CS6015: Linear Algebra and Random Processes
Lecture 3: Lines, planes, solving a system of linear equations (intuition), number of solutions to a system of linear equations
Learning Objectives
What is a line (2-D), plane(3-D), hyperplane (n-D)?
What is the row picture of a system of a linear equations?
How do you solve a system of linear equations? (high school style)
What is the intersection of lines, planes, hyperplanes?
What is the column picture of a system of linear equations?
How many solutions are possible for a system of linear equations?
(for today's lecture)
What is a line?
y = mx + c
y is a function of x
mx - y + c = 0
y = mx + c
x and y satisfy this equation
Geometrically: a line is a collection of points (x,y) which satisfy the given equation
(switch to geogebra)
Algebraically: Degree 1 polynomial
Geometrically: A flat surface
Notes: through origin, not through origin, parallel lines, intersecting lines
What is a plane?
z = ax + by + c
z is a function of x, y
ax + by -z + c = 0
x, y and z satisfy this equation
(switch to geogebra)
Algebraically: Degree 1 polynomial
Geometrically: A flat surface
Notes: through origin, not through origin, parallel planes, intersecting planes, equation with x co-efficient as 0
Geometrically: a plane is a collection of points (x,y,z) which satisfy the given equation
The (absolute) basics
The standard x-y plane is a 2 dimensional space
A line is a 1 dimensional object in this 2 dimensional space
A point is a 0 dimensional object in this 2 dimensional space

3x-2y = 0
(3,2)
Objects in this 2d space: 2d, 1d, 0d
The (absolute) basics
The standard x-y-z space is a 3 dimensional space
A line is a 1 dimensional object in this 3 dimensional space
A point is a 0 dimensional object in this 3 dimensional space
3x-2y-z = 0
Objects in this 3d space: 3d, 2d, 1d, 0d

A plane is a 2 dimensional object in this 3 dimensional space
The (absolute) basics
Consider an n dimensional space
3x-2y-z = 0
Objects in this n-d space:

n-d
(n-1)-d
(n-2)-d, (n-3)-d, ...., 2d, 1d, 0-d
(hyperplane)
What is a hyperplane?
x_n = a_1x_1 + a_2x_2 + \cdots + a_{n-1}x_{n-1} + c
is a function of
x_1, x_2, \dots, x_n
satisfy this equation
Algebraically: Degree 1 polynomial
Geometrically: A flat surface
Geometrically: a hyperplane is a collection of n-dimensional points which satisfy the given equation
x_n
x_1, x_2, \dots, x_{n-1}
a_1x_1 + a_2x_2 + \cdots + a_{n-1}x_{n-1} - x_n + c = 0
Some more basics
Intersection of two lines* (1d) is a point (0d)
Intersection of two planes* (2d) is a line (1d)
* assuming they are independent & not parallel
Intersection of three planes* (2d) is a point (0d)


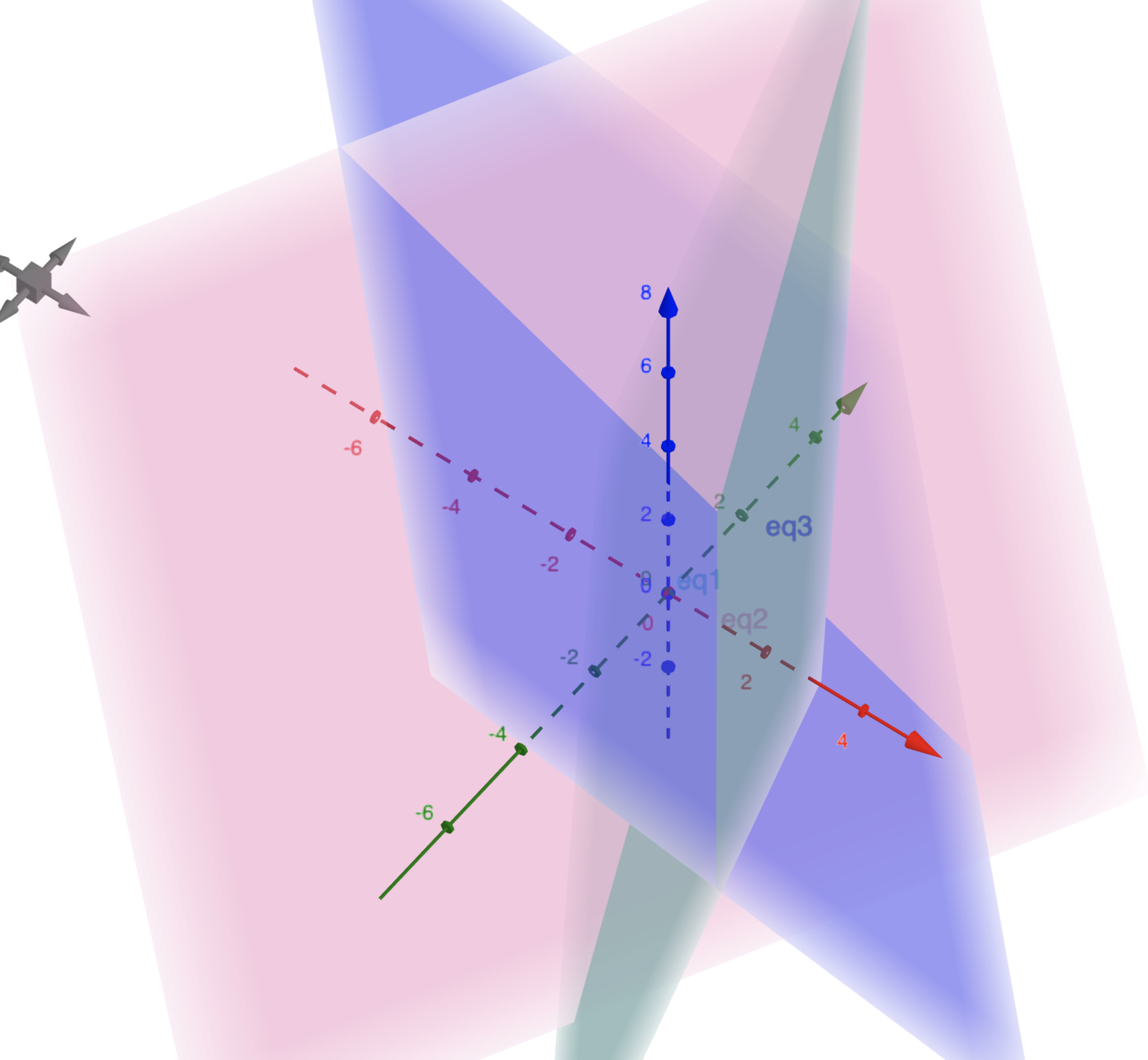
(demo in geogebra)
Two lines(1D) intersect at a point(0D)
Two planes(2D) intersect at a line(1D)
3 Planes(2D) intersect at a point(0D)
Puzzle
The intersection of 3 two dimensional planes* in a 3 dimensional space is a point
The intersection of ____ (n-1) dimensional planes* in a n dimensional space will be a point
The intersection of 2 one dimensional lines* in a 2 dimensional space is a point
n
This point will satisfy the equation of all the n planes
* assuming they are independent & not parallel
Back to system of linear equations
a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + \dots + a_{1n}x_n= b_1
a_{21}x_1 + a_{22}x_2 + a_{23}x_3 + \dots + a_{2n}x_n= b_2
a_{31}x_1 + a_{32}x_2 + a_{33}x_3 + \dots + a_{3n}x_n= b_3
a_{m1}x_1 + a_{m2}x_2 + a_{m3}x_3 + \dots + a_{mn}x_n= b_m
\dots

equations of m (n-1) dimensional planes
Our Quest: Find n-dimensional point(s) which satisfy all the given equations (i.e., lie on all the given planes)
(x_1, x_2, x_3, \dots , x_n)
Back to system of linear equations
equations of m (n-1) dimensional planes
Our Quest: Find n-dimensional point(s) which satisfy all the given equations (i.e., lie on all the given planes)
(x_1, x_2, x_3, \dots , x_n)
\begin{bmatrix}
a_{11}&a_{12}&a_{13}&\cdots&a_{1n}\\
a_{21}&a_{22}&a_{23}&\cdots&a_{2n}\\
a_{31}&a_{32}&a_{33}&\cdots&a_{3n}\\
\cdots&\cdots&\cdots&\cdots&\cdots\\
a_{m1}&a_{m2}&a_{m3}&\cdots&a_{mn}\\
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}\\
x_{3}\\
\cdots\\
x_{n}\\
\end{bmatrix}
=\begin{bmatrix}
b_{1}\\
b_{2}\\
b_{3}\\
\cdots\\
b_{m}\\
\end{bmatrix}
A
\mathbf{x}
\mathbf{b}
How many solutions are possible?
\begin{bmatrix}
1&1\\
1&1\\
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix}
= \begin{bmatrix}
1\\
2
\end{bmatrix}
\begin{bmatrix}
1&1\\
1&1\\
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix}
= \begin{bmatrix}
1\\
1
\end{bmatrix}
\begin{bmatrix}
1&1\\
1&-1\\
\end{bmatrix}
\begin{bmatrix}
x_{1}\\
x_{2}
\end{bmatrix}
= \begin{bmatrix}
3\\
1
\end{bmatrix}
* this slide is just for building intuition, there is much more to the answer than what is being revealed on the slide
0~solutions
1~solution
\infty~solutions
x_1 + x_2 = 1
x_1 + x_2 = 2
x_1 + x_2 = 3
x_1 - x_2 = 1
x_1 + x_2 = 1
x_1 + x_2 = 1
(switch to geogebra: 2d case (above examples), 3d case, a magic trick)
No solution in 3D
Magic trick(many solution)
How many solutions are possible?
* this slide is just for building intuition, there is much more to the answer than what is being revealed on the slide
Is~~m = n?
Depends on
Is~~m > n?
Is~~m < n?
How~many~unique~equations?
(the long answer)
(the short answer)
the~rank~of~the~matrix
But (the beauty of it)
there~will~always~be~0, 1~or~\infty~solutions!
How many solutions are possible?
A promise: At the end of 4 weeks you will know
How to find the number of solutions?
(0, 1~or~\infty)
How to find the solution if it exists?
(1~or~\infty)
What does this have to do with the rank of a matrix?
आरम्भः
Let's Begin
The row picture
x_1 + 2x_2 = 3
x_1 - 2x_2 = -1
x_1 + 2x_2 - x_3= 4
2x_1 - x_2 + x_3= 1
-x_1 + x_2 + 2x_3= 3
We are looking for a point which satisfies each equation (row)
x_1 + 2x_2 - x_3 + x_4 = 5
2x_1 - x_2 + x_3 - 2x_4 = -1
-x_1 + x_2 + 2x_3 - x_4= 2
Easy to solve geometrically by plotting the corresponding lines ...
-x_1 - x_2 + 2x_3 +2x_4= 1
.... but becomes messy as we go to greater than 3 dimensions
Row picture(2D)
Row Picture(3D)
The column picture
x_1 + 2x_2 = 3
x_1 - 2x_2 = -1
x_1 + 2x_2 - x_3= 4
2x_1 - x_2 + x_3= 1
-x_1 + x_2 + 2x_3= 3
We are looking for the right linear combination of the columns of A
x_1 + 2x_2 - x_3 + x_4 = 5
2x_1 - x_2 + x_3 - 2x_4 = -1
-x_1 + x_2 + 2x_3 - x_4= 2
-x_1 - x_2 + 2x_3 +2x_4= 1
.... easy to imagine even in higher dimensions
\begin{bmatrix}
1\\
1
\end{bmatrix}
+
x_1
\begin{bmatrix}
2\\
-2
\end{bmatrix}
x_2
=\begin{bmatrix}
3\\
-1\\
\end{bmatrix}
\begin{bmatrix}
1&2\\
1&-2
\end{bmatrix}
=\begin{bmatrix}
3\\
-1\\
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}
\begin{bmatrix}
1\\
2\\
-1
\end{bmatrix}
+
x_1
\begin{bmatrix}
2\\
-1\\
1
\end{bmatrix}
x_2
=\begin{bmatrix}
4\\
1\\
3\\
\end{bmatrix}
+
\begin{bmatrix}
-1\\
1\\
2
\end{bmatrix}
x_3
Linear combination of vectors in 2D
Linear Combination of vectors in 3D
The column picture
We are looking for the right linear combination of the columns of A
x_1 + 2x_2 - x_3 + x_4 = 5
2x_1 - x_2 + x_3 - 2x_4 = -1
-x_1 + x_2 + 2x_3 - x_4= 2
-x_1 - x_2 + 2x_3 +2x_4= 1
.... easy to imagine even in higher dimensions
\begin{bmatrix}
1\\
2\\
-1\\
-1
\end{bmatrix}
+
x_1
\begin{bmatrix}
2\\
-1\\
1\\
-1
\end{bmatrix}
x_2
=\begin{bmatrix}
5\\
-1\\
2\\
1
\end{bmatrix}
+
\begin{bmatrix}
-1\\
1\\
2\\
2
\end{bmatrix}
x_3
+
\begin{bmatrix}
1\\
-2\\
-1\\
2
\end{bmatrix}
x_4
The column picture
Can you think of a b such that this system of equations will not have a solution?
x_1 + x_2 = b_1
x_1 + x_2 = b_2
\begin{bmatrix}
1\\
1\\
\end{bmatrix}
+
x_1
\begin{bmatrix}
1\\
1\\
\end{bmatrix}
x_2
=\begin{bmatrix}
b_1\\
b_2\\
\end{bmatrix}
any~\mathbf{b}~where~b_1 \neq b_2
e.g., \begin{bmatrix}
1\\
2
\end{bmatrix}
, \begin{bmatrix}
2\\
-1
\end{bmatrix}
, \begin{bmatrix}
3\\
2
\end{bmatrix}
, \dots
The column picture
Can you read off (at least) one solution just by staring at the matrices?
x_1 + 2x_2 -x_3 = 1
-x_1 + 2x_2 -3x_2 = -1
\begin{bmatrix}
1\\
-1\\
2
\end{bmatrix}
+
x_1
\begin{bmatrix}
-1\\
-3\\
1
\end{bmatrix}
x_3
=\begin{bmatrix}
1\\
-1\\
2
\end{bmatrix}
\begin{bmatrix}
1\\
0\\
0
\end{bmatrix}
, \begin{bmatrix}
1\\
-1\\
1
\end{bmatrix}
, \begin{bmatrix}
1\\
-2\\
2
\end{bmatrix}
, \dots
2x_1 + x_2 +x_3 = 2
\begin{bmatrix}
2\\
2\\
1
\end{bmatrix}
x_1
+
, \begin{bmatrix}
1\\
-c\\
c
\end{bmatrix}
Solving a system of linear equations
Basic principle:
x_1 + 2x_2 - x_3 + x_4 = 5
2x_1 - x_2 + x_3 - 2x_4 = -1
-x_1 + x_2 + 2x_3 - x_4= 2
-x_1 - x_2 + 2x_3 +2x_4= 1
(high school style)
Idea:
Choose p and q such that some variables disappear in the new equation
a_{11}x_1 + a_{12}x_2 + a_{13}x_3 + a_{14}x_4 = b_1
a_{22}x_2 + a_{23}x_3 + a_{24}x_4 = b_2
a_{33}x_3 + a_{34}x_4 = b_3
a_{44}x_4 = b_4
a= b
c= d
pa + qc= pb + qd
If
then
and
Solving a system of linear equations
(high school style)
x_1 + 2x_2 = 3
x_1 - 2x_2 = -1
(equation 2 - equation 1)
x_1 + 2x_2 = 3
- 4x_2 = -4
x_2 = \frac{-4}{-4} = 1
back substitute
x_1 + 2(1) = 3
\therefore x_1 = 1
(row 2 - row 1)
\begin{bmatrix}
1&2\\
0&-4
\end{bmatrix}
=\begin{bmatrix}
3\\
-4\\
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}
\begin{bmatrix}
1&2\\
1&-2
\end{bmatrix}
=\begin{bmatrix}
3\\
-1\\
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}
Solving a system of linear equations
(high school style)
\begin{bmatrix}
1&2&-1\\
-1&2&-3\\
2&1&2
\end{bmatrix}
=\begin{bmatrix}
1\\
-5\\
6
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
x_1 + 2x_2 -x_3 = 1
-x_1 + 2x_2 -3x_3 = -5
2x_1 + x_2 + 2x_3 = 6
Solving a system of linear equations
(high school style)
\begin{bmatrix}
1&2&-1\\
-1&2&-3\\
2&1&2
\end{bmatrix}
=\begin{bmatrix}
1\\
-5\\
6
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
(equation 2 + equation 1)
(equation 3 - 2*equation 1)
\begin{bmatrix}
1&2&-1\\
0&4&-4\\
0&-3&4
\end{bmatrix}
=\begin{bmatrix}
1\\
-4\\
4
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
\begin{bmatrix}
1&2&-1\\
0&4&-4\\
0&-3&4
\end{bmatrix}
=\begin{bmatrix}
1\\
-4\\
4
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
(equation 3 + 3/4*equation 2)
\begin{bmatrix}
1&2&-1\\
0&4&-4\\
0&0&1
\end{bmatrix}
=\begin{bmatrix}
1\\
-4\\
1
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
Solving a system of linear equations
(high school style)
\begin{bmatrix}
1&2&-1\\
0&4&-4\\
0&0&1
\end{bmatrix}
=\begin{bmatrix}
1\\
-4\\
1
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
x_1 + 2x_2 -x_3 = 1
4x_2 -4x_3 = -4
x_3 = 1
back substitute
x_3 = 1
4x_2 -4(1) = -4
x_2 = 0
x_1 + 2(0) - (1) = 1
x_1 = 2
A puzzle for you
\begin{bmatrix}
1&2&-1\\
-1&2&-3\\
2&1&2
\end{bmatrix}
=\begin{bmatrix}
1\\
-5\\
6
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
\begin{bmatrix}
1&2&-1\\
0&4&-4\\
0&0&1
\end{bmatrix}
=\begin{bmatrix}
1\\
-4\\
1
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
x_3
\end{bmatrix}
How will you represent the above as matrix operations?
(row 2 + row 1)
(row 3 - 2*row 1)
(row 3 + 3/4*row 2)
Step 2,1: get 0 in position 2,1
Step 3,1: get 0 in position 3,1
Step 3,2: get 0 in position 3,2
Learning Objectives Achieved
What is a line (2-D), plane(3-D), hyperplane (n-D)?
What is the row picture of a system of a linear equations?
How do you solve a system of linear equations? (high school style)
What is the intersection of lines, planes, hyperplanes?
What is the column picture of a system of linear equations?
How many solutions are possible for a system of linear equations?
(for today's lecture)
CS6015: Lecture 3
By Mitesh Khapra
CS6015: Lecture 3
Lines, planes, solving a system of linear equations (intuition), number of solutions to a system of linear equations
- 3,647



