CS6015: Linear Algebra and Random Processes
Lecture 35: Continuous random variables, probability mass function v/s probability density function, cumulative distribution function
Learning Objectives
What are continuous random variables?
What is a probability density function?
How is it different from a probability mass function?
What is a cumulative distribution function?
Todo: add slides on
1) arbitrary pdfs
2) Expectation and variance of continuous RVs

Continuous Random Variables
Recap
Probability Mass Function

p_X(x)
1~~~2~~~3~~~4~~~5~~~6
0.2
0.4
0.6
0.8
1.0
x
Cumulative Distribution Function

p_X(x)
1~~~2~~~3~~~4~~~5~~~6
0.2
0.4
0.6
0.8
1.0
x
F_X(x)
1~~~2~~~3~~~4~~~5~~~6
0.2
0.4
0.6
0.8
1.0
x
P(X \leq x)
Cumulative Distribution Function

F_X(x)
p_X(x)
2
3
4
5
6
7
8
9
10
11
12
x
P(X \leq x)
\frac{1}{36}
\frac{2}{36}
\frac{3}{36}
\frac{4}{36}
\frac{5}{36}
\frac{6}{36}
\frac{5}{36}
\frac{4}{36}
\frac{3}{36}
\frac{2}{36}
\frac{1}{36}
\frac{1}{6}
\frac{2}{6}
\frac{3}{6}
\frac{4}{6}
\frac{5}{6}
1 = \frac{6}{6}
2
3
4
5
6
7
8
9
10
11
12
x
\frac{1}{36}
\frac{3}{36}
\frac{6}{36}
\frac{10}{36}
\frac{15}{36}
\frac{21}{36}
\frac{1}{6}
\frac{2}{6}
\frac{3}{6}
\frac{4}{6}
\frac{5}{6}
1 = \frac{6}{6}
\frac{26}{36}
\frac{30}{36}
\frac{33}{36}
\frac{35}{36}
\frac{36}{36}

Recap

p_X(x)
2
3
4
5
6
7
8
9
10
11
12
x
\frac{1}{36}
\frac{2}{36}
\frac{3}{36}
\frac{4}{36}
\frac{5}{36}
\frac{6}{36}
\frac{5}{36}
\frac{4}{36}
\frac{3}{36}
\frac{1}{36}
\frac{1}{6}
\frac{2}{6}
\frac{3}{6}
\frac{4}{6}
\frac{5}{6}
1 = \frac{6}{6}

Probability Mass Function
Total Probability = 1 (unit mass)
PMF: What share of this unit mass does each value take?
What if the random variable can take infinite values?
(continuous random variables)
Continuous Random Variables
Total Probability = 1 (unit mass)
What share of the unit probability mass does each value take?
Rainfall in Chennai:
Exactly 2 cm ?
2.01, 2.001, 1.99, 1.999
0
Infinite values possible
Continuous Random Variables
Your water intake (in litres )
Does not make sense to ask about the number of days on which you drank exactly 2 litres?
Instead it makes sense to ask about the number of days on which 1.9 < x < 2.1
1.0 1.5 2.5 2.5 3.0 3.5
\Omega
last 512 days
Continuous Random Variables
Your water intake (in litres )
Instead it makes sense to ask about the number of days on which 1.9 < x < 2.1
1.0 1.5 2.0 2.5 3.0 3.5
Continuous Random Variables
Your water intake (in litres )
1.0 1.5 2.0 2.5 3.0 3.5

probability density function


probability density function
cumulative distribution function


probability mass function
cumulative distribution function
p_X(x) \geq 0
P(a \leq X \leq b) = \sum_{x=a}^b p_X(x)
f_X(x) \geq 0
P(a \leq X \leq b) = \int_{a}^b f_X(x) dx
\int_{-\infty}^\infty f_X(x) dx = 1
\sum_x p_x(x) = 1
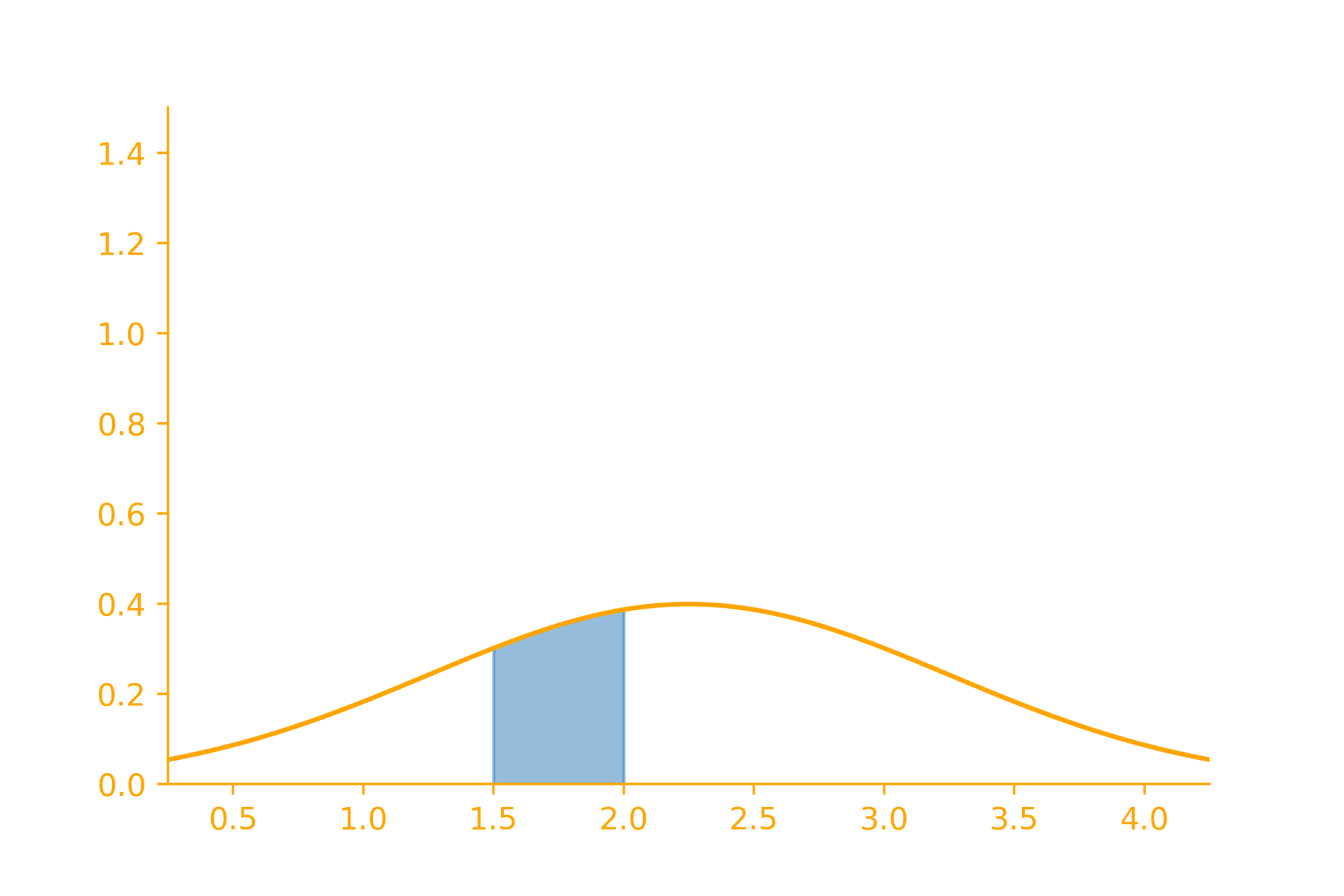
Intuition: Density v/s Mass
probability density function
probability mass function

\delta
f_X(x)
P_X(a\leq x \leq a + \delta) = f_X(x)\cdot \delta
Summary
For continuous random variables
P(X=x) = 0 \forall x
Questions of interest are
P(a\leq X \leq b)
pdf does not directly give us probability

(probability of an interval is obtained by integrating over that interval)
P_X(a\leq x \leq a + \delta) \approx f_X(x)\cdot \delta
Properties of pdf
f_X(x)\geq 0
\int_{-\infty}^\infty f_X(x) dx = 1
Learning Objectives
What are continuous random variables?
What is a probability density function?
How is it different from a probability mass function?
What is a cumulative distribution function?
Todo: add slides on
1) arbitrary pdfs
2) Expectation and variance of continuous RVs
Uniform distribution (continuous)
Discrete Uniform Distribution
\frac{1}{b - a}
b
p_X(x)
f_X(x)
Continuous Uniform Distribution
a_1
b_1
[
]
P(a_1 \leq X \leq b_1) = \frac{1}{b-a} (b_1 - a_1)
a
b
\dots
\dots
\frac{1}{b - a + 1}
a
b
Expectation

f_X(x)
p_X(x)
a
b
\dots
\dots
\frac{1}{b - a + 1}
E[X] = \sum_x xp_X(x)
E[g(X)] = \sum_x g(x) p_X(x)
Var(X) = E[X^2] - (E[X])^2
E[X] = \int_{-\infty}^{\infty} xf_X(x) dx
E[g(X)] = \int_{-\infty}^{\infty}g(x) p_X(x)dx
Var(X) = E[X^2] - (E[X])^2
Mean and variance (Uniform Distribution)
E[X] = \int_{a}^{b} x\frac{1}{b-a} dx
E[g(X)] = \int_{-\infty}^{\infty}g(x) p_X(x) dx
Var(X) = E[X^2] - (E[X])^2
\frac{1}{b - a}
b
f_X(x)
a
b
=\frac{a+b}{2}
E[X] = \int_{-\infty}^{\infty} xf_X(x) dx
E[X^2] = \int_{a}^{b} x^2\frac{1}{b-a} dx
=\frac{1}{b-a}(\frac{b^3}{3} - \frac{a^3}{3})
Var(X) = E[X^2] - (E[X])^2 = \frac{(b-a)^2}{12}
E[X] = \int_{a}^{b} x\frac{1}{b-a} dx
E[X^2] = \int_{a}^{b} x^2\frac{1}{b-a} dx
E[X] =\frac{1}{b-a} * \frac{x^2}{2} |_{a}^b
= \frac{1}{b-a} * (\frac{b^2}{2} - \frac{a^2}{2}) = \frac{1}{b-a}\frac{b^2 - a^2}{2}
= \frac{1}{b-a}\frac{(b - a)(b+a)}{2} = \frac{a+b}{2}
=\frac{1}{b-a} * \frac{x^3}{3} |_{a}^b
= \frac{1}{b-a} * (\frac{b^3}{3} - \frac{a^3}{3}) = \frac{1}{b-a}\frac{b^3 - a^3}{3}
= \frac{1}{b-a}\frac{(b - a)(a^2 + ab + b^2)}{3} = \frac{a^2 + ab + b^2}{3}
Var(X) = E[X^2] - E[X]^2
= \frac{a^2 + ab + b^2}{3} - (\frac{a+b}{2})^2
= \frac{a^2 + ab + b^2}{3} - \frac{a^2 + 2ab + b^2}{4}
= \frac{(b-a)^2}{12}
Normal Distribution
Some fun with functions

x^2
e^x

x



e^{-x}
e^{x^2}
e^{-x^2}


20 * e^{-x^2}
Some fun with functions
e^{-x^2}








Normal distribution
\mathcal{N}(0, 1) = \frac{1}{\sqrt{2 \pi}}e^{-x^2}








\int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}}e^{-x^2} dx = 1
Normal distribution
\mathcal{N}(0, 1) = \frac{1}{\sqrt{2 \pi}}e^{-x^2}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{-x^2} dx
= 0
Var[X] = E[X^2] - (E[X])^2

= 1
zero mean, unit variance
\mu = 0, \sigma = 1
Normal distribution (changing
\mathcal{N}(\mu, 1) = \frac{1}{\sqrt{2 \pi}}e^{-\frac{(x-\mu)^2}{2}}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{-\frac{(x-\mu)^2}{2}} dx
= \mu
Var[X] = E[X^2] - (E[X])^2

= 1
\mu = 2

\mu = 0
\mu = -2

\mu)
Normal distribution (changing
\mathcal{N}(0, \sigma^2) = \frac{1}{\sqrt{2 \pi}}e^{\frac{-x^2}{2\sigma^2}}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{\frac{-x^2}{2\sigma^2}} dx
= 0
Var[X] = E[X^2] - (E[X])^2
= \sigma^2
\sigma = 0.5
\sigma = 1
\sigma = 2
\sigma)



Normal distribution (changing
\mathcal{N}(\mu, \sigma^2) = \frac{1}{\sqrt{2 \pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}} dx
= \mu
Var[X] = E[X^2] - (E[X])^2
\mu = 2, \sigma = 0.5
\mu, \sigma)

= \sigma^2
The distribution is fully specified by the parameters:
\mu, \sigma^2
Normal distribution
\sigma
\sigma
\sigma
\sigma
\sigma
\sigma
\sigma
\sigma
68\%
95\%
99\%
P(\mu - \sigma \leq X \leq \mu + \sigma)
= \int_{\mu - \sigma}^{\mu + \sigma} \frac{1}{\sqrt{2\pi}} e^{ \frac{-(x - \mu)}{2 \sigma^2} } dx

\approx 0.68
P(\mu - 2\sigma \leq X \leq \mu + 2\sigma)
= \int_{\mu - 2\sigma}^{\mu + 2\sigma} \frac{1}{\sqrt{2\pi}} e^{ \frac{-(x - \mu)}{2 \sigma^2} } dx
\approx 0.95
Sampling Methods
Recap


A population is the total collection of all objects that we are interested in studying

A sample is a subgroup of the population that we study to draw inferences about the population
Population
Sample
Question: How do we select these samples?

(Let' start with some wrong ways of selecting samples)
Biased Samples
Convenience Sample
Voluntary Sample
(non-response bias)
Convenience Samples
Goal: Compute average height of students
Convenience Sample: Take the students sitting on the first bench so that you don't disturb the whole class
Bias: Shorter students sit on the first bench

Convenience Samples
Goal: Compute prevalence of COVID-19
Convenience Sample: Just consider people who are visiting ENT hospitals instead of sending out a collection team
Bias: People visiting ENT hospitals may include a higher proportion of infected people
Flu
\Omega

Convenience Samples

Goal: Predict results of presidential polls (1948)
Convenience Sample: Conduct surveys on phones
Bias: Only richer people had phones in 1948
\Omega

Convenience Samples
Goal: Draft citizens into military
Bias: People born in December were getting drafted more than others

Convenience Sample: Put the numbers 1 to 366 in a jar and then draw a number
Voluntary Samples
Goal: Predict results of presidential polls (1936)
Voluntary Sample: 1M Postal survey forms were sent to people of which 24% responded
Bias: More Republican voters responded as compared to Democratic voters

Voluntary Samples
A voluntary bias or non-response bias occurs when people who respond/participate are very different from those who do not

Voluntary Samples
Goal: Predict proportion of people who are favourable
Voluntary Sample: Check social media posts
Bias: Disgruntled citizens are more likely to post as compared to citizens who are happy with the policy

A sample that is representative of the entire population and gives each element an equal chance of being chosen

Unbiased Samples
Convenience sampling
Sampling Strategies
Simple random sampling
Systematic sampling
Cluster sampling
Stratified sampling
Convenience sampling
Sampling Strategies
Simple random sampling
Systematic sampling
Cluster sampling
Stratified sampling


import numpy as np
low = 1 //start
high = 72 //total_population
size = 9 //sample_size
np.random.randint(low, high, size)


Experimental Studies
Experiment


Apply treatment to experimental units and make observations to compare treatments
Example
Dr. Watson wants to study the effect of quantity (4-10) and type of nuts (almond, walnuts, cashews) on cholesterol levels of heart patients.
Response variable:
Cholesterol level
Experimental unit:
Heart patients
Factors:
Quantity
Factor Levels:
4 - 10
almond, walnut, cashew
Type of nuts
Treatment:
Combination of factor levels
Lurking variables:
Age, Diet, Exercise
































































































Example
12 Treatments:
Combinations of factor levels
Lurking variables:
Age, Diet, Exercise
































































































4
6
8
10




Experiments: Basic Principles
Randomization
Subjects are assigned randomly to treatment groups
Repetition
Control
Multiple subjects are given the same treatment
Control the effect of lurking variables
Placebo Effect

Actual Treatment
Experimental Group

Empty Pills
Control Group
(placebo)
Lurking variables:
Sleep, Diet, Exercise
(same sleep time, diet and exercise routine for both groups)
Single Blind Experiment
Double Blind Experiment
Subjects don't know which group they are in
Both experimenter and subjects don't know which group is which
















Types of Experiment Designs
Completely Randomized Designs
Block Randomized Designs


Males
Females

Types of Experiment Designs
Matched Pair Design




Fuel A
Fuel B
Compare
Fuel A
Fuel B
Compare
Fuel A
Fuel B
Compare
Fuel A
Fuel B
Compare
Apply all treatments to same/similar objects
Types of Experiment Designs
Matched Pair Design
Apply all treatments to same/similar objects
Does sleep deprivation affect performance on a test?
























Key Terms and Definitions
In Statistics we are always, interested in studying a large collection of people or objects

Opinion Poll: What proportion of the citizens support candidate XYZ ?
Challenge: Infeasible (expensive) to survey all citizens
























In Statistics we are always, interested in studying a large collection of people or objects

Car Testing: What is the average mileage of cars produced in a factory?
Challenge: Expensive to test all cars
Key Terms and Definitions
Randomness everywhere!
How many infections in the neighbourhood?




Examples
If he does not come out alive what is the probability that he took path A1?






P(A_1|B) = ?
B : monster encountered
i-th path taken
A_i:
P(A_1|B) = \frac{P(A_1 \cap B)}{P(B)}
P(A_1|B) = \frac{P(A_1 \cap B)}{P(A_1)\cdot P(B|A_1) + P(A_2)\cdot P(B|A_2) + P(A_3)\cdot P(B|A_3)}
P(A_1 \cap B) = P(A_1)P(B|A_1) \\
P(A_1 \cap B) = P(B)P(A_1|B)
P(A_1)=P(A_2)=P(A_3) = \frac{1}{3}
P(B|A_1) = 0.3
P(B|A_2) = 0.6
P(B|A_3) = 0.75
























Biased Samples
In Statistics we are always, interested in studying a large collection of people or objects

CS6015: Lecture 35
By Mitesh Khapra
CS6015: Lecture 35
Lecture 35: Continuous random variables, probability mass function v/s probability density function, cumulative distribution function
- 2,439



