CS6015: Linear Algebra and Random Processes
Lecture 39: Moments, Moment generating functions: What are they and why do we care?
Learning Objectives
Slides to be made
What are moments?
first moment
E[X]
E[X^2]
second moment
E[X^3]
third moment
E[X^n]
\(n\)-th moment
\dots\dots
Centred and standardized moments
E[X]
E[X^2]
How big is \(X\) on average?
How big is \(X^2\) on average?
does not add much information as based on E[X] we anyways expect E[X^2] to be greater for the red points than the blue points
(mean)
Remove the information already contained in \(E[X]\)
E[(X-E[X])^2]
(variance)
centred 2nd moment
spread of \(X\) around the mean
\underbrace{~~~~~~~~~~~~~~~}
\underbrace{~~~~~~~~~~~~~~~}
Centred and standardized moments
(skewness)
E[X^3]
E[(\frac{X-E[X]}{\sigma})^3]
Remove the information already contained in \(E[X]\) and \(\sigma = E[(X-E[X])^2]\)
centred & standardized 3rd moment
Rule of thumb
\(|skewness| > 1\)
Highly skewed
Moderately skewed
\(0.5 < |skewness| < 1\)
\(\approx symmetric\)
\(0 < |skewness| < 0.5\)
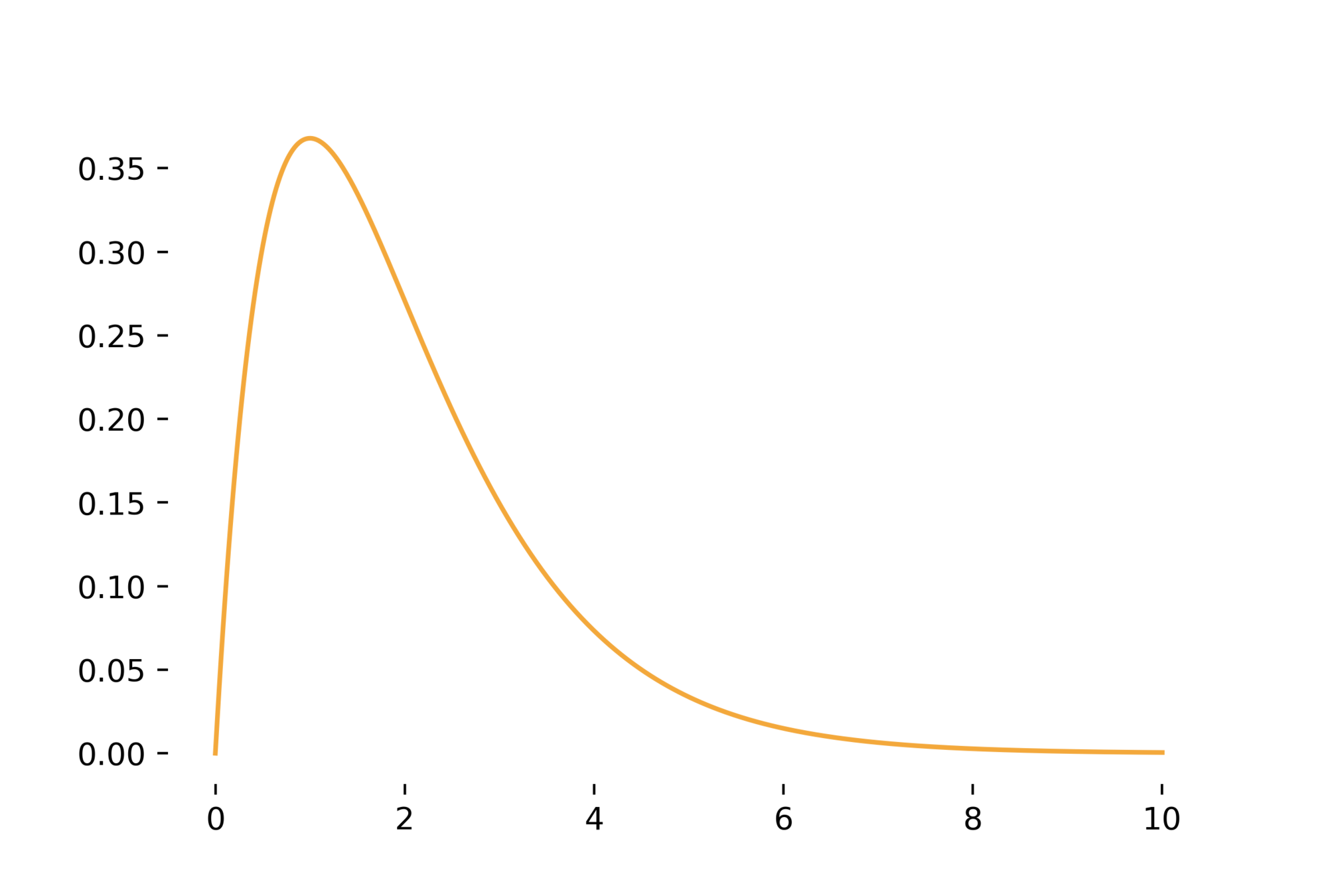
positive/right skew
E[X]
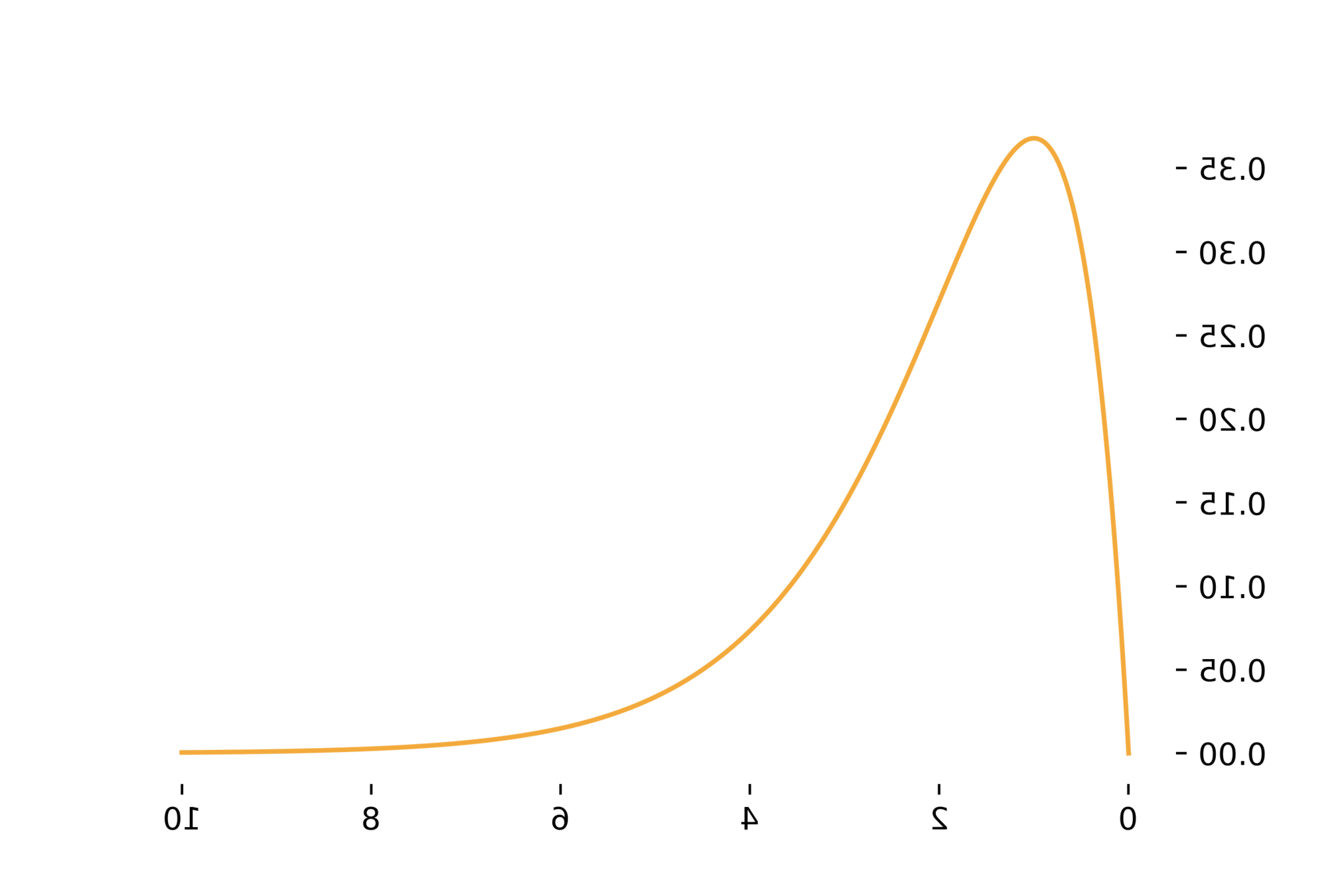
negative/left skew
E[X]
Centred and standardized moments
(kurtosis)
E[X^4]
E[(\frac{X-E[X]}{\sigma})^4]
Remove the information already contained in \(E[X]\) and \(\sigma = E[(X-E[X])^2]\)
centred & standardized 4th moment
Measures the heaviness in the tails
\(kurtosis = 3\)
Standard normal
Rule of thumb: A distribution with \(kurtosis > 3\) is said to be heavy tailed
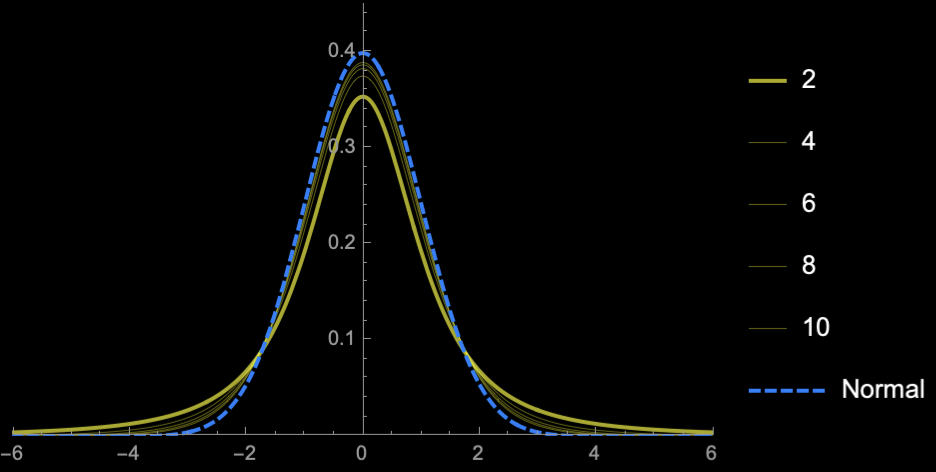
normal
Why do we care about them?
Raw
(centre of gravity)
E[X]
E[X^2]
E[X^3]
E[X^4]
E[(X-E[X])^2]
E[(\frac{X-E[X]}{\sigma})^3]
E[(\frac{X-E[X]}{\sigma})^4]
Centred
Centred + Standardised
(spread/variance)
(skewness)
(kurtosis)
Moments are a good way of summarising large data
How do we compute them?
Example 1: exponential distribution
These integrals are not very pleasant to compute
f_X(x) = \lambda e^{-\lambda x}
x \in [0, \infty)
E[X] = \int_0^{\infty} x \lambda e^{-\lambda x} dx
E[X^2] = \int_0^{\infty} x^2 \lambda e^{-\lambda x} dx
Recap:
We already saw a good way of computing these for exponential families
E[T_i(x)] = \frac{\partial A(\eta)}{\partial \eta_i}
Var[T_i(x)] = \frac{\partial^2 A(\eta)}{\partial \eta_i^2}
Moment Generating Functions
A convenient way of computing moments
How does this formula make sense?
A convenient way of computing moments
How is it convenient?
compute for exponential family
Some more examples: Poisson
show computation
Some more examples: XX
show computation
Summary
Learning Objectives
Slides to be made
CS6015: Lecture 39
By Mitesh Khapra
CS6015: Lecture 39
Lecture 39: Moments and moment generating functions: What are they and why do we care?
- 647



