APCS 實作題複習

當然，我的hackmd筆記：

here!

還有因為這是複習班，所以我不會仔細的講每個細節

題目的解釋我都會用講的 (因為再用打得我就要瘋了)

自我介紹？？？ (好像每個簡報都要放一下)

我是112班16號的翁釩予

成電38屆 教學+網管

 

興趣：打code、剪輯影片、玩minecraft

 

discord: @mlgnotcool

C++ 基礎語法

給1~2級分的

#include <bits/stdc++.h>
using namespace std;

//你的變數
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    //你的code
}

基礎架構：

#define endl '\n'
#define maxn 200005

小技巧：

define 很好用

#define int long long

signed main(){
    ...
}

想開long long時

基礎資料結構

int n1; //整數，可以存(大約) -1e9 ~ 1e9
long long n2; //整數，可以存(大約) -1e18 ~ 1e18
string s; //字串，注意如果題目的字串長度很長就要用 字元的陣列
char c; //字元
double d; //小數，可以不要用就不要用
int arr[200005] //陣列，可以存一串數字

基礎語法：

&& //and
|| //or

//如果條件，就做這件事
if (條件){
    ...
}else if (條件){
    ...
}else{
    ...
}

//如果條件，就一直做這件事直到不符合條件
while (條件){
    ...
}
for (預設; 條件; 每次做什麼){
    ...
}

其實二級是很簡單的！

我們來寫一下題目！

APCS 20250101

APCS 20240601

APCS 20231001

APCS 20241001

APCS 20250101

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int a, b, n, num, counter;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> a >> b >> n;
    for (int i=1; i<=n; ++i){
        cin >> num;
        if (num%(a+b) >= a) counter += b-(num%(a+b)-a);
    }
    cout << counter << endl;
}

APCS 20240601

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define inf 1005
using namespace std;

int n, ans, cou, b[105];
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n; b[0]=inf;
    for (int i=1; i<=n; ++i){
        cin >> b[i];

        if (b[i] < b[i-1]){
            cou++;
            ans = max(ans, cou);
        }else cou = 1;
    }
    cout << ans << endl;
}

APCS 20231001

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int x, n, l, r, sf, minl = 100, minr = -100;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> x >> n;
    for (int i=1; i<=n; ++i){
        int a; cin >> a;

        if (x > a) ++l;
        else ++r;

        minl = min(minl, a);
        minr = max(minr, a);
    }

    cout << max(l, r) << " ";
    if (l>r) cout << minl << endl;
    else cout << minr << endl;
}

APCS 20241001

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 15
using namespace std;

int n, w1, w2, h1, h2, sum[maxn], dh[maxn], maxsum;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    cin >> w1 >> w2 >> h1 >> h2;
    for (int i=1; i<=n; ++i){
        int a; cin >> a;
        sum[i] = a+sum[i-1];
    }

    for (int i=1; i<=n; ++i){
        if (sum[i] <= w1*w1*h1) dh[i] = sum[i]/(w1*w1);
        else if (sum[i] <= w1*w1*h1 + w2*w2*h2) dh[i] = h1 + (sum[i]-w1*w1*h1)/(w2*w2);
        else dh[i] = h1+h2;

        maxsum = max(maxsum, dh[i] - dh[i-1]);
    }

    cout << maxsum << endl;
}

STL, 二維陣列

給3級分的

STL 是什麼，可以吃嗎？？？

STL 是在C++裡很好用的東西 (我相信你們可以自己看的)

看文案

通常在一二題會用到的有：

struct, vector, pair, set, stack, queue

 

而在後面比較會用到的有：

map, priority_queue, bitset, unordered_set, unordered_map

int m[105][105];

通常來說

第二題考的都會是二維陣列

二維陣列要注意的：

 

不能超出邊界！

不能超出邊界！

不能超出邊界！

 

記得要檢查有沒有超出邊界！！！

二維陣列移動的方法：

int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};

for (int k=0; k<4; ++k){
    nxtx = x+dx[k]; nxty = y+dy[k];
}

1. dx, dy：

如果往哪個方向都一樣的話，就可以用dx, dy陣列

2. 每個方向去討論：

如果每個方向都有特別的條件的話，就要一個一個去討論

int f = 0;
...
if (f==0){
    ...
}else if (f==1){
    ...
}else if (f==2){
    ...
}else if (f==3){
    ...
}

二維陣列的重點：

要有耐心，完全看懂題目，小心答題，

並且好好的debug和抓edge case

如果你有耐心，其實三級是很簡單的！

我們來寫一下題目！

APCS 20241002

APCS 20240602

APCS 20240102

APCS 20231002

APCS 20230602

APCS 20221002

APCS 20250102

APCS 20241002

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int m, n, k, r, c, diamond, score, a[101][101], facing=1; bool turning=true;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> m >> n >> k >> r >> c;
    for (int i=0; i<m; ++i) for (int j=0; j<n; ++j) cin >> a[i][j];

    while (a[r][c] != 0){
        if(facing == 1){
            if ((score+a[r][c]) % k == 0 && turning){facing ++; turning = false;}
            else{
                if (c+1 >= n || a[r][c+1] == -1) facing ++;
                else{
                    turning = true;
                    score += a[r][c];
                    ++diamond;
                    --a[r][c];
                    ++c;
                }
            }
        }else if(facing == 2){
            if ((score+a[r][c]) % k == 0 && turning){facing ++; turning = false;}
            else{
                if (r+1 >= m || a[r+1][c] == -1) facing ++;
                else{
                    turning = true;
                    score += a[r][c];
                    ++diamond;
                    --a[r][c];
                    ++r;
                }
            }
        }else if(facing == 3){
            if ((score+a[r][c]) % k == 0 && turning){facing ++; turning = false;}
            else{
                if (c-1 < 0 || a[r][c-1] == -1) facing ++;
                else{
                    turning = true;
                    score += a[r][c];
                    ++diamond;
                    --a[r][c];
                    --c;
                }
            }
        }else if(facing == 4){
            if ((score+a[r][c]) % k == 0 && turning){facing ++; turning = false;}
            else{
                if (r-1 < 0|| a[r-1][c] == -1) facing ++;
                else{
                    turning = true;
                    score += a[r][c];
                    ++diamond;
                    --a[r][c];
                    --r;
                }
            }
        }
        if (facing > 4) facing = 1;
    }

    cout << diamond << endl;
}

APCS 20240602

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 25
using namespace std;

int h, w, n, a[maxn][maxn];
int r, c, t, x;
int main() {
    cin >> h >> w >> n;

    for (int i=1; i<=n; ++i){
        cin >> r >> c >> t >> x;
        ++r; ++c;

        for (int j = 1; j<=h; j++) {
            for (int l = 1; l<=w; l++) {
                if (abs(j-r) + abs(l-c) <= t) a[j][l] += x;
            }
        }
    }

    for (int i = 1; i<=h; i++) {
        for (int j = 1; j<=w; j++) {
            if (j==w) cout << a[i][j] << endl;
            else cout << a[i][j] << " ";
        }
    }
}

APCS 20240102

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int m, n, k, x, y; string nest[22]; int steps[101]; set<char> cou;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> m >> n >> k; x=m;
    for (int i=1; i<=m; ++i) cin >> nest[i];
    for (int i=1; i<=k; ++i) cin >> steps[i];

    for (int j=1; j<=k; ++j){
        int itr = steps[j];

        if (itr == 0){
            if (x-1 >= 1){
                cout << nest[x-1][y];
                cou.insert(nest[x-1][y]);
                --x;
            }else {cout << nest[x][y]; cou.insert(nest[x][y]);}
        }else if (itr == 1){
            if (y+1 <= n-1){
                cout << nest[x][y+1];
                cou.insert(nest[x][y+1]);
                ++y;
            }else {cout << nest[x][y]; cou.insert(nest[x][y]);}
        }else if (itr == 2){
            if (x+1 <= m && y+1 <= n-1){
                cout << nest[x+1][y+1];
                cou.insert(nest[x+1][y+1]);
                ++x; ++y;
            }else {cout << nest[x][y]; cou.insert(nest[x][y]);}
        }else if (itr == 3){
            if (x+1 <= m){
                cout << nest[x+1][y];
                cou.insert(nest[x+1][y]);
                ++x;
            }else {cout << nest[x][y]; cou.insert(nest[x][y]);}
        }else if (itr == 4){
            if (y-1 >= 0){
                cout << nest[x][y-1];
                cou.insert(nest[x][y-1]);
                --y;
            }else {cout << nest[x][y]; cou.insert(nest[x][y]);}
        }else{
            if (x-1 >= 1 && y-1 >= 0){
                cout << nest[x-1][y-1];
                cou.insert(nest[x-1][y-1]);
                --x; --y;
            }else {cout << nest[x][y]; cou.insert(nest[x][y]);}
        }
    }

    cout << endl;
    cout << cou.size() << endl;
}

APCS 20231002

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 45
using namespace std;

int n, m, a[maxn][maxn], cnt; bool del[maxn][maxn], clean;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >>n >> m;
    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j) cin >> a[i][j];
    }

    while (!clean){
        clean = 1;

        for (int i=1; i<=n; ++i){
            for (int j=1; j<=m; ++j){
                if (del[i][j]) continue;

                for (int k=i+1; k<=n; ++k){
                    if (a[k][j] == a[i][j]){
                        del[i][j] = 1;
                        del[k][j] = 1;
                        cnt += a[i][j];
                        clean = 0;
                    }
                    if (!del[k][j]) break;
                }
                for (int k=i-1; k>=1; --k){
                    if (a[k][j] == a[i][j]){
                        del[i][j] = 1;
                        del[k][j] = 1;
                        cnt += a[i][j];
                        clean = 0;
                    }
                    if (!del[k][j]) break;
                }
                for (int k=j+1; k<=m; ++k){
                    if (a[i][k] == a[i][j]){
                        del[i][j] = 1;
                        del[i][k] = 1;
                        cnt += a[i][j];
                        clean = 0;
                    }
                    if (!del[i][k]) break;
                }
                for (int k=j-1; k>=0; --k){
                    if (a[i][k] == a[i][j]){
                        del[i][j] = 1;
                        del[i][k] = 1;
                        cnt += a[i][j];
                        clean = 0;
                    }
                    if (!del[i][k]) break;
                }
            }
        }
    }

    cout << cnt << endl;
}

APCS 20230602

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 55
using namespace std;

int n, m, a[maxn][maxn]; vector<pair<int, int>> v;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j) cin >> a[i][j];
    }

    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j){
            int cnt=0;
            for (int x=1; x<=n; ++x){
                for (int y=1; y<=m; ++y){
                    if (abs(x-i) + abs(y-j) <= a[i][j]){
                        cnt += a[x][y];
                    }
                }
            }
            if (cnt%10 == a[i][j]) v.push_back({i-1, j-1});
        }
    }

    cout << v.size() << endl;
    for (pair<int, int> i:v){
        cout << i.first << " " << i.second << endl;
    }
}

APCS 20221002

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 55
using namespace std;

int r, c, n, t, cnt, emp; char ch; bool a[maxn][maxn], f;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> r >> c >> n;
    for (int i=1; i<=n; ++i){
        cin >> ch >> t; f=false;
        if (ch == 'A'){
            if (t >= r-3) ++cnt;
            else{
                for (int j=c+1; j>=1; --j){
                    if (a[t+1][j-1] == 1 || a[t+2][j-1] == 1 || a[t+3][j-1] == 1 || a[t+4][j-1] == 1) f=true;
                    if (f && j>c){f=false; break;}
                    if (f || j==1){
                        a[t+1][j] = 1;
                        a[t+2][j] = 1;
                        a[t+3][j] = 1;
                        a[t+4][j] = 1;
                        f=true;
                        break;
                    }
                }
            }
        }else if (ch == 'B'){
            if (t >= r) ++ cnt;
            else{
                for (int j=c+1; j>=1; --j){
                    if (a[t+1][j-1] == 1) f=true;
                    if (f && j>c-2){f=false; break;}
                    if (f || j==1){
                        a[t+1][j] = 1;
                        a[t+1][j+1] = 1;
                        a[t+1][j+2] = 1;
                        f=true;
                        break;
                    }
                }
            }
        }else if (ch == 'C'){
            if (t >= r-1) ++ cnt;
            else{
                for (int j=c+1; j>=1; --j){
                    if (a[t+1][j-1] == 1 || a[t+2][j-1] == 1) f=true;
                    if (f && j>c-1){f=false; break;}
                    if (f || j==1){
                        a[t+1][j] = 1;
                        a[t+2][j] = 1;
                        a[t+1][j+1] = 1;
                        a[t+2][j+1] = 1;
                        f=true;
                        break;
                    }
                }
            }
        }else if (ch == 'D'){
            if (t >= r-1) ++ cnt;
            else{
                for (int j=c+1; j>=1; --j){
                    if (a[t+1][j+1] == 1 || a[t+2][j-1] == 1) f=true;
                    if (f && j>c-2){f=false; break;}
                    if (f || j==1){
                        a[t+1][j+2] = 1;
                        a[t+2][j] = 1;
                        a[t+2][j+1] = 1;
                        a[t+2][j+2] = 1;
                        f=true;
                        break;
                    }
                }
            }
        }else if (ch == 'E'){
            if (t >= r-2) ++cnt;
            else{
                for (int j=c+1; j>=1; --j){
                    if (a[t+1][j] == 1 || a[t+2][j-1] == 1 || a[t+3][j-1] == 1) f=true;
                    if (f && j>c-1){f=false; break;}
                    if (f || j==1){
                        a[t+2][j] = 1;
                        a[t+3][j] = 1;
                        a[t+1][j+1] = 1;
                        a[t+2][j+1] = 1;
                        a[t+3][j+1] = 1;
                        f=true;
                        break;
                    }
                }
            }
        }

        if (!f) ++cnt;
    }

    for (int i=1; i<=r; ++i){
        for (int j=1; j<=c; ++j){
            if (a[i][j] == 0) ++emp;
        }
    }
    cout << emp << " " << cnt << endl;
}

APCS 20250102

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

string s; int n, op;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> s >> n;
    for (int i=1; i<=n; ++i){
        cin >> op;
        if (op==0){
            for (int j=0; j<s.size(); j+=2) swap(s[j], s[j+1]);
        }else if (op==1){
            for (int j=0; j<s.size(); j+=2){
                if (s[j] > s[j+1]) swap(s[j], s[j+1]);
            }
        }else{
            string temp="";
            for (int l=0, r=s.size()/2; r<s.size(); ++l, ++r){temp += s[l]; temp += s[r];}
            s = temp;
        }
    }

    cout << s << endl;
}

三級分以上的重點

演算法

第三和第四題都會是演算法，

並且還會把好幾個演算法塞在一題內，

因此接下來的章節會用演算法來分

以下會是一些要注意的東西：

1. 把全部的STL都學會

看文案

一定會用到的有：

struct, vector, pair, set, stack, queue, map, priority_queue, unordered_set, unordered_map

2. 學會如何計算時間複雜度：

 

這樣不但可以看你的方法會不會TLE，

甚至有時候可以猜出題目要考的演算法。

 

舉例來說：

n<=10，可以猜我們是把所有可能爆出來 O(n!)解

n<=20，可以猜我們是要用遞迴或回朔法 O(2^n) 解

n<=100~500，可以猜我們是三層迴圈 O(n^3)解

n<=5000，可以猜我們會是 O(n^2)解

 

** n<= 100000~1000000，可以猜我們是 O(n logn)解，

同時也可以猜我們會用到sort，或是二分搜

 

n更大，通常會是O(n)解

 

3. 多做題目！

 

看到題目時就不太會緊張，

還比較容易想到怎麼做

前綴和，差分

前綴和：

 

num為原本的數字
設一個新的陣列為pre，pre[i] = num[1] + num[2] + … + num[i]

若要找num[l] + … + num[r]的值
就會 = pre[r] - pre[l-1]

 

*提供區間查值，不能更改

前綴和模板題

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
#define ll long long
using namespace std;

ll n, num, nums[maxn]; int k;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        cin >> num;
        nums[i] = nums[i-1] + num;
    }

    for (int i=1; i<=n; ++i){
        if (i==n) cout << nums[i] << endl;
        else cout << nums[i] << " ";
    }
}

練習題！

Atcoder abc405 pC

ZeroJudge a694

Atcoder abc405 pC

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 300005
#define int long long
using namespace std;

int n, num[maxn], sub[maxn], total, ans;
signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        cin >> num[i];
        total += num[i];
        sub[i] = sub[i-1] + num[i];
    }

    for (int i=1; i<=n; ++i){
        ans += num[i] * (total-sub[i]);
    }
    cout << ans << endl;
}

ZeroJudge a694

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 505
using namespace std;

int n, m, sum[maxn][maxn], a, b, c, d;
//sum[i][j] 會是(1, 1)到(i, j)的數字加起來
int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    while (cin >> n >> m){
        for (int i=1; i<=n; ++i){
            for (int j=1; j<=n; ++j){
                cin >> a;
                sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a;
            }
        }

        for (int i=1; i<=m; ++i){
            cin >> a >> b >> c >> d;
            cout << sum[c][d] - sum[c][b-1] - sum[a-1][d] + sum[a-1][b-1] << endl;
        }
    }
}

差分：

 

sub[i] = num[i] - num[i-1]，而num就會是sub的前綴和

如果要區間[l, r]加值x，我們只要將sub[l]+=x, sub[r+1]-=x;

 如果要單點查值，就1加到要查的值

 

*區間更改，單點查值

差分模板題

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
#define ll long long
using namespace std;

ll n, num[maxn], sub[maxn]; int k;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        cin >> num[i];
        sub[i] = num[i] - num[i-1];
    }

    for (int i=1; i<=n; ++i){
        if (i==n) cout << sub[i] << endl;
        else cout << sub[i] << " ";
    }
}

練習題！

CSES - Restaurant Customers

APCS 20160303

CSES - Restaurant Customers

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int n, cnt, ans; vector<pair<int, int>> p;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        int a, b; cin >> a >> b;
        p.push_back({a, 1});
        p.push_back({b, -1});
    }

    sort(p.begin(), p.end());
    for (pair<int, int> i:p){
        cnt += i.second;
        ans = max(ans, cnt);
    }
    cout << ans << endl;
}

APCS 20160303

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int n, cnt, prevx, l; vector<pair<int, int>> v;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        int a, b; cin >> a >> b;
        v.push_back({a, 1});
        v.push_back({b, -1});
    }

    sort(v.begin(), v.end());

    for (int i=0; i<v.size(); ++i){
        if (l==0) prevx = v[i].first;
        l += v[i].second;
        if (l==0) cnt += v[i].first - prevx;
    }

    cout << cnt <<endl;
}

二分搜

有兩種主要的考法：

用lower_bound, upper_bound找最接近的值

要用二分搜找出某一個東西的最小可能值

C++中有一個好東西叫lower_bound和upper_bound

(***只能用在sort好的陣列)

 

lower_bound： 找到第一個 >= 的數字

upper_bound： 找到第一個 > 的數字 

vector<int> v;
int a[maxn]; //1~n
...
lower_bound(v.begin(), v.end(), k) - v.begin(); //回傳第一個在v裡>=k的數字的index
upper_bound(v.begin(), v.end(), k) - v.begin(); //回傳第一個在v裡>k的數字的index
lower_bound(a+1, a+1+n, k) - a; //回傳第一個在a裡>=k的數字的index
upper_bound(a+1, a+1+n, k) - a; //回傳第一個在a裡>k的數字的index

更多題目yaaa：

APCS 20200703

APCS 20220603

APCS 20200703

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
using namespace std;

int n, m, p, sum[maxn], curidx;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=n; ++i){
        int a; cin >> a;
        sum[i] = sum[i-1] + a;
    }

    for (int i=1; i<=m; ++i){
        cin >> p;
        if (sum[curidx] + p > sum[n]){
            curidx = lower_bound(sum+1, sum+n+1, p-(sum[n]-sum[curidx])) - sum;
        }else{
            curidx = lower_bound(sum+1, sum+n+1, sum[curidx]+p) - sum;
        }
    }

    cout << curidx%n << endl;
}

APCS 20220603

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 30005
using namespace std;

int n, curx, cury, f, cnt;
unordered_map<int, vector<int>> x, y;
unordered_map<int, unordered_map<int, int>> mp;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n; f = 1; curx=0; cury=0;
    for (int i=1; i<=n; ++i){
        int a, b, c; cin >> a >> b >> c;
        swap(a, b);
        mp[a][b] = c;
        x[b].push_back(a);
        y[a].push_back(b);
    }

    for (auto i=x.begin(); i!=x.end(); ++i) sort(i->second.begin(), i->second.end());
    for (auto i=y.begin(); i!=y.end(); ++i) sort(i->second.begin(), i->second.end());

    while (true){
        if (f==0){
            if (x[cury].empty()) break;
            int it = upper_bound(x[cury].begin(), x[cury].end(), curx) - x[cury].begin();

            if (it>=x[cury].size()) break;
            else{
                curx = x[cury][it];
                if (mp[curx][cury] == 0) f = 1;
                else f = 3;
            }
        }else if (f==1){
            if (y[curx].empty()) break;
            int it = upper_bound(y[curx].begin(), y[curx].end(), cury) - y[curx].begin();

            if (it>=y[curx].size()) break;
            else{
                cury = y[curx][it];
                if (mp[curx][cury] == 0) f = 0;
                else f = 2;
            }
        }else if (f==2){
            if (x[cury].empty()) break;
            int it = lower_bound(x[cury].begin(), x[cury].end(), curx) - x[cury].begin() - 1;

            if (it<0) break;
            else{
                curx = x[cury][it];
                if (mp[curx][cury] == 0) f = 3;
                else f = 1;
            }
        }else if (f==3){
            if (y[curx].empty()) break;
            int it = lower_bound(y[curx].begin(), y[curx].end(), cury) - y[curx].begin() - 1;

            if (it<0) break;
            else{
                cury = y[curx][it];
                if (mp[curx][cury] == 0) f = 2;
                else f = 0;
            }
        }

        ++cnt;
    }
    cout << cnt << endl;
}

假設題目要你k的最小值，並且k從0到最大值有單調性

(eg. 0 0 0 0 0 1 1 1 1)，就可以用二分搜找答案 

while (l < r){
    mid = (l+r)/2;

    if (nums[mid] > a) r = mid;
    else l = mid+1;
}

return r;

在這裡介紹的方法(最常用的)，是左閉右開：

更多題目 yaaaa：

APCS 20170304

APCS 20221004 (包含BFS)

APCS 20170304

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 50005
using namespace std;

int n, k, nums[maxn], l=1, r, m, d;

int check_diameter(int r){
    int x=1, curidx=nums[1];
    for (int i=1; i<=n; ++i){
        if (curidx+r < nums[i]){
            ++x;
            curidx = nums[i];
        }
    }
    return x;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> k;
    for (int i=1; i<=n; ++i){
        cin >> nums[i];
        r = max(r, nums[i]);
    }
    sort(nums+1, nums+1+n);

    while (l < r){
        m=(l+r)/2;
        d=check_diameter(m);

        if (d <= k) r = m;
        else if (d > k) l = m+1;
    }

    cout << r << endl;
}

APCS 20221004

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 305
using namespace std;

struct coord{
    int x, y, d, dep;
};

int n, a[maxn][maxn], l, r, ans, dist, finald; queue<coord> q; bool vis[maxn][maxn];
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        for (int j=1; j<=n; ++j) cin >> a[i][j];
    }

    l=0, r=1000000;
    while (l < r){
        while (!q.empty()) q.pop();
        for (int i=1; i<=n; ++i){
            for (int j=1; j<=n; ++j) vis[i][j] = 0;
        }
        q.push({1, 1, 0, 0});

        int m=(l+r)/2; ans=-1, dist=-1;
        while (!q.empty()){
            if (q.front().x == n && q.front().y == n){
                ans = q.front().d; dist=q.front().dep;
                break;
            }

            int x=q.front().x, y=q.front().y, d=q.front().d, dep=q.front().dep; q.pop();
            for (int k=0; k<4; ++k){
                int nxtx = x+dx[k], nxty = y+dy[k];
                if (nxtx < 1 || nxtx > n || nxty < 1 || nxty > n) continue;

                if (!vis[nxtx][nxty] && abs(a[x][y]-a[nxtx][nxty]) <= m){
                    vis[nxtx][nxty] = 1;
                    q.push({nxtx, nxty, max(d, abs(a[x][y]-a[nxtx][nxty])), dep+1});
                }
            }
        }

        if (ans == -1){
            l = m+1;
        }else r = m;
        if (dist != -1) finald = dist;
    }

    cout << r << endl << finald << endl;
}

遞迴

如果有認真上數學課的話，因該就知道遞迴是什麼了，

而在C++裡就是在函式裡面再叫另一個函式，一直遞迴下去

小注意：遞迴的數量是有上限的，如果你覺得太多

有可能被爆掉，有可能就要換另一種方法

(ex: dfs -> bfs)

更多題目！：

APCS 20190203

APCS 20221003

APCS 20200104

APCS 20240603

APCS 20190203

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn
using namespace std;

int curi, cnt; string s;

int calc(string s){
    int tmp = 0;
    if (s=="f"){
        cin >> s; tmp = 2*calc(s) - 3;
        return tmp;
    }else if (s=="g"){
        cin >> s; tmp += 2*calc(s);
        cin >> s; tmp += calc(s) - 7;
        return tmp;
    }else if (s=="h"){
        cin >> s; tmp += 3*calc(s);
        cin >> s; tmp -= 2*calc(s);
        cin >> s; tmp += calc(s);
        return tmp;
    }else return stoi(s);
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> s;
    cout << calc(s) << endl;
}

APCS 20221003

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 50
#define ll long long
using namespace std;

int n, depth=1; ll cnt;

void dfs(int x){
    int num;
    for (int i=1; i<=2 + (x%2); ++i){
        cin >> num;
        if (num != 0){
            cnt += abs(x-num);
            dfs(num);
        }
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    dfs(n);

    cout << cnt << endl;
}

APCS 20200104

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 2000005
#define maxm 10005
#define int long long
using namespace std;

struct t{
    int l, r;
};

int n, m, w[maxn], op[maxm], curnode; t v[maxn];

void dfs(int x, int k){
    if (x >= n){
        w[x] += k;
        curnode = x;
        return;
    }

    if (w[v[x].l] <= w[v[x].r]) dfs(v[x].l, k);
    else if (w[v[x].l] > w[v[x].r]) dfs(v[x].r, k);

    w[x] += k;
    return;
}

void build(int x){
    if (w[v[x].l] == -1) build(v[x].l);
    if (w[v[x].r] == -1) build(v[x].r);

    w[x] = w[v[x].l] + w[v[x].r];
}

signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=2*n-1; ++i) w[i] = -1;
    for (int i=1; i<=n; ++i) cin >> w[i+n-1];

    for (int i=1; i<=m; ++i) cin >> op[i];
    for (int i=1; i<=n-1; ++i){
        int a; cin >> a;
        cin >> v[a].l >> v[a].r;
    }

    build(1);

    for (int i=1; i<=m; ++i){
        dfs(1, op[i]);
        if (i==m) cout << curnode << endl;
        else cout << curnode << " ";
    }
}

APCS 20240603

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

string k, s, tmp; int n; set<string> st; bool f;

void dfs(string a, int d){
    if (f) return;
    if (d==n){
        if (st.find(a) == st.end()){
            cout << a << endl;
            f = true;
        }
        return;
    }

    for (int i=0; i<k.size(); ++i){
        if (f) return;
        dfs(a+k[i], d+1);
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> k >> n >> s;

    for (int i=0; i<s.size(); ++i){
        tmp = "";
        for (int j=i; j<=i+n-1; ++j) tmp += s[j];
        st.insert(tmp);
    }

    dfs("", 0);
}

滑動窗口

在APCS是很少見的 (只是上次有考到所以我還是放在這)

 

總而言之，就是想像一個區間的窗口在陣列移動，

找一個區間的某的值。

 

目標是用前一區間的值來算出這一區間的值，

比每次都重新找還快。

題目!!! ：

APCS 20190603

APCS 20250104

APCS 20190603

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
using namespace std;

int m, n, cnt, finalcnt; string p[maxn];
unordered_map<string, int> mp;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> m >> n;
    for (int i=1; i<=n; ++i) cin >> p[i];
    for (int i=1; i<=m; ++i){
        mp[p[i]]++;
        if (mp[p[i]] == 1) ++cnt;
    }
    if (cnt==m) ++finalcnt;

    for (int i=m+1; i<=n; ++i){
        mp[p[i-m]]--;
        if (mp[p[i-m]] == 0) --cnt;

        mp[p[i]]++;
        if (mp[p[i]] == 1) ++cnt;

        if (cnt==m) ++finalcnt;
    }

    cout << finalcnt << endl;
}

APCS 20250104

看文案

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
#define inf 1e18
#define int long long
using namespace std;

int n, k, nums[maxn], place[maxn], prevp, dp[maxn], mincount;
signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> k;
    for (int i=1; i<=n; ++i) cin >> nums[i];
    sort(nums+1, nums+1+n);

    prevp=nums[1 + ((k-1)/2)]; place[1] = 0;
    for (int i=1; i<=k; ++i) place[1] += abs(nums[i] - prevp);

    for (int i=2; i<=n-k+1; ++i){
        int mp=nums[i + ((k-1)/2)];

        //用數學去算
        if (k%2 == 0){
            place[i] = place[i-1] + nums[i-1] + nums[i+k-1] - 2*mp;
        }else{
            place[i] = place[i-1] + nums[i-1] + nums[i+k-1] - prevp - mp;
        }
        prevp = mp;
    }

    dp[1] = place[1]; mincount = inf;
    for (int i=2; i<=n-k+1; ++i){
        dp[i] = min(dp[i-1], place[i]);
        if (i>k) mincount = min(mincount, dp[i-k] + place[i]);
    }

    cout << mincount << endl;
}

貪心 greedy

greedy比較不像是演算法，但也是很重要的考點。

 

總而言之，就是我們用一種特定的方法去取東西，而不是把全部的可能爆出來，並且可以證明這樣的取法是最佳的方法。

舉簡單例子來說：

如果我們有1, 5, 10, 50元

且我們要花最少硬幣數退錢給客人，

 

則我們會greedy先取目前可以取的最大

直接帶題目來解釋greedy的技巧：

APCS 20211103

APCS 20171004

AP325 P-4-4

APCS 20230104

APCS 20211103

要搭配前面的差分來記錄區間的w[i]

並且把t[i]最短的分給w[i]最大的

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
#define ll long long
using namespace std;

int n, m, l, r, w, t[maxn], sub[maxn], val[maxn]; ll cnt;
signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=m; ++i){
        cin >> l >> r >> w;
        sub[l] += w;
        sub[r+1] -= w;
    }
    for (int i=1; i<=n; ++i){
        cin >> t[i];
        val[i] = val[i-1] + sub[i];
    }

    sort(val+1, val+n+1, greater<int>());
    sort(t+1, t+n+1);

    for (int i=1; i<=n; ++i) cnt += t[i]*val[i];
    cout << cnt << endl;
}

APCS 20171004

遇到這種要特定排序的greedy，就把他的comp函式比較寫出來，比較先選a和先選b的差別(甚至有些會被消掉)，最後再做比較

W*f_{A} + (W+w_{A})*f_{B}

假設我們目前在比較A, B哪個要排上和下，且他們上放的重量是W

A在上：

W*f_{B} + (W+w_{B})*f_{A}

B在上：

假設我們目前在比較A, B哪個要排上和下，且他們上放的重量是W

w_{A}*f_{B},\ w_{B}*f_{A}

並且可以發現可以消掉一些東西，最後要比較的就只剩這兩個：

APCS 20171004

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
#define int long long
using namespace std;

int n, curw, cnt; pair<int, int> p[maxn];

bool comp(pair<int, int> a, pair<int, int> b){
    return a.first*b.second < a.second*b.first;
}

signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i) cin >> p[i].first;
    for (int i=1; i<=n; ++i) cin >> p[i].second;
    sort(p+1, p+n+1, comp);

    for (int i=1; i<=n; ++i){
        cnt += curw * p[i].second;
        curw += p[i].first;
    }

    cout << cnt << endl;
}

AP325 P-4-4

算比較經典的greedy題，重點就是要把結束最早的排在前面，因此這樣後面才比較有機會放更多活動

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
using namespace std;

int n, counter, curtime; pair<int, int> times[maxn];
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i) cin >> times[i].second >> times[i].first;
    sort(times+1, times+1+n);

    curtime = -1;
    for (int i=1; i<=n; ++i){
        if (curtime < times[i].second){
            ++counter;
            curtime = times[i].first;
        }
    }

    cout << counter << endl;
}

APCS 20230104

和上一題類似，甚至前40%都和上一題一樣

只是我們要都考慮一個greedy，就是我們這個活動要用的機器 (如果有的化)

就會是一台機器目前活動結束時間 小於且最靠近 現在考慮的活動開始時間

 

然後我們就可以發現：

我們可以用multiset來存機器的活動結束時間，

並且用二分搜來找到要使用的機器

APCS 20230104

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
using namespace std;

int n, k, cnt; pair<int, int> p[maxn];
multiset<int> w;

bool comp(pair<int, int> a, pair<int, int> b){
    if (a.second != b.second) return a.second < b.second;
    else return a.first < b.first;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> k;
    for (int i=1; i<=n; ++i) cin >> p[i].first;
    for (int i=1; i<=n; ++i) cin >> p[i].second;
    sort(p+1, p+1+n, comp);

    for (int i=1; i<=k; ++i) w.insert(-1);

    for (int i=1; i<=n; ++i){
        auto it = w.lower_bound(p[i].first);
        if (it == w.begin()) continue;

        --it;
        ++cnt;
        w.insert(p[i].second);
        w.erase(it);
    }

    cout << cnt << endl;
}

單調隊列

直接帶題目：

AP325 P-3-4

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int n; long long counter; stack<pair<int, int>> p;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    p.push({INT_MAX, 0});
    for (int i=1; i<=n; ++i){
        int h; cin >> h;
        while (h >= p.top().first){
            p.pop();
        }
        counter += i-p.top().second;
        p.push({h, i});
    }

    cout << counter << endl;
}

若大於等於stack上方的數字則去掉
並可以保證pop的數字都比那一個數字小
新的數字若大於上個數字，則可保證上次pop的數字都比新的還小
若比較小或等於，則pop掉舊的數字，且上次pop的數字也都比較小(也是跳過)

廣度優先搜尋 bfs

可以把它想像成一層一層去做，目前在的點會是目前距離可以抵達得地方

因此提到最短距離時就要想到BFS

舉例來說：

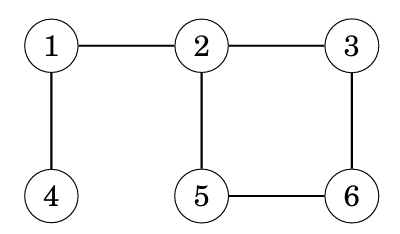
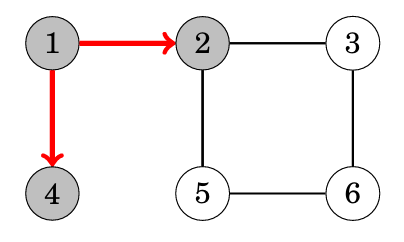
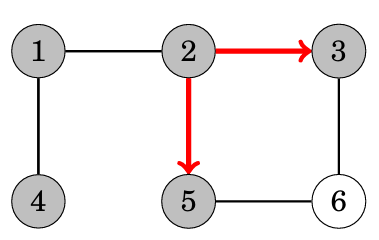
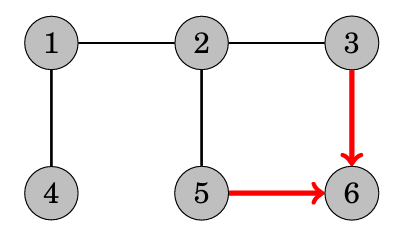
我們要使用queue來實作，用queue存放目前可以抵達的點，並且每次把queue最前面點的鄰近點丟回queue裡，

這樣就可以達到一層一層做的效果

BFS 模板題

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 805
using namespace std;

int n, m, n1, n2; bool found, vis[maxn];

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    while(cin >> n >> m){
        found=false; queue<int> q; vector<int> v[maxn];
        for (int i=1; i<=n; ++i) vis[i] = 0;

        for (int i=1; i<=m; ++i){
            int a, b; cin >> a >> b;
            v[a].push_back(b);
        }
        cin >> n1 >> n2; q.push(n1); vis[n1] = 1;

        while (!q.empty()){
            int x=q.front(); q.pop();

            for (int i:v[x]){
                if (vis[i] == 1) continue;
                if (i == n2){
                    found=true;
                    break;
                }

                vis[i] = 1;
                q.push(i);
            }
            if (found) break;
        }

        if (found) cout << "Yes!!!" << endl;
        else cout << "No!!!" << endl;
    }
}

BFS 練習題 yaaa：

ZeroJudge a982

APCS 20240103

APCS 20231003

ZeroJudge a982

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 105
using namespace std;

struct coord{
    int x, y, dist;
};

int n, a[maxn][maxn]; queue<coord> q; bool vis[maxn][maxn], f;
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        string s; cin >> s;
        for (int j=0; j<n; ++j){
            if (s[j] == '.') a[i][j+1] = 1;
            else a[i][j+1] = 0;
        }
    }

    q.push({2, 2, 1}); vis[2][2] = 1;
    while (!q.empty()){
        int x = q.front().x, y = q.front().y, d = q.front().dist; q.pop();

        if (x==n-1 && y==n-1){
            cout << d << endl;
            f=true; break;
        }
        for (int k=0; k<4; ++k){
            if (!vis[x+dx[k]][y+dy[k]] && a[x+dx[k]][y+dy[k]]){
                q.push({x+dx[k], y+dy[k], d+1});
                vis[x+dx[k]][y+dy[k]] = 1;
            }
        }
    }

    if (!f) cout << "No solution!" << endl;
}

APCS 20240103

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
using namespace std;

struct node{
    int v, d, val;
};

int p, q, r, m, in[maxn], gate[maxn], out[maxn], cnt, st[maxn]; vector<int> v[maxn];
queue<node> qu;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> p >> q >> r >> m;
    for (int i=1; i<=p; ++i){
        cin >> in[i];
        qu.push({i, 0, in[i]});
    }
    for (int i=1; i<=q; ++i){
        cin >> gate[i];
        st[i] = -1;
    }
    for (int i=1; i<=m; ++i){
        int a, b; cin >> a >> b;
        v[a].push_back(b);
    }

    while (!qu.empty()){
        int x=qu.front().v, d=qu.front().d, val=qu.front().val; qu.pop();

        for (int i:v[x]){
            if (i>p && i<=p+q){ //gate
                if (gate[i-p] == 1){
                    if (st[i-p] == -1) st[i-p] = val;
                    else qu.push({i, d+1, val&st[i-p]});
                }else if (gate[i-p] == 2){
                    if (st[i-p] == -1) st[i-p] = val;
                    else qu.push({i, d+1, val|st[i-p]});
                }else if (gate[i-p] == 3){
                    if (st[i-p] == -1) st[i-p] = val;
                    else qu.push({i, d+1, val^st[i-p]});
                }else{
                    qu.push({i, d+1, !val});
                }
            }else if (i > p+q){ //output
                out[i-p-q] = val;
                cnt = max(cnt, d);
            }
        }
    }

    cout << cnt << endl;
    for (int i=1; i<=r; ++i){
        if (i==r) cout << out[i] << endl;
        else cout << out[i] << " ";
    }
}

APCS 20231003

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 505
using namespace std;

struct coord{
    char v;
    bool n, s, e, w;
};

int n, m, cnt, maxcnt; coord a[maxn][maxn]; bool vis[maxn][maxn]; queue<pair<int, int>> q;

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j){
            cin >> a[i][j].v;
            if (a[i][j].v == 'X'){a[i][j].n=1; a[i][j].s=1; a[i][j].w=1; a[i][j].e=1;}
            else if (a[i][j].v == 'I'){a[i][j].n=1; a[i][j].s=1;}
            else if (a[i][j].v == 'H'){a[i][j].e=1; a[i][j].w=1;}
            else if (a[i][j].v == 'L'){a[i][j].n=1; a[i][j].e=1;}
            else if (a[i][j].v == '7'){a[i][j].w=1; a[i][j].s=1;}
            else if (a[i][j].v == 'F'){a[i][j].e=1; a[i][j].s=1;}
            else if (a[i][j].v == 'J'){a[i][j].n=1; a[i][j].w=1;}
        }
    }

    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j){
            if (a[i][j].v != '0' && !vis[i][j]){
                cnt = 0; vis[i][j] = 1;
                q.push({i, j});

                while (!q.empty()){
                    ++cnt;
                    int x = q.front().first, y = q.front().second; q.pop();
                    if (x+1 <= n && a[x][y].s && a[x+1][y].n && !vis[x+1][y]){
                        vis[x+1][y] = 1;
                        q.push({x+1, y});
                    }
                    if (x-1 >= 1 && a[x][y].n && a[x-1][y].s && !vis[x-1][y]){
                        vis[x-1][y] = 1;
                        q.push({x-1, y});
                    }
                    if (y+1 <= m && a[x][y].e && a[x][y+1].w && !vis[x][y+1]){
                        vis[x][y+1] = 1;
                        q.push({x, y+1});
                    }
                    if (y-1 >= 1 && a[x][y].w && a[x][y-1].e && !vis[x][y-1]){
                        vis[x][y-1] = 1;
                        q.push({x, y-1});
                    }
                }

                maxcnt = max(maxcnt, cnt);
            }
        }
    }

    cout << maxcnt << endl;
}

深度優先搜尋 dfs

可以把它想像成一直走第一個可以走的，

比BFS好寫很多，只是會有遞迴層數的問題(如果你要用stack做DFS也可以)

舉例來說：

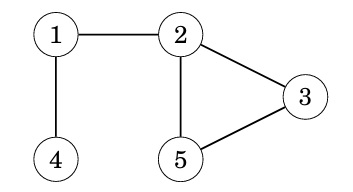
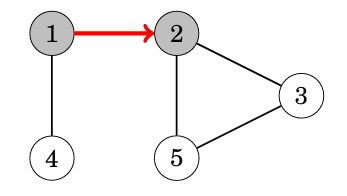
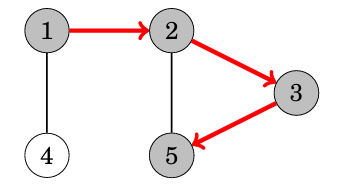
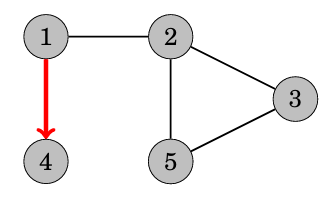
我們要使用遞迴來實作，每次就先遞迴下去可以走的

這樣就可以先走可以走的效果

我沒有模板題，所以直接帶題目：

ZeroJudge b701

APCS 20171003

APCS 20160304

ZeroJudge b701

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 515
#define inf 1e9
using namespace std;

int n, m, a[maxn][maxn], cnt, w, ns, s, e;
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};

void dfs(int x, int y){
    ++cnt; w=min(w, y); ns=min(ns, x); e=max(e, y); s=max(s, x);
    for (int k=0; k<4; ++k){
        if (a[x+dx[k]][y+dy[k]]){
            a[x+dx[k]][y+dy[k]] = 0;
            dfs(x+dx[k], y+dy[k]);
        }
    }
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j) cin >> a[i][j];
    }

    for (int i=1; i<=n; ++i){
        for (int j=1; j<=m; ++j){
            if (a[i][j] == 1){
                cnt=0; w=inf; ns=inf; s=0; e=0; a[i][j] = 0;
                dfs(i, j);
                cout << w-1 << " " << ns-1 << " " << e-1 << " " << s-1 << " " << cnt << endl;
            }
        }
    }
}

APCS 20171003

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
#define inf 1e18
#define int long long
using namespace std;

int n, k, dv[maxn], root, counter; vector<int> v[maxn];

int dfs(int x, int depth){
    if (v[x].size() == 0){
        return depth;
    }

    int mdepth=0;
    for (int i:v[x]){
        mdepth = max(mdepth, dfs(i, depth+1));
    }
    counter += (mdepth-depth);
    return mdepth;
}

signed main(){
    cin >> n;
    for (int i=1; i<=n; ++i){
        cin >> k;
        for (int j=1; j<=k; ++j){
            int a; cin >> a;
            dv[a] = i;
            v[i].push_back(a);
        }
    }

    for (int i=1; i<=n; ++i){
        if (dv[i] == 0) root = i;
    }
    cout << root << endl;

    dfs(root, 0);
    cout << counter << endl;
}

APCS 20160304

找樹的直徑：

  • 先隨便找一點dfs找最遠的點
  • 在從那一點找離他最遠的點，兩個之間的距離就是直徑
# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
#define inf 1e9
using namespace std;

int n, maxdepth, startnode;
vector<int> v[maxn];
void dfs(int x, int prenode, int depth){
    if (depth > maxdepth){
        maxdepth = depth;
        startnode = x;
    }

    for(int i:v[x]){
        if (i == prenode) continue;
        dfs(i, x, depth+1);
    }

    return;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i){
        int a, b; cin >> a >> b;
        v[a].push_back(b);
        v[b].push_back(a);
    }

    dfs(0, 0, 0);
    dfs(startnode, startnode, 0);
    cout << maxdepth << endl;
}

動態規劃

dp

dp的精神就是把大問題拆成小問題，先解出比較小數字的答案，找出規律，並寫出我們的dp轉移式

舉例來說：

費式數列：

F_{1} = 1\\ F_{2} = 1\\ F_{n} = F_{n-1} + F_{n-2} \ (n\ge3) 
dp[1] = 1;
dp[2] = 1;
for (int i=3; i<=n; ++i){
    dp[i] = dp[i-1] + dp[i-2];
}

我們先來講一些經典的dp問題，

再來寫一些APCS的題目：

1. 最大連續區間和

把dp[i]設為：我們一定取第i項，最大的值為多少

dp[i]可以是接續前面的，或是從第i項開始取。

 

最後只要找到dp裡最大的數字就是答案了。

#include <bits/stdc++.h>
#define maxn 100005
#define inf 1e9
#define endl '\n'
using namespace std;

int n; long long nums[maxn], dp[maxn], maxnum;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n;
    for (int i=1; i<=n; ++i) cin >> nums[i];

    dp[1] = nums[1]; maxnum = 0;

    for (int i=2; i<=n; ++i){
        dp[i] = max(dp[i-1] + nums[i], nums[i]);
        maxnum = max(maxnum, dp[i]);
    }

    cout << maxnum << endl;
}

2. LCS

LCS就是最長共同子序列，舉例來說：

 

s1: 2 5 7 9 3 1 2
s2: 3 5 3 2 8

LCS(s1, s2) = 5 3 2

我們第一件事就是要定義dp：

我們開一個dp[n][m]，dp[i][j]代表s1到第i項、s2到第j項 目前的LCS

第二件事就是要想轉移式：

我們先把s1[i]和s2[j]特別取出來，做比較

s1[i] == s2[j]，我們就會是取這一項的數字，那dp[i][j]就會是：

dp[i][j] = dp[i-1][j-1] + 1

s1[i] != s2[j]，我們就會是s1[i]或s2[j]取一個，dp[i][j]就會是：

dp[i][j] = max(dp[i-1][j],\ dp[i][j-1])

2. LCS

最後的程式：

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 105
using namespace std;

int n, m,  dp[maxn][maxn], n1[maxn], n2[maxn], counter;

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    while (cin >> n >> m){
        ++counter;
        if (n==0 && m==0) break;

        for (int i=0; i<n; ++i) cin >> n1[i];
        for (int i=0; i<m; ++i) cin >> n2[i];

        for (int i=1; i<=n; ++i){
            for (int j=1; j<=m; ++j){
                if (n1[i-1] == n2[j-1]){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
        cout << "Twin Towers #" << counter << endl;
        cout << "Number of Tiles : " << dp[n][m] << endl;
    }
}

2. LCS

3. LIS

LIS是最長遞增子序列，舉例來說：

 

[1 3 5 2 9] 的 LIS 是 [1 3 5 9 ]

dp會是一個vector，紀錄目前暫時的LIS
*記得我們這個dp裡的不是實際的LIS，只是拿來算的

3. LIS

並且在有一個position的陣列，

position[i] 紀錄我們剛剛把數字i 塞在哪個index裡。

我們在跑過每個數字時，我們會把這個數字放在最適合的位置，讓後面更有機會成為LIS，就會是第一個 >= 這個的數字的那一項 (用lower_bound找)，並且用vector紀錄。

最後將position的陣列從尾找到頭，假設LIS長度是l

並且找到 第一個=l 的第i項，第一個=l-1 的第i項，...，第一個=1 的第i項

最後在把全部第i項的數字反過來輸出就是LIS了

最後的程式：

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 500000
using namespace std;

int n, lis;
vector<int> nums, dp, position; stack<int> temp;
int main(){
    while (cin >> n) nums.push_back(n);

    dp.push_back(nums[0]);
    position.push_back(1);
    for (int i=1; i<nums.size(); ++i){
        if (nums[i] <= dp.back()){
            int idx = lower_bound(dp.begin(), dp.end(), nums[i]) - dp.begin();
            dp[idx] = nums[i];
            position.push_back(idx+1);
        }else{
            dp.push_back(nums[i]);
            position.push_back(dp.size());
        }
    }

    lis = dp.size();
    cout << lis << endl << "-" << endl;

    for (int i=position.size()-1; i>=0; --i){
        if (position[i] == lis){
            temp.push(nums[i]);
            --lis;
        }
        if (lis == 0) break;
    }
    while (!temp.empty()){cout << temp.top() << endl; temp.pop();}
}

3. LIS

4. 0-1背包

假設我們有一個背包可以最多裝W重量的物品，

並且我們有n個物品，每個物品有價值和重量。

 

在不超過W重量的情況下，我們如何取物品讓我們的價值是最大的

我們第一件事就是要定義dp：

我們開一個dp[n][w]，dp[i][j]會是我們討論到第n個物品，重量為j時 價值最高是多少

第二件事就是要想轉移式：

我們討論dp[i][j]拿物品或不拿物品

拿物品：

dp[i][j] = dp[i-1][j-v[i].first] + v[i].second

不拿物品：

dp[i][j] = dp[i-1][j]

4. 0-1背包

最後取max：

dp[i][j] = max(dp[i-1][j],\ dp[i-1][j-v[i].first] + v[i].second)

最後的程式：

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 105
#define maxw 100005
#define ll long long
using namespace std;

ll n, w, dp[maxn][maxw]; pair<ll, ll> v[maxn];
//v -> 存放<n, w>
//dp[第幾個物品][總共的重量] = 價值
int main(){
    ios::sync_with_stdio(0); cin.tie(0);
    
    cin >> n >> w;
    for (int i=1; i<=n; ++i) cin >> v[i].first >> v[i].second;

    for (int i=1; i<=n; ++i){
        for (int j=0; j<=w; ++j){
            if (j-v[i].first < 0) dp[i][j] = dp[i-1][j];
            else dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i].first] + v[i].second);
        }
    }

    cout << dp[n][w] << endl;
}

4. 0-1背包

 小補充：背包問題通常都可以壓空間，把 O(nw) 壓到 O(w)

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 105
#define maxw 100005
#define ll long long
using namespace std;

ll n, w, dp[maxw]; pair<ll, ll> v[maxn];
int main(){
    ios::sync_with_stdio(0); cin.tie(0);
    
    cin >> n >> w;
    for (int i=1; i<=n; ++i) cin >> v[i].first >> v[i].second;

    for (int i=1; i<=n; ++i){
        for (int j=w; j>=v[i].first; --j){
            dp[j] = max(dp[j], dp[j-v[i].first] + v[i].second);
        }
    }

    cout << dp[w] << endl;
}

4. 0-1背包

來寫APCS的題目：

APCS 20201003

APCS 20181004

APCS 20220604

APCS 20201003

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 10005
#define maxm 55
#define ll long long
using namespace std;

int n, m, a[maxm][maxn], dp[maxm][maxn], dpr[maxm][maxn], dpl[maxm][maxn], maxcnt;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> m >> n;
    for (int i=1; i<=m; ++i){
        for (int j=1; j<=n; ++j){
            cin >> a[i][j];
        }
    }

    for (int i=1; i<=m; ++i){
        for (int j=1; j<=n; ++j) dpr[i][j] = max(dp[i-1][j], dpr[i][j-1]) + a[i][j];
        for (int j=n; j>=1; --j) dpl[i][j] = max(dp[i-1][j], dpl[i][j+1]) + a[i][j];
        for (int j=1; j<=n; ++j){
            dp[i][j] = max(dpr[i][j], dpl[i][j]);
            if (i==m) maxcnt = max(maxcnt, dp[i][j]);
        }
    }

    cout << maxcnt << endl;
}

APCS 20181004

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
using namespace std;

int m, s, n, nums[maxn], dp[maxn], total;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> m >> s >> n;
    for (int i=1; i<=n; ++i){
        cin >> nums[i];
        total += nums[i];
    }
    s = max(0, m-s);

    for (int i=1; i<=n; ++i){
        for (int j=s; j>=nums[i]; --j){
            dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]);
        }
    }

    cout << total-dp[s] << endl;
}

APCS 20220604

# code yaaaa
#include <bits/stdc++.h>
#define endl '\n'
#define inf 1e18
#define int long long
#define maxn 1005
using namespace std;

int n, m, a[maxn], b[maxn], dp[maxn][maxn];
int curnum=-inf, maxnum=-inf;
signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m;
    for (int i=1; i<=n; ++i) cin >> a[i];
    for (int i=1; i<=m; ++i) cin >> b[i];

    for (int i=0; i<4; ++i){
        if (i>=1) reverse(a+1, a+1+n);
        if (i==2) reverse(b+1, b+1+m);
        curnum = -inf;

        for (int i=1; i<=n; ++i){
            for (int j=1; j<=m; ++j) dp[i][j] = -inf;
        }

        for (int i=1; i<=n; ++i){
            for (int j=1; j<=m; ++j){
                dp[i][j] = max(a[i]*b[j], dp[i-1][j-1] + a[i]*b[j]);
                curnum = max(curnum, dp[i][j]);
            }
        }

        maxnum = max(maxnum, curnum);
    }

    cout << maxnum << endl;
}

考試重點

快下課了ya

考前幾個重點：

1. 記得要一直刷題目！很重要！

2. 考前一天好好睡，不要熬夜！

 

考試幾個重點：

1. 小心作答，不要被edge case搞

(ex: 要開long long等)

2. 題目看完後先想好整個流程再開始打，這樣比較不容易錯。

3. 比較難的題目記得爭子題分數，很重要！

 

最後，助每個人都考到自己想要的分數！

(我想考 5 4 lol)

下課

ya ok bye

APCS 實作題複習

By MLGnotCOOL

Made with Slides.com

APCS 實作題複習

  • 128

More from MLGnotCOOL