Dijkstra's

演算法

要教的內容

BFS 和 Dijkstra's演算法

先從比較簡單的開始

(不是直接進入Dijkstra's演算法)

假設我們有一個無權的圖

然後要求一點到另一點的最短距離

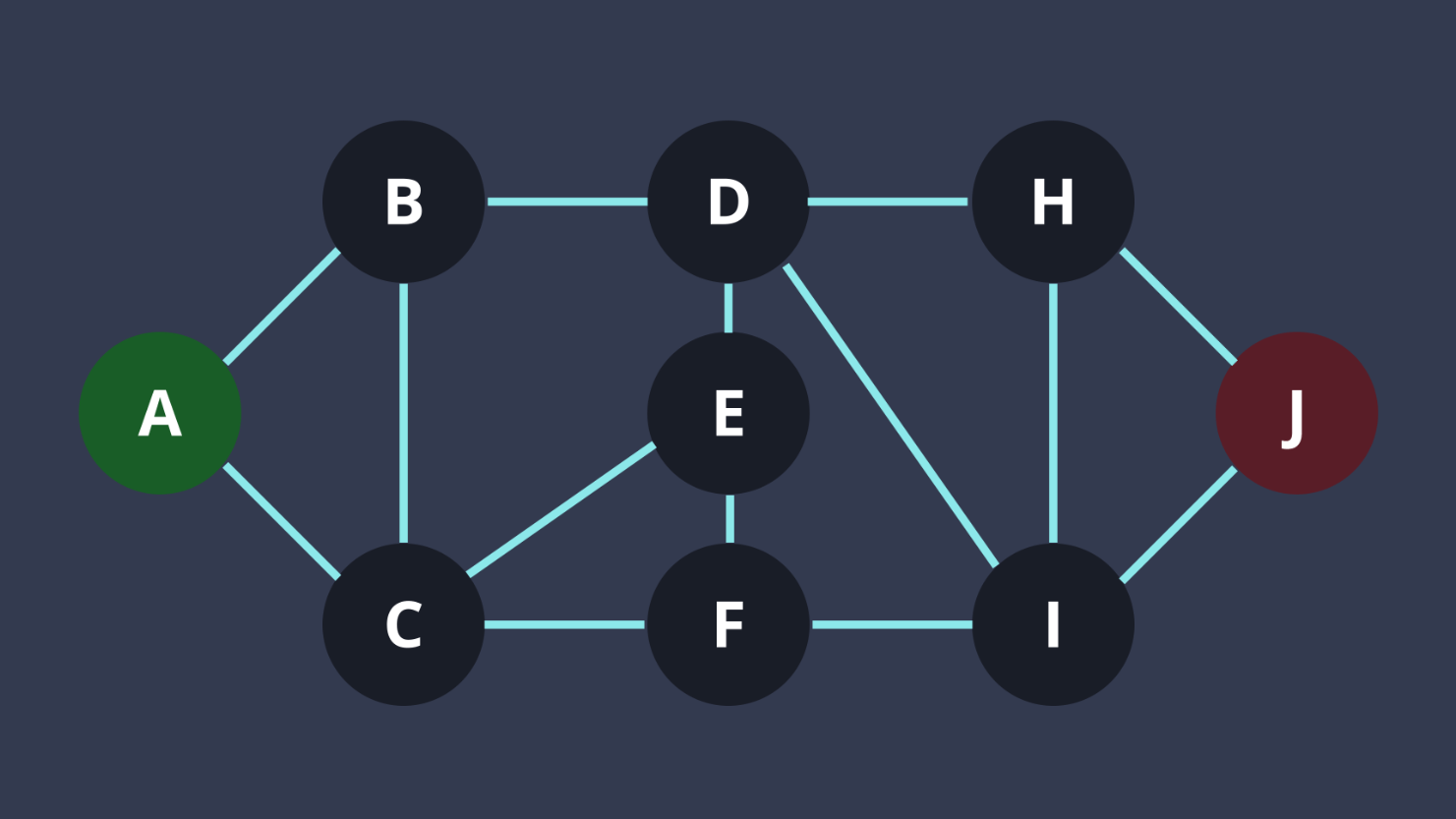
用BFS!

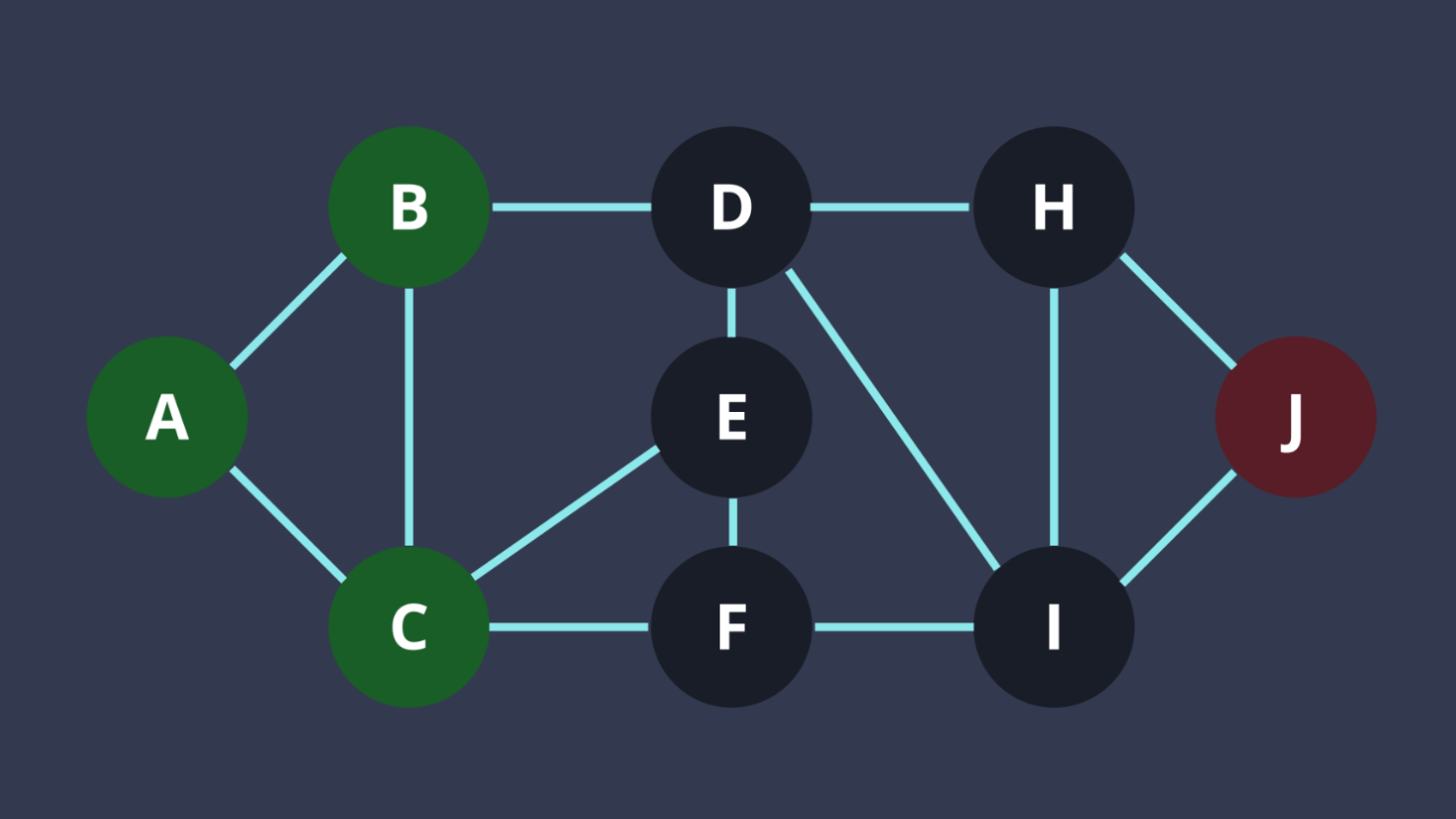
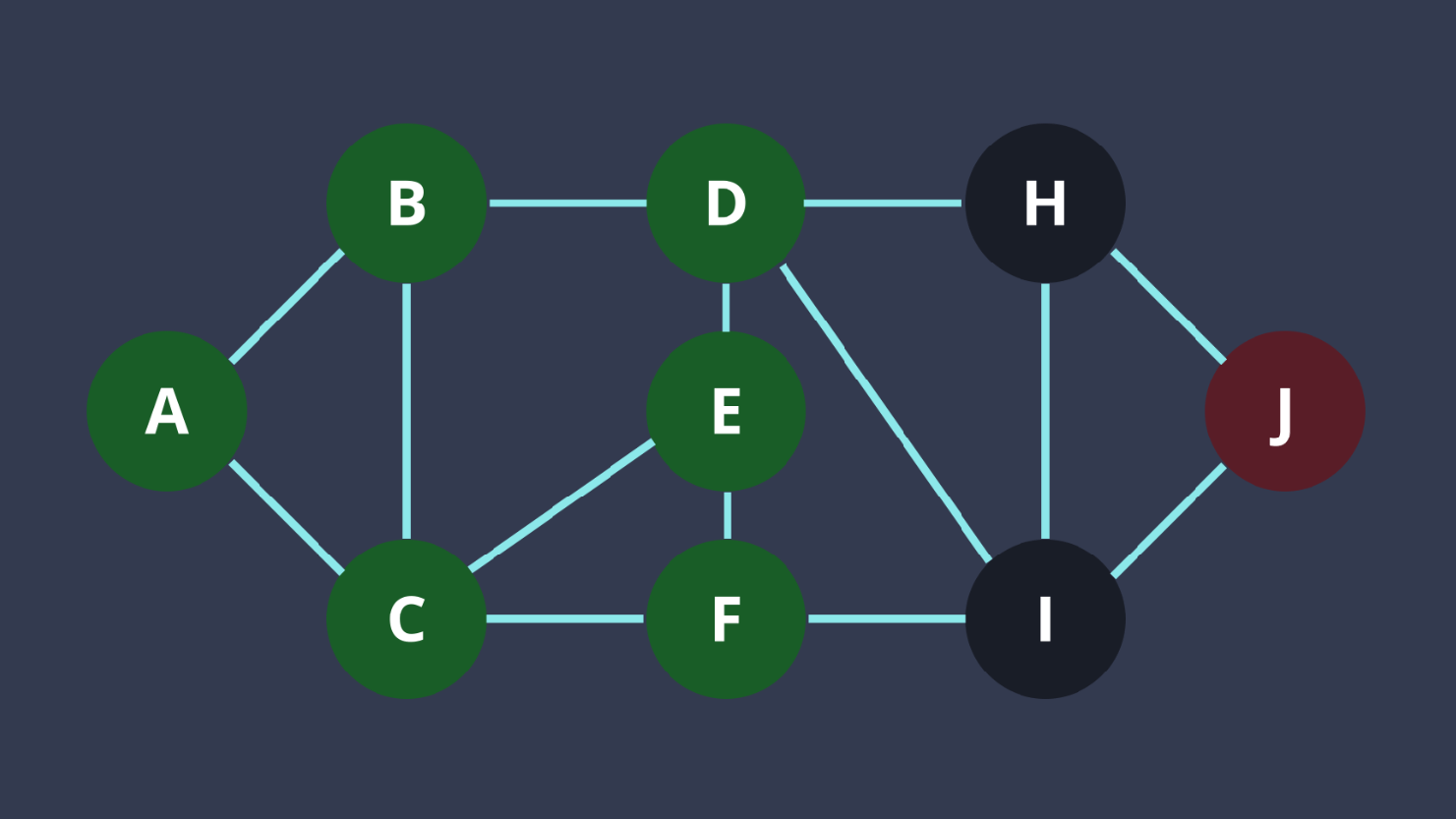
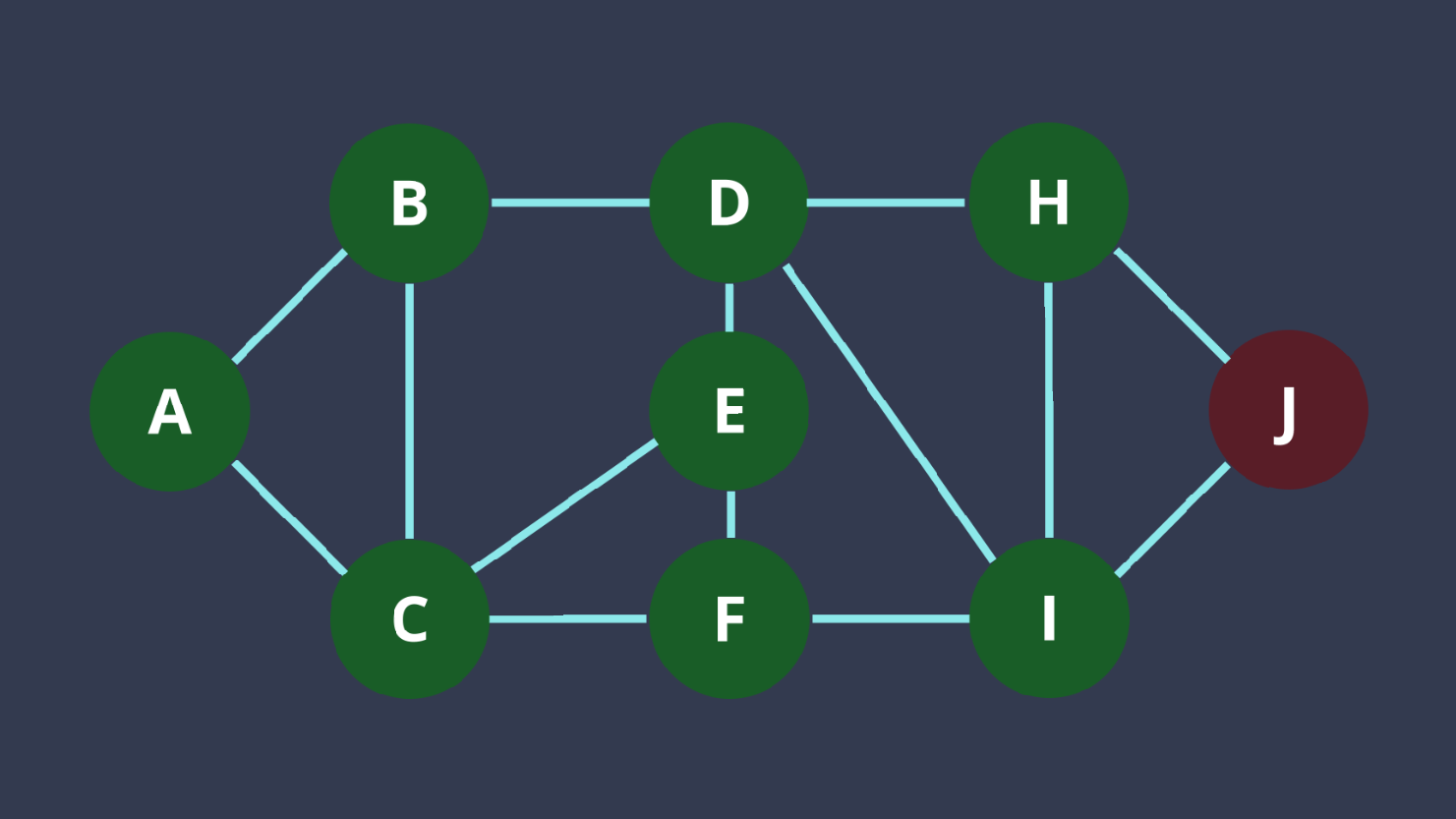
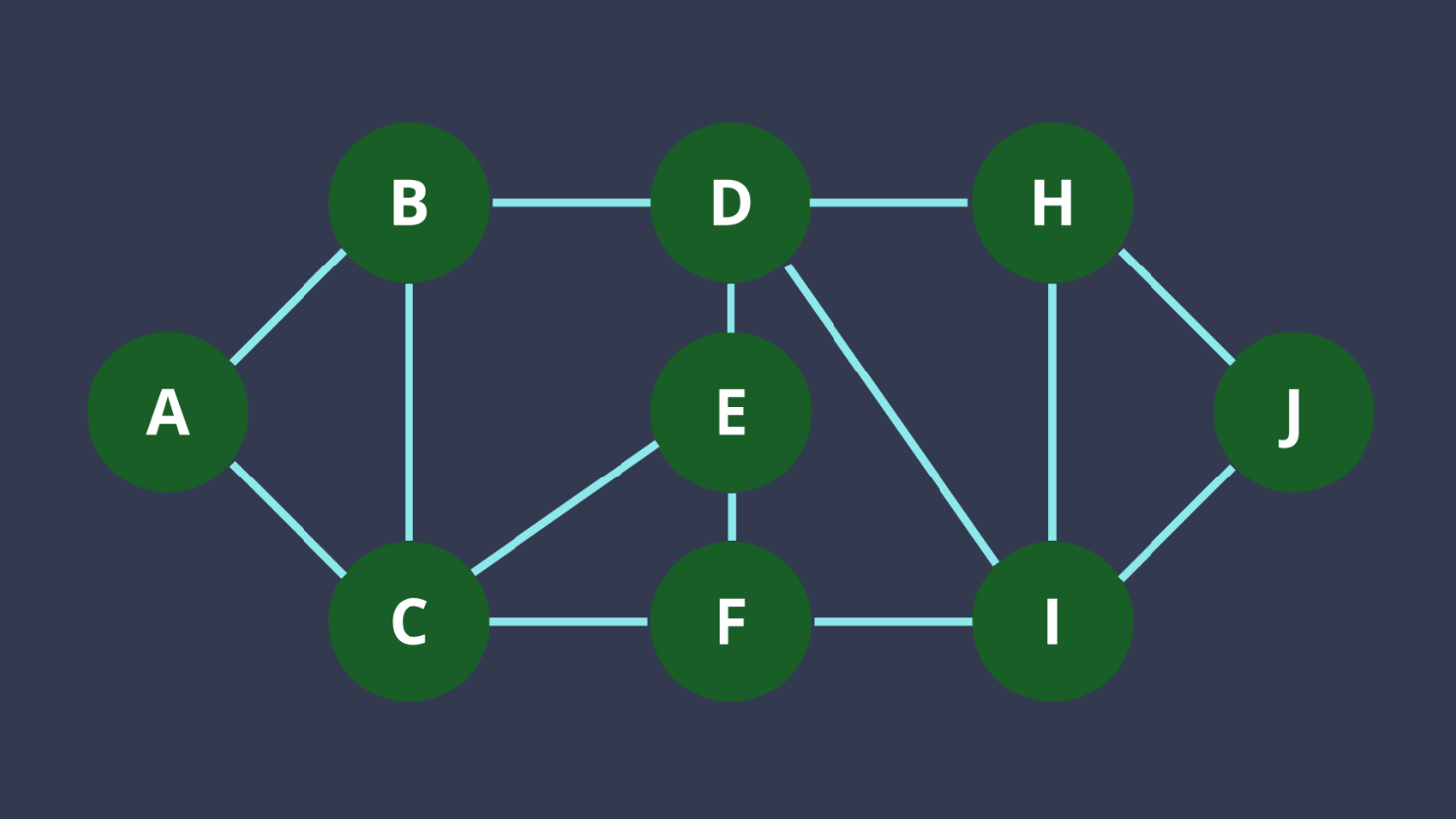
BFS 實作+題目

  • 把開始的點推到一個queue裡面
  • 一直把q.front()相連的節點推到q
  • 因為先推到q裡面的點是深度比較低的，而會先處理，做到BFS
  • 重複直到q是empty的

ZeroJudge a290 新手訓練系列 ~ 圖論https://zerojudge.tw/ShowProblem?problemid=a290

給那些點與點之間有邊(有方向性)

求可不可以從一點走到一點

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 805
using namespace std;

int n, m, n1, n2; bool found, vis[maxn];
// vis存有沒有走過這個點
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    while(cin >> n >> m){
        found=false; vector<int> v[maxn]; queue<int> q;
        //v存點之間有沒有邊 (鄰接陣列存，省空間)
        //q來做BFS
        
        for (int i=1; i<=n; ++i) vis[i] = 0;

        for (int i=1; i<=m; ++i){
            int a, b; cin >> a >> b;
            v[a].push_back(b);
        }
        //先將第一個點推到q裡，將vis的第一個點設為true
        cin >> n1 >> n2; q.push(n1); vis[n1] = 1;

        while (!q.empty()){ //重複直到q是空的
            int x=q.front(); q.pop();

            for (int i:v[x]){ //檢查全部x相鄰的點
                if (vis[i] == 1) continue; //如果已經經過則跳過
                if (i == n2){ //找到我們要的終點
                    found=true;
                    break;
                }

                vis[i] = 1;
                q.push(i); //把x相鄰的點全部推到q
            }
            if (found) break;
        }

        if (found) cout << "Yes!!!" << endl;
        else cout << "No!!!" << endl;
    }
}

# Code yaaaaa

Dijkstra's 演算法

然後要求一點到其他點的最短距離

假設我們有一個有權圖

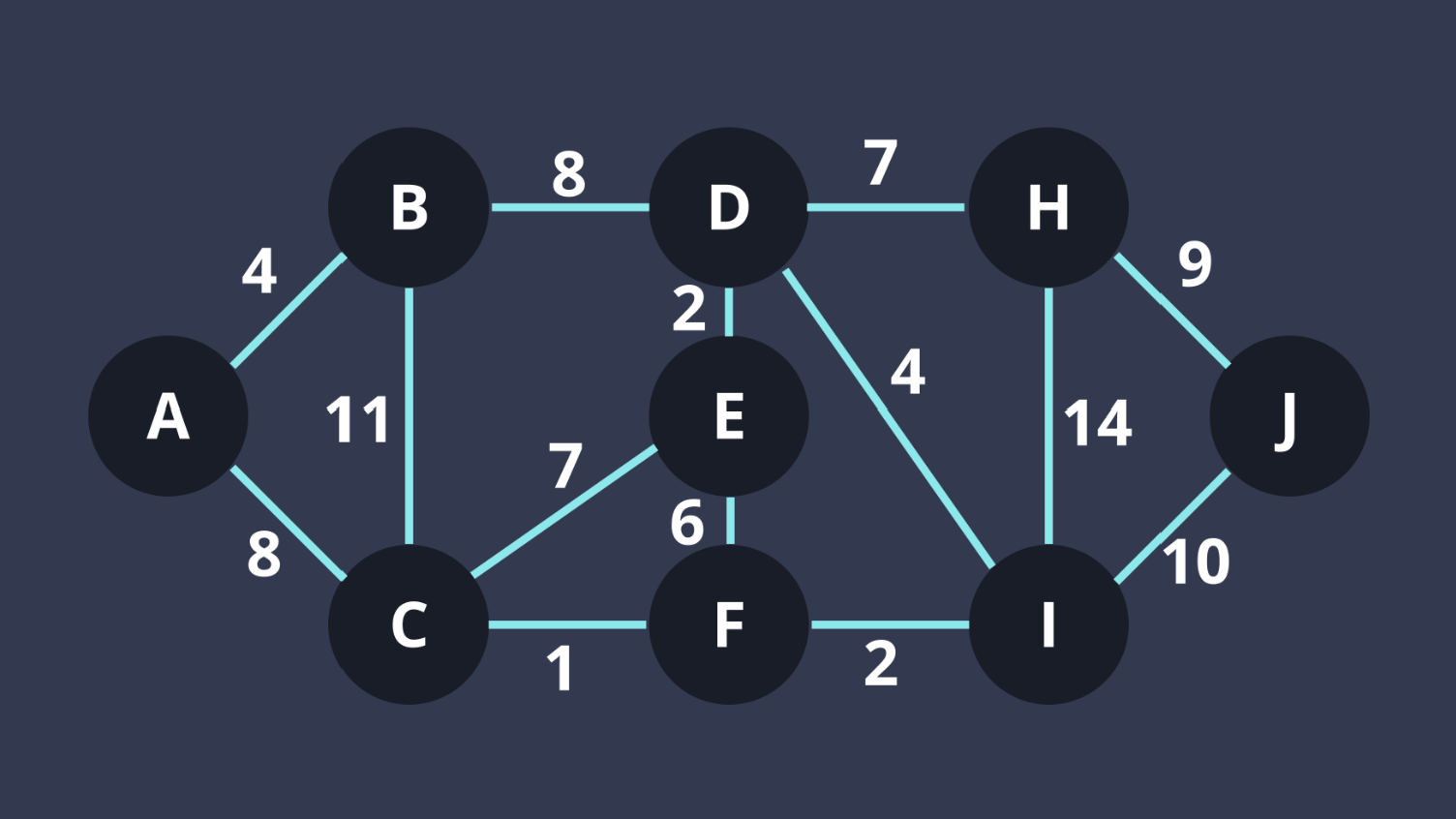
BFS ❌

BFS ❌

BFS ❌

Dijkstra✅

❓

Dijkstra's 演算法的限制：

  • 權值(邊上面的值) 不能 為負數 (否則就要用Bellmen-Ford algorithm)
  • 只能求一點到其他點的最短距離(若要求隨機兩點的最短距離，就要用Floyd-Warshall algorithm)

 

Dijkstra's 解釋

當我說距離：出發點到那一點的距離

1. 將1到n的距離存到dist[n]，並將dist全部設成無限 (dist[1]=0)

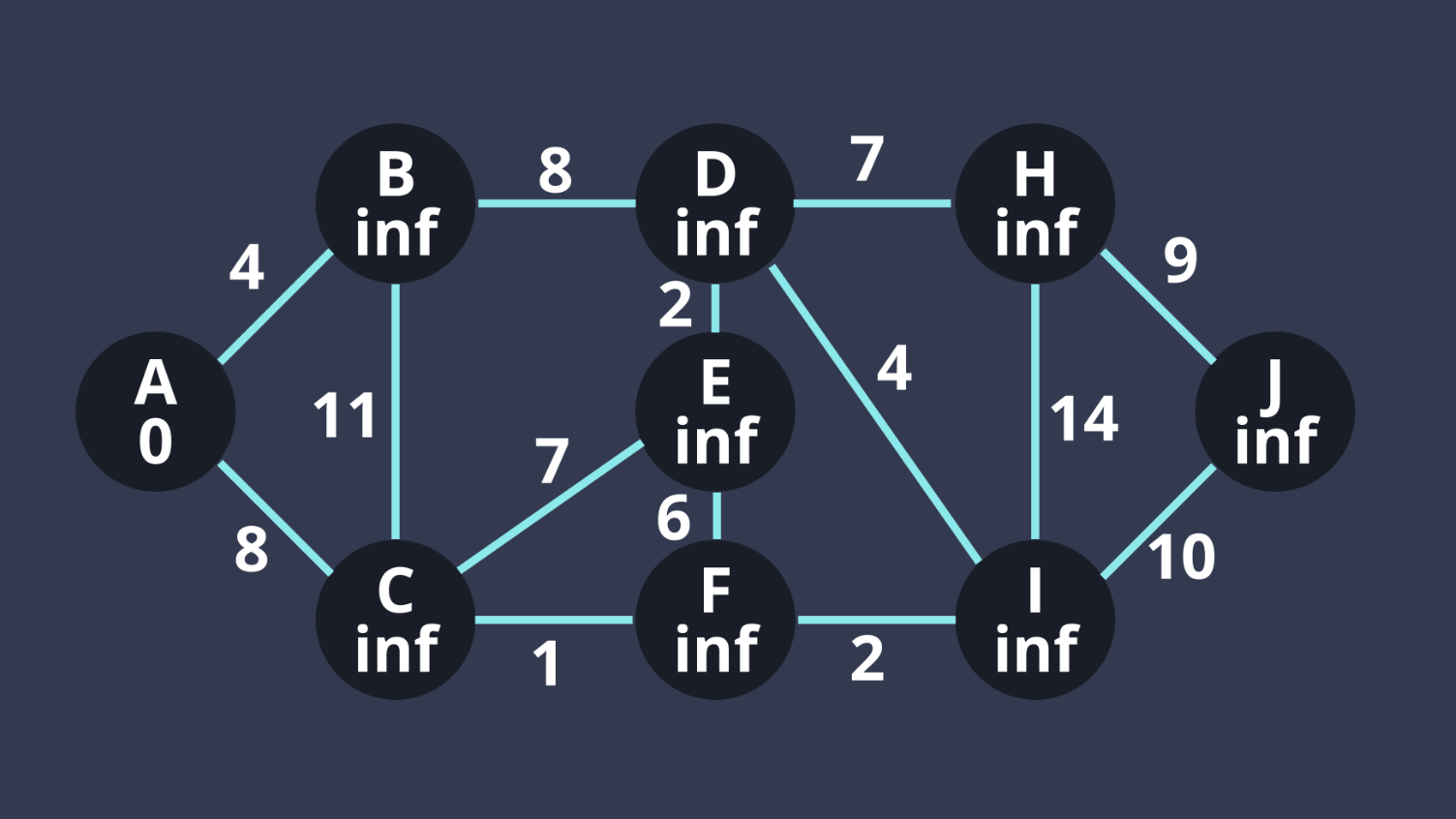
2. A連接B和C，將B,C更新：

可將dist[2]更新為4，dist[3]更新為8 (4<inf, 8<inf)

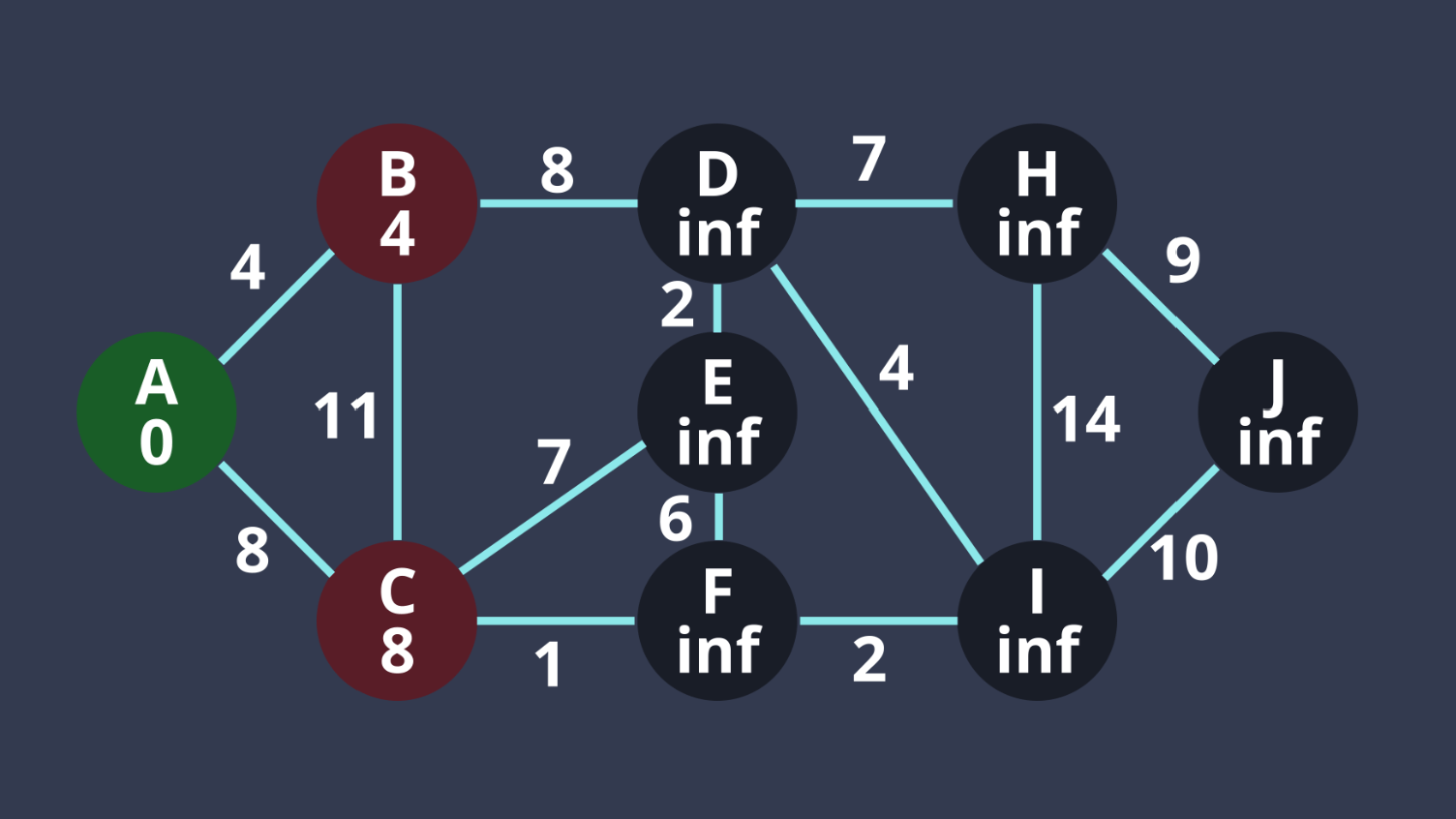
3. B距離最小，將B相鄰的點都更新
(因為C的8小於4+11，所以不用更新，也不用再加到pq)

並且若我們走過的點，則不用更新

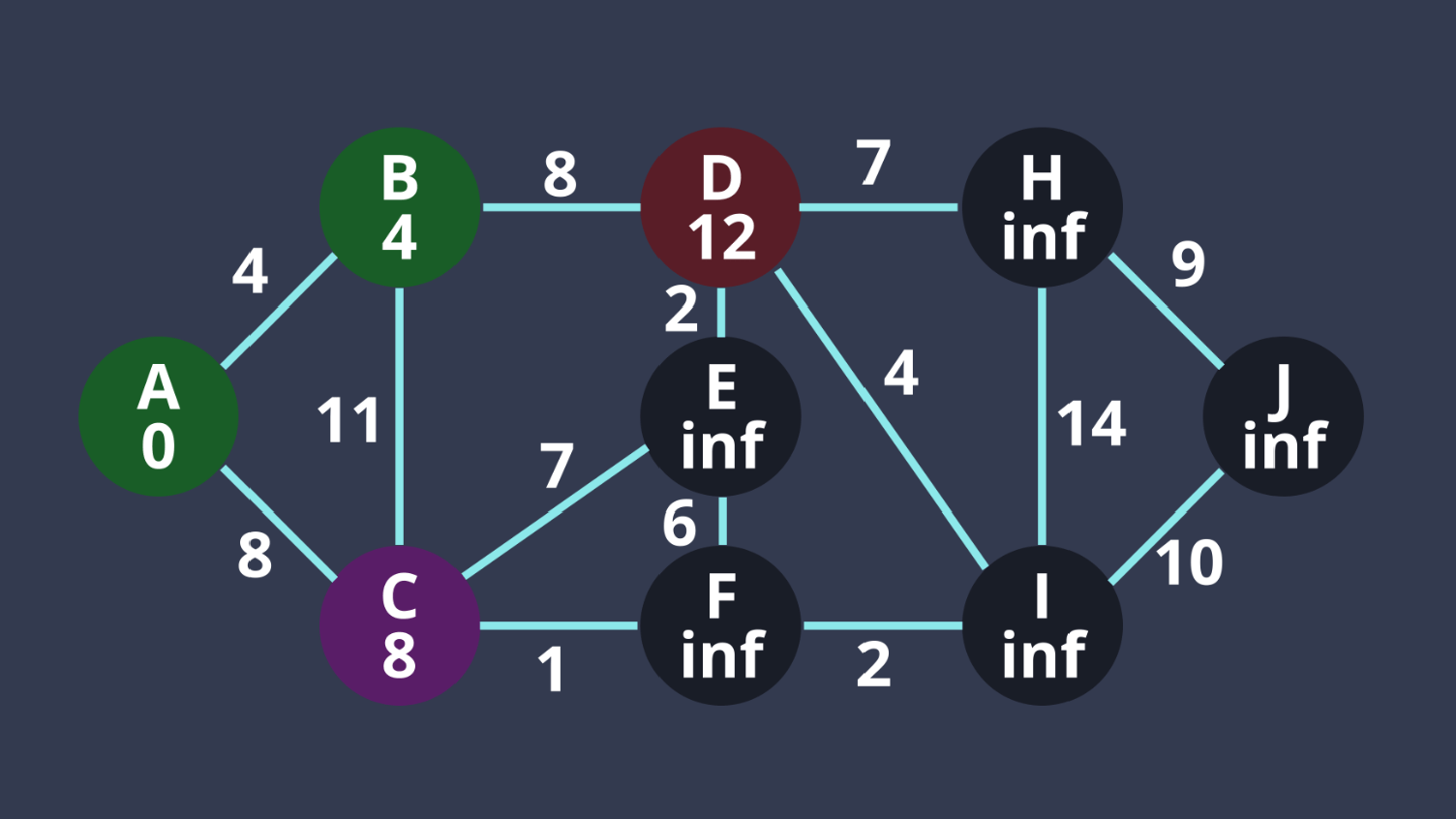
4. C距離最小，所以對C做一樣的事

(A, B走過，不用更新)

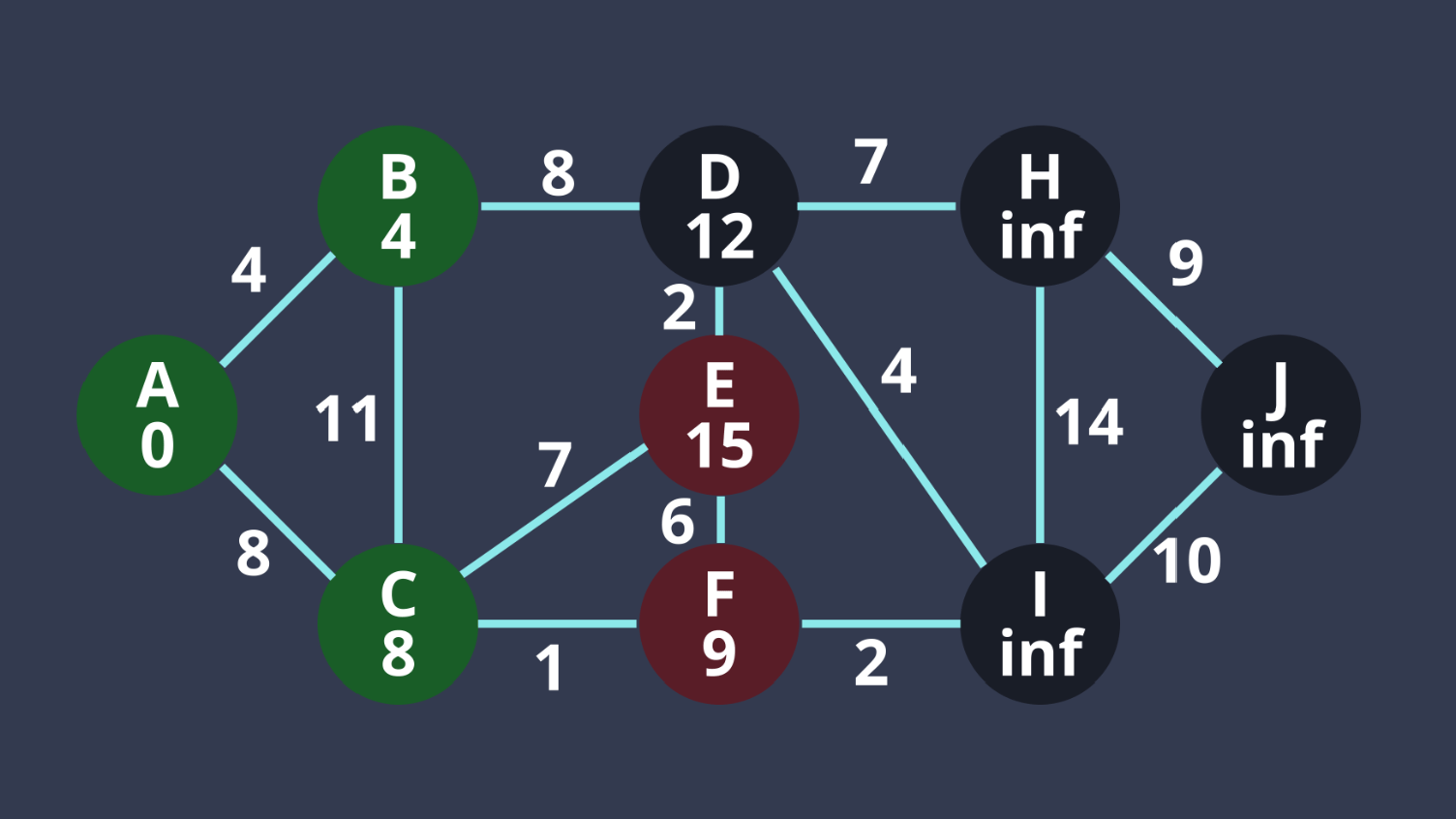
5. F距離最小

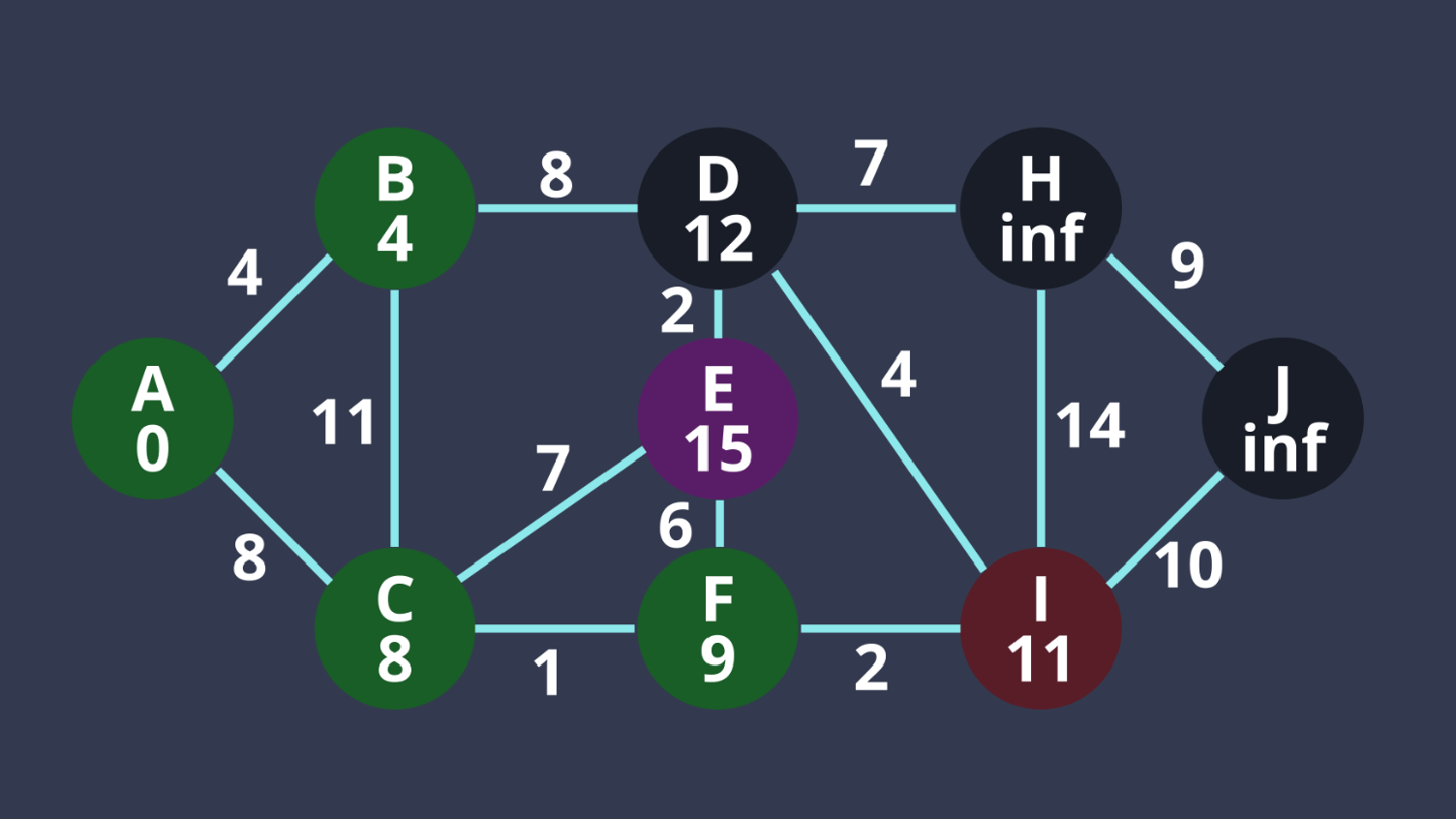
6. I距離最小

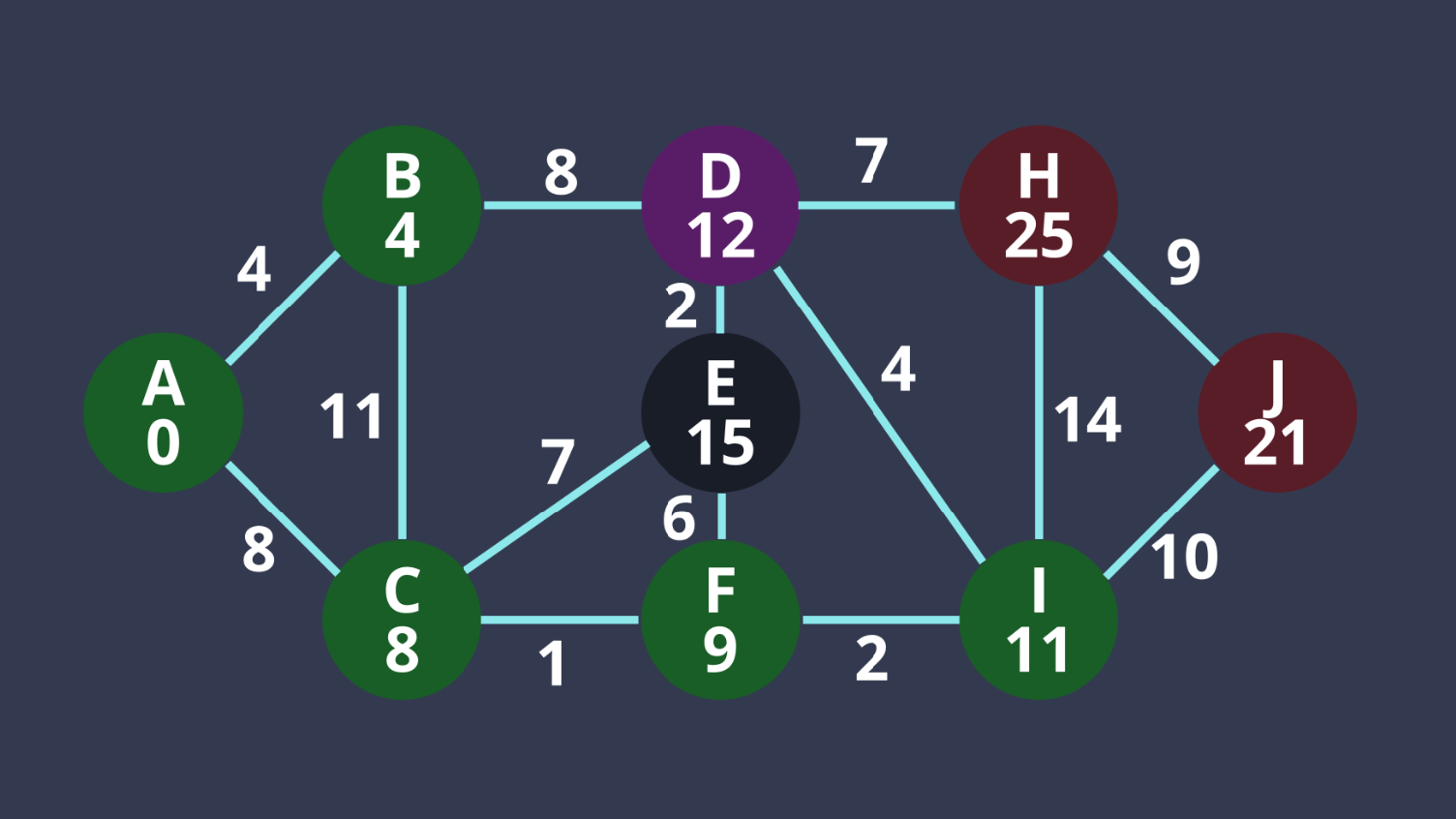
7. D距離最小

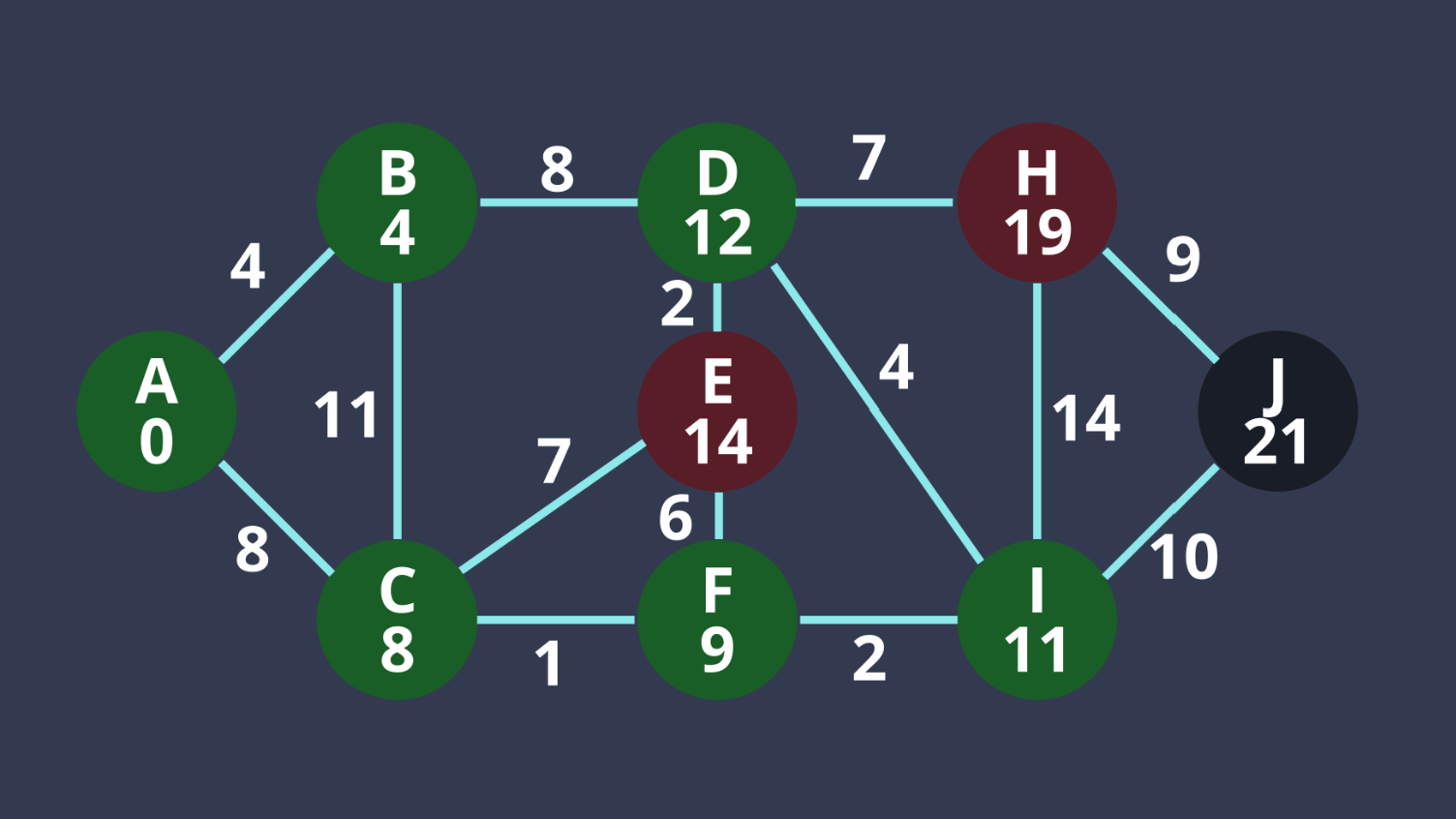
8. E距離最小

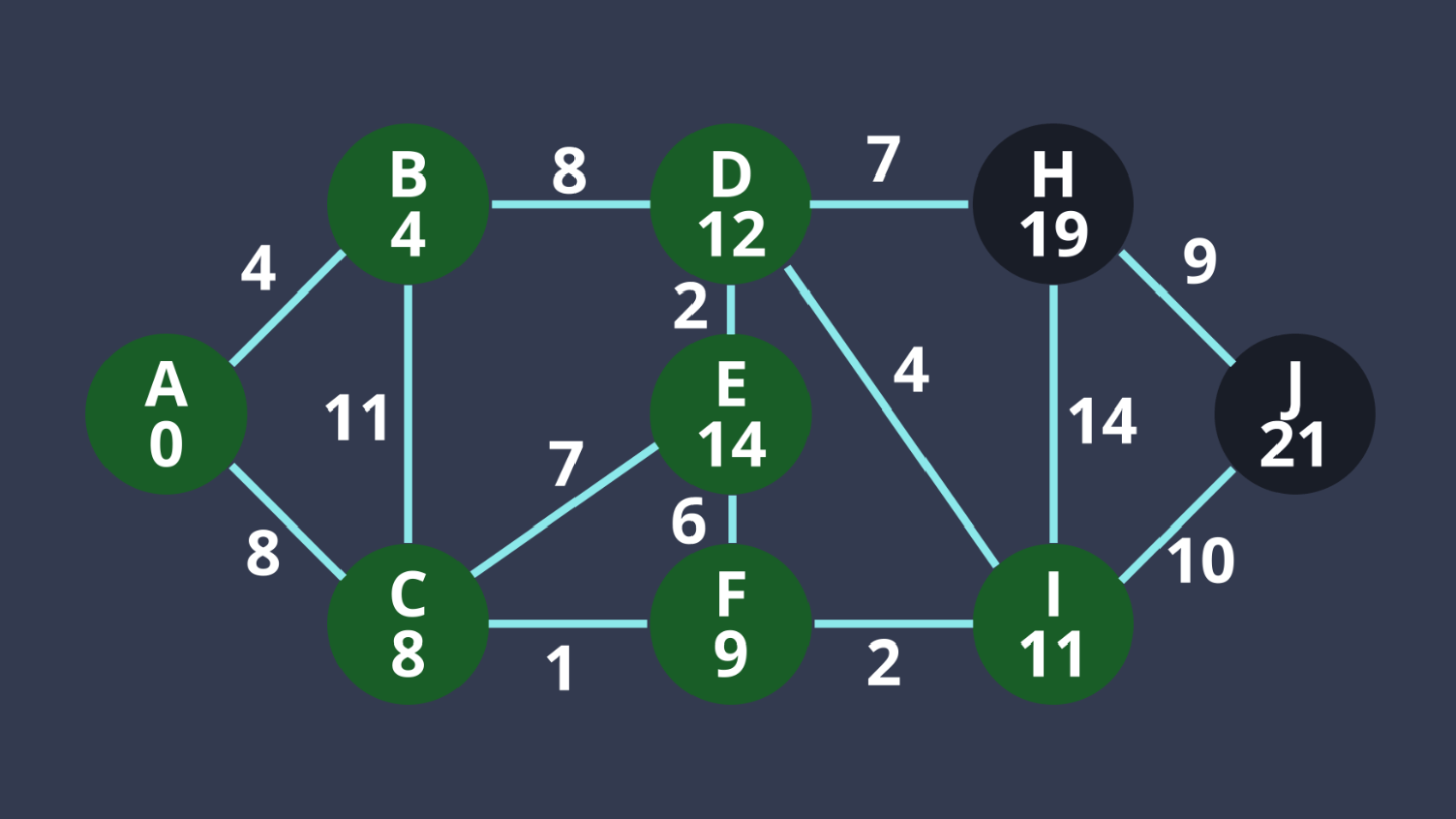
9. H距離最小

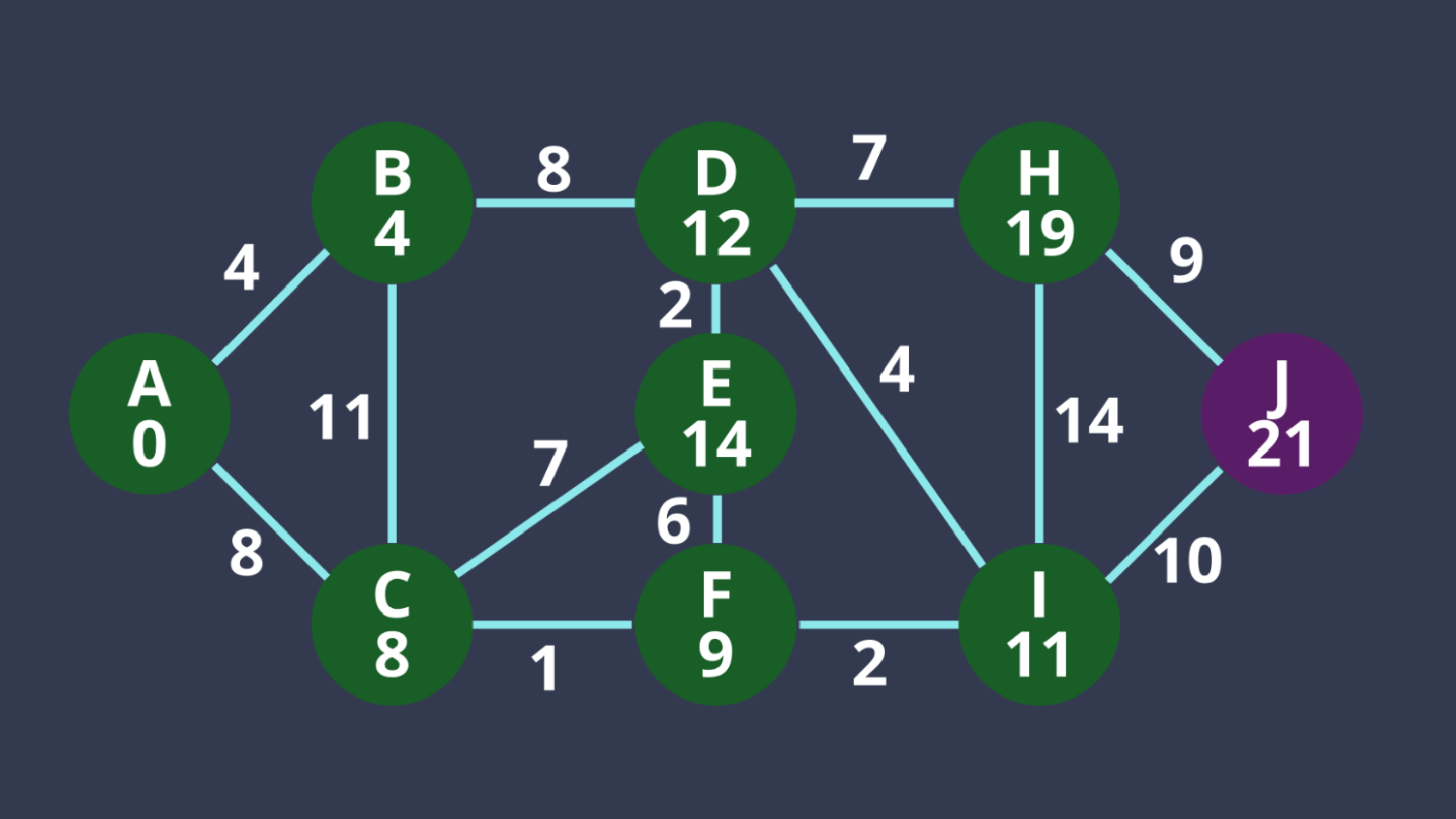
10. J距離最小

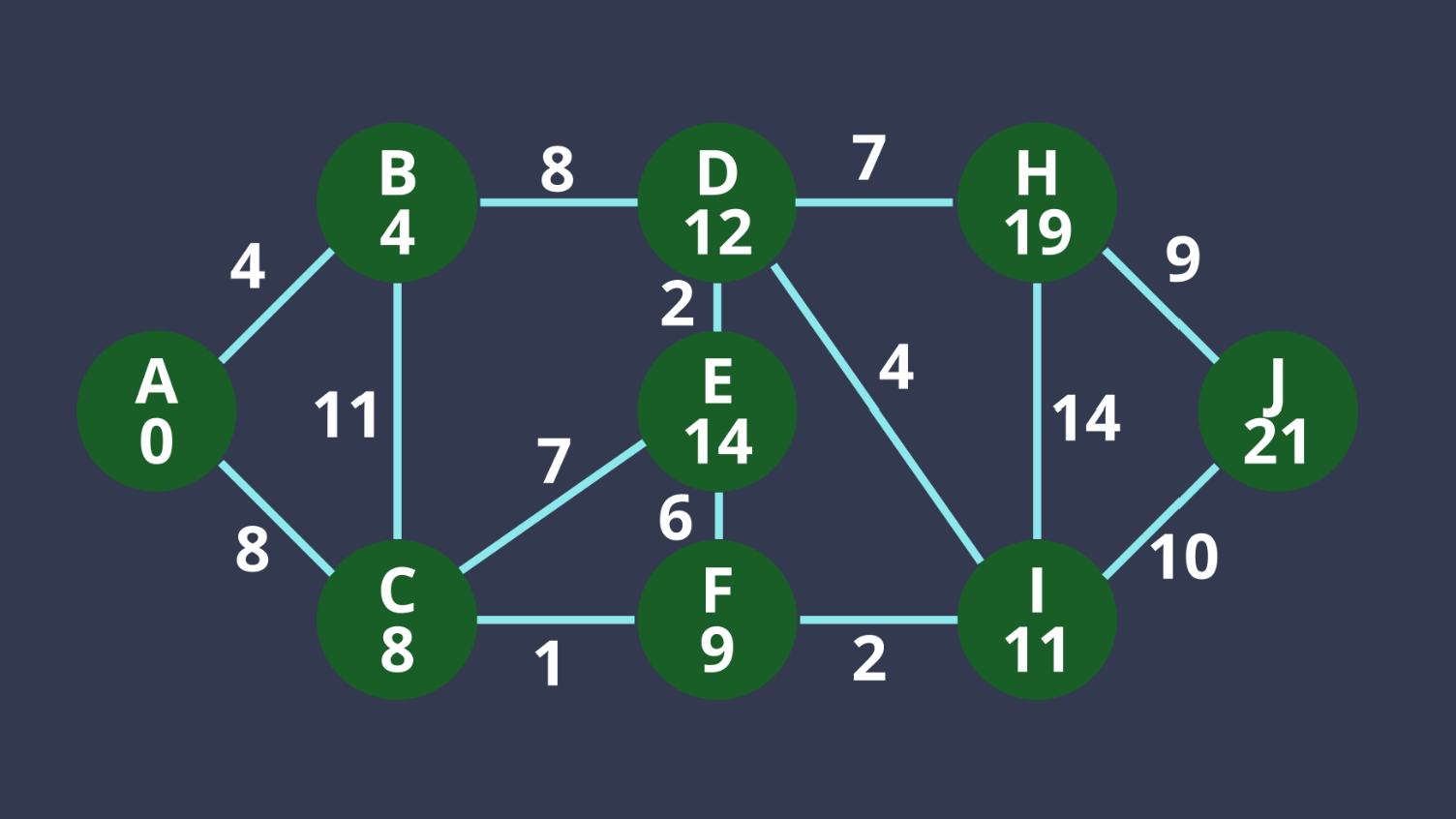
為什麼可以這樣做？？

假設一個B點，可以再被更新，那圖上的點一定會有一個小於B的距離(因為有說權值一定是0或正的)，所以圖上的那一個點會先去處理，因此當B點為全部點距離最小時，可以保證現在的距離是出發點到B點的最短距離 (同時也不用再更新B點了)

由上面可以得知：

  • 目標：從距離最小的點不斷更新他附近(且沒走過)的點，並且將可更新的點 的新的距離存到dist[i]
  • dist[i]最小的點可以用一個將 距離由小到大排列 的priority_queue來查詢，且更新dist[i]時也要把點推到pq
  • pq裡有可能有重複的點，則如果此點已經經過的話，則直接跳過(因為比較小的距離之前就處裡過了)
  • 若pq是空的就停掉

Dijkstra's 實作+題目

CSES - Shortest Routes I

https://cses.fi/problemset/task/1671

給你點與點之間的距離(有方向性)

並且要求1到全部點(1~n)的最短距離

 

保證距離>=1，1都有可能到其他點

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
#define inf LLONG_MAX
#define int long long
using namespace std;

int n, m, dist[maxn]; vector<pair<int, int>> f[maxn]; bool vis[maxn];
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
//f[i]存{j, i到j的距離}
//pq存{0到i到距離, i}

signed main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    cin >> n >> m;
    for (int i=1; i<=m; ++i){
        int a, b, c; cin >> a >> b >> c;
        f[a].push_back({b, c});
    }

    for (int i=1; i<=n; ++i) dist[i] = inf;
    dist[1] = 0;

    pq.push({0, 1});
    while (!pq.empty()){
        int p = pq.top().second; pq.pop(); //我們只需要pq最上面的點，距離是用來sort的
        if (vis[p] == 1) continue; 
        //因為有可能有重複的點被放到pq，我們只需要處裡距離最小的，
        //且pq的距離是由小排到大的，所以我們若造訪過就不用更新旁邊的了
        
        vis[p] = 1; //設為造訪過

        for (int i=0; i<f[p].size(); ++i){
            int v=f[p][i].first; //要更新的點
            int d=f[p][i].second; //現在點到要更新的點的距離

            //若沒有參訪過，且新的距離小於原本的
            if (vis[v] == 0 && dist[p]+d < dist[v]){
                dist[v] = dist[p]+d; //更新dist
                pq.push({dist[v], v}); //推進pq
            }
        }
    }

    for (int i=1; i<=n; ++i){
        if (i==n) cout << dist[n] << endl;
        else cout << dist[i] << " ";
    }
}

# Code yaaaaa

那如果我們要經過的途徑呢？

只要更新dist[i]同時，存到i點過來的點，最後從最後一點找回第一點就好了

剛剛的程式：

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 100005
#define inf LLONG_MAX
#define int long long
using namespace std;

int n, m, dist[maxn], path[maxn]; vector<pair<int, int>> f[maxn]; bool vis[maxn]; vector<int> final_path;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;

signed main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    cin >> n >> m;
    for (int i=1; i<=m; ++i){
        int a, b, c; cin >> a >> b >> c;
        f[a].push_back({b, c});
    }

    for (int i=1; i<=n; ++i) dist[i] = inf;
    dist[1] = 0;

    pq.push({0, 1});
    while (!pq.empty()){
        int p = pq.top().second; pq.pop();
        if (vis[p] == 1) continue;
        vis[p] = 1; path[1] = 0;

        for (int i=0; i<f[p].size(); ++i){
            int v=f[p][i].first;
            int d=f[p][i].second;

            if (vis[v] == 0 && dist[p]+d < dist[v]){
                dist[v] = dist[p]+d;
                path[v] = p; //加這一行
                pq.push({dist[v], v});
            }
        }
    }

    //輸出1到n點最短距離和路徑
    cout << dist[n] << endl;

    int x=n; //從n往回找
    while (x != 0){ //path[1] = 0
        final_path.push_back(x);
        x = path[x];
    }
    //反向的輸出
    for (int i=final_path.size()-1; i>=0; --i){
        if (i==0) cout << final_path[i] << endl;
        else cout << final_path[i] << " ";
    }
}

# Code yaaaaa

ok bye bye

我的hackmd筆記：

https://hackmd.io/@MLGnotCOOL/SkkoCvoakg

講完了 :)

大致上就這樣

Dijkstra's 演算法

By MLGnotCOOL

Made with Slides.com

Dijkstra's 演算法

  • 60

More from MLGnotCOOL