排程場演算法

+

約瑟夫問題

為什麼我會想講這兩個東西：

 

前幾次APCS的觀念題有考到，

然後我那時候不會寫 :)

自我介紹

我是112班16號的翁釩予

成電38屆 教學+網管

 

興趣：打code、剪輯影片、玩minecraft

 

discord: @mlgnotcool

中序infix 和 後序postfix

(是什麼可以吃嗎?)

中序 infix：

我們平常表示四則運算的方式

例如：(1+1*2)*2 = 6

後序 postfix：

電腦比較好算的方法

例如：112*+2* = 6

 

(不會有括號和先乘除的問題)

後序 怎麼算：

一直把數字加到一個stack內，如果遇到運算元時，

就把stack上的兩個數字取出來，算完之後再放回stack

舉例來說：

目前後序到哪 stack (前面進出) 說明
112*+2* 原式
12*+2* 1 1 -> 把1放進stack
2*+2* 11 1 -> 把1放進stack
*+2*   211 2 -> 把2放進stack
+2*  21 * -> 把2和1相乘
2*  3 + -> 把2和1相加
*   32 2 -> 把2放進stack
答案： 6 * -> 把3和2相乘

計算後序的題目

給大家時間寫寫看 (應該不會太難)

 

(答案在下一頁)

#include <bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;

string str; stack<int> nums;
signed main(){
    ios::sync_with_stdio(0); cin.tie(0);

    while (cin >> str){
        if (str == "+"){
            int x = nums.top(); nums.pop(); int y = nums.top(); nums.pop();
            nums.push(x + y);
        }else if (str == "-"){
            int x = nums.top(); nums.pop(); int y = nums.top(); nums.pop();
            nums.push(y - x);
        }else if (str == "*"){
            int x = nums.top(); nums.pop(); int y = nums.top(); nums.pop();
            nums.push(x * y);
        }else if (str == "/"){
            int x = nums.top(); nums.pop(); int y = nums.top(); nums.pop();
            nums.push(y / x);
        }else{
            nums.push(stoi(str));
        }
    }

    cout << nums.top() << endl;
}

排程場演算法

shunting yard algorithm

我們現在有一個中序表達式，

然後要我們轉成後序表達式：

 

排程場演算法!

這個演算法要做的事：

 

先準備一個stack來處存運算元，

並且做一個較order()的函式，來回傳這個運算元的等第

int order(char c) {
    if (c == '/' || c == '*') return 2;
    else if (c == '+' || c == '-') return 1;
    else return -1;
}

跑過中序的每個數字和運算元

1. 如果遇到數字，就直接輸出

2. 如果遇到 '('，就直接放到stack裡

3. 如果遇到 +-*/：

若stack最上方的運算元的等第>目前運算元的等第，就輸出和pop掉。

重複直到stack是空的 或 stack最上方的運算元的等第<=目前運算元的等第

 

4.如果遇到 ')'，就從stack輸出和pop最上方的運算元，直到遇到'('為止

5.最後跑完之後，把stack剩下的東西都輸出

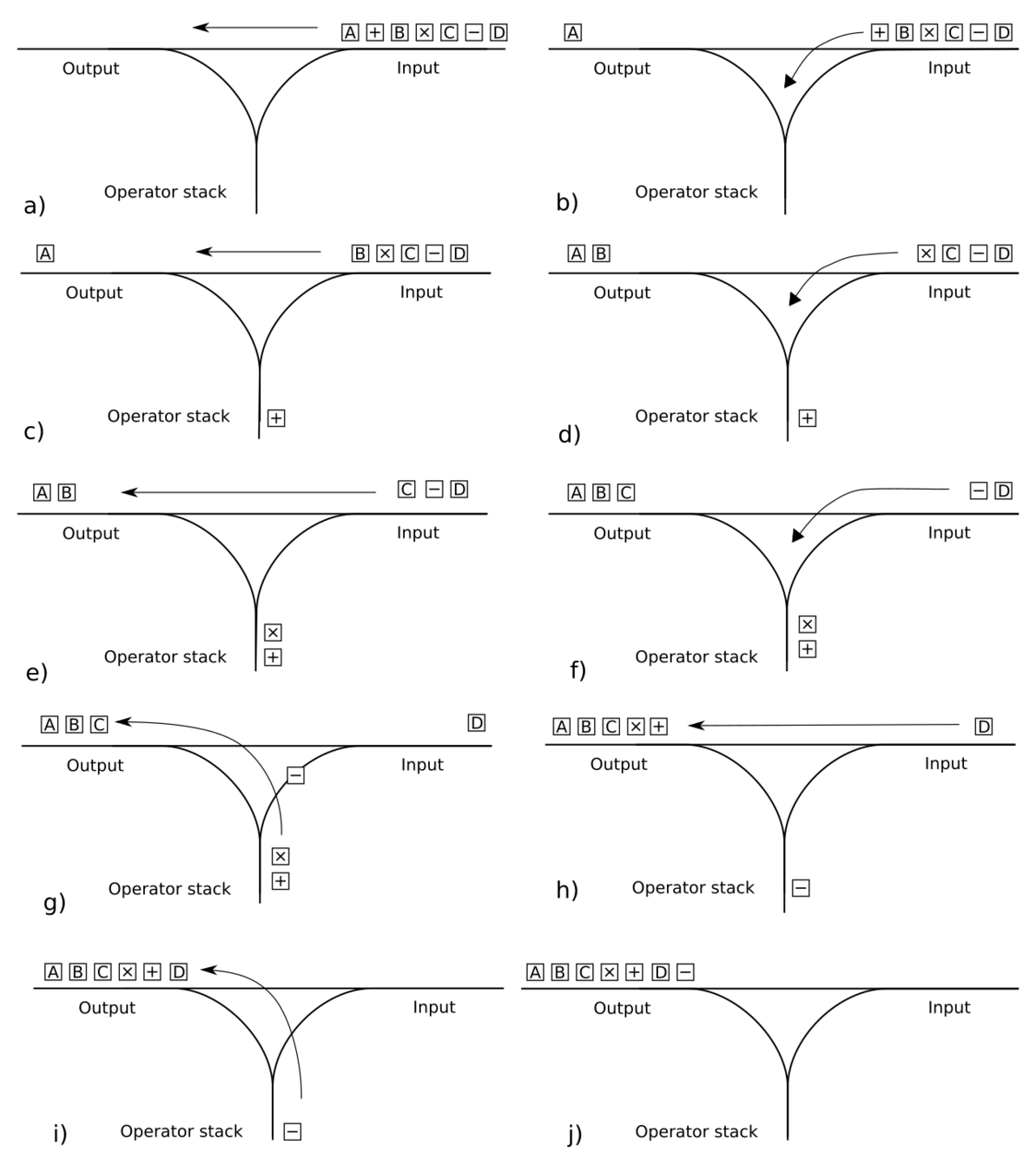
把它想像成這樣，數字直接過去，運算元要到下面的stack去

目前中序到哪 stack (前面進出) 目前輸出的
(1+1*2)*2
1+1*2)*2 (
+1*2)*2 ( 1
1*2)*2  (+ 1
*2)*2 (+ 11
2)*2 (+* 11
)*2 (+* 112
*2 112*+
2 * 112*+
* 112*+2
112*+2*

舉例來說：

為什麼會有用 (概略的解釋)：

1.因為後序是先有兩個數字，再有運算元，

因此我們遇到運算元時先放stack之後處理。

 

2. 因為中序有先乘除後加減的問題，所以遇到新的運算元時，如果目前stack上有一個等第比較大的，那就要先處理。

 

3. 如果遇到()，就會先處理()裡面的東西，因此遇到 ) 時就要一路輸出直到遇到 (

題目

 

把infix轉成postfix

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
using namespace std;

stack<char> oper; string str;
int order(char c) {
    if (c == '/' || c == '*') return 2;
    else if (c == '+' || c == '-') return 1;
    else return -1;
}
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    while (getline(cin, str)){
        for (int i=0; i<=str.size()-1; ++i){
            if (str[i] == ' ') continue;

            if (str[i] == '('){
                oper.push(str[i]);
            }else if (str[i] == '+' || str[i] == '-' || str[i] == '*' || str[i] == '/'){
                while (!oper.empty() && order(str[i]) <= order(oper.top())){
                    cout << oper.top() << " ";
                    oper.pop();
                }
                oper.push(str[i]);
            }else if (str[i] == ')'){
                while (oper.top() != '('){
                    cout << oper.top() << " ";
                    oper.pop();
                }
                oper.pop();
            }else{
                cout << str[i] << " ";
            }
        }

        while (!oper.empty()){
            cout << oper.top() << " ";
            oper.pop();
        }
        cout << endl;

    }
}

如果還是聽不懂的：

解釋影片

更多題目：

ZeroJudge a017. 五則運算

約瑟夫問題

Josephus Problem

假設我們現在有n個人排成一圈，從1開始數，

每數k個人(包含開始的那位)，

那個人就必須離開圈圈，

那我們如何求出最後一位剩下的人呢？

舉例來說，n=5, k=2：

原本的人：1 2 3 4 5

出去的順序為：2 4 1 5 3

最後一位剩下的人就會是 3

直接用陣列模擬？

O(nk)

💥💥💥TLE💥💥💥

直接用陣列模擬？

如果我們只有要找出最後一位的話

就會有更快的解法

O(n)

*如果要找順序的話，就只能用比較慢的解法

我們會用到的方式是

在k固定的情況下，把1~n個人的最後一位

計算出來，並使用前一項來計算下一項

 

(就是遞迴或dp啦)

1. 先把全部數字用 0~n-1 表示，這樣比較好算，最後答案再+1就好

2. 先把遞迴的終止條件寫出來：

n=1時 -> 答案回傳 0

3. 想我們的轉移式：

第n項 = 先把第一個人去除掉後，再加前一項f(n-1)的解果

因為我們在去除掉第一位後，可以想像成f(n-1)的每個人都往後移k位，最後再%n防止超出界線

 

最後得到遞迴式：

f(n) = (f(n-1)+k) \% n
int josephus(int n){
    if (n == 1) return 1;
    
    return (josephus(n-1) + k) % n;
}

遞迴式

dp[1] = 0;
for (int i=2; i<=n; ++i){
    dp[i] = (dp[i-1]+k)%n;
}

dp式

空間 O(1)

*記得答案最後要加1

int s = 0;
for (int i=2; i<=n; ++i){
    s = (s+k)%n;
}

題目一：

直接模擬             

CSES - Josephus Problem I

O(nk)
#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
using namespace std;

int n, curidx, p[maxn];
int main(){
    ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    cin >> n;

    for (int i=1; i<=n; ++i){
        curidx = (curidx+1) % n;
        while (p[curidx] == 1) curidx = (curidx+1) % n;

        if (i==n) cout << curidx+1 << endl;
        else cout << curidx+1 << " ";


        p[curidx] = 1;
        while (p[curidx] == 1 && i!=n) curidx = (curidx+1) % n;
    }
}

題目2：

APCS 2016 10月-3

要用到                 解，否則會TLE

O(n)
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int n, m, k;

int josephus(int n){
    if (n == 1 || k == 0) return 0;

    --k;
    return (josephus(n-1)+m)%n;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> m >> k;

    cout << josephus(n)+1 << endl;
}

還是聽不太懂的：

解釋

約瑟夫問題 進階版

more Josephus Problem

 

(或許講不到，有興趣自己回家讀)

小補充：

k=2時，有分析數據得到解果的很快方法

和Numberphile的影片

 

前面講的有更快的解法，找最後一位有 O(log n) 解

找順序有 O(n logn) 解

 

(只是我前面說的APCS應該就夠用了)

有興趣可以自己學學 :)

進階題：

CSES - Josephus Problem II

CSES - Josephus Queries

CSES - Josephus Problem II

要用到找順序的 O(n logn) 解

 

照理來說，如果用vector來存，並且用erase()

來移除要離開的那項的話，就會花到 O(n^2) 時間

 

但是我們可以用一個東西叫做 ordered set

他和set差不多，erase會是O(log n)，

只是他有順序，可以找set裡的第幾項

#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
#define ordered_set tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update>

宣告：

#include <bits/stdc++.h>
#define endl '\n'
#define maxn 200005
using namespace std;

//ordered set
#include <ext/pb_ds/assoc_container.hpp>
using namespace __gnu_pbds;
#define ordered_set tree<int, null_type, less<int>, rb_tree_tag, tree_order_statistics_node_update>

int n, k, cur; ordered_set s;
int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> n >> k;
    for (int i=1; i<=n; ++i) s.insert(i);

    for (int i=1; i<=n; ++i){
        cur = (cur + k) % s.size();

        auto it = s.find_by_order(cur);
        if (i==n) cout << *it << endl;
        else cout << *it << " ";

        s.erase(it);
    }
}

CSES - Josephus Queries

因為題目的k=2，會有一個很快的解法

我們的方法是將圈圈每次都減半，將每個人重新編號，最後有答案時再轉回原本的編號，用遞迴去做

解釋影片

O(log\ n)

最後每次的時間就會是：

遞迴的終止條件：

int josephus(int n, int k){
    if (n==1) return 1;
    if (k<=(n+1)/2){
        if (2*k>n) return (2*k)%n;
        else return 2*k;
    }
}

若剩下一個人，當然最後一個人就會是1

如果 k<=(n+1)/2 (考慮奇偶數)

 

那答案就會是2*k (可以自己列列看)

(也要考慮超出n的情況)

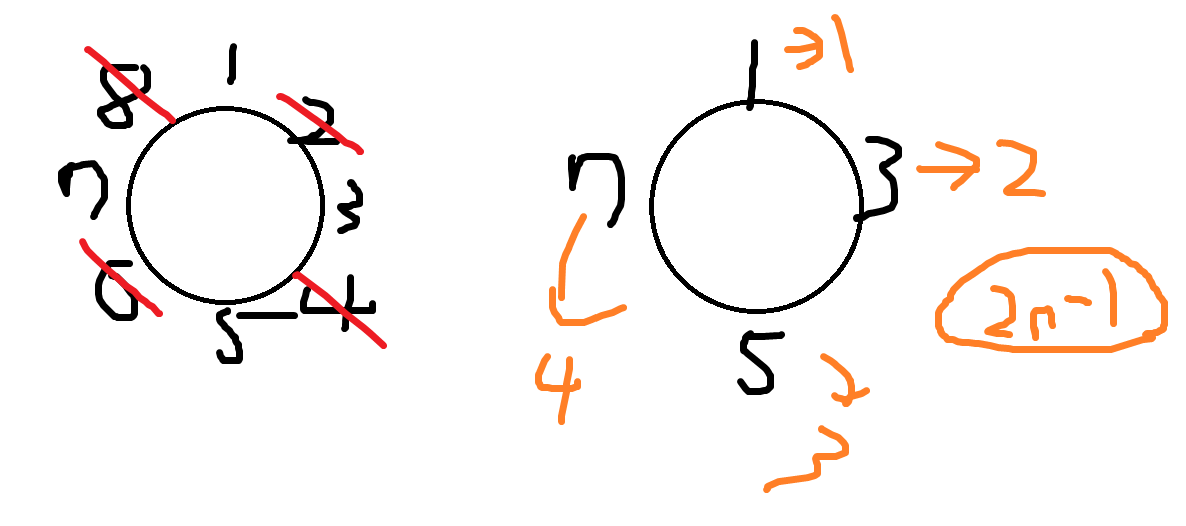
考慮n為偶數的情況，在刪掉一半和重新編號之後，轉回原本的編號只要2n-1就好了

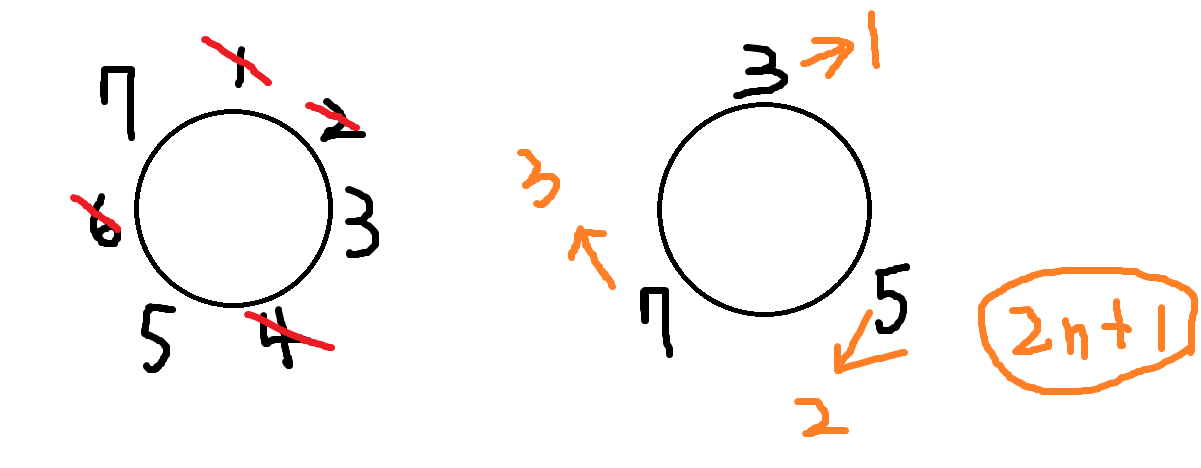
考慮n為奇數的情況，在刪掉一半和重新編號之後，轉回原本的編號只要2n+1就好了

最後的程式：

#include <bits/stdc++.h>
#define endl '\n'
using namespace std;

int q, n, k;

int josephus(int n, int k){
    if (n==1) return 1;
    if (k<=(n+1)/2){
        if (2*k>n) return (2*k)%n;
        else return 2*k;
    }

    int tmp = josephus(n/2, k-(n+1)/2);
    if (n%2==1) return 2*tmp+1;
    else return 2*tmp-1;
}

int main(){
    ios::sync_with_stdio(0); cin.tie(0);

    cin >> q;
    for (int i=1; i<=q; ++i){
        cin >> n >> k;
        cout << josephus(n, k) << endl;
    }
}

shunting yard + josephus problem

By MLGnotCOOL

Made with Slides.com

shunting yard + josephus problem

  • 88

More from MLGnotCOOL