SBAT
Classification
en modèles d'affaire
Mathieu Bernard
Le questionnaire
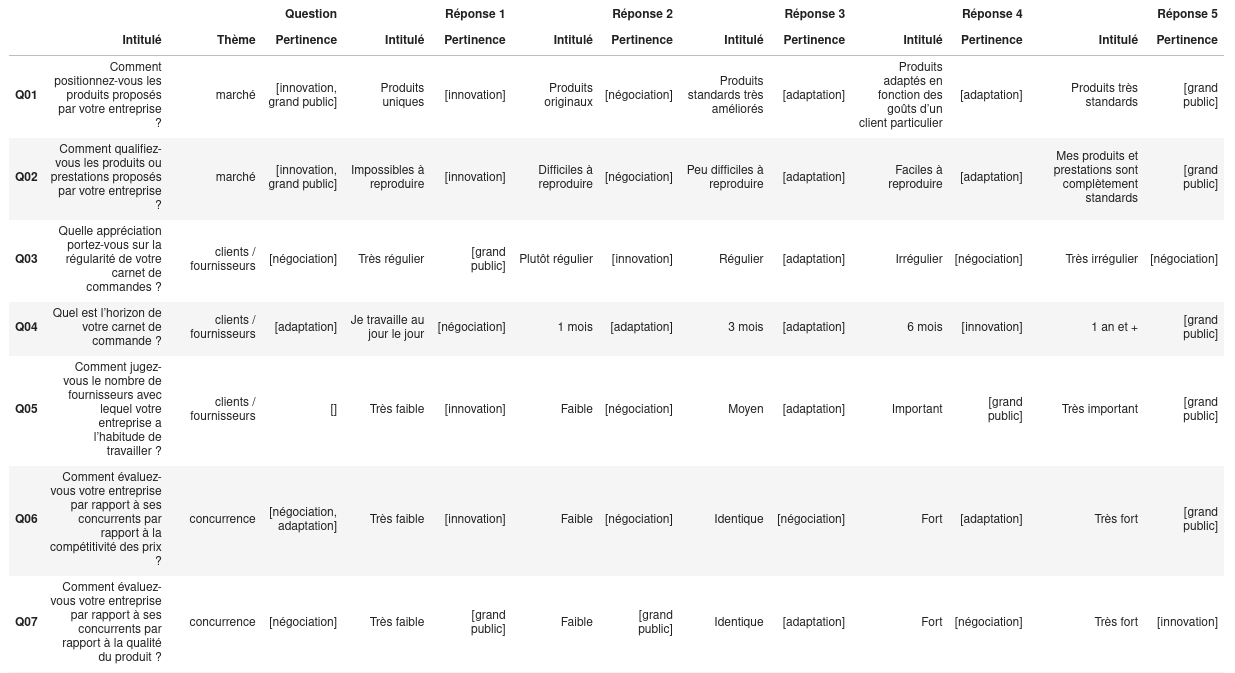

Le questionnaire
- 17 questions
- 5 réponses possibles (ou 3)
- échelle de Likert
- 4 thèmes
- marché
- clients / fournisseurs
- concurrence
- positionnement

Le questionnaire
- 17 questions
- 5 réponses possibles (ou 3)
- échelle de Likert
- 4 thèmes
- 4 modèles d'affaire
- GAIN
- pertinence par question
- pertinence par réponse
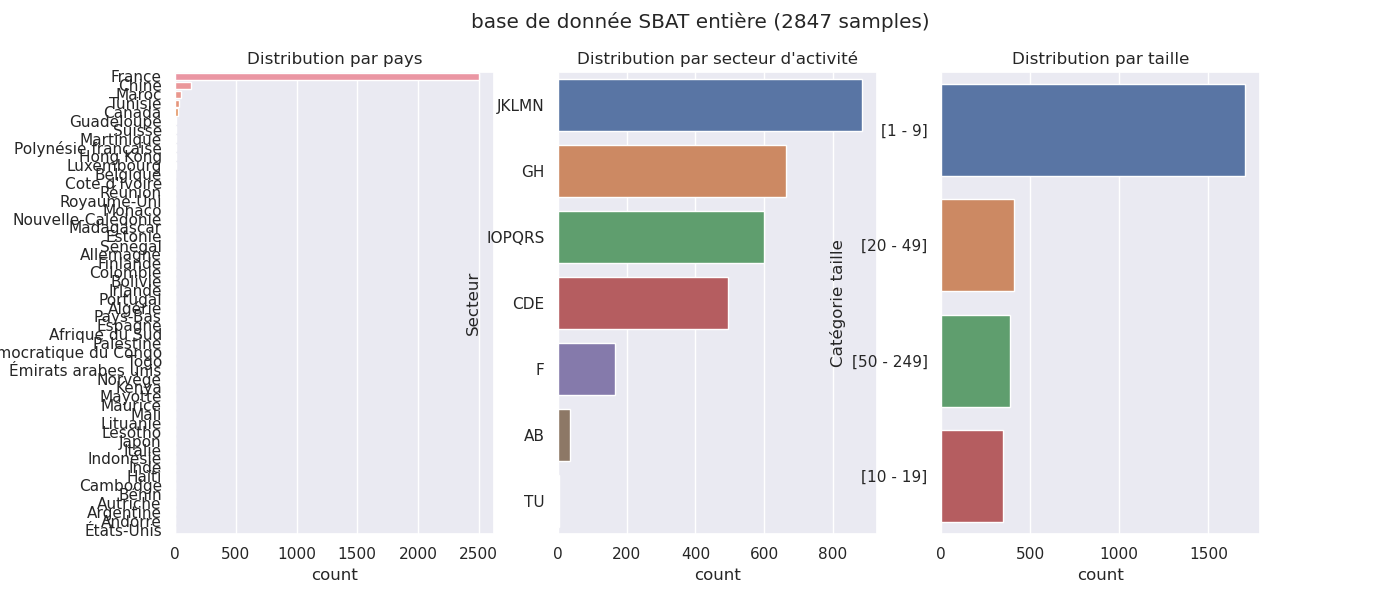
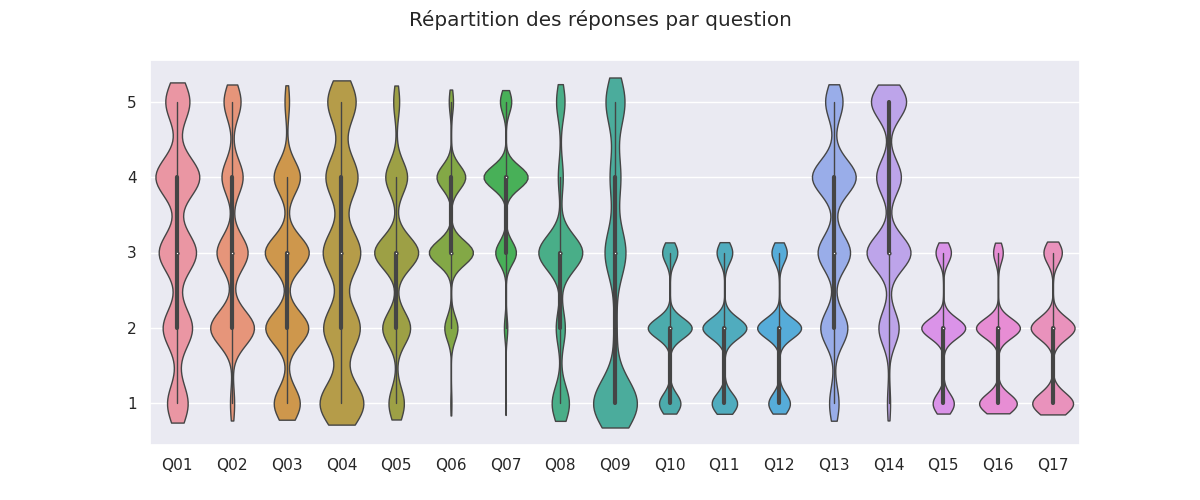
Le dataset
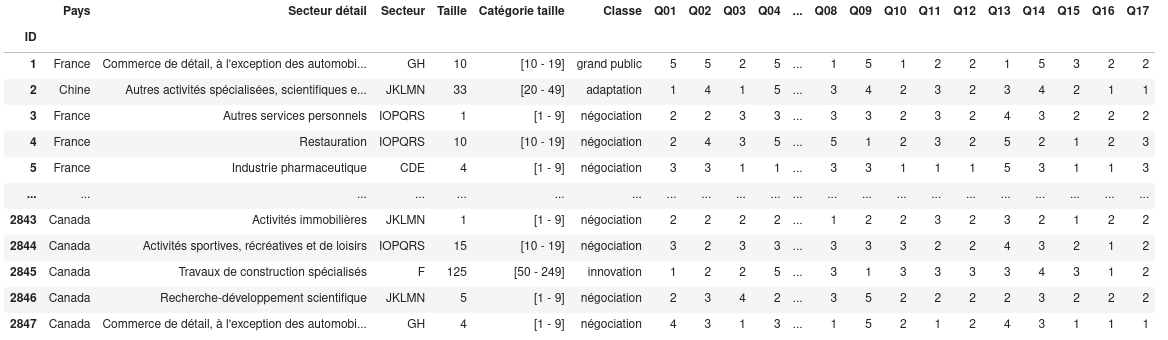
?
Dans la suite :
- restreint à la France
- sans secteurs AB et TU
Le dataset

?

Le modèle
Dataset : Réponse de l'entreprise i à la question j est k
$$D = (d_{ijk}) \in \{0, 1\}^{n \times 17 \times 5}$$
Poids : Le poids associé à la question i, à la réponse j et au modèle k
$$W = (w_{ijk}) \in \mathbb{R}_+^{17 \times 5 \times 4} $$
Avantage : Le poids assococié à la question i et au modèle j
$$A = (a_{ij}) \in \mathbb{R}_+^{17 \times 4}$$
Classification : probabilité que l'entreprise i soit du modèle j
$$C = (c_{ij}) \in [0, 1]^{n \times 4}\textrm{, avec }\sum_j c_{ij} = 1, \forall i\in [1, n]$$
$$c_{ij} = \frac{\tilde{c}_{ij}}{\sum_j \tilde{c}_{ij}}, \textrm{avec } \tilde{c}_{ij} = \sum_{k_1=1}^{17} \sum_{k_2=1}^5 a_{k_1j}w_{k_1k_2j}d_{ik_1k_2}$$
Le modèle
- trouver les poids W qui minimisent l'ambiguité de classification
- sous contrainte de poids équilibrés entre modèles d'affaire
$$\tilde{w}_{ijk} = \textrm{argmin}_{w\in W} \alpha f(w) + (1-\alpha) g(w)$$
- minimiser ambiguité de classification = maximiser l'écart-type moyen de c
$$ f(w) = -\mu(\sigma(c_{i})), \forall i\in[1, n] $$
- équilibre des poids entre modèles d'affaire = minimiser l'écart-type sur w
$$ g(w) = \sigma(\sum_i \sum_j w_{ijk}) $$
- algorithme de Nelder-Mead (downhill simplex method)
- α = 0.25, recherche dans [0, 2]
- Avantage A constant à 1 (ignoré)
Résultats
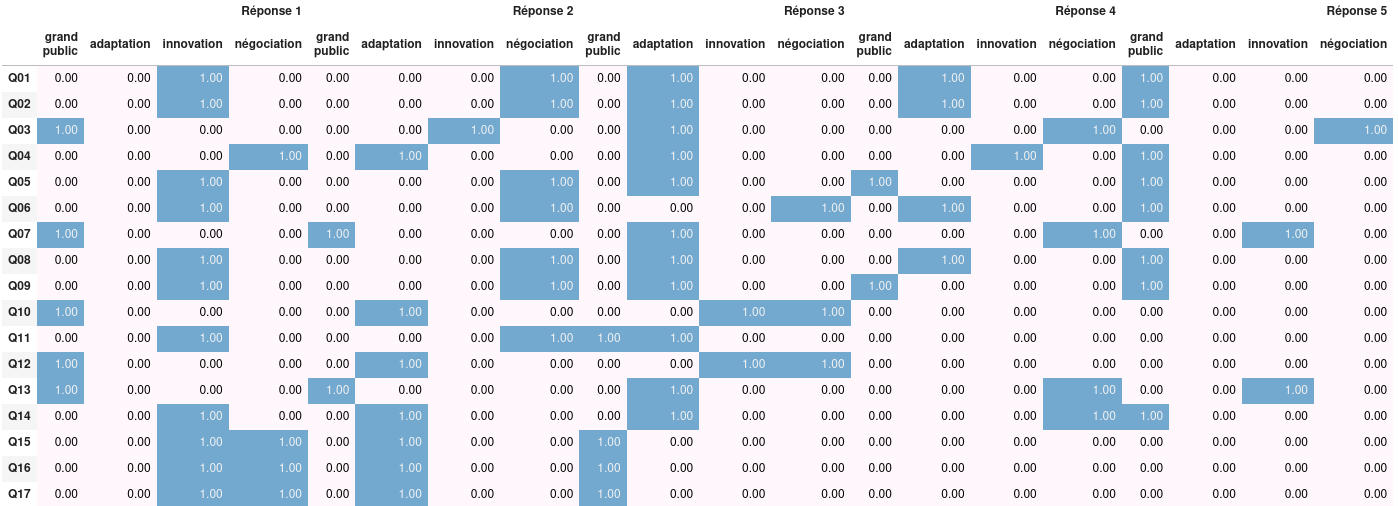
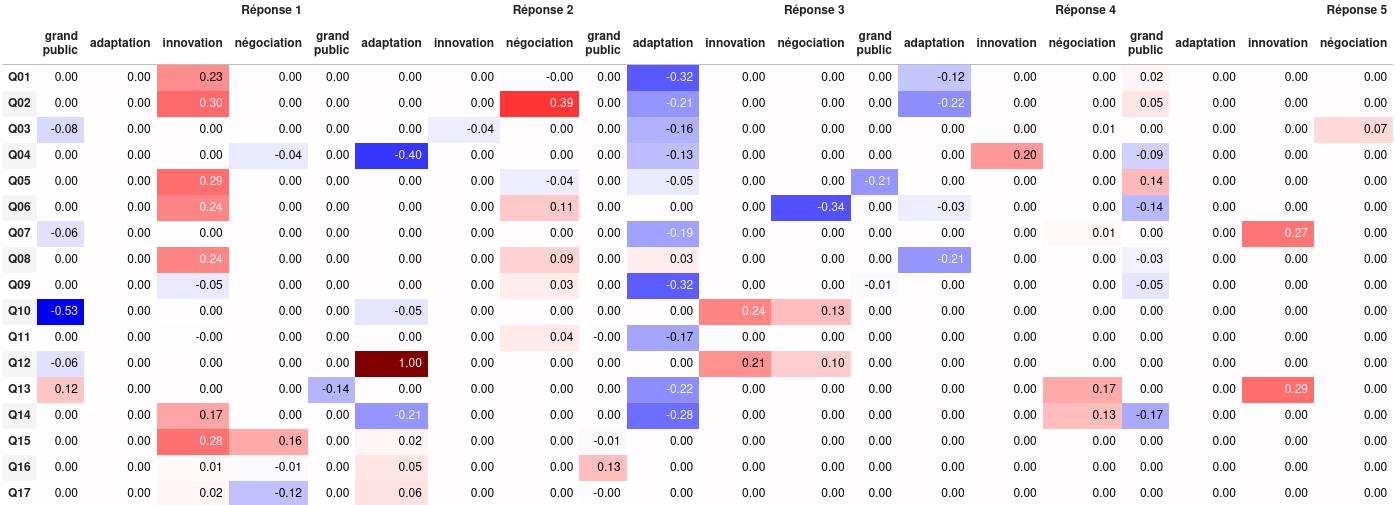
Résultats
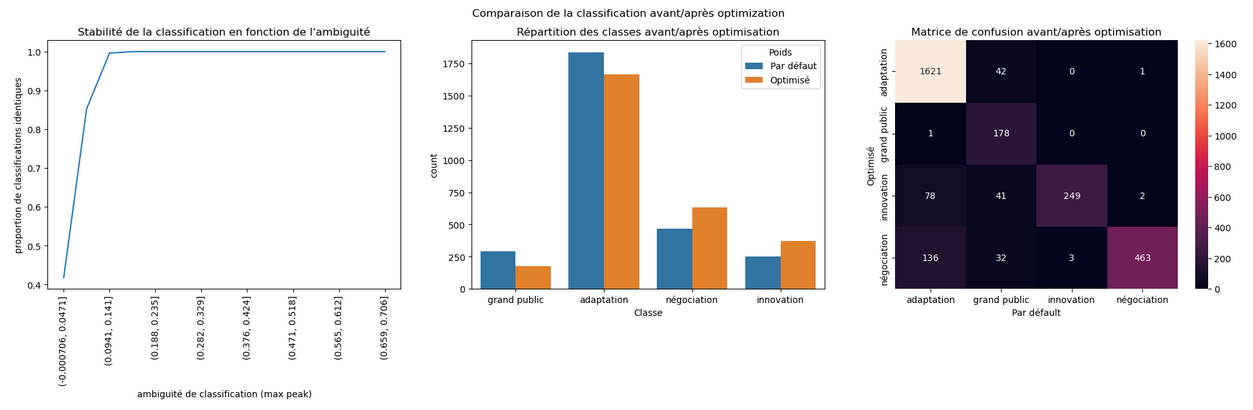
comparaison avant/après optimisation
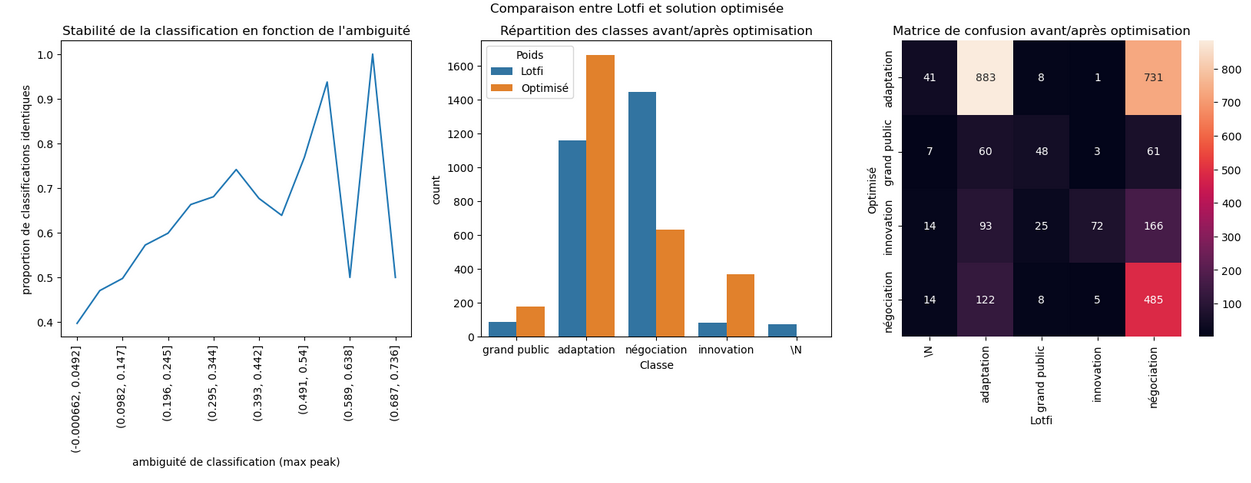
comparaison Lotfi / optimisé
deck
By mmmaat
deck
- 13



