Algorithmic Complexity Analysis

Algorithmic Complexity
Algorithmic Complexity - What is it?
- An effective way for us measure how an algorithm is affected by the size of our problem.
- We measure this both by time (time complexity) and by memory usage (space complexity)

Algorithmic Complexity
Algorithmic Complexity - Why is it important?
- Allows us to measure an Algorithms efficiency to determine its scalability.
- Most problems can be easily solved with basic approaches that result in poor time & space complexity. The real challenge is often not to find just any solution, but an efficient solution with optimal algorithmic complexity.

Algorithmic Complexity
Real World Example
- Suppose we wanted to find the largest difference between any two numbers in a set of numbers.
- We can solve this with an algorithm.
- An algorithm is defined as the system or set of steps we take in order to arrive at a solution.

Algorithmic Complexity
Real World Example
- There are different approaches (algorithms) we can take to solve a problem like this.
- Generally speaking we can expect that the bigger the data set were working with, in this case an array of numbers, the longer it will take to solve the problem.

Algorithmic Complexity
Real World Example: First Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| 2 | ||||||
| 3 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 9 |
- Compare each number against every other number
Difference

Algorithmic Complexity
Real World Example: First Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| 2 | 0 | |||||
| 3 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 9 |
- Compare each number against every other number
Difference

Algorithmic Complexity
Real World Example: First Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| 2 | 0 | 1 | ||||
| 3 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 9 |
- Compare each number against every other number
Difference

Algorithmic Complexity
Real World Example: First Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| 2 | 0 | 1 | 3 | |||
| 3 | ||||||
| 5 | ||||||
| 6 | ||||||
| 7 | ||||||
| 9 |
- Compare each number against every other number
Difference

Algorithmic Complexity
Real World Example: First Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| 2 | 0 | 1 | 3 | 4 | 5 | 7 |
| 3 | 1 | 0 | 2 | 3 | 4 | 6 |
| 5 | 3 | 2 | 0 | 1 | 2 | 4 |
| 6 | 4 | 3 | 1 | 0 | 1 | 3 |
| 7 | 5 | 4 | 2 | 1 | 0 | 2 |
| 9 | 7 | 6 | 4 | 3 | 2 | 0 |
- How many operations did we perform?
Difference

Algorithmic Complexity
Real World Example: First Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| 2 | 0 | 1 | 3 | 4 | 5 | 7 |
| 3 | 1 | 0 | 2 | 3 | 4 | 6 |
| 5 | 3 | 2 | 0 | 1 | 2 | 4 |
| 6 | 4 | 3 | 1 | 0 | 1 | 3 |
| 7 | 5 | 4 | 2 | 1 | 0 | 2 |
| 9 | 7 | 6 | 4 | 3 | 2 | 0 |
- How many operations did we perform?
- n = input size
- n = 6
- total operations is:
- n * n = n2 or 62 = 36 operations
|______________________|
n
n

Algorithmic Complexity
Real World Example: First Approach
- How does this scale?
- n = 2: 22 = 4 operations
- n = 5: 52 = 25 operations
- n = 10: 102 = 100 operations
- n = 200: 2002 = 40,000 operations

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | ||||||
| Largest? |
- Find largest and smallest numbers and compare.

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | Y | |||||
| Largest? |
- Find largest and smallest numbers and compare.

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | Y | |||||
| Largest? | Y |
- Find largest and smallest numbers and compare.

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | Y | N | ||||
| Largest? | Y |
- Find largest and smallest numbers and compare.

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | Y | N | ||||
| Largest? | Y | Y |
- Find largest and smallest numbers and compare.

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | Y | N | N | N | N | N |
| Largest? | Y | Y | Y | Y | Y | Y |
- How many operations did we perform?

Algorithmic Complexity
Real World Example: Second Approach
| 2 | 3 | 5 | 6 | 7 | 9 | |
|---|---|---|---|---|---|---|
| Smallest? | Y | N | N | N | N | N |
| Largest? | Y | Y | Y | Y | Y | Y |
- How many operations did we perform?
- n = input size
- n = 6
- total operations is:
- 2 * n = 2n or 2(6) = 12 operations
|______________________|
n
2

Algorithmic Complexity
Real World Example: Second Approach
- How does this scale?
- n = 2: 2(2) = 4 operations
- n = 5: 2(5) = 10 operations
- n = 10: 2(10) = 20 operations
- n = 200: 2(200) = 400 operations

Algorithmic Complexity
Real World Example: Third Approach
| 2 | 3 | 5 | 6 | 7 | 9 |
|---|
- What if we knew the list was already sorted?
- How many operations would this take to complete?

Algorithmic Complexity
Real World Example: Third Approach
| 2 | 3 | 5 | 6 | 7 | 9 |
|---|
- What if we knew the list was already sorted?
- How many operations would this take to complete?
- Step 1): Grab the first number
- Step 2): Grab the last number
- Step 3): Compare the difference between the first and last number
- Three Operations total

Algorithmic Complexity
Real World Example: Third Approach
- How does this scale?
- n = 2: 3(1) + 0(2)= 3 operations
- n = 5: 3(1) + 0(5) = 3 operations
- n = 10: 3(1) + 0(10) = 3 operations
- n = 200: 3(1) + 0(200) = 3 operations

Algorithmic Complexity
Real World Example: Summary
- We've discussed three approaches so far:
| Operations for n items | Approach |
|---|---|
| n2 | Compare all numbers and check for difference |
| n | Find largest and smallest numbers then calculate difference |
| 3 | Compare first and last numbers and calculate difference |

Algorithmic Complexity
Real World Example: Summary
So why isn't this 2(n)???
| Operations for n items | Approach |
|---|---|
| n2 | Compare all numbers and check for difference |
| n | Find largest and smallest numbers then calculate difference |
| 3 | Compare first and last numbers and calculate difference |

Algorithmic Complexity
Big O Notation
- Big O Notation gives an approximation of Algorithmic Complexity not an exact measurement.
- Uses general complexity types. Not exact equations.
General Complexity Types:
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<______________________________________________________>
Very Good
Very Bad

Algorithmic Complexity
Big O Notation
- Ignore Leading Coefficients:
- O(3n) would be interpreted as O(n)
- For small n the coefficient has a larger impact
- For big n the coefficient has a very small (negligible) impact
General Complexity Types:
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<______________________________________________________>
Grows Slowly
Grows Quickly

Algorithmic Complexity
Big O Notation
- Complexity is determined by analyzing the highest order function
- For this purpose we will define the highest order function as the function that grows the fastest
- Example: O(n2) + O(n) function or O(n + n2). We would interpret this as O(n2) complexity
General Complexity Types:
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<______________________________________________________>
Grows Slowly
Grows Quickly

Algorithmic Complexity
Big O Notation
- Big O Notation allows us to think about the "big picture"
- How will our function behave at small n?
- How will our function behave at big n?
General Complexity Types:
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<______________________________________________________>
Grows Slowly
Grows Quickly

Algorithmic Complexity
Big O Notation - Constant
| Name | Constant | ||||
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<___________________________________________________________________>
- Execution time is always "constant" regardless to any changes in our size n
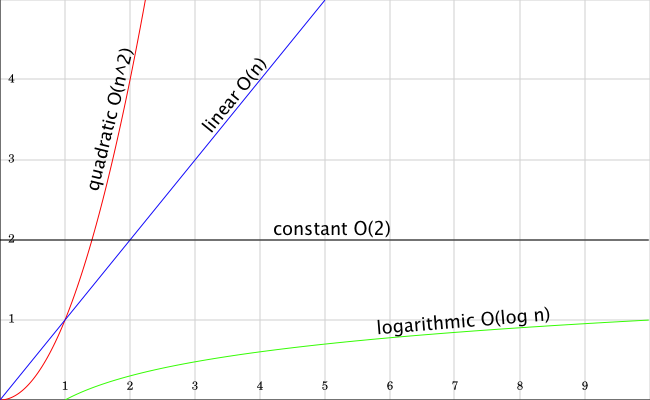
T
I
M
E
n

Algorithmic Complexity
Big O Notation - Logarithmic
| Name | Constant | Logarithmic | |||
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<___________________________________________________________________>
- Execution time increases but at a decreasing rate

T
I
M
E
n

Algorithmic Complexity
Big O Notation - Linear
| Name | Constant | Logarithmic | Linear | ||
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<___________________________________________________________________>
- As n grows so does the execution time at an equal rate

T
I
M
E
n

Algorithmic Complexity
Big O Notation - Quadriatic
| Name | Constant | Logarithmic | Linear | Quadriatic | |
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<___________________________________________________________________>
- Execution time increases at an increasing rate

T
I
M
E
n

Algorithmic Complexity
Big O Notation - Exponential
| Name | Constant | Logarithmic | Linear | Quadriatic | Exponential |
| Big O | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<____________________________________________________________________>
- Execution time increases exponentially as n grows larger
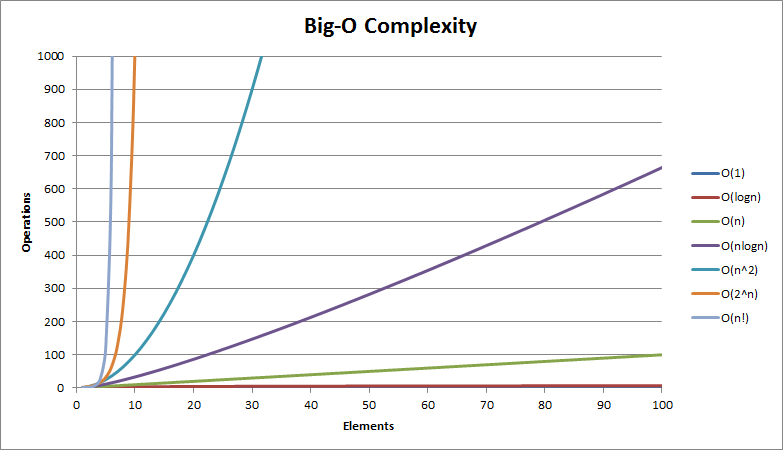
T
I
M
E
n

Algorithmic Complexity
Big O Notation - Wrapup
- Big O Notation gives an approximation of Algorithmic Complexity not an exact measurement.
- Uses general complexity types. Not exact equations.
- We've been talking primarily about time complexity, we can also measure things in space complexity.
- Space complexity follows the same rules as time complexity
- Functions will often have different space and time complexities
General Complexity Types:
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<______________________________________________________>
Grows Slowly
Grows Quickly

Algorithmic Complexity
Big O Notation - Wrapup
| Notation | O(1) | O(log n) | O(n) | O(n2) | O(cn) |
<______________________________________________________>
Grows Slowly
Grows Quickly

Algorithmic Complexity
Practice with this quiz:
http://www.codequizzes.com/computer-science/big-o-algorithms
Algorithmic Complexity Analysis
By moringaschool
Algorithmic Complexity Analysis
- 1,008



