二分搜 & 分治
一個普通ㄉ小遊戲(?
如果今天我在心裡想一個介在1~20的數字
你要猜我在想哪個數字
我會告訴你有沒有猜對
你會怎麼做
每一個都猜一遍(?
對其實就是這樣w
換一種規則
如果今天我在心裡想一個介在1~20的數字
你要猜我在想哪個數字
我會告訴你你猜的數字有沒有比我想的數字大,或是你猜對了
你會怎麼做
每一個都猜一遍?
太慢ㄌ
每次都猜中間
how?
每次都猜中間,如果我說你猜得比答案大,就把目前的左界往右移,反之則把右界往左移
看不懂沒關係
上圖
回到一開始ㄉ例子
答案是6,目前範圍1~10 中間是5
2
3
4
5
10
7
9
8
6
1
答案是6,目前範圍6~10 中間是8
2
3
4
5
10
7
9
8
6
1
答案是6,目前範圍6~7 中間是6
2
3
4
5
10
7
9
8
6
1
好耶猜到ㄌ
複雜度?
每次把一半的砍掉,複雜度\(O(log n)\)
STL裡的二分搜
lower_bound(iterator first, iterator last, k) : 回傳指向第一個鍵值大於等於 k 的迭代器。
upper_bound(iterator first, iterator last, k) :
回傳指向第一個鍵值大於 k 的迭代器。
#include <bits/stdc++.h>
using namespace std;
int main() {
vector <int> vec = {1, 3, 4, 1, 1};
sort(vec.begin(), vec.end());
sort(vec.begin(), vec.end());
auto it = lower_bound(vec.begin(), vec.end(), 1);
cout << *it << ' ' << it - vec.begin() << '\n';
it = upper_bound(vec.begin(), vec.end(), 1);
cout << *it << ' ' << it - vec.begin() << '\n';
}
/*
output:
1 0
3 3
*/陣列也可以用喔
#include <bits/stdc++.h>
using namespace std;
int main() {
int arr[15] = {1, 3, 4, 1, 1};
sort(arr, arr + 5);
auto it = lower_bound(arr, arr + 5, 1);
cout << *it << ' ' << it - arr << '\n';
it = upper_bound(arr, arr + 5, 1);
cout << *it << ' ' << it - arr << '\n';
}
/*
output:
1 0
3 3
*/set 跟 map ㄉ二分搜
s.lower_bound(k):
回傳指向第一個鍵值大於等於 k 的迭代器。
s.upper_bound(k):
回傳指向第一個鍵值大於 k 的迭代器。
#include <bits/stdc++.h>
using namespace std;
int main(){
set <int> S;
S.insert(1);
S.insert(3);
S.insert(4);
auto it = S.lower_bound(1);
cout << *it << ' ';
it = S.upper_bound(1);
cout << *it;
}
/*
output:1 3
*/#include <bits/stdc++.h>
using namespace std;
int main(){
map <int, int> mp;
mp.insert({1, 2});
mp.insert({3, 2});
mp.insert({4, 2});
auto it = mp.lower_bound(1);
cout << it->first << ' ' << it->second << '\n';
it = mp.upper_bound(1);
cout << it->first << ' ' << it->second << '\n';
}
/*
output:
1 2
3 2
*/set
map
實作
一個跟剛剛差不多的例子
我在⼼中想了⼀個介於 1 到 1000 的整數,你有辦法猜到這個數字是多少嗎?
每當你猜了⼀個數字,我可以告訴你猜的過低、過⾼或正確。但你最多只能猜 10 次。
• “lower” 如果我想的數字⽐你猜的數字⼩
• “higher” 如果我想的數字⽐你猜的數字⼤
• “correct” 如果你猜到了
自己寫寫看ㄅ
btw這是偷NPSC模擬賽的題目 沒有judge
code
#include <bits/stdc++.h>
using namespace std;
int main(){
int l = 1, r = 1000;
while(l <= r){
int mid = (l + r) / 2;
cout << mid << endl;
string str;
cin >> str;
if(str == "lower"){
r = mid - 1;
}
else if(str == "higher"){
l = mid + 1;
}
else break;
}
return 0;
}給一個有\(n\)項的序列\(A\)
\(k\)次詢問一個\(x\)在不在這個序列
若有就輸出序列\(A\)的第幾項為\(x\) 沒有則輸出\(-1\)
\(n \le 10^5\)
\(k \le 10^5\)
互動題
電腦會隨機生成一個\(1\)~\(N\)間的整數\(K\)
每次可以問一個數\(Q\)
電腦會告訴你\(Q\)「小於」\(K\)或「不小於」\(K\)
\(N \le 2 \times 10^5\)
對答案二分搜
什麼是對答案二分搜
by yungyaorz
給 \(N\) 個電信公司需要服務的據點的座標 \(x_i\)
並且最多可以架設 \(K\) 個基地台在任一座標位置
每個基地台服務的半徑範圍皆一樣
求半徑至少為多少可以覆蓋所有據點?
\(1 \le K<N \le 50000, \ 0 \le x_i \le 10^9\)
有點難?
換個問題
換一個問題
給 \(N\) 個電信公司需要服務的據點的座標 \(x_i\)
並且最多可以架設 \(K\) 個基地台在任一座標位置
每個基地台服務的半徑範圍皆一樣
給定一個半徑,問你能不能覆蓋到全部的基地台
how
每次都把半徑的最左邊卡在目前最左邊的基地台,被半徑覆蓋住的就忽略它,做到沒有基地台為止
換一個問題ㄉcode
每次都把半徑的最左邊卡在目前最左邊的基地台,被半徑覆蓋住的就忽略它,做到沒有基地台為止
bool is_legal(int r){
int cover = 0;
int stand = 0;
for(int i=0; i<n; i++){
if(arr[i] > cover){
cover = arr[i] + r;
stand++;
}
}
if(stand > k) return false;
else return true;
}回到剛剛ㄉ問題
給 \(N\) 個電信公司需要服務的據點的座標 \(x_i\)
並且最多可以架設 \(K\) 個基地台在任一座標位置
每個基地台服務的半徑範圍皆一樣
求半徑至少為多少可以覆蓋所有據點?
\(1 \le K<N \le 50000, \ 0 \le x_i \le 10^9\)
如果目前的半徑可以覆蓋所有據點
那麼比這個半徑大的都可以覆蓋所有據點
所以我們就可以對半徑二分搜!
如果目前檢查的半徑可以的話就把左界往右
不行的話就把右界往左移
題目
分治
什麼是分治
- 分而治之
- 把問題分成幾個部分再解決
Merge Sort
每次都把數列拆成左右兩半
再合併
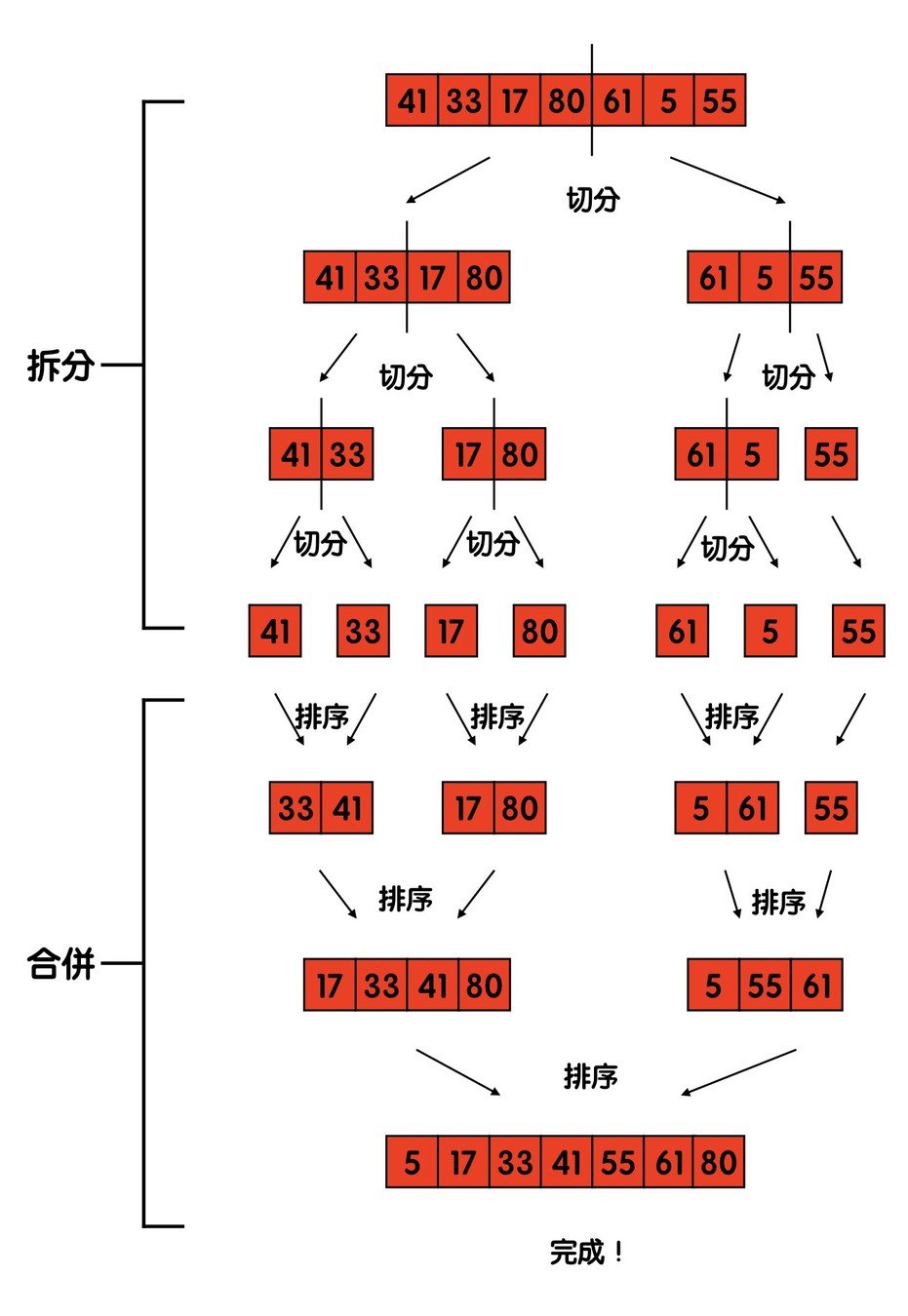
Merge Sort
int arr[N], buf[N];
void MergeSort(int l, int r){ // [l, r]
if(l > r) return;
int m = (l + r) / 2;
MergeSort(l, m), MergeSort(m+1, r);
int i = l, j = m+1, k = l;
while(i <= m && j <= r){
if(arr[i] < arr[j]) buf[k++] = arr[i++];
else buf[k++] = arr[j++];
}
while(i <= m) buf[k++] = arr[i++];
while(j <= r) buf[k++] = arr[j++];
for(int p=l ; p<=r ; p++) arr[p] = buf[p];
}
int main(){
MergeSort(0, n-1);
}題目
用merge sort寫寫看排序 zj a104
binary search
By mouyilai
binary search
- 775



