Data Structures and Algorithms

muigai unaka

Week 6

Tree

Node

Root Node

Level 0

Level 1

Level 2

Level 3

Level 4

Root Node

Height: 5

Root: A

Leaves: C, E, I, J

Preorder: ABCDEFGHIJ

Inorder: CBEDAFIHJG

Postorder: CEDBIJHGFA Breadth: ABFCDGEHIJ

// To create a Tree you will need "Nodes"
// Nodes will have data 
// (this can be a string, an integer, an object, etc) 
// and a reference to the left child Nodes and right child Nodes
function Node(data) {
    this.data = data;
    this.left = null;
    this.right = null;
}
// initiate a root node and assign the left and right
let root = new Node("A");
root.left = new Node("B");
root.right = new Node("F");
root.left.left = new Node("C");
root.left.right = new Node("D");
root.left.right.left = new Node("E");
root.right = new Node("F");
root.right.right = new Node("G");
root.right.right.left = new Node("H");
root.right.right.left.left = new Node("I");
root.right.right.left.right = new Node("J");

// To create a Tree you will need "Nodes"
// Nodes will have data 
// (this can be a string, 
// an integer, an object, etc) 
// and a reference to the left child 
// Nodes and right child Nodes
function Node(data) {
    this.data = data;
    this.left = null;
    this.right = null;
}
// initiate a root node 
// and assign the left and right
let root = new Node("A");
root.left = new Node("B");
root.right = new Node("F");
root.left.left = new Node("C");
root.left.right = new Node("D");
root.left.right.left = new Node("E");
root.right = new Node("F");
root.right.right = new Node("G");
root.right.right.left = new Node("H");
root.right.right.left.left = new Node("I");
root.right.right.left.right = new Node("J");

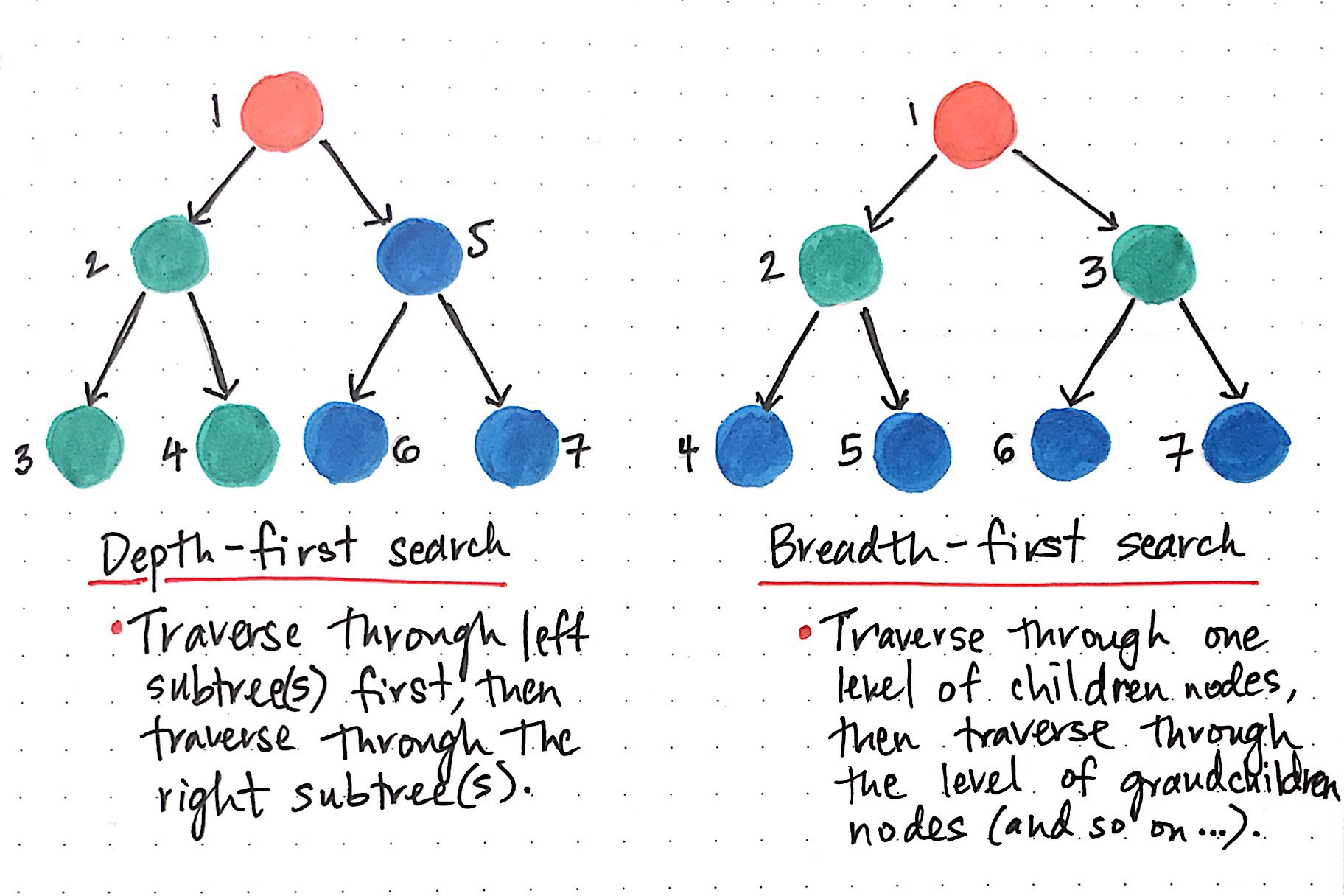
Depth First Search

/**
* Preorder traversal is used to create a copy of the tree. 
* Preorder traversal is also used to get prefix expression 
* on of an expression tree.
* <root> <left> <right>
* @param {Node} root 
function Node(data) {
    this.data = data;
    this.left = null;
    this.right = null;
}
*/
const preorderTraverse = (root) => {
    try {
        if (root == null) return;
        if (!(root instanceof Node)) {
          throw new Error("TypeError: Cannot traverse non node");
        }
        console.log(root.data);
        preorderTraverse(root.left);
        preorderTraverse(root.right);
    } catch (e) {
        throw e;
    }
}

/**
* In case of binary search trees (BST), Inorder traversal gives nodes 
* in non-decreasing order. To get nodes of BST in non-increasing order,
* a variation of Inorder traversal where Inorder traversal is reversed 
* can be used.
* <left> <root> <right>
* @param {Node} root 
function Node(data) {
    this.data = data;
    this.left = null;
    this.right = null;
}
*/
const inorderTraverse = (root) => {
    try {
        if (root == null) return;
        if (!(root instanceof Node)) {
            throw new Error("TypeError: Cannot traverse non node");
        }
        inorderTraverse(root.left);
        console.log(root.data);
        inorderTraverse(root.right);
    } catch (e) {
        throw e;
    }
}

/**
* 
* <left> <right> <root>
* @param {Node} root 
function Node(data) {
    this.data = data;
    this.left = null;
    this.right = null;
}
*/
const postorderTraverse = (root) => {
    try {
        if (root == null) return;
        if (!(root instanceof Node)) {
            throw new Error("TypeError: Cannot traverse non node");
        }
        postorderTraverse(root.left);
        postorderTraverse(root.right);
        console.log(root.data);
    } catch (e) {
        throw e;
    }
}

Breadth First Search

Breadth-first search involves search through a tree, level by level, one level at a time

// BFT uses a queue, better to do it iteratively
// Level order traversal
const bft = (node) => {
    let q = [node]
    let output = []

    while (q.length) {
        let current = q.shift()
        output.push(current.data)
        console.log(current.data)
      	// check the left node
        if (current.left) {
            q.push(current.left)
        }
      	// check the right node
        if (current.right) {
            q.push(current.right)
        }
    }
    return output
}

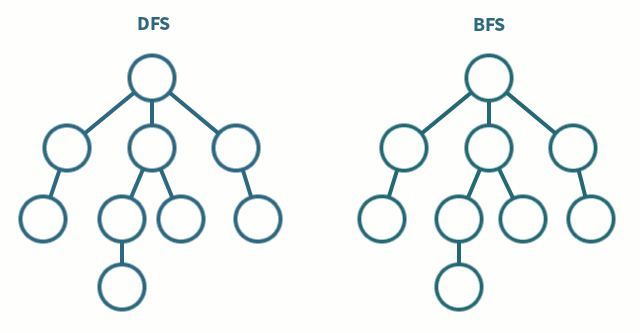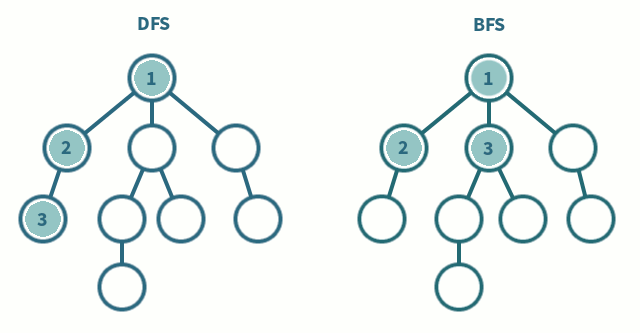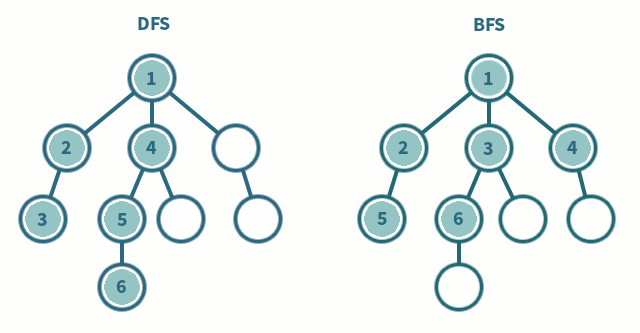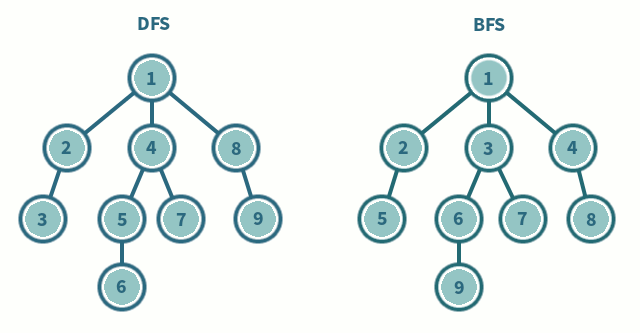
For all of these traversals - whether done recursively or iteratively - you’ll have to visit every node in the tree. That means that you’ll get a runtime complexity of 𝑂 (𝑛) - where n is the number of nodes in the binary tree.

Tree Traversal Runtime

For all of these traversals - whether done recursively or iteratively - if we don’t consider size of stack for function calls then 𝑂 (1) otherwise 𝑂 (𝑛)

Tree Traversal Space Complexity

Tree Terms

Root: the node at the top of a tree. There can only be one root node

Node: data struct that hold references to other nodes

Leaf: a node without children

Edge: a one to one connection between nodes

Path: the sequence of nodes along the edges of a tree

Visiting: accessing a node in a tree

Traversal: the act of passing through nodes in a specific way

Level: the current specific depth of a node

Depth: the number of edges from the root to the node

Height: the number of edges from the node to the deepest leaf

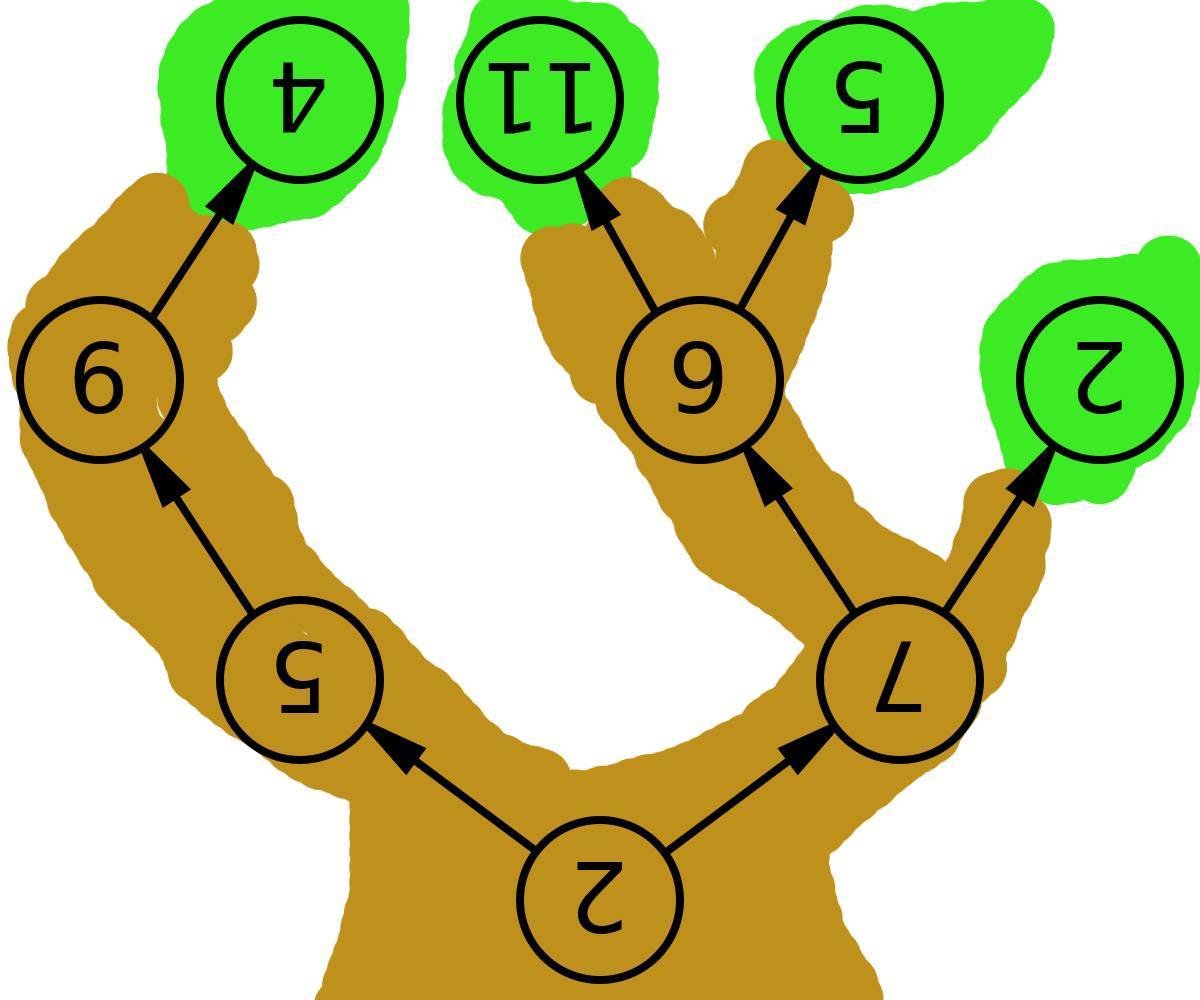
credit: shinyashanka

Tionas?

Binary Tree is a special kind of tree where each Node can have at most 2 children.

Binary Tree

All the keys (data inside the node) are distinct.
In every parent node, the left child key value is smaller than the parent node key value.
In every parent node, the right child key value is larger than the parent node key value.