BASEL PROBLEM -1899 MIX -

　バーゼル問題 -1899 MIX-

TIME　 　YEARS

5:14　　　    2017

スライド作成・発表 : たけのこ赤軍

 

The 5th Romantic Mathnight

～Presentation by TakenokoRedArmy～

バーゼル問題

\displaystyle\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}
112+122+132+⋯=π26\displaystyle\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}
\displaystyle\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}
112+122+132+⋯=π26\displaystyle\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots=\frac{\pi^2}{6}

↑       ↑　   ↑

"自然数"  1,2,3,...の2乗の逆数和

"ガウス整数"   　　　でも

同じことができないのか？

m+ni
m+nim+ni

自然な疑問

A.できます

\displaystyle \sum_{m,n=-\infty}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}
∑m,n=−∞∞1(m+ni)4=ϖ415\displaystyle \sum_{m,n=-\infty}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}

※ただし 　　は 0でない!

m,n
m,nm,n
\displaystyle \sum_{m,n=-\infty}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}
∑m,n=−∞∞1(m+ni)4=ϖ415\displaystyle \sum_{m,n=-\infty}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}

※ただし 　　は 0でない!

m,n
m,nm,n

バーゼル問題→　自然数　の　乗

これ→ガウス整数の　乗

2
22
4
44
\displaystyle \sum_{m,n=-\infty}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}
∑m,n=−∞∞1(m+ni)4=ϖ415\displaystyle \sum_{m,n=-\infty}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}

※ただし 　　は 0でない!

m,n
m,nm,n

バーゼル問題→　自然数　の　乗

これ→ガウス整数の　乗

2
22
4
44

似てる！

\varpi
ϖ\varpi

って何？

パ イ

\varpi
ϖ\varpi

って何？

→「レムニスケート周率」と呼ばれる定数

　・円周率の類似物

　・近似値は

　・「レムニスケート」という図形の周長の半分

2.62205\cdots
2.62205⋯2.62205\cdots

パ イ

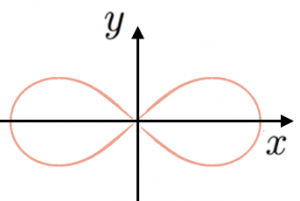
これが「レムニスケート」

は この図形の周長の半分

\varpi
ϖ\varpi
1
11
-1
−1-1

この式は なぜ成立しているか？

\displaystyle \sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}
∑m,n=−∞(m,n)≠(0,0)∞1(m+ni)4=ϖ415\displaystyle \sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=\frac{\varpi^4}{15}

示すための道具

　　　

　

示すための道具

　　　

　1.関数

　

\Delta
Δ\Delta

示すための道具

　　　

　1.関数

　2.極限公式

\Delta
Δ\Delta

示すための道具

　　　

　1.関数

　2.極限公式

　3.ゼータの分解

\Delta
Δ\Delta

示すための道具

　　　

　1.関数

　2.極限公式

　3.ゼータの分解

　4.関数

\Delta
Δ\Delta
E_4
E4E_4

1.関数

\Delta
Δ\Delta

1.関数

\Delta
Δ\Delta
\displaystyle \Delta(z)=e^{2\pi iz}\prod_{n=1}^{\infty} (1-e^{2\pi inz})^{24}
Δ(z)=e2πiz∏n=1∞(1−e2πinz)24\displaystyle \Delta(z)=e^{2\pi iz}\prod_{n=1}^{\infty} (1-e^{2\pi inz})^{24}
z=x+yi(y>0)
z=x+yi(y>0)z=x+yi(y>0)

ただし

1.関数

\Delta
Δ\Delta
\displaystyle \Delta(z)=e^{2\pi iz}\prod_{n=1}^{\infty} (1-e^{2\pi inz})^{24}
Δ(z)=e2πiz∏n=1∞(1−e2πinz)24\displaystyle \Delta(z)=e^{2\pi iz}\prod_{n=1}^{\infty} (1-e^{2\pi inz})^{24}

→なんかややこしいのでここでは定義だけ！

(あとでいっぱい出てくる)

2.極限公式

2.極限公式

\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{|mz+n|}{\sqrt{y}}=2\pi(y^6|\Delta(z)|)^{\frac{1}{12}}
∏m,n=−∞(m,n)≠(0,0)∞∣mz+n∣y=2π(y6∣Δ(z)∣)112\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{|mz+n|}{\sqrt{y}}=2\pi(y^6|\Delta(z)|)^{\frac{1}{12}}

2.極限公式

・クロネッカーが発見した公式

・言い換えはいくつかあるが、ここでは一番扱いやすいものを採用

\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{|mz+n|}{\sqrt{y}}=2\pi(y^6|\Delta(z)|)^{\frac{1}{12}}
∏m,n=−∞(m,n)≠(0,0)∞∣mz+n∣y=2π(y6∣Δ(z)∣)112\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{|mz+n|}{\sqrt{y}}=2\pi(y^6|\Delta(z)|)^{\frac{1}{12}}

2.極限公式

・クロネッカーが発見した公式

・言い換えはいくつかあるが、ここでは一番扱いやすいものを採用

\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{|mz+n|}{\sqrt{y}}=2\pi(y^6|\Delta(z)|)^{\frac{1}{12}}
∏m,n=−∞(m,n)≠(0,0)∞∣mz+n∣y=2π(y6∣Δ(z)∣)112\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{|mz+n|}{\sqrt{y}}=2\pi(y^6|\Delta(z)|)^{\frac{1}{12}}

→　を代入して二乗、という変形を行う

i
ii

2.極限公式

→計算するとこんな感じ

2.極限公式

→計算するとこんな感じ

\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty}(m^2+n^2)=4{\pi}^2\Delta(i)^{\frac{1}{6}}
∏m,n=−∞(m,n)≠(0,0)∞(m2+n2)=4π2Δ(i)16\displaystyle \prod_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty}(m^2+n^2)=4{\pi}^2\Delta(i)^{\frac{1}{6}}

3.ゼータの分解

3.ゼータの分解

\displaystyle\sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} (m^2+n^2)^{-s}=\left(\sum_{n=1}^{\infty} n^{-s}\right)\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^{-s}}\right)
∑m,n=−∞(m,n)≠(0,0)∞(m2+n2)−s=(∑n=1∞n−s)(∑n=0∞(−1)n(2n+1)−s)\displaystyle\sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} (m^2+n^2)^{-s}=\left(\sum_{n=1}^{\infty} n^{-s}\right)\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^{-s}}\right)

3.ゼータの分解

\displaystyle\sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} (m^2+n^2)^{-s}=\left(\sum_{n=1}^{\infty} n^{-s}\right)\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^{-s}}\right)
∑m,n=−∞(m,n)≠(0,0)∞(m2+n2)−s=(∑n=1∞n−s)(∑n=0∞(−1)n(2n+1)−s)\displaystyle\sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} (m^2+n^2)^{-s}=\left(\sum_{n=1}^{\infty} n^{-s}\right)\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^{-s}}\right)

「正規積」という概念を使って

左辺を和から積に変換

3.ゼータの分解

\displaystyle\sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} (m^2+n^2)^{-s}=\left(\sum_{n=1}^{\infty} n^{-s}\right)\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^{-s}}\right)
∑m,n=−∞(m,n)≠(0,0)∞(m2+n2)−s=(∑n=1∞n−s)(∑n=0∞(−1)n(2n+1)−s)\displaystyle\sum_{m,n=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} (m^2+n^2)^{-s}=\left(\sum_{n=1}^{\infty} n^{-s}\right)\left(\sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)^{-s}}\right)

「正規積」という概念を使って

左辺を和から積に変換

→積に変換すれば、さっき「2.極限公式」で示した

左辺を計算できる！

3.ゼータの分解

計算結果

3.ゼータの分解

計算結果

\displaystyle \Delta(i)=\frac{\varpi^{12}}{64\pi^{12}}
Δ(i)=ϖ1264π12\displaystyle \Delta(i)=\frac{\varpi^{12}}{64\pi^{12}}

3.ゼータの分解

計算結果

\displaystyle \Delta(i)=\frac{\varpi^{12}}{64\pi^{12}}
Δ(i)=ϖ1264π12\displaystyle \Delta(i)=\frac{\varpi^{12}}{64\pi^{12}}

が出てきてるやん！

\varpi
ϖ\varpi

4.関数

E_4
E4E_4

4.関数

E_4
E4E_4
\displaystyle E_4(z)=\frac{1}{2}\sum_{(c,d){\text{は互いに素}}}^{} \frac{1}{(c+dz)^4}
E4(z)=12∑(c,d)は互いに素1(c+dz)4\displaystyle E_4(z)=\frac{1}{2}\sum_{(c,d){\text{は互いに素}}}^{} \frac{1}{(c+dz)^4}

4.関数

E_4
E4E_4
\displaystyle E_4(z)=\frac{1}{2}\sum_{(c,d){\text{は互いに素}}}^{} \frac{1}{(c+dz)^4}
E4(z)=12∑(c,d)は互いに素1(c+dz)4\displaystyle E_4(z)=\frac{1}{2}\sum_{(c,d){\text{は互いに素}}}^{} \frac{1}{(c+dz)^4}

ちょい変形

\displaystyle =\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+nz)^4}
=12ζ(4)∑(m,n)=−∞(m,n)≠(0,0)∞1(m+nz)4\displaystyle =\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+nz)^4}

4.関数

E_4
E4E_4
i
ii

を代入

今のやつに

4.関数

E_4
E4E_4
\displaystyle E_4(i)=\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}
E4(i)=12ζ(4)∑(m,n)=−∞(m,n)≠(0,0)∞1(m+ni)4\displaystyle E_4(i)=\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}

4.関数

E_4
E4E_4
\displaystyle E_4(i)=\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}
E4(i)=12ζ(4)∑(m,n)=−∞(m,n)≠(0,0)∞1(m+ni)4\displaystyle E_4(i)=\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}

4.関数

E_4
E4E_4
\displaystyle E_4(i)=\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}
E4(i)=12ζ(4)∑(m,n)=−∞(m,n)≠(0,0)∞1(m+ni)4\displaystyle E_4(i)=\frac{1}{2\zeta(4)}\sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}

最初に出てきたやつ！！

4.関数

E_4
E4E_4

じゃあ　　　がわかったら

証明終わるんじゃね？

E_4(i)
E4(i)E_4(i)

4.関数

E_4
E4E_4

最終兵器

E_4(i)=12\Delta(i)^{\frac{1}{3}}
E4(i)=12Δ(i)13E_4(i)=12\Delta(i)^{\frac{1}{3}}

4.関数

E_4
E4E_4

最終兵器

E_4(i)=12\Delta(i)^{\frac{1}{3}}
E4(i)=12Δ(i)13E_4(i)=12\Delta(i)^{\frac{1}{3}}

「3.ゼータの分解」の最後で値は計算済み

\displaystyle \sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=12\zeta(4)\Delta(i)^{\frac{1}{3}}
∑(m,n)=−∞(m,n)≠(0,0)∞1(m+ni)4=12ζ(4)Δ(i)13\displaystyle \sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=12\zeta(4)\Delta(i)^{\frac{1}{3}}

故に、

\displaystyle \sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=12\zeta(4)\Delta(i)^{\frac{1}{3}}
∑(m,n)=−∞(m,n)≠(0,0)∞1(m+ni)4=12ζ(4)Δ(i)13\displaystyle \sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=12\zeta(4)\Delta(i)^{\frac{1}{3}}

故に、

=\displaystyle\frac{\varpi^4}{15}
=ϖ415=\displaystyle\frac{\varpi^4}{15}
\displaystyle \sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=12\zeta(4)\Delta(i)^{\frac{1}{3}}
∑(m,n)=−∞(m,n)≠(0,0)∞1(m+ni)4=12ζ(4)Δ(i)13\displaystyle \sum_{(m,n)=-\infty\atop{(m,n)\neq{(0,0)}}}^{\infty} \frac{1}{(m+ni)^4}=12\zeta(4)\Delta(i)^{\frac{1}{3}}

故に、

=\displaystyle\frac{\varpi^4}{15}
=ϖ415=\displaystyle\frac{\varpi^4}{15}

証明終了.

以上.

ご清聴ありがとうございました！

※ブログも是非！

(途中計算を詳しく載せています):

http://O-V-E-R-H-E-A-T.hatenablog.com/

ポン酢

By narcissus_strikes_back

Made with Slides.com

ポン酢

  • 1,855