CS607. Combinatorics
with Applications in Computer Science
#01. Error-Correcting Codes &
an Ice-Breaker Puzzle
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0
1 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0
Noisy Channel
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0
1 0 1 1 0 0 1 0 0 1 1 0 1 1 0 0Noisy Channel
Goal: Detect and correct as many errors as possible.
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0
1 0 1 1 0 0 1 0 0 1 1 0 1 1 1 0
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
0.33... = message | 0.66... = redundancy
\(\mathbb{F}^k_2\)
\(\mathbb{F}^n_2\)
\(\mathbb{F}^k_2\)
\(\mathbb{F}^n_2\)
Goal: Detect and correct as many errors as possible.
1 0 1 1 0 0 1 0 0 1 0 0 1 1 1 0
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
1 1 0 1
0 0 0 1
1
0.64 = message | 0.35 = redundancy
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X A B 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X A B 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 B 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 B 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 B 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 C 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 0 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 0 0 1 1 D 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1
0 0 1 1
D 0 0 1
0 0 1 11 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1
0 0 1 1
1 0 0 1
0 0 1 11 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 0 0 1 1 1 0 0 1 0 0 1 1
1 0 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
1 0 1 1 0 0 1 0 0 1 1
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 0 0 1 0 0 1 1 1 0 0 1 0 0 1 1
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
1 1 0 0 1 0 1 1 1 1 0
Goal: Detect and correct as many errors as possible.
Tools: redundancy/additional storage.
Hope: minimize tool usage: it is expensive!
A baby step: correct any one bit flip.
X 1 1 1 0 1 0 0 1 1 1 1 1 1 1 0
1 1 0 0 1 0 1 1 1 1 0
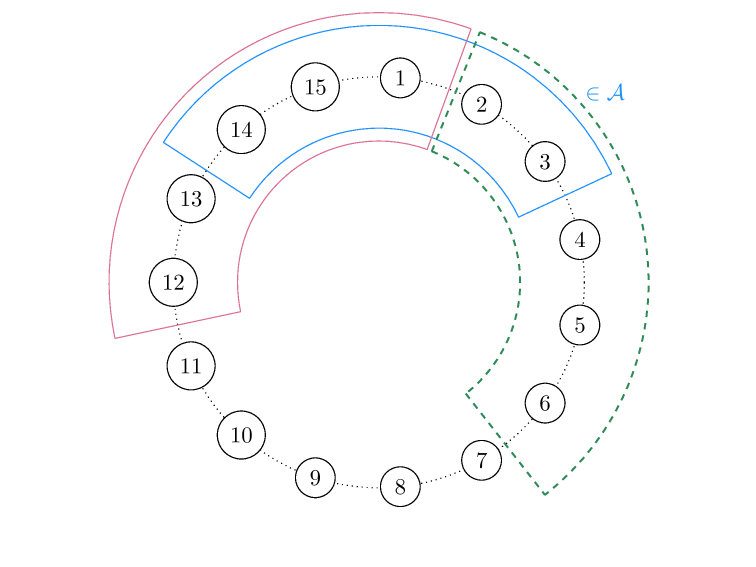
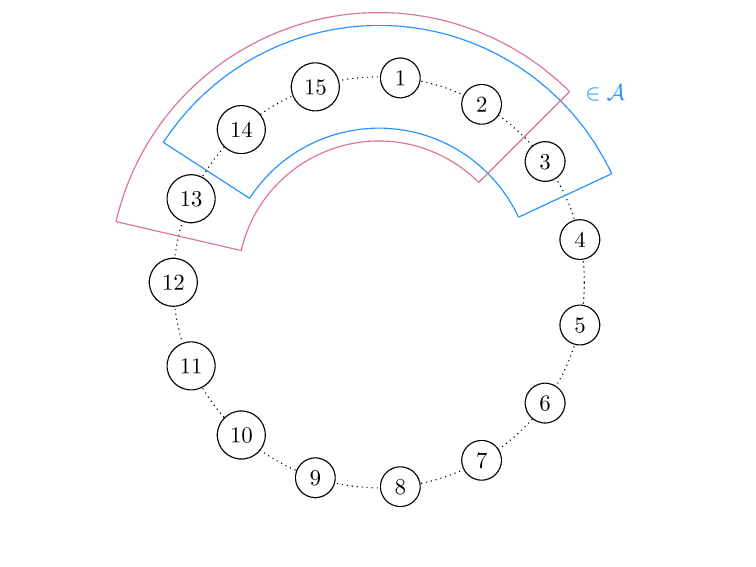
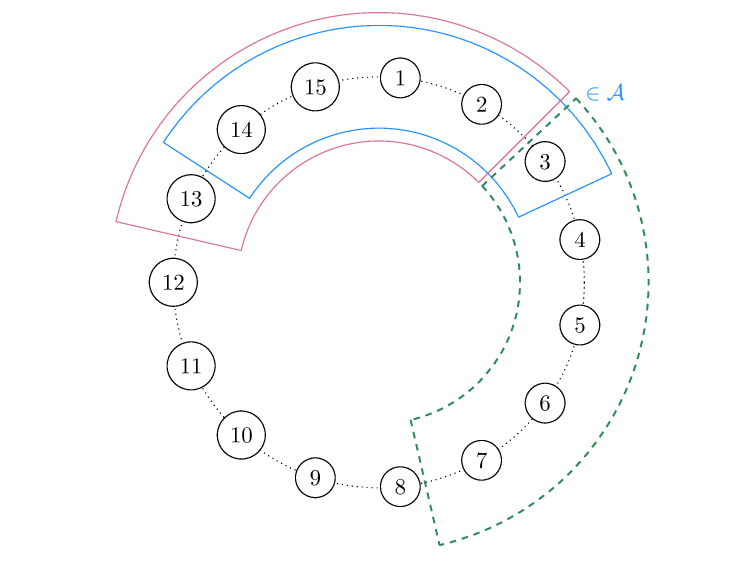
Exercise: Use the X-bit to detect if there is more than one error.
0000000100100011010001010110011110001001101010111100110111101111012345678910111213141500000001001000110100010101100111100010011010101111001101111011110123456789101112131415000000010010001101000101011001111000100110101011110011011110111101234567891011121314150000000100100011010001010110011110001001101010111100110111101111012345678910111213141500000001001000110100010101100111100010011010101111001101111011110123456789101112131415\(M_{16 \times 11} \cdot [1,1,0,0,1,0,1,1,1,1,0]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [{\color{IndianRed}1},{\color{IndianRed}1},0,{\color{IndianRed}0},{\color{IndianRed}1},0,{\color{IndianRed}1},1,{\color{IndianRed}1},1,{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [{\color{IndianRed}1},{\color{IndianRed}1},0,{\color{IndianRed}0},{\color{IndianRed}1},0,{\color{IndianRed}1},1,{\color{IndianRed}1},1,{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [{\color{IndianRed}1},1,{\color{IndianRed}0},{\color{IndianRed}0},1,{\color{IndianRed}0},{\color{IndianRed}1},1,1,{\color{IndianRed}1},{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\\star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [{\color{IndianRed}1},1,{\color{IndianRed}0},{\color{IndianRed}0},1,{\color{IndianRed}0},{\color{IndianRed}1},1,1,{\color{IndianRed}1},{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,1,0,1,1,1,1,0]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,1,0,1,1,1,1,0]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,{\color{IndianRed}1},{\color{IndianRed}0},{\color{IndianRed}0},1,0,1,{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,{\color{IndianRed}1},{\color{IndianRed}0},{\color{IndianRed}0},1,0,1,{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,1,0,1,1,1,1,0]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,{\color{IndianRed}1},{\color{IndianRed}0},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,{\color{IndianRed}1},{\color{IndianRed}0},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}1},{\color{IndianRed}0}]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,1,0,1,1,1,1,0]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\ 1 & 1 & 0 & 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1\\ 1 & 0 & 1 & 1 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\ 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\0 & 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{DodgerBlue}1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{DodgerBlue}1} \\ \end{bmatrix}\)
\(M_{16 \times 11} \cdot [1,1,0,0,1,0,1,1,1,1,0]^T = w\)
\(\begin{bmatrix} \star & \star & \star & \star & \star & \star & \star & \star & \star & \star & \star\\{\color{Blue}1} & {\color{Blue}1} & 0 & {\color{Blue}1} & {\color{Blue}1} & 0 & {\color{Blue}1} & 0 & {\color{Blue}1} & 0 & {\color{Blue}1}\\ {\color{Orange}1} & 0 & {\color{Orange}1} & {\color{Orange}1} & 0 & {\color{Orange}1} & {\color{Orange}1} & 0 & 0 & {\color{Orange}1} & {\color{Orange}1} \\ {\color{Thistle}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & {\color{SeaGreen}1} & {\color{SeaGreen}1} & {\color{SeaGreen}1} & 0 & 0 & 0 & {\color{SeaGreen}1} & {\color{SeaGreen}1} & {\color{SeaGreen}1} & {\color{SeaGreen}1}\\ 0 & {\color{Thistle}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & {\color{Thistle}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {\color{Thistle}1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \ 0 & 0 & 0 & 0 & {\color{IndianRed}1} & {\color{IndianRed}1} & {\color{IndianRed}1} & {\color{IndianRed}1} & {\color{IndianRed}1} & {\color{IndianRed}1} & {\color{IndianRed}1}\\0 & 0 & 0 & 0 & {\color{Thistle}1} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & {\color{Thistle}1} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\color{Thistle}1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{Thistle}1} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{Thistle}1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{Thistle}1} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\color{Thistle}1} \\ \end{bmatrix}\)
\(x_{1} \oplus x_{3} \oplus x_{5} \oplus x_{7} \oplus x_{9} \oplus x_{11} \oplus x_{13} \oplus x_{15} = 0 \\ x_{2} \oplus x_{3} \oplus x_{6} \oplus x_{7} \oplus x_{10} \oplus x_{11} \oplus x_{14} \oplus x_{15} = 0 \\ x_{4} \oplus x_{5} \oplus x_{6} \oplus x_{7} \oplus x_{12} \oplus x_{13} \oplus x_{14} \oplus x_{15} = 0 \\ x_{8} \oplus x_{9} \oplus x_{10} \oplus x_{11} \oplus x_{12} \oplus x_{13} \oplus x_{14} \oplus x_{15} = 0 \\\)
\(\underbrace{\begin{bmatrix} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{bmatrix}}_{\text{Parity Check Matrix: } P}\)
What is the null space of P?
The set of all valid code words.
\(\underbrace{\begin{bmatrix} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{bmatrix}}_{\text{Parity Check Matrix: } P}\)
\(Pw = P(v + e)\)
\(P(v + e) = Pv + Pe\)
\(Pv + Pe = 0 + Pe = Pe\)
\(\underbrace{\begin{bmatrix} 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{bmatrix}}_{\text{Parity Check Matrix: } P}\)
\(\begin{bmatrix} 0 \\ 0 \\ {\color{IndianRed}1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\)
\(\underbrace{\begin{bmatrix} 0 & 1 & {\color{IndianRed}0} & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & {\color{IndianRed}1} & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & {\color{IndianRed}0} & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & {\color{IndianRed}0} & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{bmatrix}}_{\text{Parity Check Matrix: } P}\)
\(\begin{bmatrix} 0 \\ 0 \\ {\color{IndianRed}1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\)
\(\underbrace{\begin{bmatrix} 0 & 1 & {\color{IndianRed}0} & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & {\color{IndianRed}1} & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 0 & {\color{IndianRed}0} & 0 & 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & {\color{IndianRed}0} & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\end{bmatrix}}_{\text{Parity Check Matrix: } P}\)
\(\begin{bmatrix} 0 \\ 0 \\ {\color{IndianRed}1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\)
\(\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}\)
=
The (4 → 7) Hamming Code
001 010 011 100 101 110 111
001 010 011 100 101 110 111
001 010 011 100 101 110 111
001
010
011
100
101
110
111001 010 011 100 101 110 111
xyzabcdx = a + b + d
y = a + c + d
z = b + c + d
I have a function \(f\) that takes a 16-bit string as input & produces a number between 0 and 15 as output.
You give me a string \(s \in \{0,1\}^{16}\) and a number \(n \in \{0,...,15\}\).
It will turn out that \(f(s) = n\).
Well, this is a bit too much :)
I have a function \(f\) that takes a 16-bit string as input & produces a number between 0 and 15 as output.
You give me a string \(s \in \{0,1\}^{16}\) and a number \(n \in \{0,...,15\}\).
It will turn out that \(f(t) = n\).
I will flip one bit in \(s\) to get \(t\).
I have a function \(f\) that takes a 16-bit string as input & produces a number between 0 and 15 as output.
You give me a string \(s \in \{0,1\}^{16}\) and a number \(n \in \{0,...,15\}\).
It will turn out that \(f(t) = n\).
I will flip one bit in \(s\) to get \(t\).
CS607. Combinatorics
with Applications in Computer Science
#02. Extremal Set Systems
08 Jan 2024
There are \(n\) citizens living in Oddtown.
Their main occupation was forming various clubs,
which at some point started threatening the very survival of the city.
⚠️ There could be as many as \(2^n\) distinct clubs!
(Well, \(2^n - 1\) if you would prefer to exclude the empty club.)
In order to limit the number of clubs, the city council decreed the following innocent-looking rules:
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
There are \(n\) citizens living in Oddtown.
Their main occupation was forming various clubs,
which at some point started threatening the very survival of the city.
⚠️ There could be as many as \(2^n\) distinct clubs!
(Well, \(2^n - 1\) if you would prefer to exclude the empty club.)
In order to limit the number of clubs, the city council decreed the following innocent-looking rules:
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
There are \(n\) citizens living in Oddtown.
Their main occupation was forming various clubs,
which at some point started threatening the very survival of the city.
⚠️ There could be as many as \(2^n\) distinct clubs!
(Well, \(2^n - 1\) if you would prefer to exclude the empty club.)
In order to limit the number of clubs, the city council decreed the following innocent-looking rules:
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
There are \(n\) citizens living in Oddtown.
Their main occupation was forming various clubs,
which at some point started threatening the very survival of the city.
⚠️ There could be as many as \(2^n\) distinct clubs!
(Well, \(2^n - 1\) if you would prefer to exclude the empty club.)
In order to limit the number of clubs, the city council decreed the following innocent-looking rules:
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Example: \(\{\{1\},\{2\}, \ldots, \{n\}\}\).
(The Singletons Clubs.)
Example: \(\{\{1,2,3\},\{1,2,4\}, \ldots, \{1,2,n\}\}\).
(Where 1 and 2 are popular.)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
subsets of \([n]\)
vectors in \(n\)-dimensional space
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
sets that satisfy (1) & (2)
linearly independent vectors
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
1
0
0
0
0
1
1
1
\(\in \mathbb{F}^n_2\)
1
0
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
1
0
0
0
0
1
1
1
1
0
\(\{1,3,5,6,7\} \subseteq [10] \longrightarrow (1,0,1,0,1,1,1,0,0,0)\)
Another Example:
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
1
0
0
0
0
1
1
1
1
0
\(\{{\color{IndianRed}1},{\color{DodgerBlue}3},{\color{SeaGreen}5},{\color{Tomato}6},{\color{Purple}7}\} \subseteq [10] \longrightarrow ({\color{IndianRed}1},0,{\color{DodgerBlue}1},0,{\color{SeaGreen}1},{\color{Tomato}1},{\color{Purple}1},0,0,0)\)
Another Example:
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 v_1 + \cdots + \alpha_i v_i + \cdots + \alpha_j v_j + \cdots + \alpha_t v_t = 0\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 (v_1 \cdot v_i) + \cdots + \alpha_i (v_i \cdot v_i) + \cdots + \alpha_j (v_j \cdot v_i) + \cdots + \alpha_t (v_t \cdot v_i) = 0\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 (v_1 \cdot v_i) + \cdots + \alpha_i ({\color{IndianRed}v_i \cdot v_i}) + \cdots + \alpha_j (v_j \cdot v_i) + \cdots + \alpha_t (v_t \cdot v_i) = 0\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
\(\{{\color{IndianRed}1},{\color{DodgerBlue}3},{\color{SeaGreen}5},{\color{Tomato}6},{\color{Purple}7}\} \subseteq [10] \longrightarrow ({\color{IndianRed}1},0,{\color{DodgerBlue}1},0,{\color{SeaGreen}1},{\color{Tomato}1},{\color{Purple}1},0,0,0)\)
\( ({\color{IndianRed}1},0,{\color{DodgerBlue}1},0,{\color{SeaGreen}1},{\color{Tomato}1},{\color{Purple}1},0,0,0)\)
\( ({\color{IndianRed}1},0,{\color{DodgerBlue}1},0,{\color{SeaGreen}1},{\color{Tomato}1},{\color{Purple}1},0,0,0)\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 (v_1 \cdot v_i) + \cdots + \alpha_i ({\color{IndianRed}v_i \cdot v_i}) + \cdots + \alpha_j (v_j \cdot v_i) + \cdots + \alpha_t (v_t \cdot v_i) = 0\)
\({\color{IndianRed}|S_i| \mod 2}\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 (v_1 \cdot v_i) + \cdots + \alpha_i ({\color{IndianRed}v_i \cdot v_i}) + \cdots + \alpha_j ({\color{DodgerBlue}v_j \cdot v_i}) + \cdots + \alpha_t (v_t \cdot v_i) = 0\)
\({\color{IndianRed}|S_i| \mod 2}\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
\(\{{\color{IndianRed}1},{\color{DodgerBlue}3},{\color{Tomato}5},{\color{Tomato}6},{\color{Tomato}7}\} \subseteq [10] \longrightarrow ({\color{IndianRed}1},0,{\color{DodgerBlue}1},0,{\color{Tomato}1},{\color{Tomato}1},{\color{Tomato}1},0,0,0)\)
\(\{{\color{IndianRed}1},{\color{DodgerBlue}3},{\color{SeaGreen}4},{\color{SeaGreen}8},{\color{SeaGreen}9}\} \subseteq [10] \longrightarrow ({\color{IndianRed}1},0,{\color{DodgerBlue}1},{\color{SeaGreen}1},0,0,0,{\color{SeaGreen}1},{\color{SeaGreen}1},0)\)
\(({\color{IndianRed}1},0,{\color{DodgerBlue}1},0,0,0,0,0,0,0)\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 (v_1 \cdot v_i) + \cdots + \alpha_i ({\color{IndianRed}v_i \cdot v_i}) + \cdots + \alpha_j ({\color{DodgerBlue}v_j \cdot v_i}) + \cdots + \alpha_t (v_t \cdot v_i) = 0\)
\({\color{IndianRed}|S_i| \mod 2}\)
\({\color{DodgerBlue}|S_i \cap S_j| \mod 2}\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\(\alpha_1 (v_1 \cdot v_i) + \cdots + \alpha_i ({\color{IndianRed}v_i \cdot v_i}) + \cdots + \alpha_j ({\color{DodgerBlue}v_j \cdot v_i}) + \cdots + \alpha_t (v_t \cdot v_i) = 0\)
\({\color{IndianRed}1}\)
\({\color{DodgerBlue}0}\)
There are \(n\) citizens living in Oddtown.
(1) Each club has to have an odd number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(n\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) forms a valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a linearly independent collection of vectors in \(\mathbb{F}_2^n\), where \(v_i := f(S_i)\).
\({\color{Silver}\alpha_i (v_1 \cdot v_i) + \cdots +} \alpha_i ({\color{IndianRed}v_i \cdot v_i}){\color{Silver} + \cdots + \alpha_j (v_j \cdot v_i) + \cdots + \alpha_t (v_t \cdot v_i)} = 0\)
\(\implies \alpha_i = 0\), \(\forall i \in [n]\)
What about Eventown?
There are \(n\) citizens living in Eventown.
(1) Each club has to have an even number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(2^{\lfloor \frac{n}{2} \rfloor}\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) is a maximal and valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a totally isotropic subspace of dimension at most \(\lfloor \frac{n}{2} \rfloor\).
Note that \(v_i \cdot v_j = 0\) for all \(1 \leqslant i,j \leqslant t\)
Let \(X := \{v_1, \ldots, v_t\}\).
In other words, \(X \perp X\), implying that \(X \subseteq X^{\perp}\).
There are \(n\) citizens living in Eventown.
(1) Each club has to have an even number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(2^{\lfloor \frac{n}{2} \rfloor}\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) is a maximal and valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a totally isotropic subspace of dimension at most \(\lfloor \frac{n}{2} \rfloor\).
Let \(X := \{v_1, \ldots, v_t\}\).
In other words, \(X \perp X\), implying that \(X \subseteq X^{\perp}\).
If \(v\) is in span\((X)\), then \(v \perp X\): therefore \(X\) is closed
(since \(\{S_1, \ldots, S_t\}\) is maximal).
There are \(n\) citizens living in Eventown.
(1) Each club has to have an even number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(2^{\lfloor \frac{n}{2} \rfloor}\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) is a maximal and valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a totally isotropic subspace of dimension at most \(\lfloor \frac{n}{2} \rfloor\).
Let \(X := \{v_1, \ldots, v_t\}\).
In other words, \(X \perp X\), implying that \(X \subseteq X^{\perp}\).
Therefore, \(X\) is a subspace.
There are \(n\) citizens living in Eventown.
(1) Each club has to have an even number of members.
(2) Every two clubs must have an even number of members in common.
Under these rules, it is impossible to form more than \(2^{\lfloor \frac{n}{2} \rfloor}\) clubs.
Claim. If \(\{S_1, \ldots, S_t\}\) is a maximal and valid set of clubs over \([n]\),
then \(\{v_1, \ldots v_t\}\) is a totally isotropic subspace of dimension at most \(\lfloor \frac{n}{2} \rfloor\).
Let \(X := \{v_1, \ldots, v_t\}\).
In other words, \(X \perp X\), implying that \(X \subseteq X^{\perp}\).
\(\dim(X) + \dim(X^\perp) = n \implies \dim(X) \leqslant \lfloor \frac{n}{2} \rfloor\).
Generalized Fisher inequality.
If \(C_1, C_2, \ldots, C_m\) are
distinct and nonempty subsets
of an \(n\)-element set
such that
all the intersections \(C_i \cap C_j, i \neq j\),
have the same size (say \(t\)),
then
\(m \leqslant n\).
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 1. \(|C_i| = t\) for some \(i \in [m]\).
At most \(n-t\) other sets.
Total # of sets \(\leqslant n-t + 1 \leqslant n\).
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(a_{i j}= \begin{cases}1 & \text { if } j \in C_i, \text { and } \\ 0 & \text { otherwise }\end{cases}\)
Let \(A\) be the \(m \times n\) matrix with entries:
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(\{{\color{IndianRed}1,2,5}\},\{{\color{DodgerBlue}2,3}\},\{{\color{DarkSeaGreen}3,4,5}\}\)
\(\left(\begin{array}{ccccc}{\color{IndianRed}1} & {\color{IndianRed}1} & 0 & 0 & {\color{IndianRed}1} \\0 & {\color{DodgerBlue}1} & {\color{DodgerBlue}1} & 0 & 0 \\ 0 & 0 & {\color{DarkSeaGreen}1} & {\color{DarkSeaGreen}1} & {\color{DarkSeaGreen}1} \end{array}\right)\)
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(B := AA^T\)
\(=\)
\(A\)
\(A^T\)
\(B\)
\(C_i\)
\(C_j\)
\(=\)
\(A\)
\(A^T\)
\(B\)
\(C_i\)
\(C_j\)
\(t\)
\(=\)
\(A\)
\(A^T\)
\(B\)
\(C_i\)
\(C_i\)
\(=\)
\(A\)
\(A^T\)
\(B\)
\(C_i\)
\(C_i\)
\(d_i\)
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(B := AA^T\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Recall that \(A\) is a \(m \times n\) matrix, so: rank\((A) \leqslant n\)
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(B := AA^T\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
\({\color{White}m = }\)rank\((B) \leqslant \) rank\((A) \leqslant n\)
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(B := AA^T\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
\(m = \) rank\((B) \leqslant \) rank\((A) \leqslant n\)
Given: \(C_1, C_2, \ldots, C_m \in 2^{[n]}\)
where \(|C_i \cap C_j| = t\) for all \(1\leqslant i < j \leqslant m\)
To Prove: \(m \leqslant n\).
Case 2. \(|C_i| > t\) for all \(i \in [m]\).
\(B := AA^T\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
\({\color{red}m = }\) rank\({\color{red}(B)} \leqslant \) rank\((A) \leqslant n\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Suffices to show: \(\mathbf{x}^T B \mathbf{x}>0 \text { for all nonzero } \mathbf{x} \in \mathbb{R}^m \text {. }\)
because once we have the above,
if \(B\mathbf{x} = \mathbf{0}\), then \(\mathbf{x}^TB\mathbf{x} = \mathbf{x}^T\mathbf{0} = 0\), hence \(\mathbf{x} = 0\).
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Suffices to show: \(\mathbf{x}^T B \mathbf{x}>0 \text { for all nonzero } \mathbf{x} \in \mathbb{R}^m \text {. }\)
We can write \(B=t J_n+D\), where \(J_n\) is the all 1's matrix and
\(D\) is the diagonal matrix with \(d_1-t, d_2-t, \ldots, d_n-t\) on the diagonal.
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
\(\left(\begin{array}{ccccc}d_1 & t & t & t \\t & d_2 & t & t \\t & t & d_3 & t \\t & t & t & d_4\end{array}\right) = \)
\(\left(\begin{array}{ccccc}0 & ~t~ & ~t~ & ~t~ \\t & ~0~ & ~t~ & ~t~ \\t & ~t~ & ~0~ & ~t~ \\t & ~t~ & ~t~ & ~0~ \end{array}\right)\)
+ \(\left(\begin{array}{ccccc}d_1 & 0 & 0 & 0 \\0 & d_2 & 0 & 0 \\0 & 0 & d_3 & 0 \\0 & 0 & 0 & d_4\end{array}\right) \)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
\(\left(\begin{array}{ccccc}~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ \\~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ \\~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ \\~~~~~~t~~~~~~ & ~~~~~~t~~~~~~ & ~~~~~t~~~~~ & ~~~~~t~~~~~ \end{array}\right)\)
+ \(\left(\begin{array}{ccccc}(d_1-t) & 0 & 0 & 0 \\0 & (d_2-t) & 0 & 0 \\0 & 0 & (d_3-t) & 0 \\0 & 0 & 0 & (d_4-t)\end{array}\right) \)
\(\left(\begin{array}{ccccc}d_1 & t & t & t \\t & d_2 & t & t \\t & t & d_3 & t \\t & t & t & d_4\end{array}\right) = \)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Suffices to show: \(\mathbf{x}^T B \mathbf{x}>0 \text { for all nonzero } \mathbf{x} \in \mathbb{R}^m \text {. }\)
We can write \(B=t J_n+D\), where \(J_n\) is the all 1's matrix and
\(D\) is the diagonal matrix with \(d_1-t, d_2-t, \ldots, d_n-t\) on the diagonal.
\(\mathbf{x}^T B \mathbf{x}=\mathbf{x}^T\left(t J_n+D\right) \mathbf{x}=t \mathbf{x}^T J_n \mathbf{x}+\mathbf{x}^T D \mathbf{x}\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Suffices to show: \(\mathbf{x}^T B \mathbf{x}>0 \text { for all nonzero } \mathbf{x} \in \mathbb{R}^m \text {. }\)
We can write \(B=t J_n+D\), where \(J_n\) is the all 1's matrix and
\(D\) is the diagonal matrix with \(d_1-t, d_2-t, \ldots, d_n-t\) on the diagonal.
\(\mathbf{x}^T B \mathbf{x}=\mathbf{x}^T\left(t J_n+D\right) \mathbf{x}=t {\color{IndianRed}\mathbf{x}^T J_n \mathbf{x}}+\mathbf{x}^T D \mathbf{x}\)
\({\color{IndianRed}\sum_{i, j=1}^n x_i x_j=\left(\sum_{i=1}^n x_i\right)^2 \geqslant 0}\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Suffices to show: \(\mathbf{x}^T B \mathbf{x}>0 \text { for all nonzero } \mathbf{x} \in \mathbb{R}^m \text {. }\)
We can write \(B=t J_n+D\), where \(J_n\) is the all 1's matrix and
\(D\) is the diagonal matrix with \(d_1-t, d_2-t, \ldots, d_n-t\) on the diagonal.
\(\mathbf{x}^T B \mathbf{x}=\mathbf{x}^T\left(t J_n+D\right) \mathbf{x}=t \mathbf{x}^T J_n \mathbf{x}+{\color{Olive}\mathbf{x}^T D \mathbf{x}}\)
\({\color{Olive}\mathbf{x}^T D \mathbf{x}=\sum_{i=1}^n\left(d_i-t\right) x_i^2>0}\)
\(B=\left(\begin{array}{ccccc}d_1 & t & t & \ldots & t \\t & d_2 & t & \ldots & t \\\vdots & \vdots & \vdots & \vdots & \vdots \\t & t & t & \ldots & d_m\end{array}\right)\)
Suffices to show: \(\mathbf{x}^T B \mathbf{x}>0 \text { for all nonzero } \mathbf{x} \in \mathbb{R}^m \text {. }\)
We can write \(B=t J_n+D\), where \(J_n\) is the all 1's matrix and
\(D\) is the diagonal matrix with \(d_1-t, d_2-t, \ldots, d_n-t\) on the diagonal.
\(\mathbf{x}^T B \mathbf{x}=\mathbf{x}^T\left(t J_n+D\right) \mathbf{x}=t \mathbf{x}^T J_n \mathbf{x}+\mathbf{x}^T D \mathbf{x}\)
\(> 0\)
Let \(L\) be a set of \(s\) nonnegative integers and
\(\mathscr{F}\) a family of subsets of an \(n\)-element set \(X\).
Suppose that for any two distinct members \(A, B \in \mathscr{F}\) we have \(|A \cap B| \in L\).
Assuming in addition that \(\mathscr{F}\) is uniform,
i.e. each member of \(\mathscr{F}\) has the same cardinality,
a celebrated theorem of D. K. Ray-Chaudhuri and R. M. Wilson asserts that:
\(|\mathscr{F}| \leqq\left(\begin{array}{l}n \\ s\end{array}\right)\).
Let \(L\) be a set of \(s\) nonnegative integers and
\(\mathscr{F}\) a family of subsets of an \(n\)-element set \(X\).
Suppose that for any two distinct members \(A, B \in \mathscr{F}\) we have \(|A \cap B| \in L\).
P. Frankl and R. M. Wilson proved that
without the uniformity assumption, we have:
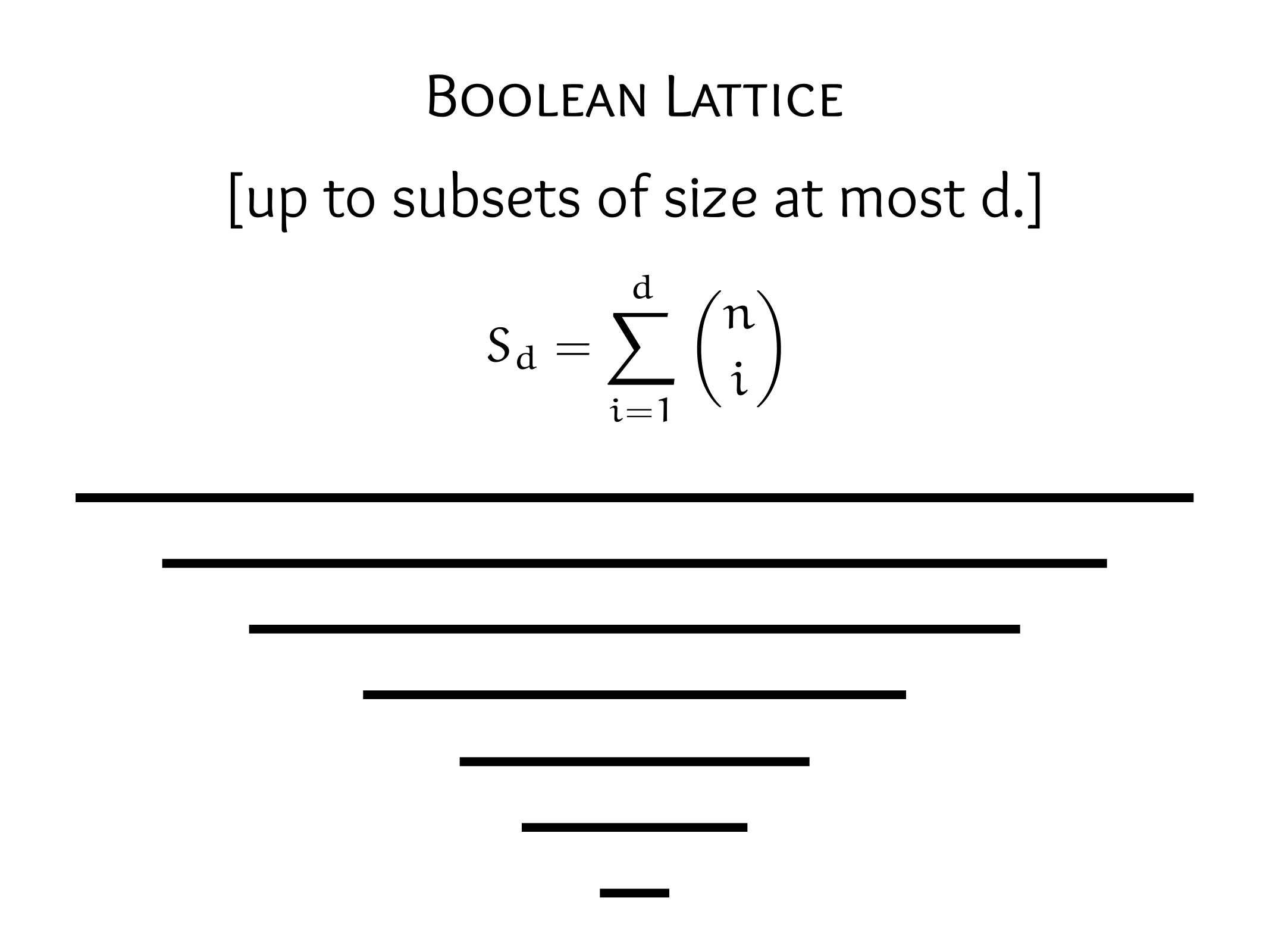
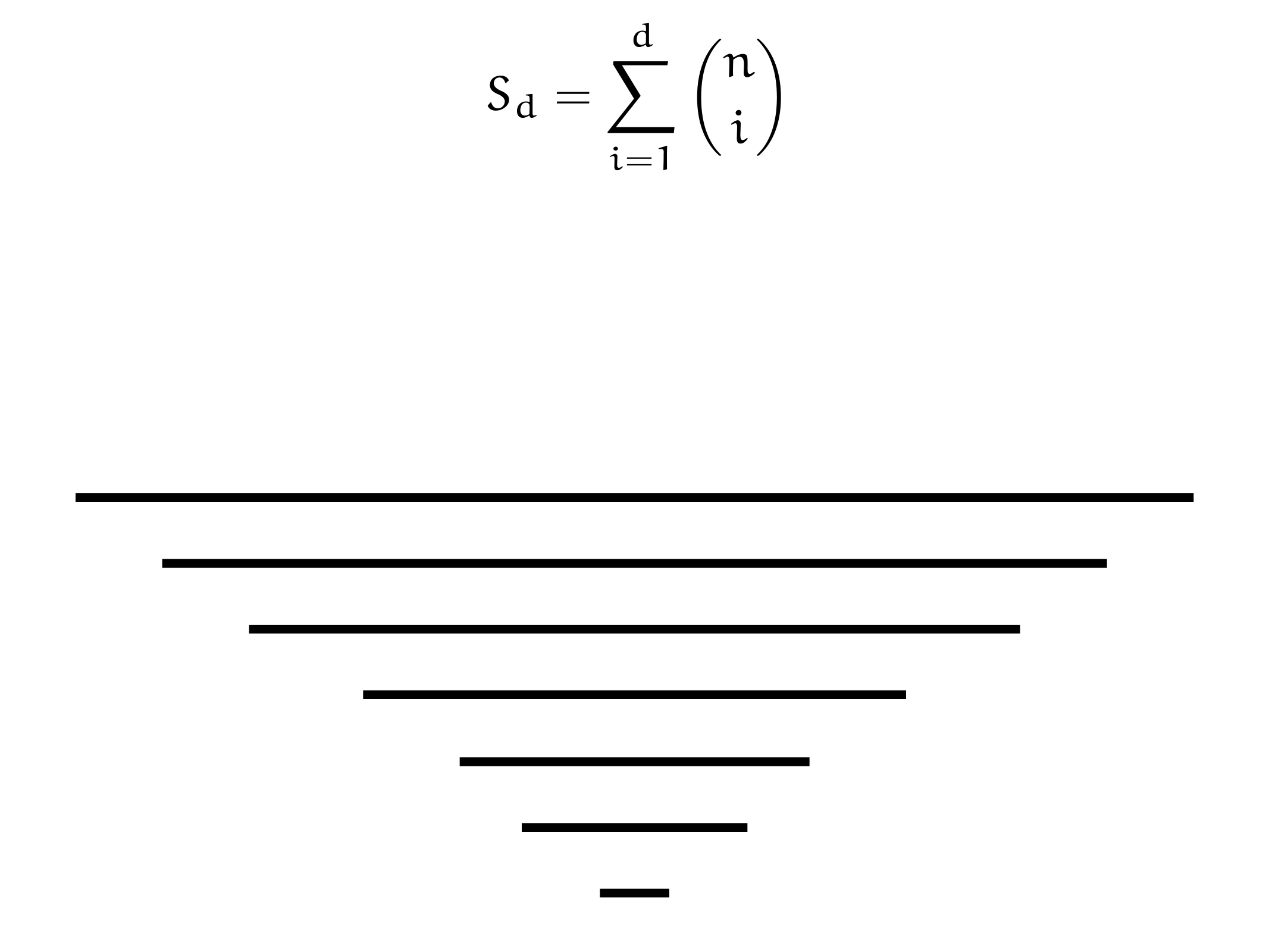
\(|\mathscr{F}| \leqq\left(\begin{array}{l}n \\s\end{array}\right)+\left(\begin{array}{c}n \\s-1\end{array}\right)+\ldots+\left(\begin{array}{l}n \\0\end{array}\right)\)

General Pattern of Question
Suppose that \(\mathcal{F}\) is a system of subsets of an \(n\)-element set.
Suppose that certain simply described configuration of sets does not occur in \(\mathcal{F}\).
What is the maximum possible number of sets in \(\mathcal{F}\)?
The Sperner lemma: If there are no two distinct sets \(A, B \in \mathcal{F}\) with \(A \subset B\), then \(|\mathcal{F}| \leq\left(\begin{array}{c}n \\ \lfloor n / 2\rfloor\end{array}\right)\).
General Pattern of Question
Suppose that \(\mathcal{F}\) is a system of subsets of an \(n\)-element set.
Suppose that certain simply described configuration of sets does not occur in \(\mathcal{F}\).
What is the maximum possible number of sets in \(\mathcal{F}\)?
The Erdős-Ko-Rado Theorem. If \(k \leqslant n / 2\), each \(A \in \mathcal{F}\) has exactly \(k\) elements, and \(A \cap B \neq \emptyset\) for every two \(A, B \in \mathcal{F}\), then \(|\mathcal{F}| \leq\left(\begin{array}{c}n-1 \\ k-1\end{array}\right)\).
General Pattern of Question
Suppose that \(\mathcal{F}\) is a system of subsets of an \(n\)-element set.
Suppose that certain simply described configuration of sets does not occur in \(\mathcal{F}\).
What is the maximum possible number of sets in \(\mathcal{F}\)?
OddTown! EvenTown! etc. etc.
Suppose that \(\mathcal{F}\) is a system of subsets of an \(n\)-element set.
Suppose that certain simply described configuration of sets does not occur in \(\mathcal{F}\).
What is the maximum possible number of sets in \(\mathcal{F}\)?
Theorem. Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Then the number of sets in \(\mathcal{F}\) is at most:
\({\color{IndianRed}|\mathcal{F}| \leqslant \left(\begin{array}{c} n \\ 0 \end{array}\right)+\left(\begin{array}{c} n \\ 1 \end{array}\right)+\cdots+\left(\begin{array}{c} n \\ p-1 \end{array}\right)}\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
A vector \(\mathbf{c}_A \in\{0,1\}^n\). This is simply the characteristic vector of \(A\), whose \(i\) th component is 1 if \(i \in A\) and 0 otherwise.
A function \(f_A:\{0,1\}^n \rightarrow \mathbb{F}_p\), given by
\(f_A(\mathbf{x}):=\prod_{s=0}^{p-2}\left(\left(\sum_{i \in A} x_i\right)-s\right)\).
With each set \(A \in \mathcal{F}\), associate:
All the arithmetic operations in the definition of \(f_A\) are in the finite field \(\mathbb{F}_p\), i.e., modulo \(p\) (and thus 0 and 1 are also treated as elements of \(\mathbb{F}_p\)).
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
A vector \(\mathbf{c}_A \in\{0,1\}^n\). This is simply the characteristic vector of \(A\), whose \(i\) th component is 1 if \(i \in A\) and 0 otherwise.
A function \(f_A:\{0,1\}^n \rightarrow \mathbb{F}_p\), given by
\(f_A(\mathbf{x}):=\prod_{s=0}^{p-2}\left(\left(\sum_{i \in A} x_i\right)-s\right)\).
With each set \(A \in \mathcal{F}\), associate:
For example, for \(p=3, n=5\), and \(A=\{2,3\}\)
we have \(\mathbf{c}_A=(0,1,1,0,0)\) and \(f_A(\mathbf{x})=\left(x_2+x_3\right)\left(x_2+x_3-1\right)\).
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
A vector \(\mathbf{c}_A \in\{0,1\}^n\). This is simply the characteristic vector of \(A\), whose \(i\) th component is 1 if \(i \in A\) and 0 otherwise.
A function \(f_A:\{0,1\}^n \rightarrow \mathbb{F}_p\), given by
\(f_A(\mathbf{x}):=\prod_{s=0}^{p-2}\left(\left(\sum_{i \in A} x_i\right)-s\right)\).
With each set \(A \in \mathcal{F}\), associate:
For example, for \(p=3, n=5\), \(A=\{2,3\}\), \(B = \{1,2,5\}\)
we have \(\mathbf{c}_A=(0,1,1,0,0)\), \(\mathbf{c}_B = (1,1,0,0,1)\),
\(f_A(\mathbf{x})=\left({\color{IndianRed}x_2+x_3}\right)\left(x_2+x_3-1\right)\) and \(f_A(\mathbf{c}_B)={\color{white}\left({\color{white}1+0}\right)\left({\color{white}1+0}-1\right).}\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
A vector \(\mathbf{c}_A \in\{0,1\}^n\). This is simply the characteristic vector of \(A\), whose \(i\) th component is 1 if \(i \in A\) and 0 otherwise.
A function \(f_A:\{0,1\}^n \rightarrow \mathbb{F}_p\), given by
\(f_A(\mathbf{x}):=\prod_{s=0}^{p-2}\left(\left(\sum_{i \in A} x_i\right)-s\right)\).
With each set \(A \in \mathcal{F}\), associate:
For example, for \(p=3, n=5\), \(A=\{2,3\}\), \(B = \{1,2,5\}\)
we have \(\mathbf{c}_A=(0,1,1,0,0)\), \(\mathbf{c}_B = (1,1,0,0,1)\),
\(f_A(\mathbf{x})=\left({\color{IndianRed}x_2+x_3}\right)\left(x_2+x_3-1\right)\) and \(f_A(\mathbf{c}_B)=\left({\color{IndianRed}1+0}\right)\left({\color{IndianRed}1+0}-1\right).\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
A vector \(\mathbf{c}_A \in\{0,1\}^n\). This is simply the characteristic vector of \(A\), whose \(i\) th component is 1 if \(i \in A\) and 0 otherwise.
A function \(f_A:\{0,1\}^n \rightarrow \mathbb{F}_p\), given by
\(f_A(\mathbf{x}):=\prod_{s=0}^{p-2}\left(\left(\sum_{i \in A} x_i\right)-s\right)\).
With each set \(A \in \mathcal{F}\), associate:
\(f_A(\mathbf{c}_B) = \prod_{s=0}^{p-2}(|A \cap B|-s)~~(\bmod p)\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
We consider the set of all functions from \(\{0,1\}^d\) to \(\mathbb{F}_p\)
as a vector space over \(\mathbb{F}_p\) in the usual way,
and we let \(V_{\mathcal{F}}\) be the subspace spanned in it by the functions \(f_A, A \in \mathcal{F}\).
Part 1. We show that the \(f_A\)'s are linearly independent, and hence \({\color{IndianRed}\operatorname{dim}\left(V_{\mathcal{F}}\right)=|\mathcal{F}|}\).
Part 2. We will bound \({\color{SeaGreen}\operatorname{dim}(V_{\mathcal F})}\) from above.
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 1. We show that the \(f_A\)'s are linearly independent, and hence \({\color{IndianRed}\operatorname{dim}\left(V_{\mathcal{F}}\right)=|\mathcal{F}|}\).
\(f_A(\mathbf{c}_B)\begin{cases} \neq 0 & \text{if } |A \cap B| \equiv p-1 \bmod p,\\ = 0 & \text{if } |A \cap B| \not\equiv p-1 \bmod p.\end{cases}\)
\(f_A(\mathbf{c}_B) = \prod_{s=0}^{p-2}(|A \cap B|-s)~~(\bmod p)\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 1. We show that the \(f_A\)'s are linearly independent, and hence \({\color{IndianRed}\operatorname{dim}\left(V_{\mathcal{F}}\right)=|\mathcal{F}|}\).
\(f_A(\mathbf{c}_B)\begin{cases} = 0 & \text{if } 0 \leqslant |A \cap B| \leqslant p-2,\\\neq 0 & \text{if } |A \cap B| = p-1 \text{ or } |A \cap B| = 2p-1,\\ = 0 & \text{if } p \leqslant |A \cap B| \leqslant 2p-2.\end{cases}\)
\(f_A(\mathbf{c}_B) = \prod_{s=0}^{p-2}(|A \cap B|-s)~~(\bmod p)\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 1. We show that the \(f_A\)'s are linearly independent, and hence \({\color{IndianRed}\operatorname{dim}\left(V_{\mathcal{F}}\right)=|\mathcal{F}|}\).
\(f_A(\mathbf{c}_B)\begin{cases} = 0 & \text{if } 0 \leqslant |A \cap B| \leqslant p-2,\\\neq 0 & \text{if } |A \cap B| = p-1 \text{ or } |A \cap B| = 2p-1,\\ = 0 & \text{if } p \leqslant |A \cap B| \leqslant 2p-2.\end{cases}\)
\(f_A(\mathbf{c}_B) = \prod_{s=0}^{p-2}(|A \cap B|-s)~~(\bmod p)\)
For \(A \neq B\): \(0 \leqslant |A \cap B| \leqslant 2p-2\), and \(|A \cap B| \neq p-1\).
For \(A = B\): \(|A \cap B| = 2p - 1\).
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 1. We show that the \(f_A\)'s are linearly independent, and hence \({\color{IndianRed}\operatorname{dim}\left(V_{\mathcal{F}}\right)=|\mathcal{F}|}\).
\(f_A(\mathbf{c}_B)\begin{cases} = 0 & \text{if } 0 \leqslant |A \cap B| \leqslant p-2,\\\neq 0 & \text{if } |A \cap B| = p-1 \text{ or } |A \cap B| = 2p-1,\\ = 0 & \text{if } p \leqslant |A \cap B| \leqslant 2p-2.\end{cases}\)
\(f_A(\mathbf{c}_B) = \prod_{s=0}^{p-2}(|A \cap B|-s)~~(\bmod p)\)
\(\sum_{A \in \mathcal{F}} \alpha_A f_A=0\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 1. We show that the \(f_A\)'s are linearly independent, and hence \({\color{IndianRed}\operatorname{dim}\left(V_{\mathcal{F}}\right)=|\mathcal{F}|}\).
\(f_A(\mathbf{c}_B)\begin{cases} = 0 & \text{if } 0 \leqslant |A \cap B| \leqslant p-2,\\\neq 0 & \text{if } |A \cap B| = p-1 \text{ or } |A \cap B| = 2p-1,\\ = 0 & \text{if } p \leqslant |A \cap B| \leqslant 2p-2.\end{cases}\)
\(f_A(\mathbf{c}_B) = \prod_{s=0}^{p-2}(|A \cap B|-s)~~(\bmod p)\)
\(\sum_{A \in \mathcal{F}} \alpha_A f_A(\mathbf{c}_B)=0 \implies \alpha_B = 0\)
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 2. We will bound \({\color{SeaGreen}\operatorname{dim}(V_{\mathcal F})}\) from above.
In general, each \(f_A\) is a polynomial in \(x_1, x_2, \ldots, x_n\) of degree at most \(p-1\), and hence it is a linear combination of monomials of the form \(x_1^{i_1} x_2^{i_2} \cdots x_n^{i_n}, i_1+i_2+\cdots+i_n \leqslant p-1\).
We can still get rid of the monomials with some exponent \(i_j\) larger than 1 , because \(x_j^2\) and \(x_j\) represent the same function \(\{0,1\}^n \rightarrow \mathbb{F}_p\) (we substitute only 0's and 1's for the variables).
Let \(p\) be a prime number and let \(\mathcal{F}\) be a system
of \((2p-1)\) element subsets of an \(n\)-element set \(X\) such that
no two sets in \({\color{SeaGreen}\mathcal{F}}\) intersect in precisely \({\color{SeaGreen}p-1}\) elements.
Part 2. We will bound \({\color{SeaGreen}\operatorname{dim}(V_{\mathcal F})}\) from above.
In general, each \(f_A\) is a polynomial in \(x_1, x_2, \ldots, x_n\) of degree at most \(p-1\), and hence it is a linear combination of monomials of the form \(x_1^{i_1} x_2^{i_2} \cdots x_n^{i_n}, i_1+i_2+\cdots+i_n \leqslant p-1\),
where \(i_j \in \{0,1\}\) for all \(1 \leqslant j \leqslant n\).
\(\operatorname{dim}\left(V_{\mathcal{F}}\right) \leq\left(\begin{array}{l}n \\ 0\end{array}\right)+\left(\begin{array}{l}n \\ 1\end{array}\right)+\cdots+\left(\begin{array}{c}n \\ p-1\end{array}\right)\)
CS607. Combinatorics
with Applications in Computer Science
#03. Extremal Set Systems (Sperner's Game)
11 Jan 2024
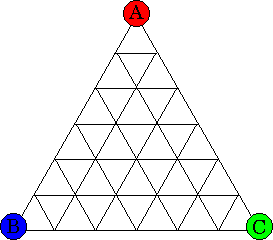
Vertices along AB may be labelled either A or B, but not C
Vertices along BC may be labelled either B or C, but not A
Vertices along CA may be labelled either C or A, but not B
Vertices inside triangle ABC may be labelled A or B or C.
Now shade in every small triangle in the subdivision that has three different labels.
Use two different shadings to distinguish the triangles which have been labelled
counterclockwise (i.e. in the same sense as triangle ABC)
from the triangles which have been labelled
clockwise (i.e. in the sense opposite to that of as triangle ABC).
Then there will be exactly one more counterclockwise triangle
than clockwise triangles.
In particular, the number of shaded triangles will be odd.
CS607. Combinatorics
with Applications in Computer Science
#04. Extremal Set Systems (VC Dimension, EKR)
15 Jan 2024
General Pattern of Question
Suppose that \(\mathcal{F}\) is a system of subsets of an \(n\)-element set.
Suppose that certain simply described configuration of sets does not occur in \(\mathcal{F}\).
What is the maximum possible number of sets in \(\mathcal{F}\)?
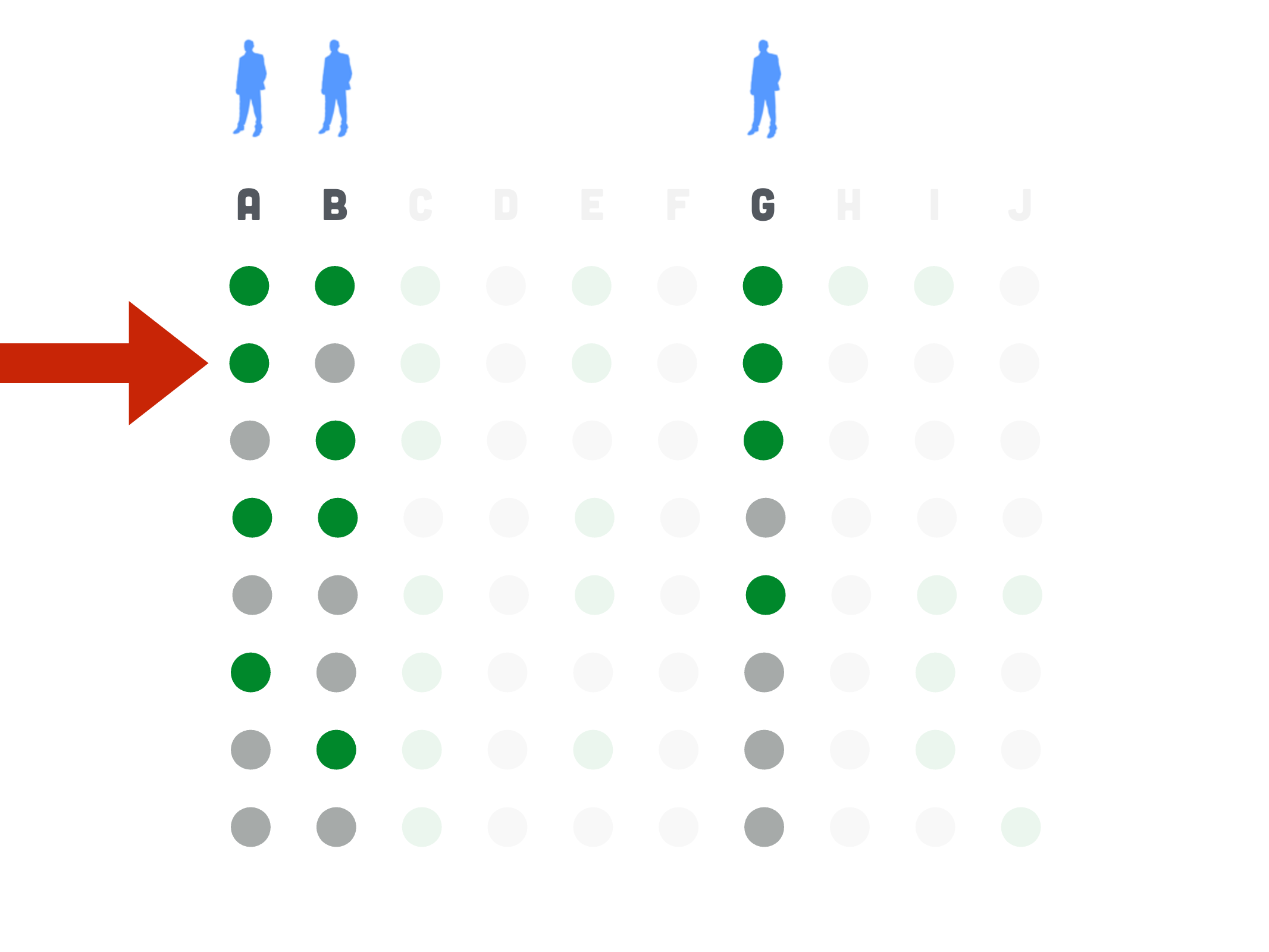
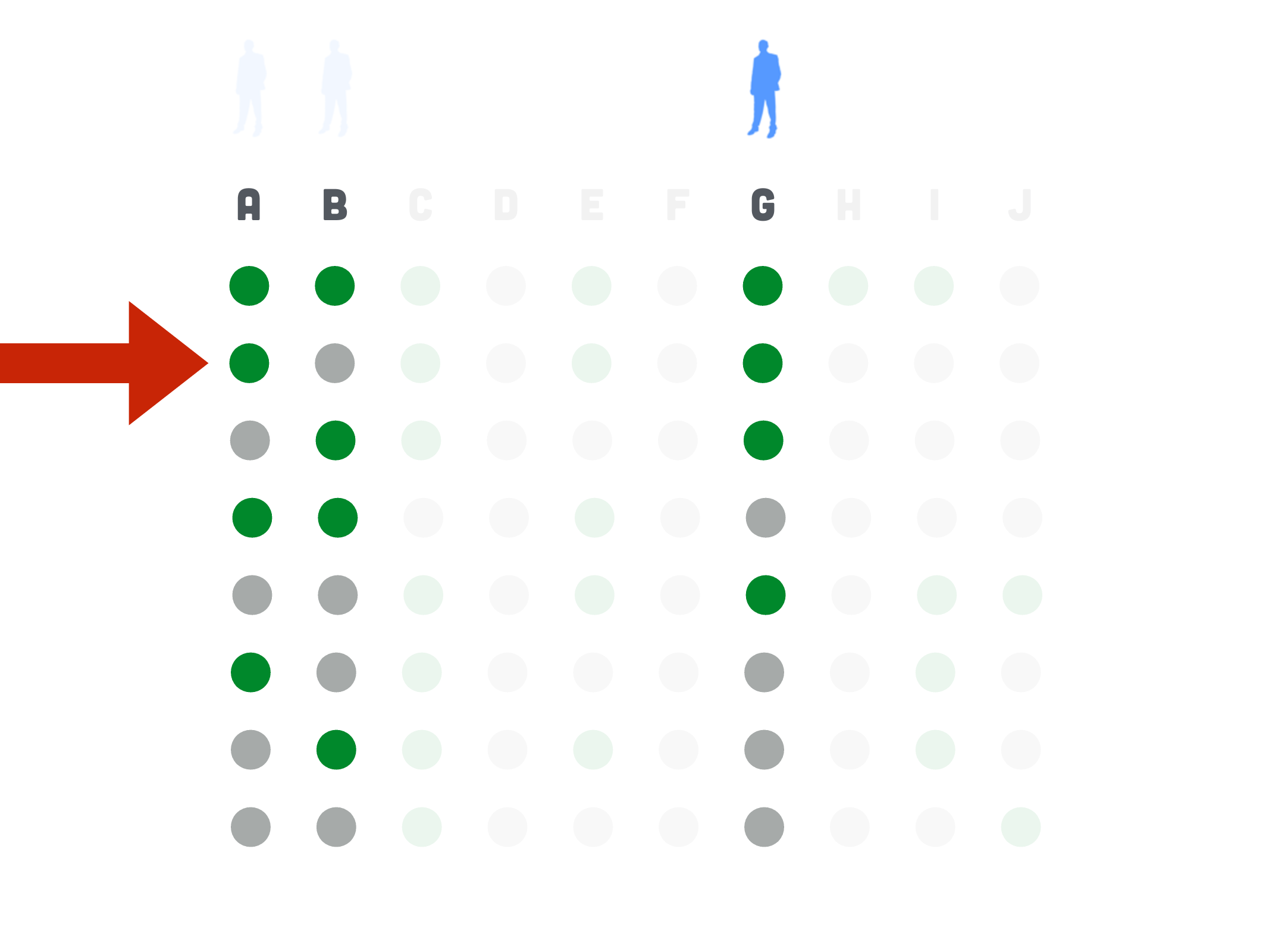
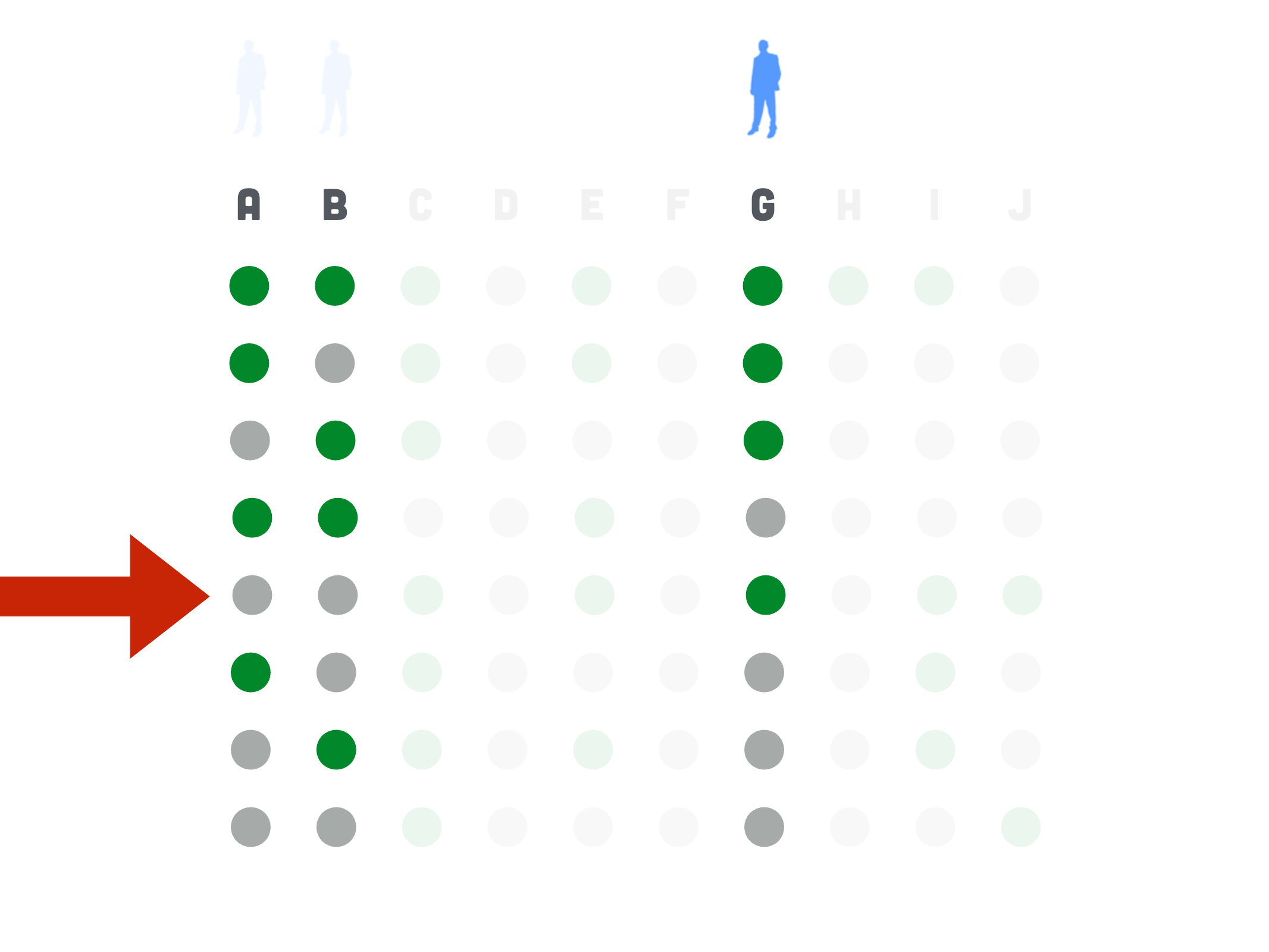
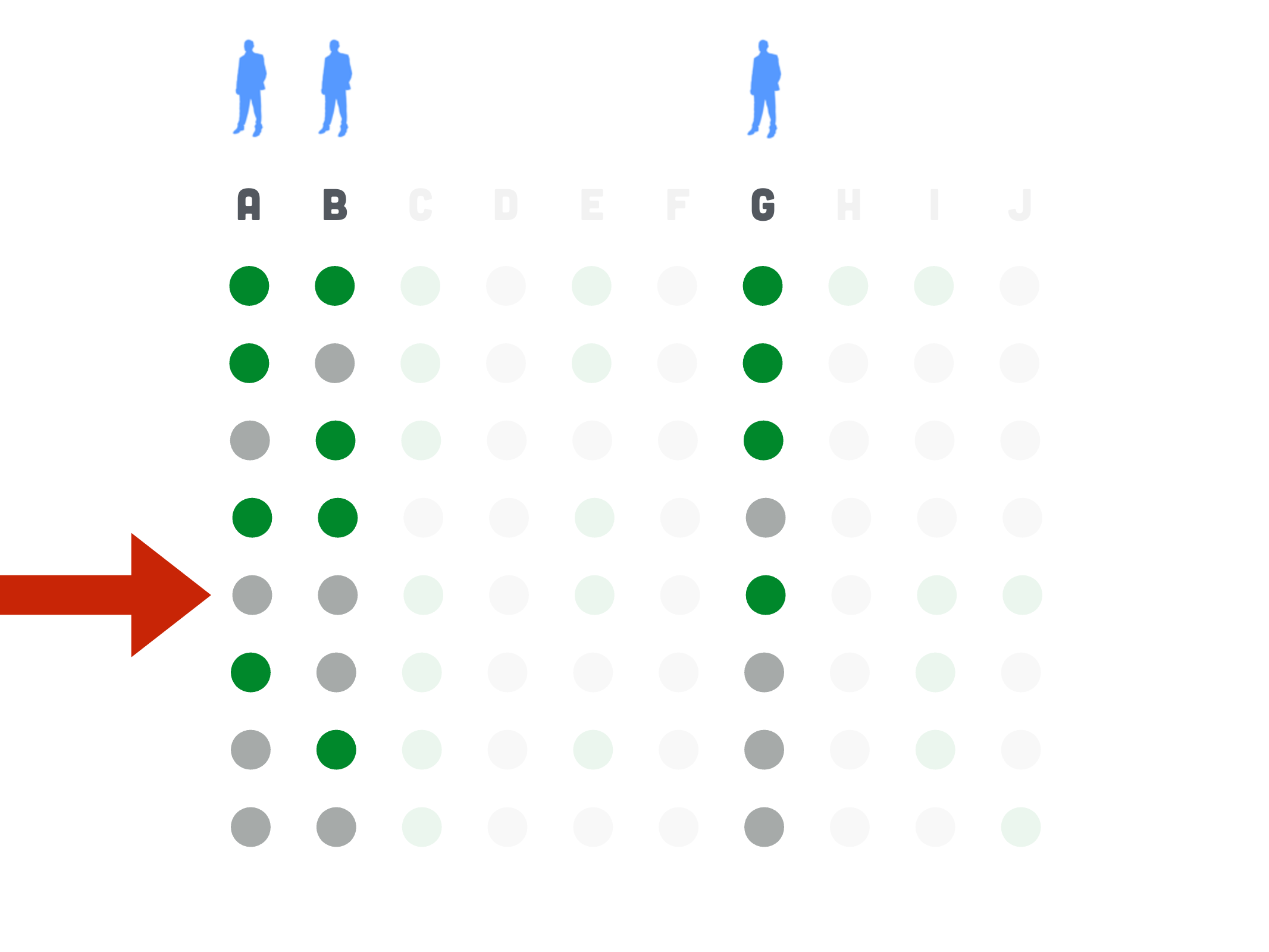
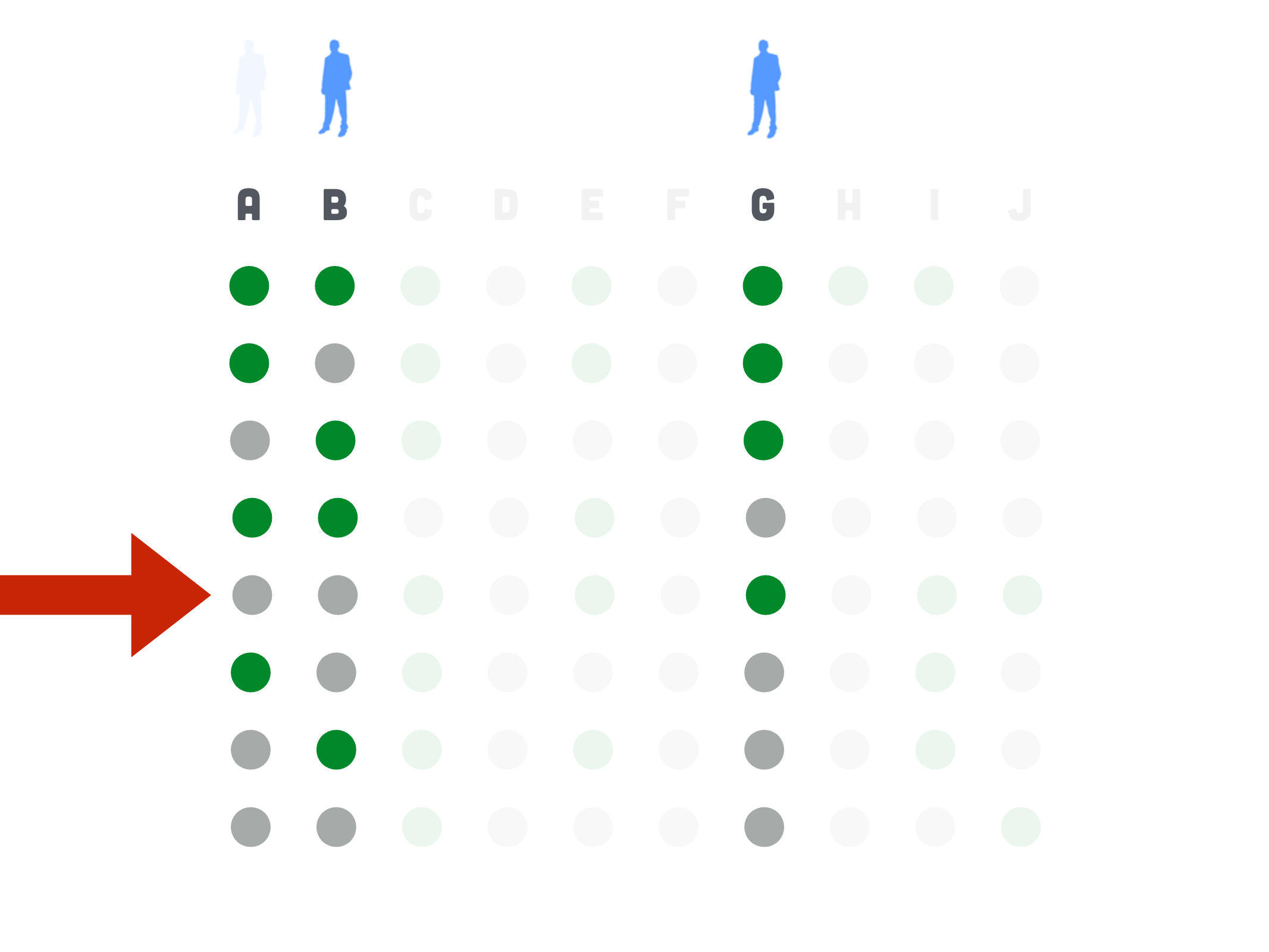
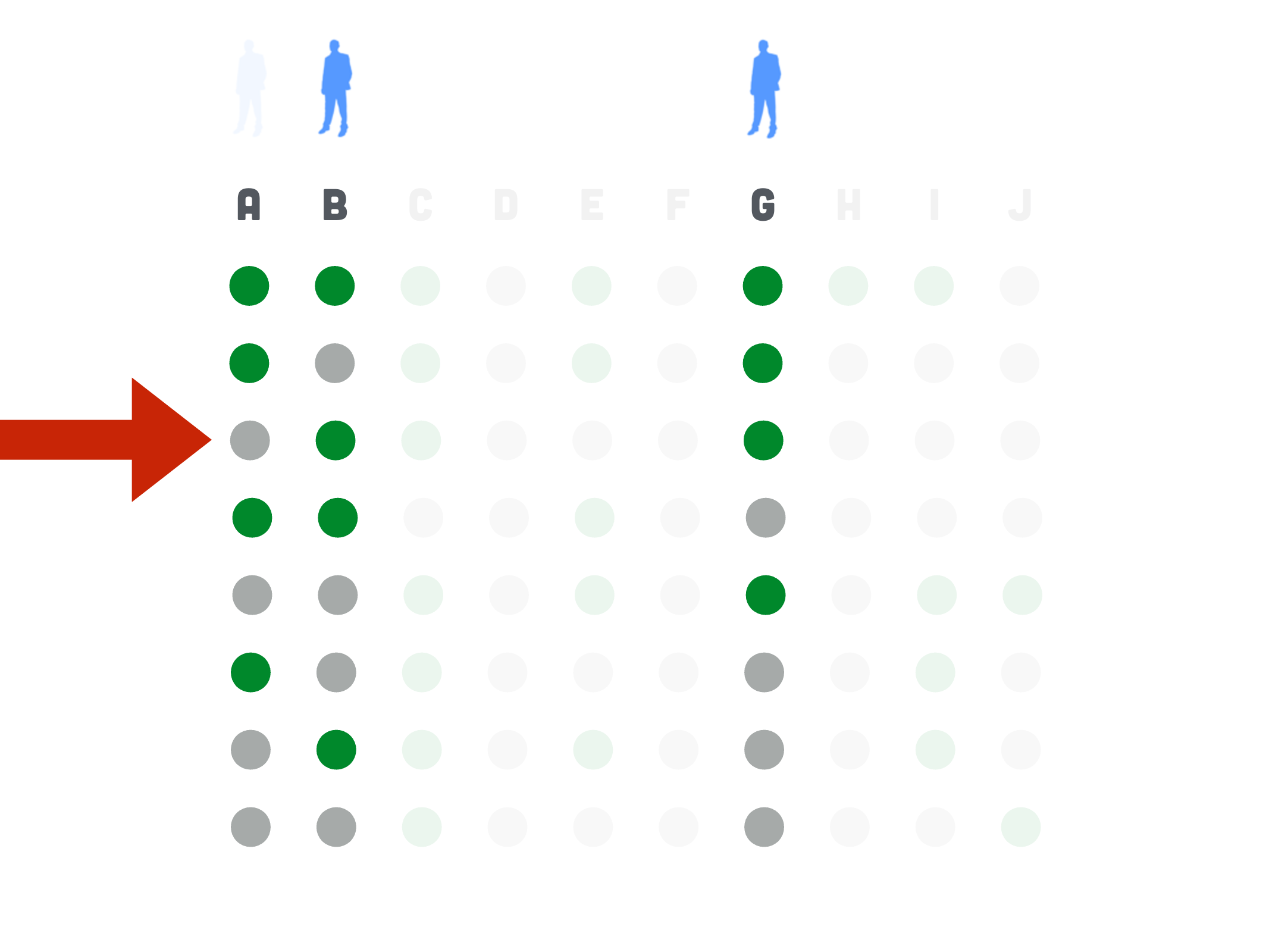
The Erdős-Ko-Rado Theorem. If \(k \leqslant n / 2\), each \(A \in \mathcal{F}\) has exactly \(k\) elements, and \(A \cap B \neq \emptyset\) for every two \(A, B \in \mathcal{F}\), then \(|\mathcal{F}| \leq\left(\begin{array}{c}n-1 \\ k-1\end{array}\right)\).






















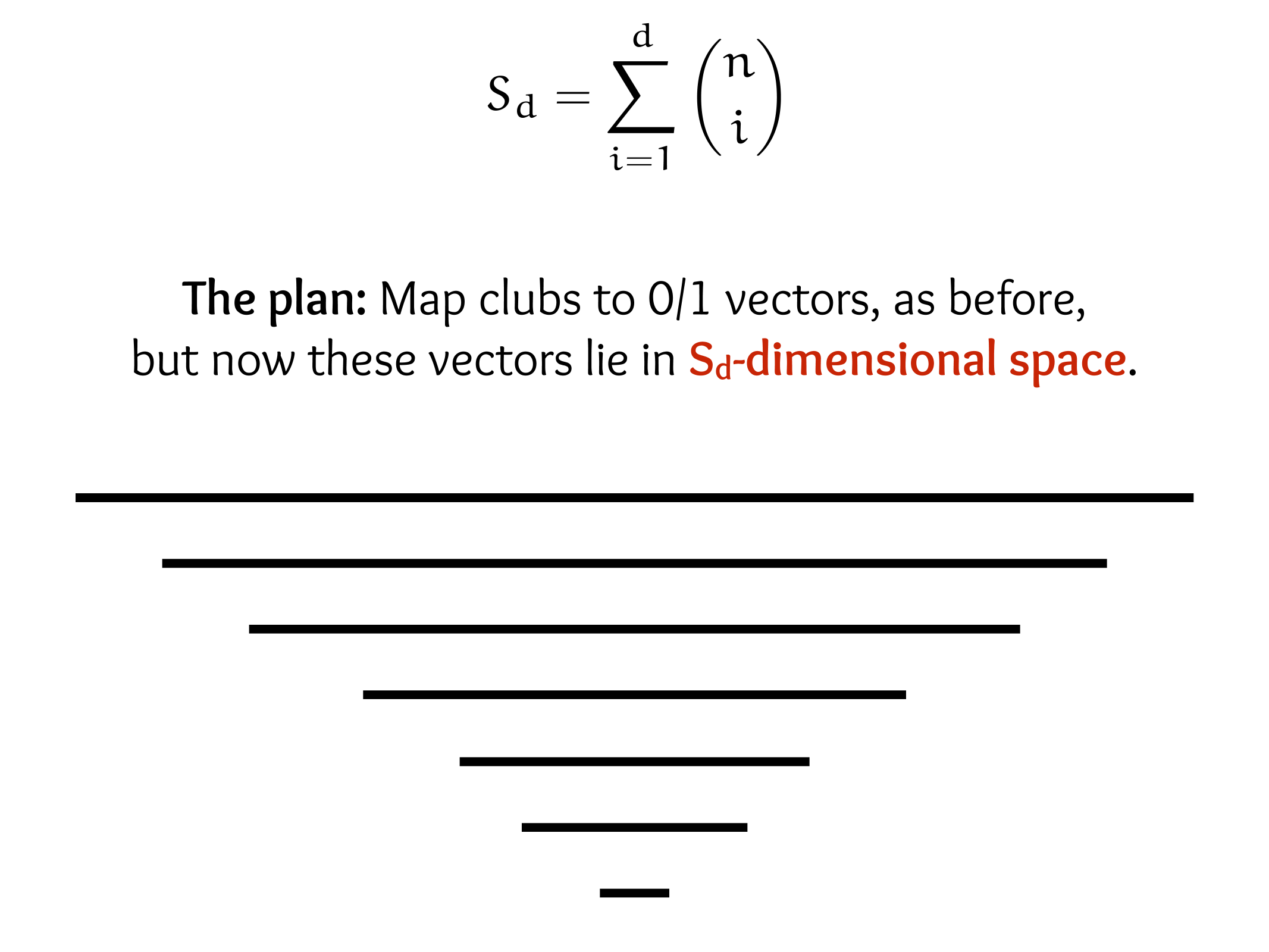
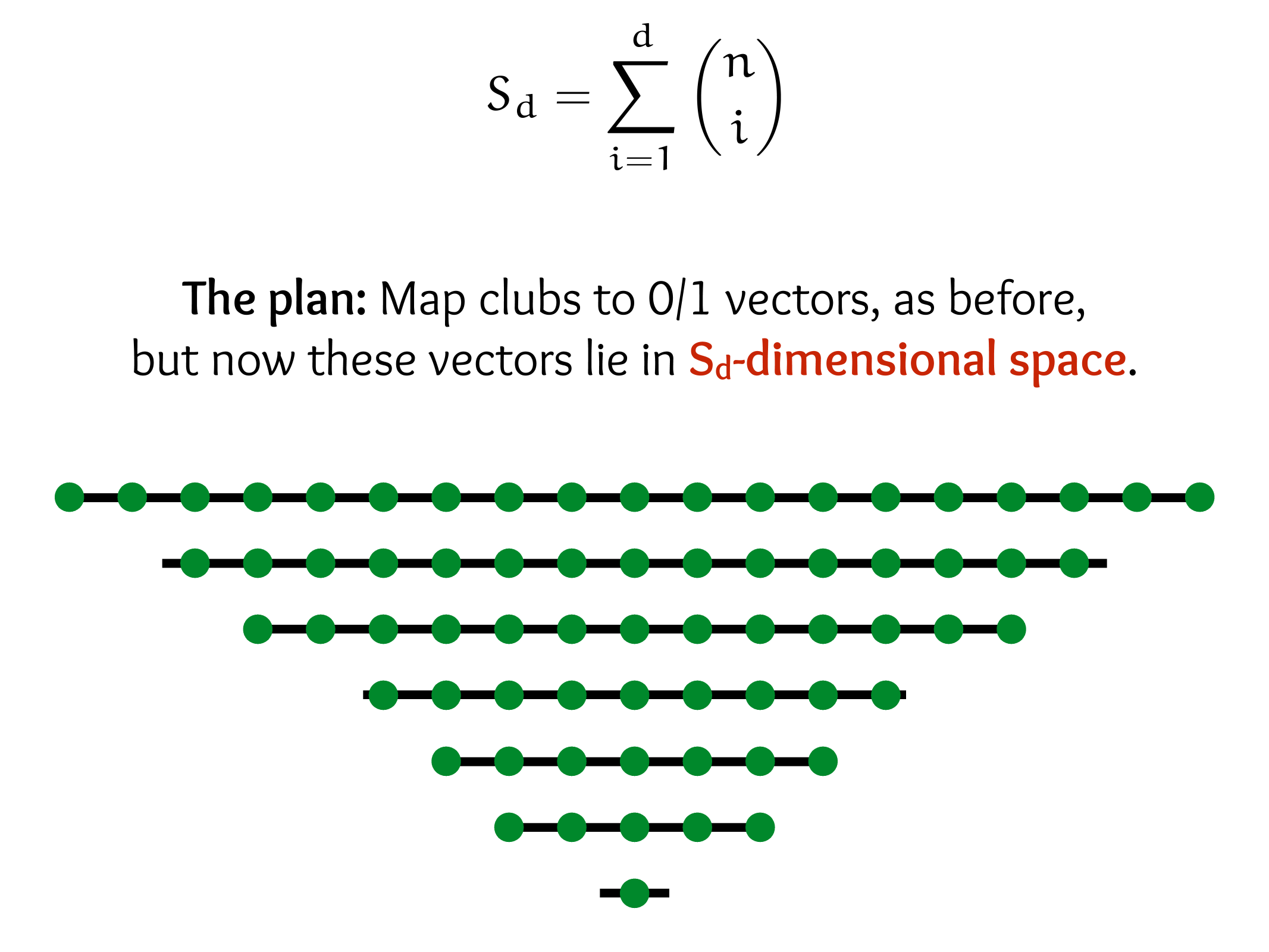
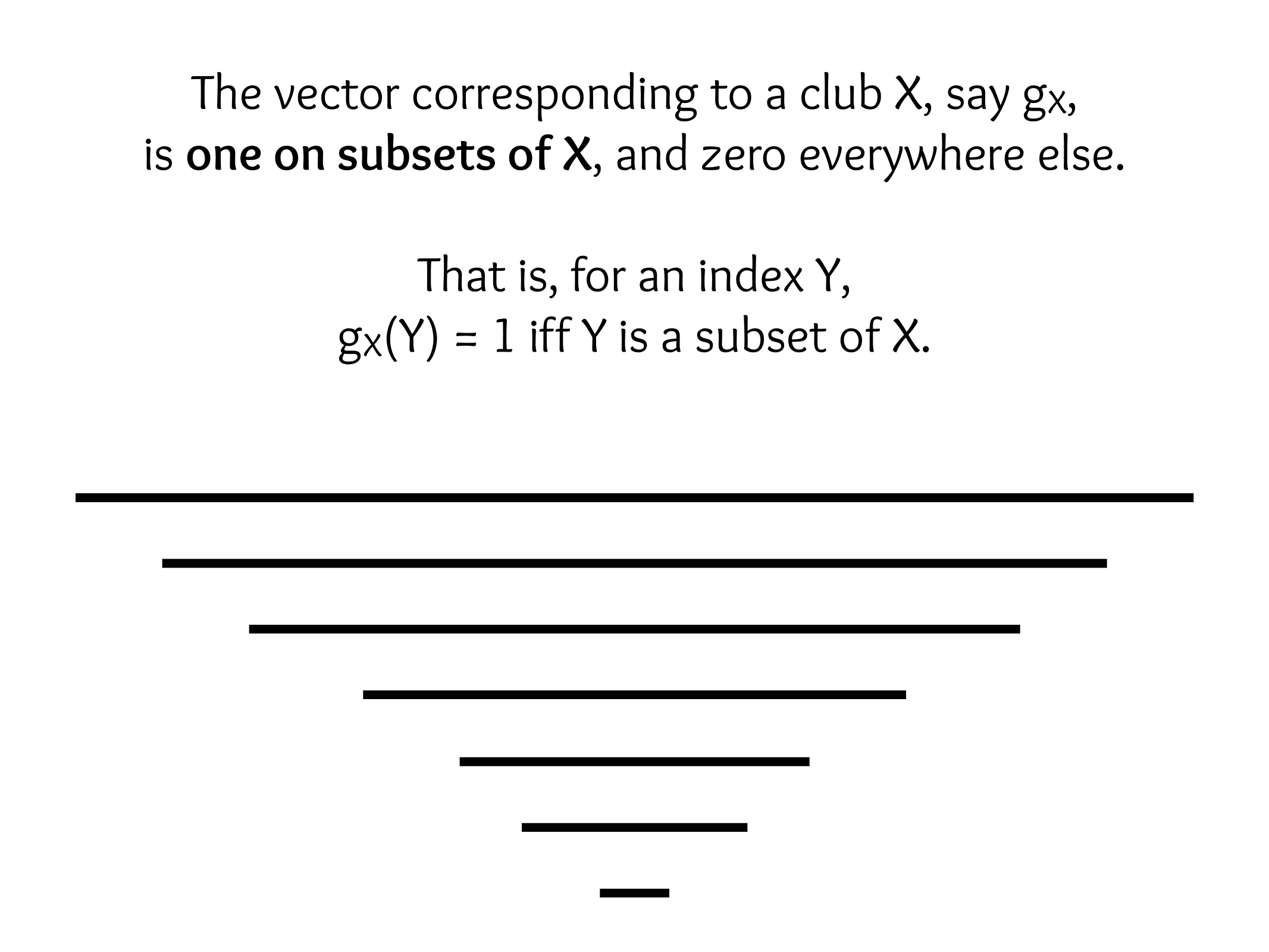
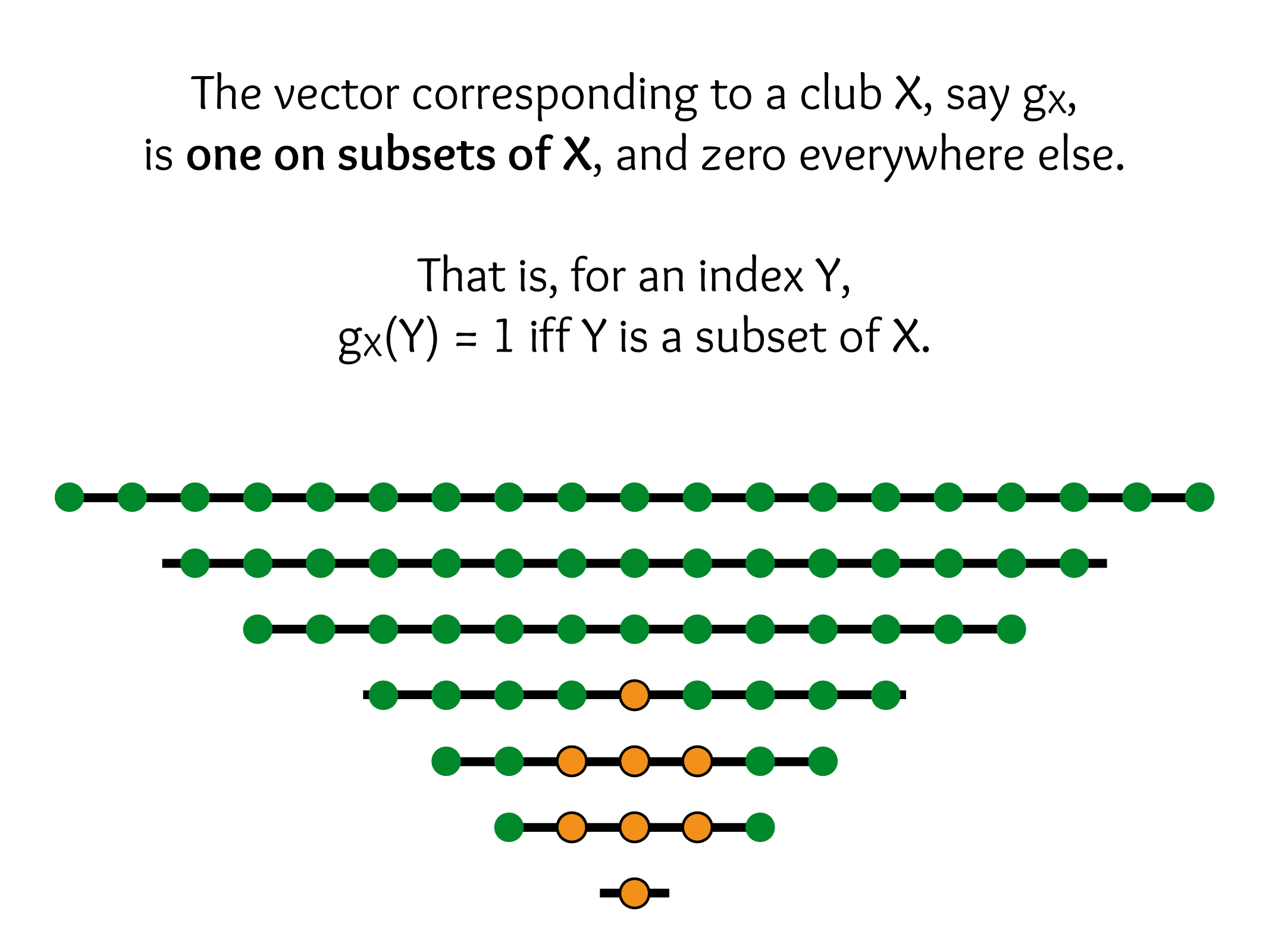





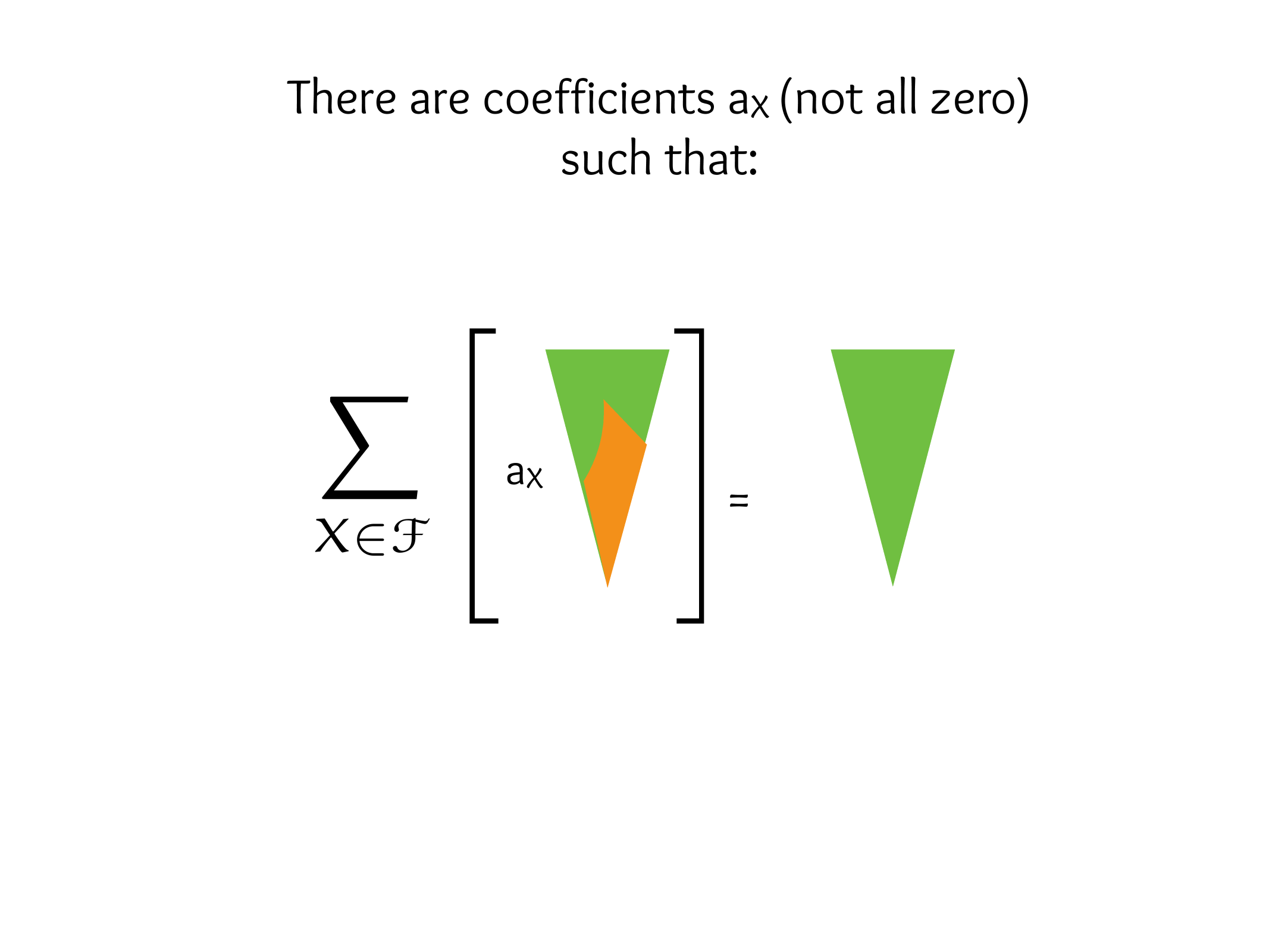
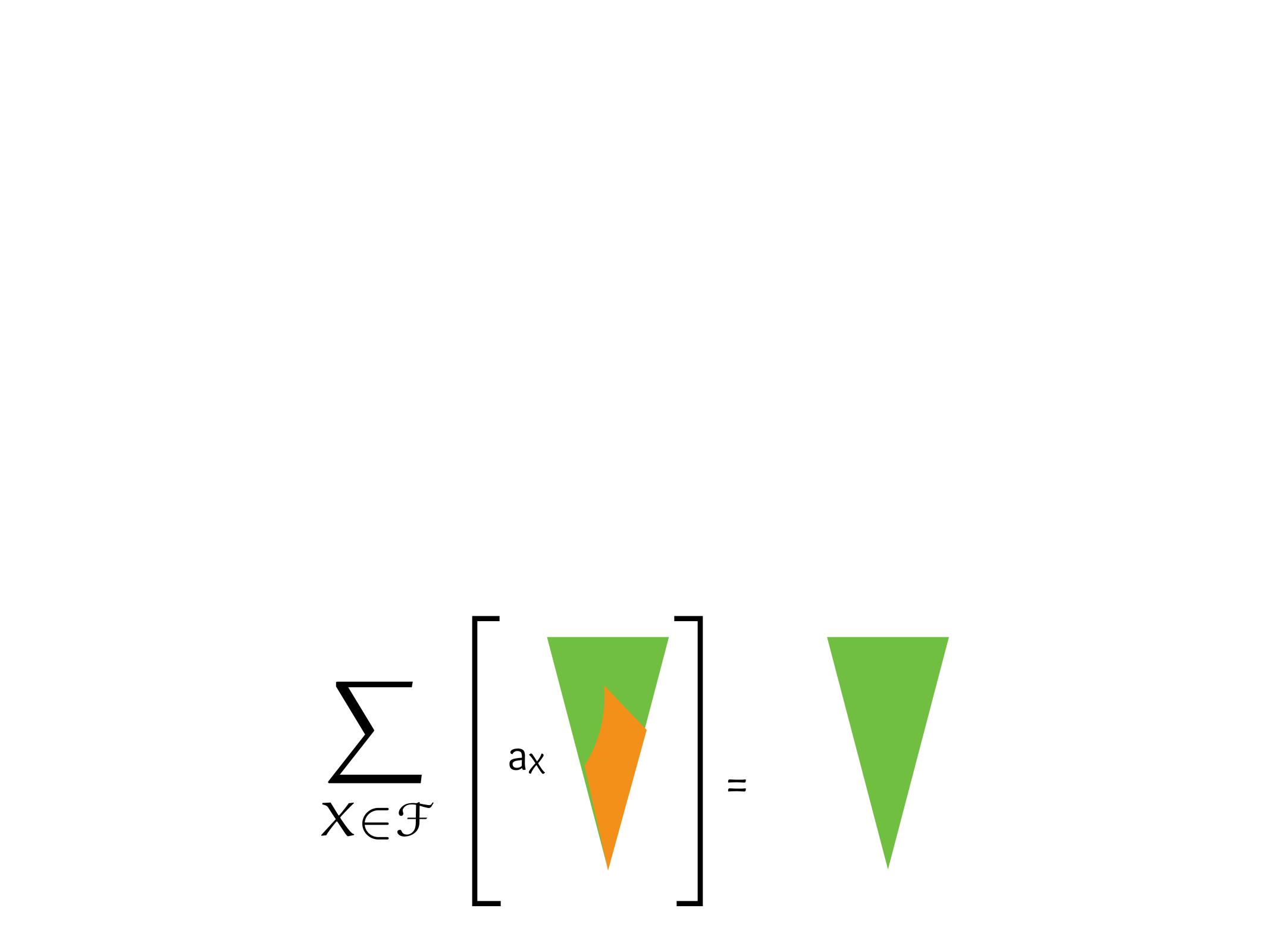
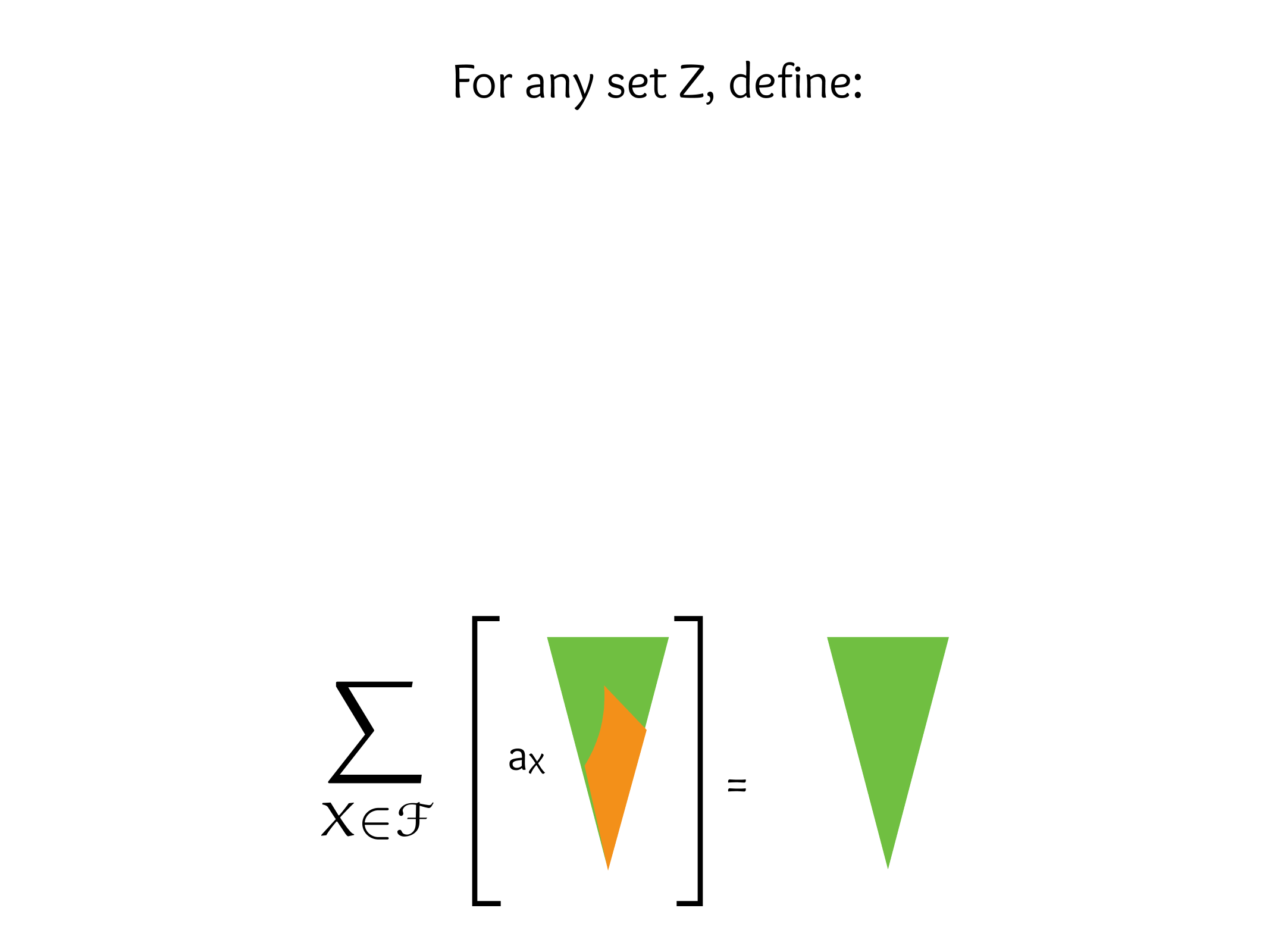
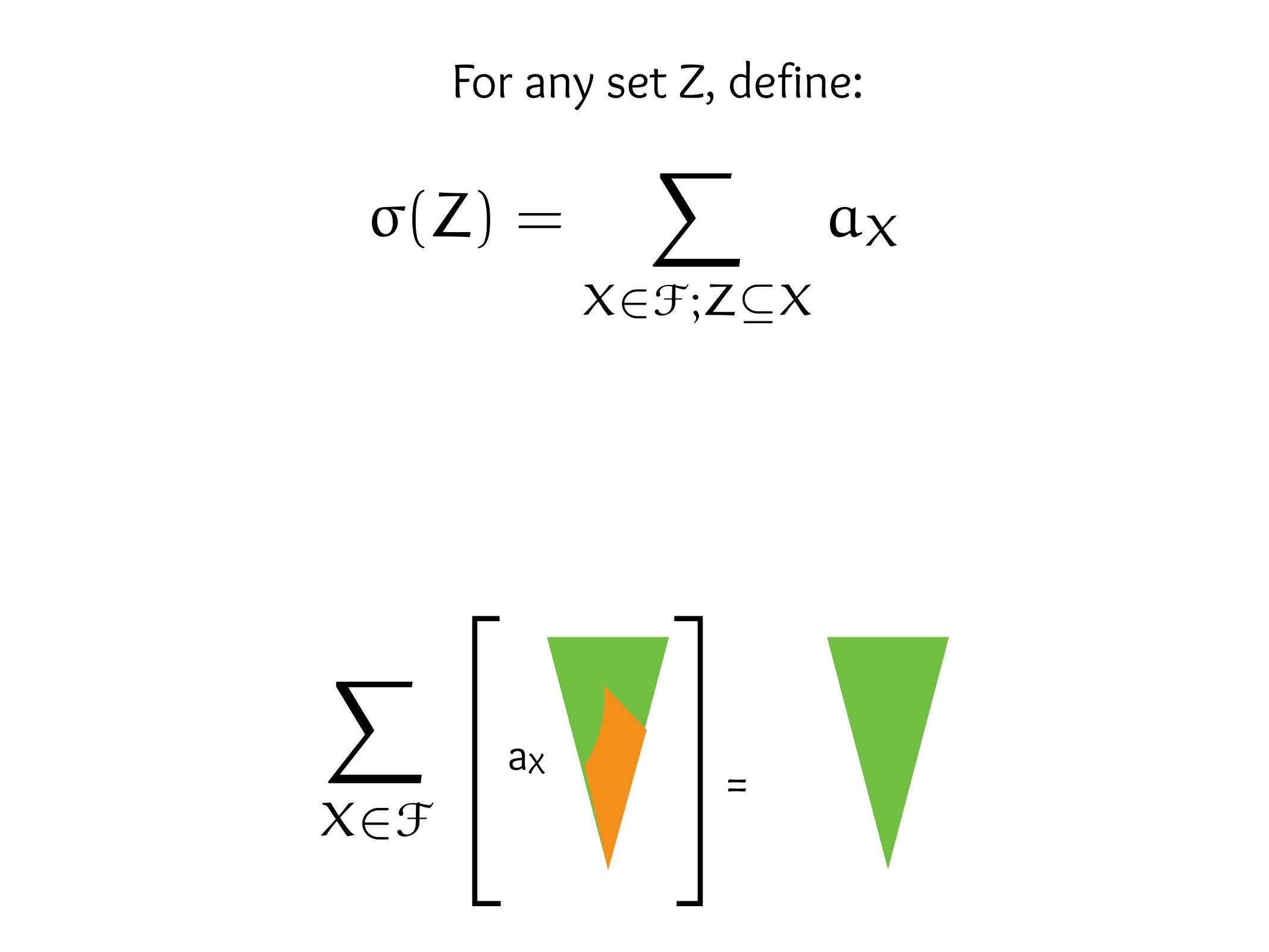
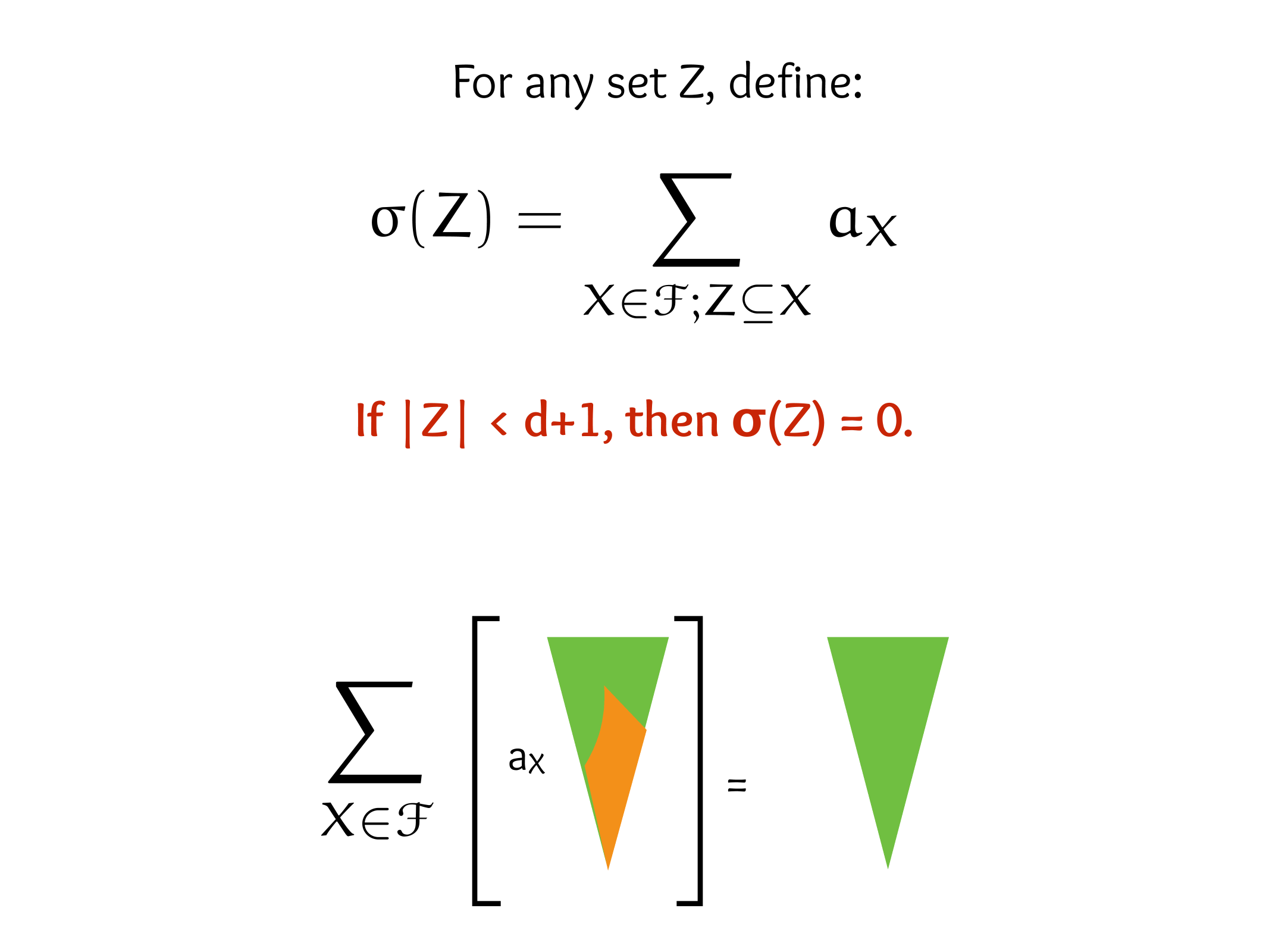
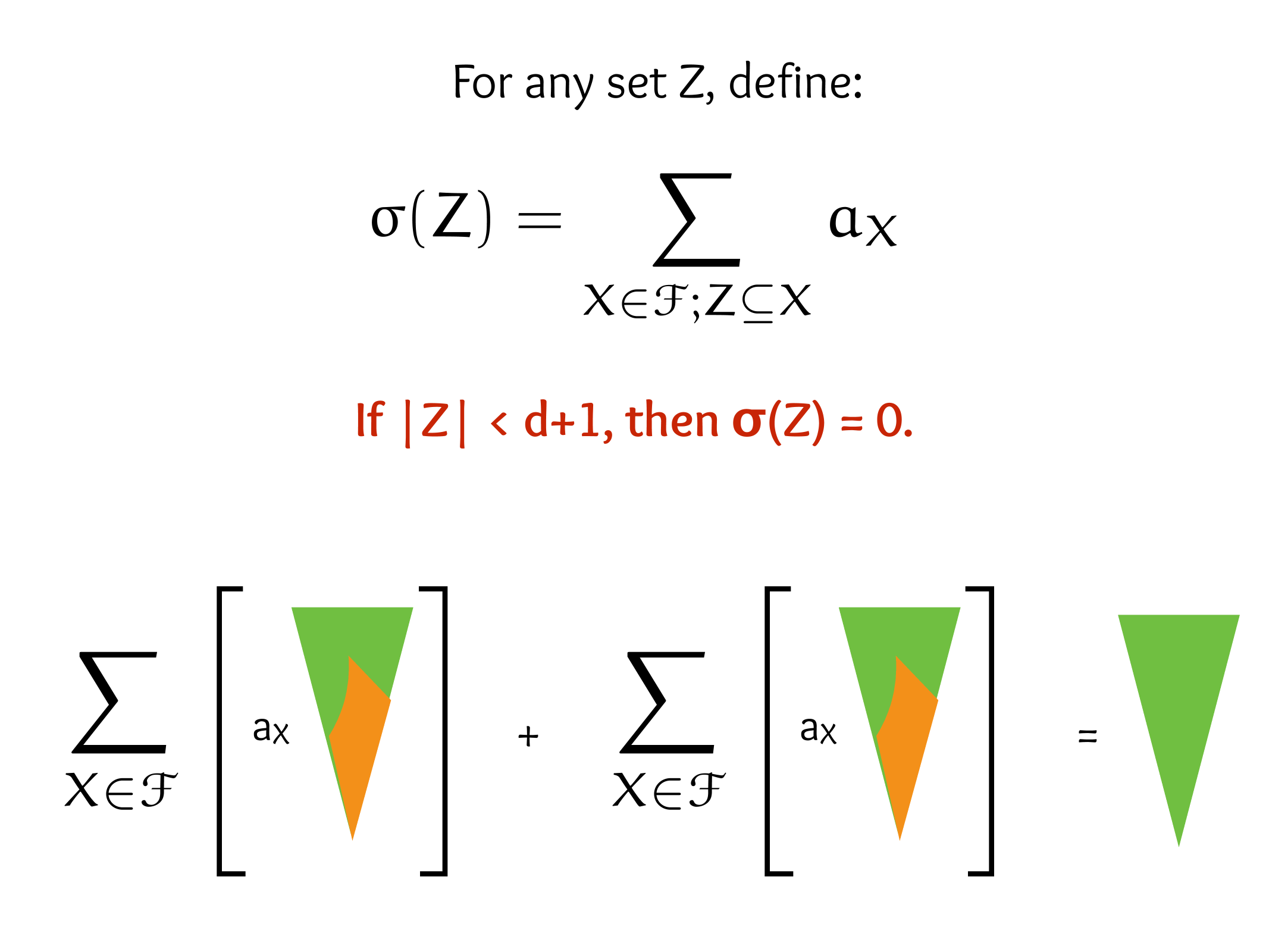
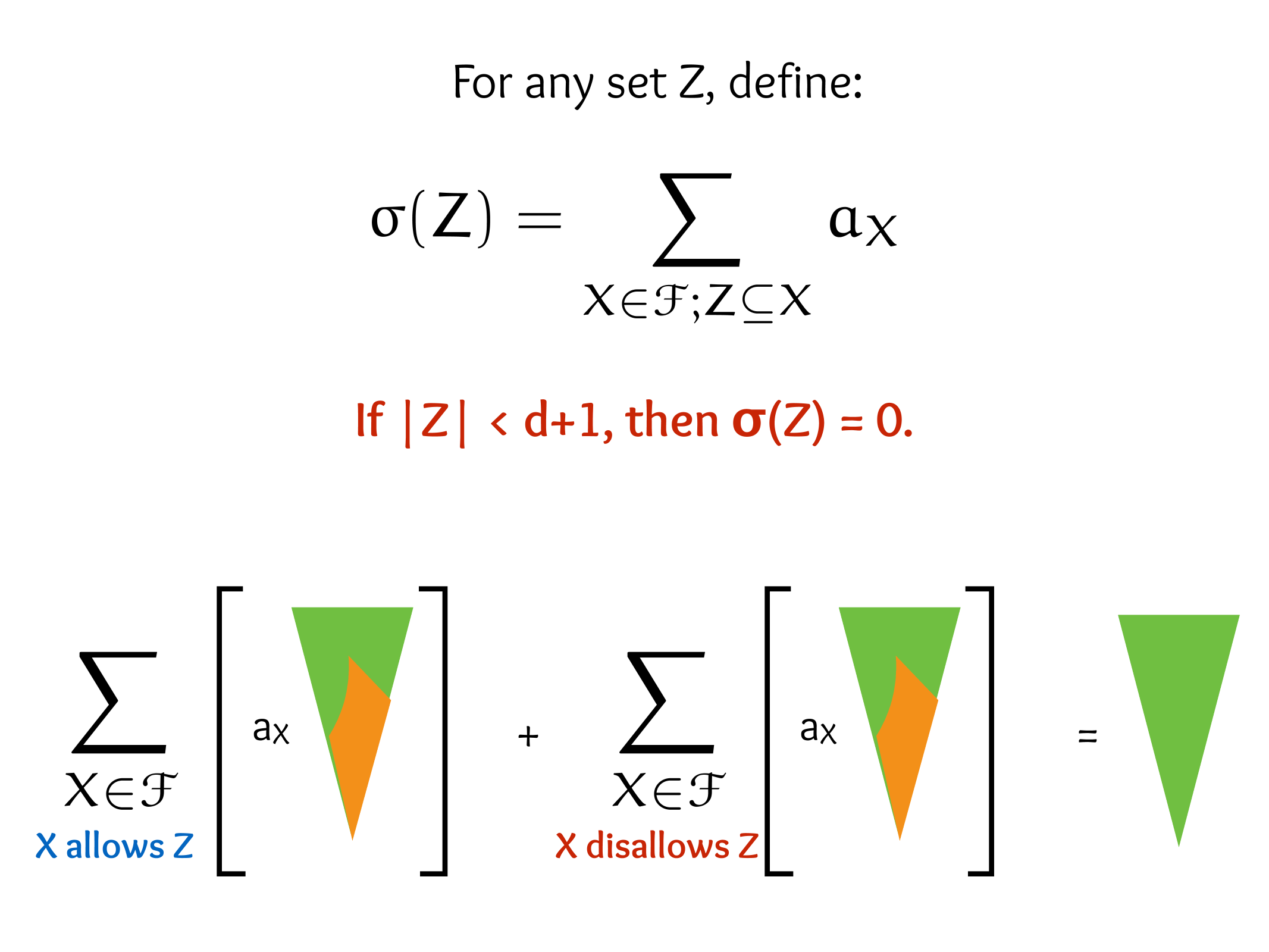
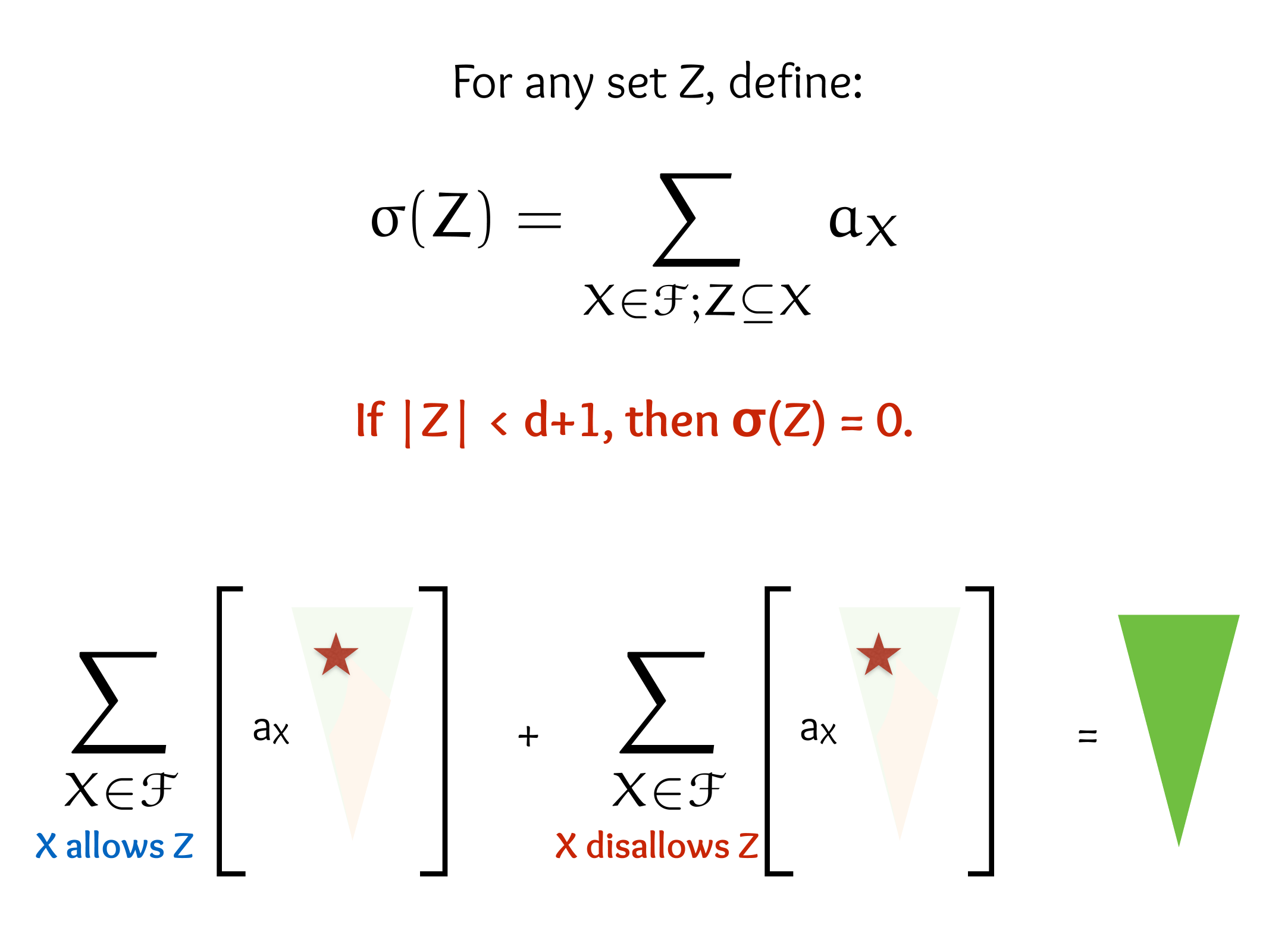
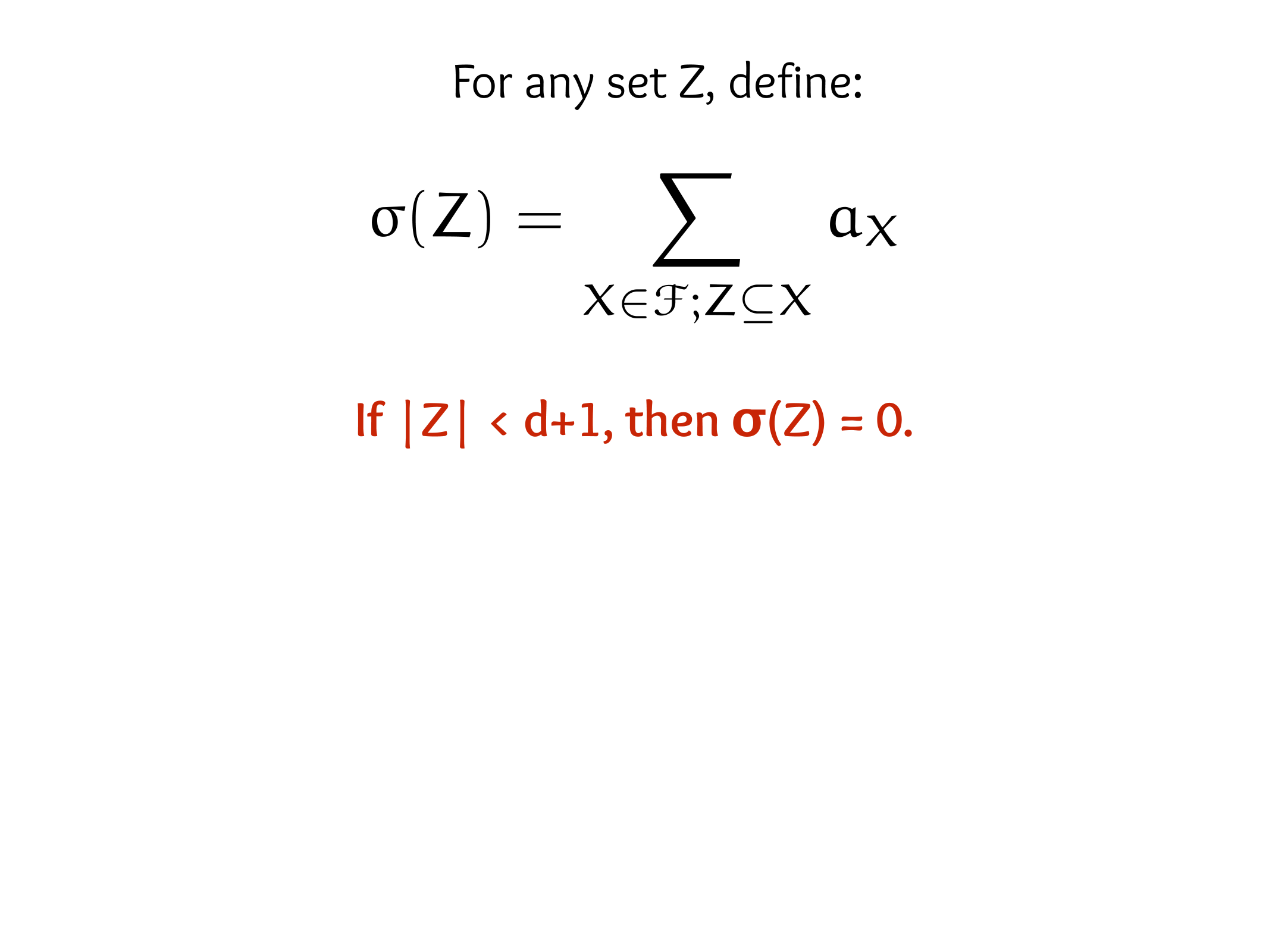

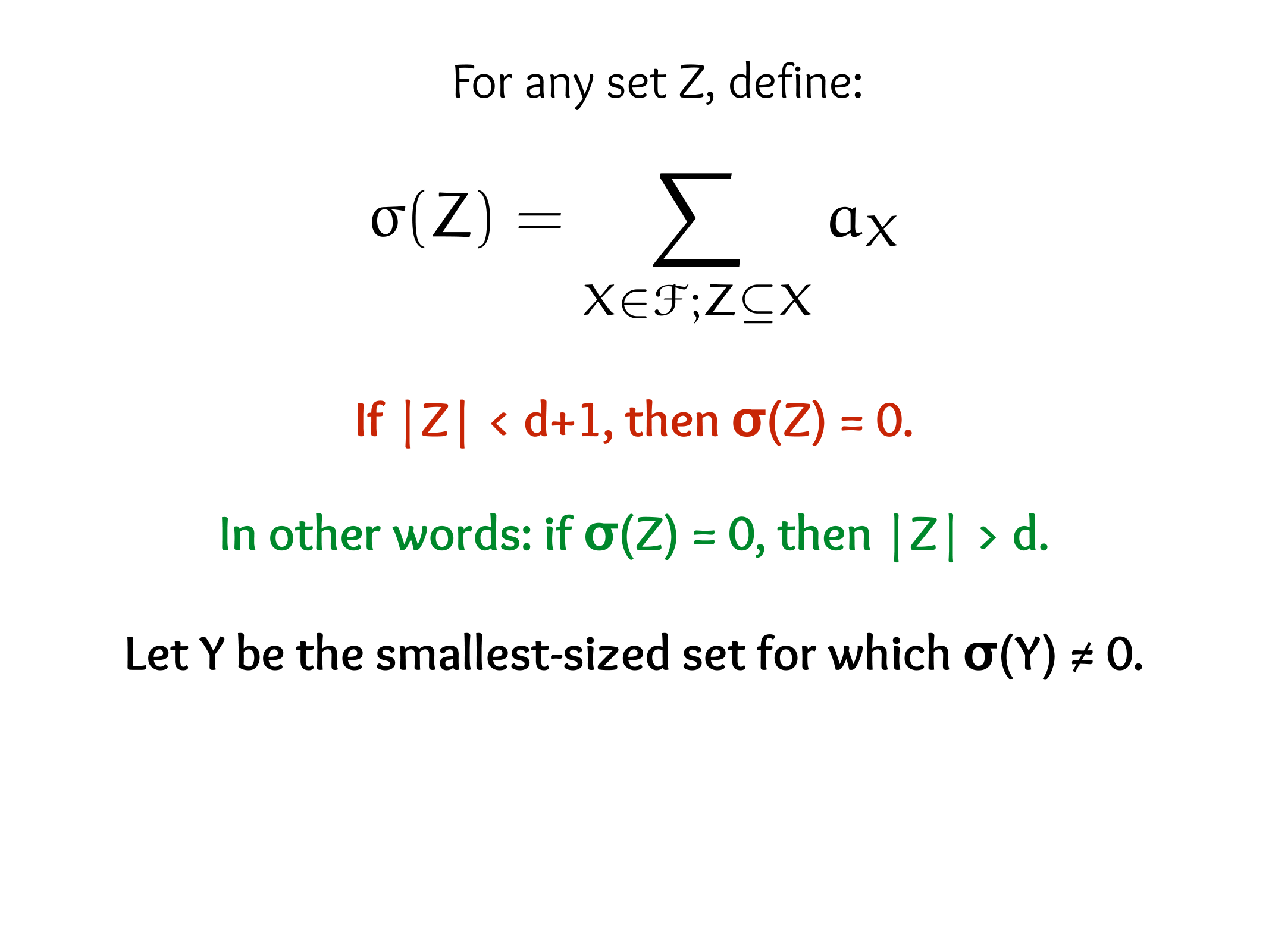
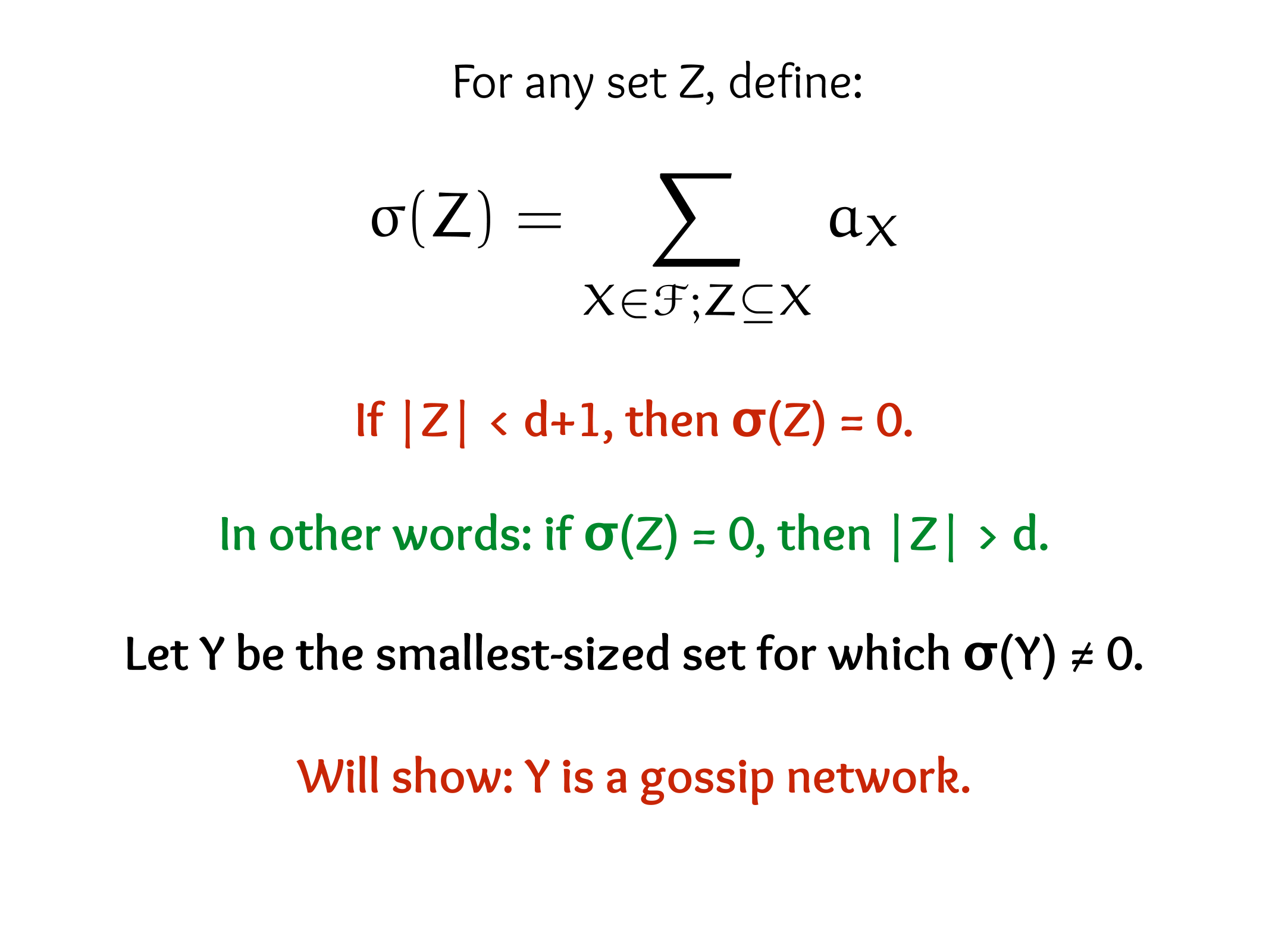
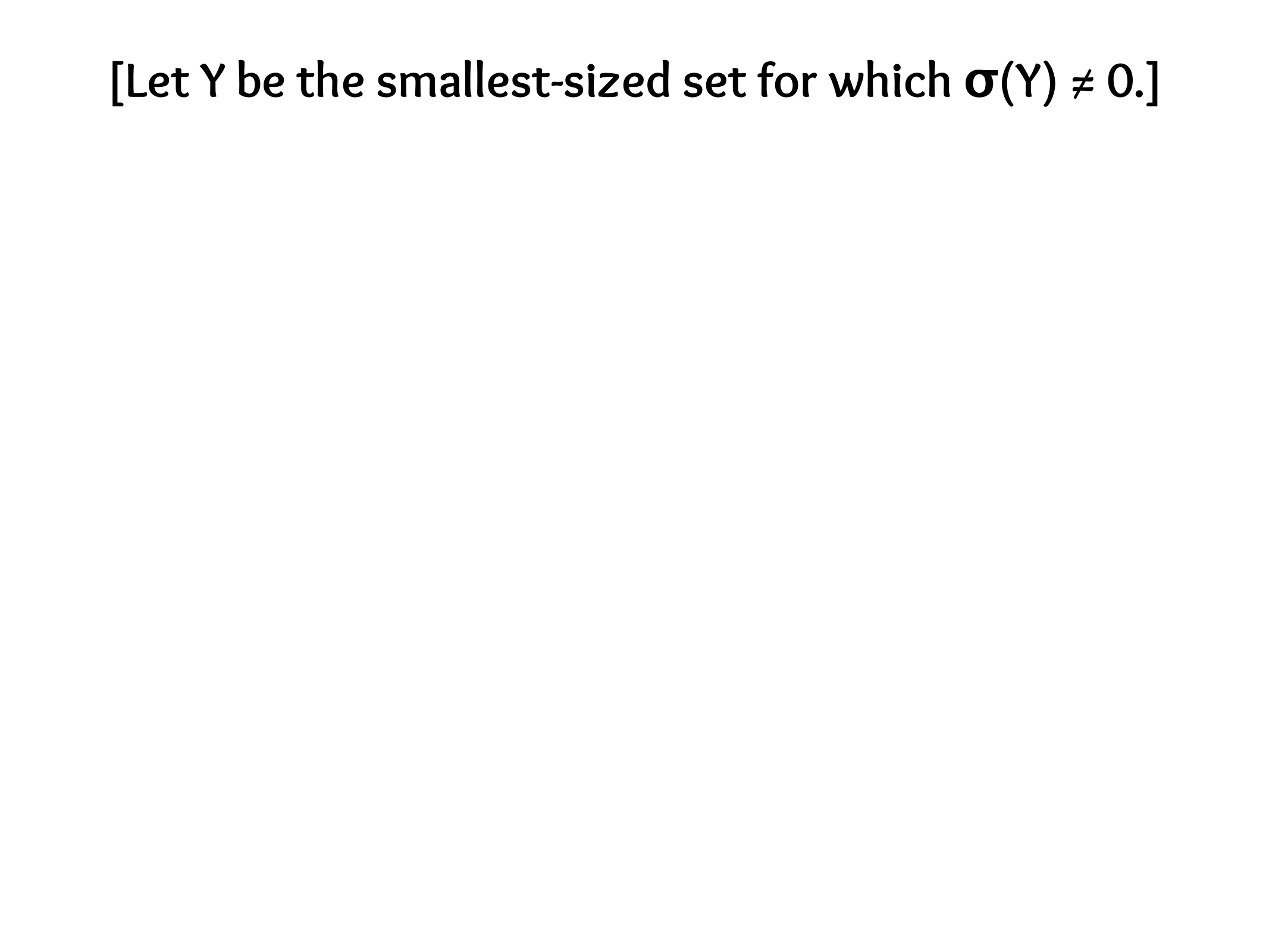

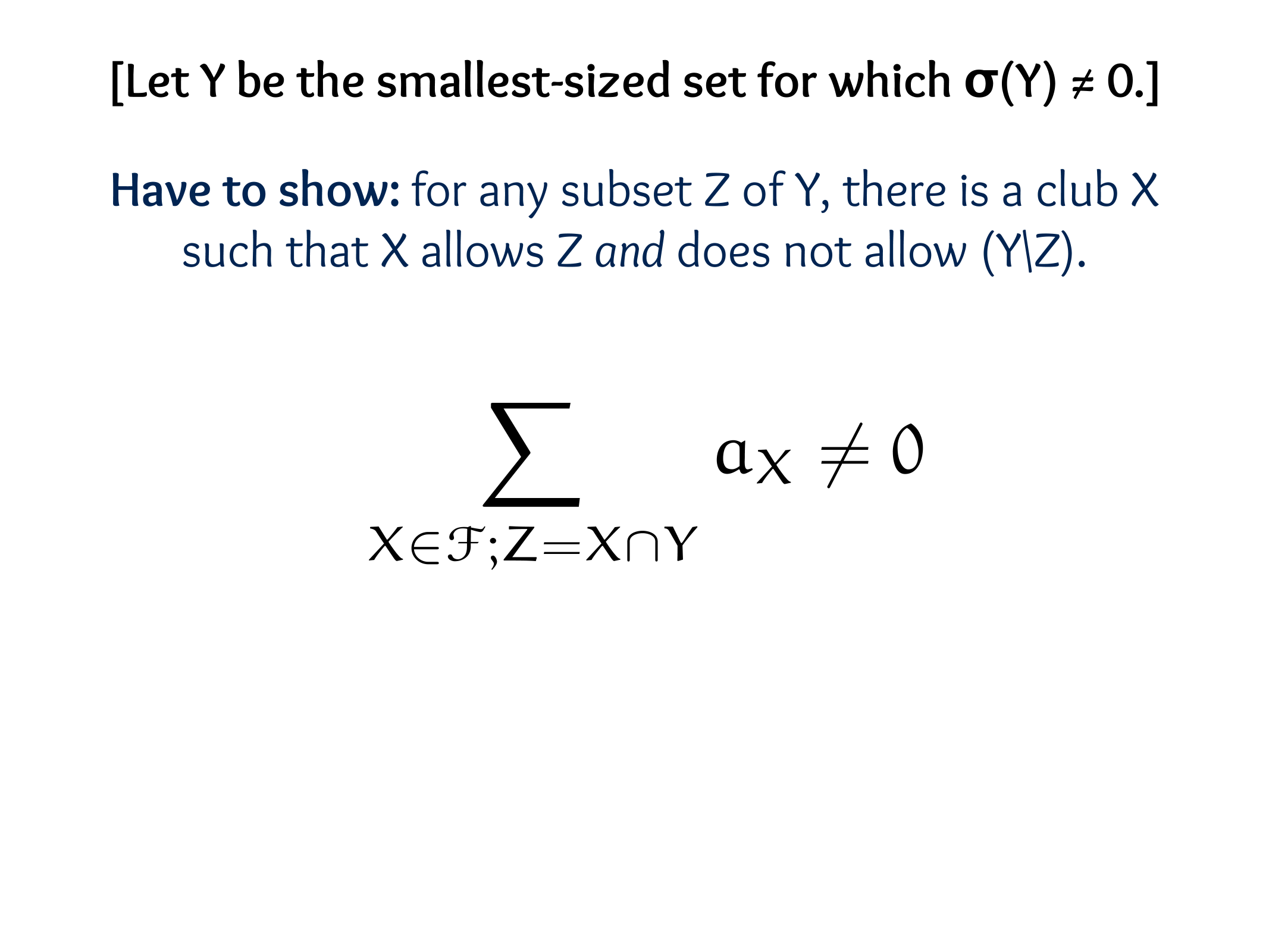


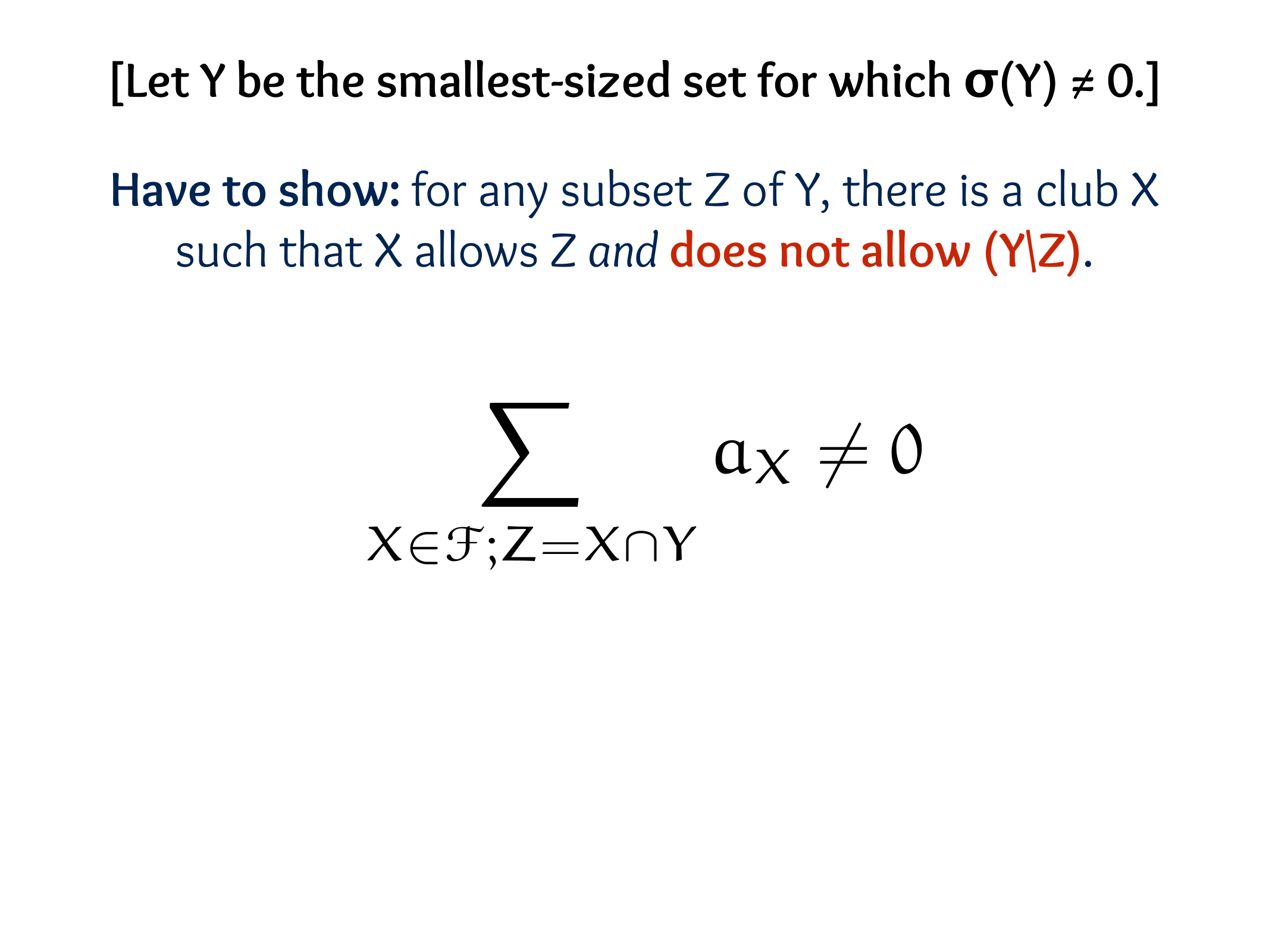









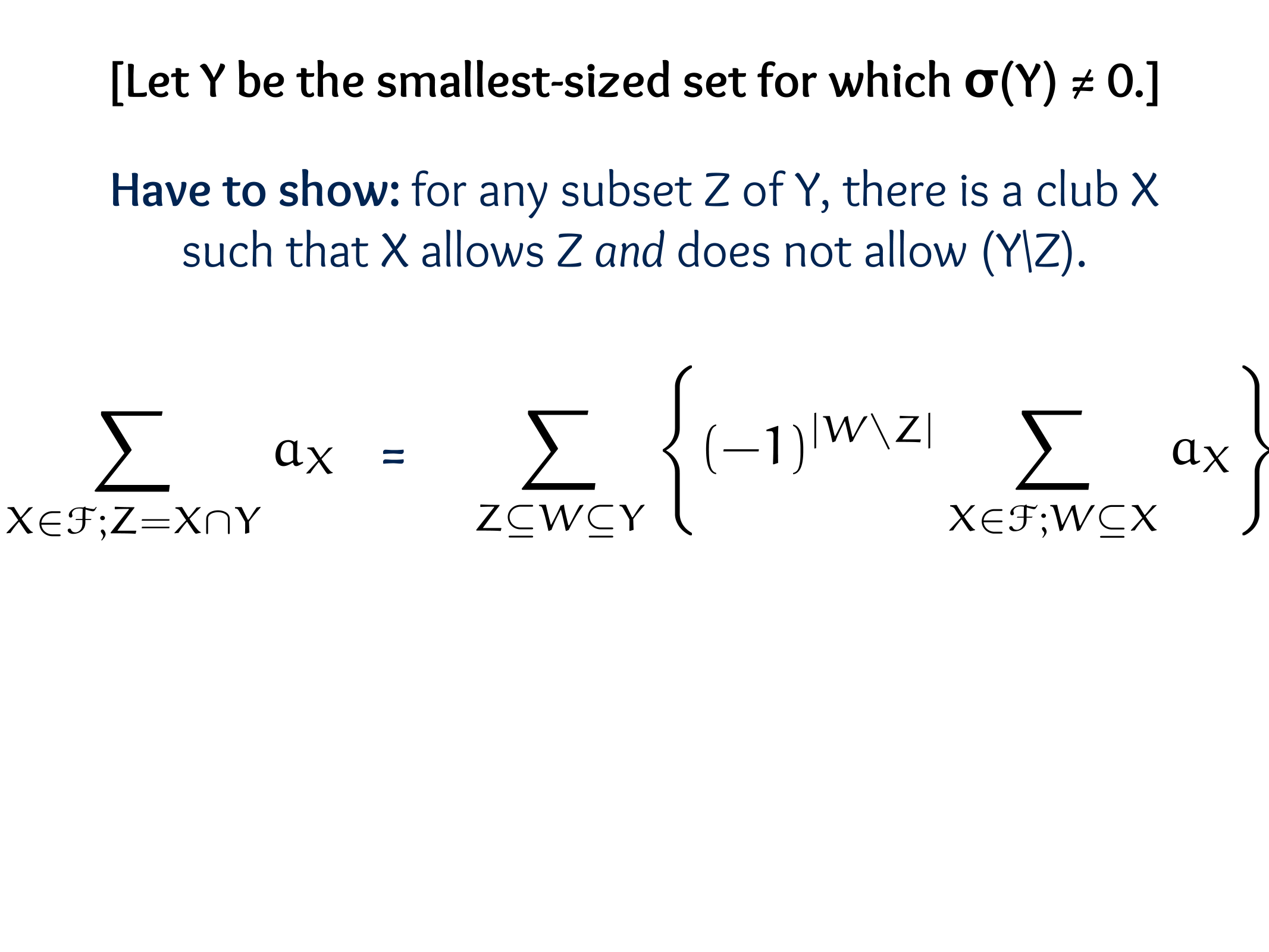
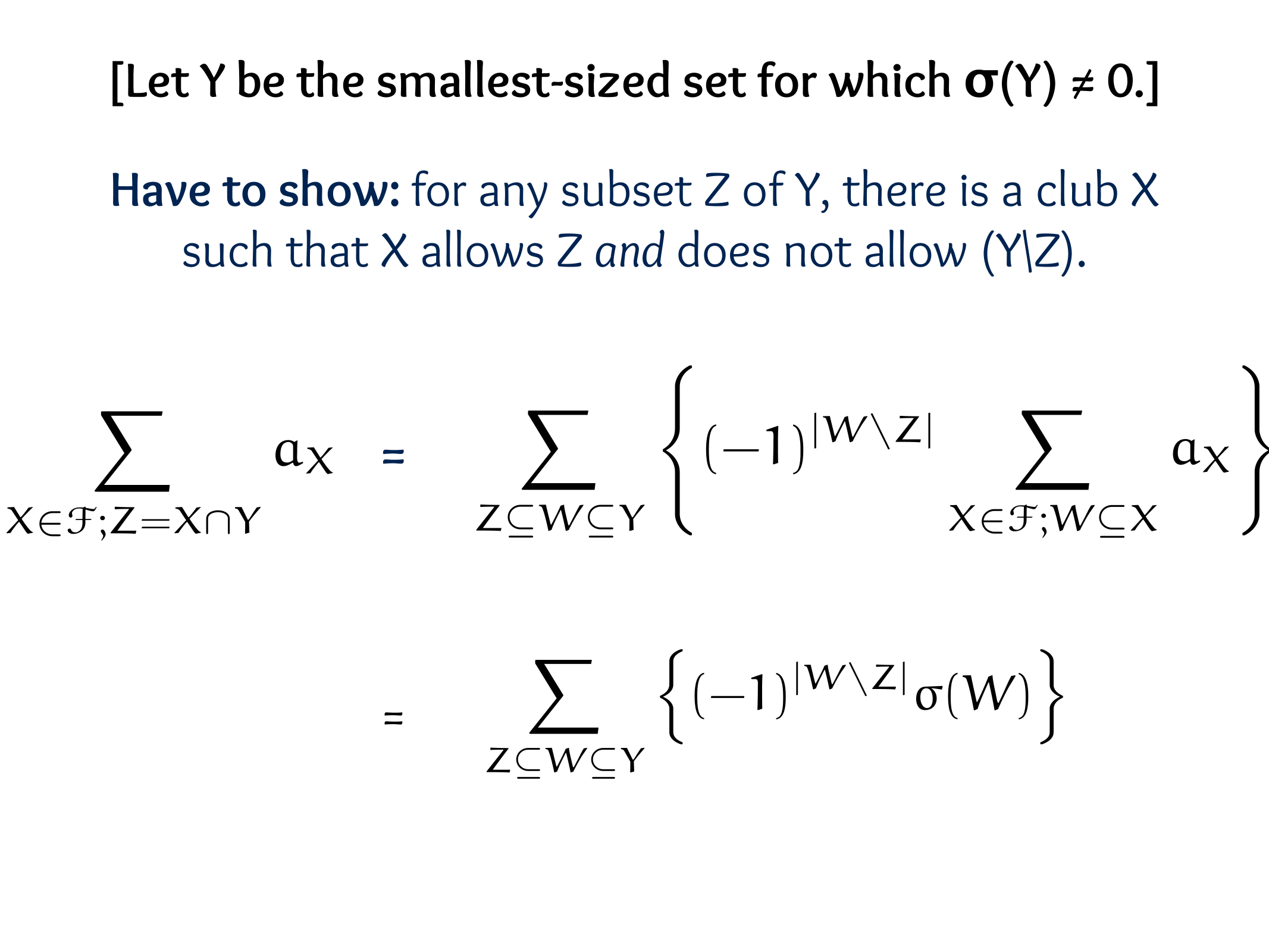
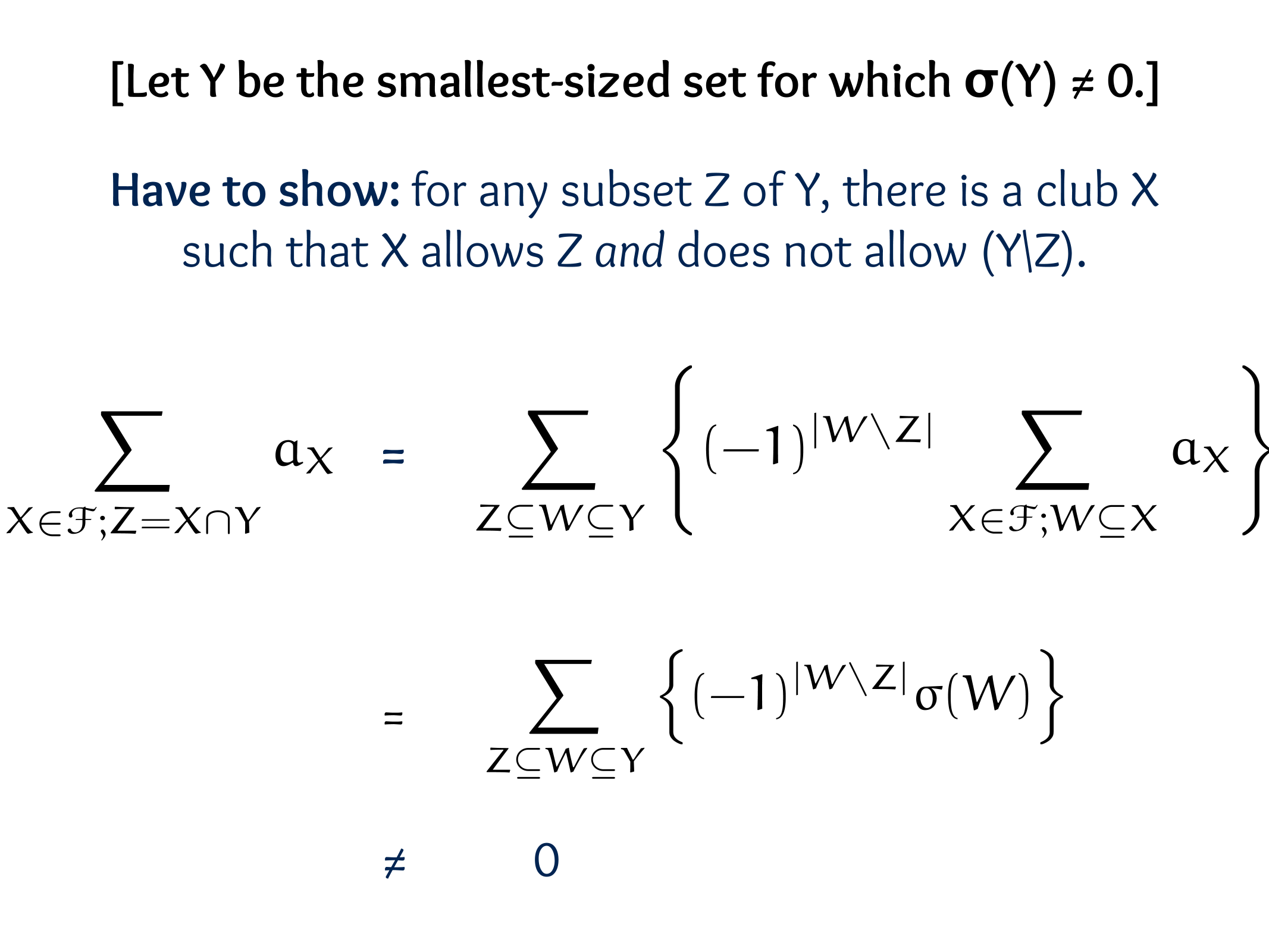






CS607. Combinatorics
with Applications in Computer Science
#05. Extremal Set Systems (sunflowers)
18 Jan 2024
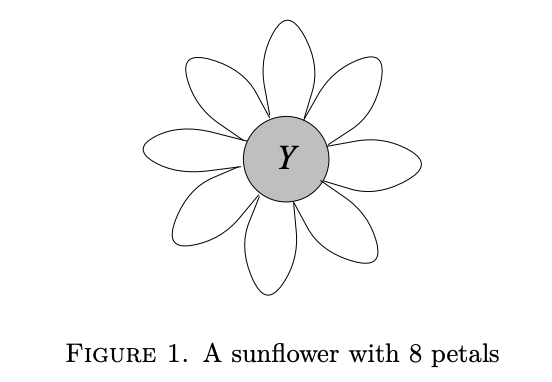
Suppose \(W\) is a set system over \(U\), that is, a collection of subsets of a set \(U\).
The collection \(W\) is a sunflower (or \(\Delta\)-system) if
there is a subset \(S\) of \(U\) such that for each distinct \(A\) and \(B\) in \(W\),
we have \(A \cap B=S\).
In other words, a set system or collection of sets \(W\) is a sunflower if
all sets in \(W\) share the same common subset of elements.
An element in \(U\) is either found the common subset \(S\) or else
appears in at most one of the \(W\) elements.
No element of \(U\) is shared by just some of the \(W\) subset,
but not others.
Suppose \(W\) is a set system over \(U\), that is, a collection of subsets of a set \(U\).
The collection \(W\) is a sunflower (or \(\Delta\)-system) if
there is a subset \(S\) of \(U\) such that for each distinct \(A\) and \(B\) in \(W\),
we have \(A \cap B=S\).
Suppose \(W\) is a set system over \(U\), that is, a collection of subsets of a set \(U\).
The collection \(W\) is a sunflower (or \(\Delta\)-system) if
there is a subset \(S\) of \(U\) such that for each distinct \(A\) and \(B\) in \(W\),
we have \(A \cap B=S\).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
(It is not clear that such an \(n\) must exist.)
Suppose \(W\) is a set system over \(U\), that is, a collection of subsets of a set \(U\).
The collection \(W\) is a sunflower (or \(\Delta\)-system) if
there is a subset \(S\) of \(U\) such that for each distinct \(A\) and \(B\) in \(W\),
we have \(A \cap B=S\).
Erdős & Rado (1960, p. 86) proved the sunflower lemma, which states that:
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}.\)
That is, if \(k\) and \(r\) are positive integers, then a set system \(W\) of cardinality
greater than or equal to \(k !(r-1)^k\) of sets of cardinality \(k\)
contains a sunflower with at least \(r\) sets.
Proof (sketch, by induction).
First, \(f(1, r) \leqslant r-1\), since...
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
Proof (sketch, by induction).
First, \(f(1, r) \leqslant r-1\), since the set system \(W\) must be a collection of distinct sets of size one, and so \(r\) of these sets make a sunflower.
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Because we assumed that \(W\) had no sunflower of size \(r\),
and a collection of pairwise disjoint sets is a sunflower, \(t<{\color{White}r}\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Because we assumed that \(W\) had no sunflower of size \(r\),
and a collection of pairwise disjoint sets is a sunflower, \(t<{\color{SeaGreen}r}\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Let \(A=A_1 \cup A_2 \cup \cdots \cup A_t\).
Since each \(A_i\) has cardinality \(k\), the cardinality of \(A\) is bounded by \({\color{White}k t \leq k(r-1)}\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Let \(A=A_1 \cup A_2 \cup \cdots \cup A_t\).
Since each \(A_i\) has cardinality \(k\), the cardinality of \(A\) is bounded by \({\color{SeaGreen}k t \leq k(r-1)}\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Define \(W_a\) for some \(a \in A\) to be \({\color{DodgerBlue}W_a=\{S \backslash\{a\} \mid a \in S, S \in W\}}\).
Every sunflower of \(W_a\) corresponds to a sunflower of \(W\). (why?)
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Define \(W_a\) for some \(a \in A\) to be \({\color{DodgerBlue}W_a=\{S \backslash\{a\} \mid a \in S, S \in W\}}\).
Every sunflower of \(W_a\) corresponds to a sunflower of \(W\).
(We can add \(a\) back to every set.)
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Define \(W_a\) for some \(a \in A\) to be \({\color{DodgerBlue}W_a=\{S \backslash\{a\} \mid a \in S, S \in W\}}\).
This means that, by our assumption that \(W\) has no sunflower of size \(r\), the size of \(W_a\) must be bounded by \({\color{white}f(k-1,r)-1}\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Define \(W_a\) for some \(a \in A\) to be \({\color{DodgerBlue}W_a=\{S \backslash\{a\} \mid a \in S, S \in W\}}\).
This means that, by our assumption that \(W\) has no sunflower of size \(r\), the size of \(W_a\) must be bounded by \({\color{IndianRed}f(k-1,r)-1}\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Define \(W_a\) for some \(a \in A\) to be \({\color{DodgerBlue}W_a=\{S \backslash\{a\} \mid a \in S, S \in W\}}\).
Since every set \(S \in W\) intersects with one of the \(A_i\)'s, it intersects with \(A\), and so it corresponds to at least one of the sets in a \(W_a\).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Proof (sketch, by induction).
The function \(f(k, r)\) for nonnegative integers \(k, r\),
is defined to be the smallest nonnegative integer \(n\) such that,
for any set system \(W\) such that every set \(S \in W\) has cardinality at most \(k\),
if \(W\) has more than \(n\) sets, then \(W\) contains a sunflower of \(r\) sets.
\({\color{IndianRed}f(k, r) \leq k !(r-1)^k}\)
In the general case, suppose \(W\) has no sunflower with \(r\) sets.
Then consider \(A_1, A_2, \ldots, A_t \in W\) to be a maximal collection of pairwise disjoint sets
(that is, \(A_i \cap A_j\) is the empty set unless \(i=j\), and every set in \(W\) intersects with some \(A_i\) ).
Define \(W_a\) for some \(a \in A\) to be \({\color{DodgerBlue}W_a=\{S \backslash\{a\} \mid a \in S, S \in W\}}\).
\(|W| \leqslant \sum_{a \in A}\left|W_a\right| \leqslant |A|(f(k-1, r)-1) \leqslant k(r-1) f(k-1, r)-|A| \leqslant k(r-1) f(k-1, r)-1\)
What if we relax the disjointness property of sunflowers, and only require
that the differences \(S_1 \backslash Y, \ldots, S_k \backslash Y\)
cannot be intersected (blocked) by a set of size smaller than some number \(t\)?
In this case we say that sets \(S_1, \ldots, S_k\) form a flower with \(t\) petals.
A blocking set of a family \(\mathcal{F}\) is a set which intersects all the members of \(\mathcal{F}\);
the minimum number of elements in a blocking set is the blocking number of \(\mathcal{F}\)
and is denoted by \(\tau(\mathcal{F})\); if \(\emptyset \in \mathcal{F}\) then we set \(\tau(\mathcal{F})=0\).
What if we relax the disjointness property of sunflowers, and only require
that the differences \(S_1 \backslash Y, \ldots, S_k \backslash Y\)
cannot be intersected (blocked) by a set of size smaller than some number \(t\)?
In this case we say that sets \(S_1, \ldots, S_k\) form a flower with \(t\) petals.
A blocking set of a family \(\mathcal{F}\) is a set which intersects all the members of \(\mathcal{F}\);
the minimum number of elements in a blocking set is the blocking number of \(\mathcal{F}\)
and is denoted by \(\tau(\mathcal{F})\); if \(\emptyset \in \mathcal{F}\) then we set \(\tau(\mathcal{F})=0\).
A restriction of a family \(\mathcal{F}\) onto a set \(Y\) is the family
\(\mathcal{F}_Y:=\{S \backslash Y: S \in \mathcal{F}, S \supseteq Y\} .\)
What if we relax the disjointness property of sunflowers, and only require
that the differences \(S_1 \backslash Y, \ldots, S_k \backslash Y\)
cannot be intersected (blocked) by a set of size smaller than some number \(t\)?
In this case we say that sets \(S_1, \ldots, S_k\) form a flower with \(t\) petals.
A blocking set of a family \(\mathcal{F}\) is a set which intersects all the members of \(\mathcal{F}\);
the minimum number of elements in a blocking set is the blocking number of \(\mathcal{F}\)
and is denoted by \(\tau(\mathcal{F})\); if \(\emptyset \in \mathcal{F}\) then we set \(\tau(\mathcal{F})=0\).
A restriction of a family \(\mathcal{F}\) onto a set \(Y\) is the family
\(\mathcal{F}_Y:=\{S \backslash Y: S \in \mathcal{F}, S \supseteq Y\} .\)
A flower with \(k\) petals and a core \(Y\) is a family \(\mathcal{F}\) such that \(\tau\left(\mathcal{F}_Y\right) \geq k\).
Note that every sunflower is a flower with the same number of petals,
but not every flower is a sunflower (give an example?).
Let \(\mathcal{F}\) be a family of sets each of cardinality \(s\), and \(k \geq 1\) and integer.
If \(|\mathcal{F}|>(k-1)^s\) then \(\mathcal{F}\) contains a flower with \(k\) petals.
In this case we say that sets \(S_1, \ldots, S_k\) form a flower with \(t\) petals.
A blocking set of a family \(\mathcal{F}\) is a set which intersects all the members of \(\mathcal{F}\);
the minimum number of elements in a blocking set is the blocking number of \(\mathcal{F}\)
and is denoted by \(\tau(\mathcal{F})\); if \(\emptyset \in \mathcal{F}\) then we set \(\tau(\mathcal{F})=0\).
A restriction of a family \(\mathcal{F}\) onto a set \(Y\) is the family
\(\mathcal{F}_Y:=\{S \backslash Y: S \in \mathcal{F}, S \supseteq Y\} .\)
A flower with \(k\) petals and a core \(Y\) is a family \(\mathcal{F}\) such that \(\tau\left(\mathcal{F}_Y\right) \geq k\).
Note that every sunflower is a flower with the same number of petals,
but not every flower is a sunflower (give an example?).
CS607. Combinatorics
with Applications in Computer Science
#05. Extremal Set Systems (applications of sunflowers)
29 Jan 2024
Application #1. Number of minterms
Let \(x_1, \ldots, x_n\) be boolean variables taking their values in \(\{0,1\}\).
A monomial is an AND of literals, and a clause is an OR of literals, where a literal is either a variable \(x_i\) or its negation \(\bar{x}_i=x_i \oplus 1\).
Thus, we have \(2^s{n \choose s}\) monomials and that many clauses of size \(s\).
A 1-term of a boolean function \(f:\{0,1\}^n \rightarrow\{0,1\}\) is a monomial \(M\) such that \(M(a) \leq f(a)\) for all inputs \(a \in\{0,1\}^n\).
That is, if we set all literals of \(M\) to 1 , then the function \(f\) is forced to take value 1 independent on what values we assign to the remaining variables.
Application #1. Number of minterms
Let \(x_1, \ldots, x_n\) be boolean variables taking their values in \(\{0,1\}\).
A monomial is an AND of literals, and a clause is an OR of literals, where a literal is either a variable \(x_i\) or its negation \(\bar{x}_i=x_i \oplus 1\).
Thus, we have \(2^s{n \choose s}\) monomials and that many clauses of size \(s\).
Dually, a 0 -term of \(f\) is a clause \(C\) such that \(C(a) \geq f(a)\) for all inputs \(a \in\{0,1\}^n\).
A minterm of \(f\) is a 1-term \(M\) of \(f\) which is minimal in the sense that deleting every single literal from \(M\) already violates this property.
Application #1. Number of minterms
Let \(x_1, \ldots, x_n\) be boolean variables taking their values in \(\{0,1\}\).
A monomial is an AND of literals, and a clause is an OR of literals, where a literal is either a variable \(x_i\) or its negation \(\bar{x}_i=x_i \oplus 1\).
A boolean function \(f\) is a \(t-\)AND\(-\)OR ( or a \(t-\)CNF ) if
it can be written as an And of an arbitrary number of clauses, each of size at most \(t\).
A minterm of \(f\) is a 1-term \(M\) of \(f\) which is minimal in the sense that deleting every single literal from \(M\) already violates this property.
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Application #1. Number of minterms
Proof (sketch).
Let \(f=C_1 \wedge \cdots \wedge C_m\), where each clause \(C_i\) has size at most \(t\).
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Application #1. Number of minterms
Proof (sketch).
Let \(f=C_1 \wedge \cdots \wedge C_m\), where each clause \(C_i\) has size at most \(t\).
We interpret the clauses as sets of their literals, and let \(\mathcal{C}=\left\{C_1, \ldots, C_m\right\}\) be the corresponding family of these sets.
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Application #1. Number of minterms
Proof (sketch).
Let \(f=C_1 \wedge \cdots \wedge C_m\), where each clause \(C_i\) has size at most \(t\).
We interpret the clauses as sets of their literals, and let \(\mathcal{C}=\left\{C_1, \ldots, C_m\right\}\) be the corresponding family of these sets.
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Let \(\mathcal{F}\) be the family of all minterms of \(f\) that have size \(s\)
(we look at minterms as sets of their literals).
Application #1. Number of minterms
Proof (sketch).
Let \(f=C_1 \wedge \cdots \wedge C_m\), where each clause \(C_i\) has size at most \(t\).
We interpret the clauses as sets of their literals, and let \(\mathcal{C}=\left\{C_1, \ldots, C_m\right\}\) be the corresponding family of these sets.
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Let \(\mathcal{F}\) be the family of all minterms of \(f\) that have size \(s\)
(we look at minterms as sets of their literals).
Then every set in \(\mathcal{C}\) intersects each set in \(\mathcal{F}\). (why?)
Application #1. Number of minterms
Proof (sketch).
Let \(f=C_1 \wedge \cdots \wedge C_m\), where each clause \(C_i\) has size at most \(t\).
We interpret the clauses as sets of their literals, and let \(\mathcal{C}=\left\{C_1, \ldots, C_m\right\}\) be the corresponding family of these sets.
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Let \(\mathcal{F}\) be the family of all minterms of \(f\) that have size \(s\)
(we look at minterms as sets of their literals).
Suppose that \(|\mathcal{F}|>t^s\).
Application #1. Number of minterms
Proof (sketch).
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Suppose that \(|\mathcal{F}|>t^s\).
Then, \(\mathcal{F}\) has a flower with \(t+1\) petals.
That is, there exists a set of literals \(Y\) such that no set of at most \(t\) literals can intersect all the members of the family
\(\mathcal{F}_Y=\{M \backslash Y: M \in \mathcal{F}, M \supseteq Y\}\)
Application #1. Number of minterms
Proof (sketch).
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Suppose that \(|\mathcal{F}|>t^s\).
\(\mathcal{F}_Y=\{M \backslash Y: M \in \mathcal{F}, M \supseteq Y\}\)
The set \(Y\) is a proper part of at least one minterm of \(f\), meaning that \(Y\) cannot intersect all the clauses in \(\mathcal{C}\).
Application #1. Number of minterms
Proof (sketch).
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Suppose that \(|\mathcal{F}|>t^s\).
\(\mathcal{F}_Y=\{M \backslash Y: M \in \mathcal{F}, M \supseteq Y\}\)
The set \(Y\) is a proper part of at least one minterm of \(f\), meaning that \(Y\) cannot intersect all the clauses in \(\mathcal{C}\).
Take a clause \(C \in \mathcal{C}\) such that \(C \cap Y=\emptyset\).
Application #1. Number of minterms
Proof (sketch).
Let \(f\) be a \(t-\)CNF function on \(n\) variables.
Then for every \(s=1, \ldots, n\) the function \(f\) has at most \(t^s\) minterms of size \(s\).
Suppose that \(|\mathcal{F}|>t^s\).
\(\mathcal{F}_Y=\{M \backslash Y: M \in \mathcal{F}, M \supseteq Y\}\)
The set \(Y\) is a proper part of at least one minterm of \(f\), meaning that \(Y\) cannot intersect all the clauses in \(\mathcal{C}\).
Take a clause \(C \in \mathcal{C}\) such that \(C \cap Y=\emptyset\).
Since this clause intersects all the sets in \(\mathcal{F}\), this means that it must intersect all the sets in \(\mathcal{F}_Y\).
Application #2. Small Depth Formulas
An s-threshold function is a monotone boolean function \(T_s^n\) which accepts
a \(0-1\) vector if and only if it has at least \(s\) ones.
That is, \(T_s^n\left(x_1, \ldots, x_n\right)=1 \text { if and only if } x_1+\cdots+x_n \geq s \text {. }\)
This function can be computed by the following formula:
\(\large{T_s^n\left(x_1, \ldots, x_n\right)=\bigvee_{I:|I|=s} \bigwedge_{i \in I} x_i .}\)
This formula is monotone (has no negated literals) and
has depth 2 (there are only two alternations between And and Or operations).
But the size of this formula (the number of literals in it) is \(s{n \choose s}\).
Can \(T_s^n\) be computed by a substantially smaller formula if we allow negated literals and/or a larger depth?
Application #2. Small Depth Formulas
An s-threshold function is a monotone boolean function \(T_s^n\) which accepts
a \(0-1\) vector if and only if it has at least \(s\) ones.
That is, \(T_s^n\left(x_1, \ldots, x_n\right)=1 \text { if and only if } x_1+\cdots+x_n \geq s \text {. }\)
Håstad (1986) proved that, for \(s=\lfloor n / 2\rfloor\), each such formula computing \(T_s^n\) must have size exponential in \(n\), even if we allow any constant depth, i.e., any constant number of alternations of AND's and OR's.
Razborov (1987) has proved that the same holds even if we allow sum modulo 2 as an additional operation.
Both these proofs employ non-trivial machinery: the switching lemma and approximations of boolean functions by low-degree polynomials.
Application #2. Small Depth Formulas
An s-threshold function is a monotone boolean function \(T_s^n\) which accepts
a \(0-1\) vector if and only if it has at least \(s\) ones.
That is, \(T_s^n\left(x_1, \ldots, x_n\right)=1 \text { if and only if } x_1+\cdots+x_n \geq s \text {. }\)
On the other hand, Håstad et al. (1995) have shown that,
at least for depth-3, one can deduce the same lower bound
in an elementary way using the flower lemma.
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
Proof (sketch). Suppose that \(F\) accepts more than \(t k^s\) vectors with precisely \(s\) ones. Then some of its And-Or subformulas \(F_i\) accepts more than \({\color{white}k^s}\) of such vectors.
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
Proof (sketch). Suppose that \(F\) accepts more than \(t k^s\) vectors with precisely \(s\) ones. Then some of its And-Or subformulas \(F_i\) accepts more than \(k^s\) of such vectors.
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
Proof (sketch). Suppose that \(F\) accepts more than \(t k^s\) vectors with precisely \(s\) ones. Then some of its And-Or subformulas \(F_i\) accepts more than \(k^s\) of such vectors.
Let \(A\) be this set of vectors with \(s\) ones accepted by \(F_i\) hence:
\(|A| > {\color{white}k^s}\)
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
Proof (sketch). Suppose that \(F\) accepts more than \(t k^s\) vectors with precisely \(s\) ones. Then some of its And-Or subformulas \(F_i\) accepts more than \(k^s\) of such vectors.
Let \(A\) be this set of vectors with \(s\) ones accepted by \(F_i\) hence:
\(|A| > k^s\)
The formula \(F_i\) has the form \(F_i=C_1 \wedge C_2 \wedge \cdots \wedge C_r\),
where \(C_1, \ldots, C_r\) are clauses with at most \(k\) positive literals in each of them.
All these vectors must be rejected by \(F_i\), since they are rejected by the whole formula \(F\).
Let \(B\) be the set of all vectors with at most \(s-1\) ones.
Plan: show that something from \(B\) is in fact accepted by \(F_i\).
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
A: large set of vectors accepted by \(F_i\) and B: all vectors with at most \(s-1\) ones.
Say that a vector \(v\) is a \(k\)-limit for \(A\) if
for every subset \(S\) of \(k\) coordinates, there exists a vector \(u \in A\) such that
\(v \leqslant u\) (vector comparision) and
\(v\) coincides with \(u\) in all the coordinates from \(S\);
that is, \(v_i \leqslant u_i\) for all \(i\) and \(v_i=u_i\) for all \(i \in S\).
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
A: large set of vectors accepted by \(F_i\) and B: all vectors with at most \(s-1\) ones.
Say that a vector \(v\) is a \(k\)-limit for \(A\) if
for every subset \(S\) of \(k\) coordinates, there exists a vector \(u \in A\) such that
\(v \leqslant u\) (vector comparision) and
\(v\) coincides with \(u\) in all the coordinates from \(S\);
that is, \(v_i \leqslant u_i\) for all \(i\) and \(v_i=u_i\) for all \(i \in S\).
\(v\)
\(A\)
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
A: large set of vectors accepted by \(F_i\) and B: all vectors with at most \(s-1\) ones.
Say that a vector \(v\) is a \(k\)-limit for \(A\) if
for every subset \(S\) of \(k\) coordinates, there exists a vector \(u \in A\) such that
\(v \leqslant u\) (vector comparision) and
\(v\) coincides with \(u\) in all the coordinates from \(S\);
that is, \(v_i \leqslant u_i\) for all \(i\) and \(v_i=u_i\) for all \(i \in S\).
\(v\)
\(A\)
Application #2. Small Depth Formulas
Let \(F=F_1 \vee F_2 \vee \cdots \vee F_t\) be an OR-AND-OR formula of bottom fan-in \(k\).
Suppose that \(F\) rejects all vectors with fewer than \(s\) ones.
Then \(F\) cannot accept more than \(k^s\) vectors with precisely \(s\) ones.
A: large set of vectors accepted by \(F_i\) and B: all vectors with at most \(s-1\) ones.
Say that a vector \(v\) is a \(k\)-limit for \(A\) if
for every subset \(S\) of \(k\) coordinates, there exists a vector \(u \in A\) such that
\(v \leqslant u\) (vector comparision) and
\(v\) coincides with \(u\) in all the coordinates from \(S\);
that is, \(v_i \leqslant u_i\) for all \(i\) and \(v_i=u_i\) for all \(i \in S\).
\(v\)
\(u\)
\(A\)
CS607. Combinatorics with Applications in Computer Science
By Neeldhara Misra
CS607. Combinatorics with Applications in Computer Science
- 1,191



