Random circuit sampling using fermionic linear optics
Michał Oszmaniec, ND, Mauro E. Morales, Zoltán Zimborás
The 5th Bangkok Workshop on Discrete Geometry, Dynamics and Statistics
24 Jan 2023
Matchgates!
Given an initial state \(|\psi\rangle\) and a family of unitary time evolutions \(\{U_{\alpha}\}_{\alpha}\),
are the \(U_{\alpha}|\psi\rangle\)'s hard to simulate on a classical computer?
-
Fundamental limit of classical computation
-
Direct applications are few and far between
- Certified random number generator (Aaronson)
- Company/Lab PR
pc: Reuters
- Introduction - What is a simulation?
- Proof strategy for classical intractability
- The fermionic case
Outline
{\bf y} \in \{0,1\}^n
String of \(n\) bits
\implies
Classical vs Quantum circuit
{\bf x}
Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)
\implies
String of \(n\) qubits
\bigotimes_{j=1}^n |\psi_j\rangle
Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)
\implies
Classical vs Quantum circuit
\implies
Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)
The result of the coin flips are just hidden bitstrings that can be included as extra inputs
Classical vs Quantum circuit
- Every Boolean circuit can be composed out of elementary gates in a universal gate set
- Most functions need an exponential-size circuit (Shannon)
- Every quantum circuit can be composed out of elementary gates in a universal gate set
- Most unitaries need an exponential-size circuit
Strong vs Weak Simulation
Strong simulation
Weak simulation
Can compute \(p_{\bf x}\)
Can sample from \(p\)
|p_{\bf x} - q_{\bf x}| \le \eta p_{\bf x}
\sum_{\bf x} |p_{\bf x} - q_{\bf x}| \le \epsilon
In practice, there need to be some notions of errors
In this talk, I will use these definitions of strong and weak simulation unless stated otherwise
Relative error
Additive error
Given an initial state \(|\psi\rangle\) and a family of unitary time evolutions \(\{U_{\alpha}\}_{\alpha}\), are the \(U_{\alpha}|\psi\rangle\)'s hard to simulate on a classical computer?
Given an initial state \(|\psi\rangle\) and a family of polynomial-depth quantum circuits \(\{U_{\alpha}\}_{\alpha}\), can there be a classical machine that approximately samples from \(p_{\bf x} = |\langle{\bf x}|U_{\alpha}|\psi\rangle|^2\) in poly\((n,\epsilon^{-1})\) time?
- Introduction - What is a simulation?
- Proof strategy for classical intractability
- The fermionic case
Outline
Proof of Classical Intractability
Given \(|\psi\rangle, \{U_{\alpha}\}_{\alpha}\)
If the RHS task is #P-hard, then \(\mathcal{C}^{\mathrm{NP}}\) would be able to solve a #P-hard problem, which we believe to be impossible
Classical sampler \(\mathcal{C}\)
\sum_{\mathbf{x}} |p_{\mathbf{x}}-q_{\mathbf{x}}| \le \epsilon
Anti-concentration of \(p_{\bf x}(U_{\alpha})\)
Ability to approximately compute \(p_{\bf 0} = |\langle {\bf 0}|U_{\alpha}|\psi\rangle|^2\) for most \(U_{\alpha}\)
\mathcal{C}^{\mathrm{NP}}
|p_{\bf 0} - q_{\bf 0}| \le \eta p_{\bf 0}
Anti-concentration
To turn relative error to additive error, we need most probabilities to be large
|p_{\bf x} - q_{\bf x}| \le \eta p_{\bf x} \longleftrightarrow \sum_{\bf x} |p_{\bf x} - q_{\bf x}| \le \epsilon
\Pr\left(p_{{\bf x}} \ge \displaystyle{\frac{C_1}{2^n}}\right) \ge C_2
\(l^2\)-distance to the uniform distribution:
\(\Vert p-p_{\mathrm{unif}}\Vert^2 = Z - \displaystyle{\frac{1}{2^n}} = Z-Z_{\mathrm{unif}}\)
Z = \mathbb{E}_U \mathbb{E}_{\bf x}\, [ p^2_{\bf x}(U)]
Z \le \displaystyle{\frac{1}{\alpha 2^n}}
\(p_{\bf{x}}(U)\) anti-concentrates if
Z_{\mathrm{unif}} = \displaystyle{\frac{1}{2^n}}
Implies \(\Pr\left(p_{{\bf x}} \ge \displaystyle{\frac{\beta}{2^n}}\right) \ge \alpha(1-\beta)^2 \) via the Paley-Zygmund inequality
\Pr\left( X\ge \beta\mathbb{E}[X] \right) \ge (1-\beta)^2 \displaystyle{\frac{\mathbb{E}[X]^2}{\mathbb{E}[X^2]}}
2
2
2
Anti-concentration
Modified from Dalzell et al., PRX Quantum 2022
Average-Case Hardness
- Average-case hardness for Boson Sampling originates from the argument for average-case hardness to compute the permanent via polynomial interpolation (Lipton 1991).
- Bouland et al., Nat Phys (2018) and Movassagh 2019 import the argument to Random Circuit Sampling
Worst-case hardness of approximately computing \(p_{\bf 0}(U_{\alpha})\)
Worst-to-average-case reduction
Hardness of approximately computing \(p_{\bf 0}(U_{\alpha})\) for most \(U_{\alpha}\)
Easy to argue based on existing results in quantum computing
- Introduction - What is a simulation?
- Proof strategy for classical intractability
- The fermionic case
Outline
Rio Grande, 2017
Fermionic Linear Optics (FLO)
X = \begin{pmatrix}0&1\\1&0 \end{pmatrix}
Y = \begin{pmatrix}0&\!\!\!-i\\i&0 \end{pmatrix}
Z = \begin{pmatrix}1&0\\0&\!\!\!-1 \end{pmatrix}
Reminder
\sigma^{\dagger} = X-iY = \begin{pmatrix}0&0\\1&0 \end{pmatrix}
\sigma^{\dagger}|0\rangle = |1\rangle
Identify computational basis states with occupation number states
Jordan-Wigner
f_j f^{\dagger}_k +f^{\dagger}_k f_j = \delta_{jk}\mathbb{I}
(f^{\dagger}_j)^2 = 0
CAR
f^{\dagger}_j \coloneqq \sigma_j^{\dagger} \displaystyle{\prod_{k=1}^{j-1}} Z_k
\(f_j^{\dagger}\) creates a fermion at site \(j\)
Pauli exclusion
Fermionic Linear Optics (FLO)
m_j^X \coloneqq X_j \displaystyle{\prod_{k=1}^{j-1}} Z_k
m_j^Y \coloneqq Y_j \displaystyle{\prod_{k=1}^{j-1}} Z_k
cf. Dirac's gamma matrices
m_{\alpha}m_{\beta} + m_{\beta}m_{\alpha} = 2 \delta_{\alpha\beta} \mathbb{I}
\alpha = (j,X\,\mathrm{or}\,Y)
Majoranas
\begin{pmatrix}
1 & & 0 \\ & \!\!\!\!\!\Large{-iX}\!\!\!\! \\ 0 & & 1
\end{pmatrix}
Non-example
\mathrm{SWAP}= \mathbb{I}\!\otimes\!\mathbb{I}\!+\!X\!\otimes\! X \!+\! Y\!\otimes \!Y \!+\! Z\!\otimes \!Z
\(Z\!\otimes\! Z\) interaction is not FLO
FLO Hamiltonians are quadratic
Antisymmetric
H_{\mathrm{FLO}} = \displaystyle{\frac{i}{4}} \sum_{\substack{\alpha,\beta \\ \alpha>\beta}} h_{\alpha\beta} [m_{\alpha},m_{\beta}]
=\begin{pmatrix}
R^{\dagger}_Z(\varphi)_{11} & & R_Z^{\dagger}(\varphi)_{12} \\ & \!\!\!\!\!\Large{R_X(\theta)}\!\!\!\! \\
R_Z^{\dagger}(\varphi)_{21} & & R_Z^{\dagger}(\varphi)_{22}
\end{pmatrix}
Fermionic Linear Optics (FLO)
Even parity
Odd parity
M(U^+,U^-) =\begin{pmatrix}
U^+_{11} & & U^+_{12} \\ & \Large{U^-} \\
U^+_{21} & & U^+_{22}
\end{pmatrix}
\det U^+ = \det U^-
FLO gates AKA Matchgates
(Valiant, SIAM J Comput 2002)
\mathrm{SWAP} = \begin{pmatrix}
1 & & 0 \\ & \!\!\!\!\Large{X}\!\!\! \\ 0 & & 1
\end{pmatrix}
Non-example
\mathrm{fSim}(\theta,\varphi) = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & -i\sin\theta & 0 \\
0 & -i\sin\theta & \cos\theta & 0\\
0 & 0 & 0 & e^{-i\varphi}
\end{pmatrix}
Classical Intractability?
Classical sampler \(\mathcal{C}\)
\sum_{\mathbf{x}} |p_{\mathbf{x}}-q_{\mathbf{x}}| \le \epsilon
Anti-concentration?
Ability to approximately compute \(p_{\bf 0} = |\langle {\bf 0}|V_{\mathrm{FLO}}|{\bf 0}\rangle|^2\) for most \(V_{\mathrm{FLO}}\)
\mathcal{C}^{\mathrm{NP}}
|p_{\bf 0} - q_{\bf 0}| \le \eta p_{\bf 0}
V_{\mathrm{FLO}}
This is easy!
Fermionic Linear Optics (FLO)
\vec{m}(t) = V^{\dagger} \vec{m} V = e^{{\bf h}t} \vec{m}
Generators of rotations SO(\(2n\))
V_{\mathrm{FLO}} = e^{iH_{\mathrm{FLO}}t}
(Defining representation)
Antisymmetric
Manipulating \(2n\times 2n\) matrices instead of \(2^n\times 2^n\) matrices!
- Only need to specify the correlation matrix (2nd moments)
- All higher moments can be extracted from \(\Sigma\) via Wick's theorem
\Sigma_{\alpha\beta} \coloneqq \frac{i}{2}\mathrm{Tr}(\rho[m_{\alpha},m_{\beta}])
p_{\bf x} = \frac{1}{i^{2^n}} \mathrm{Pf} (\Sigma)
\(\rho = (|0\rangle\langle 0|)^{\otimes n}\) is a fermionic Gaussian state
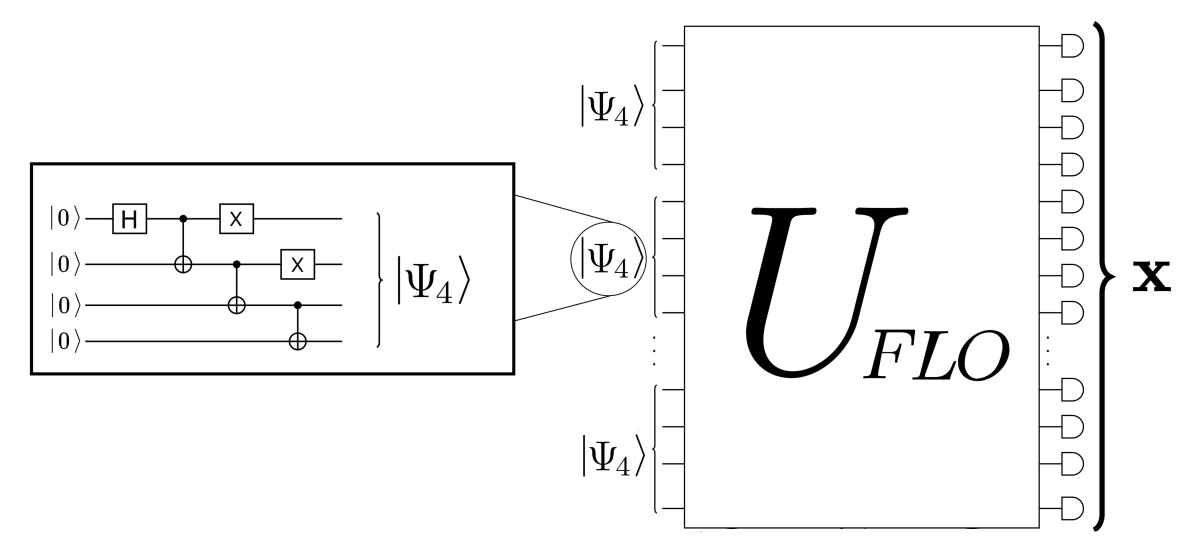
Fermion Sampling
- FLO with computational-basis input state admits strong simulation (compute \(p_{\bf x}\) up to logarithmic number of decimals)
- Not the case with non-Gaussian (magic) input state; strong simulation is #P-hard (cf. Ivanov, PRA 2017)
- Our work shows that weak simulation is also hard
V_{FLO}
|\Psi_4\rangle = \displaystyle{\frac{|0011\rangle + |1100\rangle}{\sqrt{2}}}
\mathbb{E}_V [p^2_{\bf 0}] = \int dV\, \mathrm{Tr}(V|\Psi\rangle \langle \Psi| V^{\dagger}|{\bf 0}\rangle\langle {\bf x}|)^2
= \mathrm{Tr}(|\Psi\rangle \langle \Psi| \int dV\, V^{\dagger}|{\bf 0}\rangle\langle {\bf 0}|V)^2
= \mathrm{Tr}\left[(|\Psi\rangle \langle \Psi|)^{\otimes 2} \underbrace{\int dV\, (V^{\dagger})^{\otimes 2}(|{\bf 0}\rangle\langle {\bf 0}|)^{\otimes 2}V^{\otimes 2}}\right]
Sum of projectors onto irreps by Schur's lemma under nice conditions
- SO(\(2n\)) for FLO
- U(\(n\)) for passive (number-preserving) FLO
Anti-concentration
\mathrm{Tr} \left[\mathbb{P}_{\mathrm{pas}} (|\Psi\rangle\langle\Psi |)^{\otimes 2}\right] \le \frac{1}{2N+1} \cdot \left[ 2 \sum_{k=0}^{N-1} {2N \choose k} \mathrm{Tr}(\rho_k^2) + {2N \choose N} \mathrm{Tr}(\rho_N^2) \right]
For example,
Then use combinatorics to bound the RHS
Worst-to-average-case reduction
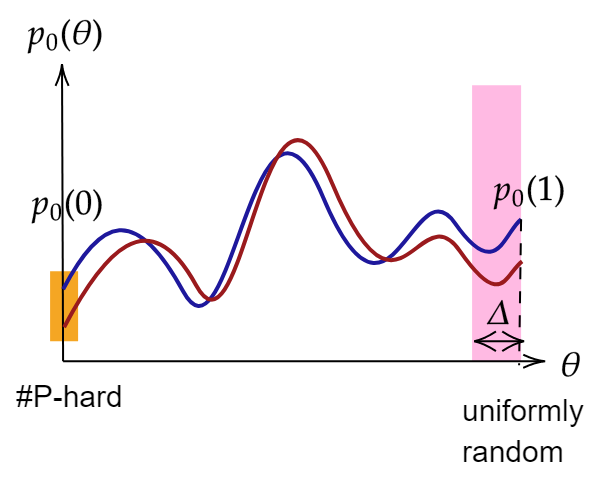
- There exists a "worst-case circuit" \(V_0\) for which \(p_{\bf 0} = |\langle \mathbf{0}|V_0|\Psi\rangle|^2\) is #P-hard to approximate
- Deform to average-case (Haar random) circuits where \(p_{\bf 0} (\theta)= |\langle \mathbf{0}|V(\theta)|\Psi\rangle|^2\) is a polynomial of low-degree \(q\)
- Sample \(\gtrsim q\) points (some can be errorneous\(\iff\)robustness) and recover \(p_{\bf 0}(\theta)\) via Berlekamp–Welch
- Plug in \(\theta = 0\) to solve a #P-hard problem!
Unitary Paths
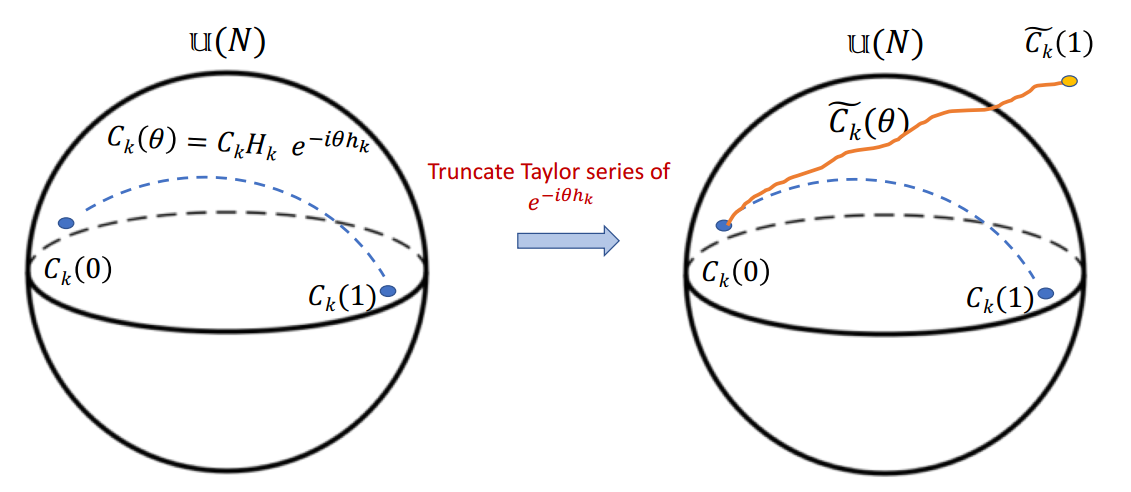
First idea: truncated exponential path
U(\theta) = U_0 e^{i\theta H}
Movassage 2019
= U_0 \left(\mathbb{I} + i\theta H + \frac{(i \theta H)^2}{2!} + \cdots \right)
Truncation gives rise to a non-unitary operator
f(X) = (\mathbb{I}-X)(\mathbb{I}+X)^{-1}
g_{\theta} = g_0
\displaystyle{
\frac{(1-\theta) \mathbb{I} +(1+\theta) g}{ (1+\theta) \mathbb{I} +(1-\theta)g }}
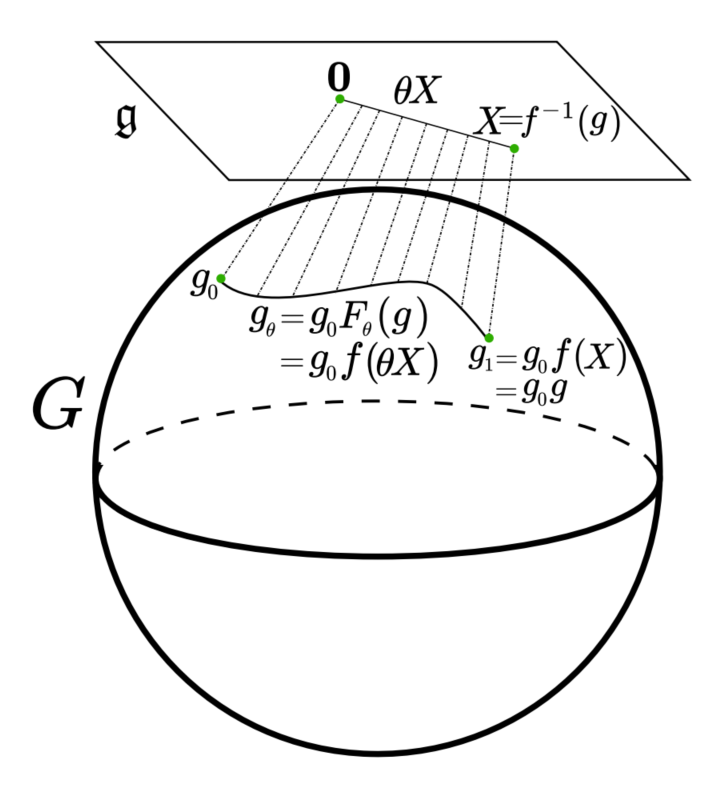
Better idea: Cayley path
Unitary
Hermitian
Hardness Guarantees
| Quantum advantage scheme | Robustness of avg-case hardness (additive error) |
Anti-concentration |
|---|---|---|
| Boson Sampling | ||
| Random circuit sampling (Google layout) | ||
| Fermion Sampling |
2^{-\tilde{O}(n)}
2^{-\tilde{O}(n^{1.5})}
2^{-\tilde{O}(n^2)}
Bouland et al., FOCS 2021
Other Results
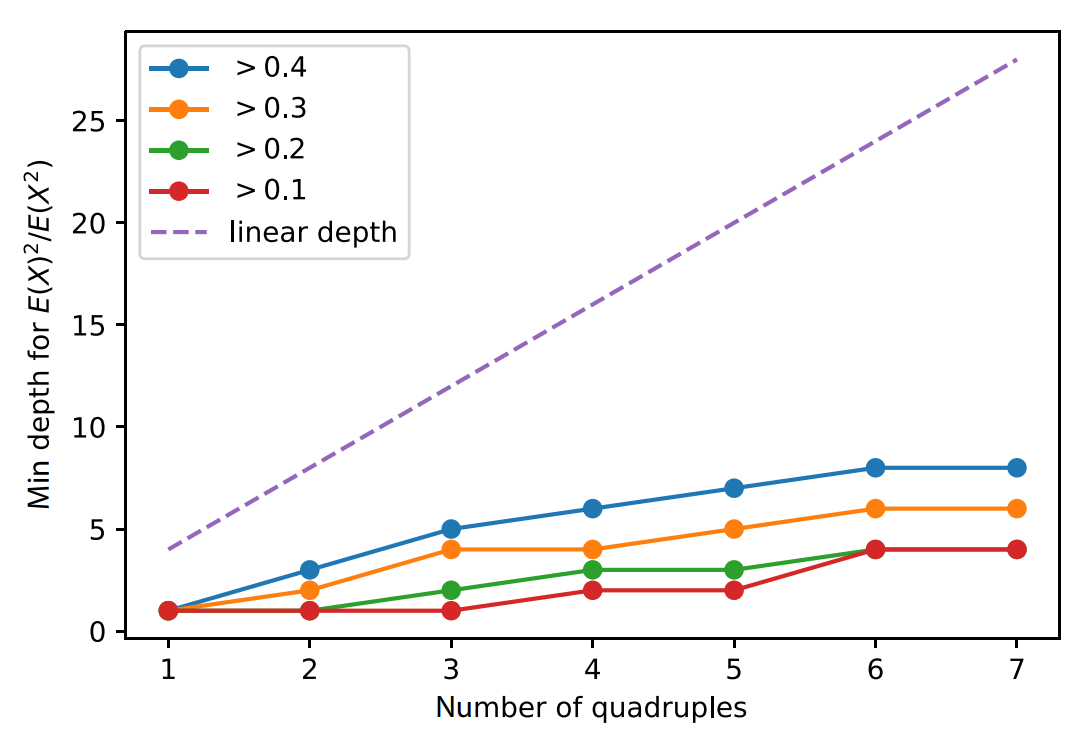
- Numerics suggest that random FLO circuits anti-concentrate in sub-linear depth
|+_X^p\rangle \\
\text{or} \\
|+_Y^p\rangle
p,p' = 1,2,\dots,d
V_{FLO}
|+_X^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_X\rangle \otimes |0\rangle^{\otimes (n-p)}
|+_Y^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_Y\rangle \otimes |0\rangle^{\otimes (n-p)}
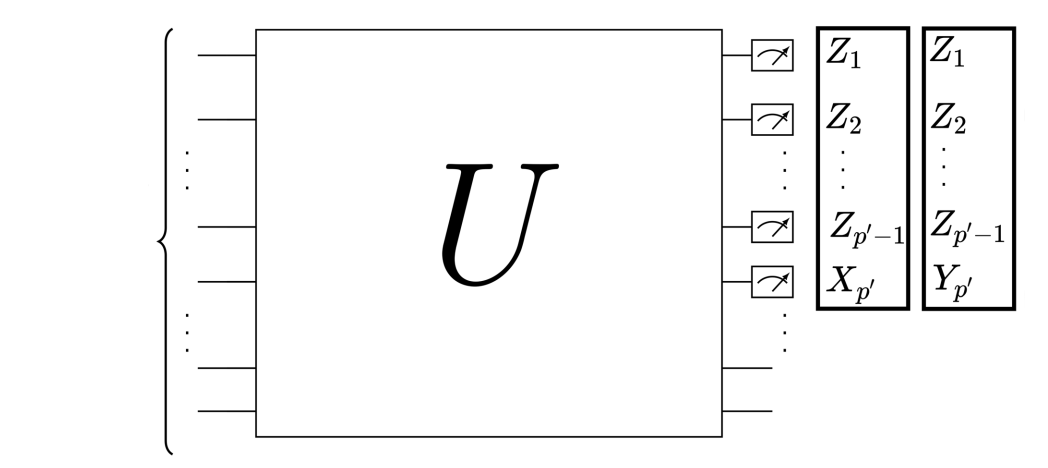
- Assuming that the circuit is FLO, circuit tomography can be performed efficiently utilizing single-mode input states and product measurements
Summary
V_{FLO}
|\Psi_4\rangle = \displaystyle{\frac{|0011\rangle + |1100\rangle}{\sqrt{2}}}
- Simulating \(U|\psi\rangle\) = Sampling from \(|\langle {\bf x}|U|\psi\rangle|^2\)
- The standard argument for hardness of sampling requires statistical data of the ensemble \(\{U_{\alpha}\}_{\alpha}\)
- When \(\{U_{\alpha}\}_{\alpha}\) has the structure of a low-dimensional Lie group, there are available techniques for computing these data
- Low-dimensionality might lead to a fast classical algorithm; but this might be circumvented by a good choice of the initial state (here a non-Gaussian state)
Thank You!
↑ for the slides
Fermion Sampling (DGDS2023)
By Ninnat Dangniam
Fermion Sampling (DGDS2023)
The 5th Bangkok Workshop on Discrete Geometry, Dynamics and Statistics (23-27 Jan 2023)
