Toward a Classical Subtheory for Matchgate Circuits
Center for Quantum Information and Control, University of New Mexico
Ninnat Dangniam, Chris Ferrie
Centre for Engineered Quantum Systems, The University of Sydney
CQuIC, 20 April 2016
Known to be
classically
simulatable
Universal
?
Gaussian
Universal
?
Matchgate/Fermionic Quantum Computation
Bravyi quant-ph/0511178
de Melo, Ćwikliński, Terhal 1208.5334
Oszmaniec, Gutt, Kuś 1406.1577
Matchgates
G(A,B)=A1100A210B11B2100B12B220A1200A22
G(A,B)=
\begin{pmatrix}
A_{11} & 0 & 0 & A_{12} \\
0 & B_{11} & B_{12} & 0 \\
0 & B_{21} & B_{22} & 0 \\
A_{21} & 0 & 0 & A_{22} \\
\end{pmatrix}
detA=detB
\det A = \det B
or
A,B∈SU(2)
A,B \in \text{SU}(2)
SWAP=1000001001000001
\text{SWAP}=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\end{pmatrix}
detI=detX
\det I \neq \det X
X∈/SU(2)
X \notin \text{SU}(2)
Non-Example
{⋅,⋅}
\{ \cdot,\cdot \}
Anti-commutator
{cα,cβ}=2δαβ
\{ c_{\alpha}, c_{\beta} \} = 2 \delta_{\alpha \beta}
c1=X1
c_1 = X_1
c2=Y1
c_2 = Y_1
c2j−1=
c_{2j-1} =
c2j=
c_{2j} =
Qubits-Fermionic Modes Isomorphism
∏k=1j−1Zk
\prod_{k=1}^{j-1} Z_k
∏k=1j−1Zk
\prod_{k=1}^{j-1} Z_k
Xj
X_j
Yj
Y_j
Majorana or Jordan-Wigner operators
Qubits-Fermionic Modes Isomorphism
∣00⋯0⟩↦∣x⟩:=∣x1x2⋯xn⟩
|0 0 \cdots 0 \rangle \mapsto |\bold{x}\rangle := | x_1 x_2 \cdots x_n \rangle
{aj†,ak}=δjk
\{ a^{\dagger}_j, a_k \} = \delta_{jk}
aj=c2j−1+ic2j
a_j = c_{2j-1} + ic_{2j}
Computational basis states = Number states
Nonlocality
-
N.N. Matchgates
-
Non-N.N. Matchgates
-
All quadratic Hamiltonians
Examples
Nonlocality
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣0⟩
|0\rangle
N.N. Matchgates
c1,c2,c3,c4
c_1,c_2,c_3,c_4
Quadratic Hamiltonians with adjacent modes
G(A,B)
G(A,B)
6 Generators
ZI
ZI
IZ
IZ
XX
XX
YY
YY
YX
YX
XY
XY
Nonlocality
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣0⟩
|0\rangle
Non-N.N. Matchgates
Quartic Hamiltonians
(Universal)
G(A,B)
G(A,B)
c1,c2,c3,c4,c5,c6
c_1,c_2,c_3,c_4,c_5,c_6
Nonlocality
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣0⟩
|0\rangle
Non-N.N. Matchgates
G(A,B)
G(A,B)
Quartic Hamiltonians
(Universal)
c1,c2,c3,c4,c5,c6
c_1,c_2,c_3,c_4,c_5,c_6
Nonlocality
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣0⟩
|0\rangle
>2-qubit gate
c1,c2,c5,c6
c_1,c_2,c_5,c_6
Quadratic Hamiltonians with nonadjacent modes
Nonlocality
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣0⟩
|0\rangle
N.N. matchgates
c1,c2,c5,c6
c_1,c_2,c_5,c_6
Quadratic Hamiltonians with nonadjacent modes
G(A,B)
G(A,B)
G(Z,X)
G(Z,X)
⋯
\cdots
G(Z,X)
G(Z,X)
c2j−1↔c2j+1
c_{2j-1} \leftrightarrow c_{2j+1}
c2j↔c2j+2
c_{2j} \leftrightarrow c_{2j+2}
∣ψ⟩∣0⟩↔∣0⟩∣ψ⟩
|\psi \rangle |0\rangle \leftrightarrow |0\rangle |\psi \rangle
Modal swap
Conditional swap
O(n3)
\mathcal{O}(n^3)
Classical Simulation
(Hand-Waving)
- The 's evolve linearly
- The outcome probability can be found from the determinant
cα
c_{\alpha}
Classical Simulation
(Hand-Waving)
1. Linearity
U†
U^{\dagger}
U
U
cα
c_{\alpha}
=∑β
= \sum_{\beta}
Rαβ
R_{\alpha \beta}
cβ
c_{\beta}
SO(2n)
\text{SO}(2n)
rotation
Quadratic Hamiltonian
c~α=
\tilde{c}_{\alpha} =
(Symplectic for bosons)
Classical Simulation
(Hand-Waving)
k≤n
k \le n
U†
U^{\dagger}
U
U
∏j=y1ykaj†aj
\prod_{j = y_1}^{y_k} a^{\dagger}_j a_j
P(y∣x)=⟨0∣
P(\bold{y}|\bold{x}) = \langle 0|
∣0⟩=Pf(M)
|0\rangle = \text{Pf}(M)
2. Counting a subset of fermions (Z measurements on k qubits)
Pf2(M)=det(M)
\text{Pf}^2 (M) = \det (M)
Determinant is easy to calculate (unlike permanent for bosons)
Some poly-size antisymmetric matrix
Quantum States at all Time
=2iTr(ρ[cα,cβ])
= \frac{i}{2} \text{Tr} (\rho [c_{\alpha} , c_{\beta}])
Vα,β
V_{\alpha,\beta}
Covariance matrix
Gaussian states
ic~2j−1c~2j)
i\tilde{c}_{2j-1} \tilde{c}_{2j})
=2n1∏j=1n(I+
= \frac{1}{2^n} \prod_{j=1}^n ( I +
λj
\lambda_j
"Williamson eigenvalue" of
V
V
ρ
\rho
=Nexp(−icTBc)
= N \exp{ \left( -i \bold{c}^T B \bold{c} \right)}
Example: number states
∣x⟩⟨x∣=∏j=1n2I−λjic2j−1c2j
|\bold{x}\rangle \langle \bold{x}| = \prod_{j=1}^n \frac{I - \lambda_j ic_{2j-1} c_{2j}}{2}
λj=(−1)xj
\lambda_j = (-1)^{x_j}
Quantum States at all Time
Wick's theorem
∏j=y1ykc2j−1c2j)=ik1Pf(
\prod_{j=y_1}^{y_k} c_{2j-1} c_{2j} ) = \frac{1}{i^k} \text{Pf} (
)=Tr(
) = \text{Tr}(
ρ
\rho
P(y∣
P(\bold{y}|
ρ
\rho
∣y)
\vert_{\bold{y}})
V
V
Quantum States at all Time
- Product input states - Single qubit Z measurement (Only linearity is required)
Variants of the Simulation Result
Jozsa, Miyake 0804.4050
- Product input states - Product basis measurements
Brod 1602.03539
- Simulating quadratic + linear Hamiltonians by quadratic Hamiltonians alone
Knill quant-ph/0108033
Jozsa, Miyake, Strelchuck 1311.3046
Product Input States - Product Basis Measurements
G(H,H)
G(H,H)
∣ψ⟩∣+⟩↦H∣ψ⟩∣+⟩
|\psi \rangle |+\rangle \mapsto H|\psi \rangle |+\rangle
Conditional Hadamard
G(Z,X)
G(Z,X)
∣ψ⟩∣0⟩↔∣0⟩∣ψ⟩
|\psi \rangle |0\rangle \leftrightarrow |0\rangle |\psi \rangle
Conditional swap
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣+⟩
|+\rangle
G(Z,X)
G(Z,X)
G(H,H)
G(H,H)
⋯
\cdots
G(Rz,Rz)
G(R_z,R_z)
G(−Z,X)
G(-Z,X)
∣ψ⟩∣1⟩↔∣1⟩∣ψ⟩
|\psi \rangle |1\rangle \leftrightarrow |1\rangle |\psi \rangle
Z
Z
G(±Z,X)
G(\pm Z,X)
Quasi-Probabilities
∣0⟩
|0\rangle
∣0⟩
|0\rangle
∣0⟩
|0\rangle
G(A,B)
G(A,B)
G(A′,B′)
G(A',B')
+
+
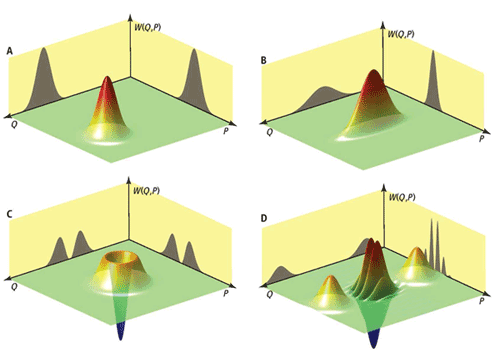
- Provide classical subtheory (hidden variable model) when quasi-probabilities are non-negative
- The negativity quantifies the resource for universal quantum computation
Why?
Classical Subtheory
ρc
\rho_c
Ec
E_c
Preparation
P(λ∣ρc)
P(\lambda|\rho_{c})
Measurement
P(Ec∣λ)
P(E_c|\lambda)
P(Ec∣ρc)=∑λP(Ec∣λ)P(λ∣ρc)
P(E_c|\rho_c) = \sum_{\lambda} P(E_c|\lambda)P(\lambda|\rho_c)
c=
c =
classical
λ=
\lambda =
"true state of the world"
ρc
\rho_c
Ec
E_c
Preparation
Tr[ρF(λ)]
\text{Tr}[\rho F(\lambda)]
Measurement
Tr[ED(λ)]
\text{Tr}[E D(\lambda)]
P(E∣ρ)=Tr{E
P(E|\rho) = \text{Tr} \{ E
(Phase Space) Quasi-Probability Model
∑λTr[ρF(λ)]D(λ)
\sum_{\lambda} \text{Tr} [\rho F(\lambda)] D(\lambda)
}
\}
∑λTr[ρ
\sum_{\lambda} \text{Tr} [ \rho
F(λ)
F(\lambda)
]
]
D(λ)
D(\lambda)
=ρ
= \rho
Frame
Dual Frame
(Phase Space) Quasi-Probability Model
(Phase point operators)
- Frame or dual frame must contain negative operators
- Negativity quantifies the amount of resource
Spekkens 0710.5549
Ferrie, Morris, Emerson 0910.3198
Veitch et al. 1307.7171
Find a classical subtheory that contains Gaussian states and fermion-counting measurements
Mission
Group-Covariance
U†(g)F(λ)U(g)=F(gλ)
U^{\dagger} (g) F(\lambda) U (g) = F(g\lambda)
G
G
-action permute phase points
- Sufficient to preserve positivity
Gross quant-ph/0602001
- Also necessary in discrete Wigner functions in odd dimensions
- Impossible for qubit discrete Wigner functions (Clifford covariance)
Zhu 1510:02619
Group-Covariance
-
How?
-
Which group?
Lie group
G
G
-covariant
G
G
F(λ,s)
F(\lambda,s)
BM
One-parameter family of
Brif, Mann quant-ph/9809052
Constructing G-Covariant Phase Spaces
D(λ,s)=F(λ,−s)
D(\lambda,s) = F(\lambda,-s)
G
G
BM
Irrep
Fiducial state
U(g)
U(g)
∣ψ⟩
|\psi \rangle
Lie group
G/
G/
Coset space
Input Data
Stabilizer of
∣ψ⟩
|\psi \rangle
H
H
Coset Space
SO(3)/SO(2)≃S2
\text{SO}(3)/\text{SO}(2) \simeq S^2
No "Good" SO(4)-covariant phase space
G(A,B)=A1100A210B11B2100B12B220A1200A22
G(A,B)=
\begin{pmatrix}
A_{11} & 0 & 0 & A_{12} \\
0 & B_{11} & B_{12} & 0 \\
0 & B_{21} & B_{22} & 0 \\
A_{21} & 0 & 0 & A_{22} \\
\end{pmatrix}
Phase space separates into odd and even parity subspaces
A,B∈SU(2)
A,B \in \text{SU}(2)
No "Good" SO(4)-covariant phase space
- In each subspace, any two pure states are connected by an SU(2) transformation (matchgate)
- So if there is just one positive pure state, then every pure state is positive.
- This is impossible for self-dual representations
- Dropping self-duality shouldn't help
The argument:
SO(2n+1)
\text{SO}(2n+1)
BM
Quadratic + linear Hamiltonians
Fiducial state
∣0⟩
|0 \rangle
SO(2n+1)/
\text{SO}(2n+1)/
U(n)
\text{U}(n)
Number-preserving Hamiltonians
Input Data
∣λ⟩=U∣0⟩
|\lambda \rangle = U|0\rangle
Coherent states
Oeckl 1408.2760
BM
Input Data
Yl,m(λ)
Y_{l,m} (\lambda)
∣⟨λ∣λ′⟩∣2=∑l,m
|\langle \lambda | \lambda' \rangle|^2 = \sum_{l,m}
τl,m
\tau_{l,m}
Orthogonal functions on the coset space
Yl,m∗(λ)Yl,m(λ′)
Y^*_{l,m} (\lambda) Y_{l,m} (\lambda')
τl,m
\tau_{l,m}
SO(2n+1)
\text{SO}(2n+1)
/U(n)
/\text{U}(n)
Dl,m=τl,m1∫G/HYl,m(λ)∣λ⟩⟨λ∣
D_{l,m} = \frac{1}{\sqrt{\tau_{l,m}}} \int_{G/H} Y_{l,m} (\lambda) | \lambda \rangle \langle \lambda |
F(λ,s)=∑l,mτl,ms1Yl,m∗(λ)Dl,m
F(\lambda,s) = \sum_{l,m} \frac{1}{\sqrt{ \tau_{l,m}^s}} Y^*_{l,m}(\lambda) D_{l,m}
BM
Heisenberg Group
- Reps of Heisenberg group are projective reps of an abelian group
- Projective reps + F.T. on non-abelian finite groups is not enough to construct a quasi-probability representation
Dangniam, Ferrie 1410.5755
- Does BM construction work on finite groups?
U=Dl,m
U = D_{l,m}
SO(2n+1)/U(n)
\text{SO}(2n+1)/\text{U}(n)
Hard
"Easy"
SO(m+1)/SO(m)≃Sm
\text{SO}(m+1)/\text{SO}(m) \simeq S^m
"Easy"
SO(5)/U(2)≃CP3
\text{SO}(5)/\text{U}(2) \simeq \mathbb{C}P^3
Need "the ring of invariant differential operators"
Barut Theory of Group Representations
Finding
Yl,m
Y_{l,m}
Open Questions
- Classical subtheory of SO(2n+1)-covariant phase space?
- General Hudson's theorem for group-covariant phase space?
- BM construction for finite groups?
Lie group
G
G
-covariant
G
G
BM
phase spaces
What I Thought It Would Be
Lie group
G
G
-covariant
G
G
BM
phase spaces
Mathematicians
What It Actually Is
Thank You
Toward a Classical Subtheory for Matchgate Circuits Center for Quantum Information and Control , University of New Mexico Ninnat Dangniam, Chris Ferrie Centre for Engineered Quantum Systems , The University of Sydney CQuIC, 20 April 2016
Matchgates (New Mexico)
By Ninnat Dangniam
Matchgates (New Mexico)
CQuIC seminar, UNM, 20 April 2016
- 755
