The Computational Power of Identical Particles
Ninnat Dangniam
Near-Term Quantum Computers Online Workshop
1 July 2020
Ph.D. in physics, University of New Mexico (2018)
Postdoctoral researcher, Fudan University (Nov 2018 - Aug 2020)
Analog quantum supremacy
with Dimitris Angelakis' group (CQT, NUS)
-
arXiv:2002.11946
- arXiv:2005.11222
Quantum state certification
with Huangjun Zhu (Fudan U)
Fermionic quasi-probability representation
with Carlton Caves & Chris Jackson (CQuIC, UNM)
Classical
Quantum
Does the computational process harness genuine quantum effects that cannot be replicated classically?
Classical simulation
Quantum advantage
?
|0\rangle, |1\rangle
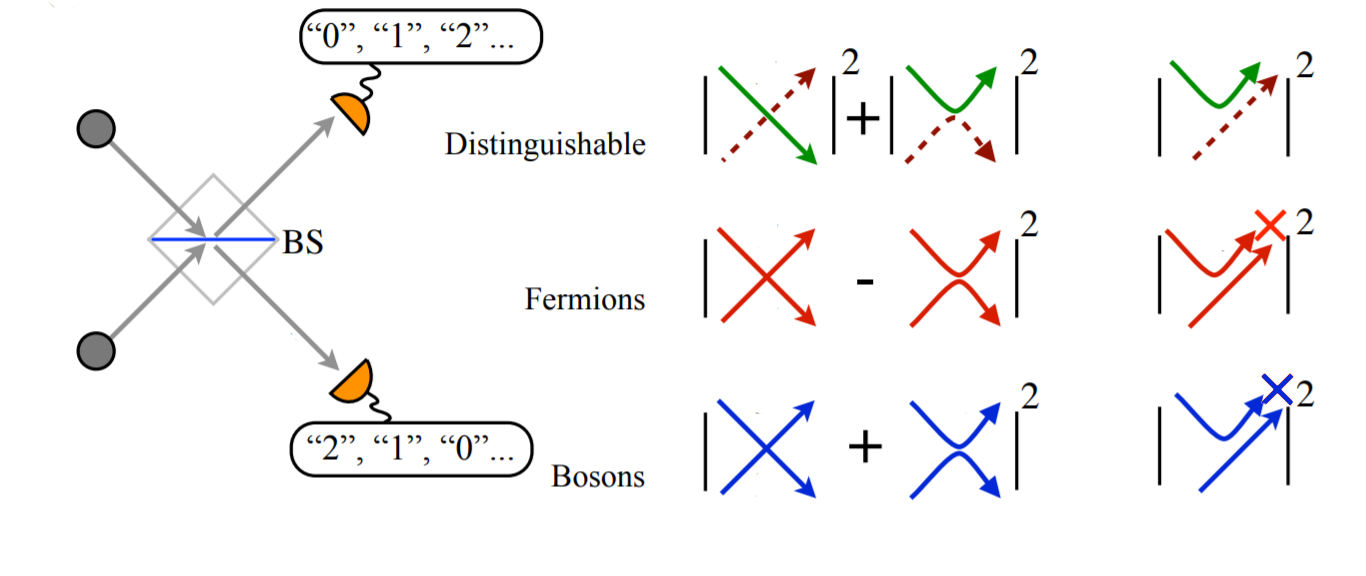
Bosons
Fermions
Qubits
Particle Interference
\mathrm{perm}\,U
= U_{11} U_{22} + U_{12} U_{21}
\det U
= U_{11} U_{22} - U_{12} U_{21}
U = \begin{pmatrix}
U_{11} & U_{12} \\
U_{21} & U_{22}
\end{pmatrix}
Hard!
Easy
Modified from Tichy, J. Phys. B 2014
\(n\) particles in \(m\) modes
U_{11}
U_{11}
U_{22}
U_{22}
U_{12}
U_{12}
U_{21}
U_{21}
if \(n \lesssim \sqrt{m} \)
no coincidence
coincidence
Pauli exclusion
Quantum Advantage by Boson Sampling
Based on certain plausible conjectures, Boson sampling is classically intractable (Aaronson & Arkhipov, STOC'11)
Wang et al., PRL 2019 performed Boson Sampling with 20 photons (6 lost) in 60 modes
State-of-the-art classical simulation algorithms?
- Boson sampling with 30 bosons in 900 modes can be classically simulated under 5 hours (Neville et al., Nat. Phys. 2017)
- Clifford & Clifford SODA'18 gives an exact algorithm in \(O(n2^n + \mathrm{poly}(m,n))\) time
Classical Simulations of Boson Sampling
- \(\log n\) remaining photons (followed from Clifford & Clifford's algorithm)
- Constant loss + constant dark-count (Rahimi-Keshari, Ralph & Caves, PRX 2016)
- Less than \(\sqrt{n}\) photons remaining (Oszmaniec & Brod, New J. Phys. 2018) and more scenarios (Brod & Oszmaniec, Quantum 2020)
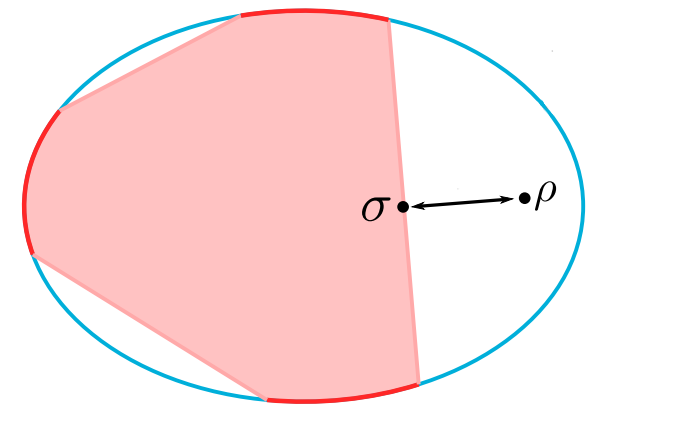
Q: How close are lossy states to classical simulable states on average?
Modified from Oszmaniec & Brod, New J. Phys. 2018
Classical
Quantum Advantage by Fermionic Linear Optics with Magic Inputs
(Passive) FLO operations such as fermionic SWAP are natural in superconducting architecture and quantum chemistry
- Google's quantum supremacy circuits
- Simulating electronic structure Hamiltonian (Kivlichan et al., PRL 2018)
|0000\rangle + |1111\rangle
"Magic" input states promote FLO to universality (Bravyi, PRA 2006)
Q: Propose a feasible quantum advantage scheme with FLO; establish average-case hardness and anti-concentration
Zoltán Zimborás, Wigner RCP
Mauro Morales, UTS
Remark: although the two problems seem to be different, they both involve statements about averaging over the unitary group!
- Boson sampling is classical intractable, while fermion sampling is classically simulable
- Non-ideal boson sampling may be classically simulable (\(\leftarrow\) our project: extend the classical simulations)
- Fermion sampling with magic inputs is classically intractable (\(\leftarrow\) our project: propose a quantum advantage scheme)
Summary
Computational power of Identical particles
By Ninnat Dangniam
Computational power of Identical particles
A short presentation of the kind of research I'll be doing at CTP PAS, Warsaw
