Robust Quantum Computational Advantage Using Fermionic Linear Optics and Magic Input States

Michał Oszmaniec¹, ‪Zoltán Zimborás², Mauro Morales³,

Ninnat Dangniam¹

AQIS, 7-9 Dec 2020

¹ Center for Theoretical Physics, Polish Academy of Sciences, ² Wigner Research Centre for Physics, ³ Centre for Quantum Software and Information, University of Technology Sydney

  • Introduction and motivations
    • Quantum computational supremacy
    • Fermion Sampling with magic input states
    • Experimental prospects
  • Results: hardness guarantees and certification
    • ​Anticoncentration
    • Robust average-case hardness by Cayley path
    • Certification
  • Summary
  • Introduction and motivations
    • Quantum computational supremacy
    • Fermion Sampling with magic input states
    • Experimental prospects
  • Results: hardness guarantees and certification
    • ​Anticoncentration
    • Robust average-case hardness by Cayley path
    • Certification
  • Summary

Quantum computational supremacy

  • Quantum supremacy: the ability of a quantum system to perform a task that classical computers cannot, regardless of whether the task is useful 

 

  • Sampling problems can demonstrate quantum supremacy with few assumptions. Boson Sampling is the canonical example (Aaronson & Arkhipov, STOC'11)

 

  • Random circuit sampling (RCS) is the leading candidate due its rigorous hardness guarantees
    • One- and two-qubit gates are chosen randomly
    • Demonstrated on the 53-qubit Sycamore quantum processor (Arute et al., Nature 2019)

Movassagh 2019

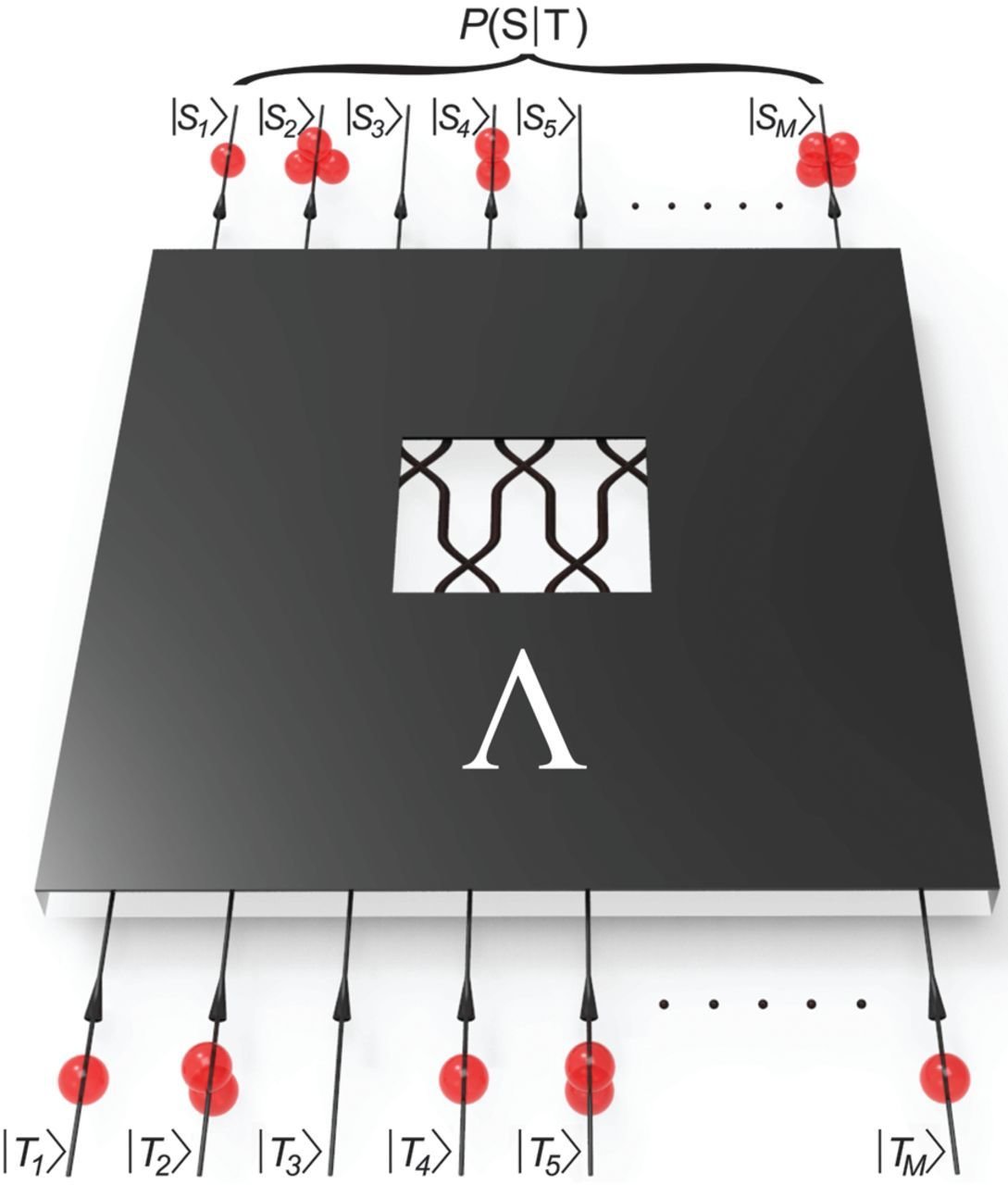
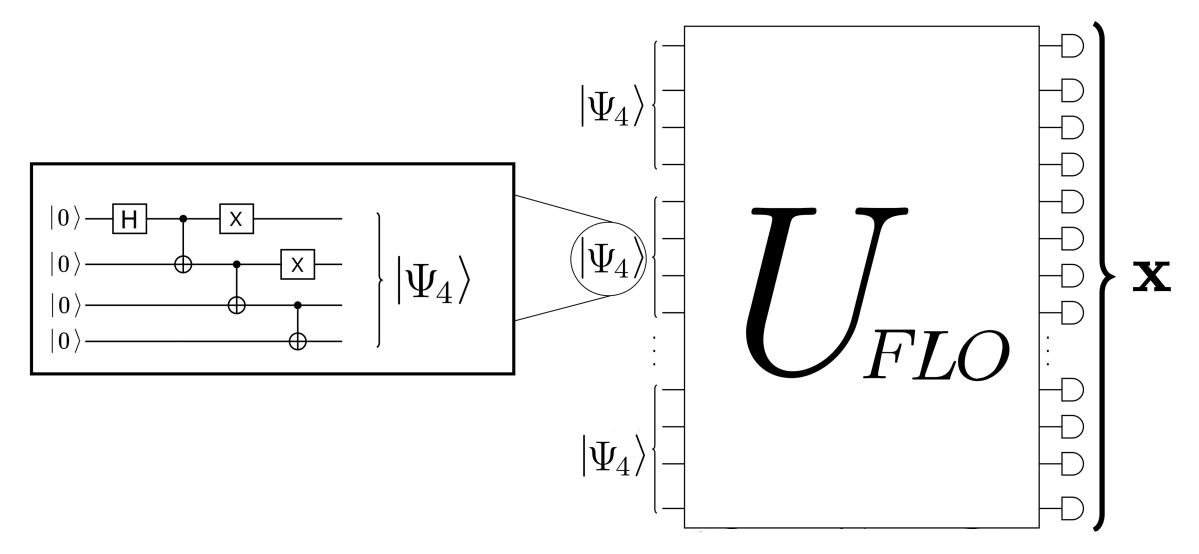
Fermion Sampling with Magic Inputs

  • Analogue of Boson Sampling: while fermionic linear optics (FLO) with fermion-number inputs are classically efficiently simulable, FLO supplemented with entangled "magic" states
|\Psi_{in}\rangle = |\Psi_4\rangle^{\otimes N} = \left( \frac{|0011\rangle + |1100\rangle}{\sqrt{2}} \right)^{\otimes N}

  • promotes (active) FLO to universal quantum computation (Bravyi & Kitaev, Ann Phys 2002, Bravyi, PRA 2006, Hebenstreit et al., 2020) 

  • leads to worst-case hard probabilities even when restricted to number-perserving (passive ) FLO (Ivanov, PRA 2017)

V_{FLO}

Experimental Prospects

FLO circuits (say under the Jordan-Wigner transformation) are native to superconducting qubit architecture

  • Two-qubit fermionic SWAP (iSWAP) gates realized with high fidelity in the demonstration of RCS on the 53-qubit Sycamore quantum processor (Arute et al., Nature 2019, Foxen et al., PRL 2020)
  • The same processor used for proof-of-principle quantum chemistry calculation (Arute et al., Science 2020), non-planar QAOA (Arute et al.  2020)

Google AI Blog

  • Introduction and motivations
    • Quantum computational supremacy
    • Fermion Sampling with magic input states
    • Experimental prospects
  • Results: hardness guarantees and certification
    • ​Anticoncentration
    • Robust average-case hardness by Cayley path
    • Certification
  • Summary

Groups of FLO transformations

\(d\) fermionic modes are described by \(d\) creation and \(d\) annihilation operators

\{f_j,f_k^\dagger\}\equiv f_j f_k^\dagger+ f_k^\dagger f_j = \delta_{j,k}

or \(2d\) majorana operators

m_{2j-1} = f_j^\dagger+f_j\, ,\qquad m_{2j} = i\, (f_j^\dagger-f_j),
  • Number-preserving (passive) FLO forms the group \(\mathrm{U}(d)\) of unitary matrices that do not mix creation and annihilation operators
  • Active FLO forms the group \(\mathrm{SO}(2d)\) are parity-preserving transformation
V_{act} = \exp\left( \frac{1}{4} \sum_{i,j=1}^{2d} \left[\log(O)\right]_{ij} m_i m_j\right),\qquad O \in \mathrm{SO}(2d)

Both groups are described by poly(\(d\)) parameters even though the groups act as circuits on Hilbert space \(\mathcal{H}\) of dimension exponential in \(d\)

Classical sampler

Result:

Anticoncentration

Approximations of \(p_{\mathbf x_0}(V,\Psi_{in})\)

on average

(over Haar distribution)

Result:

average-case hardness of approximating up to additive error \(\epsilon =\exp(-\Theta(N^6))\)

Our results supporting the supremacy conjecture

PH collapse

(conjectured to be false)

p_{\mathbf x_0}(V,\Psi_{in}) = |\langle{\mathbf x_0}|V|\Psi_{in}\rangle|^2

Conjecture: average-case hardness of approximating up to additive error \(\epsilon = (\dim\mathcal{H})^{-1}/poly(N)\)

Anticoncentration

\Pr_{V\sim \mathrm{Haar}} \left[ p_{\mathbf x_0}(V,\Psi_{in}) > \frac{\alpha}{|\mathcal{H}|} \right] > (1-\alpha)^2 C
  • We use the Paley-Zygmund inequality and moments calculated from the group-theoretic properties 
  • We do not use the 2-design property (In fact, \(\nu\) can be proven not to form a 2-design)
  • Numerics suggests that \(p_{\mathbf x_0}(V,\Psi)\) does not anticoncentrate if \(\Psi\) is Gaussian

For any \(0 < \alpha < 1\), There exists a constant \(C>0\) such that

Average-case hardness: Cayley path

(\mathcal{H})
  • Goal: construct a low-degree rational interpolation between a #P-hard FLO circuit and generic circuits
  • Use polynomial interpolation technique to recover the value of the worst-case probability from those of generic circuits 
  • To achieve the goal, we use the Cayley-path deformation (Movassagh 2019)

Difference to previous work: instead of deforming one- and two-qubit gates at the level of physical circuits, we deform at the level of the group element, which is then represented as a global circuit while maintaining the low-degree structure

\text{Passive and active FLO: }\ \ \deg = (O(N^2), O(N^2))
g_{\theta} = g_0\frac{(1-\theta) I +(1+\theta) g}{ (1+\theta) I +(1-\theta)g }

It is #P-hard to compute values of \(p_{\mathbf x_0}(V,\Psi_{in})\) with probability greater than \(\frac{3}{4}+\frac{1}{\mathrm{poly}{N}}\) over the choice of \(V\) w.r.t. the Haar measure

Average-case hardness

it is #P-hard to approximate probability \(p_{\mathbf x_0}(V,\Psi_{in})\) to within accuracy \(\epsilon =\exp(-\Theta(N^6))\) with probability greater than \(1-o(N^{-2})\) over the choice of \(V\) w.r.t. the Haar measure

Robustness

  • Movassagh's result: \(\epsilon =\exp(-\Theta(N^{4.5}))\) for the Google's layout
  • Supremacy conjecture: \(\epsilon = (\dim\mathcal{H})^{-1}/poly(N)\)

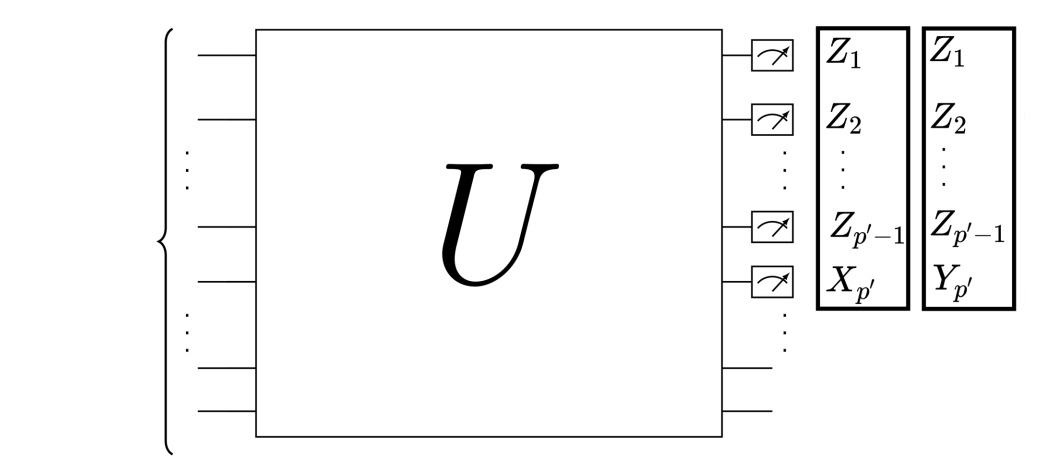
Certification

Assuming that the circuit is FLO, the circuit \(V\) can be efficiently estimated using \(poly(d,\epsilon^{-1})\) single-mode input states and computational-basis measurements, where \(\epsilon\) is the estimation error in the diamond distance

|+_X^p\rangle \\ \text{or} \\ |+_Y^p\rangle
|+_X^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_X\rangle \otimes |0\rangle^{\otimes (n-p)}, \qquad |+_Y^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_Y\rangle \otimes |0\rangle^{\otimes (n-p)}
p,p' = 1,2,\dots,d
V_{FLO}

Conclusion

  • We propose Fermion Sampling scheme with magic input states which utilize gate sets and architecture native to superconducting devices and has the potential to be realized in near-term
  • We provide state-of-the-art hardness guarantees by proving
    • Anticoncentration
    • Robust average-case hardness of computing the output probabilities
  • The hardness guarantees are comparable to RCS and surpassing Boson Sampling
  • Both results are derived using the group structure of FLO circuits
  • Assuming that we have an FLO circuit, the circuit can be certified efficiently using resources scaling polynomially with the system size

Fermionic quantum advantage

By Ninnat Dangniam

Fermionic quantum advantage

AQIS 2020 Virtual Conference, 7-9 Dec 2020. Recording available at https://www.youtube.com/watch?v=o0nm2R0FlqA

  • 455

More from Ninnat Dangniam