Quantum Sampling Advantage

How to prove it and does it matter?

The 26th International Annual Symposium on Computational Science and Engineering

20 Jul 2023

Ninnat Dangniam

The Institute for Fundamental Study (IF)

Naresuan University

PC: Google Quantum AI

  • Introduction - What is a simulation?
  • Case I: Periodically-driven thermalized quantum systems
  • Case II: Fermion Sampling
  • Does it matter?

Outline

Quantum Advantage

  • Computational quantum advantage, or quantum supremacy, refers to the ability of a quantum system to perform a task that classical computers cannot, regardless of whether the task is useful 
  • Certain sampling tasks provide provable quantum advantages based on a plausible complexity-theoretic assumption (but weaker than P \(\neq\) NP). 
  • Quantum-sampling-advantage tasks are very different in nature from e.g. fast integer factorization using Shor's algorithm

Given an initial state \(|\psi\rangle\) and a family of unitary time evolutions \(\{U_{\alpha}\}_{\alpha}\),

are the \(U_{\alpha}|\psi\rangle\)'s hard to simulate on a classical computer?

Quantum advantage (informal)

{\bf y} \in \{0,1\}^n

String of \(n\) bits

\implies

Classical vs Quantum circuit

{\bf x}

Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)

\implies

String of \(n\) qubits

\bigotimes_{j=1}^n |\psi_j\rangle

Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)

\implies

Classical vs Quantum circuit

\implies

Output distribution over \(2^n\) bitstrings \(p({\bf x}) = p_{\bf x}\)

The result of the coin flips are just hidden bitstrings that can be included as extra inputs

Strong vs Weak Simulation

Strong simulation

Weak simulation

Can compute \(p_{\bf x}\) 

Can sample from \(p\)

|p_{\bf x} - q_{\bf x}| \le \eta p_{\bf x}
\sum_{\bf x} |p_{\bf x} - q_{\bf x}| \le \epsilon

In practice, there need to be some notions of errors

In this talk, I will use these definitions of strong and weak simulation unless stated otherwise

Relative error

Additive error

Given an initial state \(|\psi\rangle\) and a family of unitary time evolutions \(\{U_{\alpha}\}_{\alpha}\), are the \(U_{\alpha}|\psi\rangle\)'s hard to simulate on a classical computer?

Given an initial state \(|\psi\rangle\) and a family of polynomial-depth quantum circuits \(\{U_{\alpha}\}_{\alpha}\), can there be a classical machine that approximately samples from \(p_{\bf x} = |\langle{\bf x}|U_{\alpha}|\psi\rangle|^2\) in poly\((n,\epsilon^{-1})\) time?

(Quantum sampling advantage)

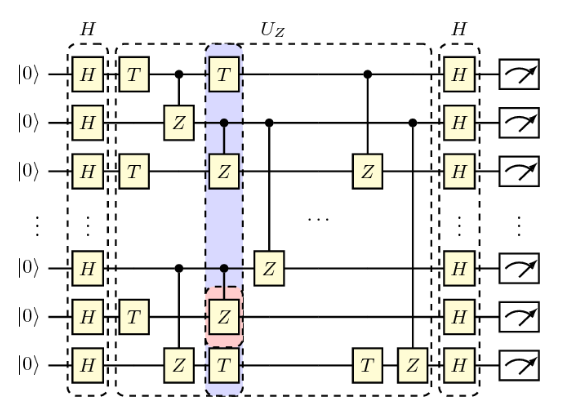
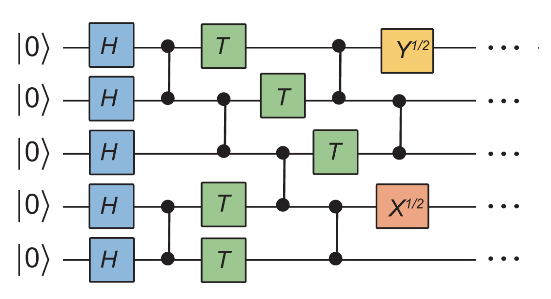
Boson sampling

Commuting circuit sampling

Random circuit sampling (RCS)

Instantaneous quantum polynomial (IQP)

Aaronson and Arkhipov, STOC'11

Bremner et al., Proc. R. Soc. A (2011)

Bremner et al., PRL (2016)

Boixo et al., Nat. Phys. (2018)

Bouland et al., Nat. Phys. (2018)

Quantum simulators

Translation-invariant Hamiltonians

Bermejo-Vega et al., PRX (2018)

Haferkamp et al., PRL (2020)

Novo et al., Quantum (2021)

Energy measurement

MBQC

Difficulty

P: problems solvable in polynomial time

  • Eulerian cycle
  • Multiplication
  • Primality testing

NP: problems checkable in polynomial time 

  • Hamiltonian cycle
  • Traveling salesman
  • Packing
  • Graph coloring

#P: counting the number of solutions to an NP problem

BQP: problems solvable in polynomial time on a quantum computer

  • Factoring
  • Discrete log
  • Jones polynomial

Proof of Classical Intractability

Proof of Classical Intractability

Given \(|\psi\rangle, \{U_{\alpha}\}_{\alpha}\)

Classical sampler \(\mathcal{C}\) for all \(U_{\alpha}\)

\sum_{\mathbf{x}} |p_{\mathbf{x}}-q_{\mathbf{x}}| \le \epsilon

Weak simulation

Strong simulation

|p_{\bf 0} - q_{\bf 0}| \le \eta p_{\bf 0}

Anti-concentration of \(p_{\bf 0}(U_{\alpha})\)

Ability to approximately compute \(p_{\bf 0} = |\langle {\bf 0}|U_{\alpha}|\psi\rangle|^2\) for most \(U_{\alpha}\)

\mathcal{C}^{\mathrm{NP}}

Collapse of the polynomial hierarchy if the RHS is a #P-hard problem

Anti-concentration

To turn relative error to additive error, we need most probabilities to be large

|p_{\bf x} - q_{\bf x}| \le \eta p_{\bf x} \longleftrightarrow \sum_{\bf x} |p_{\bf x} - q_{\bf x}| \le \epsilon
\Pr\left(p_{{\bf x}} \ge \displaystyle{\frac{C_1}{2^n}}\right) \ge C_2

Average-Case Hardness

  • Average-case hardness for Boson Sampling originates from the argument for average-case hardness to compute the permanent via polynomial interpolation (Lipton 1991).
  • Bouland et al., Nat. Phys. (2018) and Movassagh 2019 import the argument to Random Circuit Sampling

Worst-case hardness of approximately computing \(p_{\bf 0}(U_{\alpha})\)

Worst-to-average-case reduction

Hardness of approximately computing \(p_{\bf 0}(U_{\alpha})\) for most \(U_{\alpha}\)

Easy to argue based on existing results in quantum computing

Jirawat Tangpanitanon, Supanut Thanasilp, Marc-Antoine Lemonde, ND, Dimitris G. Angelakis, Quantum Sci. Technol. 8, 025019 (2023)

  • Introduction - What is a simulation?
  • Case I: Periodically-driven thermalized quantum systems
  • Case II: Fermion Sampling
  • Does it matter?

Outline

Periodically-Driven Thermalized Quantum Systems

U_F = \mathcal{T} \exp\left[-\frac{i}{\hbar}\int_0^T dt\,H(t)\right] \equiv \exp(-\frac{i}{\hbar}H_F T)

Time-dependent Hamiltonian with a periodic driving

Floquet operator

Floquet Hamiltonian

Multiple periods \(M\) of evolutions until thermalize

|\psi_M\rangle = U_F^M |\psi_0\rangle

External drive

H(t) = H_0 + f(t) H_{\textrm{drive}}
f(t+T)
=

Periodically-Driven Thermalized Quantum Systems

External drive

A
B

In what sense a closed quantum system thermalize?

Subsystem thermalization

\rho_A = \mathrm{Tr}_B |\psi\rangle\langle\psi|_{\textrm{total}} = \displaystyle{\frac{e^{-H/k_B T}}{Z}}
U_F \longleftrightarrow U_{\textrm{COE}}

Floquet eigenstate thermalization hypothesis (ETH)

Observables' statistics  are well described by a unitary matrix randomly drawn from the circular orthogonal ensemble

Time-reversal symmetry

Periodically-Driven Thermalized Quantum Systems

Commuting quantum circuit

We show

  • Anticoncentration of \(M \gg 2\pi/ET \) periods of COE evolutions
  • Worst-case hardness of strong simulation

Undriven

Driven

Kim et al., PRE (2014)

Lazarides et al., PRE (2014)

Mori et al., PRL (2016)

The Role of Drive

  • ETH applies to a wider part of the energy spectrum
  • Long range effective interaction (Magnus expansion analysis)
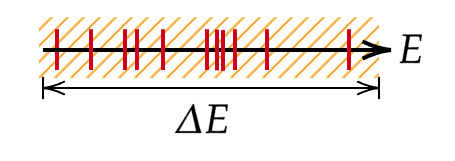
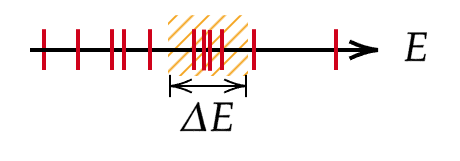
H_0^{\mathrm{Ising}} = \sum_{j=1}^L \mu_j Z_j + J \sum_{jk} Z_jZ_k \\ H^{\mathrm{Ising}}_{\textrm{drive}} = \sum_{j=1}^L X_j
  • We numerically show that the eigenstate statistics are approximated well by COE statistics and anti-concentrate (close to the Porter-Thomas distribution ) for the driven disordered Ising chain and driven Bose-Hubbard model
H^{\mathrm{BH}}_0 = \sum_{j=1}^L \left(\mu_j a_j^{\dagger}a_j + \frac{U}{2} a_j^{\dagger 2} a_j^2 \right) \\ V^{\mathrm{BH}}_{\textrm{drive}} = \sum_{j=1}^{L-1} \left( a_j^{\dagger} a_{j+1} + \mathrm{H.C.} \right)

The Role of Drive

Evidences of quantum sampling advantage for driven, thermalized quantum systems by anti-concentration and the worst-case hardness

Not clear if average-case hardness holds because random matrix instances are not the same as the physical instances

  • Introduction - What is a simulation?
  • Case I: Periodically-driven thermalized quantum systems
  • Case II: Fermion Sampling
  • Does it matter?

Outline

Michał Oszmaniec, ND, Mauro E. Morales, Zoltán Zimborás, PRX Quantum 3, 020328 (2022)

=\begin{pmatrix} R^{\dagger}_Z(\varphi)_{11} & & R_Z^{\dagger}(\varphi)_{12} \\ & \!\!\!\!\!\Large{R_X(\theta)}\!\!\!\! \\ R_Z^{\dagger}(\varphi)_{21} & & R_Z^{\dagger}(\varphi)_{22} \end{pmatrix}

Fermionic Linear Optics (FLO)

Even parity

Odd parity

M(U^+,U^-) =\begin{pmatrix} U^+_{11} & & U^+_{12} \\ & \Large{U^-} \\ U^+_{21} & & U^+_{22} \end{pmatrix}
\det U^+ = \det U^-

FLO gates AKA Matchgates

(Valiant, SIAM J Comput 2002)

\mathrm{SWAP} = \begin{pmatrix} 1 & & 0 \\ & \!\!\!\!\Large{X}\!\!\! \\ 0 & & 1 \end{pmatrix}

Non-example

Google AI Blog

\mathrm{fSim}(\theta,\varphi) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\theta & -i\sin\theta & 0 \\ 0 & -i\sin\theta & \cos\theta & 0\\ 0 & 0 & 0 & e^{-i\varphi} \end{pmatrix}

Classical Intractability?

Classical sampler \(\mathcal{C}\)

\sum_{\mathbf{x}} |p_{\mathbf{x}}-q_{\mathbf{x}}| \le \epsilon

Anti-concentration?

Ability to approximately compute \(p_{\bf 0} = |\langle {\bf 0}|V_{\mathrm{FLO}}|{\bf 0}\rangle|^2\) for most \(V_{\mathrm{FLO}}\)

\mathcal{C}^{\mathrm{NP}}
|p_{\bf 0} - q_{\bf 0}| \le \eta p_{\bf 0}
V_{\mathrm{FLO}}

This is easy!

Jordan-Wigner

f^{\dagger}_j \coloneqq (X_j-iY_j) \displaystyle{\prod_{k=1}^{j-1}} Z_k

FLO

Free-fermionic evolution

Fermion Sampling

  • FLO with computational-basis input state admits strong simulation (compute \(p_{\bf x}\) up to logarithmic number of decimals)
  • Not the case with non-Gaussian (magic) input state; strong simulation is #P-hard (cf. Ivanov, PRA 2017)
  • Our work shows that weak simulation is also hard
V_{FLO}
|\Psi_4\rangle = \displaystyle{\frac{|0011\rangle + |1100\rangle}{\sqrt{2}}}

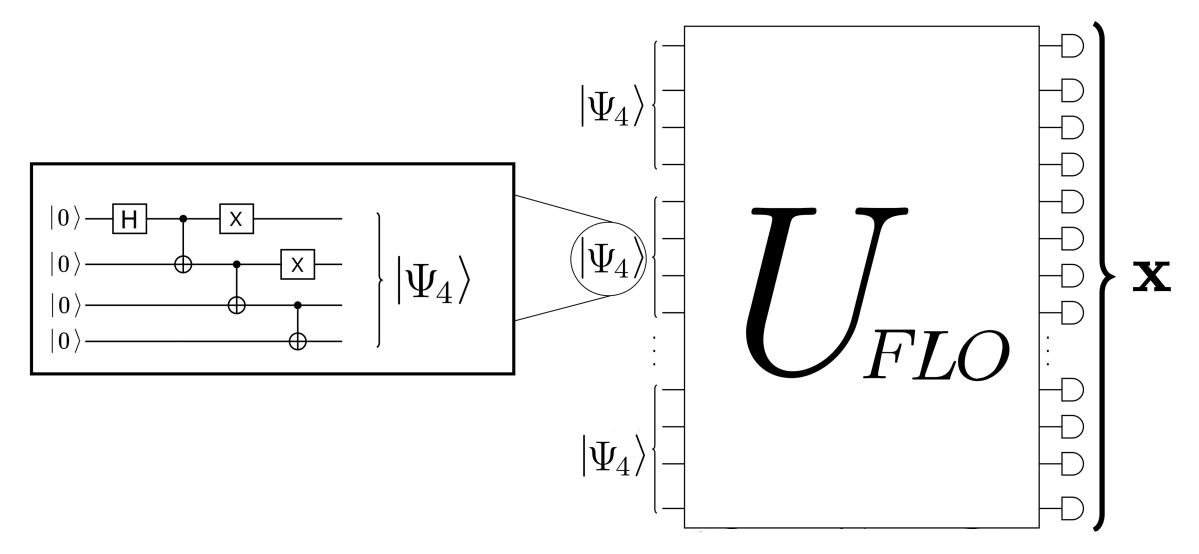
Fermion Sampling

We analytically show both anti-concentration and average-case hardness, the two ingredients needed in the proof of sampling quantum advantage

  • SO(\(2n\)) for FLO
  • U(\(n\)) for passive (number-preserving) FLO
|+_X^p\rangle \\ \text{or} \\ |+_Y^p\rangle
p,p' = 1,2,\dots,d
V_{FLO}
|+_X^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_X\rangle \otimes |0\rangle^{\otimes (n-p)}
|+_Y^p\rangle = |0\rangle^{\otimes (p-1)} \otimes |+_Y\rangle \otimes |0\rangle^{\otimes (n-p)}
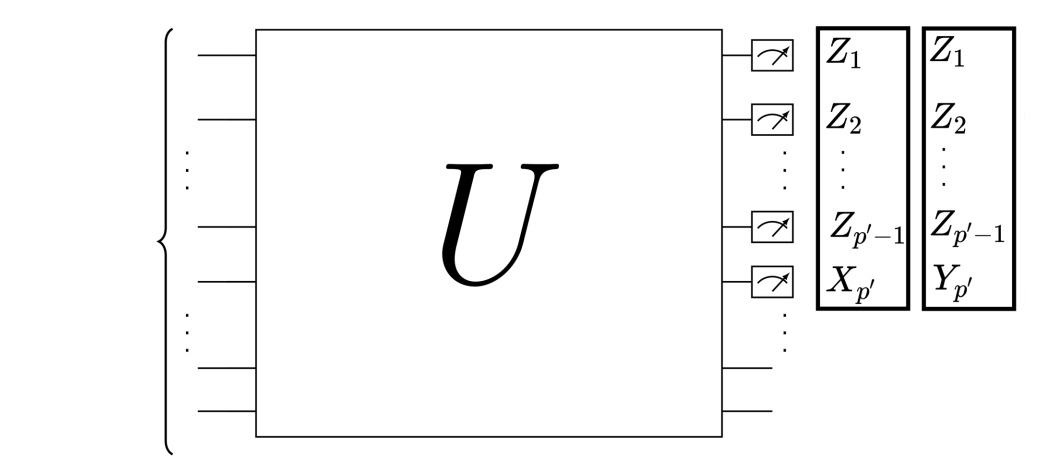
  • The low dimensionality also allows an efficient tomography of the FLO circuit using single-mode input states and product measurements
  • Introduction - What is a simulation?
  • Case I: Periodically-driven thermalized quantum systems
  • Case II: Fermion Sampling
  • Does it matter?

Outline

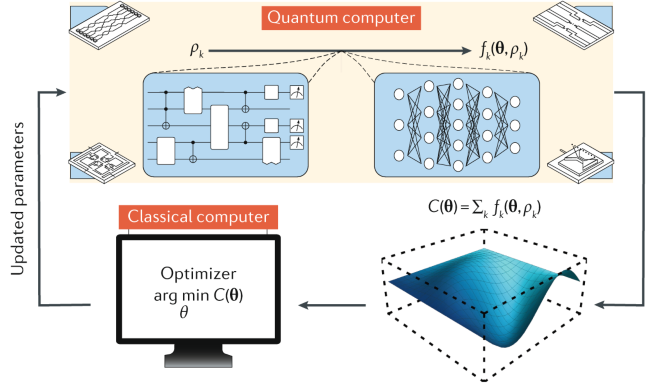
  • Variational quantum algorithm (VQA)
    • Hybrid classical-quantum algorithm
    • Generate distribution that is hard to sample from classically, but heuristic optimization by classical computers

Cerezo et al., Nat. Rev. Phys. (2021)

Does It Matter for "Real" Tasks?

* Semi-informed personal opinion

  • Optimization problems and quantum machine learning
    • Mapping to unnatural instances of NP problems e.g. factoring
  • Repertoire of hard tasks for cryptographic uses e.g. Blockchain agreement arXiv:2305.19865

Provable quantum advantage, or weaker one (advantageous compared to existing classical algorithms e.g. exponential speedup by Shor's algorithm)

Summary

  • Simulating \(U|\psi\rangle\) = Sampling from \(|\langle {\bf x}|U|\psi\rangle|^2\) (Weak simulation)
  • The standard argument for sampling quantum advantage requires statistical data of the ensemble \(\{U_{\alpha}\}_{\alpha}\), namely anti-concentration and hardness "on average" (most instances)
  • Driven thermalized quantum systems are candidates that may provide quantum advantage
  • Fermion Sampling provides strong hardness guarantees, comparable to those of random circuit sampling but with smaller gate sets
  • So far it is not clear that proofs of quantum advantage for application-oriented tasks such as optimization and machine learning are actually relevant to real-world applications

Tent Rock National Monument 2017

Extra Slides

50-100 qubits

1,000

10,000

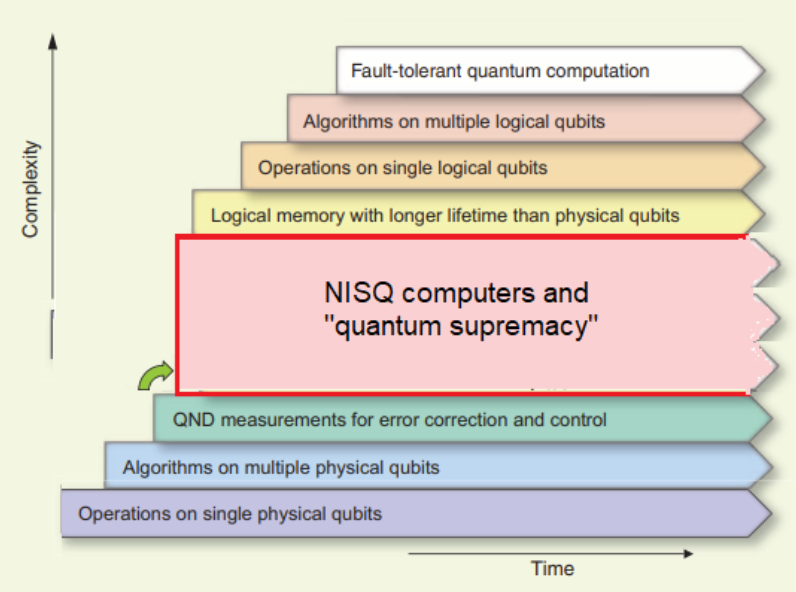
1,000,000

...

Fault-tolerant, universal quantum computing

Gil Kalai, modified from Devoret and Schoelkpf, Science (2013)

Noisy, intermediate-scale quantum (NISQ) devices

\underbrace{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\:}

Commercially-relevant applications, unambiguous quantum advantage

10 years?

A Quantum Future

BBC

Codebreaking

iStock/sergunt

Quantum chemistry simulation

Modified from Bremner, QIP2018

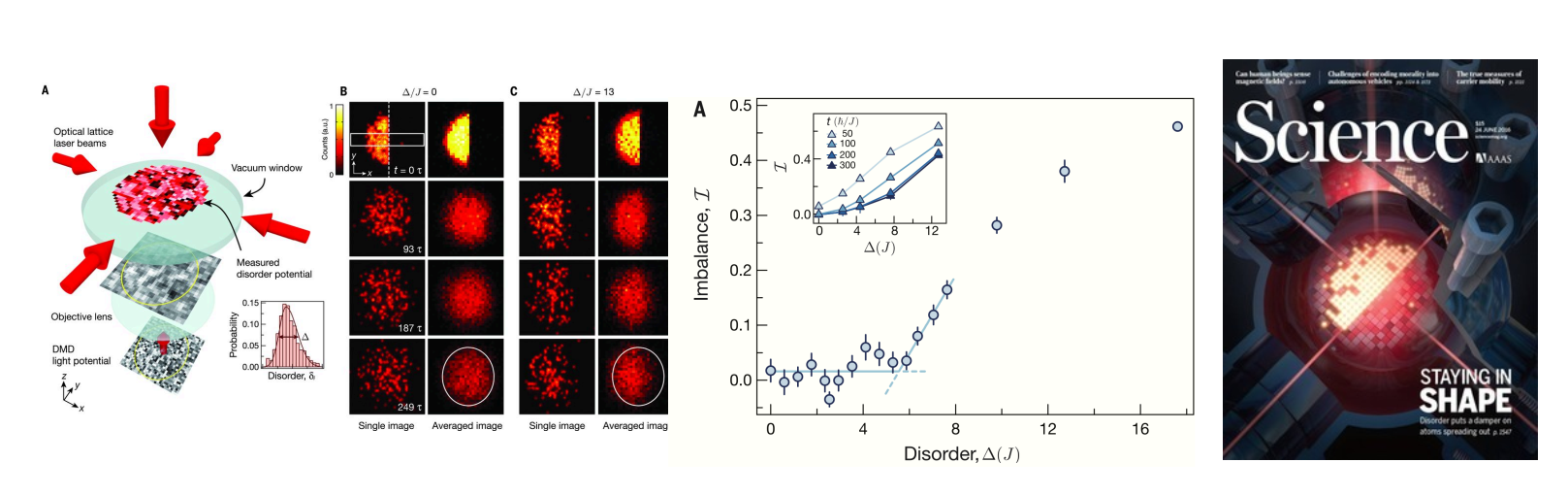
Immanuel Bloch's group

Quantum simulations are natural, useful, and appear to be hard for classical computers.

Choi et al., Sci. 2016 uses cold atoms in optical lattices to compute many-body localization transition in 2D, which cannot be efficiently done with existing numerical techniques

But are they provably hard?

Fermionic Linear Optics (FLO)

X = \begin{pmatrix}0&1\\1&0 \end{pmatrix}
Y = \begin{pmatrix}0&\!\!\!-i\\i&0 \end{pmatrix}
Z = \begin{pmatrix}1&0\\0&\!\!\!-1 \end{pmatrix}

Reminder

\sigma^{\dagger} = X-iY = \begin{pmatrix}0&0\\1&0 \end{pmatrix}
\sigma^{\dagger}|0\rangle = |1\rangle

Identify computational basis states with occupation number states

Jordan-Wigner

f_j f^{\dagger}_k +f^{\dagger}_k f_j = \delta_{jk}\mathbb{I}
(f^{\dagger}_j)^2 = 0

CAR

f^{\dagger}_j \coloneqq \sigma_j^{\dagger} \displaystyle{\prod_{k=1}^{j-1}} Z_k

\(f_j^{\dagger}\) creates a fermion at site \(j\)

Pauli exclusion

Fermionic Linear Optics (FLO)

m_j^X \coloneqq X_j \displaystyle{\prod_{k=1}^{j-1}} Z_k
m_j^Y \coloneqq Y_j \displaystyle{\prod_{k=1}^{j-1}} Z_k

cf. Dirac's gamma matrices

m_{\alpha}m_{\beta} + m_{\beta}m_{\alpha} = 2 \delta_{\alpha\beta} \mathbb{I}
\alpha = (j,X\,\mathrm{or}\,Y)

Majoranas

\begin{pmatrix} 1 & & 0 \\ & \!\!\!\!\!\Large{-iX}\!\!\!\! \\ 0 & & 1 \end{pmatrix}

Non-example

\mathrm{SWAP}= \mathbb{I}\!\otimes\!\mathbb{I}\!+\!X\!\otimes\! X \!+\! Y\!\otimes \!Y \!+\! Z\!\otimes \!Z

\(Z\!\otimes\! Z\) interaction is not FLO

FLO Hamiltonians are quadratic

Antisymmetric

H_{\mathrm{FLO}} = \displaystyle{\frac{i}{4}} \sum_{\substack{\alpha,\beta \\ \alpha>\beta}} h_{\alpha\beta} [m_{\alpha},m_{\beta}]

Fermionic Linear Optics (FLO)

\vec{m}(t) = V^{\dagger} \vec{m} V = e^{{\bf h}t} \vec{m}

Generators of rotations SO(\(2n\))

V_{\mathrm{FLO}} = e^{iH_{\mathrm{FLO}}t}

(Defining representation)

Antisymmetric

Manipulating \(2n\times 2n\) matrices instead of \(2^n\times 2^n\) matrices!

  • Only need to specify the correlation matrix (2nd moments)
  • All higher moments can be extracted from \(\Sigma\) via Wick's theorem
\Sigma_{\alpha\beta} \coloneqq \frac{i}{2}\mathrm{Tr}(\rho[m_{\alpha},m_{\beta}])
p_{\bf x} = \frac{1}{i^{2^n}} \mathrm{Pf} (\Sigma)

\(\rho = (|0\rangle\langle 0|)^{\otimes n}\) is a fermionic Gaussian state

\(l^2\)-distance to the uniform distribution:

\(\Vert  p-p_{\mathrm{unif}}\Vert^2 = Z - \displaystyle{\frac{1}{2^n}} = Z-Z_{\mathrm{unif}}\)

Z = \mathbb{E}_U \mathbb{E}_{\bf x}\, [ p^2_{\bf x}(U)]
Z \le \displaystyle{\frac{1}{\alpha 2^n}}

\(p_{\bf{x}}(U)\) anti-concentrates if

Z_{\mathrm{unif}} = \displaystyle{\frac{1}{2^n}}

Implies \(\Pr\left(p_{{\bf x}} \ge \displaystyle{\frac{\beta}{2^n}}\right) \ge \alpha(1-\beta)^2 \) via the Paley-Zygmund inequality

\Pr\left( X\ge \beta\mathbb{E}[X] \right) \ge (1-\beta)^2 \displaystyle{\frac{\mathbb{E}[X]^2}{\mathbb{E}[X^2]}}
2
2
2

Anti-concentration

Modified from Dalzell et al., PRX Quantum 2022

\mathbb{E}_V [p^2_{\bf 0}] = \int dV\, \mathrm{Tr}(V|\Psi\rangle \langle \Psi| V^{\dagger}|{\bf 0}\rangle\langle {\bf x}|)^2
= \mathrm{Tr}(|\Psi\rangle \langle \Psi| \int dV\, V^{\dagger}|{\bf 0}\rangle\langle {\bf 0}|V)^2
= \mathrm{Tr}\left[(|\Psi\rangle \langle \Psi|)^{\otimes 2} \underbrace{\int dV\, (V^{\dagger})^{\otimes 2}(|{\bf 0}\rangle\langle {\bf 0}|)^{\otimes 2}V^{\otimes 2}}\right]

Sum of projectors onto irreps by Schur's lemma under nice conditions 

  • SO(\(2n\)) for FLO
  • U(\(n\)) for passive (number-preserving) FLO

Anti-concentration

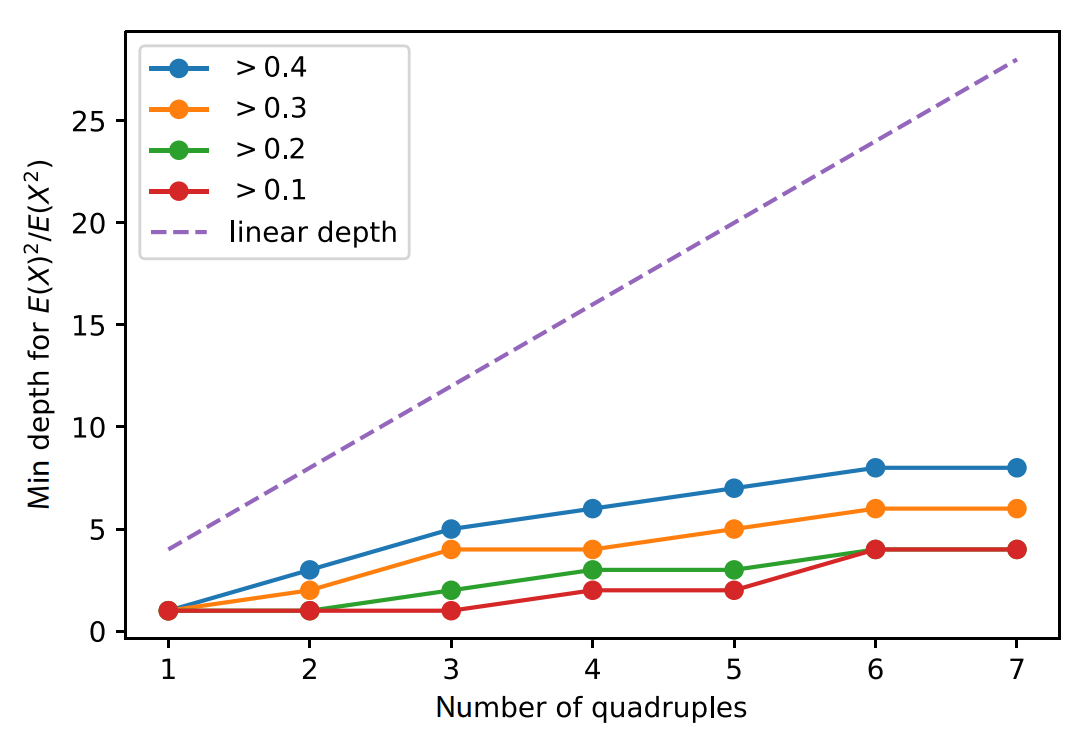
  • Numerics suggest that random FLO circuits anti-concentrate in sub-linear depth

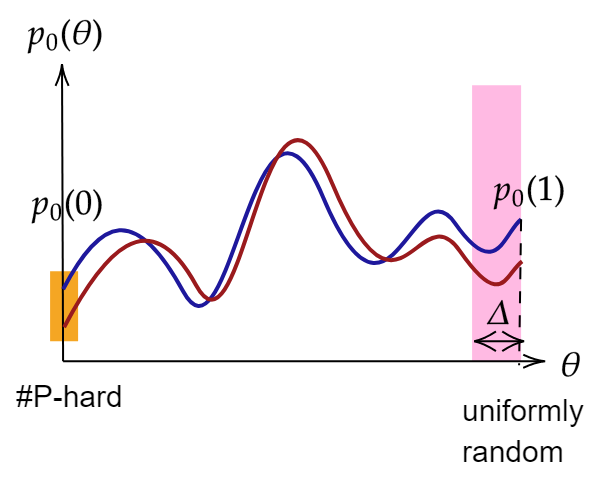
Worst-to-average-case reduction

  • There exists a "worst-case circuit" \(V_0\) for which \(p_{\bf 0} = |\langle \mathbf{0}|V_0|\Psi\rangle|^2\) is #P-hard to approximate
  • Deform to average-case (Haar random) circuits where \(p_{\bf 0} (\theta)= |\langle \mathbf{0}|V(\theta)|\Psi\rangle|^2\) is a polynomial of low-degree \(q\)
  • Sample \(\gtrsim q\) points (some can be errorneous\(\iff\)robustness) and recover \(p_{\bf 0}(\theta)\) via Berlekamp–Welch
  • Plug in \(\theta = 0\) to solve a #P-hard problem! 

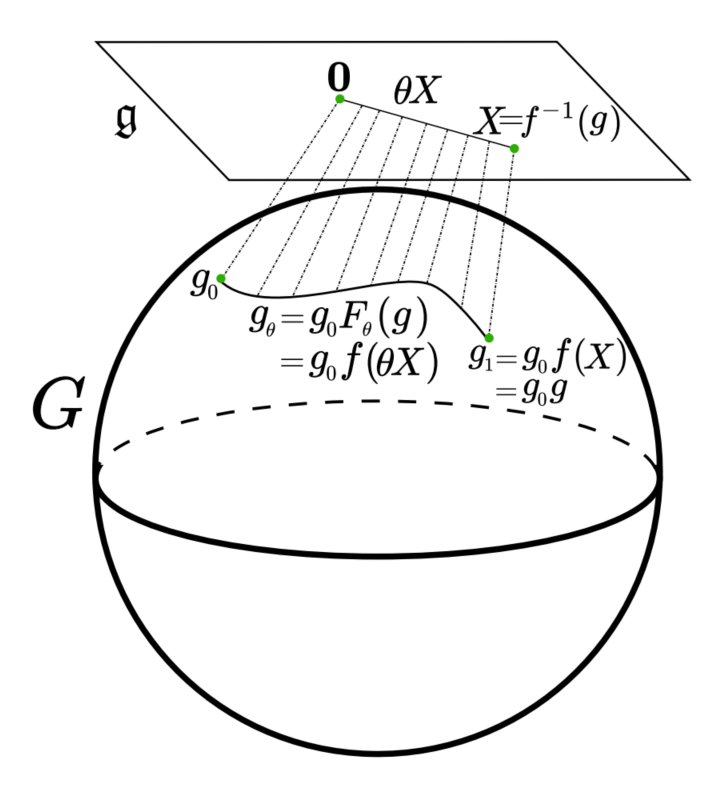
Unitary Paths

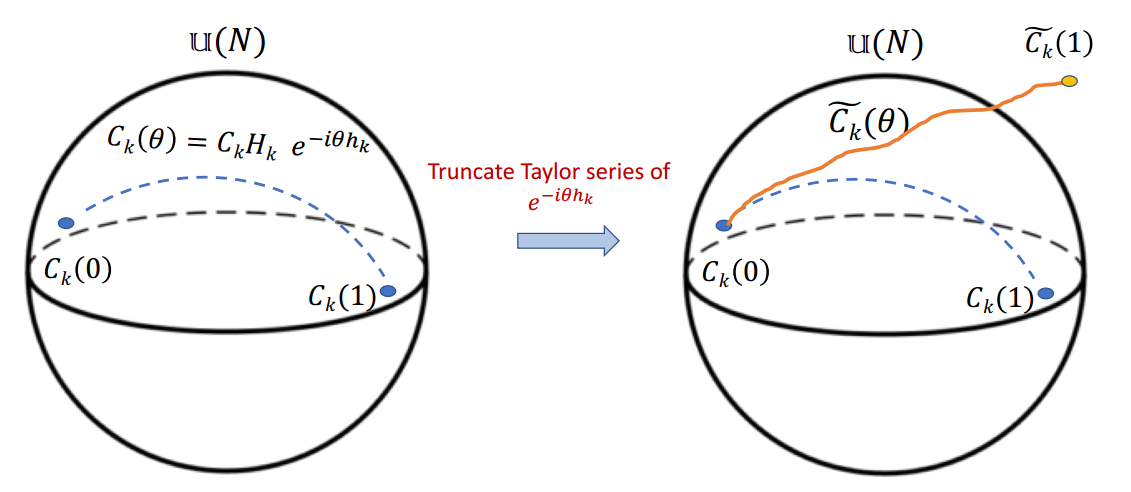
First idea: truncated exponential path

U(\theta) = U_0 e^{i\theta H}

Movassage 2019

= U_0 \left(\mathbb{I} + i\theta H + \frac{(i \theta H)^2}{2!} + \cdots \right)

Truncation gives rise to a non-unitary operator

f(X) = (\mathbb{I}-X)(\mathbb{I}+X)^{-1}
g_{\theta} = g_0 \displaystyle{ \frac{(1-\theta) \mathbb{I} +(1+\theta) g}{ (1+\theta) \mathbb{I} +(1-\theta)g }}

Better idea: Cayley path

Unitary

Hermitian

Hardness Guarantees

Quantum advantage scheme Robustness of avg-case hardness
(additive error)		 Anti-concentration
Boson Sampling
Random circuit sampling (Google layout)
Fermion Sampling
2^{-\tilde{O}(n)}
2^{-\tilde{O}(n^{1.5})}
2^{-\tilde{O}(n^2)}

Bouland et al., FOCS 2021

Sampling Advantage (ANSCSE2023)

By Ninnat Dangniam

Sampling Advantage (ANSCSE2023)

The 26th International Annual Symposium on Computational Science and Engineering (20-21 Jul 2023)

  • 184

More from Ninnat Dangniam