Topologikus fázisátmenet vizsgálata mikroméretű buborékok segítségével
Tajkov Zoltán, Nanoszerkezetek laboratórium
EK MFA szeminárium, 2022. április 27.
összefoglalás
EK MFA szeminárium, 2022. április 27.
EK MFA szeminárium, 2022. április 27.
EK MFA szeminárium, 2022. április 27.
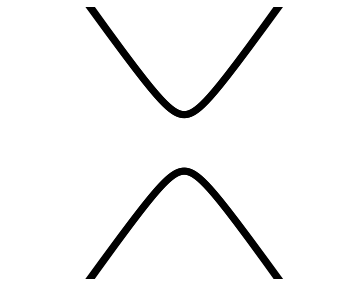
$$ E $$
$$ E $$
Szigetelő?
Topológia?
$$ \frac{1}{2\pi}\int K \mathrm{d}A = 2(1-g) $$
EK MFA szeminárium, 2022. április 27.
$$ \frac{1}{2\pi}\int K \mathrm{d}A = 2(1-g) $$
Su-Schrieffer-Heeger
H_{\mathrm{véges}}=\begin{pmatrix}
0 & v & 0 & 0 & 0 & 0 \\
v & 0 & w & 0 & 0 & 0 \\
0 & w & 0 & v & 0 & 0 \\
0 & 0 & v & 0 & w & 0 \\
0 & 0 & 0 & w & 0 & v \\
0 & 0 & 0 & 0 & v & 0
\end{pmatrix}
H_{\mathrm{per.}}=\begin{pmatrix}
0 & v & 0 & 0 & 0 & w \\
v & 0 & w & 0 & 0 & 0 \\
0 & w & 0 & v & 0 & 0 \\
0 & 0 & v & 0 & w & 0 \\
0 & 0 & 0 & w & 0 & v \\
w & 0 & 0 & 0 & v & 0
\end{pmatrix}
H(k)=\begin{pmatrix}
0 & v+w\mathrm{e}^{ik} \\
v+w\mathrm{e}^{-ik} & 0
\end{pmatrix}
FT
E(k)=\pm\sqrt{v^2+w^2+2vw\cos{(k)}}
J. K. Asbóth, et. al., vol. 909 of Lecture Notes in Physics. Springer International Publishing, 1st ed., 2016.
EK MFA szeminárium, 2022. április 27.
$$ \frac{1}{2\pi}\int K \mathrm{d}A = 2(1-g) $$
Su-Schrieffer-Heeger
H(k)=\begin{pmatrix}
0 & v+w\mathrm{e}^{ik} \\
v+w\mathrm{e}^{-ik} & 0
\end{pmatrix}
E(k)=\pm\sqrt{v^2+w^2+2vw\cos{(k)}}
H(k)=d_x(k) \mathbf{\sigma}_x + d_y(k) \mathbf{\sigma}_y + d_z(k) \mathbf{\sigma}_z
\mathbf{d}(k)=\begin{pmatrix}
d_x(k) \\
d_y(k) \\
d_z(k)
\end{pmatrix} =
\begin{pmatrix}
v+w\cos{(k)} \\
w\sin{(k)} \\
0
\end{pmatrix}
\nu = \frac{1}{2\pi}\int \left( \tilde{\mathbf{d}}(k) \times \frac{\mathrm{d}}{\mathrm{d}k} \tilde{\mathbf{d}}(k) \right)_z\mathrm{d}k
csavarodási szám
J. K. Asbóth, et. al., vol. 909 of Lecture Notes in Physics. Springer International Publishing, 1st ed., 2016.
EK MFA szeminárium, 2022. április 27.
Kétdimenziós példa
A Chern-szám
Q=\frac{1}{2\pi}\int_{\mathrm{BZ}}F_{xy}\mathrm{d}^2k
\sigma_{xy}=-\frac{e^2}{2\pi\hbar}Q
EK MFA szeminárium, 2022. április 27.
Mire jók a topoligikus szigetelők?
- Robusztusak
- Tulajdonságaik nem lokálisak
- Csak fundamentális konstansoktól függnek
- Kvantum-számítástechnika
- Alapvető konstansok mérése
- Spintronika
- Topologikusan védett élállapotok
EK MFA szeminárium, 2022. április 27.
A topologikus szigetelők ritkák!
25%
EK MFA szeminárium, 2022. április 27.
Cirkónium pentatellurid - ZrTe5
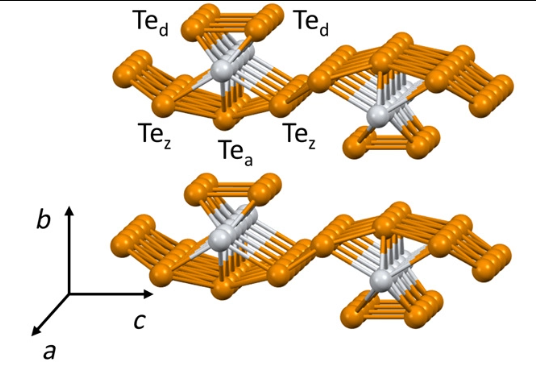
Mutch, J., Chen, et. al. Science Advances, 2019 5(8).
EK MFA szeminárium, 2022. április 27.
Cirkónium pentatellurid - ZrTe5
Mutch, J., Chen, et. al. Science Advances, 2019 5(8).
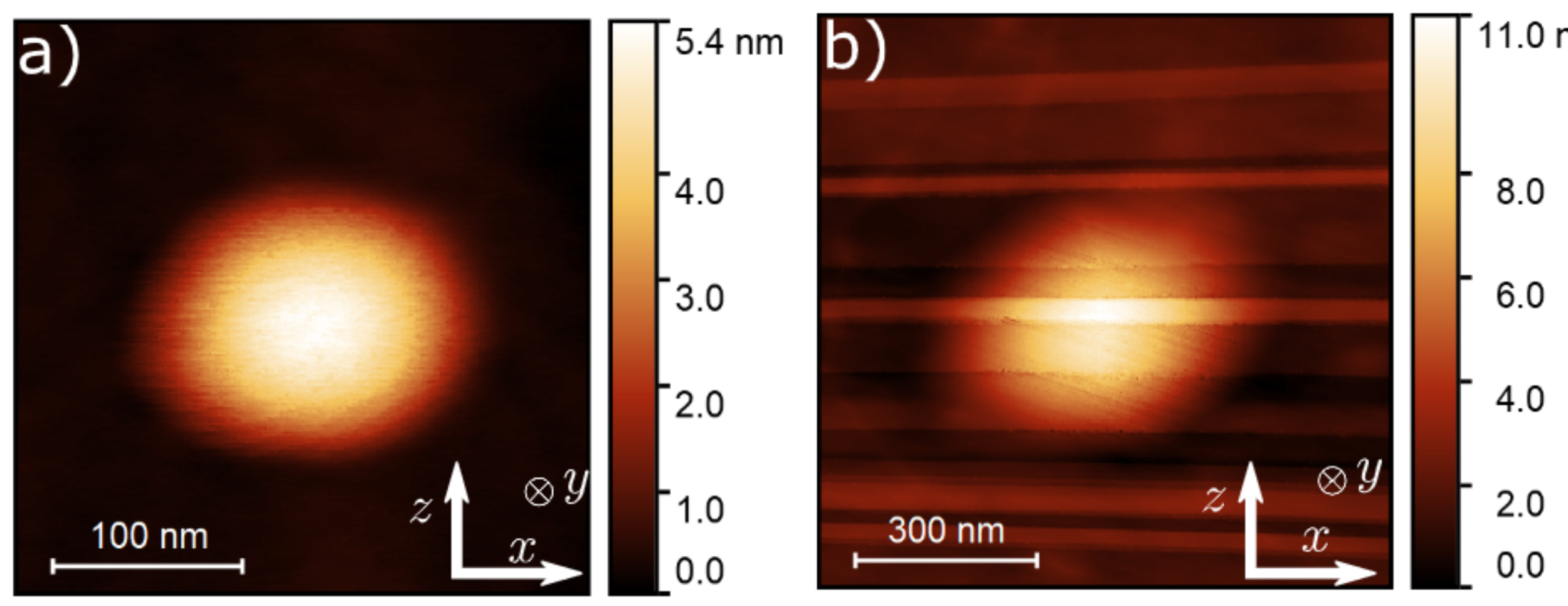
EK MFA szeminárium, 2022. április 27.
Cirkónium pentatellurid - ZrTe5
$$ \#1 $$
$$ \#2 $$
$$ d $$
$$ h$$
$$ R_1 $$
$$ R_2 $$
$$ Ang $$
55
49
1015
813
178
90
6000
4560
EK MFA szeminárium, 2022. április 27.
Cirkónium pentatellurid - ZrTe5
$$ O_x $$
$$ \mathcal{A}_1 $$
$$ \mathcal{B}_1 $$
$$ C $$
$$ O_z$$
$$ O_x $$
$$ \mathcal{A}_1 $$
$$ \mathcal{B}_1 $$
$$ C $$
$$ O_z$$
Merevség tenzor illesztése (DFT)
Végeselem módszer
Elektromos tulajdonságok (DFT)
EK MFA szeminárium, 2022. április 27.
Cirkónium pentatellurid - ZrTe5
COMSOL eredmények
EK MFA szeminárium, 2022. április 27.
Cirkónium pentatellurid - ZrTe5
Elsőelves eredmények
Minimal
By novidad21
