Lecture 3: Biophysical basis of excitability
1. THE NERST EQUATION
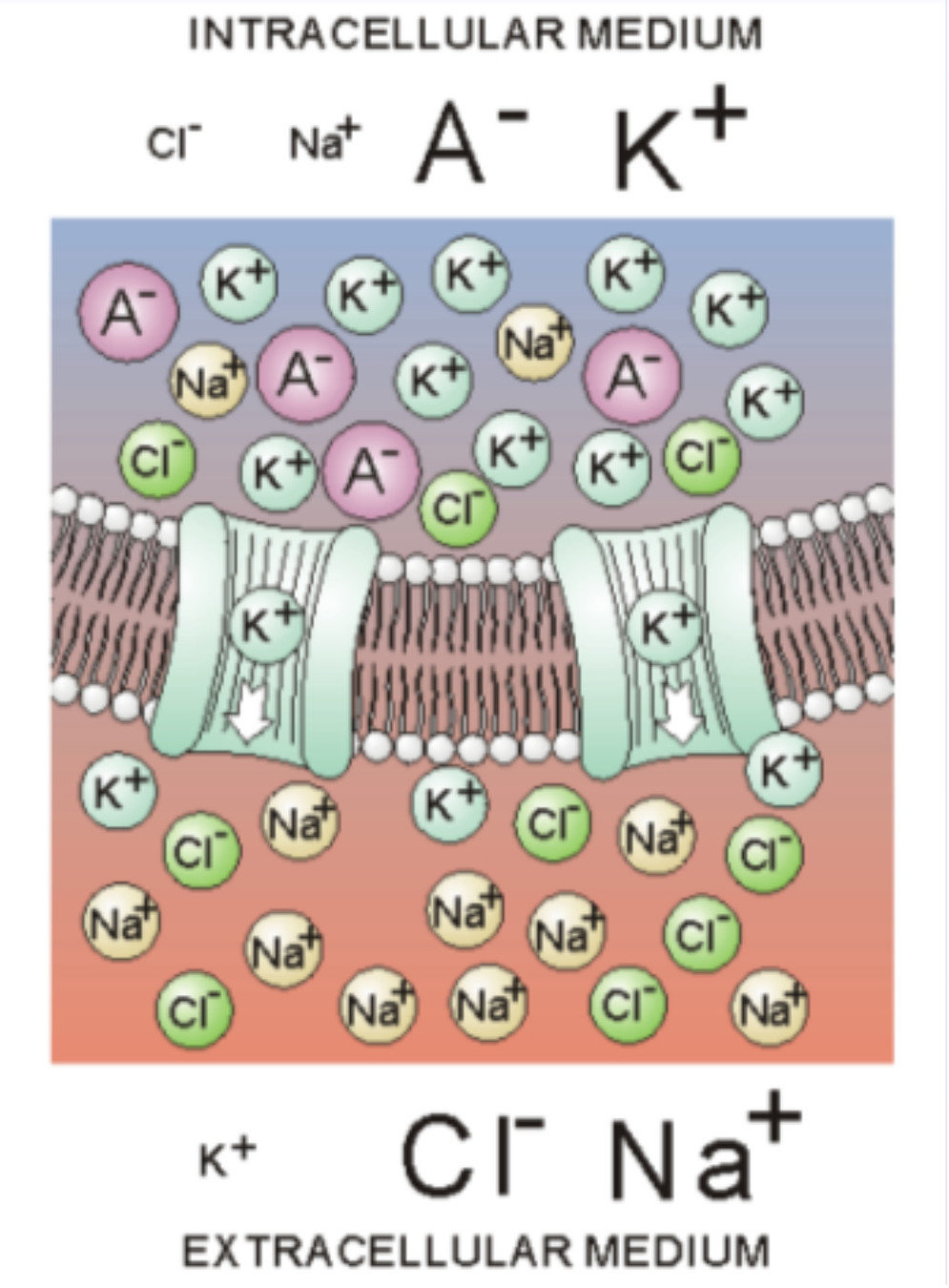
The membrane: contains channels which can open and close
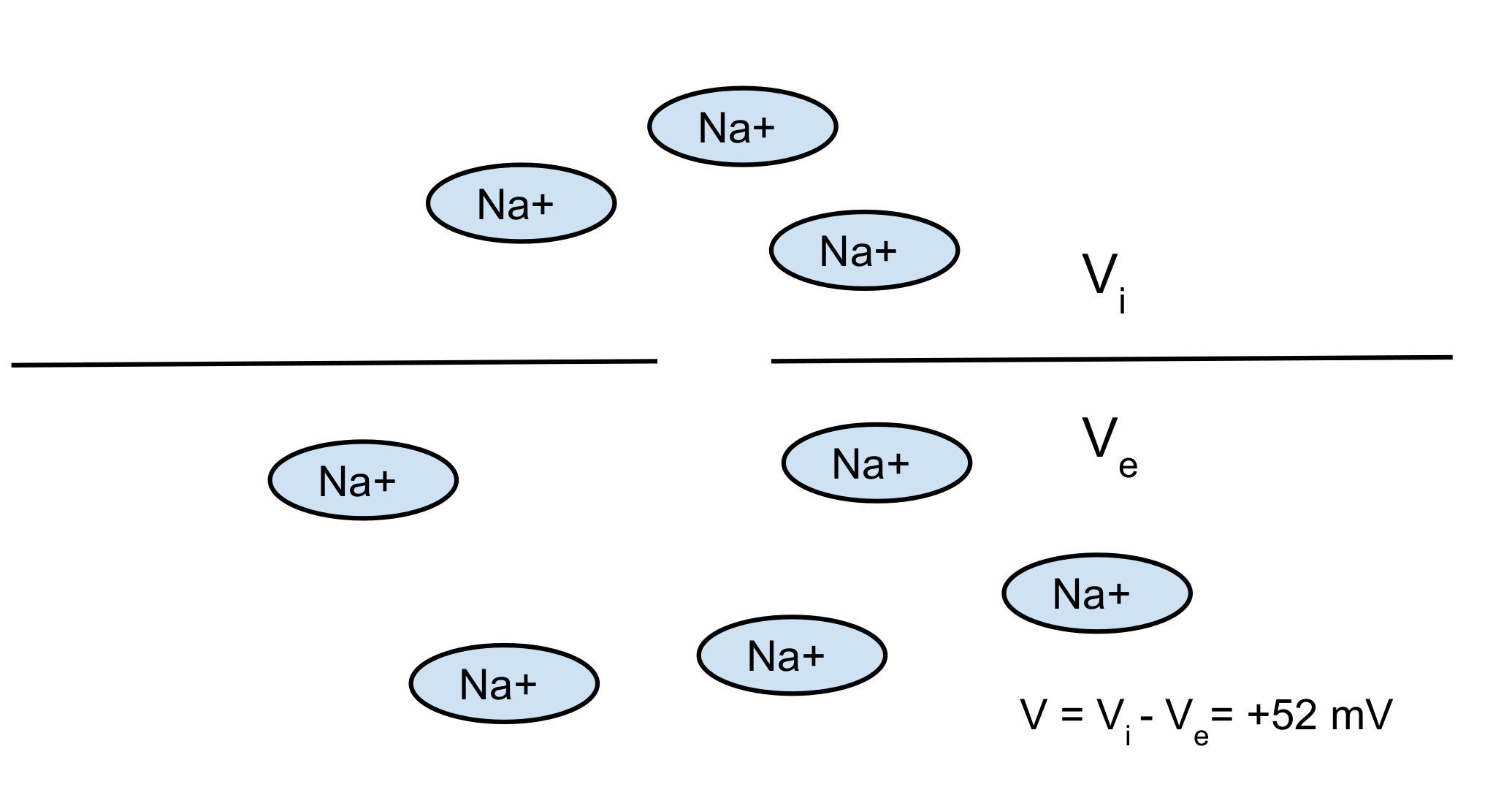
In the sea -> salty water -> high concentrations of Na+
Nerst potential: 2 opposite forces:
- diffusion
- electrical force
You can find the equilibrium which gives you the Nerst potential
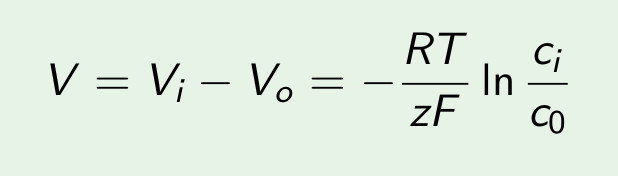
Diffusive flux: (Fick's first law)
D= diffusion coefficient
[D] = m^2/s
C = concentration
[C] = mol/m^3
J = diffusive flux
[J] = mol/(s m^2)
Take a uniform electric field:
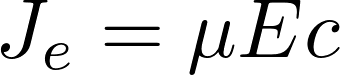
concentration
[C] = mol/m^3
Electric field
[E] = V/m
mobility
[μ] = m^2/(Vs)
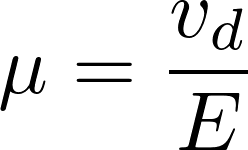
J = flux due to electric field
[J] = mol/(s m^2)
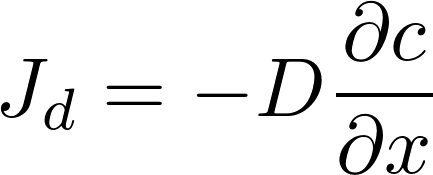
Diffusive flux: (Fick's first law)
D= diffusion coefficient
[D] = m^2/s
C = concentration
[C] = mol/m^3
J = diffusive flux
[J] = mol/(s m^2)
Take a uniform electric field:
concentration
[C] = mol/m^3
Potential
[ϕ] = V
mobility
[μ] = m^2/(Vs)
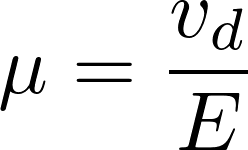
J = flux due to electric field
[J] = mol/(s m^2)
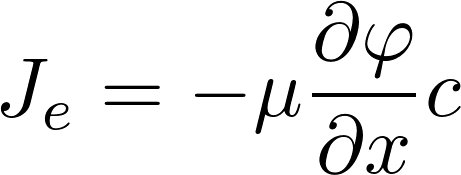
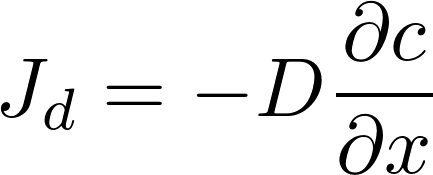
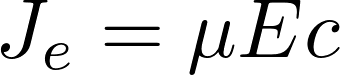
Diffusive flux: (Fick's first law)
Take a uniform electric field:
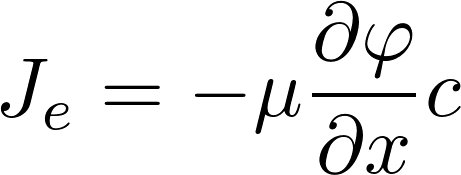
Einstein relation
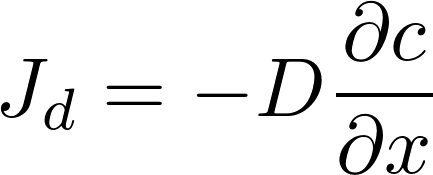
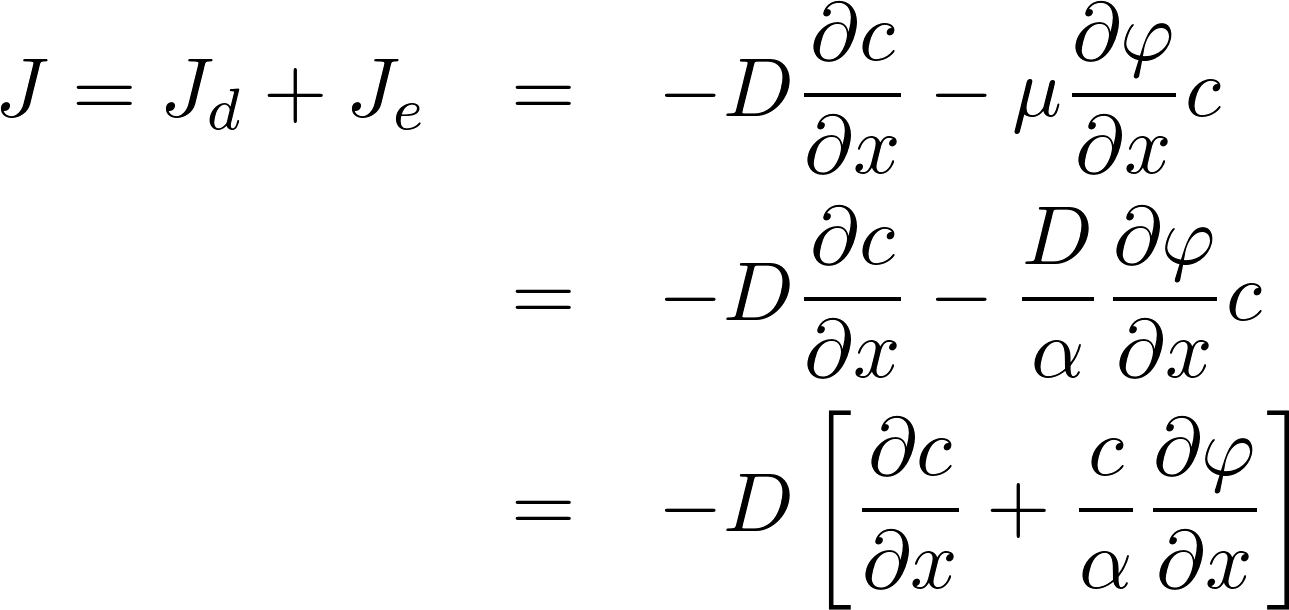
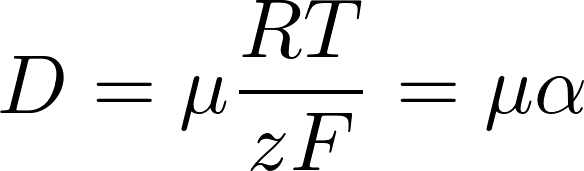
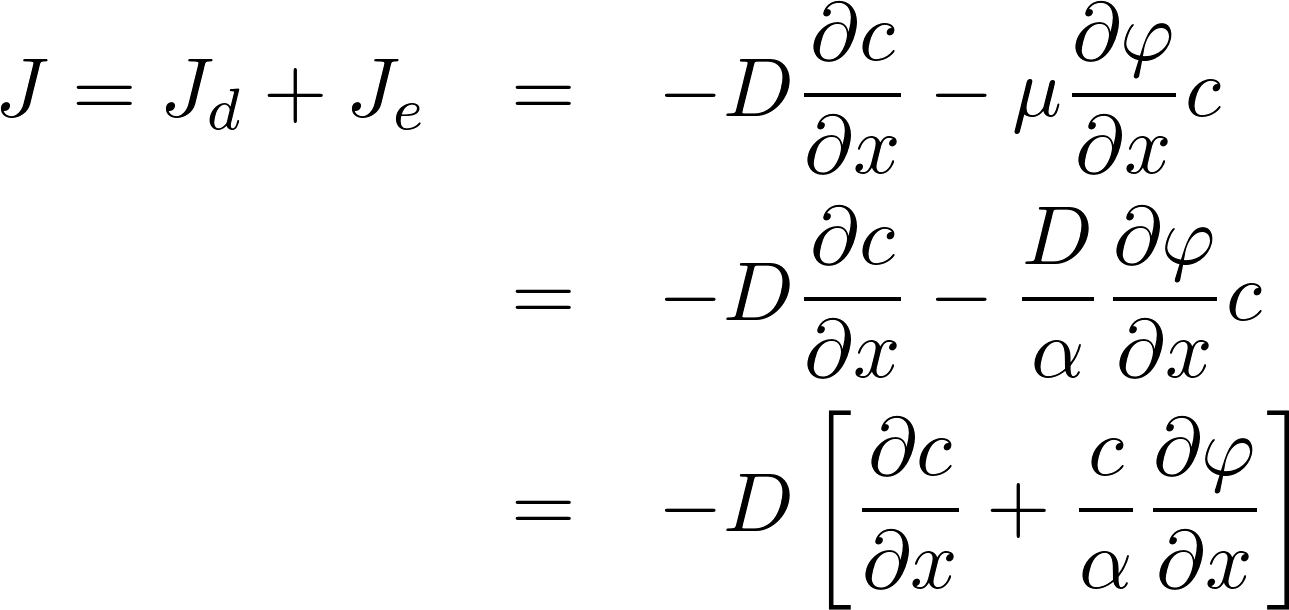
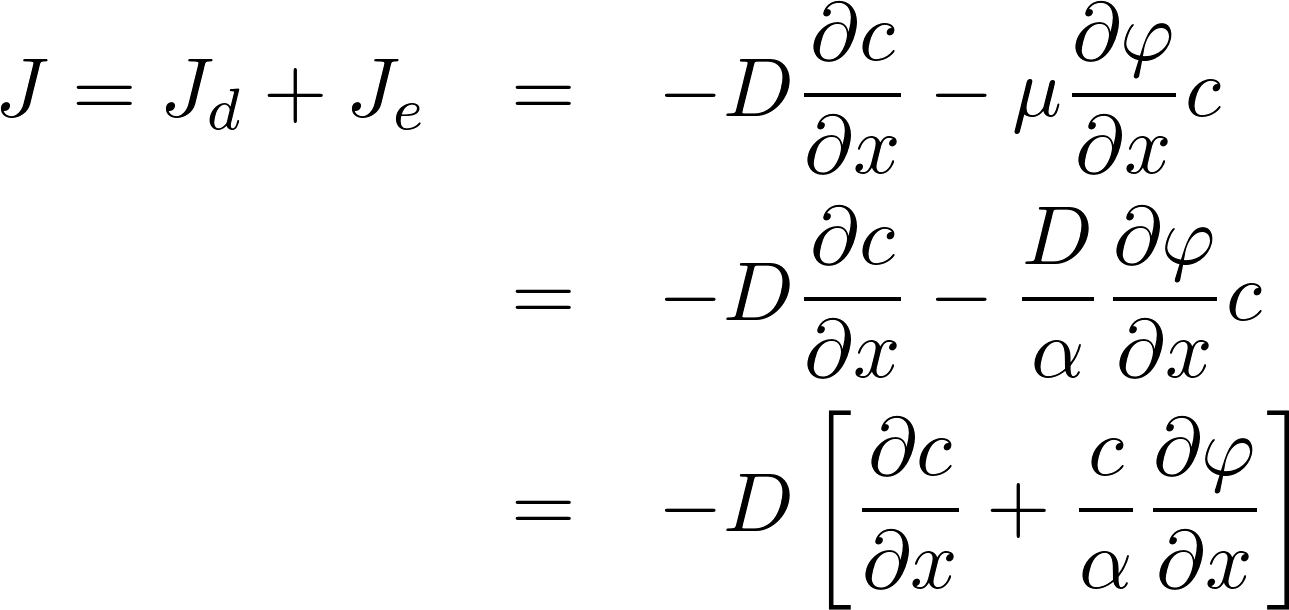
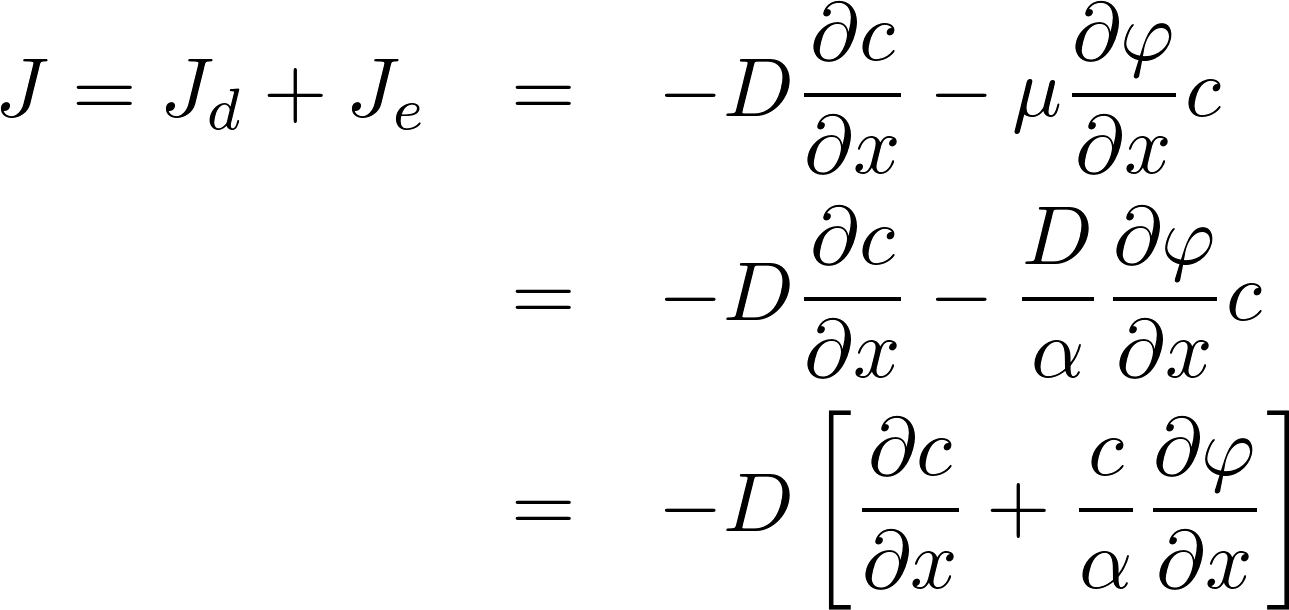
In equilibrium, J = 0
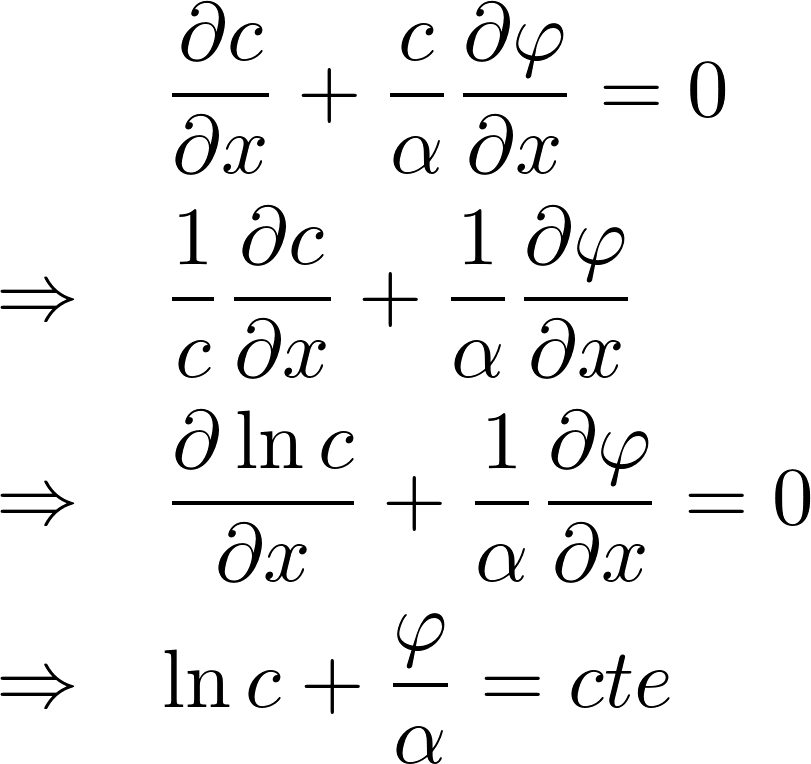
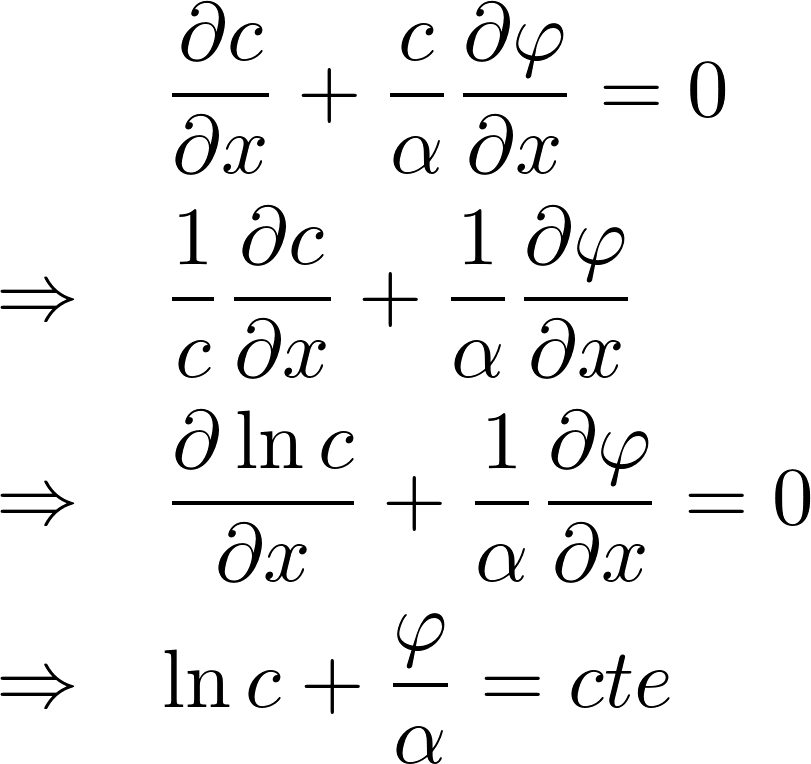
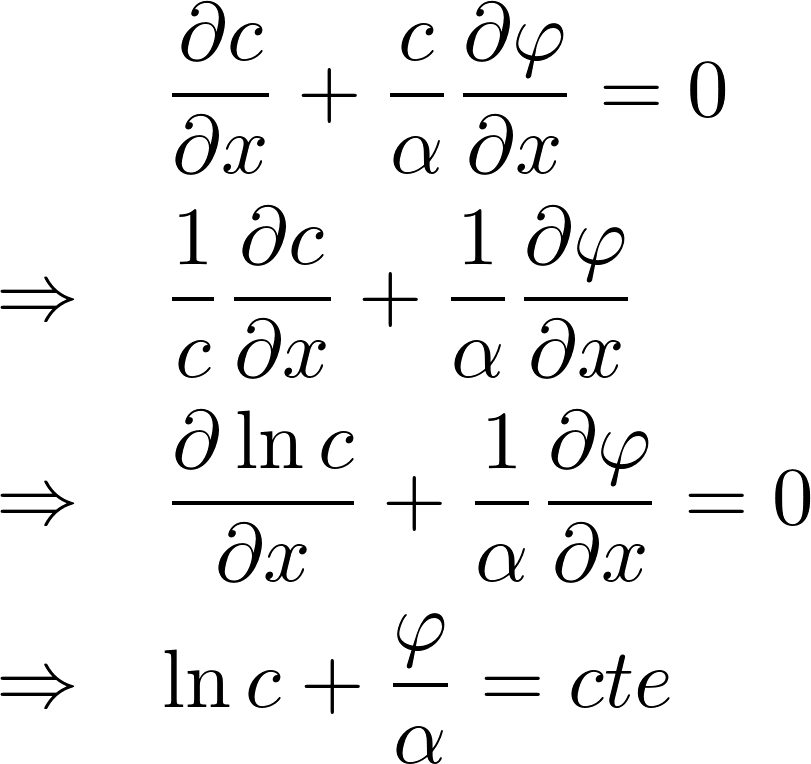
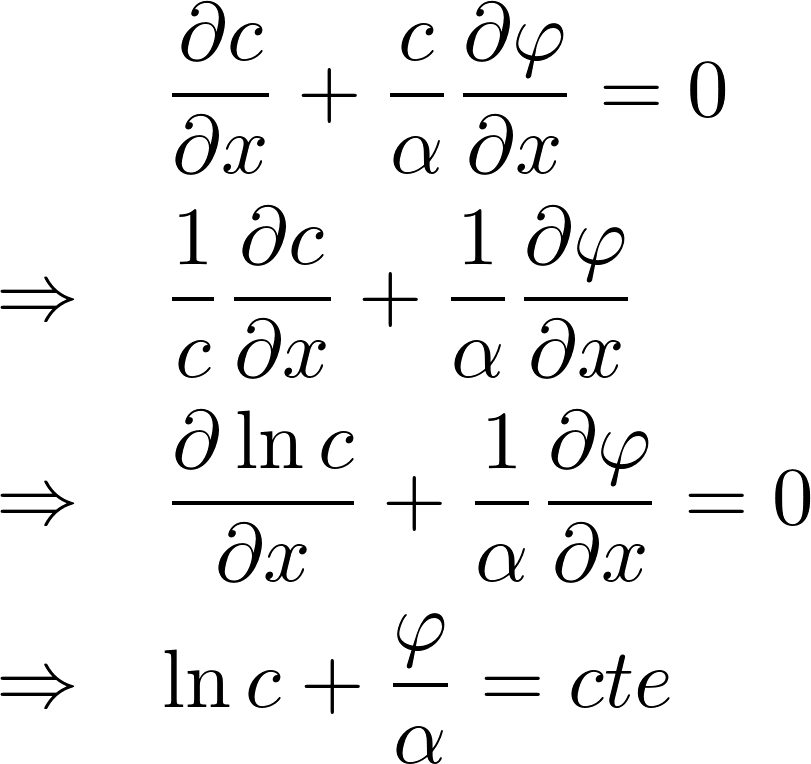
i: inside the cell
o: outside the cell
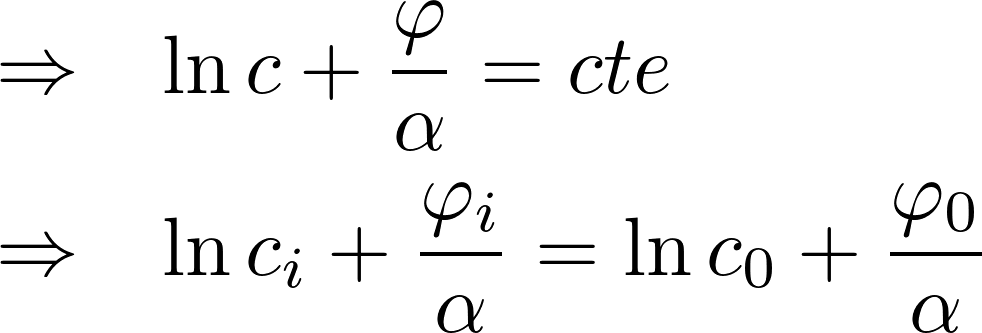
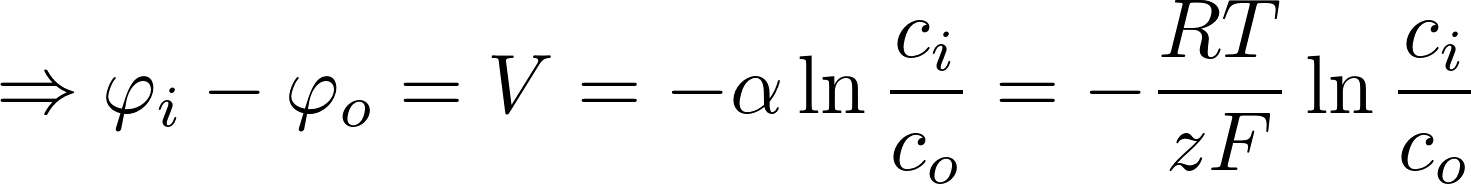
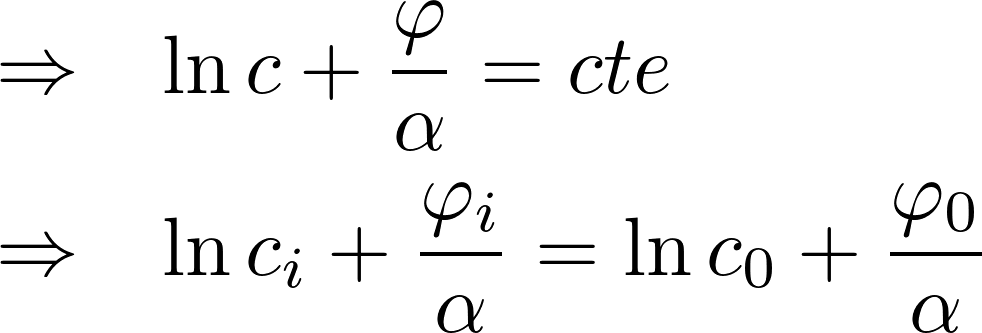
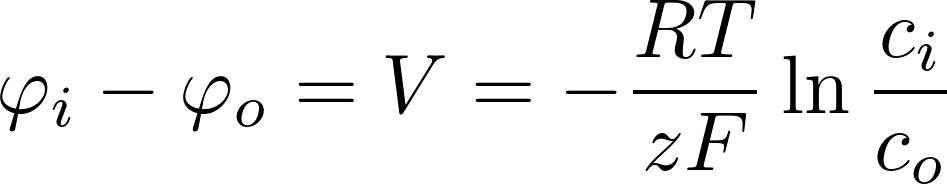
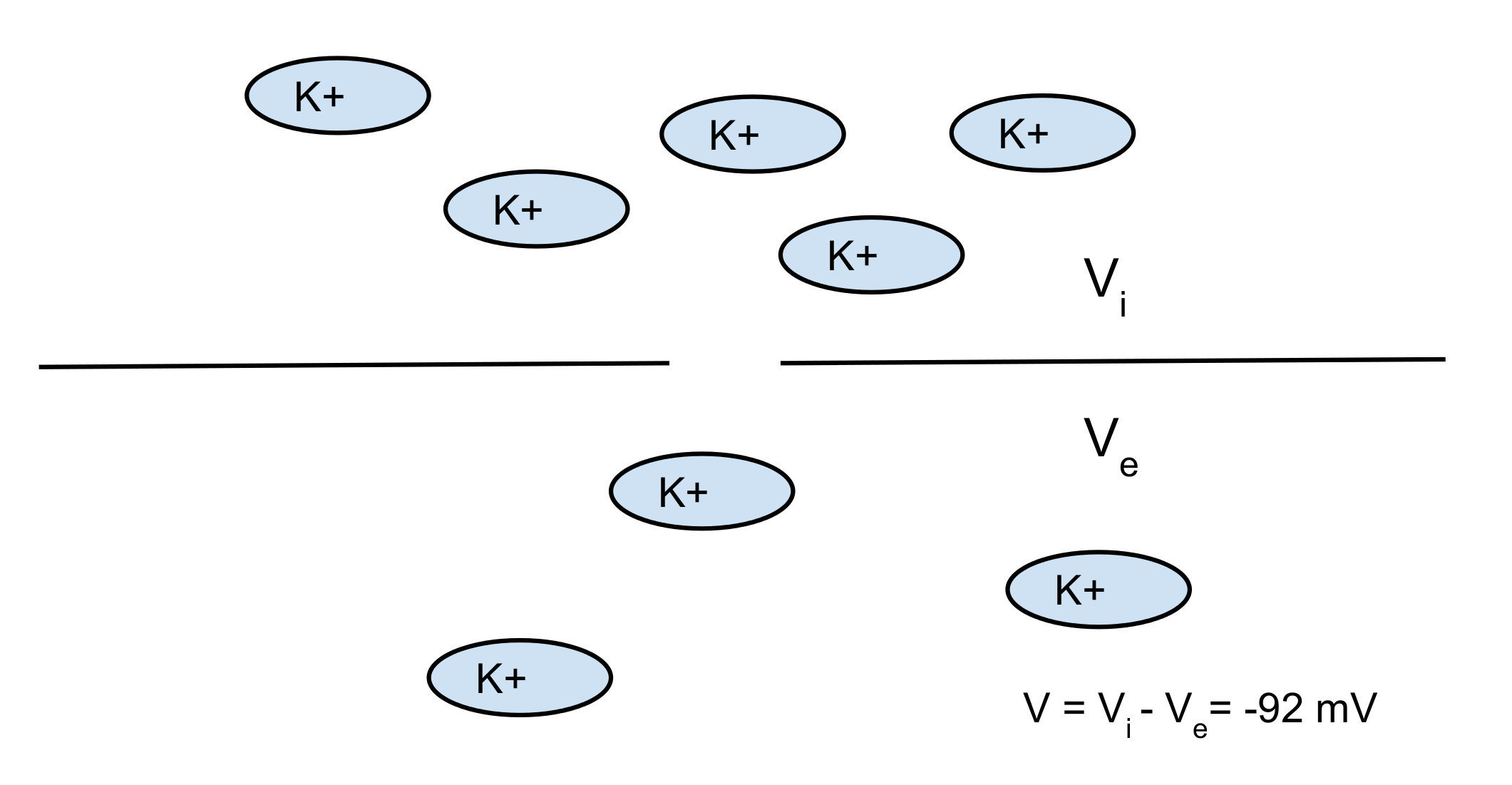
Potassium K+:
- room temp: RT/F = 25 mV
- [K]i = 140 mM
- [K]o = 2.5 mM
=> V = -101 mV
Nerst potential: 2 opposite forces:
- diffusion
- electrical force
You can find the equilibrium which gives you the Nerst potential
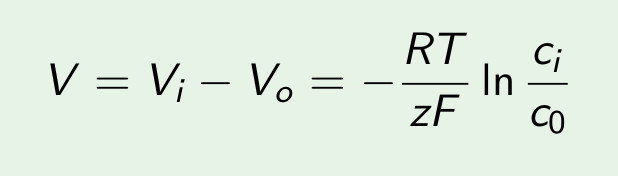
Nerst potential: 2 opposite forces:
- diffusion
- electrical force
You can find the equilibrium which gives you the Nerst potential
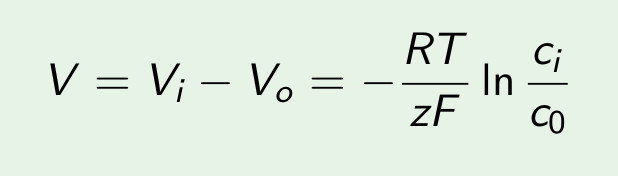
2. GOLDMAN-HODGKIN-KATZ
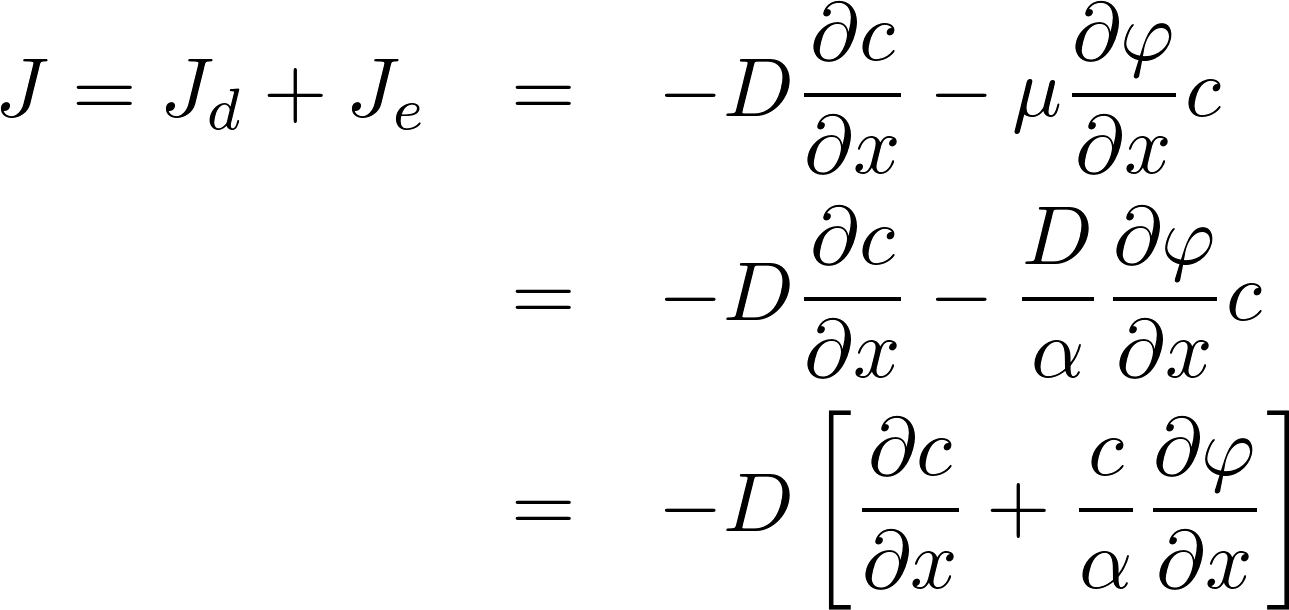
This time we assume that the flux is not zero, we are in a non-stationairy situation
We assume that is a linear function of x
X-axis: goes from inside to outside
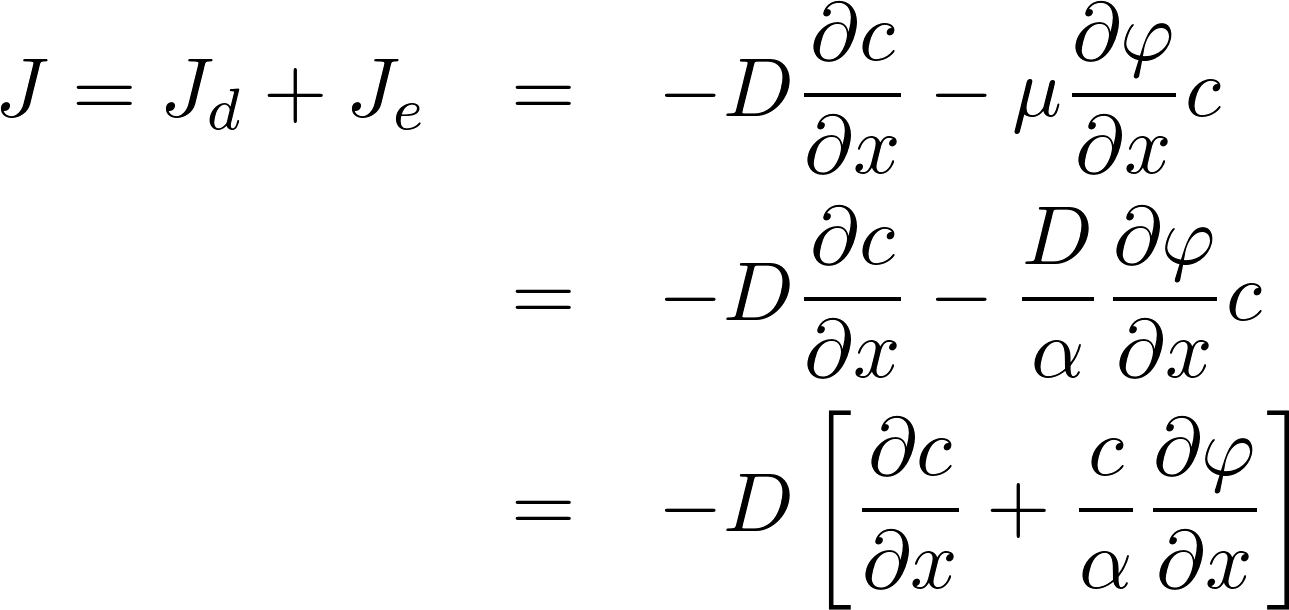
inside
outside
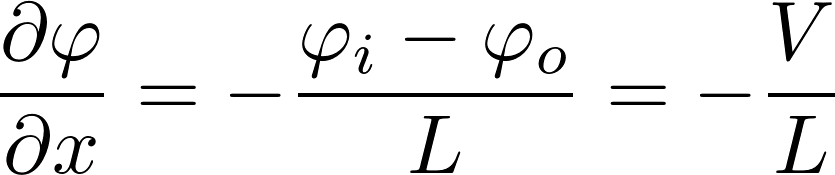
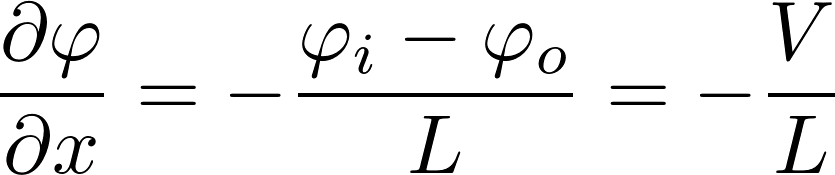
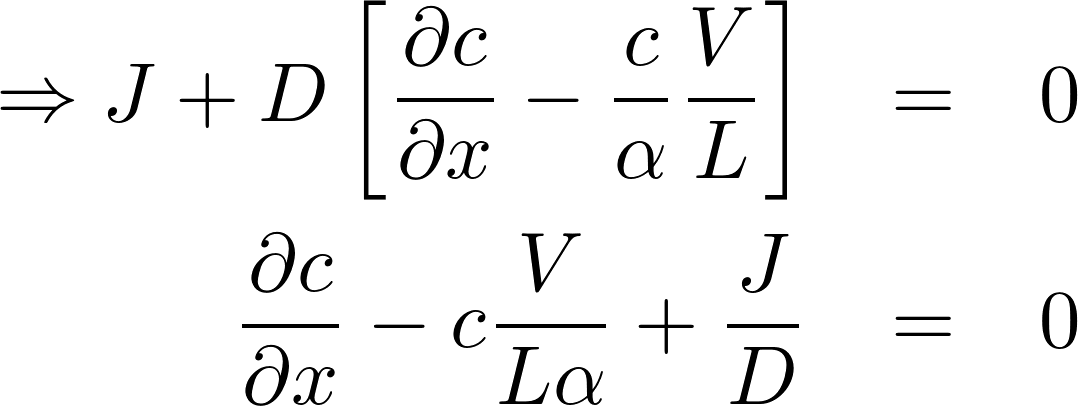
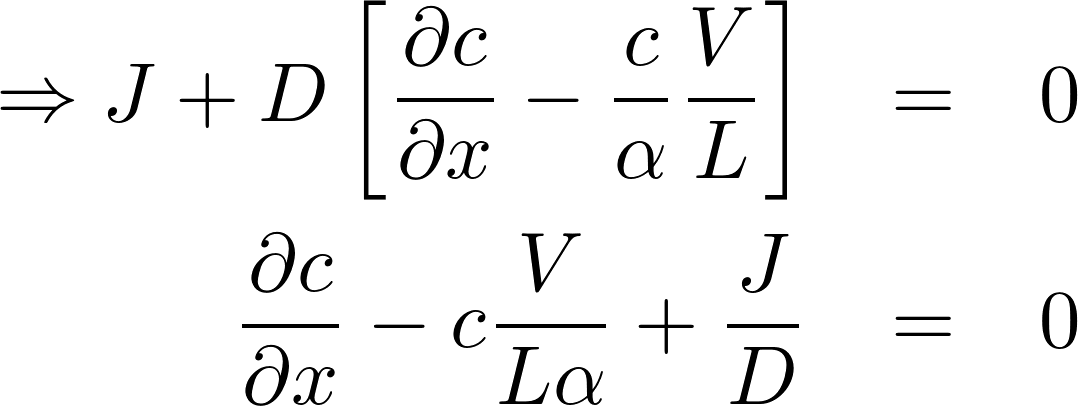
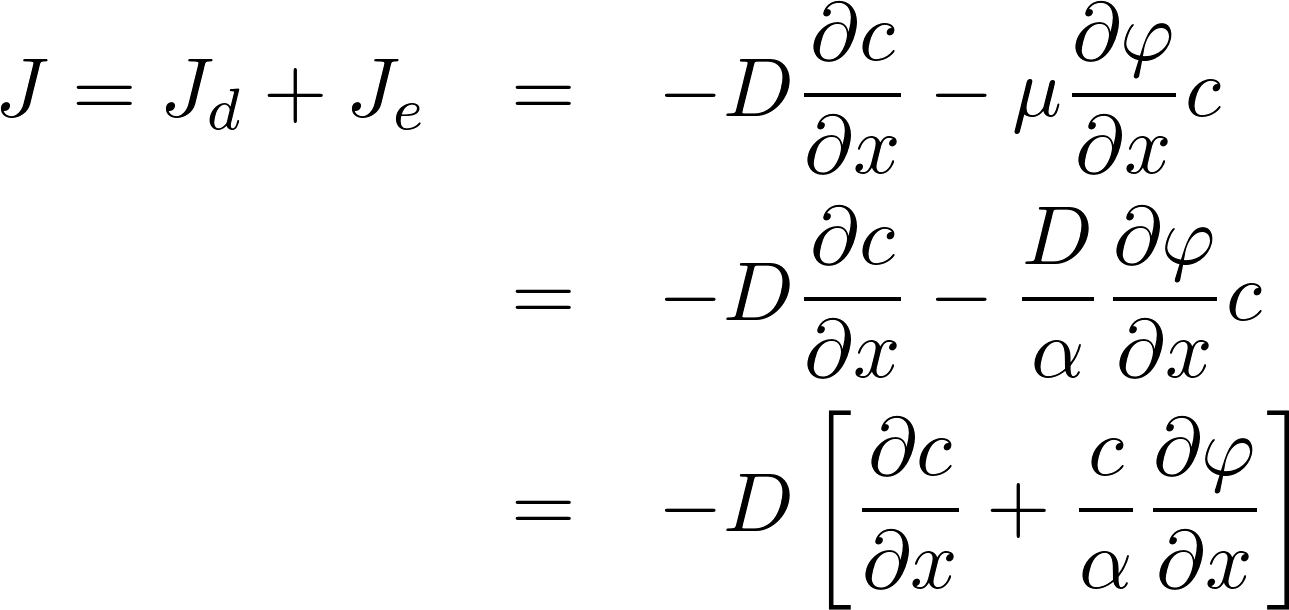
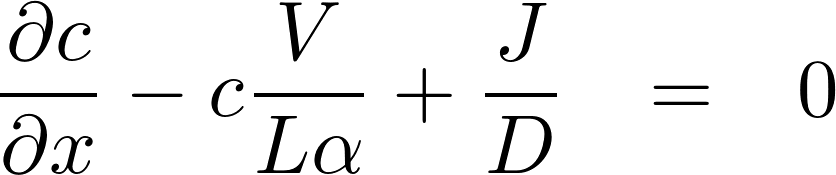
The homogeneous equation:
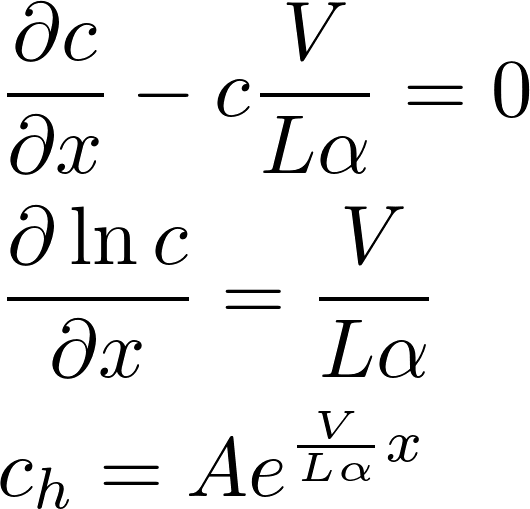
A particular solution:
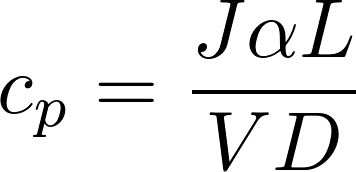
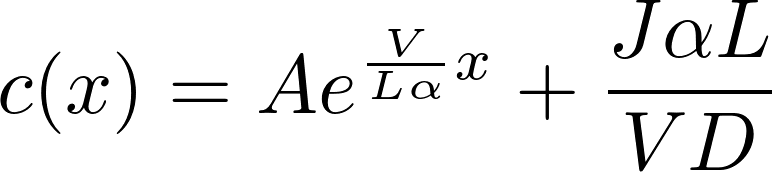
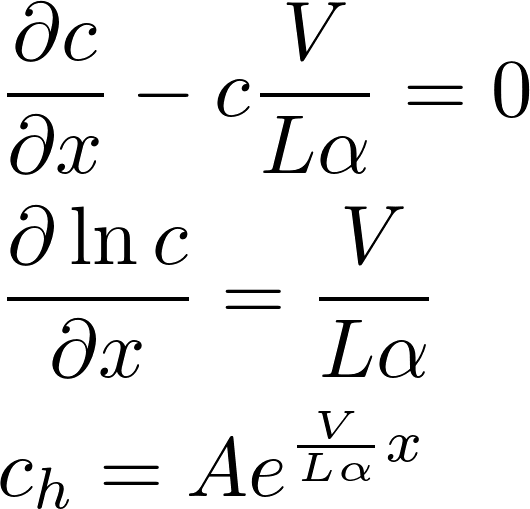
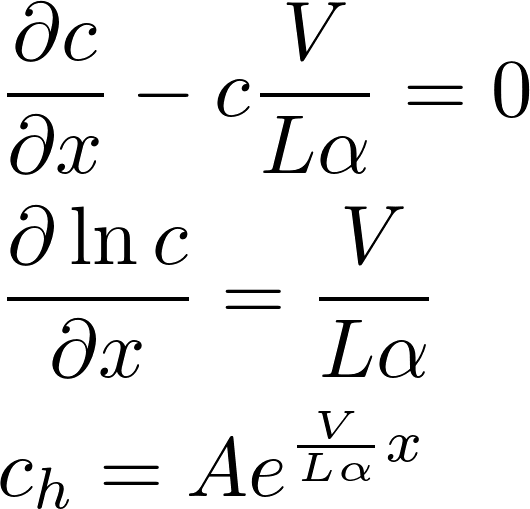
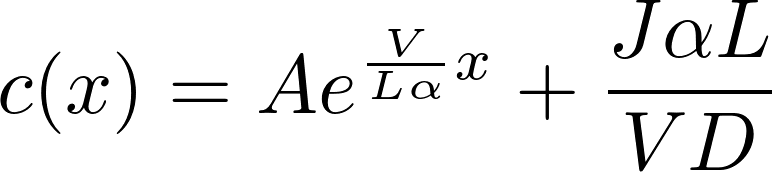
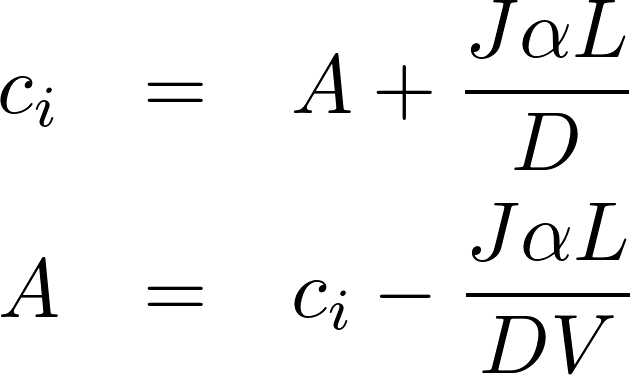
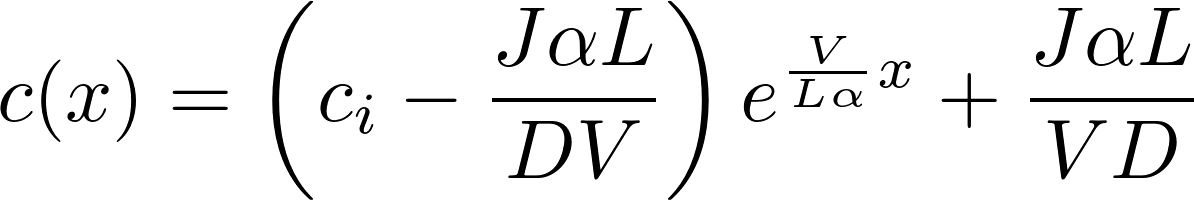
inside
outside
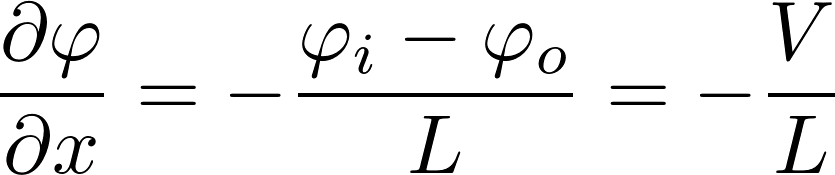
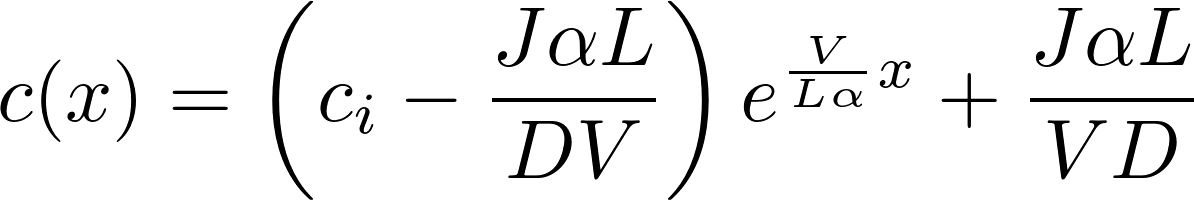
inside
outside
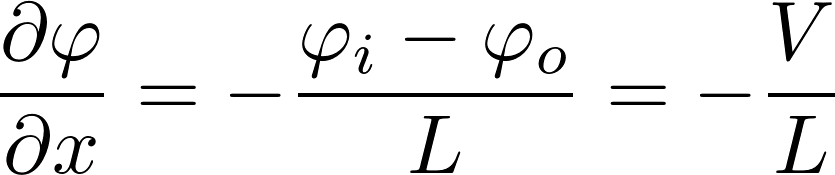
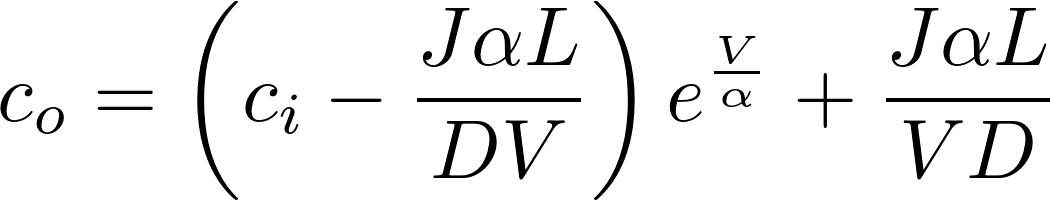
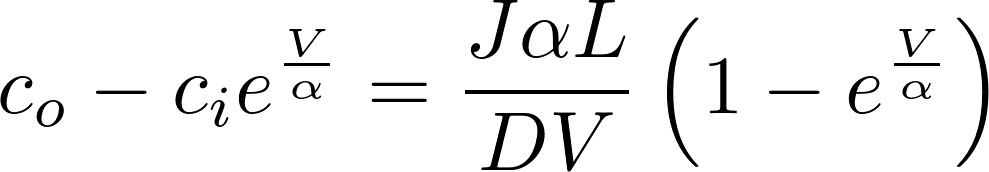
Denote P = D/L as the permeability of the membrane to the substance.
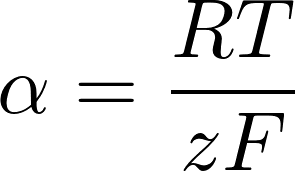
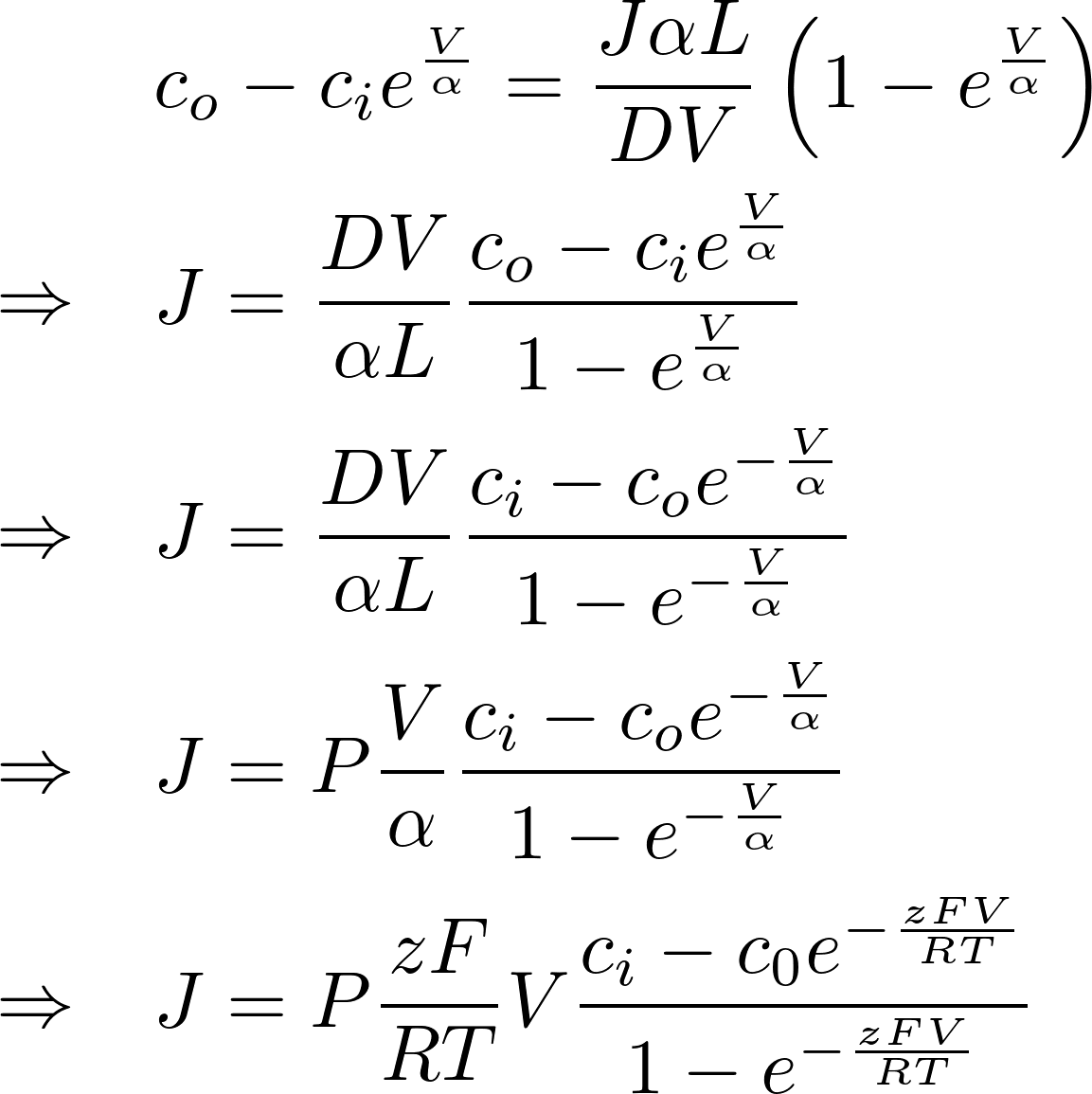
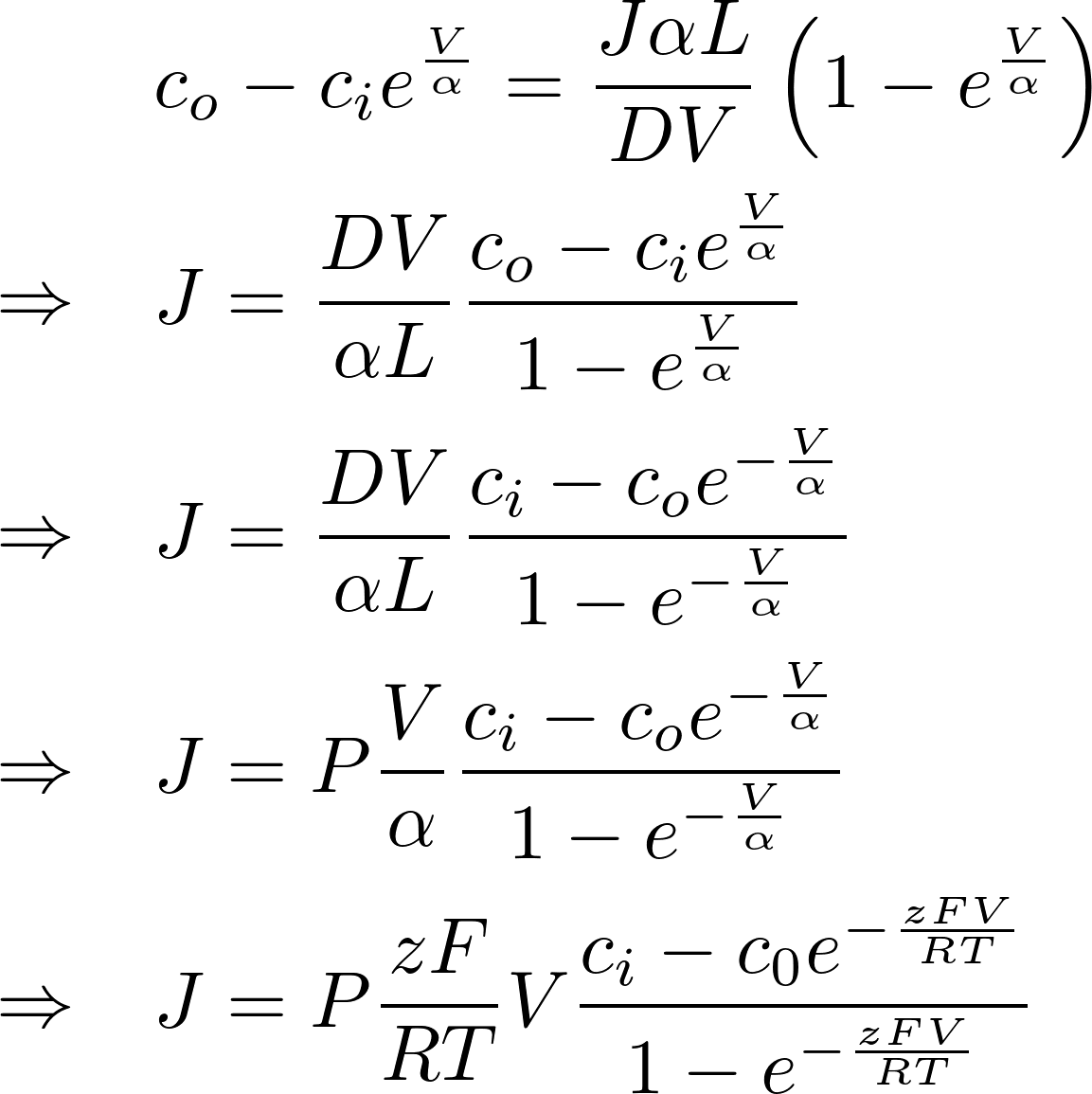
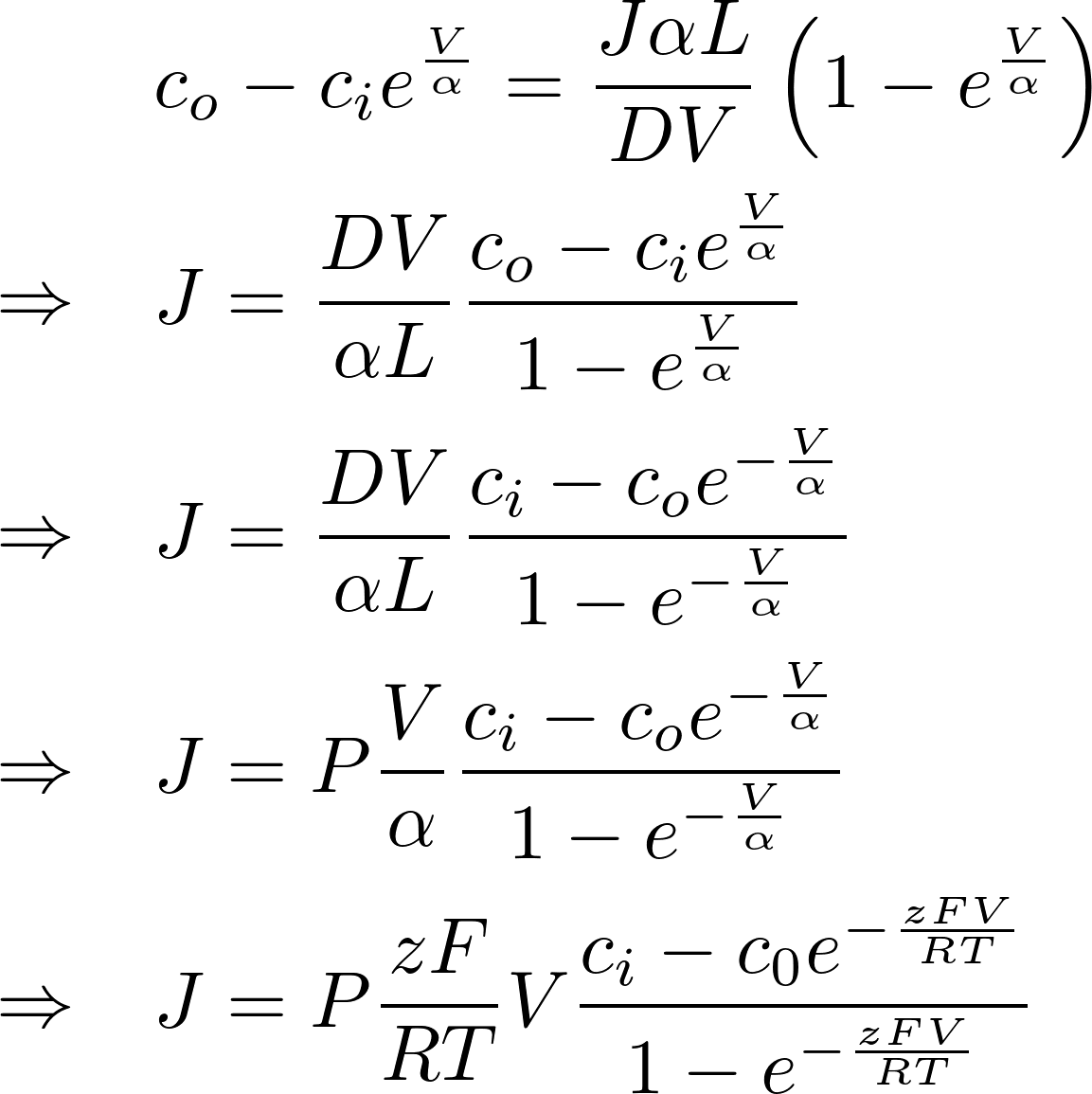
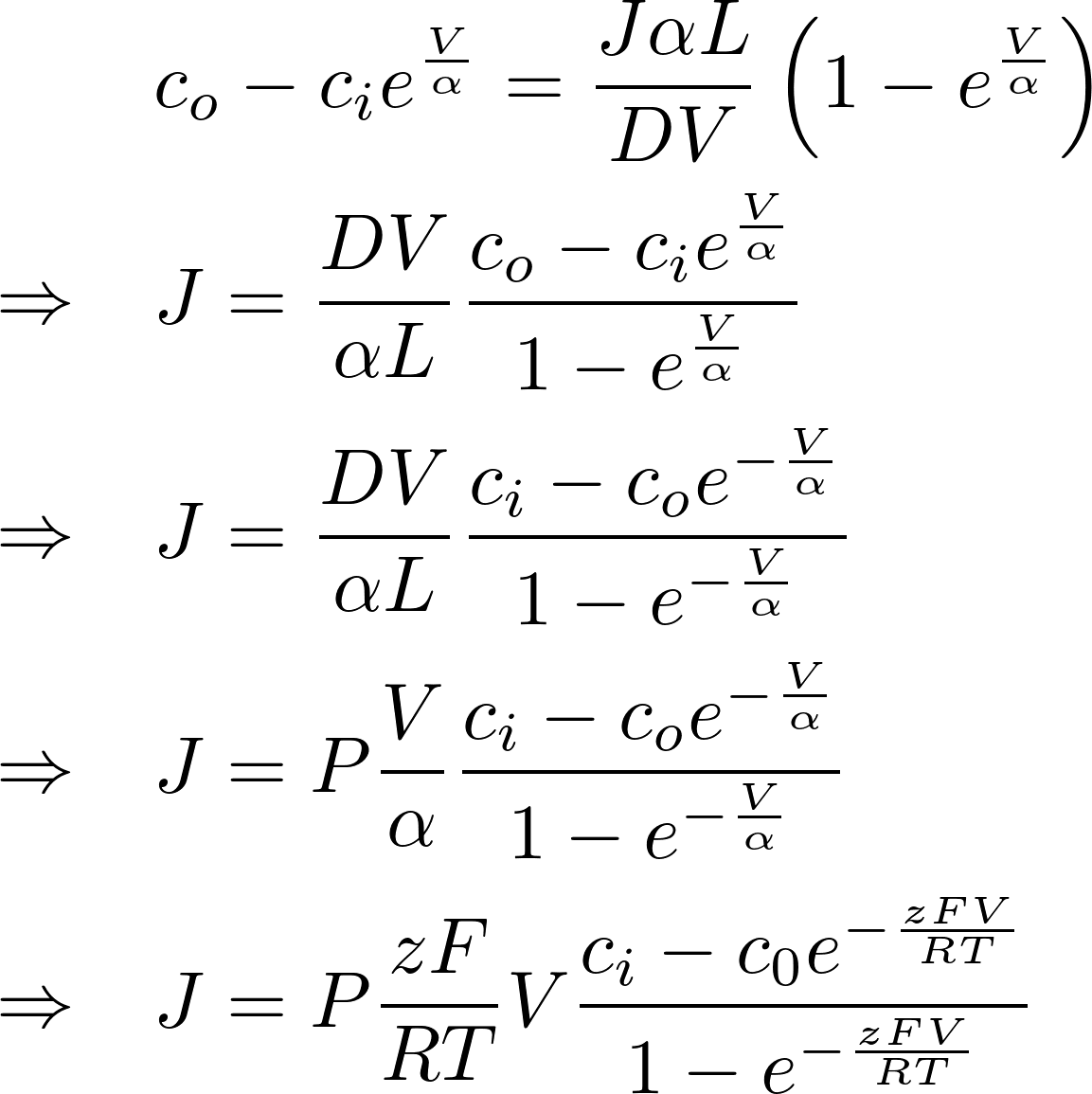
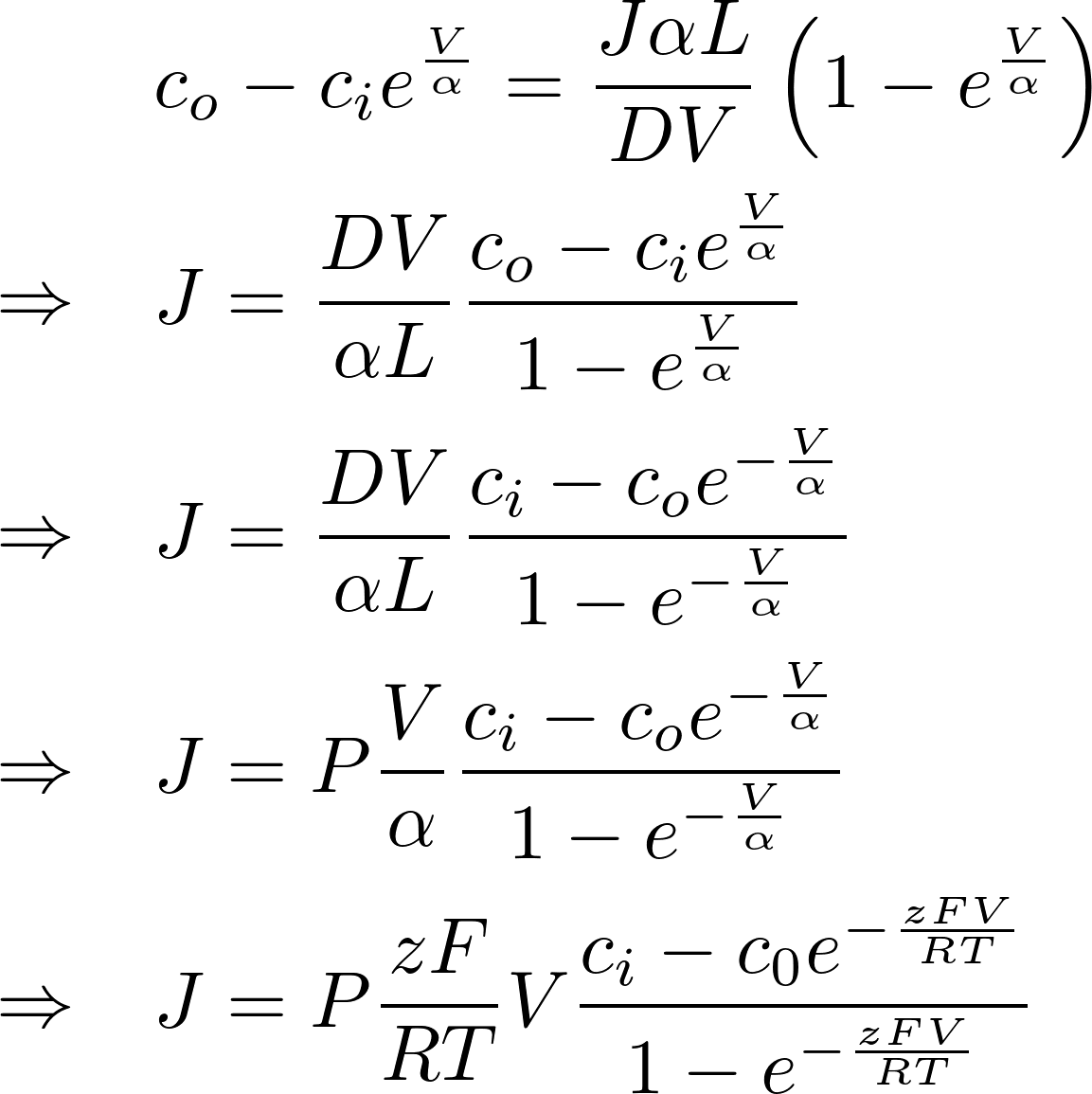
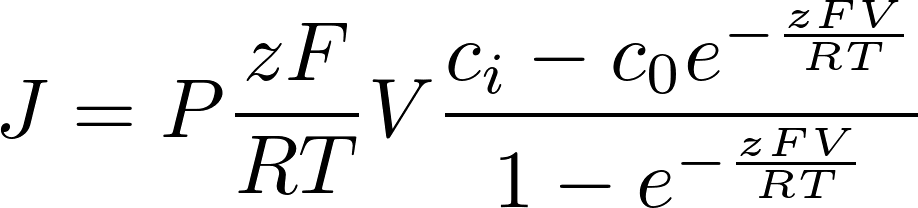
[J] = mol / s m^2
To find the electric current, we multiply by the amount of charge conveyed by a mole (zF): [zF] = C/mol
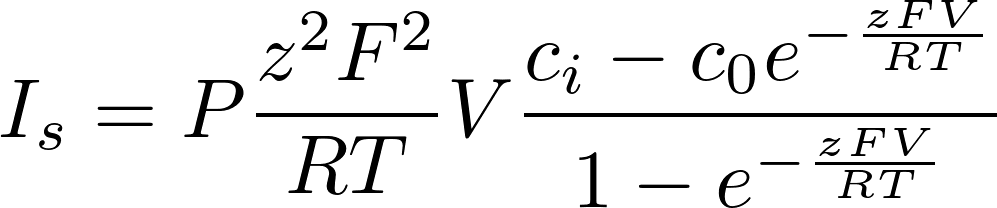
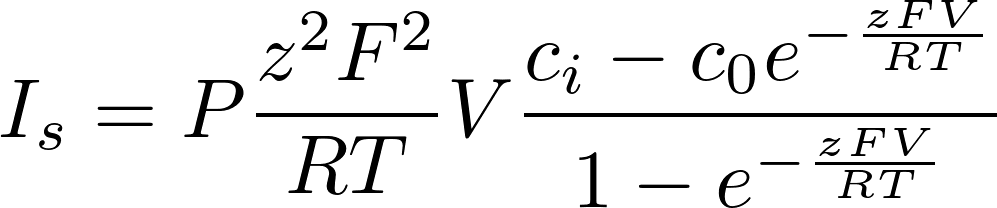
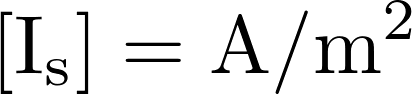
This is the famous GHK equation, which gives the relation between the value of the current and the concentrations.
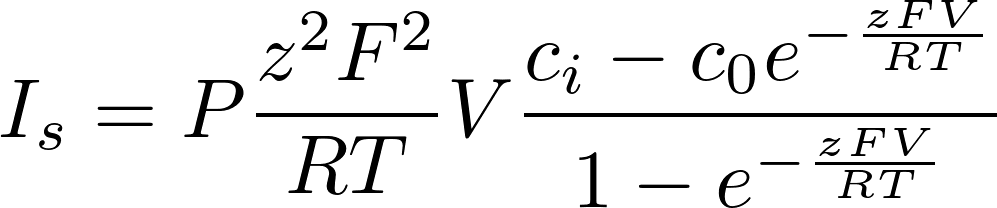
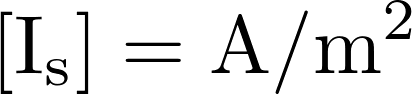
For z < 0
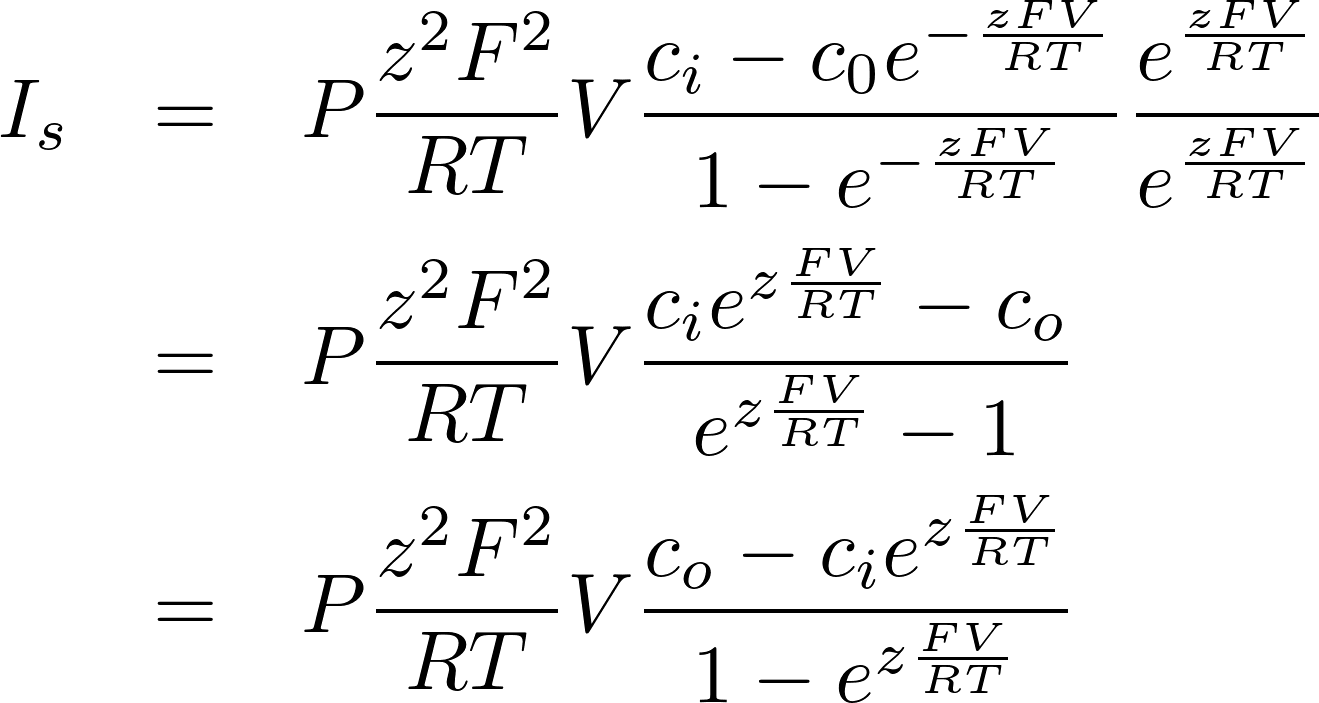
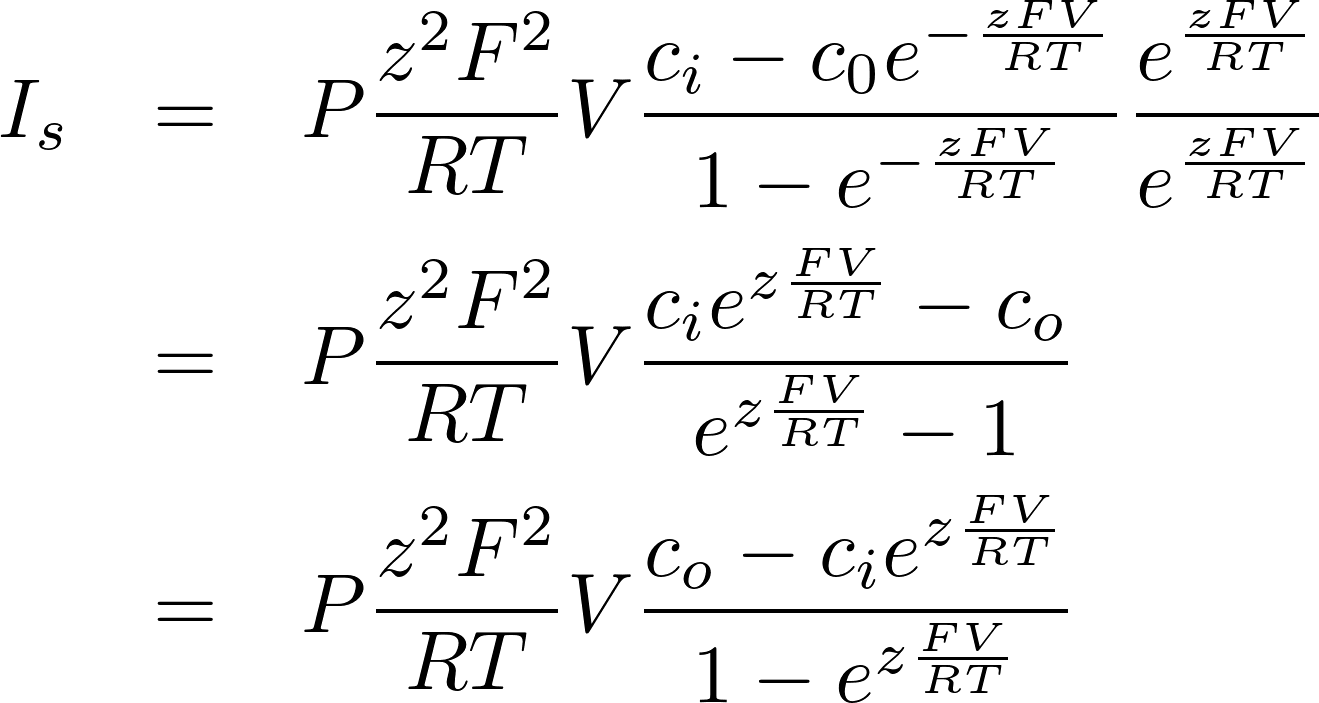
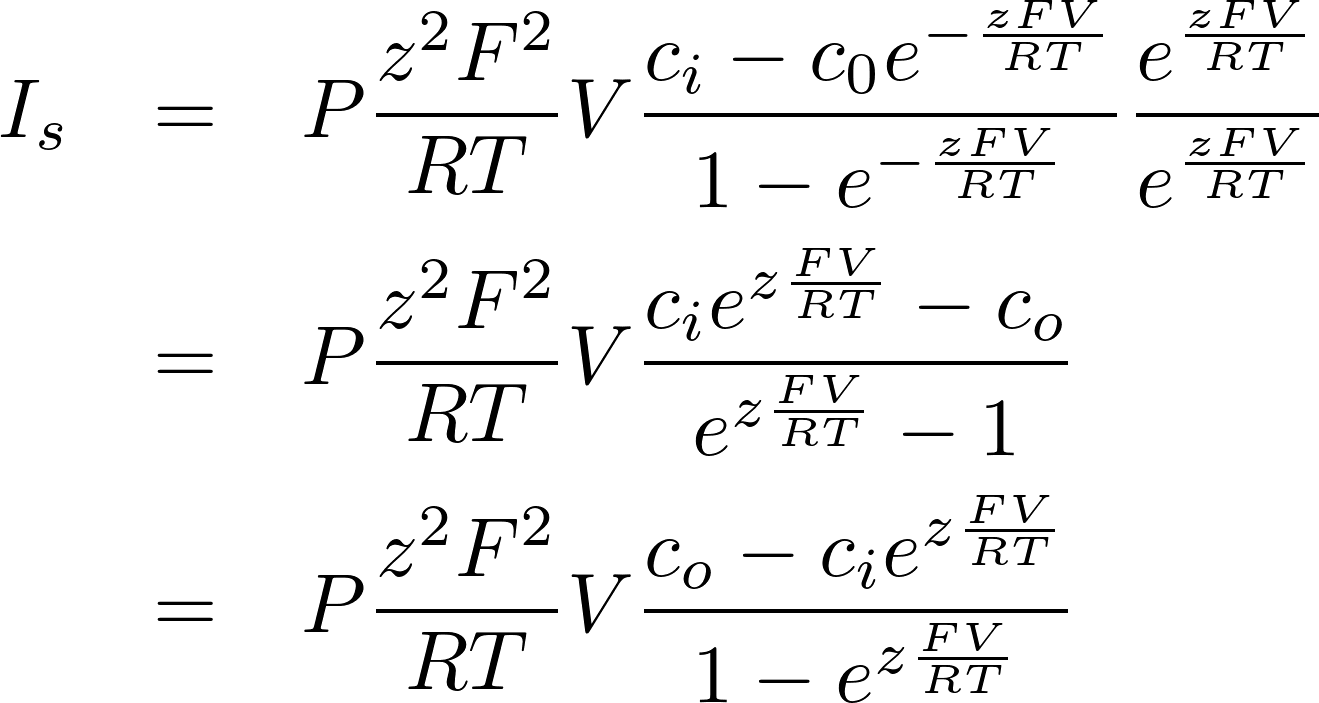
Thus for z = +1
Thus for z = -1
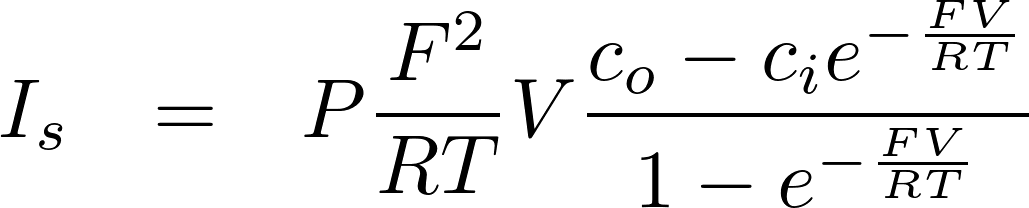
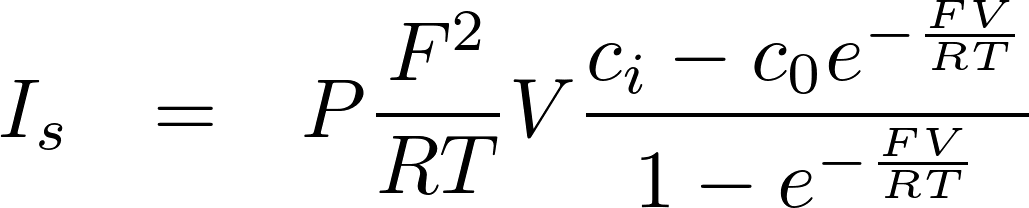
Just change c0 and ci
3. GOLDMAN-HODGKIN-KATZ IN A MIXTURE OF IONS
- Now we can account for the situation where we have a mixture of several ions.
- In that case the total current through the membrane must be zero, so the potential does not change.
- Assume ions with charge +1 (Na+, K+) and -1 (Cl-)
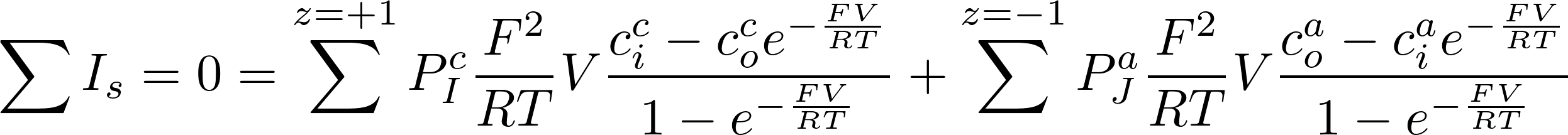
Thus for z = +1
Thus for z = -1
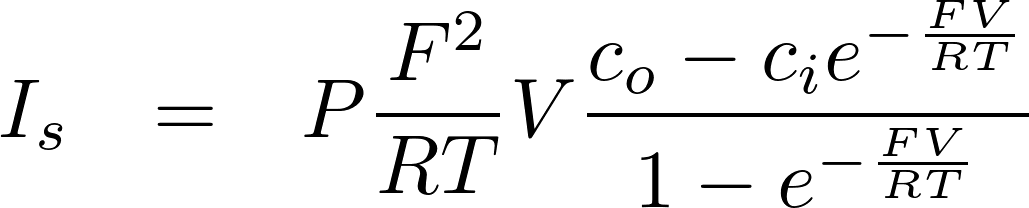
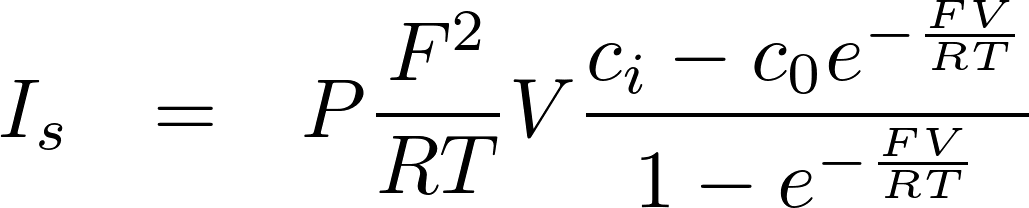
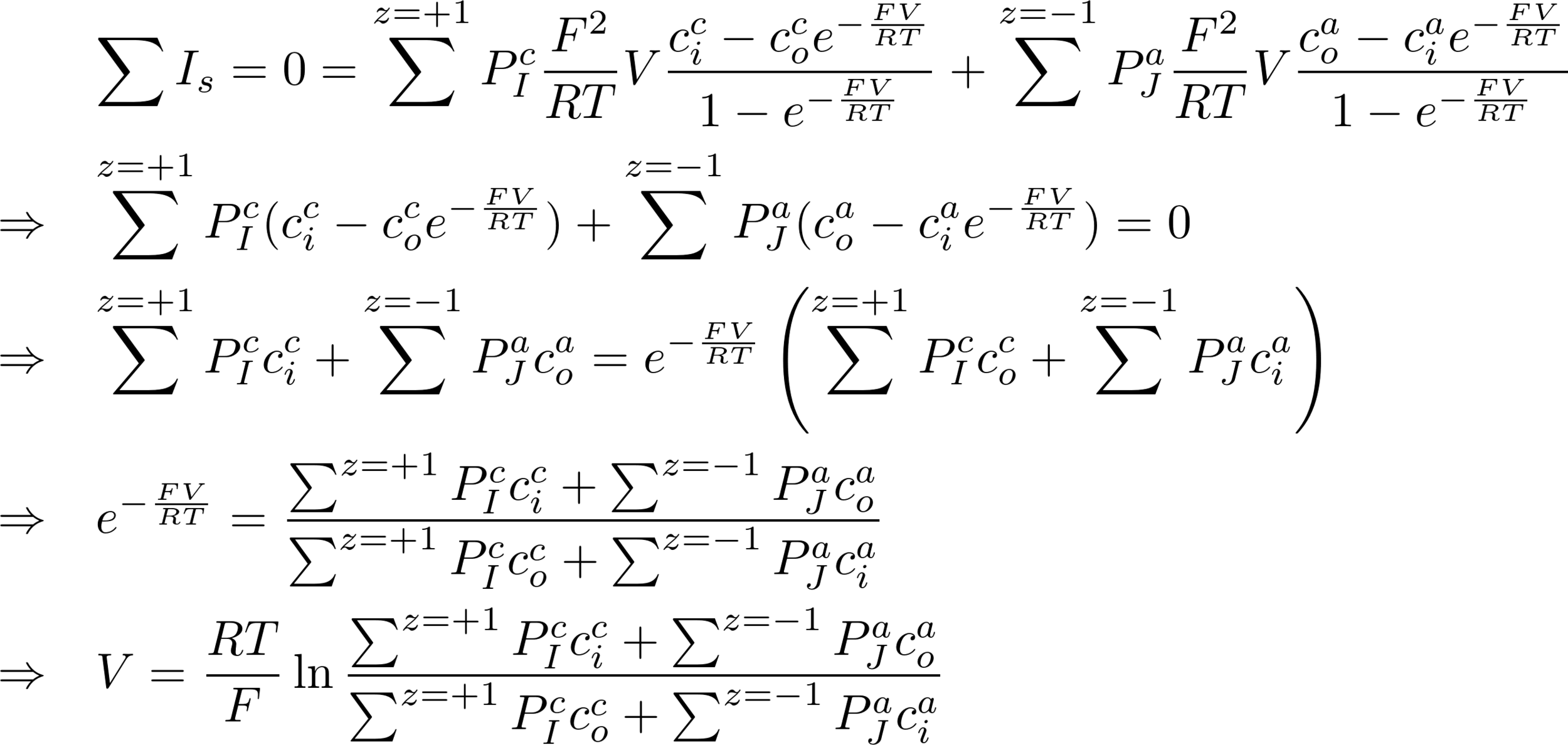
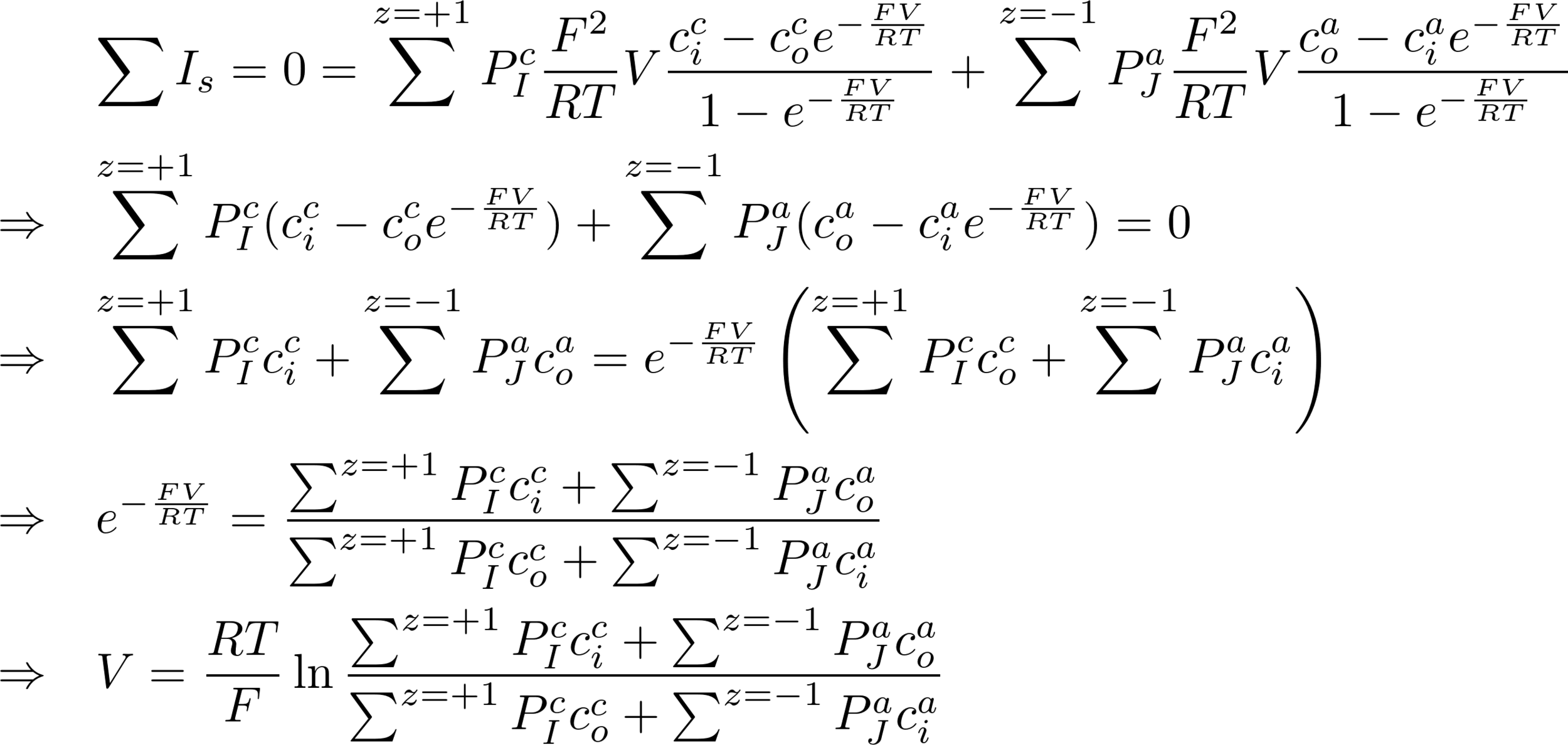
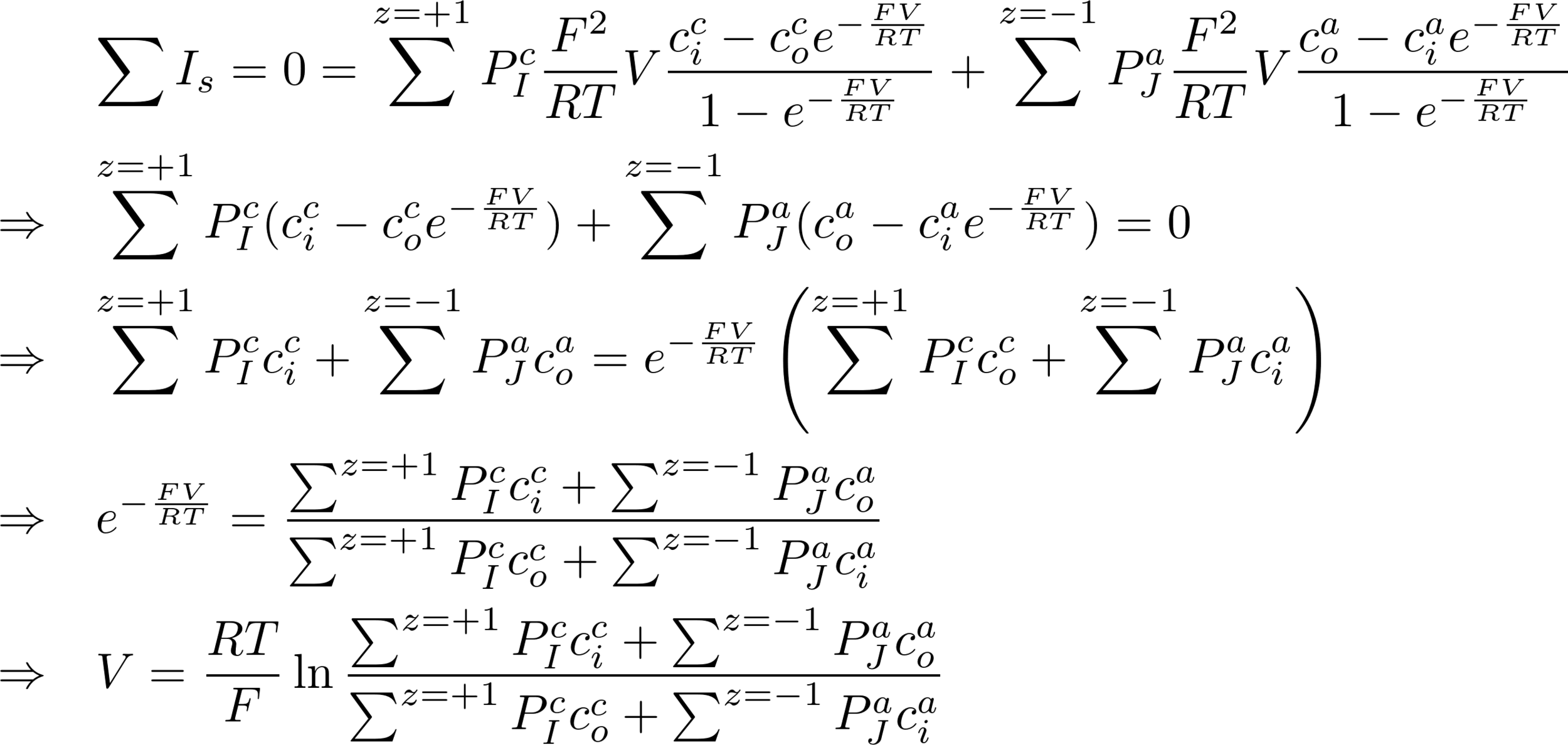
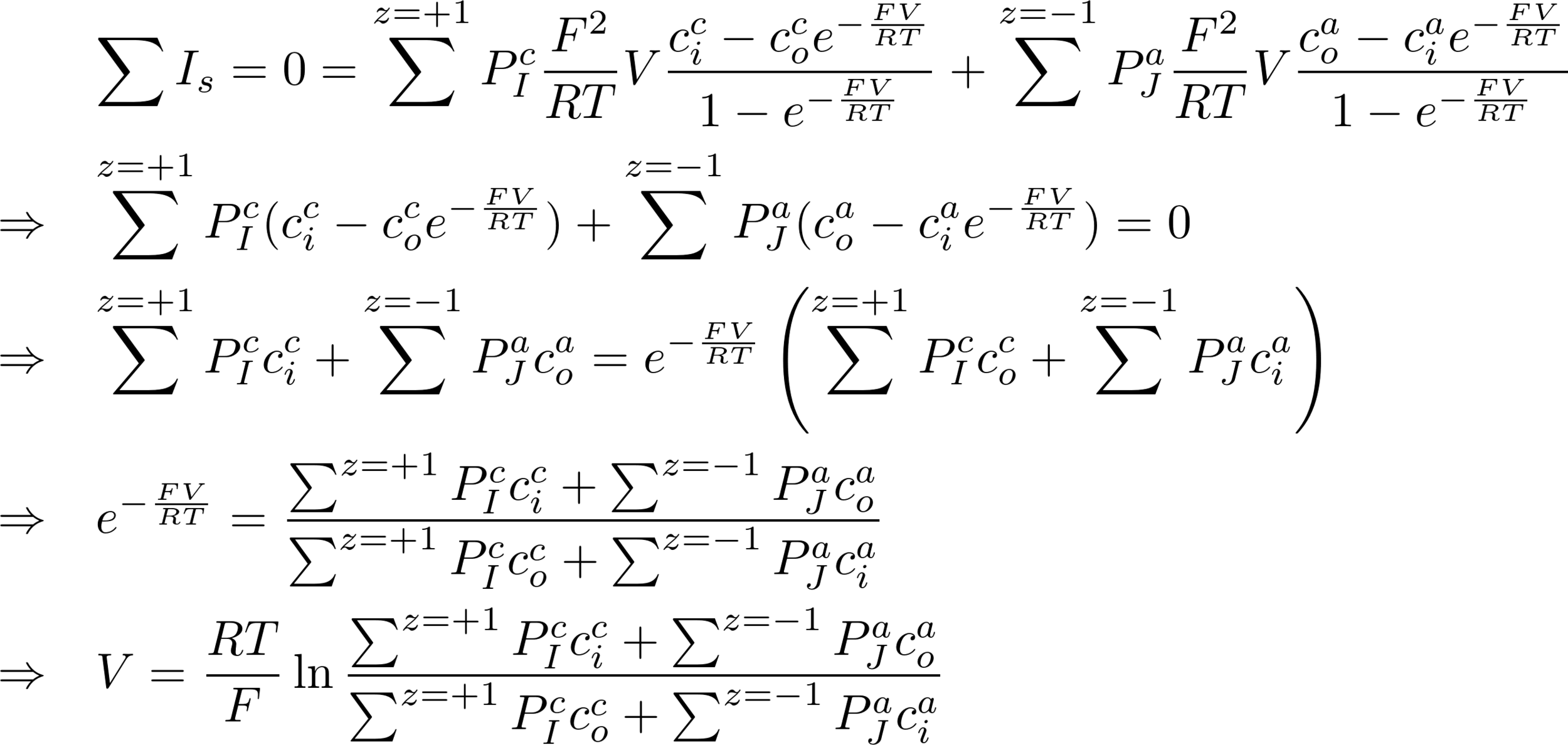
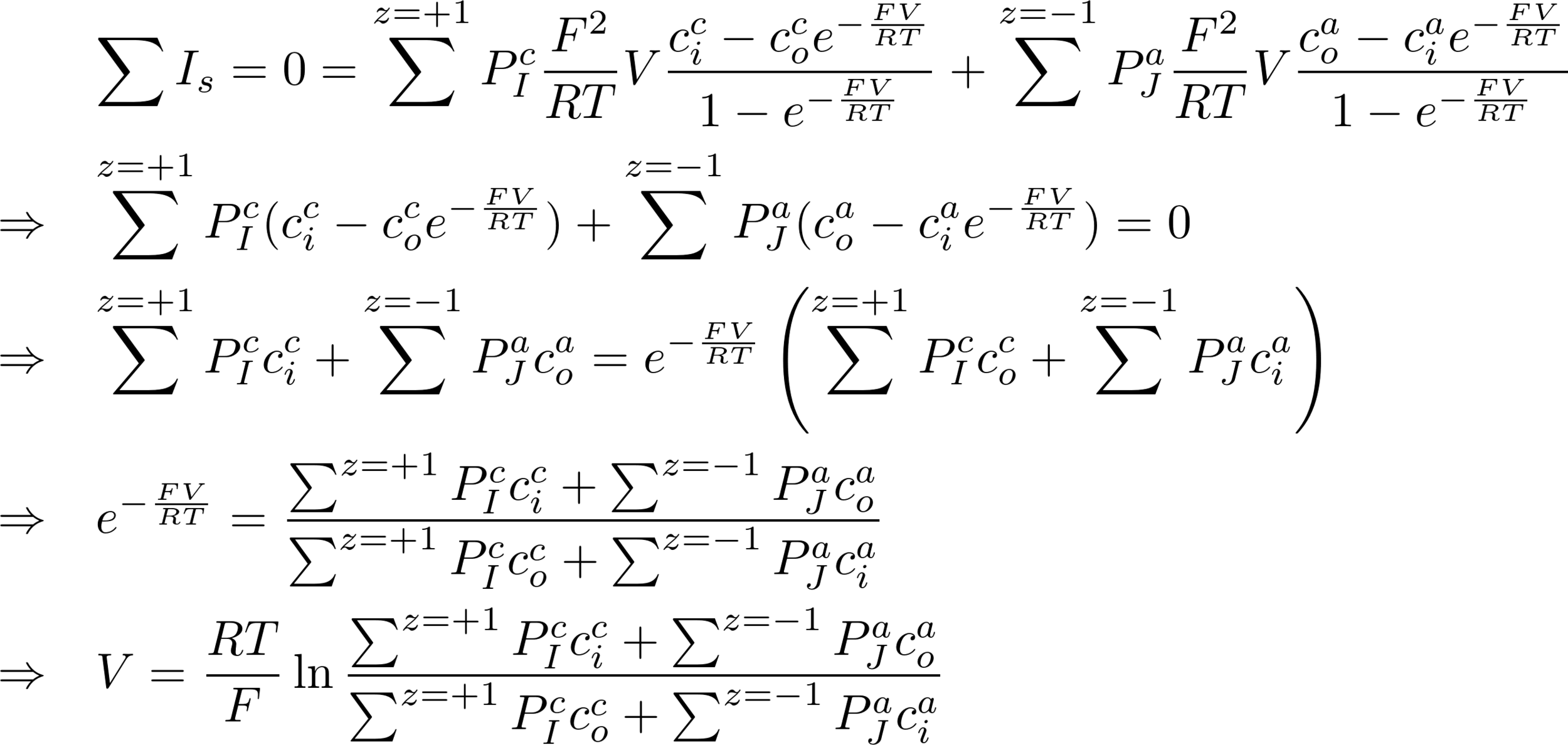
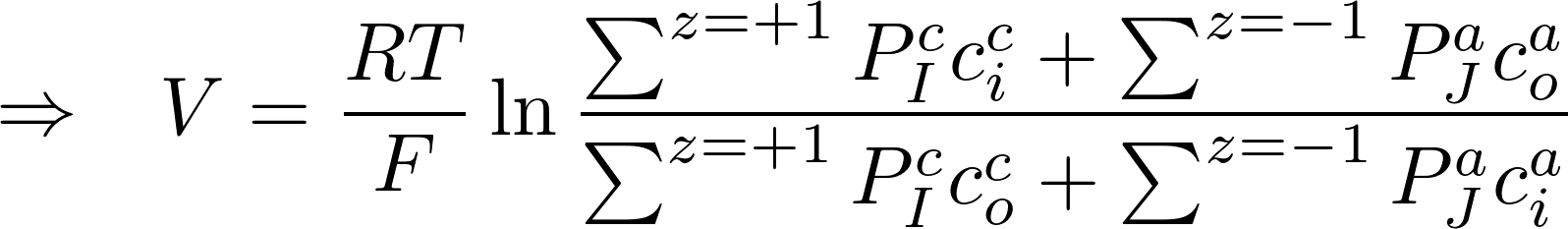
Consider K+ and Na+:
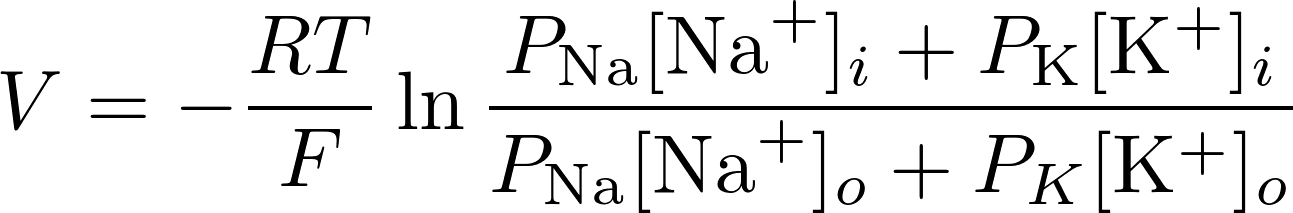
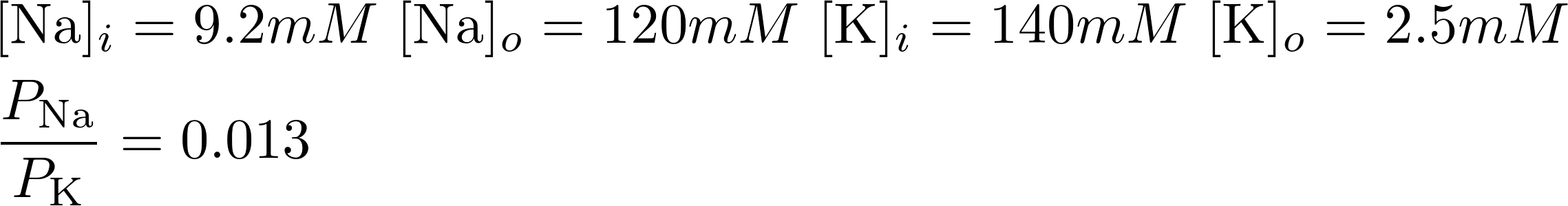
V = -88.53 mV
V = -88.53 mV
This is already a big difference with previous value of only considering K+ (-101 mV)
Real value V = -90 mV -> so this is a good estimate!
4. Electrodynamics of a cell
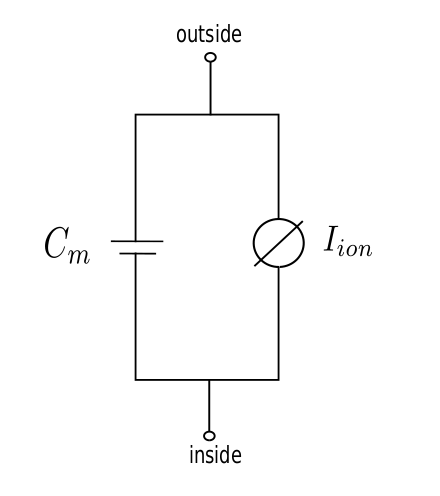
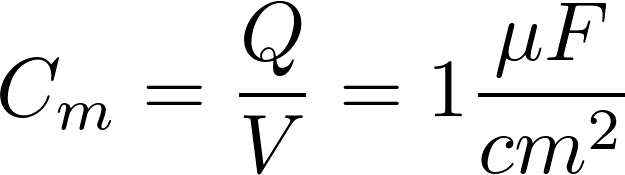
Text
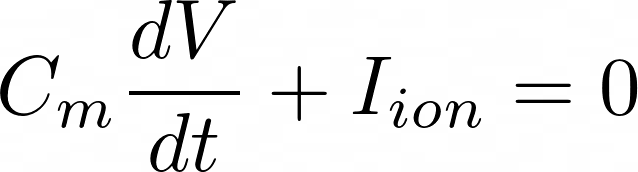
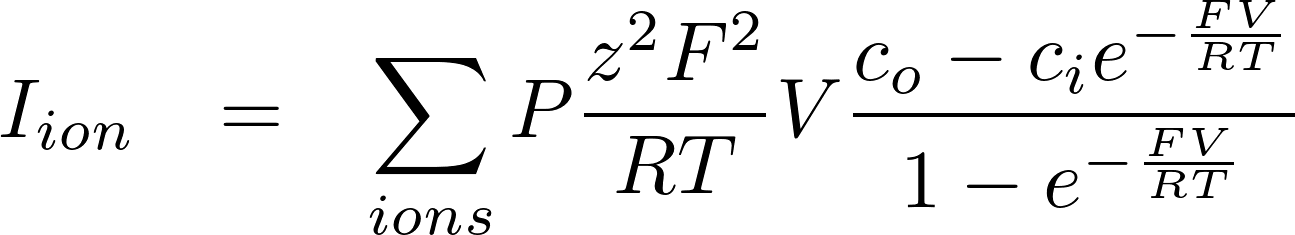
1. GHK expression
2. Linear approximation
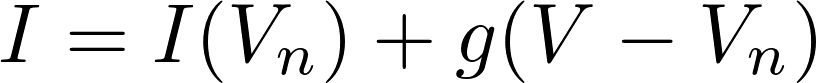
= 0
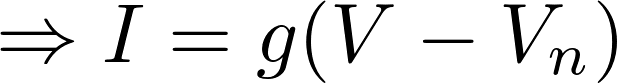
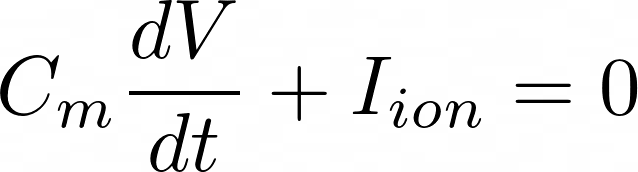
Lecture 3: Biophysical basis of excitability
By Nele Vandersickel
