Lecture 4: the hodkin and Huxley model
Special thanks to Prof. Sobie for sharing his slides
Sir Alan Hodgkin

Sir Andrew Huxley
The Hodgkin-Huxley model

1914-1998
1914-1998
Noble prize 1963
Brief historical note
Action potential recorded at the Marine Biological Association at Plymouth
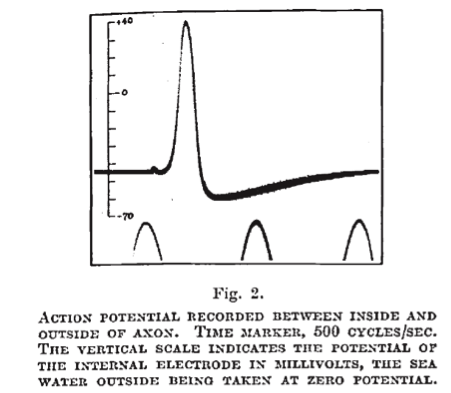
Hodkin and Huxley (1939) Nature 144:710-711
Hodgkin & Huxley left Plymouth: August 30, 1939
Hilter invaded Poland: September 1, 1939
"We published this result in a letter in Nature (1939) with no discussion or explanation. In a full paper (1945) we gave four possible explanations, all wrong" Huxley (2002), J. Physiol. 539: 2
Single cell
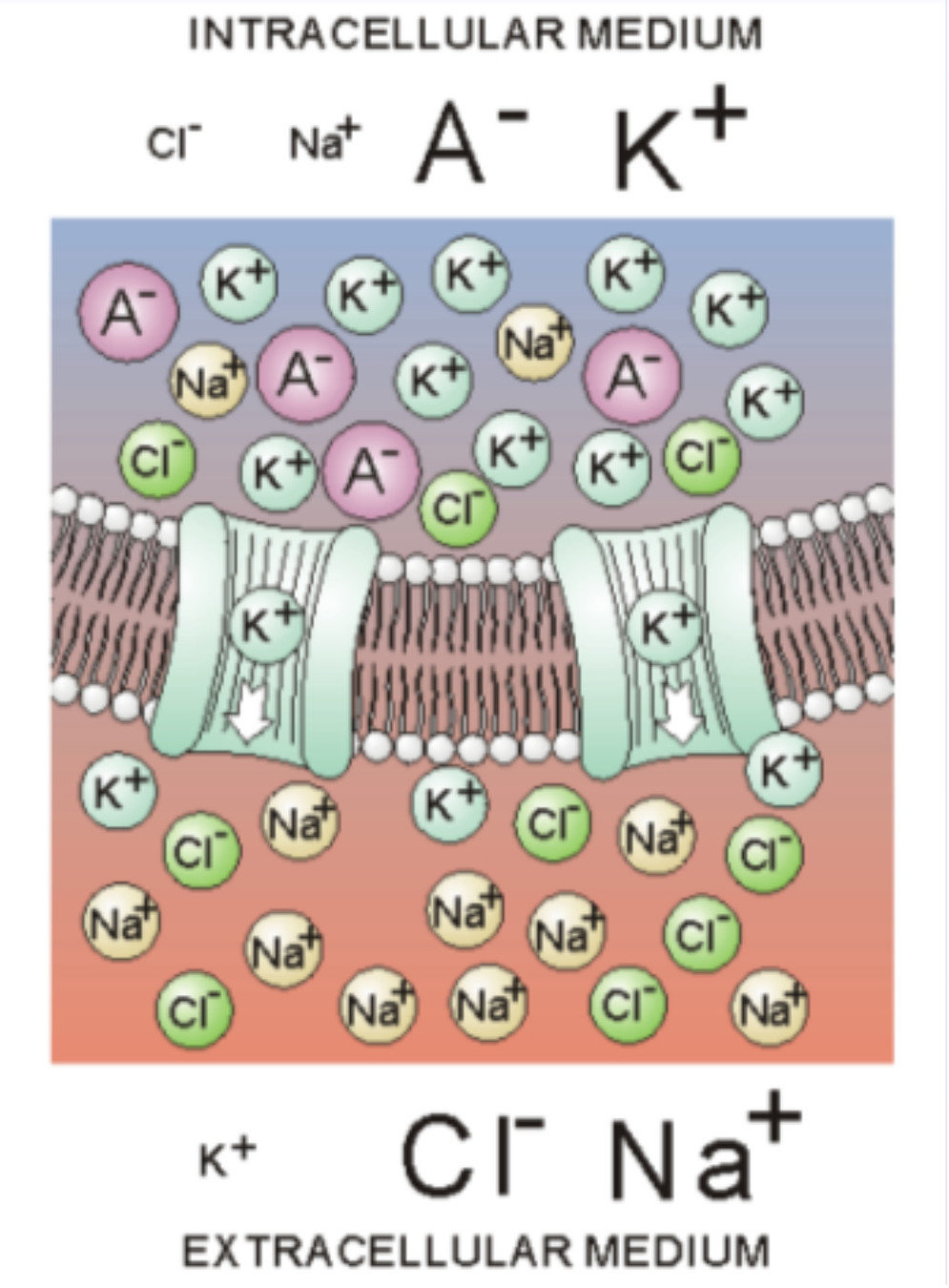
The membrane: contains channels which can open and close
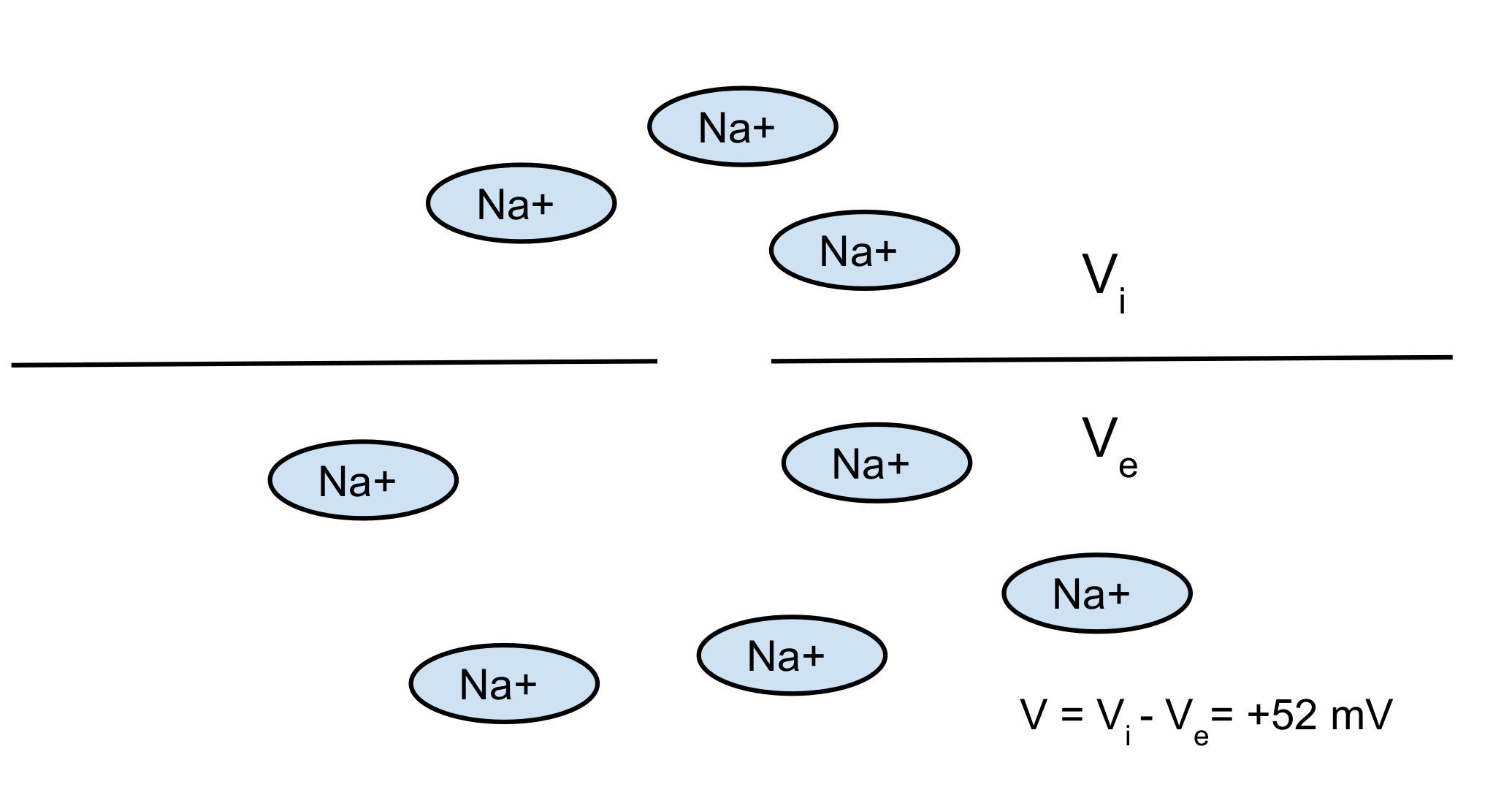
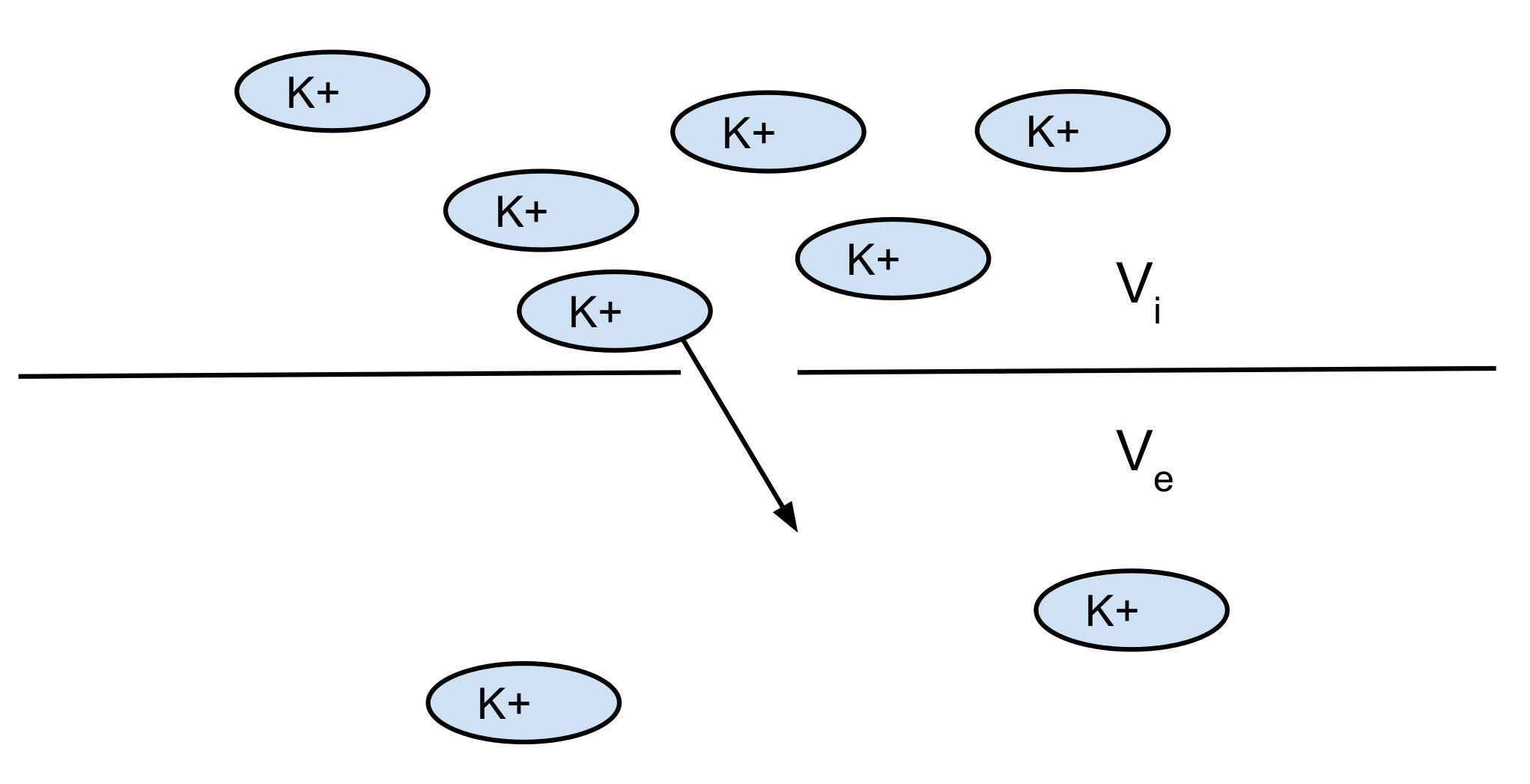
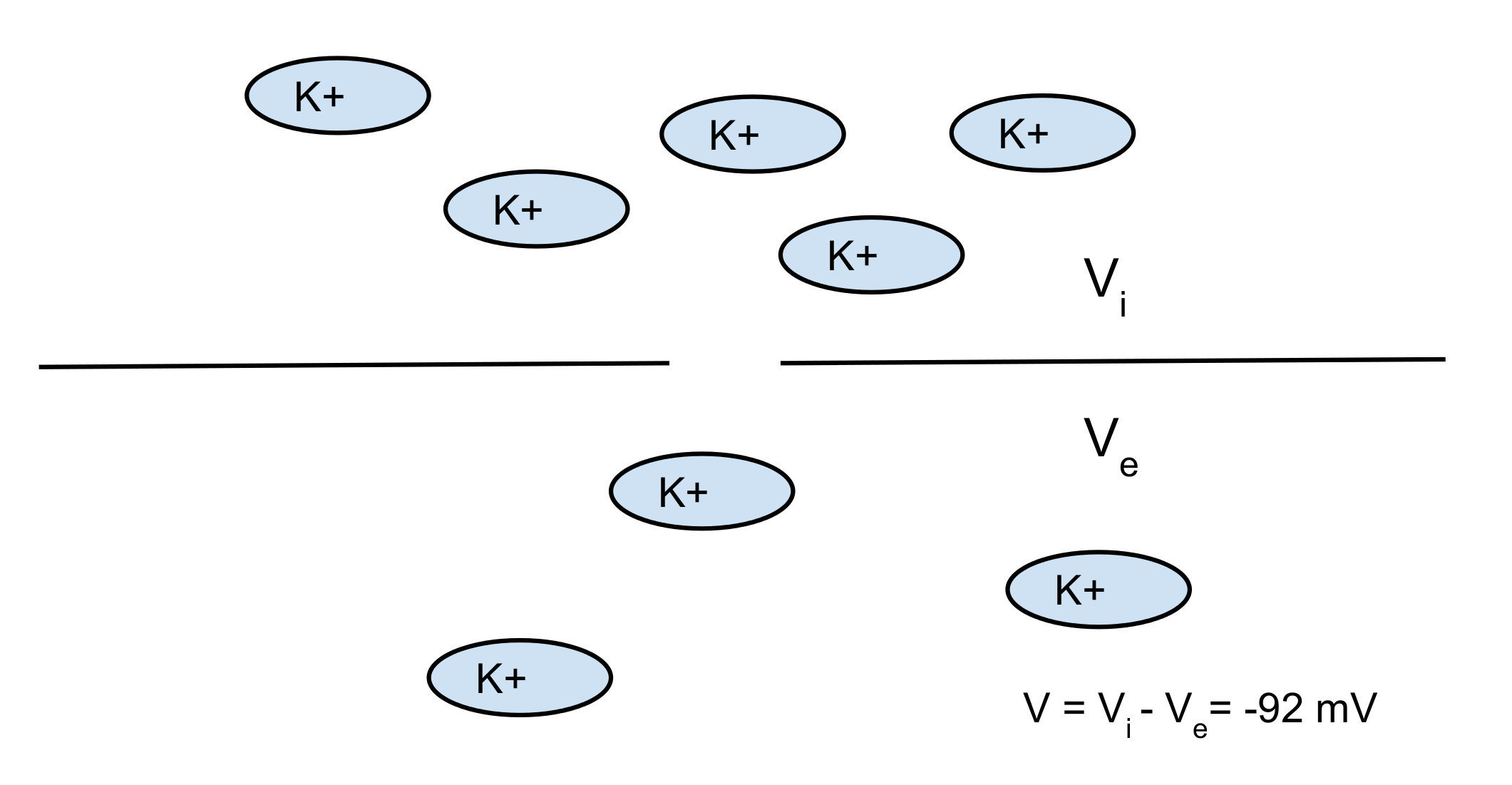
Nerst potential: 2 opposite forces:
- diffusion
- electrical force
You can find the equilibrium which gives you the Nerst potential
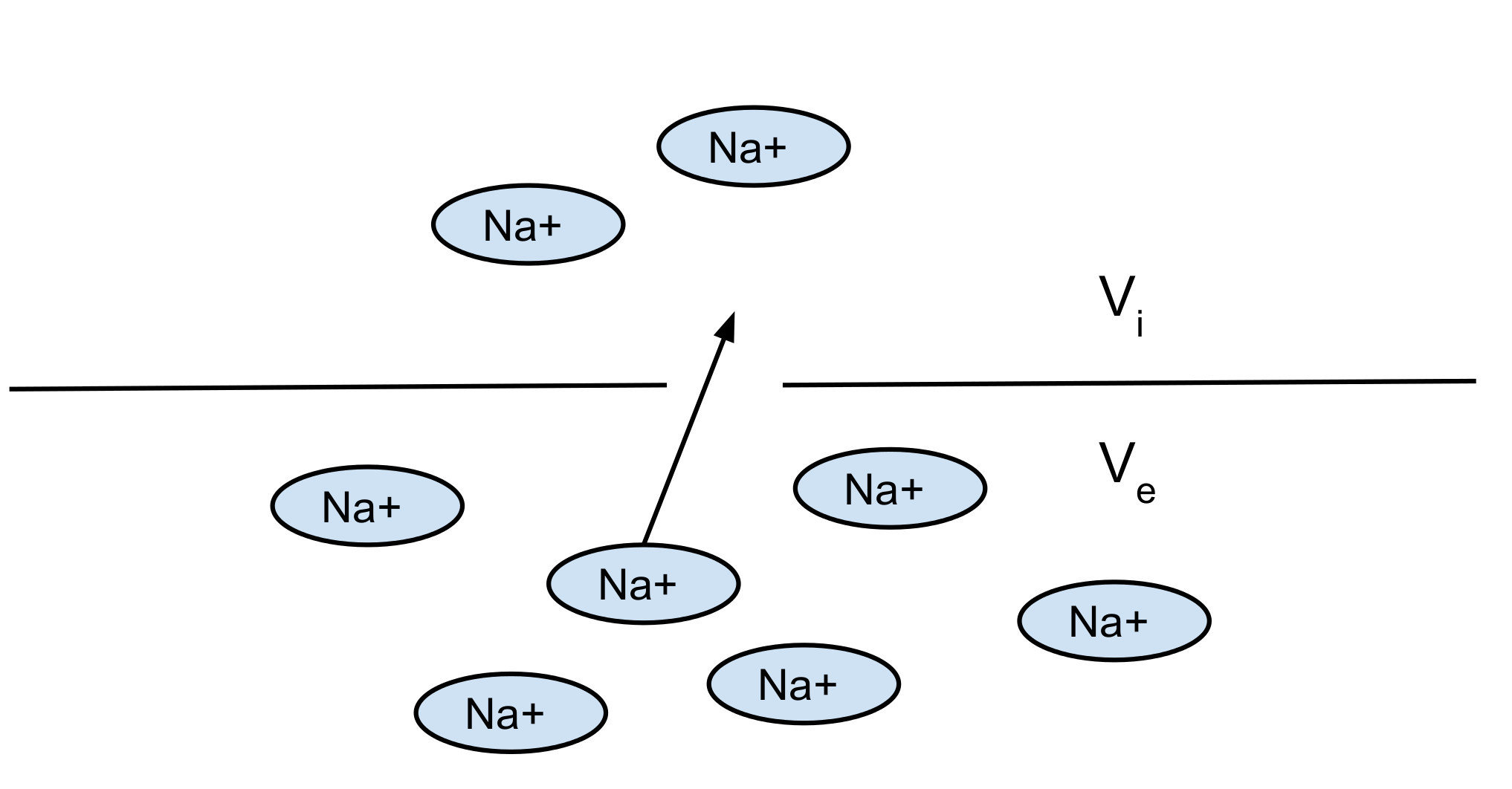
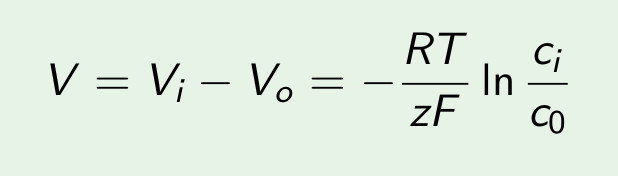
Nerst potential: 2 opposite forces:
- diffusion
- electrical force
You can find the equilibrium which gives you the Nerst potential
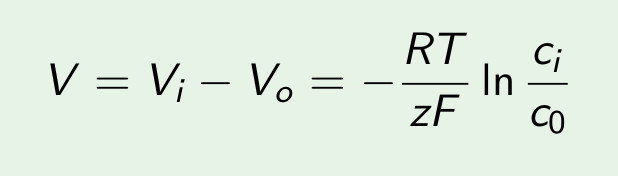
Most easy model: Hodgkin huxley (nerve cell)
Most easy model: Hodgkin huxley (nerve cell)
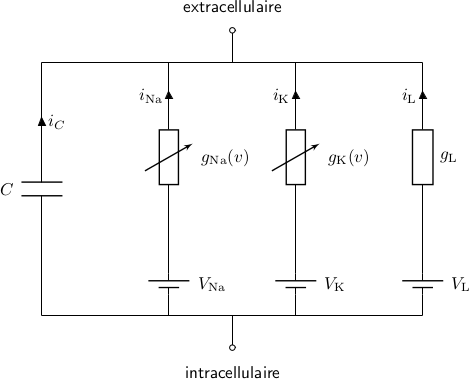
Most easy model: Hodgkin huxley (nerve cell)
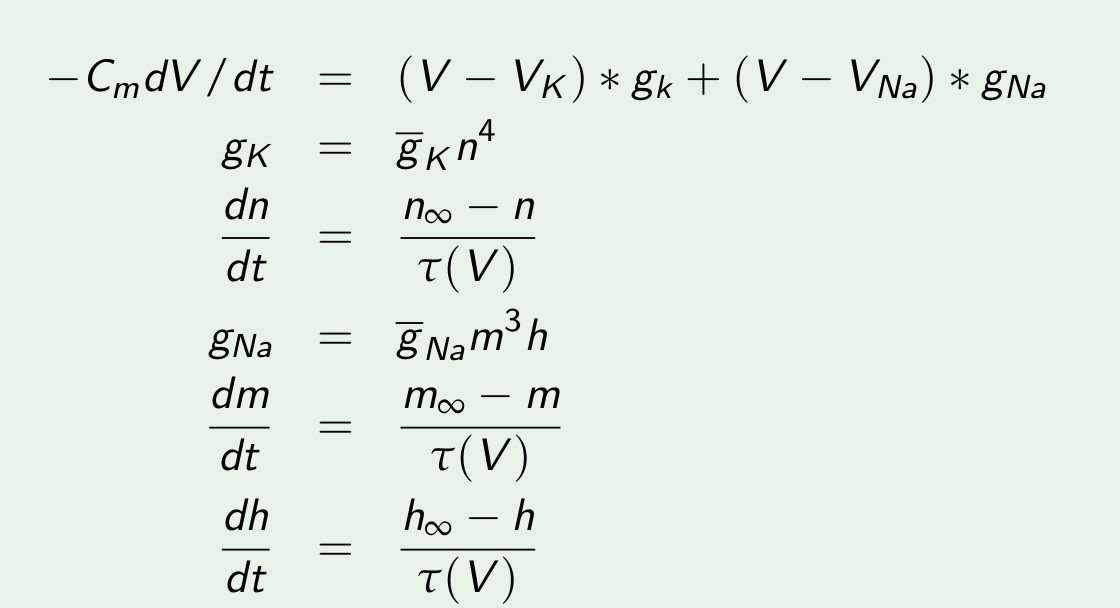
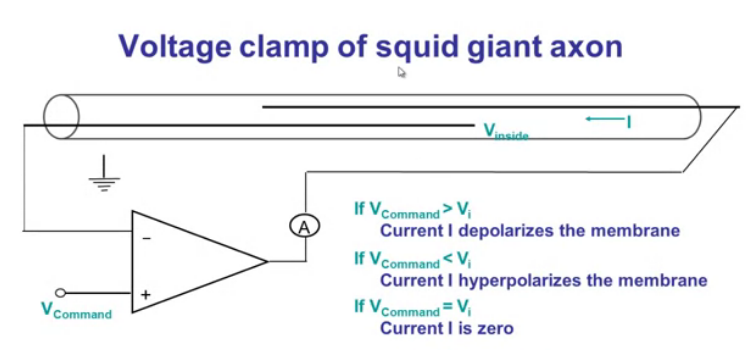
Current I required to keep Vcommand = Vi is equal in magnitude
to current flowing across the membrane
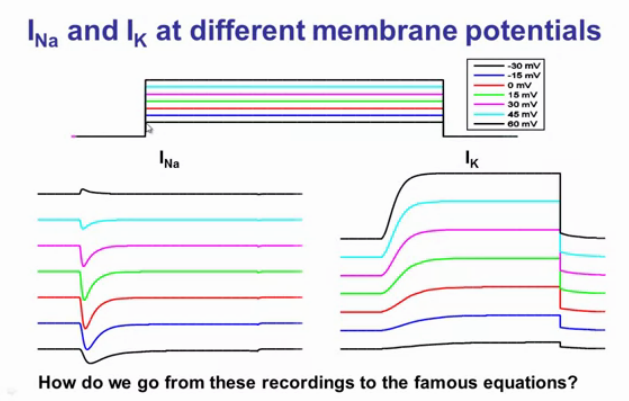
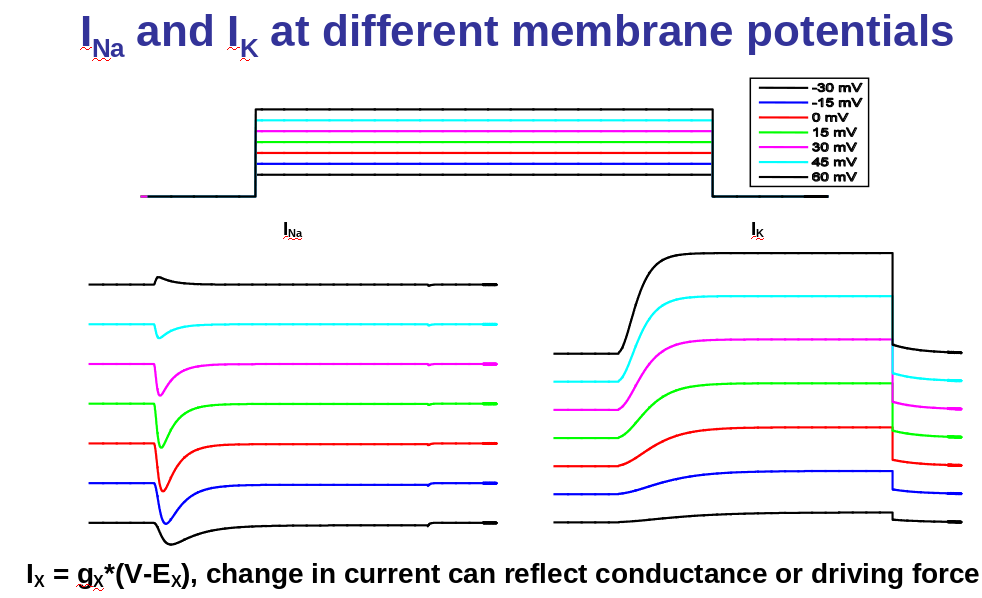
How to separate INa and IK?
V
time
I
time

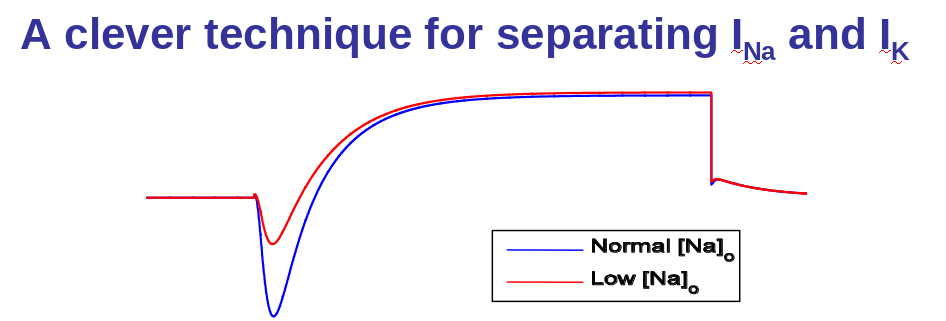
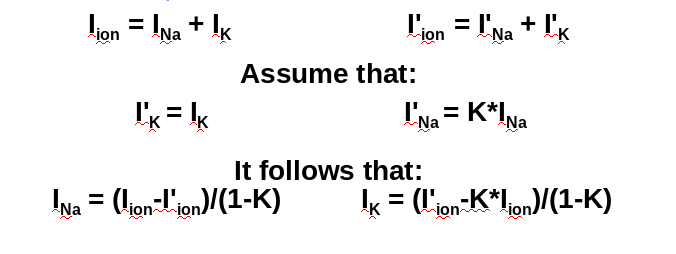
Why did they have to develop the voltage clamp technique?
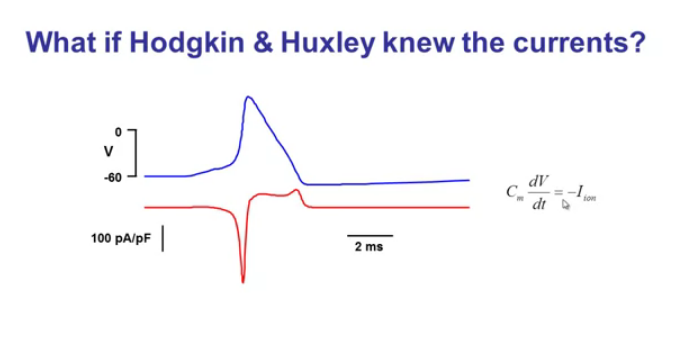
Imagine that we can magically separate INa and IK
Intermezzo:
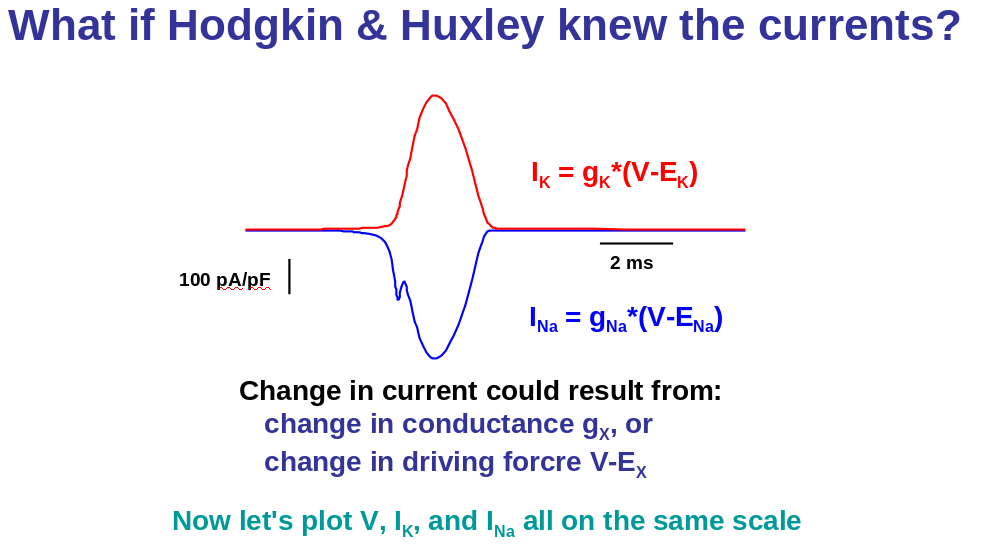
Problem 1:
Problem 2:
Intermezzo:
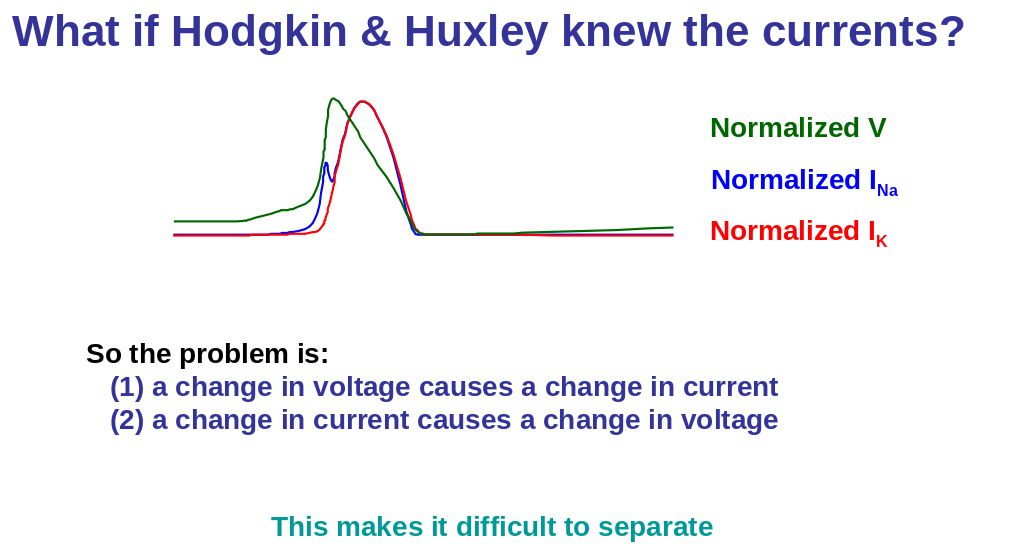
Intermezzo:

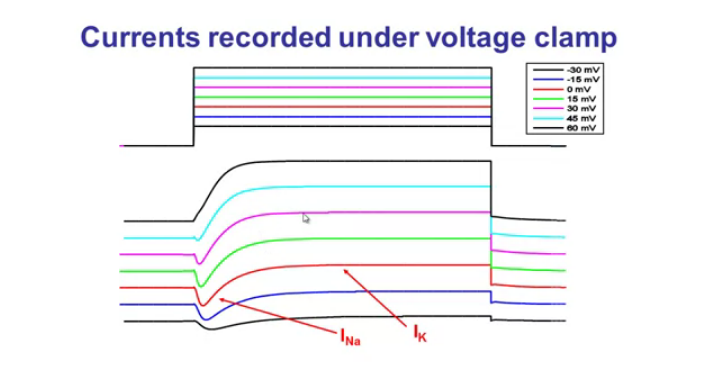
Hudgkin and Huxley found a way to control the voltage so they could measure the currents
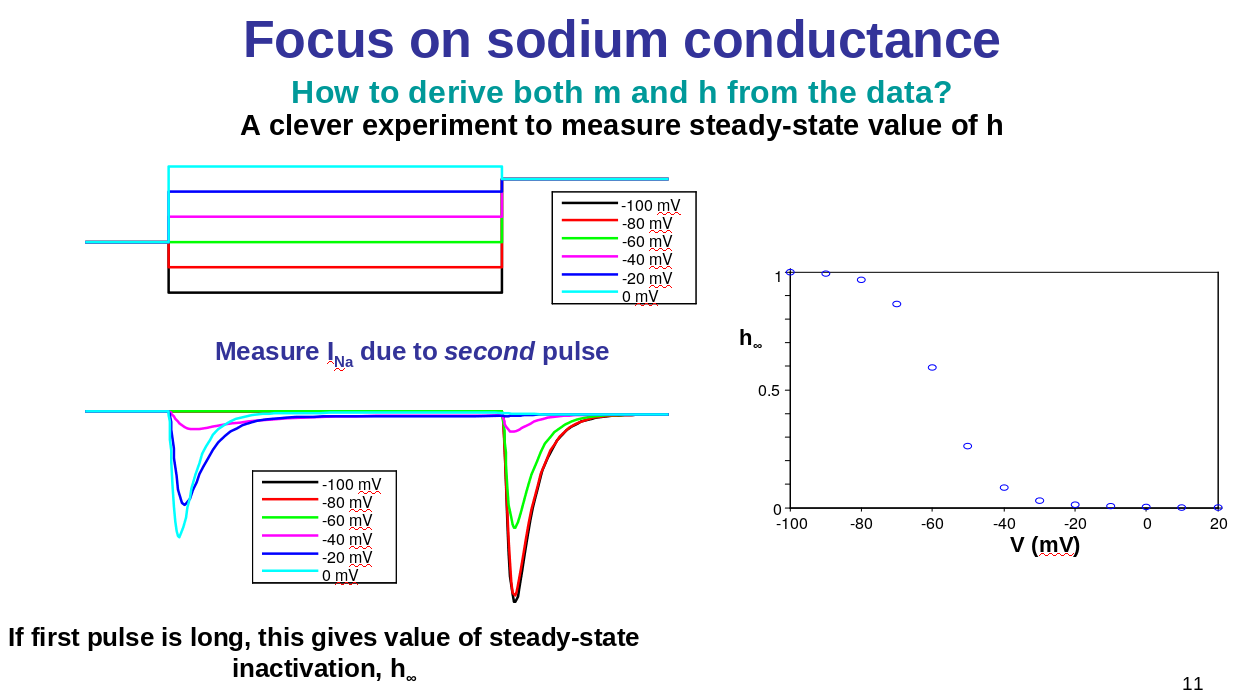
We will now derive the model equations from the experimental recordings.
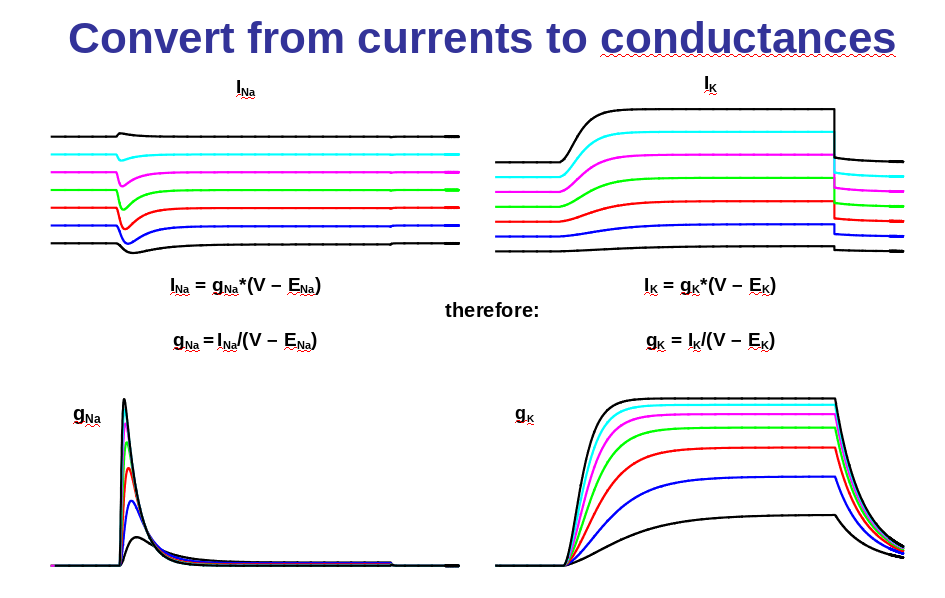
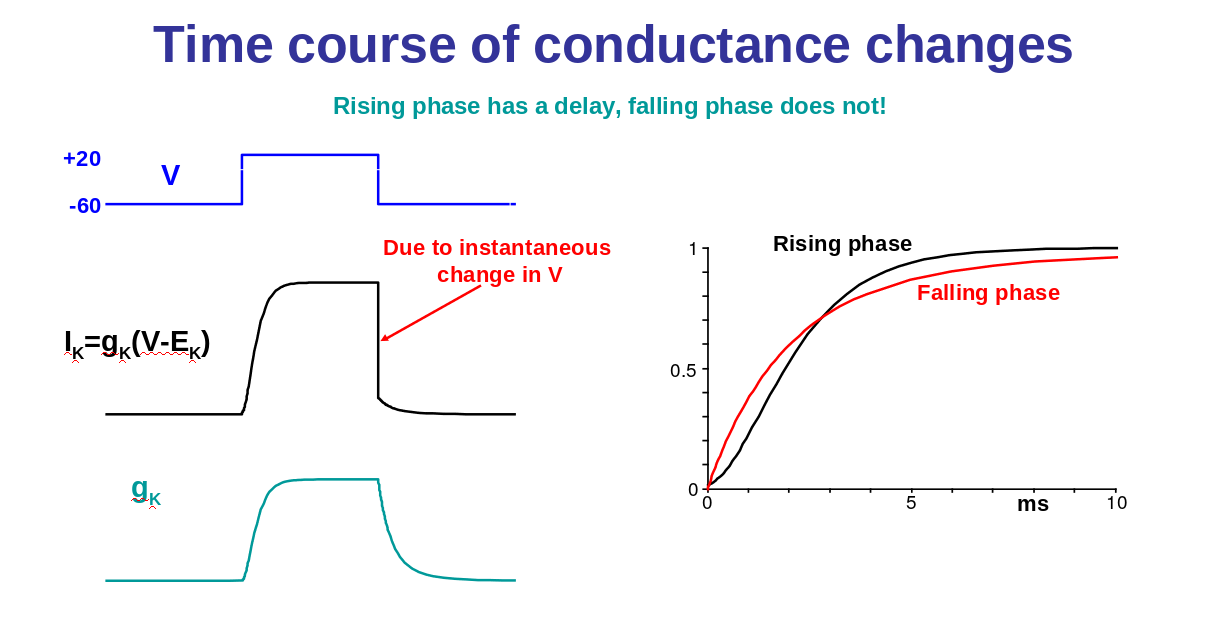
We will convert the currents to conductance:
- K+ conductance: will increase with a delay
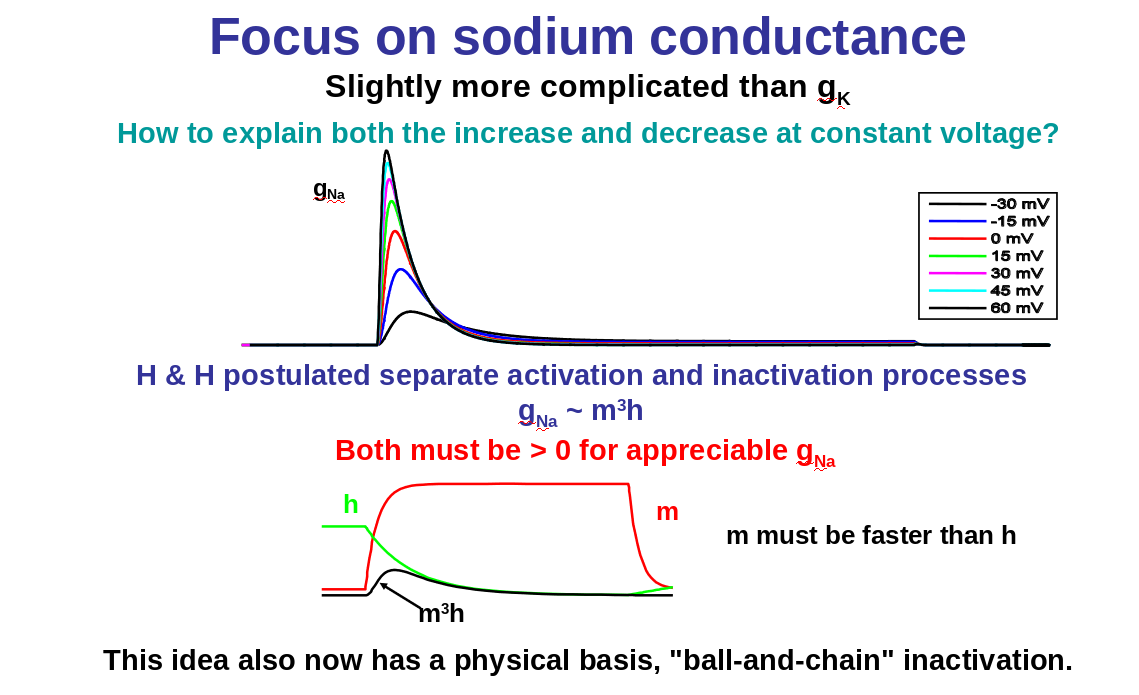
- Na+ conductance: increase and then decrease or inactivate

How do we go from these measurements to the famous equations of Hudgkin and Huxley?
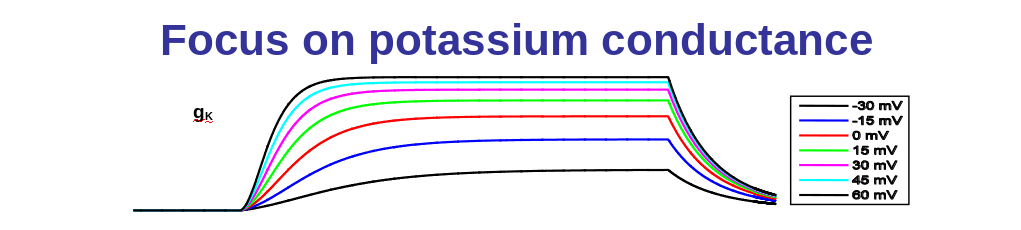
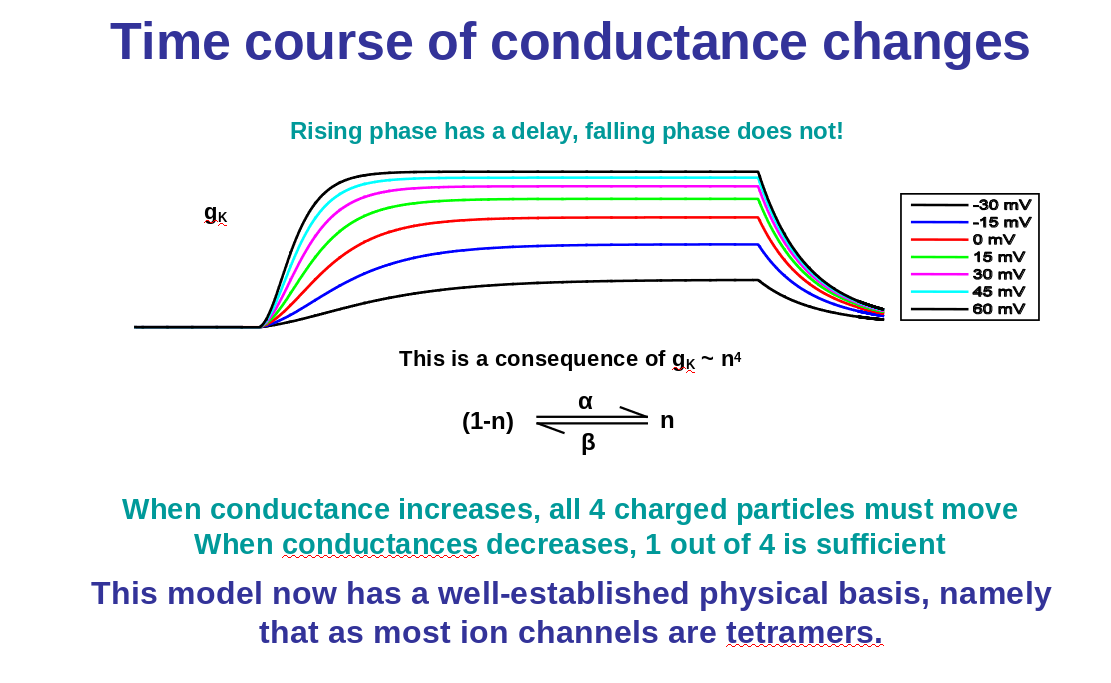
1) Changing V changes both steady-state gK and rate of rise
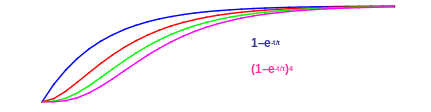
2) Time course of gK: increase similar to an exponential raised to a power
time
time

time
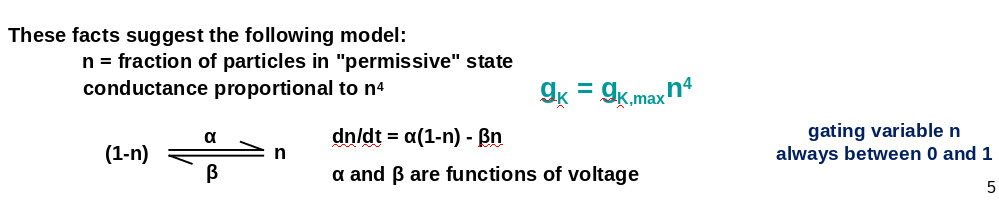
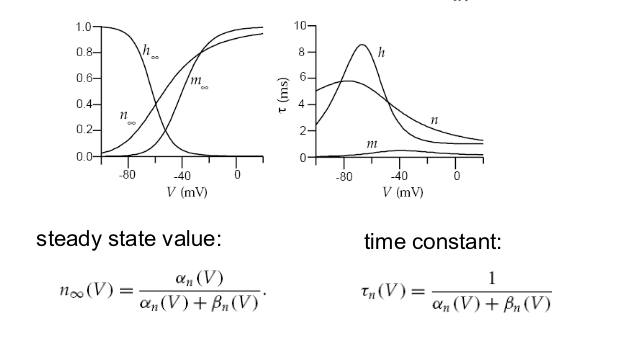
n is a gating variable, which is always between 0 and 1
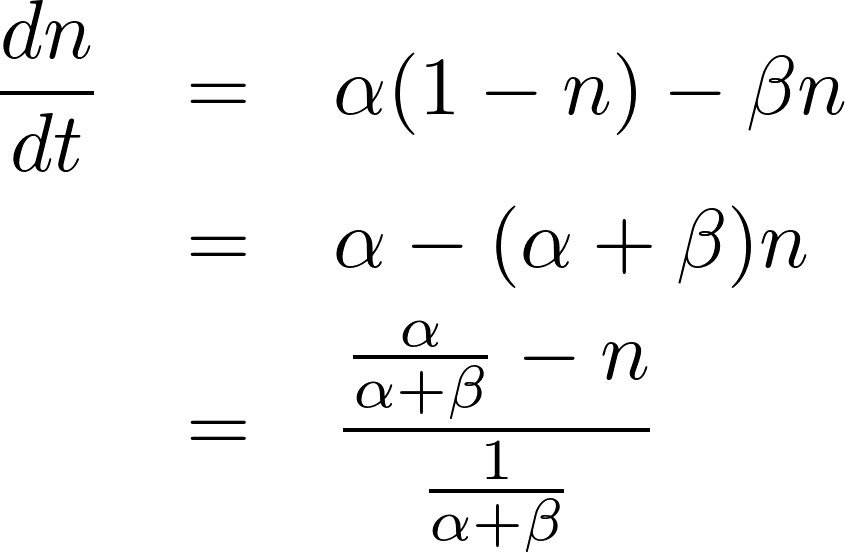
We can rewrite this equation as:
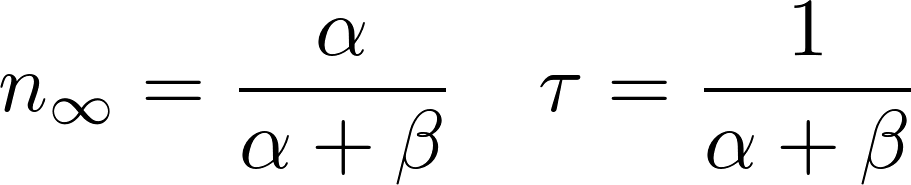
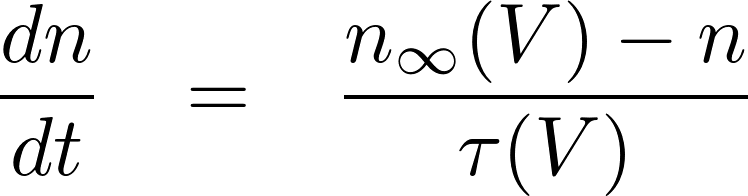
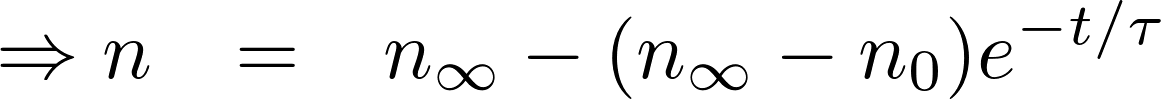
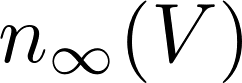
and
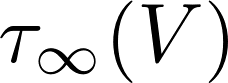
can be extracted from the data
How?
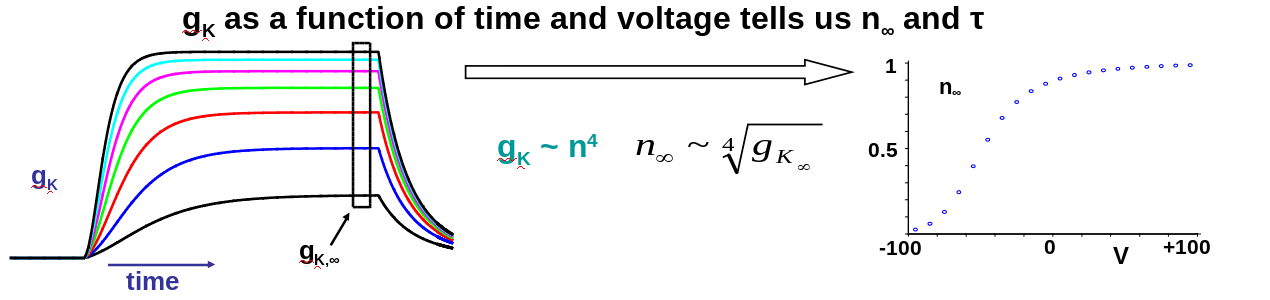
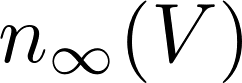
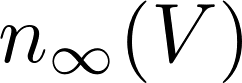
and
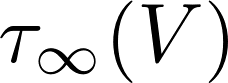
can be extracted from the data
How?
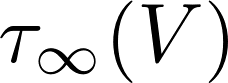
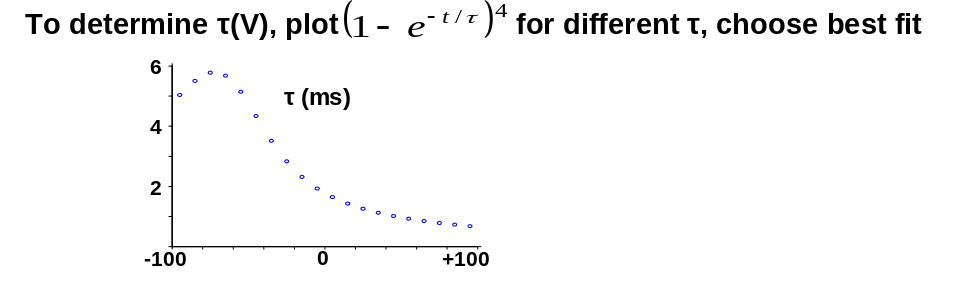

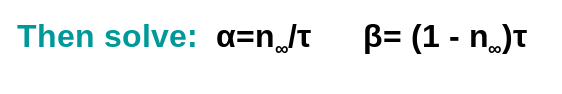

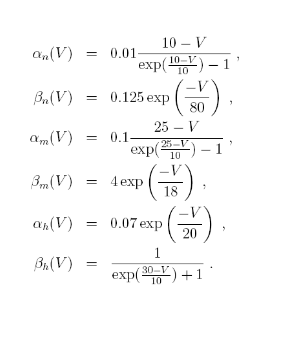

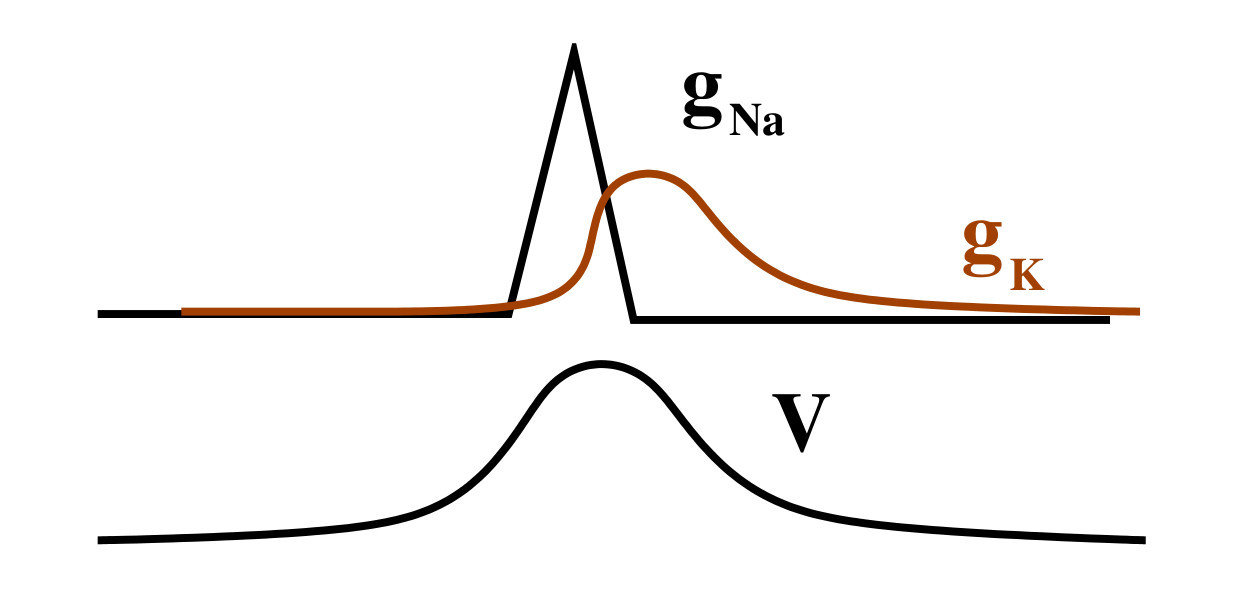
Initial situation: V= -80 mV
Fast activation of m-channel: INa large
Inactivation of h-channel -> INa equal to zero
n-channel open -> makes V lower again, gates closes
Lecture 4: the hodkin and Huxley model
By Nele Vandersickel
Lecture 4: the hodkin and Huxley model
- 751



