Logic, machines
&
sequent calculus
Alexander Gryzlov
Adform
19/12/2018
Lists
data List : Type -> Type where
Nil : List a -- aka []
(::) : a -> List a -> List aList membership
These are natural numbers in disguise!
data Elem : a -> List a -> Type where
Here : Elem x (x::xs)
There : Elem x xs -> Elem x (y::xs)data Nat : Type where
Z : Nat
S : Nat -> NatListS as sets
Subset : List a -> List a -> Type
Subset {a} xs ys =
{x : a} -> Elem x xs -> Elem x ysLambda calculus
A formal rewriting system at the heart of FP
Untyped :
x (variable) λx.M (abstraction) M N (application)
+ β-reduction
(λx.M) N → M[x:=N]
untyped Lambda calculus
DeBrujin indices
Term0 : Term
Term0 = App (Lam $ App (Var Z) (Var Z))
(Lam $ Var Z)
Term1 : Term
Term1 = App (App (Lam $ Var Z) (Lam $ Var Z))
(Lam $ Var Z)
Term2 : Term
Term2 = App (Lam $ Var Z)
(App (Lam $ Var Z) (Lam $ Var Z))data Term = Var Nat
| Lam Term
| App Term Term(λ x. x x) (λ x. x)
((λ x. x) (λ x. x))
(λ x. x)
(λ x. x)
((λ x. x) (λ x. x))

untyped Lambda calculus
1.
(λ x. x x) (λ x. x)
~
(λ x. x) (λ x. x)
~
(λ x. x)
2.
((λ x. x) (λ x. x))
(λ x. x)
~
(λ x. x) (λ x. x)
~
(λ x. x)
3.
(λ x. x)
((λ x. x) (λ x. x))
~
(λ x. x) (λ x. x)
~
(λ x. x)
simply-typed Lambda calculus
data Ty = A | Imp Ty Ty
infix 5 ~>
(~>) : Ty -> Ty -> Ty
(~>) = Imp
data Term : List Ty -> Ty -> Type where
Var : Elem a g -> Term g a
Lam : Term (a::g) b -> Term g (a~>b)
App : Term g (a~>b) -> Term g a -> Term g b
TestTy : Ty
TestTy = A ~> A
-- Term1 not typeable because of self-application!
Term2 : Term [] TestTy
Term2 = App (App (Lam $ Var Here) (Lam $ Var Here)) (Lam $ Var Here)
Term3 : Term [] TestTy
Term3 = App (Lam $ Var Here) (App (Lam $ Var Here) (Lam $ Var Here))
Result : Term [] TestTy
Result = Lam $ Var Here (structural) Proof theory
A branch of logic studying proofs as mathematical objects
Curry-Howard iso:
Theorem ~ Type
Proof ~ Term
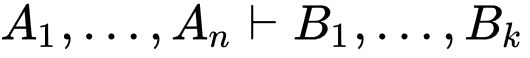
Sequent:
For now, let's restrict the RHS to a single formula:
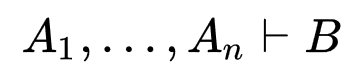
natural deduction
Minimal propositional logic:
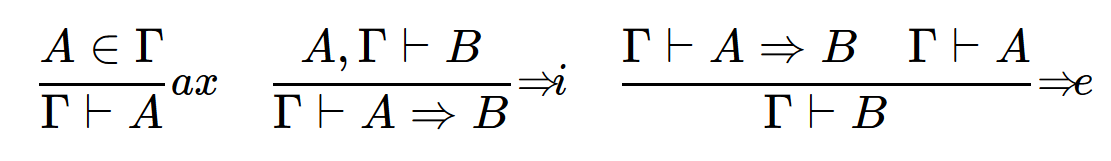
Var :
Elem a g ->
Term g aLam :
Term (a::g) b ->
Term g (a~>b)App :
Term g (a~>b) ->
Term g a ->
Term g b
Sequent calculus
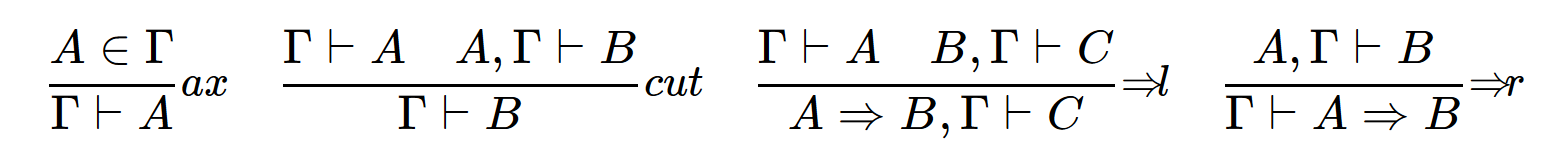
VarS :
Elem a g ->
TermS g a
Cut :
TermS g a ->
TermS (a::g) b ->
TermS g b
ImpL :
TermS g a ->
TermS (b::g) c ->
TermS ((a~>b)::g) c
ImpR :
TermS (a::g) b ->
TermS g (a~>b)structural properties
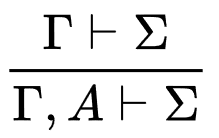
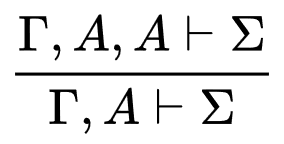
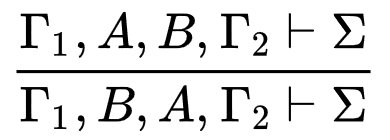
weakening contraction permutation
Gentzen's LJ
data LJ : List Ty -> Ty -> Type where
AxJ : LJ [a] a
CutJ : LJ g a -> LJ (a::g) b -> LJ g b
ImpLJ : LJ g a -> LJ (b::g) c -> LJ ((a~>b)::g) c
ImpRJ : LJ (a::g) b -> LJ g (a~>b)
WSJ : LJ g b -> LJ (a::g) b
CSJ : LJ (a::a::g) b -> LJ (a::g) b
PSJ : LJ (g ++ a::b::d) c -> LJ (g ++ b::a::d) ctwo-sided Sequent calculus
Splits sequents into kinds
and adds activation rules:
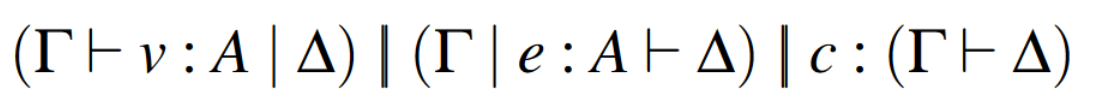

+ structural rules for both sides!
two-sided Sequent calculus
mutual
data Cmd : List Ty -> List Ty -> Type where
C : Term g a d -> CoTerm g a d -> Cmd g d
CWL : ...
CCL : ...
CPL : ...
CWR : ...
data Term : List Ty -> Ty -> List Ty -> Type where
Var : Term [a] a []
Mu : Cmd g (a::d) -> Term g a d
...
data CoTerm : List Ty -> Ty -> List Ty -> Type where
CoVar : CoTerm [] a [a]
Mut : Cmd (a::g) d -> CoTerm g a d
...aka Gentzen's LK
two-sided Sequent calculus
mutual
data Cmd : List Ty -> List Ty -> Type where
C : Term g a d -> CoTerm g a d -> Cmd g d
data Term : List Ty -> Ty -> List Ty -> Type where
Var : Elem a g -> Term g a d
Mu : Cmd g (a::d) -> Term g a d
data CoTerm : List Ty -> Ty -> List Ty -> Type where
CoVar : Elem a d -> CoTerm g a d
Mut : Cmd (a::g) d -> CoTerm g a d
internalise structurals
Subset : List a -> List a -> Type
Subset {a} xs ys = {x : a} -> Elem x xs -> Elem x ys
data IsSubset : List a -> List a -> Type where
Id : IsSubset l l
Cons2 : IsSubset l m -> IsSubset (a::l) (a::m)
shift : IsSubset l m -> Subset l m
shift Id el = el
shift (Cons2 s) Here = Here
shift (Cons2 s) (There el) = There $ shift s el
mutual
shiftCmd : IsSubset g g1 -> IsSubset d d1
-> Cmd g d -> Cmd g1 d1
shiftTerm : IsSubset g g1 -> IsSubset d d1
-> Term g a d -> Term g1 a d1
shiftCoTerm : IsSubset g g1 -> IsSubset d d1
-> CoTerm g a d -> CoTerm g1 a d1 Connectives
E.g., we can add function, tuples & discriminated unions:
data Ty = A | Imp Ty Ty | Prod Ty Ty | Sum Ty Ty
mutual
data Cmd : List Ty -> List Ty -> Type where
C : Term g a d -> CoTerm g a d -> Cmd g d
data Term : List Ty -> Ty -> List Ty -> Type where
Var : Elem a g -> Term g a d
Mu : Cmd g (a::d) -> Term g a d
Lam : Term (a::g) b d -> Term g (Imp a b) d
Pair : Term g a d -> Term g b d -> Term g (Prod a b) d
Inl : Term g a d -> Term g (Sum a b) d
Inr : Term g b d -> Term g (Sum a b) d
data CoTerm : List Ty -> Ty -> List Ty -> Type where
CoVar : Elem a d -> CoTerm g a d
Mut : Cmd (a::g) d -> CoTerm g a d
AppC : Term g a d -> CoTerm g b d -> CoTerm g (Imp a b) d
MatP : Cmd (a::b::g) d -> CoTerm g (Prod a b) d
MatS : Cmd (a::g) d -> Cmd (b::g) d -> CoTerm g (Sum a b) dAbstract machines
Like a virtual machine, but abstract :)
Usually includes closures, stacks & environments
KRivine Abstract machine
Lazy (call by name)
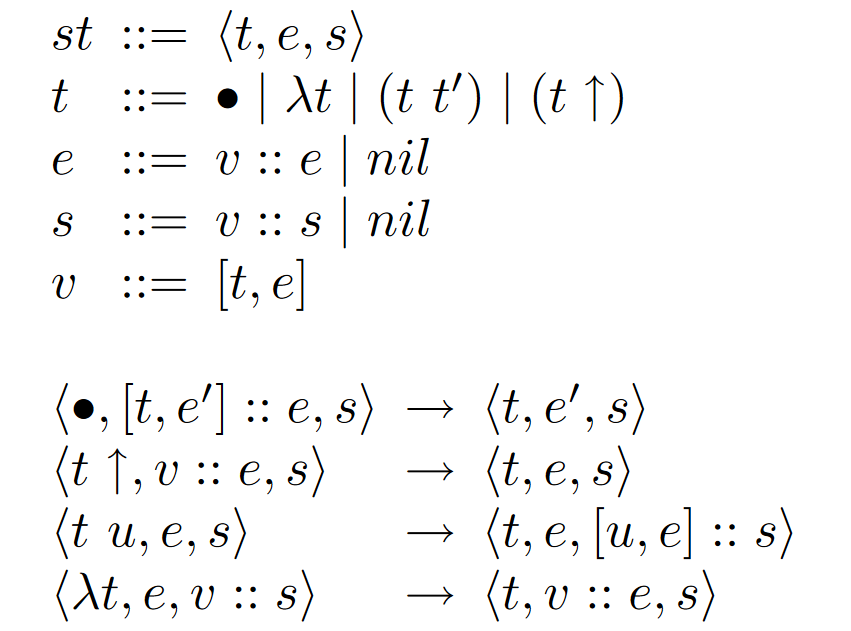
KRivine Abstract machine
mutual
Env : Type
Env = List Clos
data Clos = Cl Term Env
Stack : Type
Stack = List Clos
State : Type
State = (Term, Env, Stack)
step : State -> Maybe State
step (Var Z , Cl t e::_, s) = Just ( t, e, s)
step (Var (S n), _::e, s) = Just (Var n, e, s)
step (Lam t , e, c::s) = Just ( t, c::e, s)
step (App t u , e, s) = Just ( t, e, Cl u e::s)
step _ = Nothingcek
Control + Environment + Kontinuation
Eager (call by value)
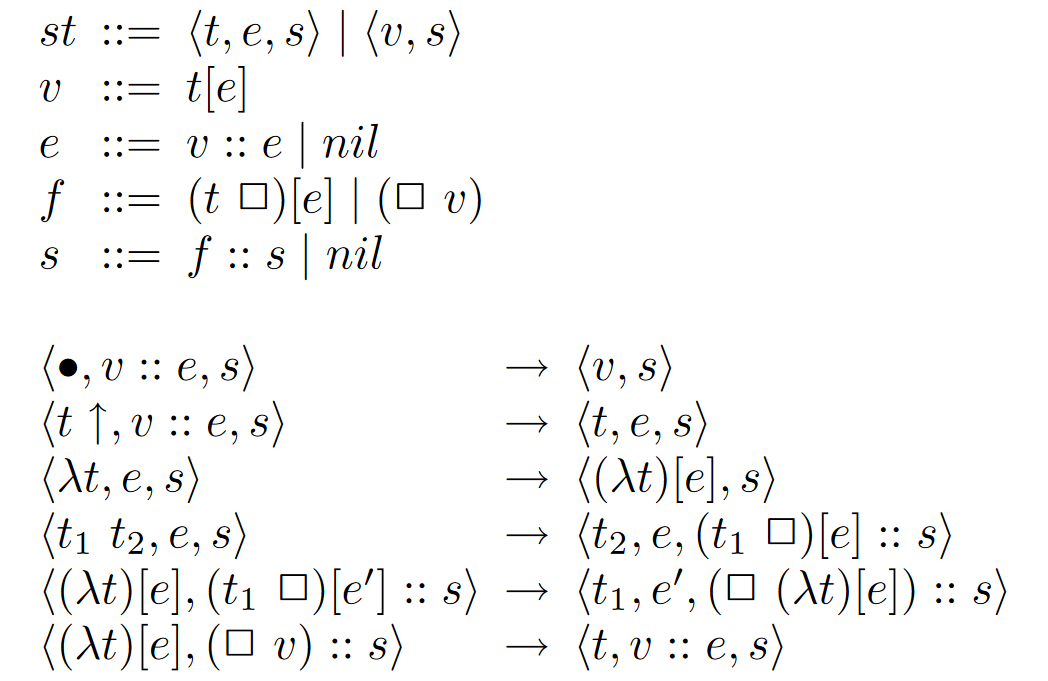
cek
mutual
Env : Type
Env = List Clos
data Clos = Cl Term Env
data Frame = Fun Term Env | Arg Clos
Stack : Type
Stack = List Frame
data State = L Term Env Stack | R Clos Stack
step : State -> Maybe State
step (L (Var Z) (v::_) s ) = Just $ R v s
step (L (Var (S n)) (_::e) s ) = Just $ L (Var n) e s
step (L (Lam t) e s ) = Just $ R (Cl (Lam t) e) s
step (L (App t u) e s ) = Just $ L u e (Fun t e::s)
step (R (Cl (Lam t) e) (Fun t1 e1::s)) = Just $ L t1 e1 (Arg (Cl (Lam t) e)::s)
step (R (Cl (Lam t) e) ( Arg v::s)) = Just $ L t (v::e) s
step _ = NothingDeconstructing
application, lambdas & LET
(λx.t) u → t[x:=u] <λx.t | u·e> → <t[x:=u] | e>
<μ(x·α).c | u·e> → c[x:=u,α:=e]
λx.t === μ(x·α).<t|α>
<t u | e> → <t | u·e>
<μα.c | e> → c[α:=e]
t u === μα.<t|u·α>
let x=t in u === μα.<t|μ~x.<u|α>>
Deconstructing
application & lambdas
mutual
data Cmd : List Ty -> List Ty -> Type where
C : Term g a d -> CoTerm g a d -> Cmd g d
data Term : List Ty -> Ty -> List Ty -> Type where
Var : Elem a g -> Term g a d
Mu : Cmd g (a::d) -> Term g a d
MatC : Cmd (a::g) (b::d) -> Term g (Imp a b) d
data CoTerm : List Ty -> Ty -> List Ty -> Type where
CoVar : Elem a d -> CoTerm g a d
Mut : Cmd (a::g) d -> CoTerm g a d
AppC : Term g a d -> CoTerm g b d -> CoTerm g (Imp a b) d
lam : Term (a::g) b d -> Term g (Imp a b) d
lam t =
MatC $ C (shiftTerm t) (CoVar Here)
app : Term g (Imp a b) d -> Term g a d -> Term g b d
app t u =
Mu $
C (shiftTerm t) (AppC (shiftTerm u) (CoVar Here))
let_ : Term g a d -> Term (a::g) b d -> Term g b d
let_ t u = Mu $ C (shiftTerm t)
(Mut $ C (shiftTerm u) (CoVar Here))call/cc
callcc : Term g (Imp (Imp a b) a) (a::d) -> Term g a d
callcc f =
Mu $ C f
(AppC
(MatC $ C (Var Here) (CoVar $ There Here))
(CoVar Here))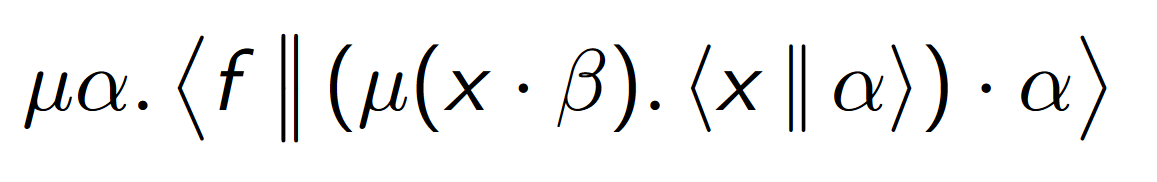
reduction
reduce : Cmd g d -> Maybe (Cmd g d)
reduce (C (Mu c) e ) = Just $ cosubst c e
reduce (C t (Mut c) ) = Just $ subst c t
reduce (C (MatC c) (AppC t e)) = Just $ subst
(cosubst c (shiftCoTerm e))
(shiftTerm t)
reduce _ = Nothing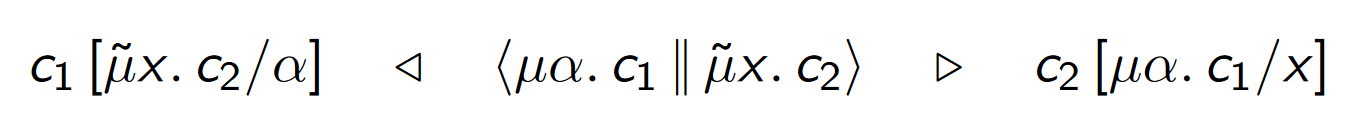
critical pair!
Dual reduction - LKT
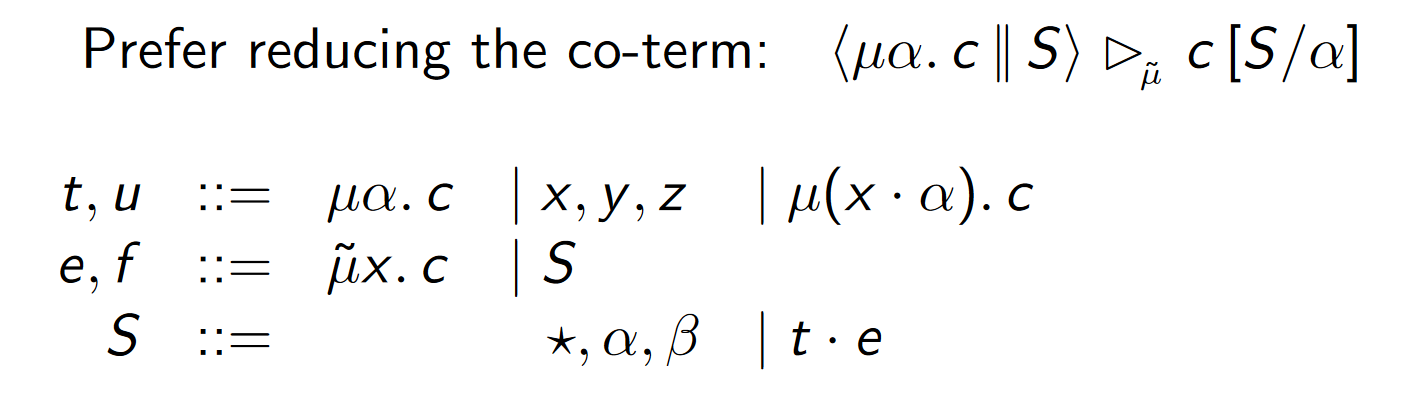
Amounts to lazy evaluation
Dual reduction - LKT
mutual
data Cmd : List Ty -> List Ty -> Type where
C : Term g a d -> CoTerm g a d -> Cmd g d
data Term : List Ty -> Ty -> List Ty -> Type where
Var : Elem a g -> Term g a d
Mu : Cmd g (a::d) -> Term g a d
MatC : Cmd (a::g) (b::d) -> Term g (Imp a b) d
data CoTerm : List Ty -> Ty -> List Ty -> Type where
CoVal : CoValue g a d -> CoTerm g a d
Mut : Cmd (a::g) d -> CoTerm g a d
data CoValue : List Ty -> Ty -> List Ty -> Type where
Empty : CoValue g a d
CoVar : Elem a d -> CoValue g a d
AppC : Term g a d -> CoValue g b d
-> CoValue g (Imp a b) d
Dual reduction - LKQ
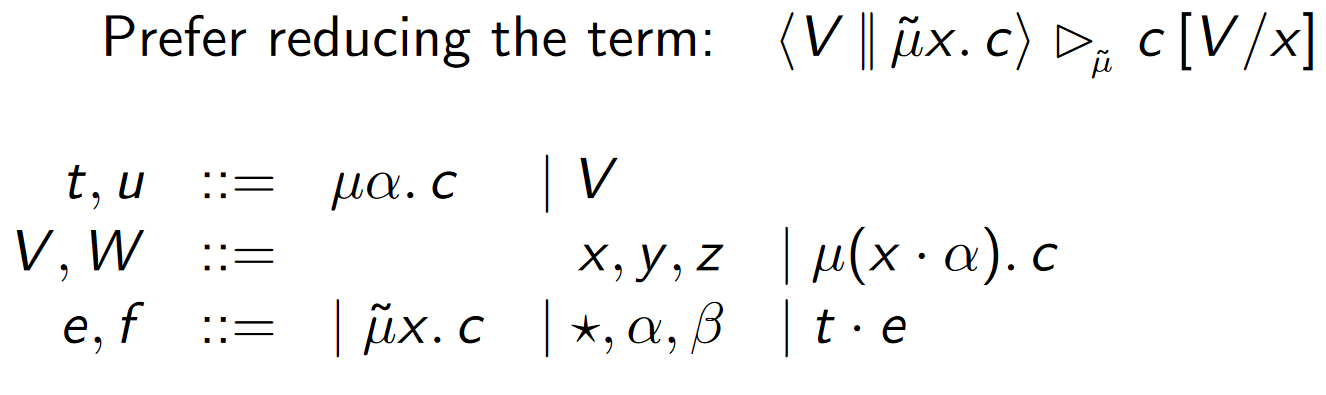
Amounts to eager evaluation
Dual reduction - LKQ
mutual
data Cmd : List Ty -> List Ty -> Type where
C : Term g a d -> CoTerm g a d -> Cmd g d
data Term : List Ty -> Ty -> List Ty -> Type where
Val : Value g a d -> Term g a d
Mu : Cmd g (a::d) -> Term g a d
data Value : List Ty -> Ty -> List Ty -> Type where
Var : Elem a g -> Value g a d
MatC : Cmd (a::g) (b::d) -> Value g (Imp a b) d
data CoTerm : List Ty -> Ty -> List Ty -> Type where
CoVar : Elem a d -> CoTerm g a d
Empty : CoTerm g a d
Mut : Cmd (a::g) d -> CoTerm g a d
AppC : Value g a d -> CoTerm g b d
-> CoTerm g (Imp a b) dPolarization
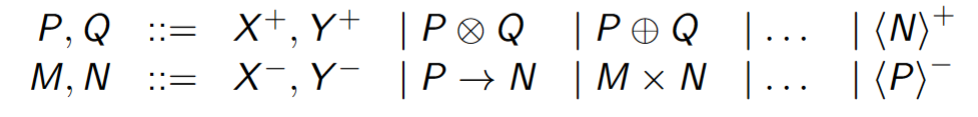
Types
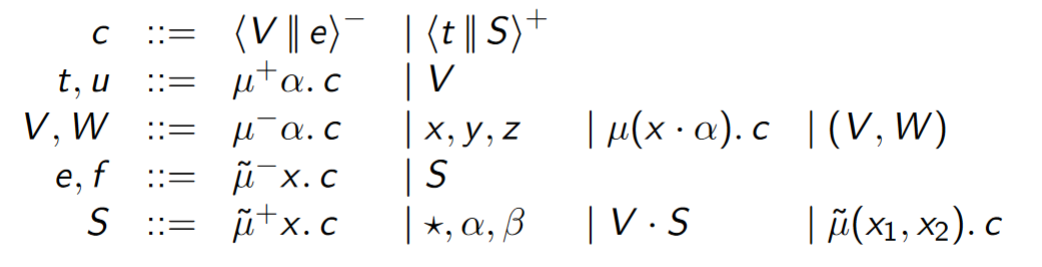
Terms
more polarities
call by need! (true laziness)
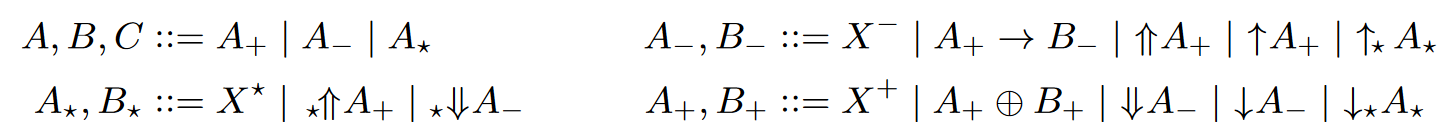
effects
reduce : Monad m => Cmd g d -> m (Cmd g d)
...
Adjunction f g => Monad (Compose g f)
???generalizing connectives
Move to
- inductive sums of products and
- coinductive records of functions/matches
Infinite structures become first class
polymorphism
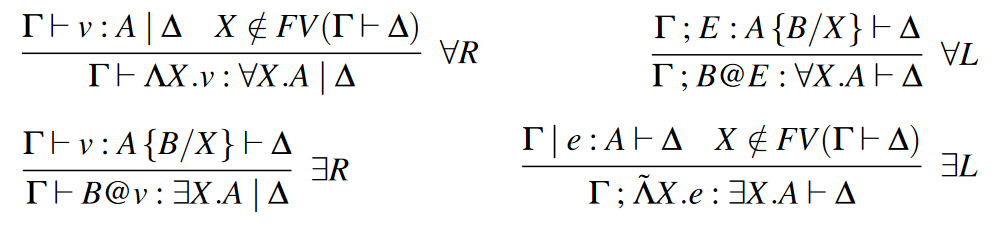
Both universal and existential
dependent types

Literature
Thanks!
Copy of Logic, machines and sequent calculus
By Oleg Nizhnik
Copy of Logic, machines and sequent calculus
- 1,212


