Dinámica de mecanismos
Unidad 2: Análisis cinemático de Levas y Engranajes
Ing. Oscar Alonso Rosete Beas
Semana 7 Marzo Rev:1 ciclo 2023-1
oscarrosete.com
oscarrosete.com

Agenda
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes
oscarrosete.com
Unidad 1
oscarrosete.com

Agenda
oscarrosete.com

oscarrosete.com
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Introducción

oscarrosete.com
oscarrosete.com
El análisis de velocidad y aceleración en mecanismos articulados requiere un estudio detallado, muy diferente al que se hace con las partículas


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Consideraciones

oscarrosete.com
oscarrosete.com
- Las ecuaciones cinemáticas son ecuaciones vectoriales. Por esta razón requieren una solución vectorial gráfica y(o) analítica.
- Existen diferentes tipos de velocidades y aceleraciones. Por ejemplo, velocidades y aceleraciones angulares de los eslabones, velocidades y aceleraciones tangenciales en los nodos y(o) uniones y velocidades rectilíneas en las correderas, entre otras.

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Consideraciones

oscarrosete.com
oscarrosete.com
- Los métodos gráficos permiten solucionar ecuaciones de velocidad y aceleración mediante trazos vectoriales, en especial para el cálculo en un instante dado del mecanismo.
- No obstante, lo anterior no aplica para los métodos analíticos, en los que es posible establecer ecuaciones representativas de velocidad y aceleración en cualquier instante, obteniendo resultados más exactos en comparación con los métodos gráficos.

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Conceptos básicos

oscarrosete.com
oscarrosete.com
Velocidad se define como la magnitud del cambio de la posición con respecto al tiempo.
Aceleración es el cambio en la magnitud de la velocidad respecto al tiempo.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
El análisis de velocidad en los elementos de un mecanismo radica principalmente en comprender la relación vectorial que existe entre la velocidad de rotación en un eslabón y la velocidad tangencial en cada uno de sus nodos de articulación.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
Para dejar en claro lo anterior, considérese el mecanismo manivela-corredera de la figura, el cual dispone de una manivela 2, con un movimiento de rotación alrededor del nodo O2.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
Por su parte, el nodo A transmite el movimiento del eslabón 2 al eslabón 3 y tiene una trayectoria circular, mientras que el nodo B transmite el movimiento del eslabón 3 al 4, al tiempo que, debido a que forma parte de la corredera 4, tiene una trayectoria rectilínea.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
Como primer paso del análisis cinemático de mecanismos se establecen las ecuaciones de velocidad aislando cada elemento, en las cuales el cambio de posición se expresa como un vector desplazamiento Δr




Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad angular

oscarrosete.com
oscarrosete.com
La velocidad angular, o de rotación, puede presentarse en los eslabones con movimiento de rotación alrededor de un punto.
La velocidad angular promedio e instantánea se define como:



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad tangencial

oscarrosete.com
oscarrosete.com
La velocidad tangencial se encuentra en los nodos de un eslabón y es tangente a la trayectoria generada por el nodo durante el movimiento.



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad

oscarrosete.com
oscarrosete.com
Cuando un eslabón tiene movimiento de rotación, como en el caso de la figura a), cada nodo del eslabón experimenta un desplazamiento lineal, que se denota por ΔrA, el cual, después de ser dividido por el lapso de tiempo, proporciona la velocidad de desplazamiento, o velocidad tangencial (VT ):

Velocidad tangencial


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Relación entre velocidad tangencial y angular

oscarrosete.com
oscarrosete.com
En los eslabones que tienen movimiento de rotación existe una relación entre la velocidad angular del eslabón (ω) y la velocidad lineal de algún nodo del eslabón (V), conocida como velocidad tangencial. Si la longitud de arco en una circunferencia es s=rθ, entonces para pequeños desplazamientos del nodo A de la manivela se tiene ds=rAdθ; por tanto:



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad

oscarrosete.com
oscarrosete.com
Así, se establece una relación entre la magnitud de la velocidad lineal de un nodo VTA con la velocidad de rotación (ω) y el radio de giro (rA), siempre y cuando no cambie la magnitud del radio de giro.



Relación entre velocidad tangencial y angular
Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad

oscarrosete.com
oscarrosete.com
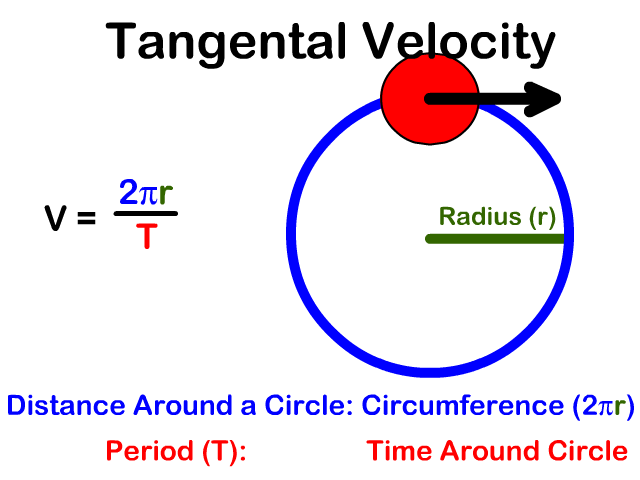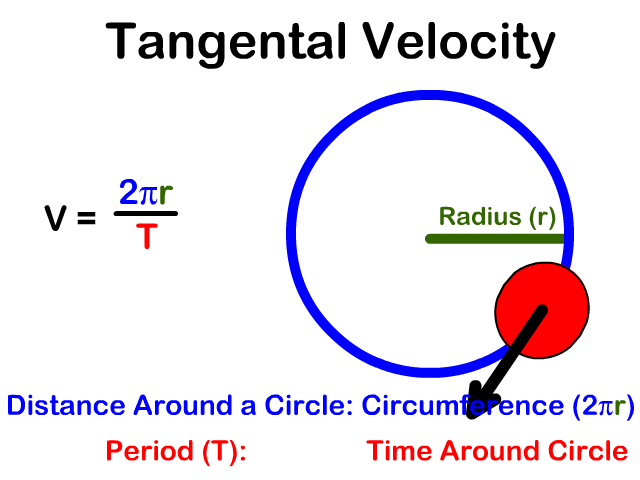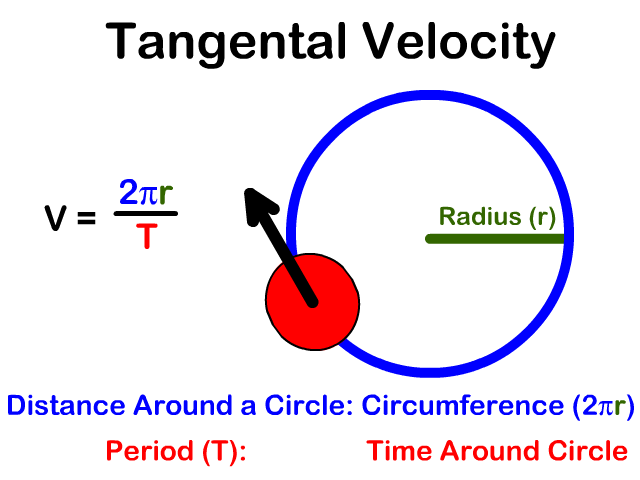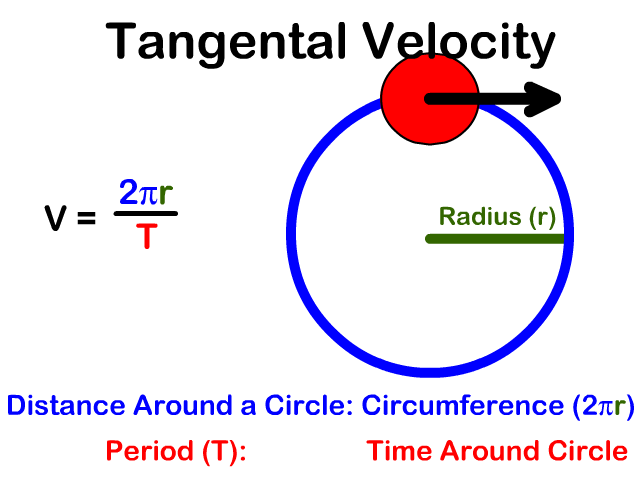
Tanto la posición de un mecanismo como la velocidad tangencial de uno de sus nodos son cantidades vectoriales, y como vector la velocidad tangencial es perpendicular al radio de giro, cuyo sentido depende del movimiento del eslabón.


Relación entre velocidad tangencial y angular
Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad rectilínea

oscarrosete.com
oscarrosete.com
Considérese ahora el caso de un sólido rígido que tiene un movimiento de translación rectilínea, como el de la figura. Cada partícula de un sólido rígido tiene los mismos desplazamientos; además, debido a que las trayectorias entre dos nodos del mismo eslabón son siempre paralelas, la velocidad en cada partícula siempre es lineal e idéntica, la cual se conoce como velocidad rectilínea o lineal VL y se define como:



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad rectilínea

oscarrosete.com
oscarrosete.com
Vectorialmente, la dirección de la velocidad rectilínea VL es paralela al movimiento de la corredera en el sentido de esta, como se muestra en la figura



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Tanto la velocidad tangencial como la velocidad rectilínea se conocen como velocidades absolutas, ya que ambas se miden desde un marco de referencia fijo.



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Asimismo, existe otro tipo de velocidad, conocida como velocidad relativa, vector que se mide tomando como origen un nodo del sólido rígido que se encuentra en movimiento.
Un ejemplo de estas velocidades lo constituyen las bielas, debido a que en este eslabón todos sus nodos están en movimiento.

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
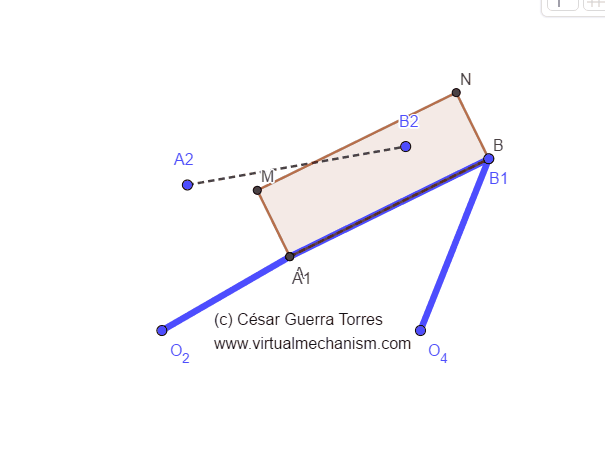
Para el análisis de velocidad relativa considérese un observador que está situado en el nodo A de un sólido rígido, el cual desea determinar la velocidad de otro nodo, al que se denomina nodo B.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Con base en lo anterior, ¿cómo es el desplazamiento del nodo B visto desde A, es decir, (ΔrB/A)? Entonces, para hallar la velocidad se fija el nodo A y se trazan ambas posiciones relativas (ΔrB1/A1 y ΔrB2 /A2), como se muestra en la figura.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
De lo anterior puede deducirse que, en términos generales, las trayectorias de los nodos A y B son des- conocidas, ya que dependen del eslabón al cual habrán de articularse.



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Sin embargo, independientemente de las trayectorias absolutas de A y B, la trayectoria relativa de B vista desde A es siempre conocida y circular, por lo que la velocidad relativa (VB/A) puede determinarse mediante la ecuación:



Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Como la trayectoria relativa de dos puntos de una misma barra siempre es circular, entonces la dirección de la velocidad relativa es perpendicular al radio de giro como dirección.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Método del polígono de velocidad

oscarrosete.com
oscarrosete.com
Al considerar dos puntos p y q de cualquier eslabón rígido en un mecanismo, la ecuación de velocidad entre dichos puntos quedará determinada de la siguiente manera:


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Método del polígono de velocidad

oscarrosete.com
oscarrosete.com
Si la ecuación fuera algebraica, entonces se requerirían dos datos (de tres) para su solución, pero como es una ecuación vectorial que posee magnitud y dirección por vector, entonces se requiere de cuatro datos (de seis) para su solución.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Método del polígono de velocidad

oscarrosete.com
oscarrosete.com
Las velocidades Vp y Vq se conocen como velocidades absolutas, y su magnitud y dirección dependen de los eslabones a los que se encuentran articulados.
Por otra parte, la velocidad relativa (Vp/q) puede calcularse mediante la expresión Vp/q=(ωp/q)(rp/q), ya que siempre es de trayectoria circular y, por tanto, perpendicular al radio de giro rp/q.


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
1. Identificar el dato conocido de velocidad, ya sea velocidad angular (por parte de un eslabón) o velocidad tangencial (por parte de un nodo).
2. Si se conoce la velocidad angular de un eslabón, establecer ecuaciones de puntos de la misma barra p y q que pertenezcan al mismo eslabón mediante:


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
3. La ecuación vectorial tendrá solución si se tienen como máximo dos incógnitas. Si se tienen más incógnitas, deberá establecerse otra ecuación que relacione el punto de interés con otro nodo del eslabón, del cual por lo menos se conozca su trayectoria.
Las incógnitas pueden ser la magnitud y(o) la dirección por cada vector; si la trayectoria del nodo es circular o rectilínea, entonces se dice que es conocida; de ser circular, será perpendicular al radio de giro; y si es rectilínea, será paralela a la línea de desplazamiento.

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
4. Se tiene un caso específico cuando se plantea la ecuación de velocidad de dos puntos de la misma barra en una manivela, ya que la velocidad en uno de sus nodos (Vp) es igual a la velocidad relativa del nodo vista desde el pivote Ox (Vp/Ox), el cual al estar siempre fijo es de magnitud nula:


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
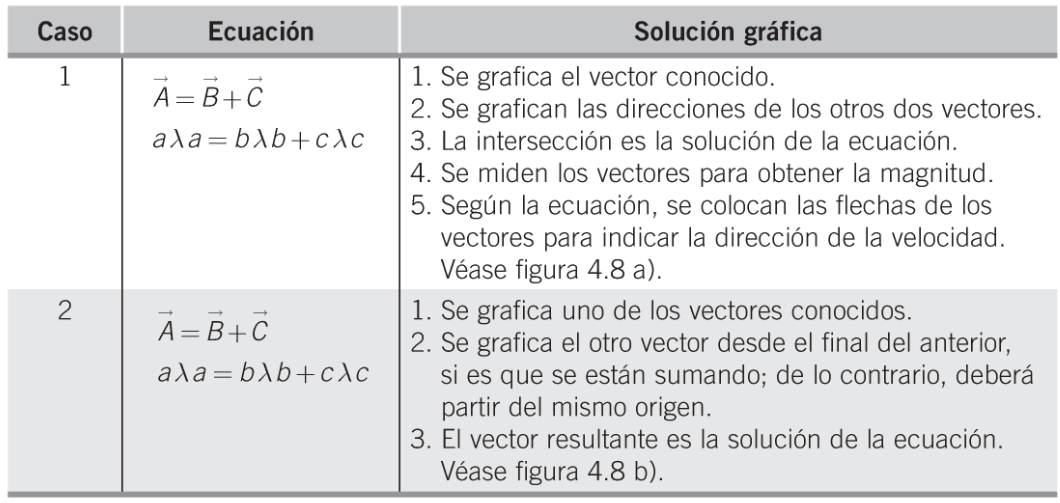
5. Resolver las ecuaciones vectoriales en el orden permitido. Una ecuación vectorial contiene vectores representados por magnitud y dirección, y tendrá solución solo si se tienen dos incógnitas.
Para la solución de la ecuación vectorial se pueden presentar dos opciones, como se muestra en la siguiente tabla

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com


Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Ejemplo

oscarrosete.com
oscarrosete.com
El mecanismo de la figura representa el diagrama cinemático de un mecanismo manivela-oscilador. La manivela 2 se mueve a una velocidad constante de 5 rad/s, cmr (en sentido contrario al movimiento de las manecillas del reloj).

Sem-7
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Ejemplo
oscarrosete.com
oscarrosete.com
Determinar la velocidad del centro de gravedad G de la biela 3 mediante el uso del método gráfico del polígono de velocidad.


Sem-7
oscarrosete.com
oscarrosete.com
Ejercicio de tarea
oscarrosete.com
oscarrosete.com
La barra AB del mecanismo de cuatro articulaciones de la figura gira con una velocidad angular w1 de 9 rad/s en sentido antihorario. Determine las velocidades angulares w2 y w3 de las barras BC y CD, en la posición mostrada




0.3
Sem-7
oscarrosete.com
oscarrosete.com
Ejercicio de refuerzo
oscarrosete.com
oscarrosete.com

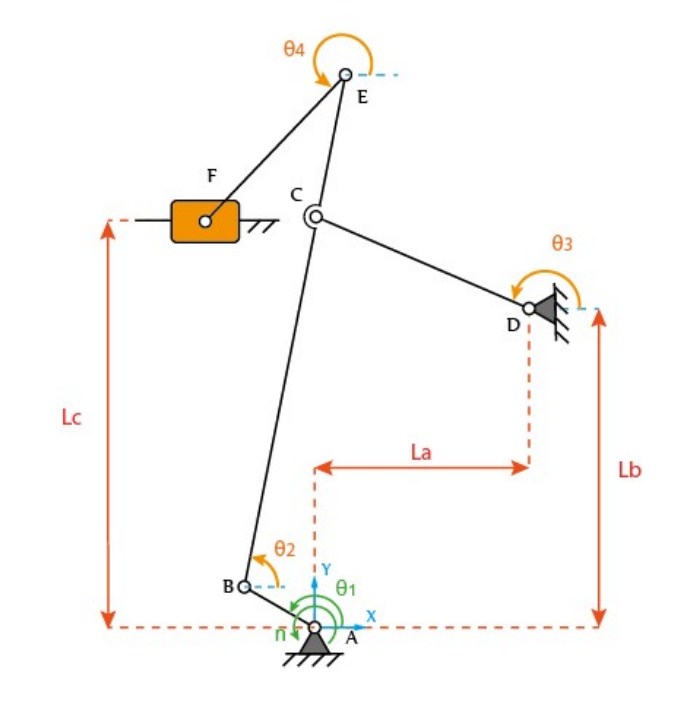
n= 10 rad/s
AB= 0.140 m
DC= 0.400 m
BC= 0.650 m
EF= 0.350 m
CE= 0.250 m.
Datos:
θ1=150
La= 0.370 m
Lb= 0.550 m
Lc= 0.700 m
Determine la totalidad de velocidades tangenciales y angulares
Sem-7

oscarrosete.com
oscarrosete.com
oscarrosete.com
oscarrosete.com
Para la cortadora manual mostrada en la figura use el método de velocidad relativa para determinar gráficamente la velocidad angular requerida del mango, para pasar la hoja de corte a través del metal a una velocidad de 3 mm/s. Calcule asimismo la velocidad lineal del punto X.
Sem-8



Ejercicios de aplicación
oscarrosete.com
oscarrosete.com
Ejercicios de aplicación
oscarrosete.com
oscarrosete.com
Para el mecanismo del limpiador del cristal trasero mostrado en la figura, use el método de velocidad relativa para determinar gráficamente la velocidad angular del brazo del limpiador, conforme la manivela gira a 40 rpm en sentido antihorario.



Sem-8
oscarrosete.com
oscarrosete.com
oscarrosete.com
oscarrosete.com
El dispositivo de la figura es un chapoteadero que se usa para lavar productos vegetales. Para la configuración mostrada, utilice el método de la velocidad relativa para determinar gráficamente la velocidad angular del tanque de agua, conforme la manivela es impulsada a 100 rpm en sentido antihorario.



Sem-8
Ejercicios de aplicación
oscarrosete.com
oscarrosete.com
oscarrosete.com
oscarrosete.com
La figura muestra un mecanismo triturador de rocas, se usa en una máquina donde se coloca una roca grande en una tolva vertical y cae hacia la cámara de trituración. las rocas del tamaño adecuado, que pasan a través de un cribador, se descargan por la parte inferior.
Determine la velocidad angular del ariete triturador, en la configuración mostrada, conforme la manivela gira a 120 rpm en sentido horario.

Sem-8
Ejercicios de aplicación

Agenda
oscarrosete.com

oscarrosete.com
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes
Sem-8
oscarrosete.com

oscarrosete.com
Levas
Una leva es un elemento común de un mecanismo que impulsa un componente aparejada conocida como seguidor.
Desde un punto de vista funcional, un arreglo de leva-seguidor es muy similar a los eslabonamientos estudiados previamente.
La leva acepta un movimiento de entrada parecido al de una manivela e imparte movimiento al seguidor.
Sem-8
oscarrosete.com

oscarrosete.com
Levas
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de levas
Hay una gran variedad de levas de compañías especializadas en su diseño y manufactura.
Los fabricantes clasifican las levas en subcategorías y las comercializan según las diferentes aplicaciones o configuraciones. No obstante, la gran mayoría de las levas se agrupan en los tres tipos generales siguientes:
- levas de placa
- leva cilíndrica
- leva lineal
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de levas
Levas de placa o de disco
Son el tipo de levas mas simples y comunes. Este tipo de leva se moldea sobre un disco o una placa. La distancia radial a partir del centro del disco varia a lo largo de la circunferencia de la leva. Si se hace que un seguidor se mueva sobre el extremo exterior, se proporciona al seguidor un movimiento radial.


Seguidor
Leva
Movimiento de la leva
Sem-8

Tipos de levas
Leva cilíndrica o de tambor
Esta clase de leva se moldea sobre un cilindro. Se corta una ranura en el cilindro con un emplazamiento variable a lo largo de su eje de giro. Enganchando un seguidor que se mueve en la ranura, se da al seguidor un movimiento a lo largo del eje rotación.
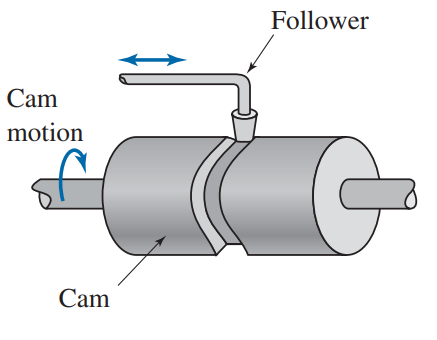

Seguidor
Leva
Movimiento de la leva
Barrel cam follower
oscarrosete.com
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de levas
Leva lineal
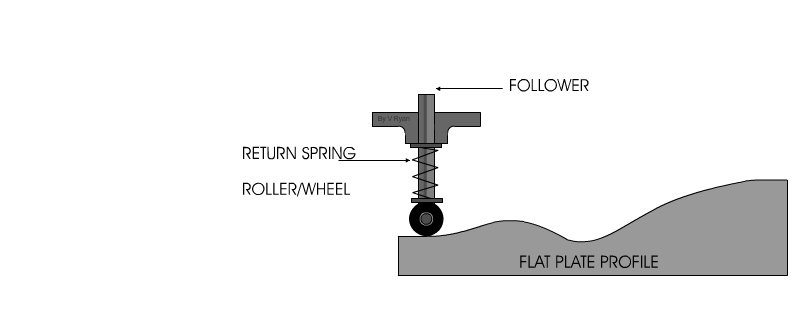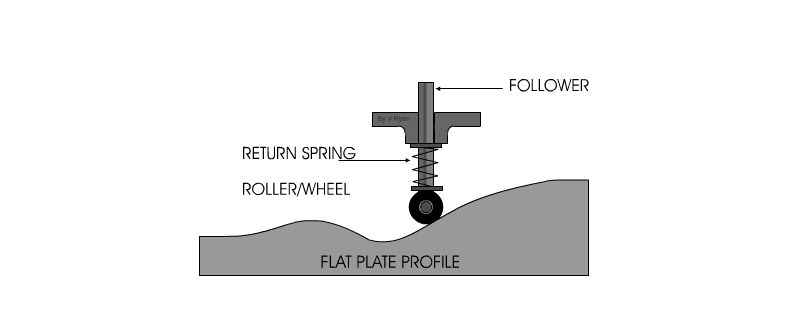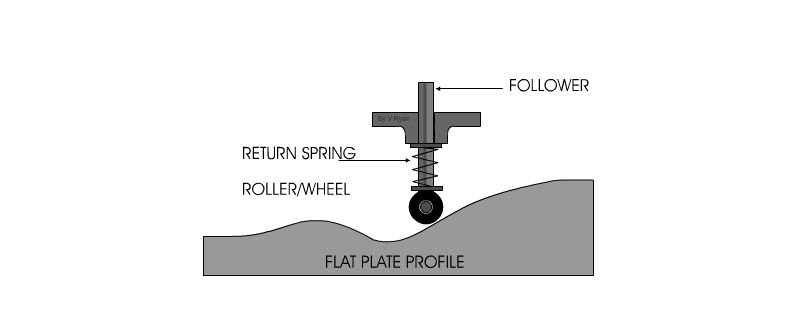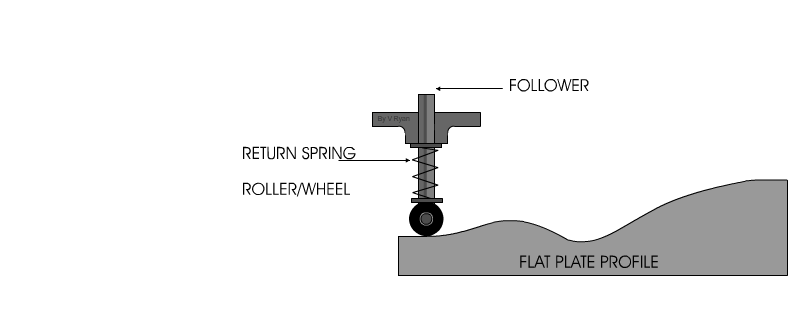
Este tipo de leva se moldea sobre un bloque de traslación. Se corta una ranura en el bloque con una distancia que varia desde el plano de traslación. Al sujetar un seguidor que se mueve en la ranura, se proporciona al seguidor un movimiento perpendicular al plano de traslación.

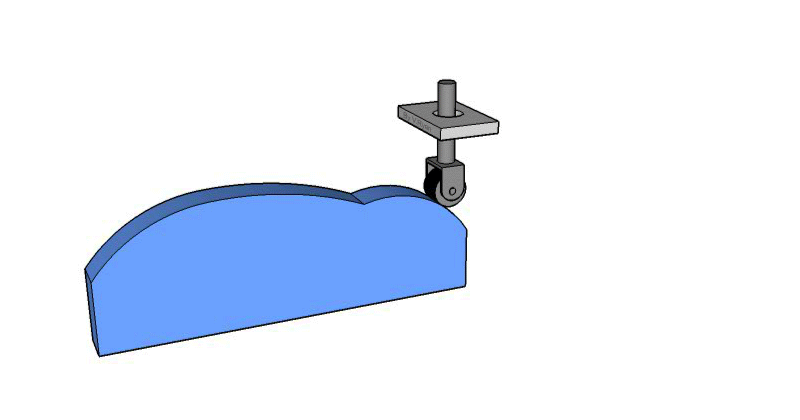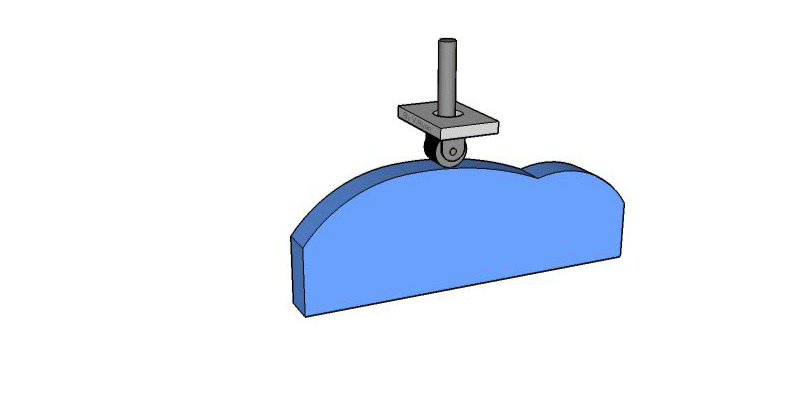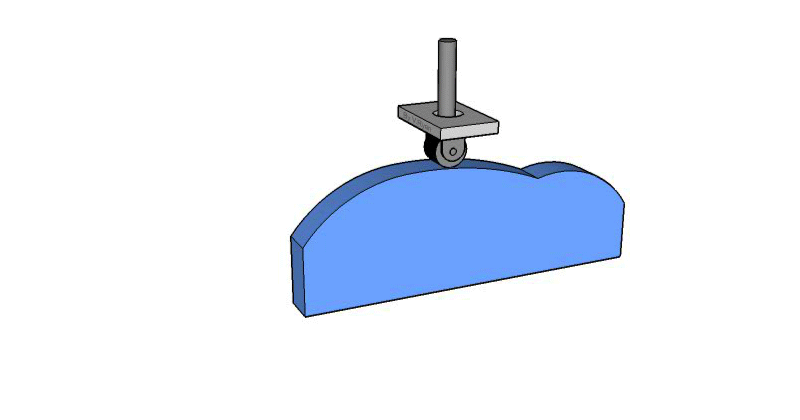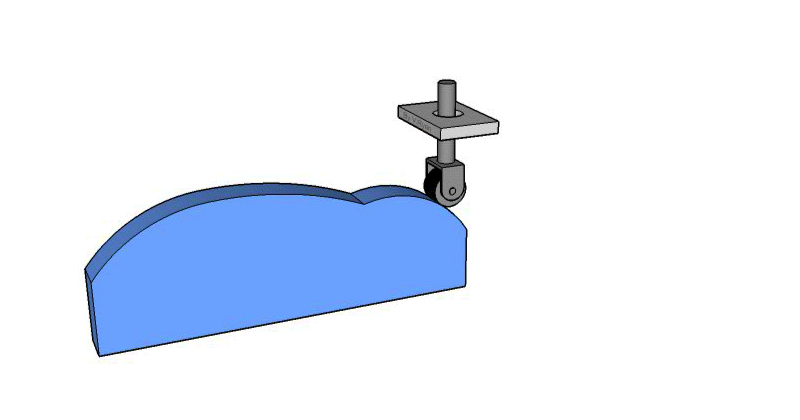
Flat Plate Cam/ Linear Cam
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Los seguidores se clasifican por su movimiento, su forma y su posición.
Movimiento del seguidor
El movimiento del seguidor se clasifica en las dos categorías siguientes:
- Seguidores de traslación
- Seguidores con brazo oscilante
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Los seguidores de traslación están restringidos a movimientos en linea recta.


Seguidor de cuña, en línea

Seguidor de cara plana, descentrado
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Los seguidores con brazo oscilante o con pivote están restringidos a movimiento giratorio


Seguidor de rodillo, con pivote
Seguidor de cara esférica, con pivote
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Posición del seguidor
La posición del seguidor, en relación con el centro de rotación de la leva, se ve afectada generalmente por los requerimientos de espacio de la máquina.
La posición de los seguidores de traslación se divide en dos categorías:
- Seguidor en línea
- Seguidor descentrado
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Seguidor en línea
Tiene movimiento en línea recta, de modo que la línea de traslación se extiende a través del centro de rotación de la leva

Seguidor de cuña, en línea
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Seguidor descentrado
La línea de movimiento no pasa por el centro de rotación de la leva.
En el caso de seguidores con pivote, no hay necesidad de distinguir entre seguidores en línea y descentrados, ya que tienen la misma cinemática

Seguidor de cara plana, descentrado
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Formas del seguidor
La forma del seguidor se agrupa en las cuatro categorias siguientes:
- seguidor de cuña
- seguidor de rodillo
- seguidor de cara plana
- seguidor de cara esférica

Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
El seguidor de cuña
Consiste en un seguidor formado por un punto, que se arrastra sobre el borde de la leva.
Es la forma más simple, pero el extremo puntiagudo produce altos esfuerzos de contacto y se desgasta rápidamente.

Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Seguidor de rodillo
Consiste en un seguidor que tiene una parte separada: el rodillo que esta sujeto a la espiga del seguidor.
El seguidor más comúmente utilizado.
Se puede atascar durante un desplazamiento abrupto de la leva.
Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
El seguidor de cara esférica
Consiste en un seguidor formado con un radio de la cara que entra en contacto con la leva

Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Seguidor de cara plana
consiste en un seguidor formado por una superficie grande y plana de contacto con la leva.

Sem-8
oscarrosete.com

oscarrosete.com
Tipos de seguidores
Estos dos tipos de seguidor se utiliza con un movimiento abrupto de la leva sin que se atasque.
Se puede combinar cualquier forma de seguidor con cualesquiera de sus movimientos o posición.

Sem-8
oscarrosete.com
oscarrosete.com
Competencia Individual leva de placa
- Identificar una aplicación de la leva de placa o de la leva lineal y documentarla en una presentación.
- Realizar su propio mecanismo planar donde se involucre una leva de placa, de preferencia que se alinea a la aplicación que ustedes definieron.
- Investigar diagramas "SVAJ", selección de funciones (conexión diagrama de desplazamiento) y ley fundamental del diseño de levas.
- Diseñar y explicar criterios de diseño utilizados en la presentación
El mejor proyecto individual tendrá puntuación adicional para el examen del segundo parcial.


Sem-8
oscarrosete.com
oscarrosete.com
Potencial
Sem-8

oscarrosete.com

oscarrosete.com
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes
Agenda
Sem-8
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

El diseño de levas es conocido comúnmente como diseño del perfil de leva, y consiste en la construcción de la geometría o la forma de la leva, que al estar en contacto con el seguidor produce un movimiento determinado y establecido en las condiciones del diseño.

Sem-8
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

Este diseño se logra al aplicar la cinemática inversa en el diagrama de desplazamiento del seguidor, esto se refiere a que, dadas las condiciones de diseño de movilidad del seguidor, se puede formar el diagrama de desplazamiento y después envolver dicho diagrama sobre una circunferencia.

Sem-8
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

El primer parámetro se conoce como círculo base, el cual se refiere a partir de dónde se construirá la geometría de la leva. El radio del círculo base rb está condicionado al tipo del seguidor y depende principalmente de los factores de espacio donde se montará la leva y de la afectación del ángulo de presión ejercido sobre el seguidor. Sin embargo, entre mayor sea el diámetro, mejor transmisión de fuerza se tendrá.

Sem-8
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

Considerando giro de leva en el sentido de las manecillas del reloj, los ejes de medición que determinan la posición inicial de la leva se iniciarán en el eje vertical positivo con respecto a un plano cartesiano. Enseguida, y debido al sentido del giro de la leva, los ángulos se medirán contra el movimiento de la leva, como se indica en la figura.

Sem-8
oscarrosete.com
oscarrosete.com
Etapas de diseño y elaboración



Módulo CamSim de Mekanize© para el diseño de perfil de leva.
Sem-8
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño
Diagrama de desplazamiento
El diagrama de desplazamiento de una leva, también conocido como tipo de movimiento del rodillo o parte del diagrama SVAJ , se refiere a la gráfica de comportamiento que genera la posición del seguidor en función de la posición de la leva.

Sem-8

oscarrosete.com
oscarrosete.com
Ejemplo

Elabore un diagrama de desplazamiento y determine la rapidez requerida de la leva cuando la secuencia del movimiento del seguidor es como sigue:
- Se eleva 2 in en 1.2 s
- Paro de movimiento durante 0.3 s
- Desciende 1 in en 0.9 s
- Paro durante 0.6 s
- Desciende 1 in en 0.9 s



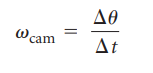
Sem-8
oscarrosete.com
oscarrosete.com
Ejercicios en clase

Elabore un diagrama de desplazamiento y determine la rapidez requerida de la leva cuando la secuencia del movimiento del seguidor es como sigue:
- Permanecer cerrado por 0.03 s
- Abrirse una distancia de 0.25 in, a partir de la posición cerrada, en 0.01 s
- Permanecer en posición abierta durante 0.002 s
- Moverse a la posición cerrada en 0.01 s
Sem-8
oscarrosete.com
oscarrosete.com

Motion:
The disc cam rotates at constant velocity transmitting the following uniform motion to the wedge shaped follower:
- Rises 15 mm during the first 60° of rotation
- Remains stationary for the next 90° of rotation
- Rises 20 mm for the next 60° of rotation
- Remains stationary for the 90° of rotation
- Return to the starting position to complete one revolution.

Ejercicios en clase
Sem-8
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño
Diagrama de desplazamiento
El diagrama de desplazamiento de una leva, también conocido como tipo de movimiento del rodillo o parte del diagrama SVAJ , se refiere a la gráfica de comportamiento que genera la posición del seguidor en función de la posición de la leva.

Sem-8
oscarrosete.com

oscarrosete.com
Levas
Sem-8
oscarrosete.com
oscarrosete.com
Competencia Individual leva de placa
- Identificar una aplicación de la leva de placa o de la leva lineal y documentarla en una presentación.
- Realizar su propio mecanismo planar donde se involucre una leva de placa, de preferencia que se alinea a la aplicación que ustedes definieron.
- Investigar diagramas "SVAJ", selección de funciones (conexión diagrama de desplazamiento) y ley fundamental del diseño de levas.
- Diseñar y explicar criterios de diseño utilizados en la presentación
El mejor proyecto individual tendrá puntuación adicional para el examen del segundo parcial.

Sem-8
oscarrosete.com
oscarrosete.com
Potencial


Sem-8
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento prescrito del seguidor
Como se ha indicado, la característica única de una leva es que imparte movimientos muy diferentes a su seguidor. Desde luego, el movimiento del seguidor depende de la tarea requerida y puede definirse con todo detalle.

Sem-8
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento prescrito del seguidor
Supongamos una leva utilizada para recolectar papel
- Permanecer cerrado por 0.03 s
- Abrirse una distancia de 0.25 in, a partir de la posición cerrada, en 0.01 s
- Permanecer en posición abierta durante 0.002 s
- Moverse a la posición cerrada en 0.01 s
En la realidad, los requerimientos del movimiento del seguidor se expresa en términos del desplazamiento angular de la leva en lugar del tiempo.
Sem-8
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento prescrito del seguidor
El mismo movimiento prescrito, establecido en términos de la rotación de la leva, se lista como sigue:
- Permanecer cerrado en 154.3° de rotación de la leva.
- Abrirse una distancia de 0.25 in, a partir de la posición cerrada, en 51.4° de rotación de la leva.
- Permanecer en posición abierta en 102.9° de rotación de la leva.
- Moverse a la posición cerrada en 51.4° de rotación de la leva.
Sem-8
oscarrosete.com
oscarrosete.com

Motion:
The disc cam rotates at constant velocity transmitting the following uniform motion to the wedge shaped follower:
- Rises 15 mm during the first 60° of rotation
- Remains stationary for the next 90° of rotation
- Rises 20 mm for the next 60° of rotation
- Remains stationary for the 90° of rotation
- Return to the starting position to complete one revolution.

Design walk-through/ workshop
Mar/25
oscarrosete.com
oscarrosete.com
Ejercicio de tarea


Se va a diseñar una leva para una parte de un cargador automático, como se muestra en la figura. Empleando las ecuaciones de movimiento, construya una tabla que ilustre los desplazamientos del seguidor contra el tiempo y contra la rotación de la leva.
También grafique estos datos cuando el movimiento prescrito de esta aplicación sea como sigue
Abr/1
oscarrosete.com
oscarrosete.com
Ejercicio de tarea

- Elevación de 50 mm en 1.5s con el esquema de movimiento de velocidad constante.
- Retorno en 2.0 s con el uso del esquema de movimiento cicloidal.
- Detención en 0.75 s.
- Se repite la secuencia

Abr/1

oscarrosete.com
oscarrosete.com
Ejemplo de diagrama de desplazamiento
- Elevación de 50 mm en 1.5s con el esquema de movimiento de velocidad constante.
- Retorno en 2.0 s con el uso del esquema de movimiento cicloidal
- Detención en 0.75 s.
- Se repite la secuencia

Abr/1

oscarrosete.com
oscarrosete.com
Ejercicio de tarea
Dos levas son utilizadas para controlar una pinza de sujeción en un sistema mecánico de manipulación de partes. Las dos levas pueden generar movimientos independientes horizontales y verticales al gripper. Estas máquinas pueden reubicar partes de manera similar a un robot manipulador con una fracción de su costo.
Abr/4



oscarrosete.com
oscarrosete.com
Ejercicio de tarea
Dibuje el diagrama de desplazamiento y el perfil de leva considerando que el movimiento prescrito para una de las levas es el siguiente:
1. Elevación de 1.5 in. en 1.5 s utilizando movimiento armónico
4. Permanecer 2 s.
3. Retorno en 1.5 s utilizando movimiento armónico
4. Permanecer 2 s.
5. Repetir la secuencia.
El radio del círculo base será de 3.5 in.

Abr/4

oscarrosete.com

oscarrosete.com
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes
Agenda
Sem-9
oscarrosete.com
oscarrosete.com
Competencia Individual leva de placa
- Identificar una aplicación de la leva de placa o de la leva lineal y documentarla en una presentación.
- Realizar su propio mecanismo planar donde se involucre una leva de placa, de preferencia que se alinea a la aplicación que ustedes definieron.
- Investigar diagramas "SVAJ", selección de funciones (conexión diagrama de desplazamiento) y ley fundamental del diseño de levas.
- Diseñar y explicar criterios de diseño utilizados en la presentación
El mejor proyecto individual tendrá puntuación adicional para el examen del segundo parcial.

Sem-9

oscarrosete.com
oscarrosete.com
Potencial

Sem-9
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

El diseño de levas es conocido comúnmente como diseño del perfil de leva, y consiste en la construcción de la geometría o la forma de la leva, que al estar en contacto con el seguidor produce un movimiento determinado y establecido en las condiciones del diseño.

Sem-9
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

Este diseño se logra al aplicar la cinemática inversa en el diagrama de desplazamiento del seguidor, esto se refiere a que, dadas las condiciones de diseño de movilidad del seguidor, se puede formar el diagrama de desplazamiento y después envolver dicho diagrama sobre una circunferencia.

Sem-9
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

El primer parámetro se conoce como círculo base, el cual se refiere a partir de dónde se construirá la geometría de la leva. El radio del círculo base rb está condicionado al tipo del seguidor y depende principalmente de los factores de espacio donde se montará la leva y de la afectación del ángulo de presión ejercido sobre el seguidor. Sin embargo, entre mayor sea el diámetro, mejor transmisión de fuerza se tendrá.

Sem-9
oscarrosete.com
oscarrosete.com
Nociones del diseño del perfil de leva

Considerando giro de leva en el sentido de las manecillas del reloj, los ejes de medición que determinan la posición inicial de la leva se iniciarán en el eje vertical positivo con respecto a un plano cartesiano. Enseguida, y debido al sentido del giro de la leva, los ángulos se medirán contra el movimiento de la leva, como se indica en la figura.

Sem-9
oscarrosete.com
oscarrosete.com
Etapas de diseño y elaboración



Módulo CamSim de Mekanize© para el diseño de perfil de leva.
Sem-9
oscarrosete.com
oscarrosete.com

Motion:
The disc cam rotates at constant velocity transmitting the following uniform motion to the wedge shaped follower:
- Rises 15 mm during the first 60° of rotation
- Remains stationary for the next 90° of rotation
- Rises 20 mm for the next 60° of rotation
- Remains stationary for the 90° of rotation
- Return to the starting position to complete one revolution.

Design walk-through/ workshop
Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Una vez que el movimiento del seguidor esta prescrito, es conveniente registrarlo en forma gráfica.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
El diagrama de desplazamiento de una leva, también conocido como tipo de movimiento del rodillo o parte del diagrama SVAJ , se refiere a la gráfica de comportamiento que genera la posición del seguidor en función de la posición de la leva.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
El eje horizontal representa el tiempo, medido en segundos, minutos, o bien, desplazamientos angulares de la leva, medidos en grados o en fracciones de una revolución.
El eje vertical representa el desplazamiento lineal.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
En el diagrama de desplazamiento no existe una función única que determine todo el comportamiento de la leva, ya que habrá subidas, bajadas, retenciones y aceleraciones.
El diagrama contiene tramos de funciones


Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
En dicha figura se muestran las funciones S1(θ), S2(θ),... Sn(θ), que denotan un tipo de movimiento del seguidor. Es importante hacer notar que existen diferentes tipos de movimiento estandarizados con sus ecuaciones representativas


Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
Los cuales para su estudio utilizan la siguiente nomenclatura, que se puede apreciar en la figura
- Intervalo de tiempo del sistema (Ti). Tiempo total en que ocurre el movimiento; es decir, Ti = Tf * To.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
- Ángulo inicial y final del movimiento de la leva (θ0,θf). Se refiere al ángulo en grados con el que inicia y termina el movimiento.
- Posición inicial y final del seguidor (S0,Sf). Se refiere al valor que determina la posición del seguidor al iniciar y terminar el movimiento.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
- Alzada del seguidor en la ventana del movimiento (Si). Esto indica la altura máxima alcanzada por el seguidor en el tramo de interés; es decir, Si=Sf-S0.
- Intervalo de rotación de la leva (Bi). Desplazamiento de Ia leva en grados en el tramo de interés; es decir, Bi=θf-θi.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
Si la leva se mueve a velocidad constante w, lo cual sucede en la mayoría de las aplicaciones, entonces para cada movimiento la relación entre el desplazamiento angular de la Bi de la leva y el tiempo en el cual ocurre Ti es:


Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
Sin embargo, el que la leva se mueva a velocidad constante no implica que el seguidor también lo hará. De hecho, el seguidor tendrá su propio movimiento, independientemente de que la leva se mueva a velocidad constante, ya que dicho movimiento lo define la geometría de la leva.


Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
A continuación se presentan las ecuaciones y los diagramas de desplazamiento de algunos de los movimientos típicos en el diseño de levas, las cuales están planteadas para un rango de valores desde 0 hasta bi con el uso de los siguientes parámetros:
- Velocidad constante de la biela: w.
- Variable de la posición angular en grados: θ.
- Variable del tiempo: t.
Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento a velocidad constante del seguidor
El movimiento más simple para un seguidor consiste en la elevación o el descenso a una velocidad constante, lo cual implica un desplazamiento proporcional y una aceleración nula, excepto en los extremos, donde la aceleración aparece con magnitudes infinitas, lo que presenta una desventaja para velocidades altas debido a que aparecen fuerzas inerciales.

Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento a velocidad constante del seguidor
Las ecuaciones cinemáticas de posición, velocidad y aceleración para este tipo de movimiento son:


Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento a velocidad constante del seguidor
Las ecuaciones cinemáticas de posición, velocidad y aceleración para este tipo de movimiento son:


Sem-9
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

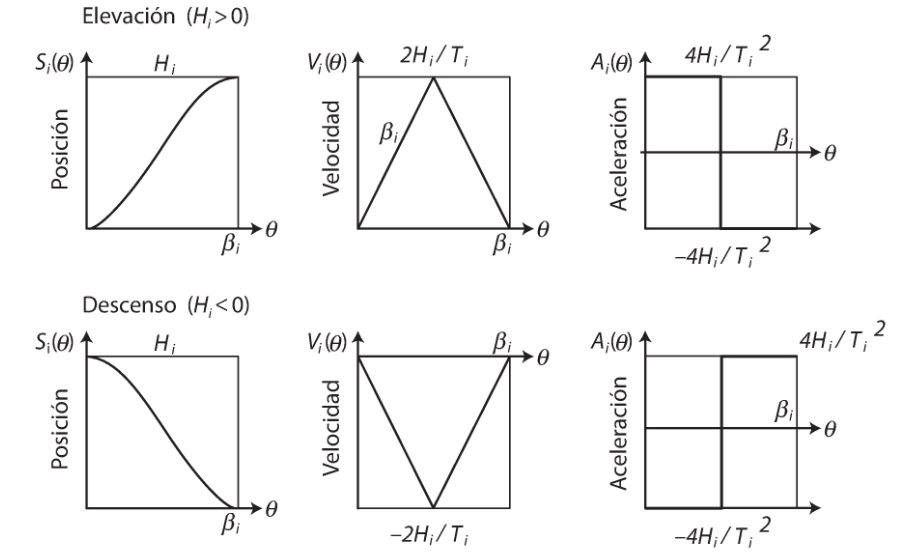
Movimiento parabólico
Las ecuaciones cinemáticas de posición, velocidad y aceleración para este tipo de movimiento son:


Sem-9
oscarrosete.com
oscarrosete.com
Ley fundamental de diseño de levas

Cualquier leva diseñada para operar a velocidades diferentes de las muy bajas debe diseñarse con las siguientes restricciones: La función de leva debe ser continua en la primera y segunda derivadas de desplazamiento a través de todo el intervalo (360 grados)


Movimiento armónico
Movimiento cicloidal
Sem-9
oscarrosete.com
oscarrosete.com
Ley fundamental de diseño de levas


Desplazamiento y aceleración medidos en el seguidor de una leva excéntrica

Sem-9
oscarrosete.com
oscarrosete.com
Etapas de diseño y elaboración
Sem-9
oscarrosete.com
oscarrosete.com
Diseño gráfico de perfil de una leva de disco

La forma más eficiente de describir la construcción de una leva con un seguidor de cuña es a través de la construcción real.
Para construir gráficamente un perfil de este tipo se dispone del siguiente procedimiento general:
- Traza el círculo base de radio Rb. El tamaño normalmente está en función de las restricciones espaciales de la aplicación.

Sem-9
oscarrosete.com
oscarrosete.com

- Dibujar el seguidor en la posición de entrada.
- Trazar líneas radiales del centro de la leva, en correspondencia con los ángulos de la leva identificados sobre el diagrama de desplazamiento. Para efectos de construcción, la leva permanecerá inmóvil y el seguidor girará en dirección opuesta al giro real de la leva.

Diseño gráfico de perfil de una leva
Sem-9
oscarrosete.com
oscarrosete.com

4. Transferir los desplazamientos del diagrama de desplazamiento a las líneas radiales. Estos desplazamientos se miden desde el círculo base.
5. Dibujar una curva suave a través de los desplazamientos prescritos.
6. Para construir un perfil con una precisión consistente con el diagrama de desplazamiento, es necesario transferir puntos intermedios adicionales de los intervalos de elevación y descenso.

Diseño gráfico de perfil de una leva
Sem-9
oscarrosete.com
oscarrosete.com


Diseño gráfico de perfil de una leva

Sem-9
oscarrosete.com
oscarrosete.com

Diseño gráfico de perfil de una leva
No es posible iniciar el diseño del perfil de una leva, sino hasta determinar primero el tipo de seguidor, así como la ubicación y el tamaño del círculo base.
Tales decisiones dependen normalmente de la magnitud de las fuerzas transmitidas y de los requerimientos de tamaño de la maquinaria impulsada por la leva.
Sem-9
oscarrosete.com
oscarrosete.com

Given information
- The detail of a wedge shaped follower for a disc cam in its starting position
- The cam shaft
- The minimum distance from the cam shaft centre to the cam profile
Specifications
Rotation: clockwise

Design walk-through/ workshop
Sem-9
oscarrosete.com
oscarrosete.com

Motion:
The disc cam rotates at constant velocity transmitting the following uniform motion to the wedge shaped follower:
- Rises 15 mm during the first 60° of rotation
- Remains stationary for the next 90° of rotation
- Rises 20 mm for the next 60° of rotation
- Remains stationary for the 90° of rotation
- Return to the starting position to complete one revolution.

Design walk-through/ workshop
Sem-9
oscarrosete.com
oscarrosete.com

Instructions
- Using a horizontal scale of 30° equal to 6 mm and a displacement scale 1:1 draw the displacement graph for the given motion.
- Label the displacement graph and include the scale.
- Project and draw the cam profile from the displacement graph.
- Show the direction of rotation on the cam profile.
- Hatch the shaft (closely spaced parallel lines)
- Show all necessary construction.

Design walk-through/ workshop
Sem-9
oscarrosete.com
oscarrosete.com
Walk-through reference
Sem-9
oscarrosete.com

oscarrosete.com
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes
Agenda
Sem-10
oscarrosete.com
oscarrosete.com
Competencia Individual leva de placa
- Identificar una aplicación de la leva de placa o de la leva lineal y documentarla en una presentación.
- Realizar su propio mecanismo planar donde se involucre una leva de placa, de preferencia que se alinea a la aplicación que ustedes definieron.
- Investigar diagramas "SVAJ", selección de funciones (conexión diagrama de desplazamiento) y ley fundamental del diseño de levas.
- Diseñar y explicar criterios de diseño utilizados en la presentación
El mejor proyecto individual tendrá puntuación adicional para el examen del segundo parcial.


Sem-10
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Diagrama de desplazamiento
A continuación se presentan las ecuaciones y los diagramas de desplazamiento de algunos de los movimientos típicos en el diseño de levas, las cuales están planteadas para un rango de valores desde 0 hasta bi con el uso de los siguientes parámetros:
- Velocidad constante de la biela: w.
- Variable de la posición angular en grados: θ.
- Variable del tiempo: t.
Sem-10
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento a velocidad constante del seguidor
El movimiento más simple para un seguidor consiste en la elevación o el descenso a una velocidad constante, lo cual implica un desplazamiento proporcional y una aceleración nula, excepto en los extremos, donde la aceleración aparece con magnitudes infinitas, lo que presenta una desventaja para velocidades altas debido a que aparecen fuerzas inerciales.

Sem-10
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento a velocidad constante del seguidor
Las ecuaciones cinemáticas de posición, velocidad y aceleración para este tipo de movimiento son:


Sem-10
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento a velocidad constante del seguidor
Las ecuaciones cinemáticas de posición, velocidad y aceleración para este tipo de movimiento son:


Sem-10
oscarrosete.com
oscarrosete.com
Criterios básicos de diseño

Movimiento parabólico
Las ecuaciones cinemáticas de posición, velocidad y aceleración para este tipo de movimiento son:


Sem-10
oscarrosete.com
oscarrosete.com
Ley fundamental de diseño de levas

Cualquier leva diseñada para operar a velocidades diferentes de las muy bajas debe diseñarse con las siguientes restricciones: La función de leva debe ser continua en la primera y segunda derivadas de desplazamiento a través de todo el intervalo (360 grados)


Movimiento armónico
Movimiento cicloidal
Sem-10
oscarrosete.com
oscarrosete.com
Ley fundamental de diseño de levas


Desplazamiento y aceleración medidos en el seguidor de una leva excéntrica

Sem-10
oscarrosete.com
oscarrosete.com

Motion:
The disc cam rotates at constant velocity transmitting the following uniform motion to the wedge shaped follower:
- Rises 15 mm during the first 60° of rotation
- Remains stationary for the next 90° of rotation
- Rises 20 mm for the next 60° of rotation
- Remains stationary for the 90° of rotation
- Return to the starting position to complete one revolution.

Design walk-through/ workshop
Sem-10
oscarrosete.com
oscarrosete.com
Ejercicio


Se va a diseñar una leva para una parte de un cargador automático, como se muestra en la figura. Empleando las ecuaciones de movimiento, construya una tabla que ilustre los desplazamientos del seguidor contra el tiempo y contra la rotación de la leva.
También grafique estos datos cuando el movimiento prescrito de esta aplicación sea como sigue
Sem-10
oscarrosete.com
oscarrosete.com
Ejercicio

- Elevación de 50 mm en 1.5s con el esquema de movimiento de velocidad constante.
- Retorno en 2.0 s con el uso del esquema de movimiento cicloidal.
- Detención en 0.75 s.
- Se repite la secuencia

Sem-10

oscarrosete.com
oscarrosete.com
Ejemplo de diagrama de desplazamiento
- Elevación de 50 mm en 1.5s con el esquema de movimiento de velocidad constante.
- Retorno en 2.0 s con el uso del esquema de movimiento cicloidal
- Detención en 0.75 s.
- Se repite la secuencia


Sem-10
oscarrosete.com
oscarrosete.com
Ejercicio en clase
Dos levas son utilizadas para controlar una pinza de sujeción en un sistema mecánico de manipulación de partes. Las dos levas pueden generar movimientos independientes horizontales y verticales al gripper. Estas máquinas pueden reubicar partes de manera similar a un robot manipulador con una fracción de su costo.


Sem-11

oscarrosete.com
oscarrosete.com
Dibuje el diagrama de desplazamiento y el perfil de leva considerando que el movimiento prescrito para una de las levas es el siguiente:
1. Elevación de 1.5 in. en 1.5 s utilizando movimiento armónico
4. Permanecer 2 s.
3. Retorno en 1.5 s utilizando movimiento armónico
4. Permanecer 2 s.
5. Repetir la secuencia.
El radio del círculo base será de 3.5 in.

Sem-11

Ejercicio en clase

oscarrosete.com
oscarrosete.com
Sem-11
Ejercicio en clase

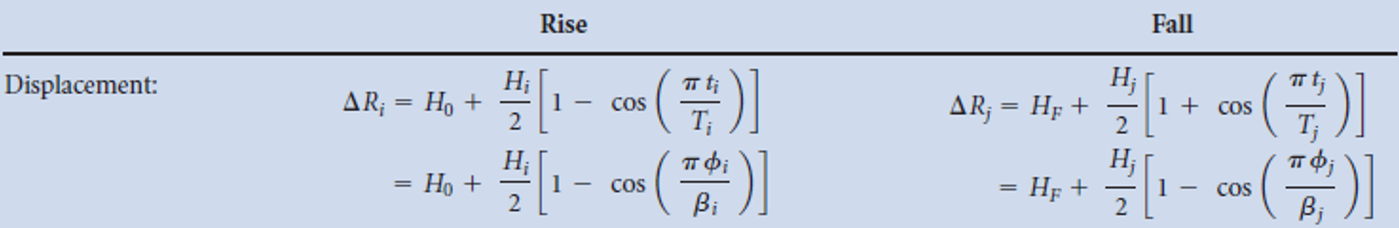


oscarrosete.com
oscarrosete.com
Ejercicio de tarea
Se usa una leva para impulsar un mecanismo que mueve una herramienta en un proceso automático de maquinado de tornillos.
- El seguidor de la leva se debe elevar hacia afuera 24 mm oon movimiento armónico en 0.2 s.
- Hacer una detención de 0.3 s.
- Descender 10 mm con movimiento armónico en 0.3 s.
- Hacer una detención de 0.2 s.
- Descender 14 mm con movimiento armónico en 0.2 s y, luego, repetir la secuencia.
Determine la velocidad requerida de la leva y elabore gráficamente el diagrama de desplazamiento del seguidor.
Sem-11


oscarrosete.com
oscarrosete.com
Ejercicio de repaso
Sem-11

El dispositivo de la figura es un chapoteadero que se usa para lavar productos vegetales. Para la configuración mostrada, utilice el método de la velocidad relativa para determinar gráficamente la velocidad angular del tanque de agua, conforme la manivela es impulsada a 50 rpm en sentido antihorario.

oscarrosete.com
oscarrosete.com
Ejercicio de repaso
Sem-11

En la figura se muestra un mecanismo triturador de rocas. Posicione gráficamente los eslabones en la configuración mostrada. Luego, reposicione los eslabones conforme la manivela gira 30° en el sentido horario.
Determine el desplazamiento angular resultante del ariete triturador.

75°
Agenda
oscarrosete.com
oscarrosete.com
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes

Sem-12
Cinématica de los engranes
Los engranes son ruedas dentadas cilíndricas que se usan para transmitir movimiento y potencia desde un eje giratorio hasta otro
No debemos confundir engrane con engranaje.
Engrane se refiere al elemento y engranaje al conjunto de elementos interconectados.

oscarrosete.com
Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
Un engrane es conductor/impulsor cuando inicia el movimiento y es conducido/impulsado si recibe el movimiento. Además, el engrane de menor diámetro se conoce comúnmente como piñón, mientras que el de mayor longitud se designa como rueda.


Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
Los dientes de un engrane conductor encajan con precisión en los espacios entre los dientes del engrane conducido


Sem-12
Cinématica de los engranes

oscarrosete.com
Sem-12
Cinématica de los engranes
Los dientes del impulsor empujan a los dientes del impulsado, lo cual constituye una fuerza perpendicular al radio del engrane. Con esto se transmite un par torsional, y como el engrane es giratorio también se transmite potencia

oscarrosete.com

Sem-12
oscarrosete.com
oscarrosete.com
Cinématica de los engranes
Con frecuencia se emplean engranes para producir un cambio en la velocidad angular del engrane conducido relativa a la del engrane conductor.
En la figura previa, el engrane superior menor, llamado piñón, impulsa al engrane inferior, mayor, que a veces se le llama simplemente engrane; el engrane mayor gira con más lentitud.


Sem-12
oscarrosete.com
oscarrosete.com
Cinématica de los engranes
La cantidad de reducción de velocidad depende de la relación del número de dientes en el piñón entre el número de dientes en el engrane mayor, de acuerdo con la relación siguiente:



Sem-12
oscarrosete.com
oscarrosete.com
Cinématica de los engranes
Considere que el piñón de la figura previa gira a 1800 rpm.
Se puede identificar que el número de dientes del piñón es 11, y en el engrane es 18.

Sem-12
oscarrosete.com
oscarrosete.com
Cinématica de los engranes
Entonces, se calcula la velocidad angular del engrane al despejar nG de la ecuación:


Sem-12
oscarrosete.com
oscarrosete.com
Cinématica de los engranes
Cuando existe una reducción de la velocidad angular del engrane, existe un incremento proporcional simultáneo en el par torsional del eje unido al engrane.
Se usan con frecuencia varios tipos de engranes que tienen distintas geometrías de diente.
Los tipos principales que se describirán serán: engranes rectos, helicoidales, cónicos y conjuntos de tornillo sinfín y corona.

Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Los engranes rectos tienen dientes rectos y paralelos al eje del árbol que los sostiene. La forma curva de las caras de los dientes de engranes rectos tiene una geometría especial, llamada curva involuta.

Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Con esta forma, es posible que dos engranes trabajen juntos con una transmisión de potencia uniforme y positiva.
En la figura se muestra la vista lateral de los dientes de engranes rectos, donde se aprecia con claridad la forma de la curva involuta en los dientes.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Los ejes que sostienen los engranes son paralelos.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Los dientes de los engranes helicoidales forman un ángulo con respecto al eje del árbol.
El ángulo se llama ángulo de hélice y puede ser virtualmente cualquier ángulo. Los ángulos típicos van desde unos 10 hasta unos 30°, pero son prácticos los ángulos hasta de 45°.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Los dientes helicoidales trabajan con más uniformidad que los dientes rectos, y los esfuerzos son menores.
En consecuencia, se puede diseñar un engrane helicoidal menor para determinada capacidad de transmisión de potencia, en comparación con los engranes rectos


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Una desventaja de los engranes helicoidales es que se genera una fuerza axial, llamada fuerza de empuje, además de la fuerza de impulsión que actúa tangente al cilindro básico sobre el que se disponen los dientes.
Debe considerar la fuerza de empuje al seleccionar cojinetes, para que sostengan al eje durante su operación.
Adicional se desgastan de manera más fácil que los engranes rectos debido a la naturaleza de sus dientes, los cuales pueden recibir un fuerte cambio de velocidad al inicar el contacto.

Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Los engranes cónicos tienen dientes colocados como elementos sobre la superficie de un cono. Los dientes de los engranes cónicos rectos parecen semejantes a los del engrane recto, pero tienen lados inclinados entre sí, son más anchos en el exterior y más estrechos hacia la parte
superior del cono.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
En forma típica, operan en ejes a 90° entre sí. En realidad, con frecuencia ésta es la causa para especificar engranes cónicos en un sistema de transmisión.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Cuando se fabrican los engranes cónicos con sus dientes formando un ángulo de hélice similar al de los engranes helicoidales, se les llama engranes cónicos espirales. Trabajan en forma más constante que los cónicos rectos, y pueden ser menores para determinada capacidad de transmisión de potencia.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Cuando ambos engranes cónicos en un par tienen el mismo número de dientes, se les llama engranes de inglete; sólo se usan para cambiar 90° la dirección del eje.
No existe cambio de velocidad.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes

Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Una cremallera es un engrane en línea recta que se mueve en línea, en vez de girar.
Cuando un engrane circular encaja en una cremallera, como se ve en el lado inferior derecho de la figura, a la combinación se le llama accionamiento por piñón y cremallera.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Un tornillo sinfín o gusano y su respectiva rueda sinfín trabajan en ejes que forman 90° entre sí. En el caso típico, tienen una relación de reducción de velocidad bastante grande, en comparación con otros tipos de engranes.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
El sinfín es el impulsor, y su corona es el engrane impulsado. Los dientes del sinfín parecen roscas de tornillo, y en realidad con frecuencia se les llama roscas y no dientes. Los dientes de la corona para el sinfín pueden ser rectos, como los dientes de engranes rectos, o pueden ser helicoidales.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranes
Con frecuencia, la forma del perfil de la punta de los dientes de la corona se agranda para envolver parcialmente las roscas del sinfín, y mejorar la capacidad de transmisión del conjunto.
Una desventaja de la transmisión con sinfín y corona es que tiene una eficiencia mecánica algo menor que la mayor parte de los demás tipos de engranes, porque tiene mucho contacto con frotamiento entre las superficies de las roscas del gusano y los lados de los dientes de la corona.

Sem-12
oscarrosete.com
oscarrosete.com
Actividad en equipos
En equipos realizar presentación a exponer el día Viernes 28 de Abril respecto al tipo de engrane asignado (duración máxima de 15 minutos)
- Características
- Ventajas, inconvenientes y aplicaciones.
- Explicación del proceso de diseño
Sem-12
oscarrosete.com
oscarrosete.com
Actividad en equipos
- Herringbone:
- Planetario:
- Sinfin-Corona:
- Cónicos:
- Helicoidales:
- Cremallera-piñon:
Sem-12

oscarrosete.com
oscarrosete.com
Actividad en equipos
Sem-12
Equipo 1: Alfredo González, Eric Siqueiros, Luis Rodriguez, Raul Velazquez
Equipo 2: Axel Juárez Melendrez, Daniel Murrieta García, Aristides González Pacheco Ronzón
Equipo 3: Rodrigo Vargas, José Acosta, Mireya Rodríguez
Equipo 4: Amalinalli Ruiz, Diana Vargas, Carlo Mendez, Luiz Ojeda del Cid
Equipo 5: Jose Manuel Gonzales, Carlos Quintero, Ederik Diaz, Mariana Mariscal
Equipo 6: Alfredo Santaella, Jesus de la Torre, Miguel Mendoza, Oscar Moreno

oscarrosete.com
oscarrosete.com
Actividad independiente
Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
Dos engranes se pueden unir para una transmisión solo si disponen del mismo paso diametral, por lo que para su análisis son considerados como dos ruedas, como se muestra en la figura


Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
Un engrane es conductor cuando inicia el movimiento y es conducido si recibe el movimiento. Además, el engrane de menor diámetro se conoce comúnmente como piñón, mientras que el de mayor longitud se designa como rueda.


Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
Para iniciar el estudio cinemático de un engranaje, considérese un engrane conductor con un radio del círculo de paso llamado rEi , que significa radio del engrane inicial, y un engrane conducido, con un radio llamado rEf .


Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
Si los dos engranes tienen el mismo paso diametral, entonces la relación de velocidad (Rv), según la teoría de centros instantáneos,
donde wEi y wEf son la velocidad angular de los engranes i y f, respectivamente, r es el radio del círculo de paso y N es el número de dientes.


Sem-12
oscarrosete.com
oscarrosete.com
Cinemática de engranes
La relación expresada en la ecuación se conoce como ley fundamental del engranaje, que expresa:
La relación de la velocidad angular entre elementos de una transmisión de engranes debe permanecer constante en toda la conexión.


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranajes y nomenclatura
Mientras que un engranaje o tren de engranes es una sucesión de dos o más engranes interconectados cuya función es efectuar un cambio de velocidad, torque o giro en forma constante, el conjunto de engranes interconectados y dentro de una caja recibe el nombre de caja de engranes, y los accesos a esta se denominan flecha o eje de entrada y flecha o eje de salida, respectivamente, como se muestra en la figura:


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranajes y nomenclatura
La relación cinemática del eje de salida vs. la relación cinemática y el eje de entrada (posición, velocidad o aceleración) recibe el nombre de relación del engranaje o valor del tren (e), que en función de la posición (θ), la velocidad (w) o la aceleración (a) angular se expresa como:



Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranajes y nomenclatura
Si en un engranaje la relación de transmisión es positiva, entonces no hay cambio de giro entre la flecha de entrada y salida, pero si es negativa indica un cambio de giro entre ambas flechas.
Además, si:


Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranajes y nomenclatura
En una caja de engranaje, el uso del término reductor o atenuador es relativo, ya que si en un sentido es reductor, en sentido opuesto será atenuador.
Es por eso que algunos fabricantes colocan una placa en la caja del engranaje en la que se indica la relación de la forma θent:θsal; por ejemplo, la relación 2:1 significa que por cada vuelta de entrada del lado izquierdo de la placa habrá una vuelta a la salida, es decir, e=1/2=0.5.

Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranajes y nomenclatura
Un tren de engranes es cualquier conjunto de dos o más engranes conectados. En un tren de engranes simple cada eje porta sólo un engrane, el ejemplo de dos engranes más básico se muestra en la figura





Sem-12
oscarrosete.com
oscarrosete.com
Tipos de engranajes y nomenclatura
Para obtener una relación de tren de más de 10:1 con engranes rectos, helicoidales o cónicos (o con cualquier combinación de los mismos) es necesario un tren de engranes del tipo compuesto (a menos que se utilice un tren epicíclico).
Un tren compuesto es aquel en el que por lo menos un eje tiene más de un engrane.
Éste será un arreglo en paralelo o en serieparalelo, en lugar de las conexiones en serie puras del tren de engranes simple

Sem-12
oscarrosete.com
oscarrosete.com
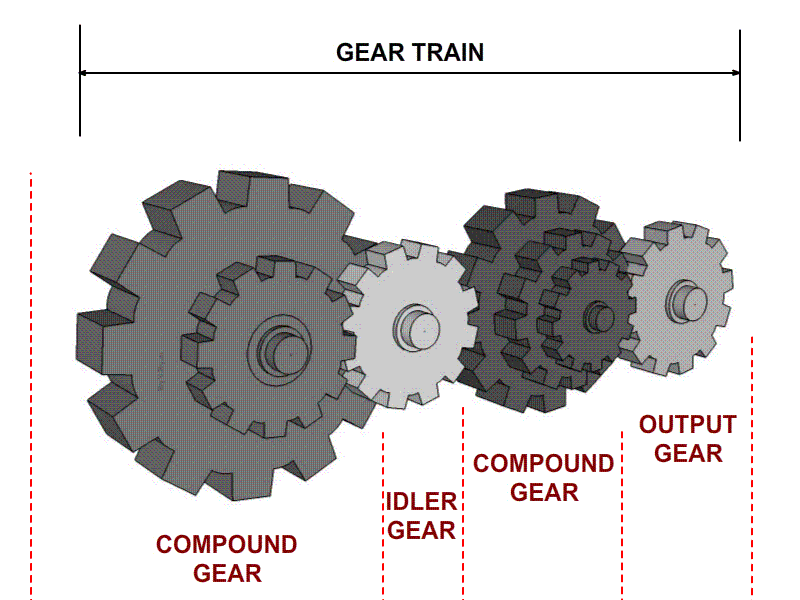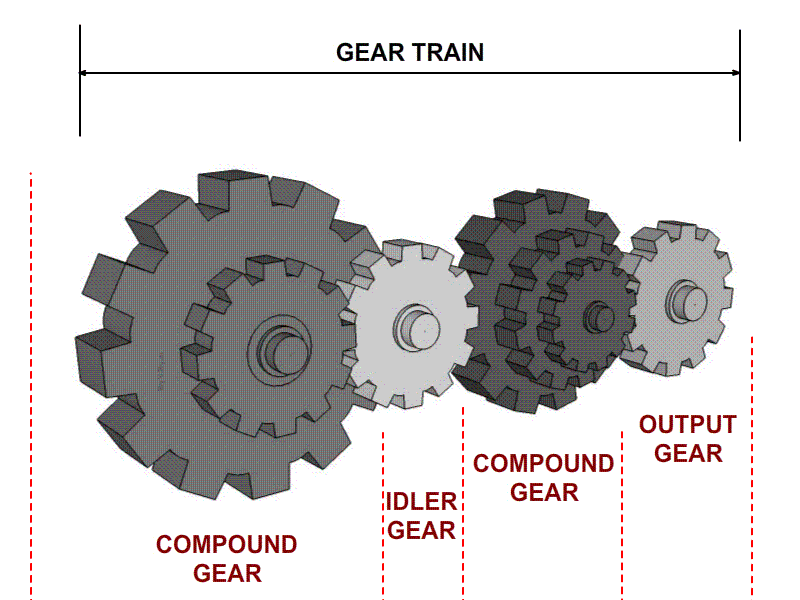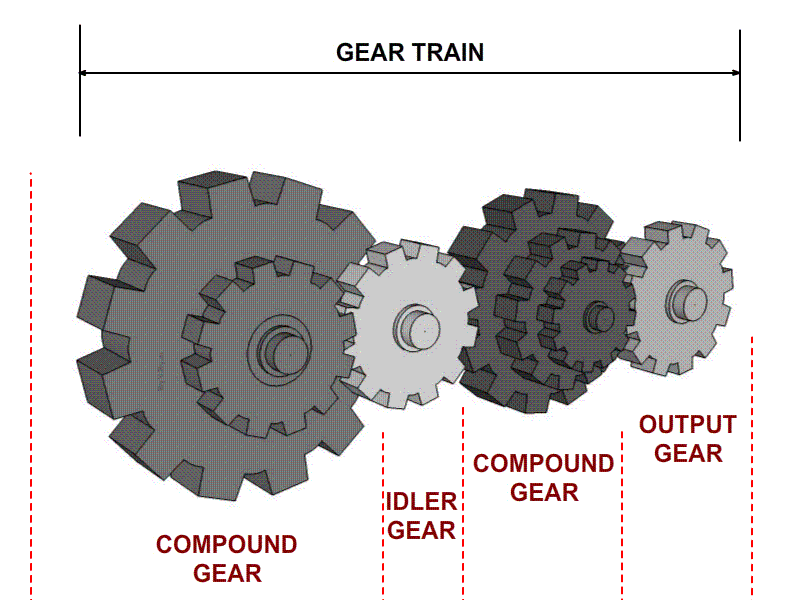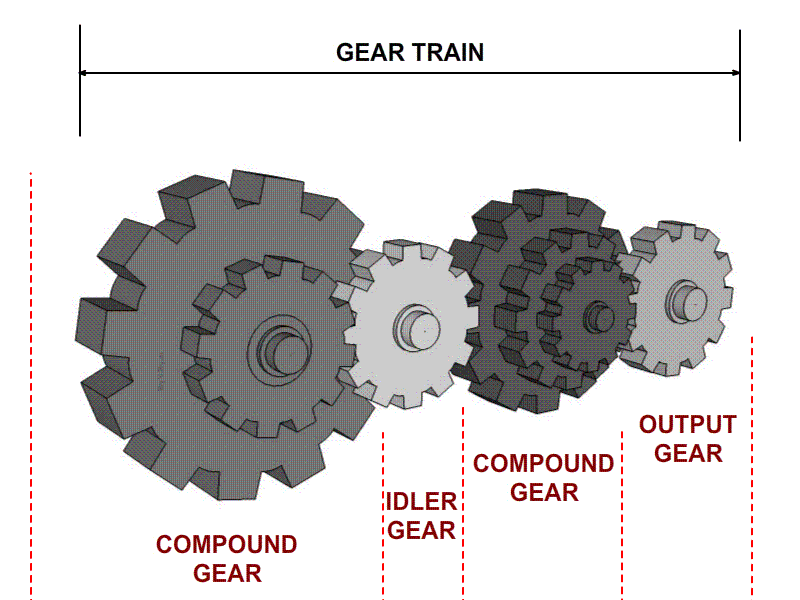
Tipos de engranajes y nomenclatura
Un tren compuesto es aquel en el que por lo menos un eje tiene más de un engrane.




Sem-12
oscarrosete.com
oscarrosete.com
Ejemplo de aplicación


Determine la velocidad y dirección de rotación de los engranes 4 y 6 si w1=5rad/s en sentido horario para el tren de engranajes mostrado abajo
Sem-12
oscarrosete.com
oscarrosete.com
Ejercicio alumno 1

Determine la velocidad y direccion de rotación del engrane 4 si w2=25 rad/s en sentido antihorario para el tren de engranajes mostrado abajo con Pd=20.

Sem-12

oscarrosete.com
oscarrosete.com
Ejercicio alumno 2
Un conjunto de engranes se utiliza para reducir la velocidad del eje de un motor eléctrico.
El engrane del eje de motor tiene un piñon con paso diametral de 10, tiene 15 dientes y trabaja a 1800 rpm sentido horario.
Determina la velocidad del engrane conectado que tiene 45 dientes. También calcula la velocidad en la linea de paso(ft/min).

Sem-12


oscarrosete.com
oscarrosete.com
Cinemática de engranes
Dos engranes se pueden unir para una transmisión solo si disponen del mismo paso diametral, por lo que para su análisis son considerados como dos ruedas, como se muestra en la figura


Sem-13
oscarrosete.com
oscarrosete.com
El círculo del que se derivan los perfiles evolventes de los dientes es denominado círculo base.

Terminología
Sem-13

oscarrosete.com
oscarrosete.com
Terminología

Diametro de paso
Es la dimensión principal del circulo que representa el tamaño del rodillo de fricción correspondiente que podría sustituir al engrane.
Tales rodillos equivalentes es muestran en la figura.


Sem-13
oscarrosete.com
oscarrosete.com

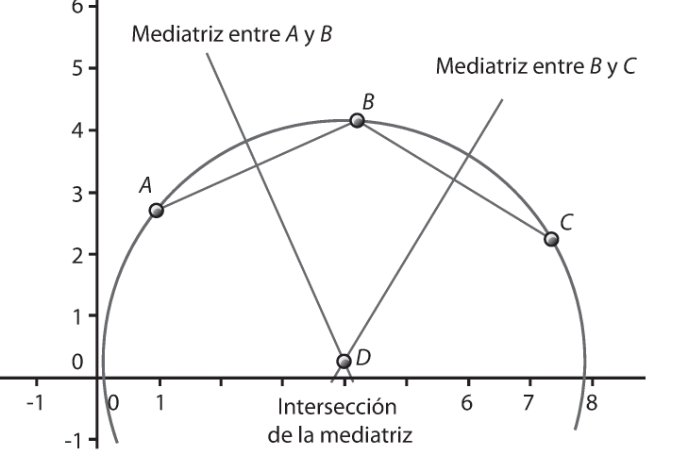
Cuando dos engranes se acoplan, sus círculos de paso son tangentes en el punto de contacto sobre la linea que une el centro de ambos círculos.
El punto de paso es el punto de contacto de los dos círculos de paso.


Terminología
Sem-13
oscarrosete.com
oscarrosete.com

El paso diametral Pd (dientes/pulg), o simplemente paso, se refiere en realidad al tamaño del diente, que se ha convertido en un estándar de especificación para el tamaño del mismo. Formalmente el paso diametral es el numero de dientes por pulgada del diámetro de paso.



Terminología
Sem-13
oscarrosete.com
oscarrosete.com

El paso de dos engranes engranados debe ser idéntico.

Terminología
Sem-13
oscarrosete.com
oscarrosete.com

La distancia entre centros C se define como la distancia de un centro a otro entre dos engranes acoplados, que también es la distancia entre los ejes que soportan los engranes.
Terminología
Sem-13

oscarrosete.com
oscarrosete.com

Ejemplo de aplicación
Sem-13

En la figura se muestra un tren de engranes.
Los engranes tienen las siguientes propiedades: N1=16 dientes y Pd=16; d2=8 in; N3=20 dientes; y N4=50 dientes. Determine la velocidad del engrane 4 cuando el engrane 1 impulsa a 1800 rpm.
oscarrosete.com
oscarrosete.com
En la figura se muestra un tren de engranes. Los engranes tienen las siguientes propiedades. Determine la velocidad angular del engrane 7 cuando el engrane 2 impulsa a 1800 rpm en sentido antihorario.
Sem-13
Ejemplo de aplicación (Tren Compuesto)


oscarrosete.com
oscarrosete.com
En la figura se muestra un tren de engranes. Los engranes tienen las siguientes propiedades: N2=15 dientes; N3 = 90 dientes y Pd = 16; N4 = 15 dientes; N5 = 75 dientes; N6 = 75 dientes y Pd = 12; N7 = 15 dientes; y N8 = 60 dientes y Pd = 8. Determine la velocidad del engrane 8 cuando el engrane 2 impulsa a 3600 rpm en sentido horario. Determine asimismo la
distancia entre centros de los engranes 2 y 8.
Sem-13
Ejercicio alumno 1


oscarrosete.com
oscarrosete.com
En la figura se ilustra el ventilador de escape de un engrane impulsado y la carcasa.
Para mejorar el flujo de aire la velocidad del ventilador necesita incrementarse a 460 rpm, o bien, acercarse a esta velocidad tanto como sea posible.
Se utilizará el motor existente de 3 hp que funciona a 1750 rpm. La carcasa no se deberla alterar, pues tiene un sistema de soporte con una distancia entre centros de 95 in. Seleccione un conjunto de engranes para esta aplicación.
Sem-13
Ejercicio alumno 2


oscarrosete.com
oscarrosete.com
Seleccione un conjunto de engranes para las siguientes aplicaciones (proponer distinto paso diametral para cada engrane):
500 rpm a 1500 rpm distancia entre centros de 4 in
500 rpm a 1000 rpm distancia entre centros de 3 in
500 rpm a 2500 rpm distancia entre centros de 2 in
Sem-13
Ejercicio alumno 2


oscarrosete.com
oscarrosete.com
Actividad en equipos
Son los encargados del diseño mecánico de robots velocistas, teniendo como principal meta la obtención de la velocidad máxima de salida en el eje de acoplamiento para las ruedas.


Sem-12
oscarrosete.com
oscarrosete.com
Actividad en equipos
La velocidad de entrada ubicada en el engrane motriz es de 11,000 rpm, el paso diametral de 48, cuenta con 12 dientes, angulo de presión de 20 y el diámetro de paso es de 1/4 de pulgada.
Torque de entrada 0.5 kg*cm
Buscamos lograr que el robot se mueva, con la mayor velocidad posible


Abr/18
oscarrosete.com
oscarrosete.com
Actividad en equipos
Equipo 1: Peso del robot: 1 kg , diámetro de llantas: 10 cm
Equipo 2: Peso del robot: 2 kg, diámetro de llantas: 8 cm
Equipo 3: Peso del robot: 3 kg, diámetro de llantas: 6cm
Equipo 4: Peso del robot: 4 kg, diámetro de llantas: 4 cm
Equipo 5: Peso del robot: 5 kg, diámetro de llantas: 2 cm
Abr/18

Agenda
oscarrosete.com
oscarrosete.com
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes

Sem-13
oscarrosete.com
oscarrosete.com
En la figura se muestra un tren de engranes. Los engranes tienen las siguientes propiedades: N2=15 dientes; N3 = 90 dientes y Pd = 16; N4 = 15 dientes; N5 = 75 dientes; N6 = 75 dientes y Pd = 12; N7 = 15 dientes; y N8 = 60 dientes y Pd = 8. Determine la velocidad del engrane 8 cuando el engrane 2 impulsa a 3600 rpm en sentido horario. Determine asimismo la
distancia entre centros de los engranes 2 y 8.
Sem-13
Ejercicio alumno 1


oscarrosete.com
oscarrosete.com
En la figura se ilustra el ventilador de escape de un engrane impulsado y la carcasa.
Para mejorar el flujo de aire la velocidad del ventilador necesita incrementarse a 460 rpm, o bien, acercarse a esta velocidad tanto como sea posible.
Se utilizará el motor existente de 3 hp que funciona a 1750 rpm. La carcasa no se deberla alterar, pues tiene un sistema de soporte con una distancia entre centros de 95 in. Seleccione un conjunto de engranes para esta aplicación.
Sem-13
Ejercicio alumno 2


oscarrosete.com
oscarrosete.com
En la figura se ilustra el ventilador de escape de un engrane impulsado y la carcasa.
Para mejorar el flujo de aire la velocidad del ventilador necesita incrementarse a 460 rpm, o bien, acercarse a esta velocidad tanto como sea posible.
Se utilizará el motor existente de 3 hp que funciona a 1750 rpm. La carcasa no se deberla alterar, pues tiene un sistema de soporte con una distancia entre centros de 95 in. Seleccione un conjunto de engranes para esta aplicación.
Sem-13
Ejercicio alumno 2


oscarrosete.com
oscarrosete.com
Procedure
1. Calculate the pitch diameter and draw pitch circles tangential to each other
In the example shown, the module has been selected as m=2.5, the number of teeth in the pinion 20, and in the gear 50. So dP=2.5x20=50 mm and dG=2.5x50=125mm.


Sem-13
oscarrosete.com
oscarrosete.com
Procedure
2. Draw a line perpendicular to the line of centres through the pitch point (this is the point of tangency of the pitch circles). Draw the pressure line at an angle equal to the pressure angle from the perpendicular. It is called the pressure line because the resultant tooth force is along this line during meshing. Here the pressure angle is 20°.


Sem-13
oscarrosete.com
oscarrosete.com
Procedure
3. Construct perpendiculars OPA and OGB to the pressure line through the centres of each gear.The radial distances of each of these lines are the radii of the base circles of the pinion and gear, respectively. Draw the base circles.


Sem-13
oscarrosete.com
oscarrosete.com
Procedure
4. Draw an involute curve on each base circle. This is illustrated on the gear. First divide the base circle in equal parts A0, A1, A2, A3, A4, A5,…,An. Construct radial lines OGA0,OGA1, OGA2,OGA3,…,OGAn.Construct perpendiculars to these radial lines. The involute begins at A0.


Sem-13
oscarrosete.com
oscarrosete.com
Procedure
4. The second point is obtained by measuring off the distance A0A1 on the perpendicular through A1.The next point is found by measuring off twice the distance A0A1 on the perpendicular through A2 and so on. The curve constructed through these points is the involute for the gear.The involute for the pinion is constructed in the same way on the base circle of the pinion.


Sem-13
oscarrosete.com
oscarrosete.com
Procedure
5. Calculate the circular pitch
The width of the teeth and the width of the spaces are equal to half the circular pitch. Mark these distances off on the pitch circles (p= pi x 2.5).



Sem-13
oscarrosete.com
oscarrosete.com
Procedure
6. Draw the addendum and dedendum circles for the pinion and gear. Here a tooth system has been selected with



Sem-13
oscarrosete.com
oscarrosete.com
Procedure
7. Mirror the involute profile about a line constructed using a distance half the tooth width along the pitch circle and the gear centre. Using a polar array generate all of the teeth for the gear. Construct the root fillets as appropriate. Construct the tooth top and bottom lands.


Sem-13
oscarrosete.com
oscarrosete.com
Final Result


Sem-13
oscarrosete.com
oscarrosete.com
Actividad independiente/ Práctica CAD #1
Siga los pasos mostrados en el siguiente video para realizar el diseño de dos engranes cilíndricos de dientes rectos.
En caso de no contar con software CAD, será aceptado de manera alternativa diseño gráfico manual y elaboración de prototipo.


Sem-13
oscarrosete.com
oscarrosete.com
Actividad independiente/ Práctica CAD #1

Sem-13


oscarrosete.com
oscarrosete.com
Requisitos básicos
Se debe hacer un reporte del ejercicio de laboratorio, que incluirá los siguientes elementos:
- Portada con nombre de la materia, nombre de la práctica, fecha de la práctica, nombre completo del estudiante con matrícula.
- Además el reporte debe contener:
- Introducción,
- Marco teórico
- Descripción de los engranes cilíndricos de dientes rectos
- Proceso de diseño
- Terminología básica utilizada
- Formulas utilizadas para cálculo de parámetros de interés
- Desarrollo
- Observaciones
- Conclusiones
- El reporte .doc, y el diseño deberá ser presentado en la actividad de blackboard en .zip o .rar con el formato Matricula1_PracticaN.

Sem-13
Agenda
oscarrosete.com
oscarrosete.com

Sem-14
Unidad 3: Síntesis de mecanismos
1.1 Introducción.
- Tipos de síntesis.
- Error estructural y error mecánico
1.2 Espaciado de los puntos de precisión en el diseño de mecanismos.
1.3 Diseño de un mecanismo de 4 barras articuladas.
- Generador de función.
- Para valores instantáneos de velocidad y aceleración.
- Para posiciones definidas en el acoplador.
1.4 Análisis del torque de inercia en rotores.
1.5 Par de salida de un motor.
Agenda
oscarrosete.com
oscarrosete.com
Unidad 4: Cinemática de las maquinas

4.1 Movimiento de una partícula.
- Lineal.
- Angular.
- Relativo.
4.2 Métodos de análisis de velocidad y aceleración.
- Análisis de velocidad y aceleración con matemáticas vectoriales.
- Centros instantáneos. Teorema de Kennedy.
- Componente de Coriolis de la Aceleración.
- Análisis cinemático mediante números complejos
Sem-14
Agenda
oscarrosete.com
oscarrosete.com
Unidad 5: Vibraciones mecánicas

5.1 Vibración natural.
5.2 Vibración forzada.
5.3 Transmisibilidad.
5.4 Amortiguación.
5.5 Rotación excéntrica de flechas.
- Frecuencia natural y velocidad crítica.
- Frecuencia natural de una flecha con varias masas.
- Flechas con diámetro variable.
- Velocidades críticas de mayor orden.
5.6 Vibraciones torsionales.
- Flechas escalonadas.
- Sistema de torsión con engranaje
Sem-14
oscarrosete.com
oscarrosete.com
Análisis vs Síntesis
La cinemática de mecanismos no consiste solo en el estudio de los movimientos, sino también en los métodos para crearlos.
El estudio de los movimientos en mecanismos se conoce como análisis de mecanismos o cinemática directa.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de mecanismos consiste en lo siguiente:
Dada la topología y las dimensiones del mecanismo, establecer y solucionar ecuaciones para determinar su posición, velocidad y(o) aceleración, mediante el uso de herramientas gráficas, analíticas y(o) computacionales. Esto es:


Análisis vs Síntesis
Sem-14
oscarrosete.com
oscarrosete.com
Por otro lado, la segunda parte del estudio de mecanismos consiste en los métodos necesarios para crearlos. Esta parte se conoce de manera más específica como síntesis de mecanismos o cinemática inversa y consiste en lo siguiente:
Dados los requerimientos cinemáticos en un proceso mecánico, determinar la topología y las dimensiones de un mecanismo para satisfacer las necesidades de diseño. Esto es:


Análisis vs Síntesis
Sem-14
oscarrosete.com
oscarrosete.com
Consideramos dos tipos de análisis de mecanismos.
El primero consiste en establecer las técnicas para el estudio cinemático y cinético de un mecanismo ya diseñado.
El segundo consiste en utilizar las técnicas utilizadas con antelación para validar los resultados de la síntesis cinemática.

Tipos de Análisis
Sem-14
oscarrosete.com
oscarrosete.com
Existen diferentes clasificaciones para el análisis de mecanismos:
- Topológico
- Cinemático
- Cinético

Tipos de Análisis

Sem-14
oscarrosete.com
oscarrosete.com
Topológico: Permite definir y clasificar a los mecanismos en función de sus componentes, comportamiento, conexiones, distribución y aplicaciones.
Cinemático: Consiste en establecer y solucionar las ecuaciones de posición, velocidad y aceleración de los elementos y conectores del mecanismo aislando el análisis de fuerzas.
Cinético: Determina el efecto de las fuerzas alrededor de los componentes y conectores de un mecanismo.

Tipos de Análisis
Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Un método gráfico alterno al método del polígono y que facilita el cálculo de velocidades se conoce con el nombre de centros instantáneos de velocidad (CIV), el cual permite determinar la ubicación de un nodo en el espacio plano de un mecanismo común para dos eslabones, ya sea articulados, en contacto o separados.
Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Un centro instantaneo de velocidad (CIV) es un nodo de ubicación instantánea que relaciona el movimiento relativo de un par de eslabones y común para ambos eslabones.
Un CIV es un nodo que puede existir o no de forma físico en un mecanismo, todas las uniones cinemáticas son un CIV.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Si un mecanismo dispone de n eslabones, entonces el número de centros instantáneos (NCI) es el número de combinaciones por par de eslabones.


Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Ya que un CIV es un nodo en el espacio de un mecanismo que relaciona o comunica dos de sus eslabones, es posible determinar velocidades angulares desconocidas a partir de velocidades angulares conocidas mediante la velocidad del nodo de contacto, la cual es una velocidad común para ambos eslabones.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Formas de determinar un CIV
Por observación
Un CIV se puede obtener por “simple observación”, ya que toda junta cinemática (como la de una articulación) es un CIV.
Estos CIV se denotan por Oij , donde i y j son los eslabones i y j.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por definición de velocidad
Al saber que una velocidad tangencial es perpendicular al radio de giro, entonces un nodo de rotación es un CIV que relaciona el eslabón M con el eslabón fijo 1, que se denota por C1M , el cual se puede obtener al prolongar e intersecar los radios de giro, como se muestra en la figura.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Siempre que se dispongan tres eslabones i, j y k en un mecanismo con movimiento relativo en un plano, existirán tres CIV sobre una línea en el espacio del mecanismo, denotados por Oij, Oik y Ojk, respectivamente.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Por ejemplo, si se asigna el elemento 1 al eslabón fijo, entonces los CIV de los eslabones 1, i, j se encuentran en la llamada línea de Kennedy, como se muestra en la figura.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Teorema de Kennedy: Siempre que se tengan tres elementos en movimiento coplanario, existirá sobre una línea, llamada Línea de Kennedy, la ubicación de los tres centros instantáneos que relaciona los tres elementos.

Sem-14
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Existe un artificio gráfico que permite determinar cualquier centro instantáneo en el plano de un mecanismo basado en el teorema de Kennedy, conocido como círculo de centros, el cual permite la construcción de líneas de Kennedy.

Sem-14
oscarrosete.com
oscarrosete.com
Ejercicio en clase

Determine las velocidades angulares y tangencial de las barras AB y corredera A, en la posición mostrada utilizando el método de centros instantáneos por definición de velocidad.
Sem-14

oscarrosete.com
oscarrosete.com

Análisis de velocidad centros instantáneos
Sem-14
oscarrosete.com
oscarrosete.com
Ejercicio de tarea
La barra AB del mecanismo de cuatro articulaciones de la figura gira con una velocidad angular w1 de 9 rad/s en sentido antihorario. Determine las velocidades angulares w2 y w3 de las barras BC y CD, en la posición mostrada utilizando el método de centros instantáneos por definición de velocidad.


0.3m
Sem-14

oscarrosete.com
oscarrosete.com

Síntesis y Análisis (systems thinking)
Sem-14
oscarrosete.com
oscarrosete.com
En el estudio de mecanismos es importante diferenciar los conceptos síntesis y diseño.
Así, en términos generales, la palabra diseño proviene del italiano (disegn) y significa lo por venir. Se refiere al procedimiento de búsqueda para formular una solución a un problema.
Por su parte, el término síntesis forma parte del diseño donde se proporciona la solución en una esencia ingenieril al problema de diseño.

Sem-15
Síntesis de mecanismos
oscarrosete.com
oscarrosete.com
De manera específica, el diseño de mecanismos consiste en proporcionar una solución total a una necesidad de movimiento sincronizado, automatizado o especializado.
La síntesis de mecanismos se refiere al uso de técnicas analíticas, gráficas y(o) computacionales para solucionar el problema de diseño, una vez que se ha especificado en lenguaje ingenieril o técnico.

Síntesis de mecanismos
Sem-15
oscarrosete.com
oscarrosete.com
En términos específicos del diseño de mecanismos, este se compone de una serie de etapas, que inicia desde el planteamiento de la necesidad en un lenguaje no técnico hasta la solución entregable.
Las etapas que comprende son:
1. Necesidad. En esta etapa se presenta la problemática a resolver en un lenguaje no necesariamente técnico.
2. Interpretación técnica. Aquí se plantea la necesidad a resolver en un lenguaje técnico o ingenieril.

Etapas de diseño
Sem-15
oscarrosete.com
oscarrosete.com
Las etapas que comprende son:
3. Estudio preliminar. En este punto se establece si la necesidad a resolver es factible, o bien si parte de esta lo es mediante la implementación de un mecanismo. Además, aquí se determina la necesidad del diseño como un requerimiento de diseño.
4. Soluciones existentes. Etapa que consiste en verificar si existen o no soluciones a los requerimientos de diseño, todo derivado de una investigación bibliográfica.
5. Planteamiento del problema. Se establecen el problema a resolver y las necesidades de diseño en términos de síntesis de mecanismos.

Etapas de diseño
Sem-15
oscarrosete.com
oscarrosete.com
Las etapas que comprende son:
6. Síntesis. Consiste en la utilización de técnicas o estrategias gráficas, analíticas y(o) computacionales para solucionar el problema de diseño. El resultado final es un tipo de mecanismo y sus dimensiones. Aquí primero se tiene que sintetizar el tipo de mecanismo y enseguida se hace una síntesis dimensional.
7. Posible replanteamiento. Si los resultados obtenidos por la síntesis no satisfacen las necesidades, o bien aparecen nuevos problemas, entonces se replantea la problemática y se buscan nuevas soluciones.

Etapas de diseño
Sem-15
oscarrosete.com
oscarrosete.com
Las etapas que comprende son:
8. Prototipo. Consiste en implementar el mecanismo en un modelo a escala, con el fin de verificar si el rango de error de implementación no afecta el resultado; además, aquí se determina el tipo de material y de uniones, entre otros aspectos.
9. Escalamiento. Reside en la construcción final del producto a su escala natural y con los componentes reales. Lo más seguro es que en esta etapa se establezcan nuevas necesidades relacionadas con la resistencia del material, el diseño de uniones, los componentes motrices, etcétera; no obstante, estas nuevas necesidades deberán solucionarse en otra etapa de diseño.

Etapas de diseño
Sem-15
oscarrosete.com
oscarrosete.com
Para solucionar problemas del diseño mecánico por medio de mecanismos se puede hacer uso de diferentes tipos de síntesis, entre los cuales se pueden mencionar los siguientes:
- Síntesis de tipo
- Síntesis dimensional
- Síntesis gráfica
- Síntesis analítica
- Síntesis basada en algoritmos computacionales
- Síntesis de generación de trayectorias
- Síntesis con puntos de precisión

Tipos de Síntesis
Sem-15
oscarrosete.com
oscarrosete.com
- Síntesis de tipo o de Reuleaux. Consiste en la elección de los tipos de eslabones y mecanismos a emplear (levas, engranajes, resortes, palancas) en la solución de problemas, en función de criterios de equivalencia y diversas cualidades de los mecanismos.
- Síntesis dimensional o de Burmester. Algunos reservan este nombre para las síntesis geométrico-planas que elaboró Burmester, consideraremos como síntesis dimensional al procedimiento para determinar las dimensiones de los elementos del mecanismo, las posiciones límites y las geometrías de las piezas y con un rendimiento específico.

Tipos de Síntesis
Sem-15
- Síntesis gráfica. Utiliza técnicas basadas en las propiedades geométricas del movimiento. Si bien las técnicas y los procedimientos que se usan en este tipo de síntesis pueden ser simples o metódicos, el resultado es una solución aproximada, debido a la incertidumbre en los trazos gráficos.
- Síntesis analítica. Se basa en la solución de un conjunto de ecuaciones cinemáticas y(o) cinéticas para satisfacer una serie de necesidades. Este tipo de síntesis utiliza ecuaciones de geometría analítica, álgebra vectorial y álgebra compleja, entre otros. Es más preciso que el de la síntesis gráfica, pues solo puede variar por errores de punto flotante.

Tipos de Síntesis
oscarrosete.com
Sem-15
- Síntesis basada en algoritmos computacionales. Utiliza técnicas modernas para solucionar problemas en los que el procedimiento gráfico y(o) analítico está limitado para dar una solución. Este tipo de síntesis se basa en algoritmos iterativos mediante el uso de una computadora. El resultado final de esta síntesis es un mecanismo aproximado que satisface restricciones más complejas que la síntesis gráfica o analítica.
- Síntesis de generación de trayectorias. Este tipo de síntesis afronta el problema de ubicar los puntos de las barras de un mecanismo a lo largo de trayectorias preestablecidas.

Tipos de Síntesis
oscarrosete.com
Sem-15
- Síntesis con puntos de precisión. Se denomina así a las síntesis exactas de un número finito de especificaciones, por ejemplo, la síntesis de generación de funciones con cinco puntos de precisión o la síntesis de generación de trayectorias con nueve puntos de precisión.

Tipos de Síntesis
oscarrosete.com
Sem-15
El proceso de síntesis comprende diversas etapas, entre las que destacan las siguientes:
- Recolección de información.
- Síntesis de tipo.
- Síntesis dimensional.
- Validación de resultados.
- Posible replanteamiento.

Etapas de la Síntesis
oscarrosete.com
Sem-15
1. Recolección de información. En esta etapa se recoge la información de la necesidad en lenguaje técnico, como dimensiones, limitantes y espacio de trabajo, entre otros.
2. Síntesis de tipo. Una vez que se tiene la información, se procede a la selección del tipo de mecanismo que permita dar solución a la necesidad.
3. Síntesis dimensional. Luego de definir el tipo de mecanismo, lo siguiente es dimensionar los elementos con el uso de técnicas de síntesis analíticas, gráficas y computacionales.

Etapas de la Síntesis
oscarrosete.com
Sem-15
4. Validación de resultados. Etapa que consiste en validar si la solución obtenida por la síntesis dimensional satisface los requerimientos, además de validar si el mecanismo no se va a agarrotar. Esto se logra mediante las técnicas de análisis vistas en los capítulos anteriores y(o) mediante el uso de software especializado.
5. Posible replanteamiento. En caso de que surjan problemas en el paso anterior, se procede a plantear una nueva solución, la cual puede iniciar desde cambiar el tipo de mecanismo.

Etapas de la Síntesis
oscarrosete.com
Sem-15
En la síntesis cinemática por lo común se plantean los siguientes tipos de tareas:
1. Generación de función.
2. Generación de trayectoria.
3. Generación de movimiento.

Tareas de la Síntesis
oscarrosete.com
Sem-15
En la tarea de generación de función, la síntesis consiste en establecer una relación entre la posición de un eslabón de un mecanismo (por lo general el eslabón de salida), con respecto a la posición del eslabón de entrada mediante una función específica y=f(x), donde y es la posición del eslabón de salida y x es la posición del eslabón de entrada.

Tareas de la Síntesis
oscarrosete.com
Sem-15
Para comprender mejor la tarea de generación de función imagínese un mecanismo dentro de una caja negra, la cual dispone de dos perillas, una para mover el elemento de entrada y otra que muestra la posición del elemento de salida, como las que se muestra en la figura, entonces la posición de la perilla de salida estará en función de la posición de la perilla de entrada.

Tareas de la Síntesis
oscarrosete.com

Sem-15
La generación de trayectoria consiste en sintetizar un mecanismo para controlar la trayectoria de un nodo de uno de sus eslabones (generalmente de un acoplador) para que siga una trayectoria específica. Por lo general, esta tarea se logra mediante la implementación de un mecanismo de al menos cuatro barras, donde un punto del acoplador traza una trayectoria específica.

Tareas de la Síntesis
oscarrosete.com

Sem-15
Generación de movimiento
La tarea de generación de movimiento, también conocida como guiado de sólido, se define como el control del movimiento de una línea perteneciente a un sólido rígido en un plano.

Tareas de la Síntesis
oscarrosete.com

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis

Síntesis de dos posiciones
La síntesis de dos posiciones se subdivide en dos categorías:
- salida de balancín (rotación pura) y
- salida de acoplador (movimiento complejo).

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis

Salida balancín
Dos posiciones con desplazamiento angular
Mecanismo de Grashof (clase I): s+l<p+q
Puede dar vueltas completas

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Dos posiciones con desplazamiento complejo
Mecanismo de Grashof (clase I): s+l<p+q
Puede dar vueltas completas


Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Dos posiciones con desplazamiento complejo
Problema:
Diseñe un eslabonamiento de cuatro barras para mover el eslabón CD de la posición C1D1 a C2D2.

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Solución:
- Dibuje el eslabón CD en sus posiciones deseadas C1D1 y C2D2 como se muestra en el plano.
- Trace líneas de construcciones del punto C1 a C2 y del punto D1 a D2.
- Bisecte la línea C1C2 y la línea D1D2 y extienda sus bisectrices perpendiculares hasta intersectar a O4. Su intersección es el rotopolo.
- Seleccione un radio conveniente y trace un arco alrededor del rotopolo para cortar ambas líneas O4C1 y O4C2.
Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Rotopolo
Algunas técnicas para la síntesis cinemática se basan en la ubicación de un centro de giro para algunos nodos en el plano cartesiano llamado rotopolo, el cual puede determinarse mediante la definición de una circunferencia, de modo que en un plano cartesiano un solo nodo puede pertenecer a una familia infinita de circunferencias, cuyo centro de giro puede ubicarse en cualquier coordenada del plano cartesiano.

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Rotopolo
Por su parte, dos puntos en el plano cartesiano pueden pertenecer a una familia infinita de circunferencias, pero el centro de giro se limita sobre una línea recta, como se muestra en la figura

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Rotopolo
Sin embargo, tres puntos en el plano cartesiano pertenecen solo a una circunferencia, como se muestra en la figura

Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Rotopolo
Para los casos en los que se desea determinar el rotopolo para dos puntos de precisión en un plano, puede obtenerse mediante el trazo de la mediatriz entre estos dos puntos; luego, sobre la mediatriz se selecciona un punto arbitrario que será el centro de la circunferencia que pasará por los dos puntos.
Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Rotopolo
Por último, cuando se dispone de tres puntos de precisión (A, B, C ) en el plano, solo existe una coordenada de posición para el rotopolo, el cual puede obtenerse al intersecar las rectas de la mediatriz de AB y de BC, como se muestra en la figura
Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Solución:
- Marque las intersecciones como B1 y B2.
- Replique el procedimiento visto para síntesis de dos posiciones con desplazamiento angular.
- Elabore un modelo del mecanismo y ármelo para comprobar su funcionamiento y sus ángulos de transmisión.
Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Dos posiciones con desplazamiento complejo
Mecanismo de Grashof (clase I): s+l<p+q
Puede dar vueltas completas


Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Dos posiciones con desplazamiento complejo
Mecanismo de Grashof (clase II): s+l>p+q


Sem-15
oscarrosete.com
oscarrosete.com

Ejemplos de Síntesis
Salida balancín
Dos posiciones con desplazamiento complejo
Mecanismo no Grashof (clase II): s+l>p+q
Triple balancín


Página 93
Sem-15
oscarrosete.com
oscarrosete.com
Síntesis de mecanismos

Sem-15
oscarrosete.com
oscarrosete.com
Síntesis de mecanismos
Ejercicio en clase
Siga los pasos mostrados en el vídeo para realizar la síntesis de dos posiciones con un mecanismo clase II.
Seleccionar dimensiones distintas a las vistas en el vídeo.


Sem-15
oscarrosete.com
oscarrosete.com
Síntesis de mecanismos
Ejercicio en clase
Siga los pasos mostrados en el sitio web para realizar la síntesis de un mecanismo de doble balancin.
Seleccionar dimensiones distintas a las vistas en el sitio web.

Sem-15
Agenda
oscarrosete.com
oscarrosete.com
Abr/22
Levas, con diferentes tipos de seguidores.
Bases del diseño de levas
Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
Engranajes Cónicos.
Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes

oscarrosete.com
oscarrosete.com
Tipos de engranes
El perfil de diente que más se usa en los engranes rectos es la forma involuta de profundidad total.
La involuta es uno de los tipos de curvas geométricas llamadas curvas conjugadas. Cuando dos dientes con esos perfiles engranan y giran, existe una relación constante de velocidad angular entre ellos.


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
Desde el momento del contacto inicial hasta el desengrane, la velocidad del engrane motriz está en una proporción constante respecto a la del engrane conducido.

Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
La acción que resulta en los dos engranes es muy uniforme.
Si no fuera así, habría algo de aceleraciones y desaceleraciones durante el engrane y desengrane, y las aceleraciones resultantes causarían vibración, ruido y oscilaciones torsionales peligrosas en el sistema.


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
Se puede visualizar con facilidad una curva de involuta al tomar un cilindro y enredarle un cordón alrededor de su circunferencia. Amarre un lápiz en el extremo del cordón, y después comience con el lápiz apretado contra el cilindro, con el cordón tenso. Mueva el lápiz y aléjelo del cilindro, mientras mantiene tenso el cordón. La curva que trazará será una involuta.


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
El círculo que representa el cilindro se llama círculo base. Observe que en cualquier posición de la curva, el cordón representa una línea tangente al círculo base y, al mismo tiempo, el cordón es perpendicular a la involuta.


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
Si dibuja otro círculo base en la misma línea de centro, en una posición tal que la involuta que resulte sea tangente a la primera, demostrará que en el punto de contacto las dos rectas tangentes a los círculos base coinciden, y se mantendrán en la misma posición a medida que giren los círculos base. Eso es lo que sucede
cuando están engranados dos dientes de engrane


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
Un principio fundamental de la cinemática, el estudio del movimiento, es que si la recta trazada perpendicular a las superficies de dos cuerpos en rotación, en el punto de contacto, siempre cruza la línea entre los dos cuerpos en el mismo lugar, entonces la relación de velocidad angular de los dos cuerpos será constante.


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes
Es un enunciado de la ley de engrane. Los dientes de engranes que tienen la forma de involuta siguen esta ley.
Naturalmente, sólo la parte del diente del engrane que realmente se pone en contacto con su diente correspondiente, es la que debe tener la forma de involuta.


Abr/22
oscarrosete.com
oscarrosete.com
Tipos de engranes



Los términos y símbolos se apegan, en inglés, a las normas de la American Gear Manufacturers Association (AGMA)
Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Diametro de paso
Es la dimensión principal del circulo que representa el tamaño del rodillo de fricción correspondiente que podría sustituir al engrane.
Tales rodillos equivalentes es muestran en la figura.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Cuando dos engranes se acoplan, sus círculos de paso son tangentes en el punto de contacto sobre la linea que une el centro de ambos círculos.
El punto de paso es el punto de contacto de los dos círculos de paso.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

El paso circular p es la distancia medida a lo largo del circulo de paso de un punto sobre un diente al punto correspondiente, en el diente adyacente del engrane.
El paso circular se calcula a partir del numero de dientes y el paso diametral del engrane.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Es una longitud de arco, por lo general en pulgadas. Para calcular el valor del paso circular, se toma la circunferencia del círculo de paso y se divide en un número de partes iguales, que corresponde al número de dientes del engrane.
El paso de dos engranes engranados debe ser idéntico.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

El paso diametral Pd (dientes/pulg), o simplemente paso, se refiere en realidad al tamaño del diente, que se ha convertido en un estándar de especificación para el tamaño del mismo. Formalmente el paso diametral es el numero de dientes por pulgada del diámetro de paso.



Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Como tal, sus unidades son pulgadas -1. Sin embargo, casi nunca se indican las unidades, y a los engranes se les indica como paso 8 o paso 20, por ejemplo. Una de las ventajas del sistema de paso diametral es que hay una lista de pasos normalizados, y la mayor parte de los pasos tienen valores enteros.
A los de paso 20 o mayor se les llama paso fino y los de paso 20 o menor, paso grueso.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Como tal, sus unidades son pulgadas -1. Sin embargo, casi nunca se indican las unidades, y a los engranes se les indica como paso 8 o paso 20, por ejemplo. Una de las ventajas del sistema de paso diametral es que hay una lista de pasos normalizados, y la mayor parte de los pasos tienen valores enteros.
A los de paso 20 o mayor se les llama paso fino y los de paso 20 o menor, paso grueso.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

La tolerancia (clearance), c, es la cantidad en la cual el dedendo excede al adendo. Este es el espacio superior del diente del engrane y la parte inferior del diente del engrane acoplado.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

El módulo también es una medida relativa del tamaño del diente y, en teoría, el reciproco del paso diametral, utilizada en el SI de unidades definida como la razón entre el diámetro de paso y el numero de dientes de engrane.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

El adendo es la distancia radial del circulo de paso a la parte superior del diente del engrane.
El dedendo es la distancia radial del circulo de paso a la parte inferior del diente del engrane.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Espesor del diente (t): Es la longitud del arco, medida en el círculo de paso, de un lado de un diente al otro lado. A veces a esto se le llama espesor circular y su valor teórico es la mitad del paso circular.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Espacio entre dientes: Es la longitud de arco, medida desde el lado derecho de un diente hasta el lado izquierdo del siguiente. Teóricamente, es igual al espesor del diente, pero por razones prácticas, se hace mayor

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Juego: Si el espesor del diente se hiciera idéntico al valor del espacio entre dientes, como lo es en teoría, la geometría del diente debería tener una precisión absoluta para que funcionaran los dientes, y no habría espacio para lubricar las superficies de los dientes. Para resolver estos problemas, los engranes prácticos se fabrican con el espacio entre dientes, un poco mayor que el espesor del diente, y a la diferencia se le llama juego.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

La magnitud del juego depende de la precisión deseada en el par de engranes, y del tamaño y el paso de ellos. En realidad, es una decisión de diseño para balancear el costo de producción y el funcionamiento deseado. La American Gear Manufacturers Associaton (AGMA) emite recomendaciones del juego en sus normas

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

El ángulo de presión es el que forma la tangente a los círculos de paso y la línea trazada normal (perpendicular) a la superficie del diente del engrane
A veces, a esta línea normal se le llama línea de acción. Cuando dos dientes están engranados y transmiten potencia, la fuerza que pasa del diente del engrane motriz al del conducido actúa a lo largo de la línea de acción.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

La forma real del diente del engrane depende del ángulo de presión, como se ve en la figura .

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

En esa figura se trazaron los dientes de acuerdo con las proporciones de un engrane de 20 dientes, paso 5, de 4.000 pulgadas de diámetro de paso.
Los tres dientes tienen el mismo espesor porque sólo depende del paso. La diferencia que se ve entre los tres dientes se debe a los distintos ángulos de presión, porque el ángulo de presión determina el tamaño del círculo base.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Por consiguiente, el diámetro del círculo base se puede calcular con
La norma actual para los ángulos de presión son los mostrados en la figura. Las ventajas y desventajas de los distintos valores de angulo de presión se relaciona con la resistencia de los dientes, interferencia y magnitud de fuerzas ejercidos sobre el eje.


Abr/22
oscarrosete.com
oscarrosete.com
Terminología

Como en la mayoría de los procesos se utilizan herramientas especializadas, desde el punto de vista económico es deseable estandarizar el tamaño de los engranes.
La AGMA es la principal organización que supervisa este esquema de estandarización, una agrupación que representa a cerca de 400 fabricantes, la mayoría de sus estándares están certificados por ANSI.
Abr/22
oscarrosete.com
oscarrosete.com
Terminología

La mayoría de las características de un diente de engrane están estandarizadas en relación con el paso diametral y el angulo de presión.
Estas relaciones son actualizadas por la AGMA, que revisa y publica los estándares nuevos cada año.

Abr/22
oscarrosete.com
oscarrosete.com
Terminología

La mayoría de las características de un diente de engrane están estandarizadas en relación con el paso diametral y el angulo de presión.
Estas relaciones son actualizadas por la AGMA, que revisa y publica los estándares nuevos cada año.
Abr/22
oscarrosete.com
oscarrosete.com
Terminología

En el sistema Internacional los parametros principales se calculan con respecto al modulo.



Abr/22
oscarrosete.com
oscarrosete.com
Ejemplo de selección de engrane


Pitch or Diametral Pitch(3DP, 4DP, 2CP, etc.)
Abr/22
oscarrosete.com
oscarrosete.com
Ejemplo de selección de engrane


Abr/22
Agenda
oscarrosete.com
oscarrosete.com

Unidad 4: Cinemática de las maquinas
4.1 Movimiento de una partícula.
- Lineal.
- Angular.
- Relativo.
4.2 Métodos de análisis de velocidad y aceleración.
- Análisis de velocidad y aceleración con matemáticas vectoriales.
- Centros instantáneos. Teorema de Kennedy.
- Componente de Coriolis de la Aceleración.
- Análisis cinemático mediante números complejos
May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Un método gráfico alterno al método del polígono y que facilita el cálculo de velocidades se conoce con el nombre de centros instantáneos de velocidad (CIV), el cual permite determinar la ubicación de un nodo en el espacio plano de un mecanismo común para dos eslabones, ya sea articulados, en contacto o separados.
May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Un centro instantaneo de velocidad (CIV) es un nodo de ubicación instantánea que relaciona el movimiento relativo de un par de eslabones y común para ambos eslabones.
Un CIV es un nodo que puede existir o no de forma físico en un mecanismo, todas las uniones cinemáticas son un CIV.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Si un mecanismo dispone de n eslabones, entonces el número de centros instantáneos (NCI) es el número de combinaciones por par de eslabones.


May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Ya que un CIV es un nodo en el espacio de un mecanismo que relaciona o comunica dos de sus eslabones, es posible determinar velocidades angulares desconocidas a partir de velocidades angulares conocidas mediante la velocidad del nodo de contacto, la cual es una velocidad común para ambos eslabones.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Formas de determinar un CIV
Por observación
Un CIV se puede obtener por “simple observación”, ya que toda junta cinemática (como la de una articulación) es un CIV.
Estos CIV se denotan por Oij , donde i y j son los eslabones i y j.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por definición de velocidad
Al saber que una velocidad tangencial es perpendicular al radio de giro, entonces un nodo de rotación es un CIV que relaciona el eslabón M con el eslabón fijo 1, que se denota por C1M , el cual se puede obtener al prolongar e intersecar los radios de giro, como se muestra en la figura.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Siempre que se dispongan tres eslabones i, j y k en un mecanismo con movimiento relativo en un plano, existirán tres CIV sobre una línea en el espacio del mecanismo, denotados por Oij, Oik y Ojk, respectivamente.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Por ejemplo, si se asigna el elemento 1 al eslabón fijo, entonces los CIV de los eslabones 1, i, j se encuentran en la llamada línea de Kennedy, como se muestra en la figura.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Teorema de Kennedy: Siempre que se tengan tres elementos en movimiento coplanario, existirá sobre una línea, llamada Línea de Kennedy, la ubicación de los tres centros instantáneos que relaciona los tres elementos.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
Existe un artificio gráfico que permite determinar cualquier centro instantáneo en el plano de un mecanismo basado en el teorema de Kennedy, conocido como círculo de centros, el cual permite la construcción de líneas de Kennedy.

May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
El círculo de Centros es una herramienta gráfica visual que sirve para determinar C.I. que no se pueden obtener por observación cuyo procedimiento se describe a continuación:
- Dibujar un circulo, a mano alzada recomendablemente en el mecanismo a analizar, éste círculo será llamado Círculo de Centros.
May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
- Distribuir uniformemente puntos sobre el Círculo de Centros, según el número de eslabones del mecanismo incluyendo el elemento fijo, en cada punto enumerar del 1 a n, donde n es el número de eslabones..
- Determinar todos los C.I. por observación.
May/9
oscarrosete.com
oscarrosete.com
Análisis de velocidad centros instantáneos

Por el teorema de Kennedy
- Unir en el Círculo de Centros dos puntos por medio de un segmento(conocidos)
- Para determinar el C.I. desconocido trazar un segmento punteado.
- El C.I. desconocido se podrá localizar en el mecanismo si pertenece a un par de C.I. conocidos
- Si el C.I. se puede localizar bajo el punto anterior, entonces localizarlo en el mecanismo trazando las rectas correspondientes.
May/9
oscarrosete.com
oscarrosete.com
Ejercicio en clase

Determine las velocidades angulares y tangencial de las barras AB y corredera A, en la posición mostrada utilizando el método de centros instantáneos por definición de velocidad.
May/9
oscarrosete.com
oscarrosete.com
Ejercicio de tarea
La barra AB del mecanismo de cuatro articulaciones de la figura gira con una velocidad angular w1 de 9 rad/s en sentido antihorario. Determine las velocidades angulares w2 y w3 de las barras BC y CD, en la posición mostrada utilizando el método de centros instantáneos por definición de velocidad.



May/9
0.3m
oscarrosete.com
oscarrosete.com
Ejercicio en clase
May/18
Localiza los centros instantáneos del mecanismo mostrado.
Si el eslabón 2 esta girando en sentido horario a 60 rad/s, determina la velocidad lineal de los puntos C y B utilizando centros instantáneos, así como la velocidad ángular CD.



oscarrosete.com
oscarrosete.com
Aceleración
Ecuaciones de aceleración
En la cinemática de mecanismos, el número de componentes vectoriales en una ecuación de aceleración se incrementa debido a que existen aceleraciones que no solo dependen del cambio en la magnitud del vector velocidad sino también del cambio en la dirección del vector velocidad.

May/20
oscarrosete.com
oscarrosete.com
Aceleración
Ecuaciones de aceleración
En un mecanismo articulado, la aceleración puede presentarse en las siguientes modalidades:
Aceleración angular, aceleración tangencial, aceleración normal y aceleración relativa.

May/20
oscarrosete.com
oscarrosete.com
Aceleración
Aceleración angular
Considérese un nodo p de un sólido rígido con movimiento de rotación alrededor de un punto fijo O del mismo sólido rígido. La aceleración angular (a) del eslabón se puede obtener así:
donde Δω es el desplazamiento angular, Δt es el desplazamiento del tiempo, aprom es la aceleración promedio, dω/dt es la derivada de la velocidad angular con respecto al tiempo y a es la aceleración instantánea, respectivamente.


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Aceleración tangencial
Considérese un nodo p de un sólido rígido con movimiento de rotación alrededor de un punto fijo O del mismo sólido rígido. La aceleración tangencial, aT, del nodo p, el cual depende del cambio de la magnitud de la aceleración angular del sólido rígido, se define como:


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Aceleración normal
Considérese un nodo p de un sólido rígido con movimiento de rotación alrededor de un punto fijo O del mismo sólido rígido. La aceleración normal, aN, del nodo p depende del cambio de la dirección de la velocidad angular y se define como:


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Al igual que la velocidad tangencial, las componentes de aceleración normal y tangencial son vectores, por lo que tienen dirección y sentido.
La aceleración normal depende solo del cambio de dirección de la velocidad tangencial y se encuentra a 180° en el sentido de la dirección de la velocidad angular, es decir, paralelo al radio de giro, con un sentido del punto de análisis al pivote.

May/20
oscarrosete.com
oscarrosete.com
Aceleración
Asimismo, la aceleración tangencial depende de la aceleración angular y es perpendicular al radio de giro en el sentido de la aceleración angular; ambas aceleraciones se muestran en la figura


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Existencia y significado de las componentes de aceleración
los vectores Vi y Vf se agrupan sobre un mismo origen, como se muestra en la figura, puede apreciarse un cambio de velocidad en dirección ΔV1 dirigido de a hasta b, así como un cambio de velocidad en magnitud ΔV2, que se muestra desde el origen hasta c.




May/20
oscarrosete.com
oscarrosete.com
Aceleración
ΔV1 produce la componente de aceleración normal aN, depende por tanto de la velocidad angular y del radio de giro.
ΔV2 produce una componente de aceleración tangencial aT, que depende solo de la aceleración angular y del radio de giro.




May/20
oscarrosete.com
oscarrosete.com
Aceleración
Método del polígono de aceleración
La solución usando el método del polígono de aceleración es similar al método del polígono de velocidades, pues la única diferencia radica en que en una ecuación de aceleración pueden aparecer más de tres vectores de aceleración debido a la existencia de aceleraciones normales y tangenciales por nodo.

May/20
oscarrosete.com
oscarrosete.com
Aceleración
Método del polígono de aceleración
Así, sean dos puntos p y q cualesquiera de un eslabón rígido, la ecuación de aceleración que relaciona estos puntos se expresa por:
Los vectores de aceleración de la ecuación son las aceleraciones totales que pueden contener componentes de aceleración normal y tangencial.


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Método del polígono de aceleración
Si las aceleraciones totales ap y aq pertenecen a nodos con trayectorias curvas, entonces estos vectores de aceleración deberán descomponerse en sus componentes normal y tangencial.
Por su parte, como la aceleración relativa ap/q siempre tiene trayectoria circular, tendrá componentes normal y tangencial. De este modo, la ecuación de aceleración de puntos de la misma barra puede representarse de la siguiente forma:


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Método del polígono de aceleración
Donde aN es la componente de aceleración normal de dirección paralela al radio de giro, cuyo sentido se origina desde el punto de análisis al pivote, y aT es la componente de aceleración tangencial, que es perpendicular al radio de giro en el sentido dado por el sentido de la aceleración angular.


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Método del polígono de aceleración
Un mecanismo manivela-corredera, como el que se ilustra en la figura, es impulsado por una manivela 2 de 2.36 cm, la cual gira a una velocidad constante de 5 rad/s, cmr.
En la figura se muestra el resultado del análisis de velocidad.


May/20
oscarrosete.com
oscarrosete.com
Aceleración
Método del polígono de aceleración
Determinar:
a) la aceleración de la corredera.
b) la aceleración angular de la biela.
c) la aceleración de un nodo G colocado en el centro entre A y B.

May/20
Mecanismos Unidad 2
By Oscar Rosete
Mecanismos Unidad 2
- 811