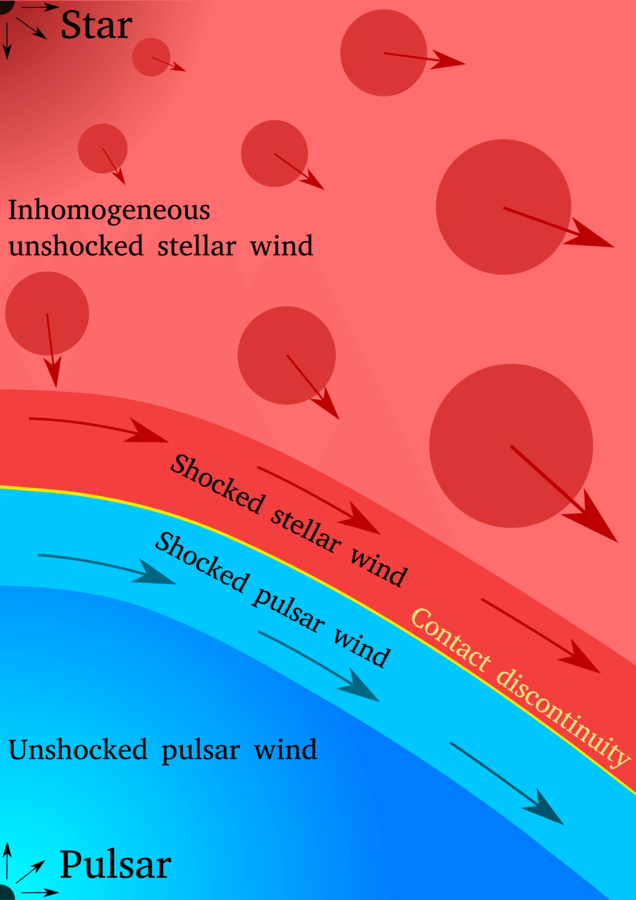
High-energy radiation from

pulsar-star wind colliding binaries

Víctor Moreno de la Cita

Heidelberg, 6th May 2015

Valentí Bosch-Ramon

Dmitry Khangulyan

We performed a 2D axisymmetric RHD simulation (Paredes-Fortuny et al. 2015) of the pulsar-star wind collision followed by a computation of the evolution of the non-thermal particles and their IC and synchrotron radiation.

Gamma ray binaries as

early type star + compact object.

We consider the gamma-ray production in the colliding wind region of binaries with a non-accreting pulsar

We consider an inhomogeneous stellar wind, with a clump placed between the pulsar and the star. 

To do so, we first impose an homogeneous wind until we reach a stationary state and then we add a clump of a given size and density.

Our workframe 

​Paredes-Fortuny et al. 2015

We fix our coordinate system with the y axis in the line connecting the pulsar and the star. The shock is formed where the ram pressures of the two winds are balanced.

Our workframe

T_{\star} = 4\times 10^4 \text{ K}
T⋆=4×104 KT_{\star} = 4\times 10^4 \text{ K}
L_{\star} = 10^{39} \text{erg s}^{-1}
L⋆=1039erg s−1L_{\star} = 10^{39} \text{erg s}^{-1}
\vec{v}_{wind,\star} = 3000 \text{ km s}^{-1}
v⃗wind,⋆=3000 km s−1\vec{v}_{wind,\star} = 3000 \text{ km s}^{-1}
\dot{M}_\star = 10^{-7} M_\odot \text{yr}^{-1}
M˙⋆=10−7M⊙yr−1\dot{M}_\star = 10^{-7} M_\odot \text{yr}^{-1}

The star is a O type with the following data:

R_c = 1 \text{ or }5 \text{ in units of } a, \text{ with }\,\, a = 8\times 10^{10} \text{ cm}
Rc=1 or 5 in units of a, with a=8×1010 cmR_c = 1 \text{ or }5 \text{ in units of } a, \text{ with }\,\, a = 8\times 10^{10} \text{ cm}

Clump radius:

Our workframe

The pulsar has a spin-down luminosity of:

And a wind Lorentz factor of:

L_{sd} = 10^{37}\text{ erg s}^{-1}
Lsd=1037 erg s−1L_{sd} = 10^{37}\text{ erg s}^{-1}
\Gamma = 5
Γ=5\Gamma = 5

Giving rise to a pulsar-to-star wind momentum ratio of :

\eta = \dfrac{F_{pw}S_{pw}}{F_{sw}S_{sw}}\approx\dfrac{L_{sd}}{\dot{M}v_{sw}c}\approx 0.2
η=FpwSpwFswSsw≈LsdM˙vswc≈0.2\eta = \dfrac{F_{pw}S_{pw}}{F_{sw}S_{sw}}\approx\dfrac{L_{sd}}{\dot{M}v_{sw}c}\approx 0.2
y_\star = 4.4\times 10^{12} \text{ cm}
y⋆=4.4×1012 cmy_\star = 4.4\times 10^{12} \text{ cm}
y_p = 4\times 10^{11} \text{ cm}
yp=4×1011 cmy_p = 4\times 10^{11} \text{ cm}

Star

Pulsar

Our workframe

Star

Pulsar

Although the RHD simulation is 2D, we take this information and scramble the different lines around the y axis, giving each line a random azimuthal angle phi, so the result is more similar to the 3D real scenario.

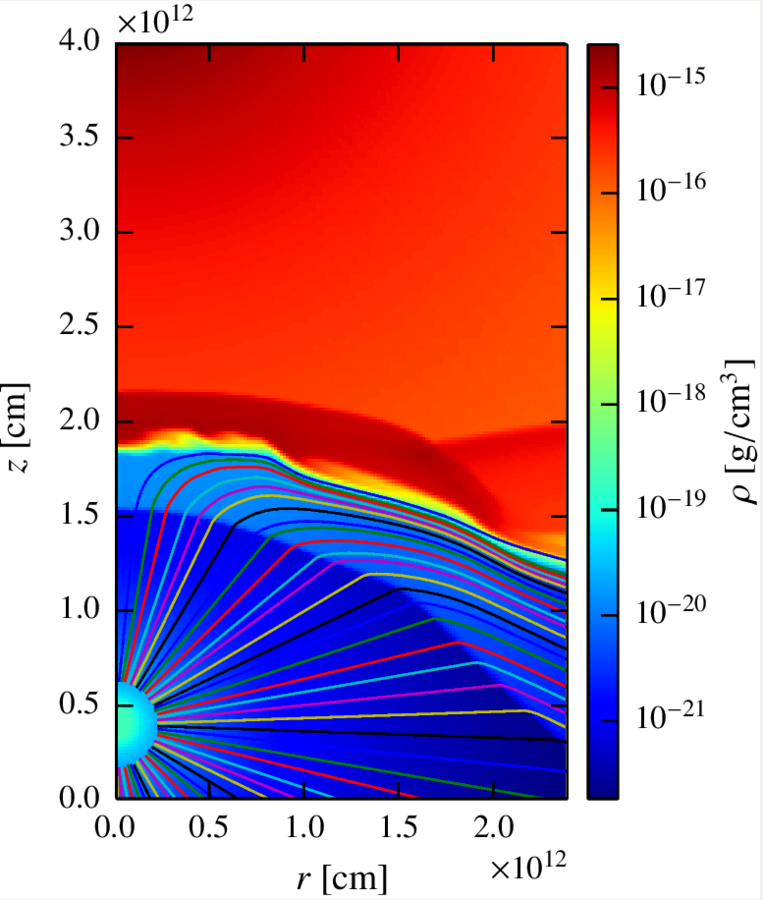
Going into details. hidrodynamic setup.

Dealing with fluid mixing

The fluid is divided in 40 lines with 200 cells each, describing an axisymmetric 2D space of:

r\in[0,2.4\times10^{12}\text{ cm}]
r∈[0,2.4×1012 cm]r\in[0,2.4\times10^{12}\text{ cm}]

However, not every line contains shocked material, so we can ignore some. Also, given that the two winds can mix through the fluid lines, we have had to cut the lines at a certain point. 

y\in[0,4\times10^{12}\text{ cm}]
y∈[0,4×1012 cm]y\in[0,4\times10^{12}\text{ cm}]

Going into details. Physical assumptions i.

Prescription for acceleration in strong shocks (Drury 1983)

t_{gain} = t_{loss}
tgain=tlosst_{gain} = t_{loss}
t_{loss} = \min
tloss=mint_{loss} = \min
\{
{\{
t_{sync}=\dfrac{1}{a_sB^2E}
tsync=1asB2Et_{sync}=\dfrac{1}{a_sB^2E}
t_{diff} = \dfrac{R^2}{2D}, \,\,\,D=k\cdot r_g\cdot c/3
tdiff=R22D,D=k⋅rg⋅c/3t_{diff} = \dfrac{R^2}{2D}, \,\,\,D=k\cdot r_g\cdot c/3
t_{gain} = \tilde\eta \dfrac{E}{qBc}
tgain=η~EqBct_{gain} = \tilde\eta \dfrac{E}{qBc}
\tilde\eta=2\pi(c/v)^2
η~=2π(c/v)2\tilde\eta=2\pi(c/v)^2

with

We inject non-thermal particles when a shock takes place:

Internal energy goes up

and

fluid velocity goes down

Where and how do we inject non-thermal particles

Going into details. Physical assumptions ii.

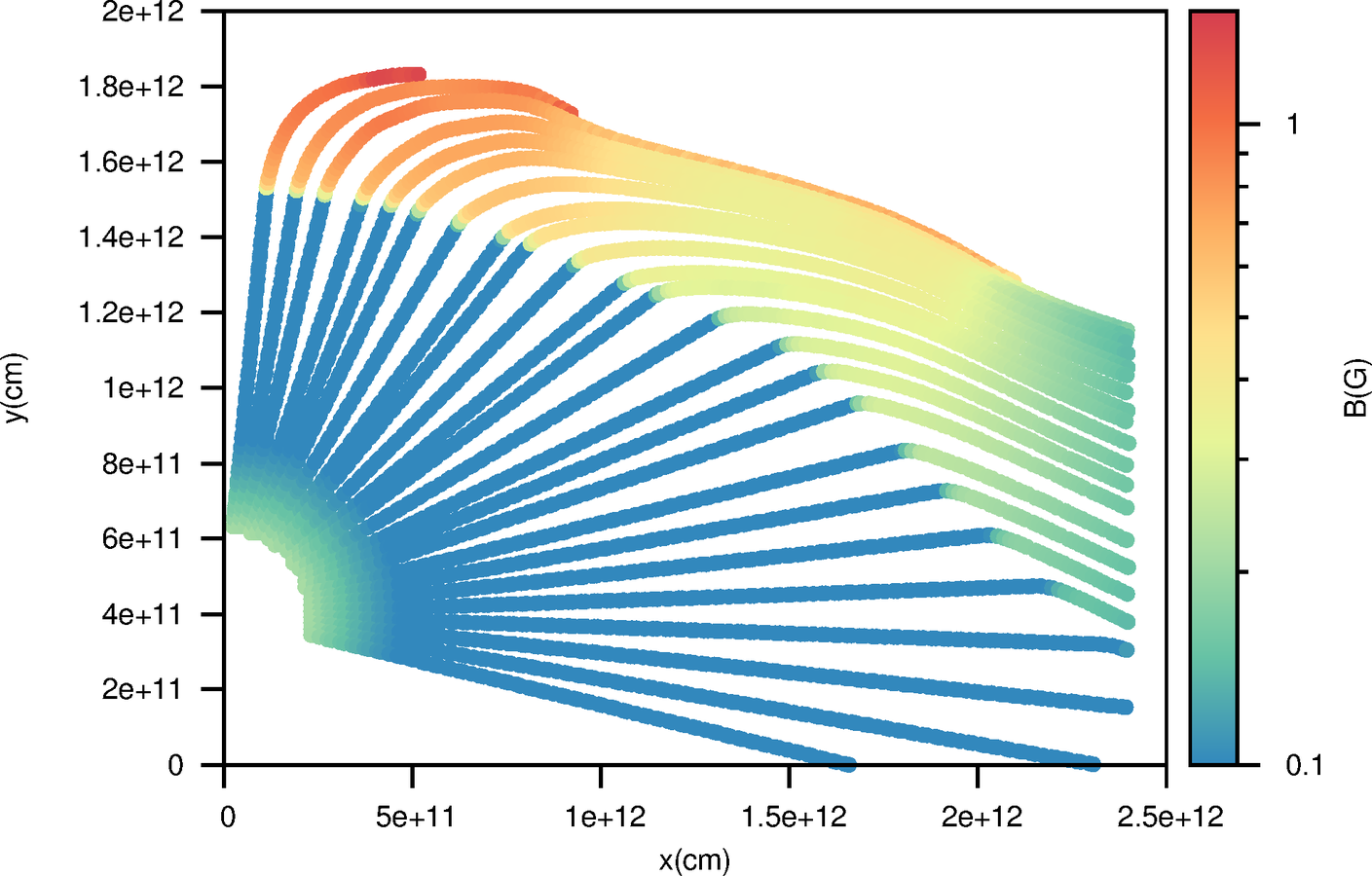
Magnetic field perpendicular to the fluid line

B_0^\prime = \Gamma_0^{-1}\sqrt{\eta_B \times 8\pi e_0}
B0′=Γ0−1ηB×8πe0B_0^\prime = \Gamma_0^{-1}\sqrt{\eta_B \times 8\pi e_0}
e_0 = \Gamma_0^2\rho_0h_0c^2 - \Gamma_0\rho_0 c^2 -p_0
e0=Γ02ρ0h0c2−Γ0ρ0c2−p0e_0 = \Gamma_0^2\rho_0h_0c^2 - \Gamma_0\rho_0 c^2 -p_0
B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
Bk′=B0′(ρkv0Γ0ρ0vkΓk)1/2B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
\eta_B = 10^{-4}, 1
ηB=10−4,1\eta_B = 10^{-4}, 1

Definition of the magnetic field at the beginning of the line:

Evolution of the B field in the different cells k:

(Low, high magnetic field)

Free energy density
Fraction of total energy that goes to magnetic energy

Going into details. some notes on the code.

  1. We let the particles evolve until they reach a steady state so we can consider the medium stationary, in other words, every loss time (e.g. synchrotron) or cell-crossing time is much shorter than the dynamical time on large scales. 
  2. All the computation is done in the (relativistic) frame of the fluid, so every relevant quantity has to be transformed, including the angles between fluid, gamma photons and target photons velocities.
  3. The section evolution is computed imposing conservation of energy in the fluid frame.
S = S_0\dfrac{\Gamma_0^2\rho_0h_0v_0}{\Gamma^2\rho hv}
S=S0Γ02ρ0h0v0Γ2ρhvS = S_0\dfrac{\Gamma_0^2\rho_0h_0v_0}{\Gamma^2\rho hv}

Going into details. Structure of the shock. 

​Paredes-Fortuny et al. 2015

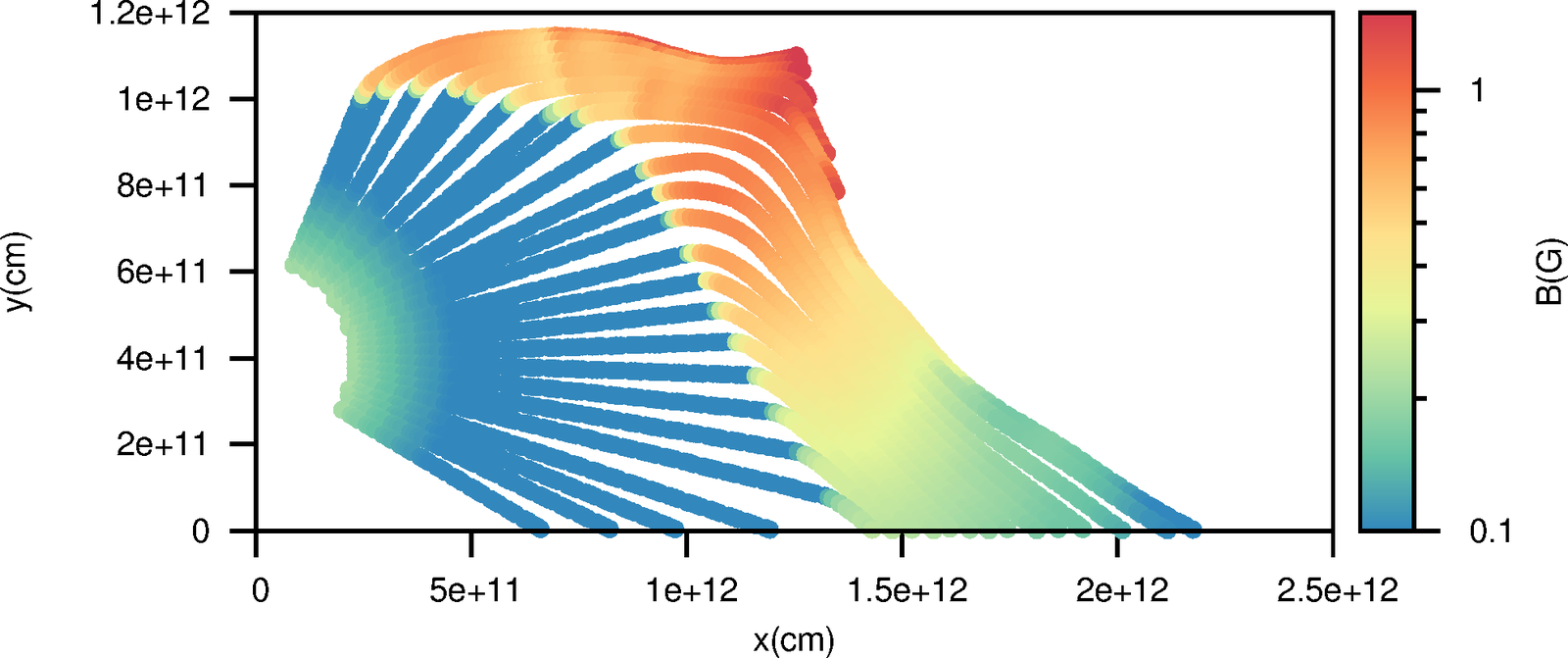
Going into details. Magnetic field. 

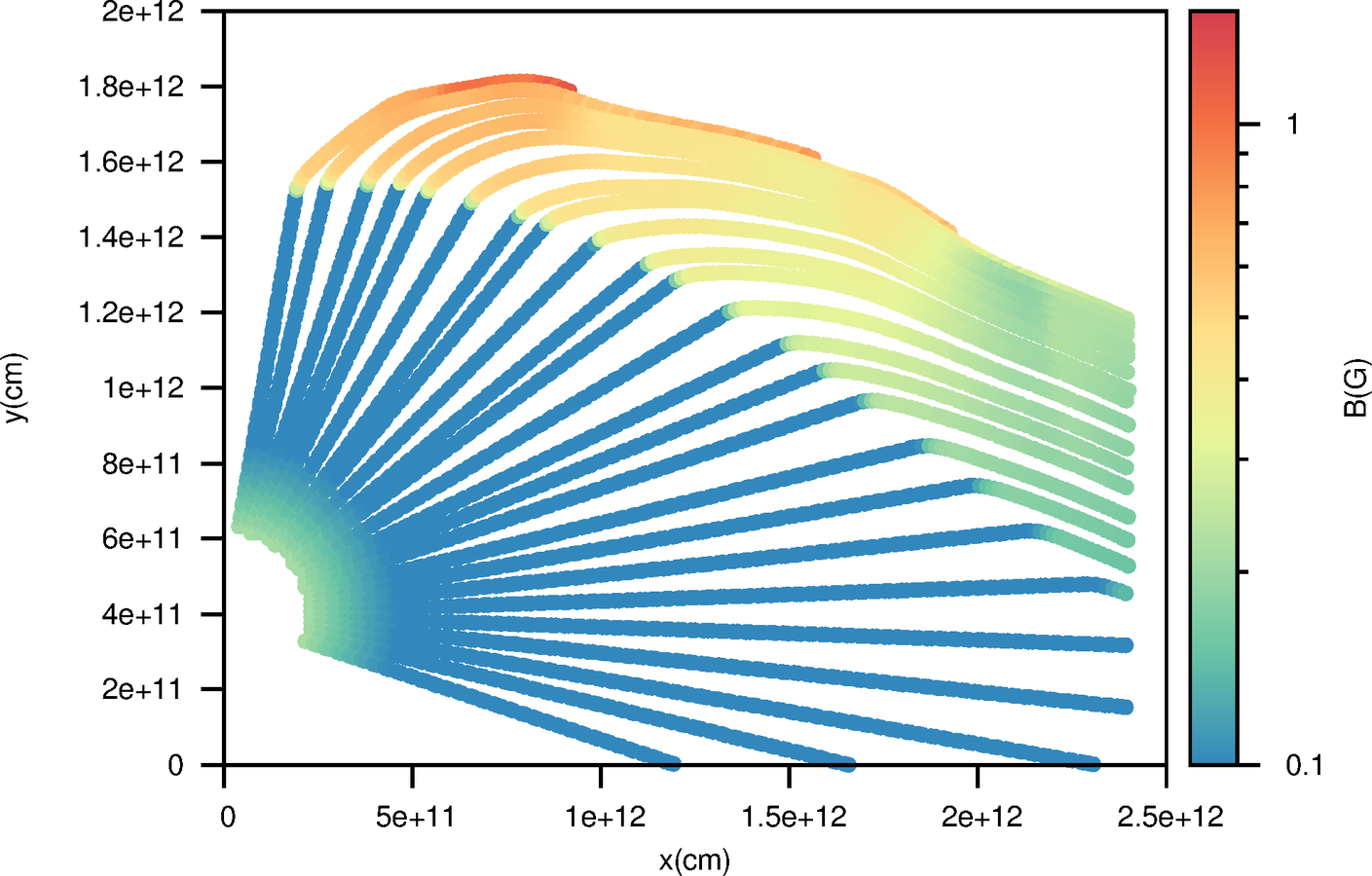
No clump
Small clump
Big clump
As proposed by Bosch-Ramon 2013

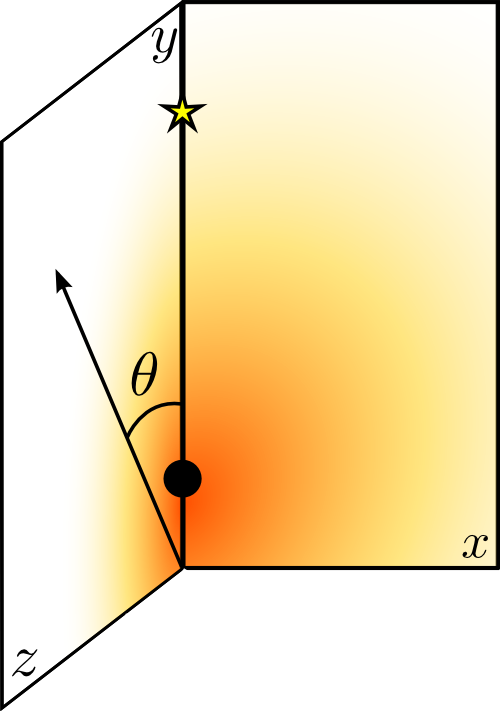
Going into details. Observer angle.

Star

Pulsar

To avoid eclipses, we do not simulate the most extreme cases:

\theta = 0,\,\theta=180^\circ
θ=0,θ=180∘\theta = 0,\,\theta=180^\circ

Instead, we take just three angles: 45º for the case of the observer closer to the star, 135º for the one closer to the pulsar and 90º, when the observer is placed in the z axis.

The observer will be placed in the z-y plane forming an angle theta with the vertical axis. 

Results. Low magnetic field, no clump.

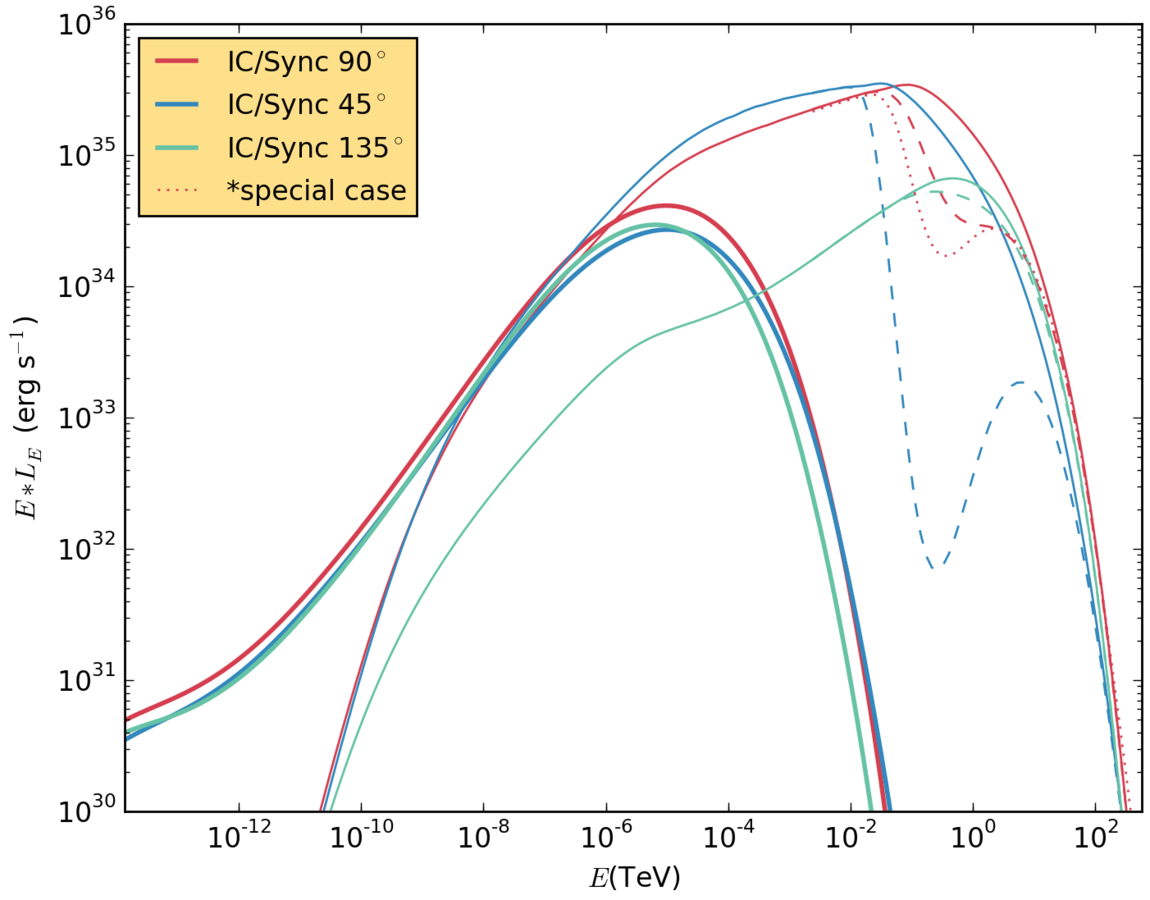
Very similar sync. emission, the IC depends stronger on the viewing angle.

The absorption due to pair production depends on the position of the observer and the extent of the IC source. 

Results. Low magnetic field, 90 degrees.

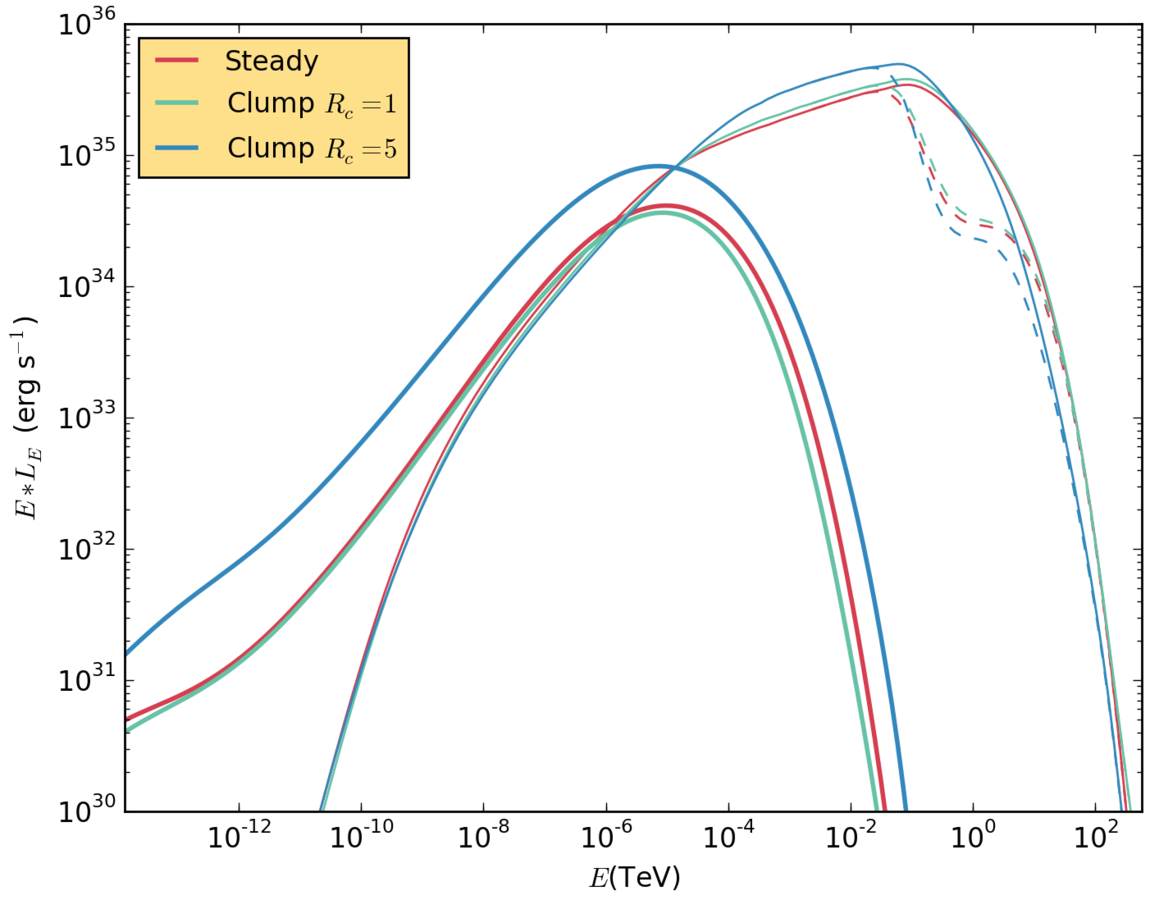
Small clumps do not seem to change importantly the emission of the homogeneous wind. However, if the clump is big enough, an increase on both synchrotron and IC emission is expected.

Results. small clump with different B fields.

With a B field 100 times stronger, the IC radiation  becomes weaker and presents a cutoff at lower energy.

The synchrotron emisson becames much more important, specially at low energies.

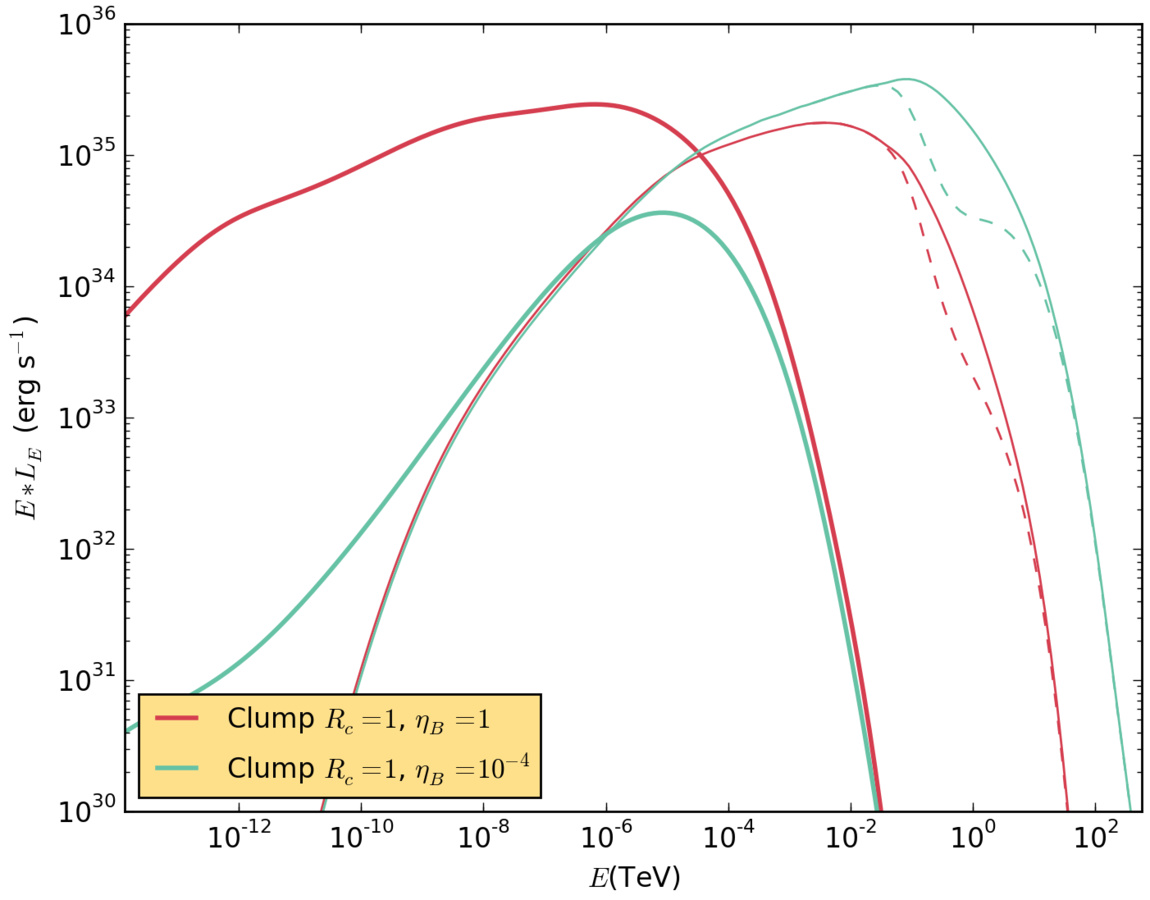
Results. big clump with different B fields.

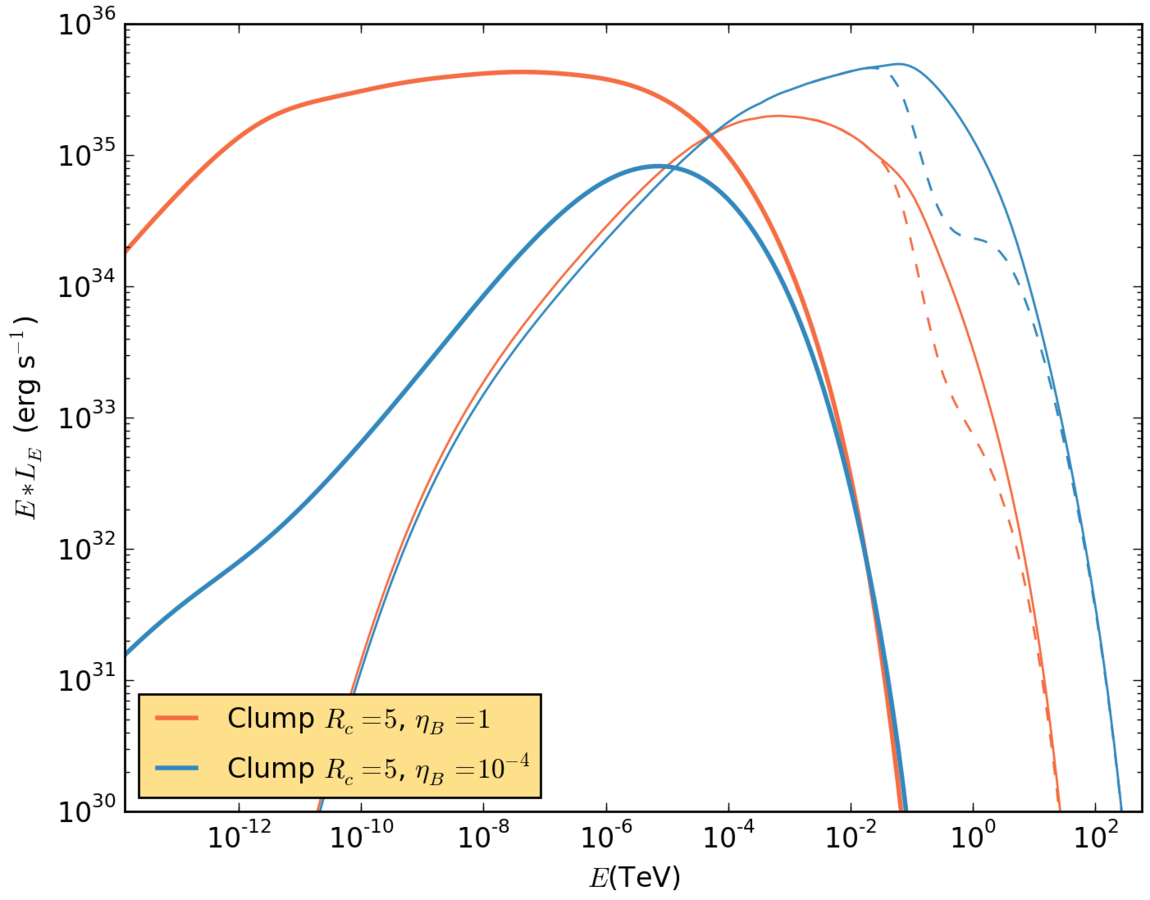
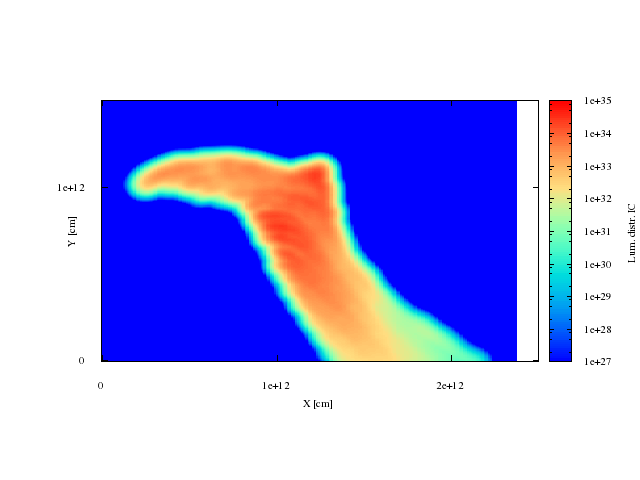
Maps. IC radiation, big clump.

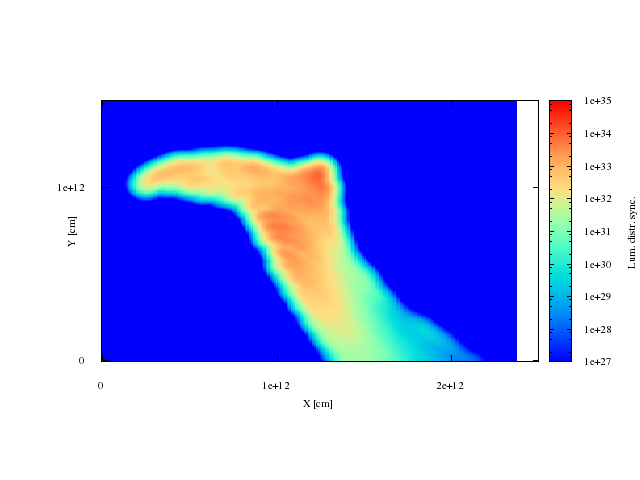
Maps. synchrotron radiation, Big clump.

Discussion. Conclusions and future work.

The next step could be to get a more realistic 3D scenario computing a larger number of lines to make the scramble.

With this method we should be able to:

  1. Explore different scenarios of academical interest
  2. Try to explain the gamma-ray emission of some sources such as PSR B1259-63 or LS I +61 303.

Thank You.

Backup slide. Fixing the line ending.

Given that the two winds can mix through the fluid lines, we have had to cut the lines at a certain point. To do so, we can impose that the amount of material that crosses the section do not get larger than a certain threshold:

\text{if: } S\rho v\Gamma > 2\times S_0\rho_0v_0\,\rightarrow\, \text{end of the line}
if: SρvΓ>2×S​0​​ρ​0​​v​0​​→end of the line

Backup slide. Injected Luminosity.

The injected non-thermal particles have a lumisosity given by:

L_{inj} = \chi \times \dfrac{L_T}{ \Gamma^2} \dfrac{v_{rel}}{v}
L​inj​​=χ×​Γ​2​​​​L​T​​​​​v​​v​rel​​​​
L_T= U_T\Gamma^2vS
L​T​​=U​T​​Γ​2​​vS

With the pre-factor varying between 0 and 1 and the total luminosity being:

heidelberg2015

By otnoesmusica

Made with Slides.com

heidelberg2015

High-energy radiation from pulsar-star wind colliding binaries

  • 1,172

More from otnoesmusica