圖論
黃博崇
- 成功高中電子計算機研習社35th 總務/教學
講師介紹
目錄
- 介紹圖
- 圖的存取
- 名詞解釋
- 圖的遍歷
- 拓樸排序
- 最短距離
- 樹
- 並查集
- 最小生成樹
圖(graph)
由一些節點(vertices/node)和邊(edge)組成
每個節點有自己的編號
圖(graph)
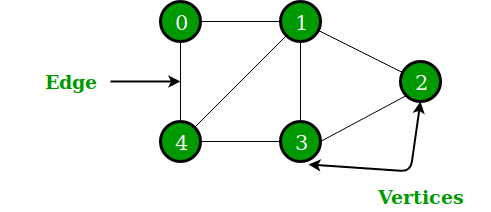
邊(egde)
分為有向邊和無向邊
如果在一張圖中全部都是無向邊稱為無向圖
否則是有向圖
1
2
3
無向圖
1
2
3
有向圖
邊(edge)
邊可能有帶權重
1
2
3
無向帶權圖
1
2
3
有向帶權圖
4
7
2
3
度數(degree)
入度(in degree)代表有多少邊指向這個節點
出度(out degree)代表有多少邊從這個節點出去
1
2
3
4
| in degree | out degree | |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0 | 2 |
| 3 | 2 | 1 |
| 4 | 1 | 0 |
圖的存取
假設一張圖有n個點m個邊
宣告一個二維陣列v[ n ][ n ]
v[ i ][ j ]代表i~j邊的長度
空間複雜度為O(n^2)
鄰接矩陣
3
2
1
4
4
2
8
| v | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 4 | 0 | 0 | 0 |
| 3 | 0 | 0 | 2 | 0 | 0 |
| 4 | 0 | 8 | 0 | 0 | 0 |
優點:
- 能夠O(1)直接獲得兩點間的邊權
鄰接矩陣
缺點:
- 空間複雜度為O(n^2)容易爆掉
code
#include <bits/stdc++.h>
using namespace std;
int v[10005][10005];
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < m; i++){
int a, b, w;
cin >> a >> b >> w;
v[a][b] = w;
//v[b][a] = w; 無向圖
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
cout << v[i][j] << ' ';
}
cout << '\n';
}
}
宣告一個長度為n存pair的vector v[n]
v[i].push_back({j, w})代表新增點i連到點j長度為w的邊
空間複雜度O(m)
鄰接串列
3
2
1
4
4
2
8
v[ 1 ] = {{2, 4}, {4, 8}}
v[ 2 ] = {{3, 2}}
優點:
- 相較鄰接矩陣能夠省許多空間
鄰接串列
缺點:
- 無法快速獲得兩點間的邊權
code
#include <bits/stdc++.h>
using namespace std;
vector <pair <int, int> > v[10005];
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < m; i++){
int a, b, w;
cin >> a >> b >> w;
v[a].push_back({b, w});
v[b].push_back({a, w});
}
for(int i = 1; i <= n; i++){
cout << i << " : ";
for(auto j : v[i]){
cout << j.first << ", " << j.second << " ";
}
cout << '\n';
}
}
宣告一個struct存邊的兩端點和長度
邊陣列
3
2
1
4
4
2
8
edge[0]={1,2,4}
edge[1]={2,3,2}
edge[2]={1,4,8}
code
#include <bits/stdc++.h>
using namespace std;
struct e{
int u, v, w;
}edge[100005];
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < m; i++){
int a, b, w;
cin >> a >> b >> w;
edge[i] = {a, b, w};
}
for(int i = 0; i < m; i++){
cout << edge[i].u << " " << edge[i].v << " " << edge[i].w << '\n';
}
}
名詞解釋
一個連通塊中的任兩點間都一定有路徑連通
連通塊
2
1
5
4
3
6
7
環上的點能經過一些邊再回到原本的點
環
2
1
5
4
3
有向且無環的圖
DAG
2
1
5
4
3
有n個點n-1條邊的圖
Tree
2
1
5
4
3
類似迷宮的圖
網格圖
把點分成兩種顏色
相鄰的點都是不同的顏色
二分圖
圖的遍歷
通常以遞迴實作
- 到達一個點並標記為已走過
- 看他能夠走到哪些還沒被走過的點
- 往下個點走
DFS
2
1
5
4
3
6
7
順序
- 1 2 5 3 4 6 7
- 1 3 5 4 6 7 2
code
bool visit[100005];
vector <int> g[100005];
void dfs(int v){
visit[v] = true;
for(int i : g[v]){
if(!visit[i]){
dfs(i);
}
}
return;
}一個DFS可以跑完一個連通塊
如果題目不只一個連通塊記得跑完所有點
for(int i = 1; i <= n; i++){
if(!visit[i]){
dfs(i);
}
}像倒水一樣慢慢擴散,通常用queue實作
- 從queue裡拿出點
- 看他能夠走到哪些還沒被走過的點
- 把它們丟進queue裡並標記已走到過
- 直到queue裡沒東西
BFS
2
1
5
4
3
6
7
順序
- 1 2 5 3 7 6 4
- 1 5 2 3 7 6 4
code
bool visit[100005];
vector <int> g[100005];
void bfs(){
queue <int> q;
visit[1] = true;
q.push(1);
while(!q.empty()){
int v = q.front();
q.pop();
for(int i : g[v]){
if(!visit[i]){
q.push(i);
visit[i] = true;
}
}
}
return;
}網格圖的BFS
code(暴力版)
string g[105];
bool visit[105][105];
bool bfs(){
queue <pair <int, int>> q;
visit[1][1] = true;
q.push({1, 1});
while(!q.empty()){
int x = q.front().first, y = q.front().second;
if(x == n - 2 && y == n - 2){
return true;
}
q.pop();
if(g[y - 1][x] == '.' && !visit[y - 1][x]){ //up
q.push({x, y - 1});
visit[y - 1][x] = true;
}
if(g[y + 1][x] == '.' && !visit[y + 1][x]){ //down
q.push({x, y + 1});
visit[y + 1][x] = true;
}
if(g[y][x - 1] == '.' && !visit[y][x - 1]){ //left
q.push({x - 1, y});
visit[y][x - 1] = true;
}
if(g[y][x + 1] == '.' && !visit[y][x + 1]){ //right
q.push({x + 1, y});
visit[y][x + 1] = true;
}
}
return false;
}code(比較不暴力版)
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
string g[105];
bool visit[105][105];
bool bfs(){
queue <pair <int, int>> q;
visit[1][1] = true;
q.push({1, 1});
while(!q.empty()){
int x = q.front().first, y = q.front().second;
if(x == n - 2 && y == n - 2){
return true;
}
q.pop();
for(int i = 0; i < 4; i++){
int nextx = x + dir[i][0], nexty = y + dir[i][1];
if(g[nexty][nextx] == '.' && !visit[nexty][nextx]){
q.push({nextx, nexty});
visit[nexty][nextx] = true;
}
}
}
return false;
}例題
拓樸排序
在DAG中將所有點排成一個序列
滿足所有點都是由前向後的
拓樸排序不是唯一的
介紹
2
1
5
4
3
6
7
拓樸排序
- 1 2 3 5 4 6 7
- 1 3 2 4 5 6 7
在DAG上DP就可以使用拓樸排序
需要記錄入度
- 將入度為0的點放入序列
- 將這個點連到的所有點入度減1(把邊拔掉)
- 重複直到所有點都放入序列
可用queue實作
2
1
5
4
3
6
7
拓樸排序
- 1 2 3 5 4 6 7
- 1 3 2 4 5 6 7
code
vector <int> g[100005];
int indeg[100005];
vector <int> topo;
void toposort(){
queue <int> q;
for(int i = 1; i <= n; i++){
if(indeg[i] == 0) q.push(i);
}
while(!q.empty()){
int v = q.front();
q.pop();
topo.push_back(v);
for(auto i : g[v]){
indeg[i]--;
if(indeg[i] == 0) q.push(i);
}
}
}例題
最短距離
負環
2
1
5
4
3
每走一圈距離會變更少
和負環連接的點不會有最短距離
-2
3
-4
-10
1
假設任兩點i、j間的當前最短距離是dis[i][j]
如果有一點k存在且dis[i][k]+dis[k][j]<dis[i][j]
那麼就可以更新dis[i][j]的值
鬆弛
i
j
k
12
4
5
- 暴力枚舉三個點i、j、k
- 將k看成i、j的中點
- 對i、j鬆弛
時間複雜度為O(n^3)
Floyd-Warshall Algorithm
code
for(int k = 1; k <= n; k++){
for(int i = 1; i <= n; i++){
for(int j = 1; j <= n; j++){
if(dis[i][k] + dis[k][j] < dis[i][j]){
dis[i][j] = dis[i][k] + dis[k][j];
}
}
}
}單源點最短距離
起點只有一個
詢問起點到任意點的最短距離
Dijkstra's Algorithm
陣列dis[i]代表起點到i的最短距離
- 尋找距離起點最近的點當作"已確認最短路徑的點"
- 用這個點鬆弛其他能被走到的點
用priority_queue來實作
時間複雜度為O(mlogm)
無法處理負邊權
code
#define f first
#define s second
typedef pair <int, int> pii;
int dis[100005];
vector <pii> g[100005];
priority_queue <pii, vector <pii>, greater <pii> > pq;
void dijkstra(int n, int st){
for(int i = 1; i <= n; i++){
dis[i] = 1e9;
}
dis[st] = 0;
pq.push({0, st});
while(!pq.empty()){
pii tmp = pq.top();
pq.pop();
if(dis[tmp.s] != tmp.f){
continue;
}
for(auto i : g[tmp.s]){
int newdis = dis[tmp.s] + i.s;
if(newdis < dis[i.f]){
dis[i.f] = newdis;
pq.push({dis[i.f], i.f});
}
}
}
}例題
樹
名詞解釋
2
1
5
4
3
6
子樹
根
葉
父節點
子節點
二元樹
2
1
5
4
3
6
每個節點最多只有2個子節點
樹直徑
2
1
5
4
3
6
樹上最長的1條路徑
也就是樹上最遠兩個點的距離
7
樹直徑
- 從任一點dfs到最遠的點
- 再從那個點dfs到最遠點,所走的路徑長就是樹直徑
只能在非負邊權使用
code
vector <int> g[100005];
int far_d, far_v;
void dfs(int v, int fa, int d = 0){
if(d > far_d){
far_d = d;
far_v = v;
}
for(auto i : g[v]){
if(i == fa) continue;
dfs(i, v, d + 1);
}
}
int diam(){
far_d = -1;
dfs(1, 1);
far_d = -1;
dfs(far_v, far_v);
return far_d;
}樹重心
2
1
5
4
3
6
一個樹會存在1或2個樹重心
樹重心的最大子樹是所有點中最小的
且子樹大小不大於n/2
樹重心
需紀錄目前重心和大小、每個點所有子樹加自己大小總和
- 從任一點開始dfs
- 找到他的最大子樹
- 檢查是否比目前重心的最大子樹小
code
vector <int> g[100005];
int G, Gsize;
int sz[100005];
void dfs(int v, int fa){
int maxsz = 0;
sz[v] = 1;
for(auto i : g[v]){
if(i == fa) continue;
dfs(i, v);
maxsz = max(maxsz, sz[i]);
sz[v] += sz[i];
}
maxsz = max(maxsz, n - sz[v]);
if(maxsz < Gsize){
Gsize = maxsz;
G = v;
}
}例題
zerojudge b967
並查集(disjoint set)
介紹
一種處理集合的樹狀資料結構
- 能夠查詢元素所在的集合
- 能夠合併兩集合
ex:
a、b是同學,b、c是同學
所以a、c也是同學
查詢
宣告一個陣列root[]代表每個點的"根",初始化每個點的根都是自己
要查詢時,不停往上找根直到根是自己
當兩個點最終找到的根一樣代表位於同個集合
1
2
3
4
5
6
root[1]=2
root[2]=3
root[3]=3
root[4]=3
root[5]=6
root[6]=6
合併
在兩個點中找到其中一個點最終的根
將另一個點的根直接設為它
1
2
3
4
5
6
root[1]=2
root[2]=3
root[3]=3
root[4]=3
root[5]=6
root[6]=6(3)
code
int root[100005];
int findroot(int x){
if(root[x] == x) return x;
return findroot(root[x]);
}
void connect(int x, int y){
root[findroot(y)] = findroot(x);
}好像有點慢?
啟發式合併
把較小的樹合進較大的樹
1
2
3
4
5
6
小合進大
root[1]=2
root[2]=3
root[3]=3
root[4]=3
root[5]=6
root[6]=3
大合進小
root[1]=2
root[2]=3
root[3]=6
root[4]=3
root[5]=6
root[6]=6
時間複雜度為O(logn)
code
void connect(int x, int y){
if(findroot(x) == findroot(y)) return;
if(size[findroot(x)] > size[findroot(y)]){
size[findroot(x)] += size[findroot(y)];
root[findroot(y)] = findroot(x);
}
else{
size[findroot(y)] += size[findroot(x)];
root[findroot(y)] = findroot(y);
}
}路徑壓縮
每次查詢某個點完後
直接將根設為最後找到的根
1
2
3
4
1
2
3
4
時間複雜度為alpha(n)
code
int findroot(int x){
if(root[x] == x) return x;
root[x] = findroot(root[x]);
return root[x];
}給一些點和邊
有兩種操作
- 移除某兩點間的邊
- 詢問兩點是否連通
並查集要怎麼把點移出集合?
能夠只靠合併集合做到嗎?
1
2
3
4
5
6
離線(倒著做)
- 先將所有操作紀錄起來且不要建圖
- 只建沒在操作中被移除的邊
- 把紀錄的操作反過來,如果是詢問操作就照目前建的圖查看連通性,如果是移除操作就把它變成增加邊
ex:
- 移除2、3的邊
- 查詢1、6連通性
- 移除4、6的邊
- 查詢2、5連通性
1
2
3
4
5
6
原圖
例題
最小生成樹(MST)
介紹
生成樹代表包含了一張圖所有點的樹
一張圖有可能有很多生成樹
最小生成樹代表邊權和最小的生成樹
1
2
3
4
5
9
2
3
5
7
15
6
Kruskal's Algorithm
- 將所有邊以權重由小排到大
- 如果目前選到的邊兩端點已經在生成樹中就無視這條邊,反之將這條邊加進生成樹中
以並查集維護
時間複雜度為O(mlogm))
code
struct e{
int u, v, w;
};
vector <e> edge;
bool cmp(e a, e b){
return a.w < b.w;
}
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < m; i++){
int a, b, w;
cin >> a >> b >> w;
edge.push_back({a, b, w});
}
sort(edge.begin(), edge.end(), cmp);
int sum = 0;
for(int i = 0; i < m; i++){
int u = edge[i].u, v = edge[i].v, w = edge[i].w;
if(findroot(u) != findroot(v)){
connect(u, v);
sum += w;
}
}
}Prim's Algorithm
和Dijkstra類似
改成每次尋找離目前最小生成樹最近的點
用priority_queue維護
code
#define f first
#define s second
typedef pair <int, int> pii;
bool visit[100005];
vector <pii> g[100005];
priority_queue <pii, vector <pii>, greater <pii> > pq;
int prim(){
int sum = 0;
pq.push({0, 1});
while(!pq.empty()){
pii tmp = pq.top();
pq.pop();
if(visit[tmp.s]) continue;
visit[tmp.s] = true;
sum += tmp.f;
for(auto i : g[tmp.s]){
pq.push({i.s, i.f});
}
}
return sum;
}例題
參考資料
- ap325
- 2021建中校內培訓簡報
- 2022 ION Camp
- 賴阿蘭放課簡報
進階圖論
- DFS Tree
- 關節點和橋
- 強連通分量scc
- LCA
- 樹壓平
- 樹鏈剖分
圖論
By patrickh
圖論
- 349


