What is Deep Learning?

Deep Learning is a stack of automation algorithms that converts one form of data into another using the concept of Neural Networks

How Neural Network learns...

Point to Remember

Without being told how well it's predictions are, it cannot learn. This will be important to remember.

Data Privacy

When you homomorphically encrypt data, you can't read it but you still maintain most of the interesting statistical structure. This has allowed people to train models on encrypted data (CryptoNets)

Encrypting NNs

Many state-of-the-art neural networks can be created using only the following operations:

• Addition
• Multiplication
• Division
• Subtraction
• Sigmoid
• Tanh
• Exponential

Merging the boundaries

Can we Homomorphically Encrypt NN?

• Addition - works out of the box
• Multiplication - works out of the box
• Division - works out of the box? - simply 1 / multiplication
• Subtraction - works out of the box? - simply negated addition
• Sigmoid - hmmm... perhaps a bit harder
• Tanh - hmmm... perhaps a bit harder
• Exponential - hmmm... perhaps a bit harder

The Missing Ingredient

The activation functions and other non trivial stuffs are...non trivial

Let's resolve this...

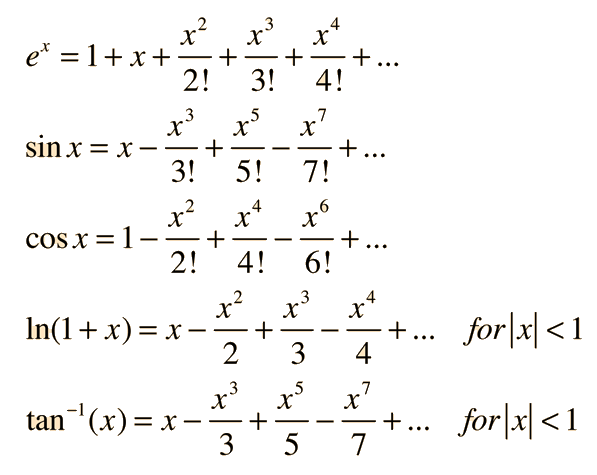
Choosing an Encryption Algorithm

The quest for a fully homomorphic scheme seeks to find an algorithm that can efficiently and securely compute the various logic gates required to run arbitrary computation. The general hope is that people would be able to securely offload work to the cloud with no risk that the data being sent could be read by anyone other than the sender.

Constraints

In general, most Fully Homomorphic Encryption schemes are incredibly slow relative to normal computers (not yet practical). This has sparked an interesting thread of research to limit the number of operations to be Somewhat homomorphic so that at least some computations could be performed. Less flexible but faster, a common tradeoff in computation.

Choices Despite Constraints

• Efficient Homomorphic Encryption on Integer Vectors and Its Applications

• Yet Another Somewhat Homomorphic Encryption (YASHE)

• Somewhat Practical Fully Homomorphic Encryption (FV)

• Fully Homomorphic Encryption without Bootstrapping

Best Choice...

The best one to use here is likely either YASHE or FV. YASHE was the method used for the popular CryptoNets algorithm, with great support for floating point operations.

Choice For This talk...

YASHE and FV are pretty complex. For the purpose of making this talk easy and fun to play around with, we're going to go with the slightly less advanced (and possibly less secure) Efficient Integer Vector Homomorphic Encryption.