Generative Image Modeling using Style and Structure Adversarial Networks
Xiaolong Wang, Abhinav Gupta
Robotics Institute, Carnegie Mellon University
Presenter: Wei YANG, CUHK
Xiaolong Wang
Ph.D. Student @ RI, CMU
- Object Detection/Segmentation
- 3D Scene Understanding, Video Analysis.
- Deep Learning, Unsupervised Learning.
Abhinav Gupta
Machine Learning Dept.
- Learning representation
- Language ~ Vision
- Actions and objects
PAMI Young Researcher Award 2016
Unsupervided Learning of Visual Representation
Discriminative Framework
Generative Framework
Discriminative Framework
Use auxiliary tasks such that ground truth can be generated without labeling
Generative Framework
-
Non-parametric matching
-
Parametric modeling: RBMs, VAE, GAN ...
Generative Adversarial Networks
G
Generator
D
Discriminator
Random Noise
Generated
Real
X_i
G(z_i)
z_i
Generative Adversarial Networks
Real samples
Random noise sampled from uniform distribution
\mathbf{X} = (X_1,\cdots, X_M)
\mathbf{Z} = (z_1,\cdots, z_M)
Loss for D network
L^D(\mathbf{X}, \mathbf{Z}) = \sum_{i=1}^{M/2} L(D(X_i), 1) + \sum_{i=M/2+1}^{M} L(D(G(z_i)), 0).
Where L is the binary cross-entropy loss,
L(y^*, y) = -[y\log(y^*) + (1-y)\log(1-y^*)].
Generative Adversarial Networks
Real samples
Random noise sampled from uniform distribution
\mathbf{X} = (X_1,\cdots, X_M)
\mathbf{Z} = (z_1,\cdots, z_M)
Loss for G network
L^G(\mathbf{Z}) = \sum_{i=M/2+1}^{M} L(D(G(z_i)), 1).
It tries to fool the discriminator D to classify the generated sample as real sample
What does the GAN really learns?
- Structure?
- Texture?
Underlying Principles of image formation
=
+
Structure
Style (texture)
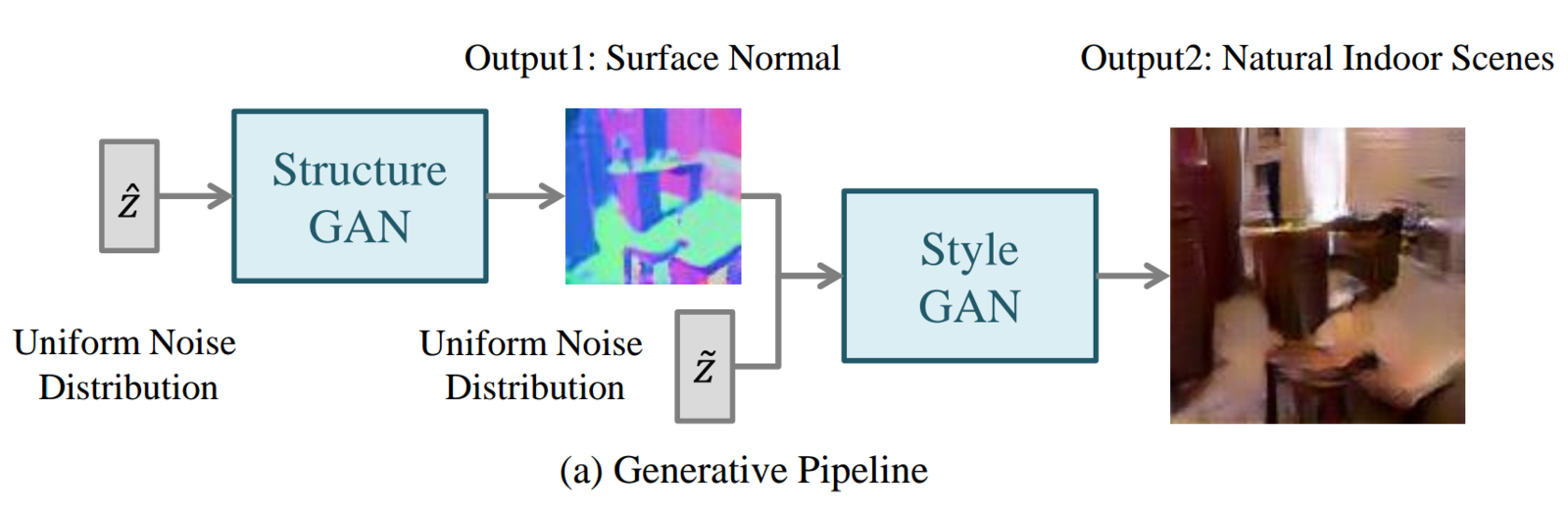
SS-GAN
Style and Structure Adversarial Networks
-
Simplifies the generative process
-
More interpretable
-
Unsupervided learning of RGBD representation
-
Style-GAN as a rendering engine
SS GAN
Dataset: NYU v2 RGBD dataset
Structure-GAN + Style-GAN
Generated Examples
Structure-GAN
Style-GAN
Synthetic Scene Rendering
Style-GAN
Ground truth
Structured-GAN
generates surface normals from sampled
\hat{z}
Generator
Input
100-d vector sampled from uniform distribution
Output
72*72*3 surface normal map
Discriminator
Input
Surface normal maps (1/2 generated, 1/2 ground truth)
Output
Binary classification (generated or ground truth)
\hat{z}
G(\hat{z})
D(\cdot)
\pm1
X_i
\hat{z}
Style-GAN
Conditional GAN
Conditional GAN
Generator is conditioned on additional information
Input
100-d vector sampled from uniform distribution
RGB images
Ground truth surface normal
Output
128*128*3 scene image
\tilde{z}
G(C_i, \hat{z})
C_i
C_i
\tilde{z}
X_i
L_{cond}^D(\mathbf{X, C, \tilde{Z}}) = \sum_{i=1}^{M/2}L(D(C_i, X_i), 1) + \sum_{i=M/2+1}^{M}L(D(C_i, G(C_i, \tilde{z_i}), 0),
L_{cond}^G(\mathbf{C, \tilde{Z}}) = \sum_{i=M/2+1}^{M}L(D(C_i, G(C_i, \tilde{z_i}), 1),
Style-GAN Generator
Style-GAN: full architecture
Drawback
The generated images are noisy
Edges are not well aligned with the surface normal
Style-GAN: full architecture
Multi-task learning with pixel-wise constraints
Assumption: if the generated image is real enough, it can be used for reconstructing the surface normal maps
Style-GAN: full architecture
L_{multi}^G(\mathbf{C, \tilde{Z}}) = L_{cond}^G(\mathbf{C, \tilde{Z}}) + L^{FCN}(G(\mathbf{C, \tilde{Z}}), C)
L^{FCN}(\mathbf{X, C}) = \sum_{i=1}^{M} \sum_{k=1}^{K\times K} softmax (F_k{X_i}, C_{i,k}),
FCN loss
Full loss
Style-GAN: full architecture
EM-like training algorithm
- Fix the generator G, optimize the discriminator D
- Fix the FCN and the discriminator D, optimize the generator G
- Fix the generator G, fine-tune FCN using generated and real images.
Joint Learning for SS-GAN
Experiments
Style-GAN Visualization
Style-GAN
visulized results (gt from NYUv2 test set)
Style-GAN
with/without pixel-wise constraints
Rendering on Synthetic Scene
Inputs are 3D model annotations.
SS-GAN Visualization
DCGAN: Radford et al. "Unsupervised representation learning with deep convolutional generative adversarial networks." arXiv preprint arXiv:1511.06434 (2015).
LAPGAN: Denton et al. "Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks." NIPS, 2015.
Walking the latent space
interpret the model by manipulating the latent space
\hat{z}, \tilde{z}
"Growing" 3D cubic
Shutdown window
Nearest Neighbors Test
Quantitative Results
Scene Classification
Object Detection
Thank you.
https://github.com/xiaolonw/ss-gan
ssgan
By Wei Yang
