Rare-event asymptotics and estimation for dependent random sums
Exit Talk of Patrick J. Laub
University of Queensland & Aarhus University



PhD outline


| 2015 | Aarhus |
| 2016 Jan-Jul | Brisbane |
| 2016 Aug-Dec | Aarhus |
| 2017 | Brisbane/Melbourne |
| 2018 Jan-Apr (end) | China |
Supervisors: Søren Asmussen, Phil Pollett, and Jens L. Jensen

10101
Sums of random variables
Asymptotic analysis / rare-events
Monte Carlo simulation
What is applied probability?
Data
Fitted model
Decision
Statistics
App. Prob.
You have some goal..
Insurance
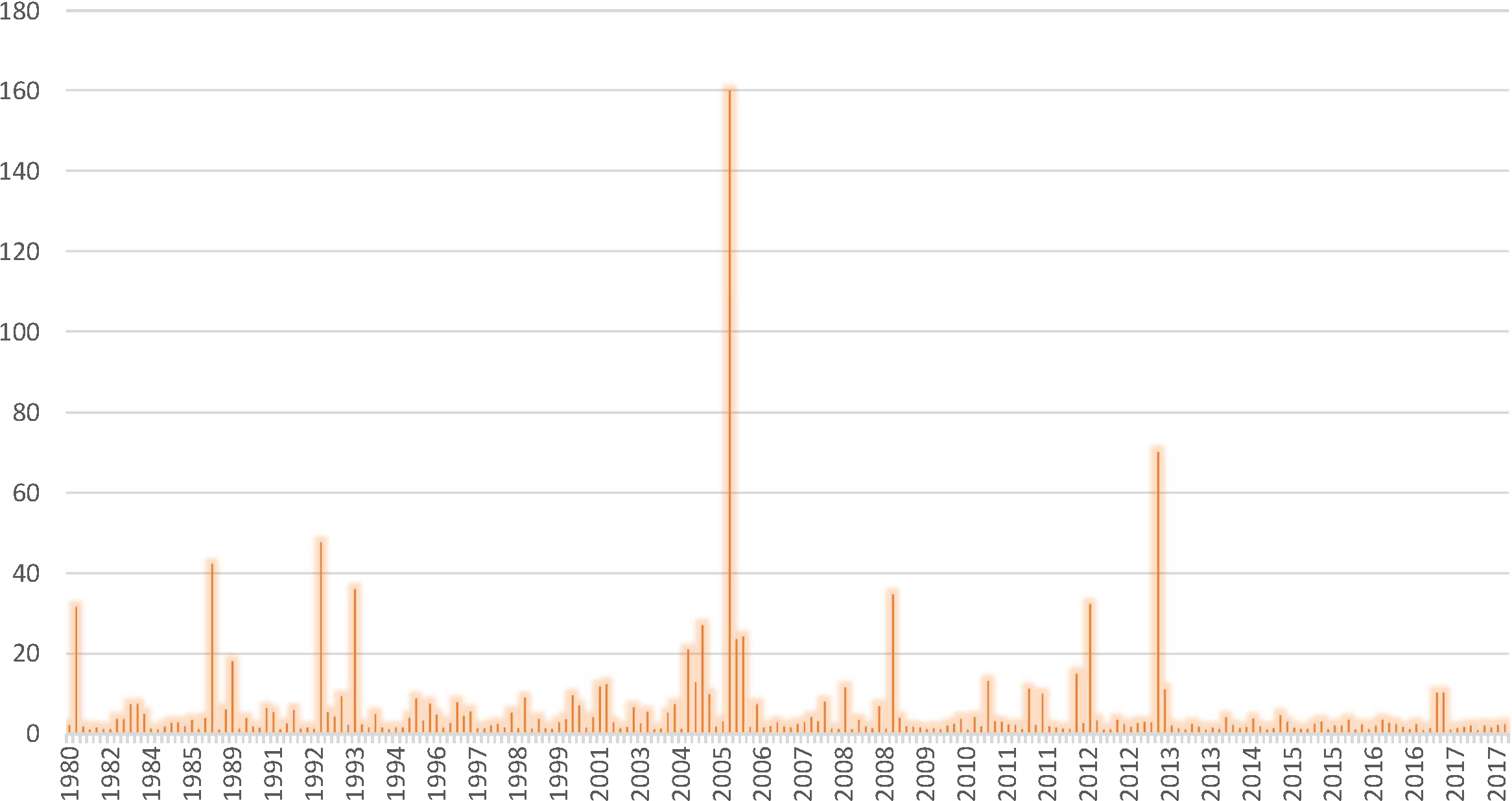
Estimated financial cost of the natural disasters in the USA which cost over $1bn USD. Source: National Centers for Environmental Information
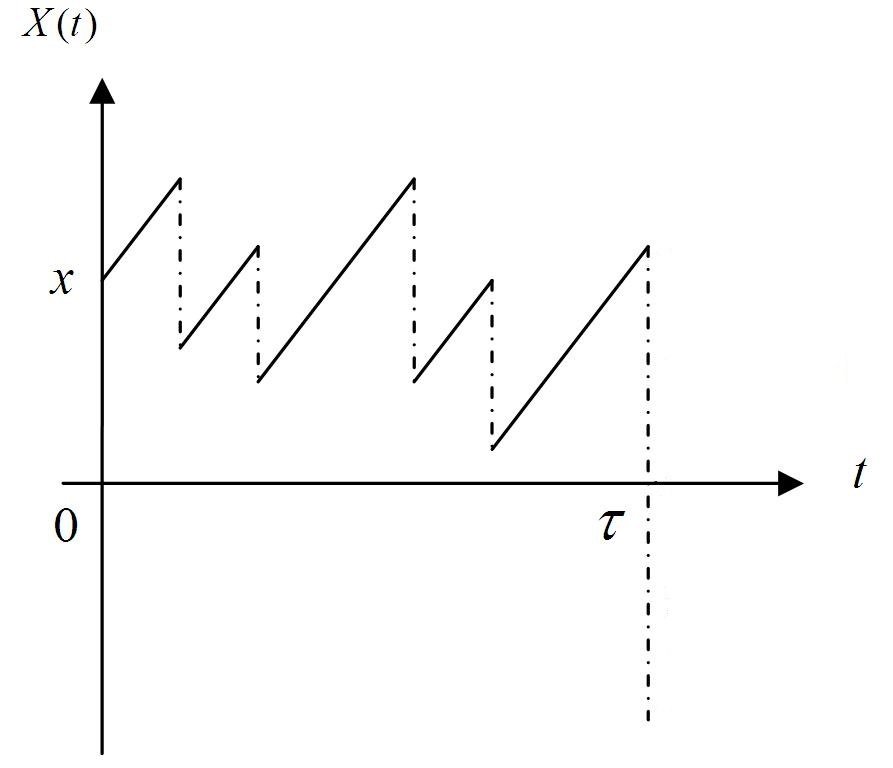
Cramér-Lundberg model
Interested in
- Probability of ruin (bankruptcy) in the next 10 years
- Probability of ruin eventually
- Stop-loss premiums
E.g. guaranteed benefits
An investor's problems
Want to know:
- cdf values
- value at risk
- expected shortfall
Modelling stock prices
Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of political economy


Fischer Black Myron Scholes
Can you tell which is BS?
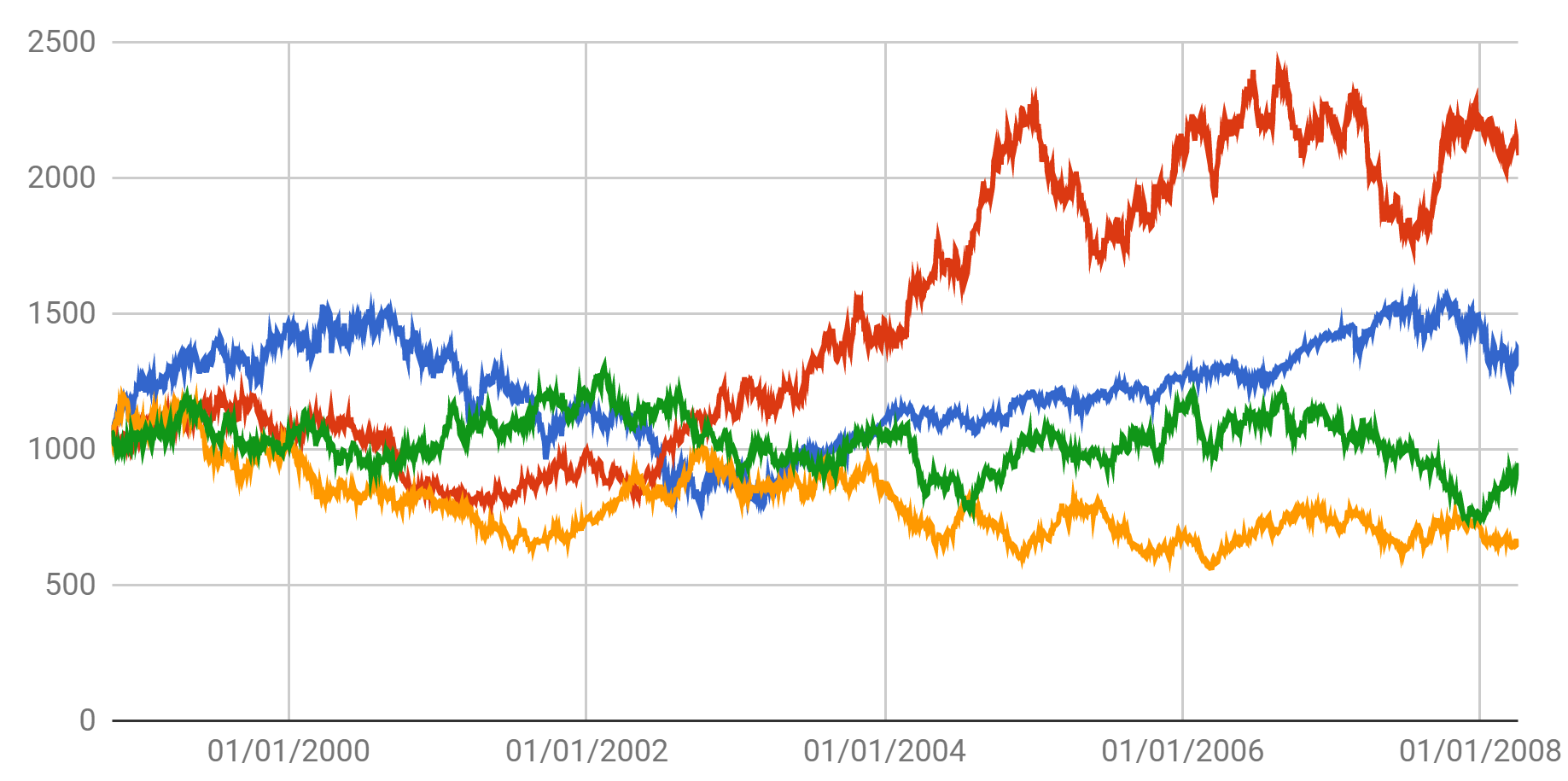
S&P 500 from Oct 1998 to Apr 2008
Google Finance

Geometric Brownian motion
In words, Stock Price = (Long-term) Trend + (Short-term) Noise
That's just the beginning..
General diffusion processes...
Stochastic volatility processes...
SV with jumps...
SV with jumps governed by a Hawkes process with etc...
Monte Carlo

Quasi-Monte Carlo
For free, you get a confidence interval
Sum of lognormals distributions
where
What is that?
Start with a multivariate normal
Then set
Then add them up
What's known about sums?
Easy to calculate interesting things with the density
Density can be known..
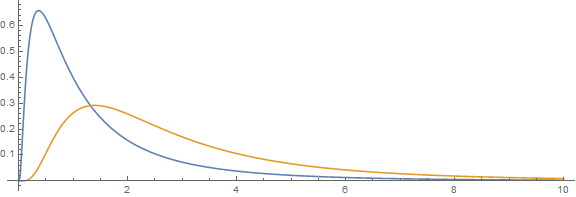
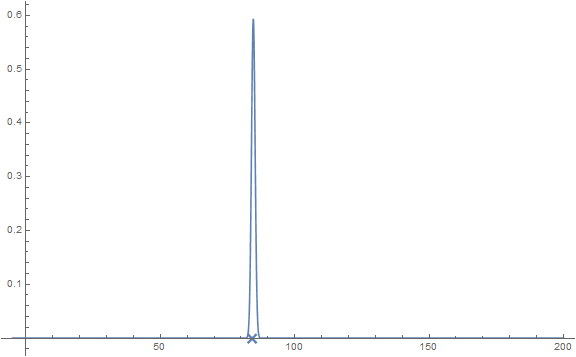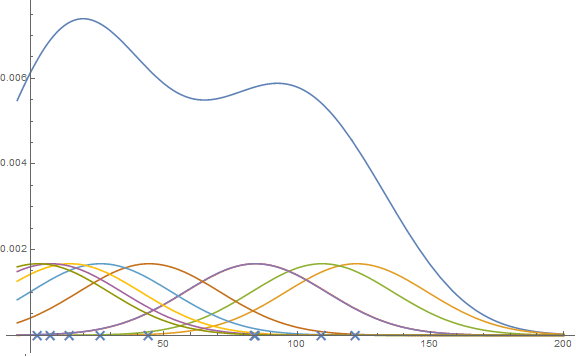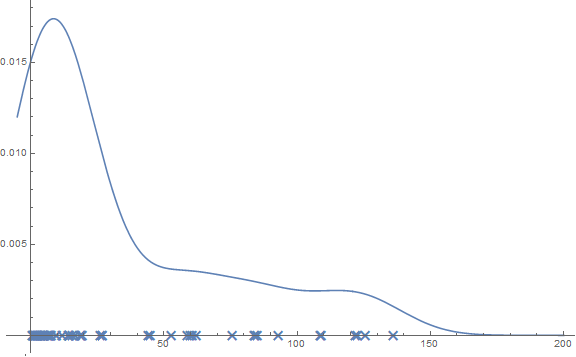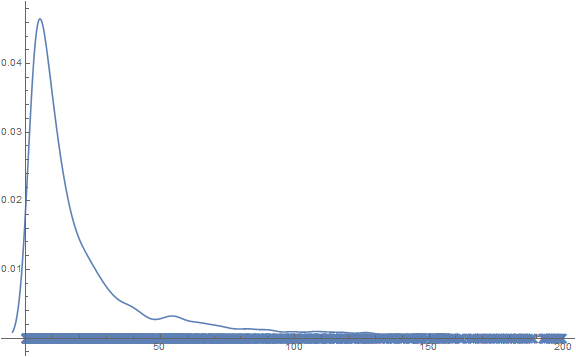
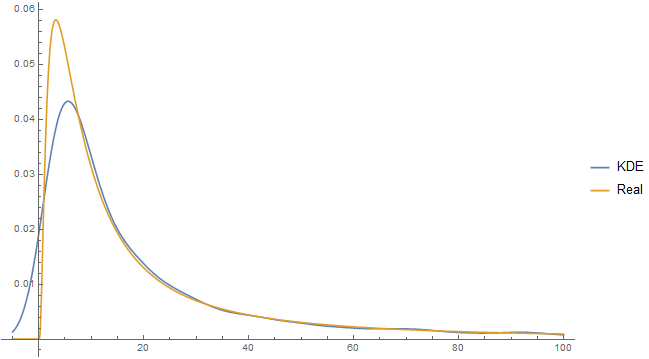
Example
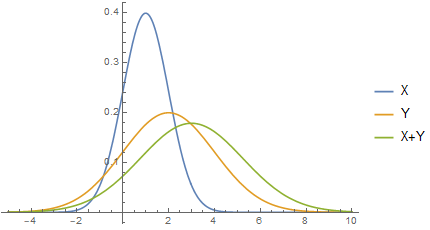
Kernel-density estimation
Laplace transform approximation
No closed-form exists for a single lognormal
Asmussen, S., Jensen, J. L., & Rojas-Nandayapa, L. (2016). On the Laplace transform of the lognormal distribution. Methodology and Computing in Applied Probability


Generalise to d dimensions
- Setup Laplace's method
- Find the maximiser
- Apply Laplace's method
Laub, P. J., Asmussen, S., Jensen, J. L., & Rojas-Nandayapa, L. (2016). Approximating the Laplace transform of the sum of dependent lognormals. Advances in Applied Probability








Generalise to d dimensions
- Setup Laplace's method
- Find the maximiser
- Apply Laplace's method
Solve numerically:
What is the maximiser?

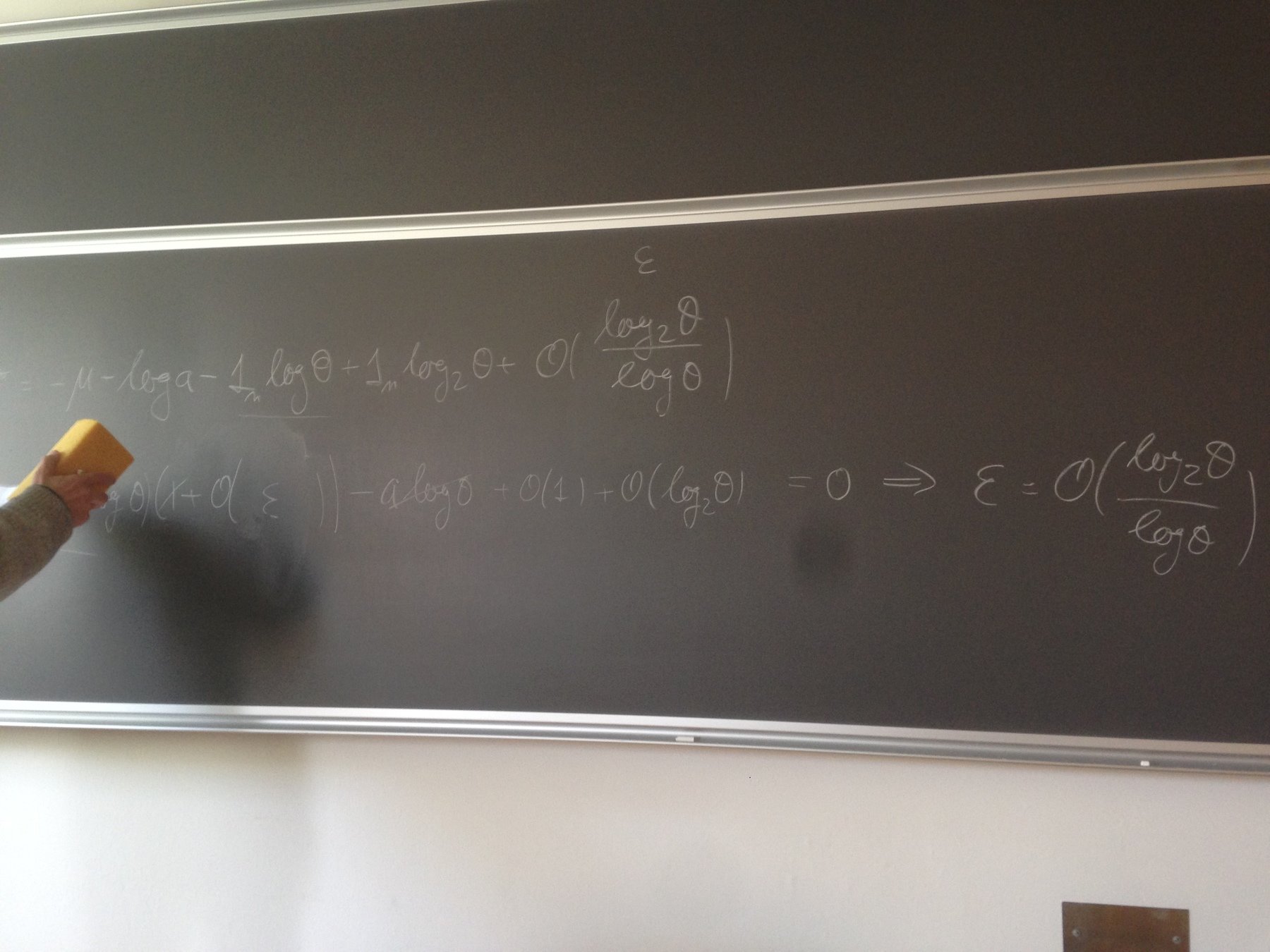
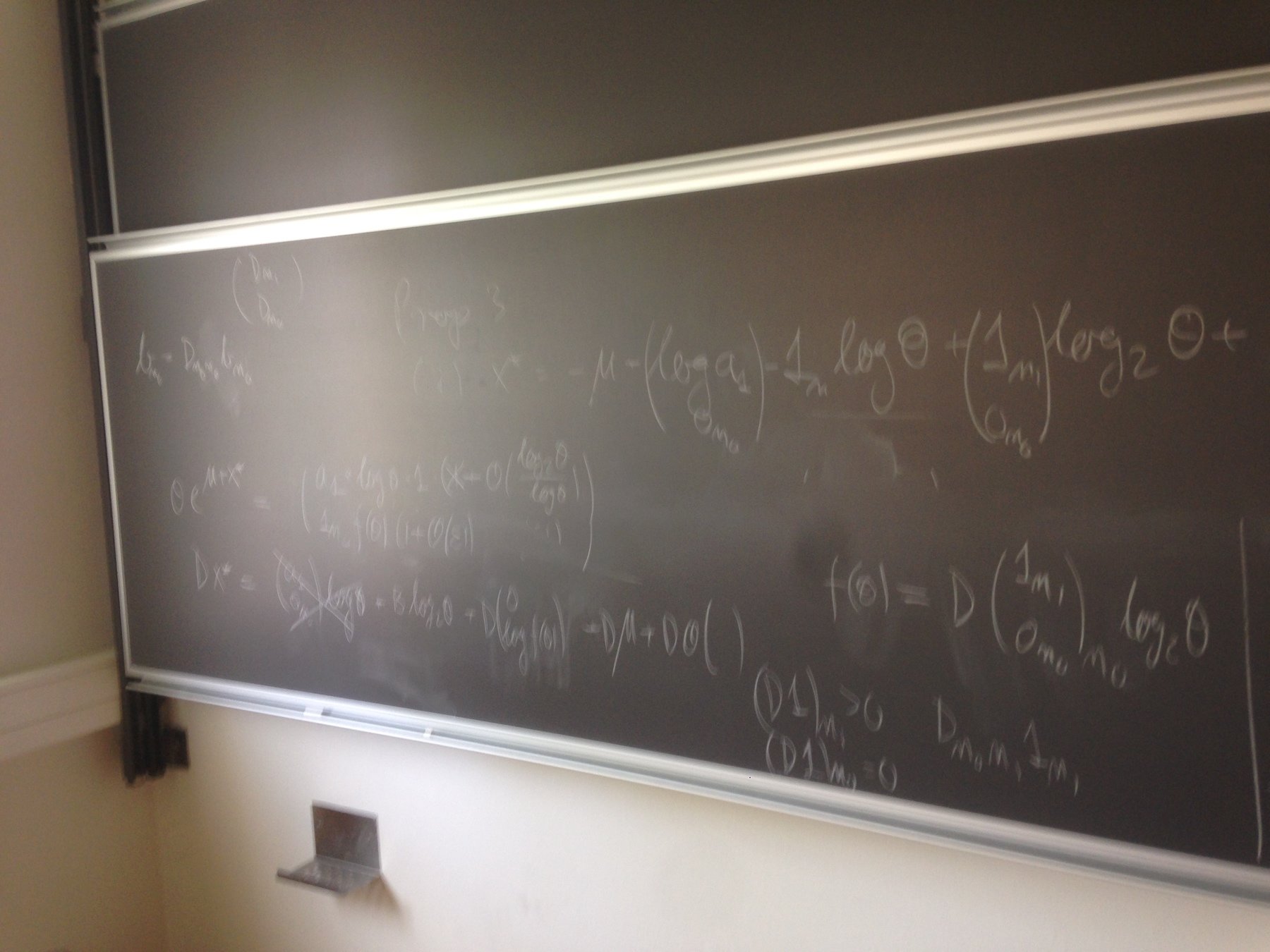
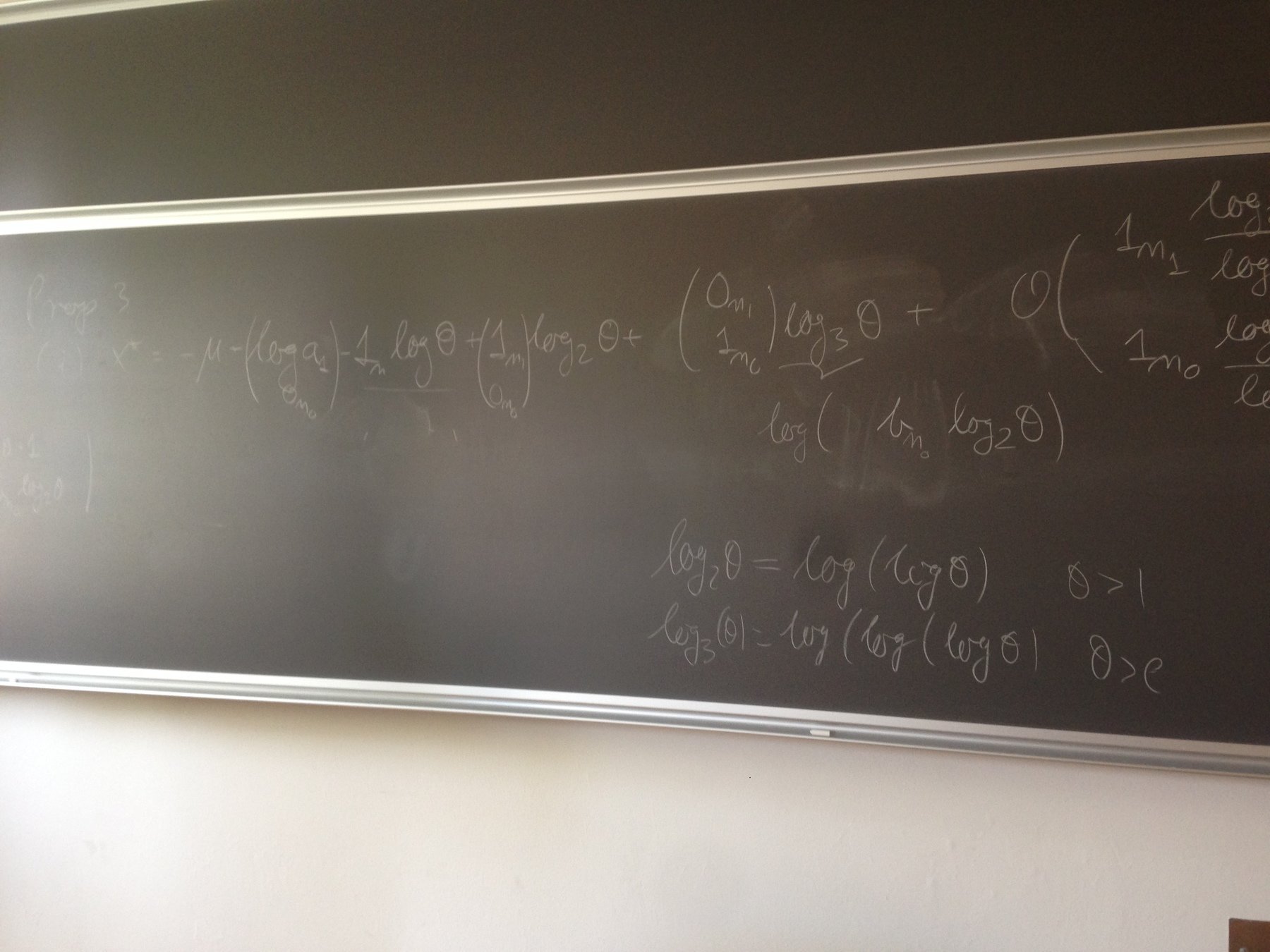

Savage condition
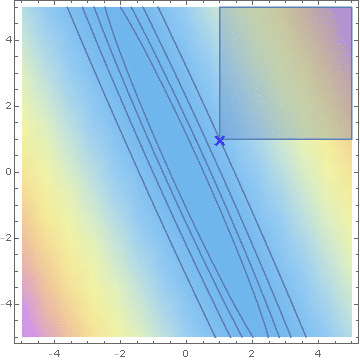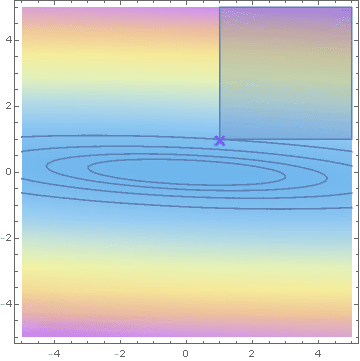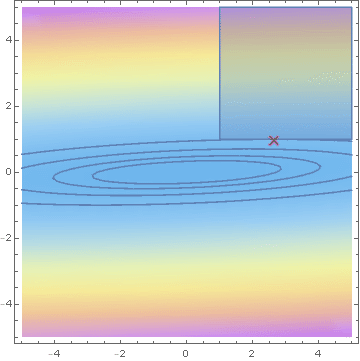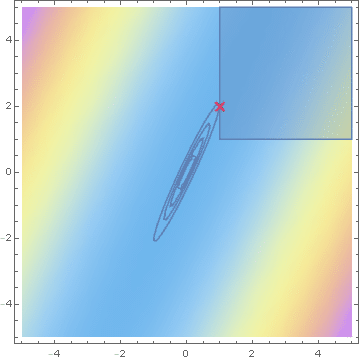
Hashorva, E. (2005), 'Asymptotics and bounds for multivariate Gaussian tails', Journal of Theoretical Probability
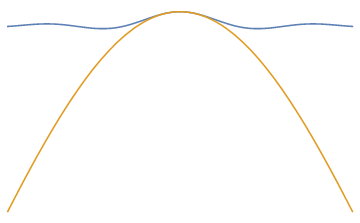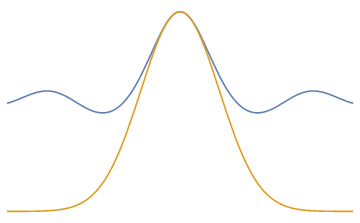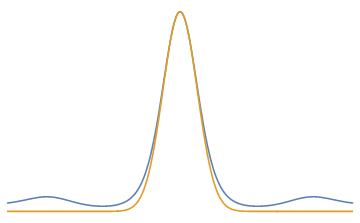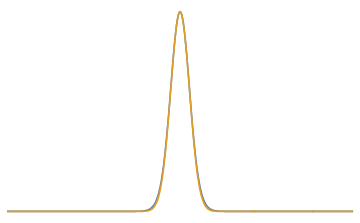
Laplace's method
Find
Expand with 2nd order Taylor series about the maximiser
Example
Orthogonal polynomial expansions
- Choose a reference distribution, e.g,
2. Find its orthogonal polynomial system
3. Construct the polynomial expansion

Pierre-Olivier Goffard
Asmussen, S., Goffard, P. O., & Laub, P. J. (2017). Orthonormal polynomial expansions and lognormal sum densities. Risk and Stochastics - Festschrift for Ragnar Norberg (to appear).
Orthogonal polynomial systems
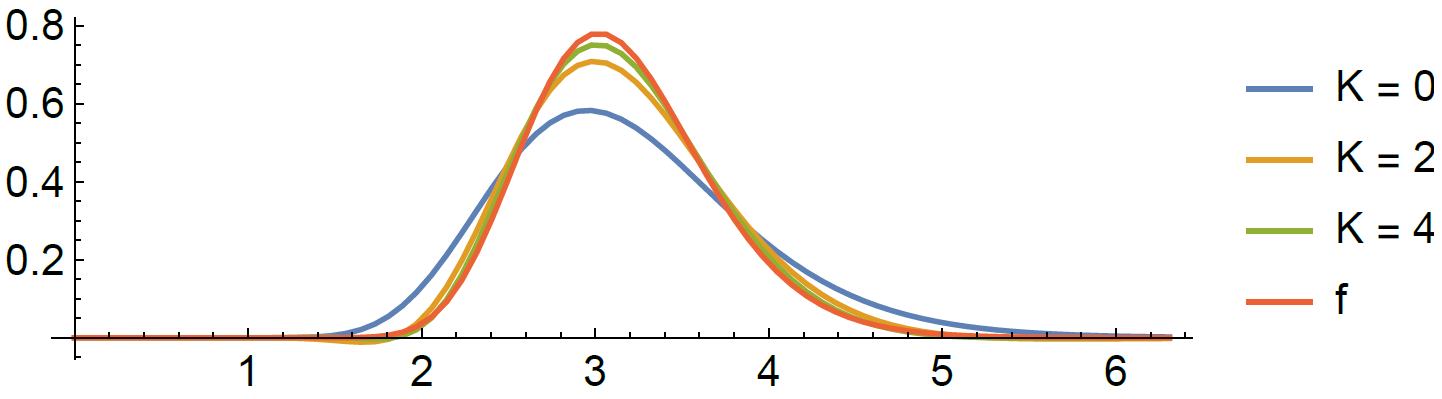
Example: Laguerre polynomials
If the reference is Gamma
then the orthonormal system is
For r=1 and m=1,
Final steps
Final final step: cross fingers & hope that the q's get small quickly...
Calculating the coefficients
1. From the moments
2. Monte Carlo Integration
3. (Dramatic foreshadowing) Taking derivatives of the Laplace transform...
Applied to sums
- Moments
- Monte Carlo Integration
- Taking derivatives
- Gauss Quadrature
Title Text
Subtitle
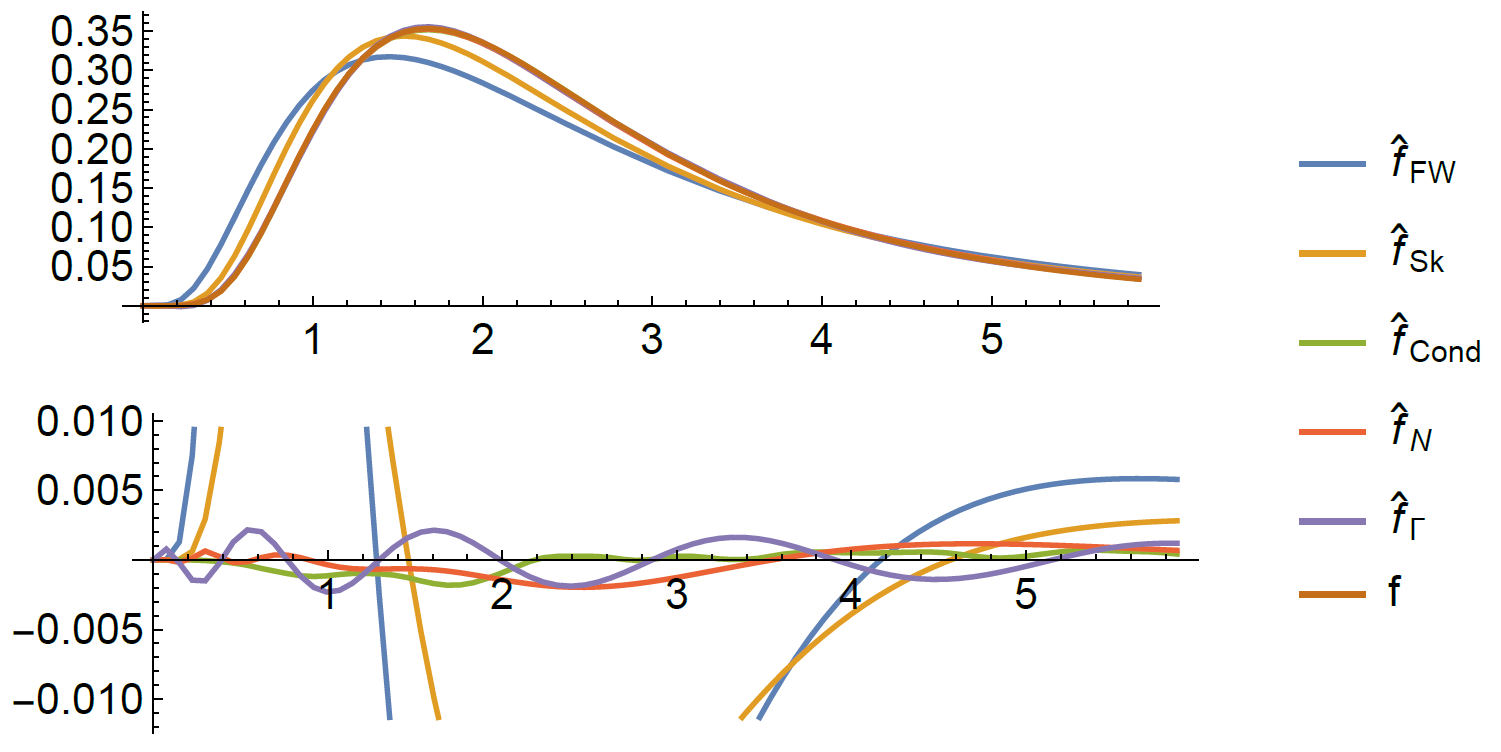
An example test
Applications to option pricing
Dufresne, D., & Li, H. (2014).
'Pricing Asian options: Convergence of Gram-Charlier series'.
Goffard, P. O., & --- (2017). 'Two numerical methods to evaluate stop-loss premiums'. Scandinavian Actuarial Journal (submitted).
Extension to random sums
Say you don't know how many summands you have...
Imagine you are an insurance company;
there's a random amount of accidents to pay out (claim frequency),
and each costs a random amount (claim size)
Approximate S using orthogonal polynomial expansion
A simplification
where
The stuff we want to know
As
and using
we can write
Laplace transform of random sum
With we can deduce
and just take derivatives

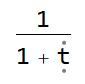
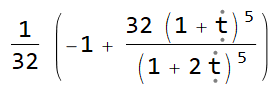
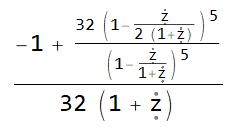
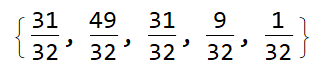
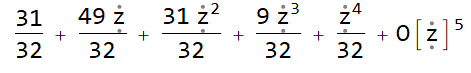
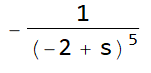
Another example test
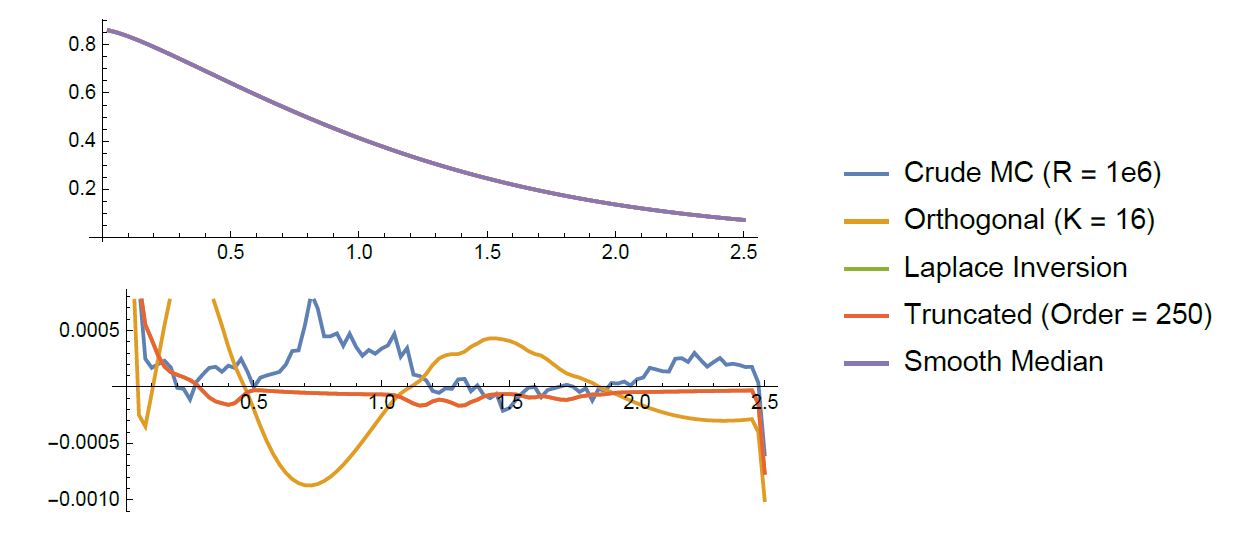
Other things I don't have time to talk about
- Andersen, L.N., ---, Rojas-Nandayapa, L. (2017) ‘Efficient simulation for dependent rare events with applications to extremes’. Methodology and Computing in Applied Probability
- Asmussen, S., Hashorva, E., --- and Taimre, T. (2017) ‘Tail asymptotics of light-tailed Weibull-like sums’. Polish Mathematical Society Annals.
In progress:
- Taimre, T., ---, Rare tail approximation using asymptotics and polar coordinates
- Salomone, R., ---, Botev, Z.I., Density Estimation of Sums via Push-Out, Mathematics and Computers in Simulation
- Asmussen, S., Ivanovs, J., ---, Yang, H., 'A factorization of a Levy process over a phase-type horizon, with insurance applications


Thomas Taimre
Robert Salomone
Thanks for listening!
and a big thanks to UQ/AU/ACEMS for the $'s
And thanks to my supervisors





Rare-event asymptotics and estimation for dependent random sums – an exit talk, with applications to finance and insurance
By plaub
Rare-event asymptotics and estimation for dependent random sums – an exit talk, with applications to finance and insurance
- 3,021



