Algorithms and Data Structures

Requests

Don't feel shy.
Don't reveal the answers.
Correct me.

Algorithms

A procedure to solve a problem.

What kind of problem?

Suppose you have a list of random phone numbers and you want to check duplicates.

How you will tackle this problem in your routine life?

Take the first number, will look through the whole list for duplicates and repeat the same for each number.

Lets Code it !

The phone numbers are stored in a Array named pnum.

pnum[n]
flag=0
for i=0 to n
    for j=0 to n
        if i not equals j and pnum[i] equals pnum[j]
            flag=1
            break
if flag equals 1
    Print "Duplicates found"
else
    Print "No Duplicates"

Pseudcode

Is it the best way to solve it or better ways are there?

Will try to find out as the lecture proceeds.

Lets try one more example !

You are working as a secret officer in an intelligence agency. You got an assignment to find the real message from a set of messages which are interaction of two Aliens. Each message contain two words which may or may not be meaningless. The real message is the longest common subsequence of the two words. You have to do it fast to save us.

Come on lets save the world.

Let's try Hit and Trial method.

Take every subsequence of first string and try to find it in second. List all the subsequences and the biggest will be the message.

Oh No! Timesup!

We have to something better.

Analysis of Algorithms

Why to do so ?

Because time and space are not infinite.

Ex: Aliens are invading us and we have to decode there message asap.

We are given a character and we want to build a String containing that character n number of times.

Problems Everywhere

public static String repeat(char c, int n){
    String answer="";
    for(int j=0;j<n;++j)
        answer=answer+c;
    return answer;
}

public static String repeat2(char c, int n){
    StringBuilder sb=new StringBuilder();
    for(int i=0;j<n;++j)
        sb.append(c);
    return sb.toString();
}

Method 1 using String

Method 2 using StringBuilder

Method 2 takes 13.5 seconds !

More than one half of the time to run 100 meters.

Guess how much Method 1 will take to do this !

Suppose we have a String of 12.8 million characters. How much time it will take?

Never try this!

It will take 26,569,642.1seconds which is more than 3 days.

Analyzing running time of algorithms

Assigning a value to a variable
Performing an Arithmetic operation
Comparing two numbers
Accessing a single element of an array by Index

Primitive Operations

Which takes constant time to execute

Focusing on worst case Input

Measuring operations as a Function of Input Size

Constant function
Logarithm function
Linear function
N Log-N function
Quadratic function
Polynomial function
Exponential function

The seven functions

f(n) = C

f(n) = logN

f(n)=n

f(n)=nlogn

f(n)=n^2

f(n) = n^a (a=3,4,..)

f(n) = b^n

Let f(n) and g(n) be functions mapping positive integers to positive real numbers. We say f(n) is O(g(n)) if there is a real constant c>0 and an integer constant n'>=1 such that

f(n) <= c.g(n) , for n >= n'

The Big-Oh notation

The Big-Oh notation allows us to ignore constant factors and lower order terms.

Focus on main components of a function that affect its growth.

For example

5n^4 + 3n^3 + 2n^2 + 4n +1 is O(n^4)
8n + 5 is O(n)
5n^2 + 3nlogn + 2n +5 is O(n^2)
3logn + 2 is O(logn)
2^(n+2) is O(2^n)
2n + 100logn is O(n)
54 is O(1)

Finding Big-Oh of algorithms designed so far.

The duplicate number problems.

Comparing, assignment and increment are primitive operations.
Two for loops each running for n times.

The LCS problem

Trying each subsequence and checking its existence.

The String building problem

Method 1

Method 2

A for loop running n times.
String concatenation operation.

A for loop running n times.
Appending a character at the end of string.

Time complexity

Duplicate number problem : O(n^2)
LCS problem : O(2^n)
String Building(Method 1) : O(n^2)
String Building(Method 2) : O(n)

Digging Deeper

The Algorithm Design Manual (Steven Skiena) : Chapter 2
Introduction to Algorithm (CLRS) : Chapter 2 and 3
Algorithm Unlocked (Thomas H. Cormen) : Chapter 2

Its enough analyzing, lets learn new algorithms and analyze them

Sorting and Searching Algorithms

Sorting refers to arranging the elements of an array in certain order generally ascending.
Searching refers to finding elements in an array.

Bubble Sort

Each time move the biggest element to the last.

Algorithm used

Checking two consecutive elements, if the left one is bigger than right one, swap. Repeat this N times.

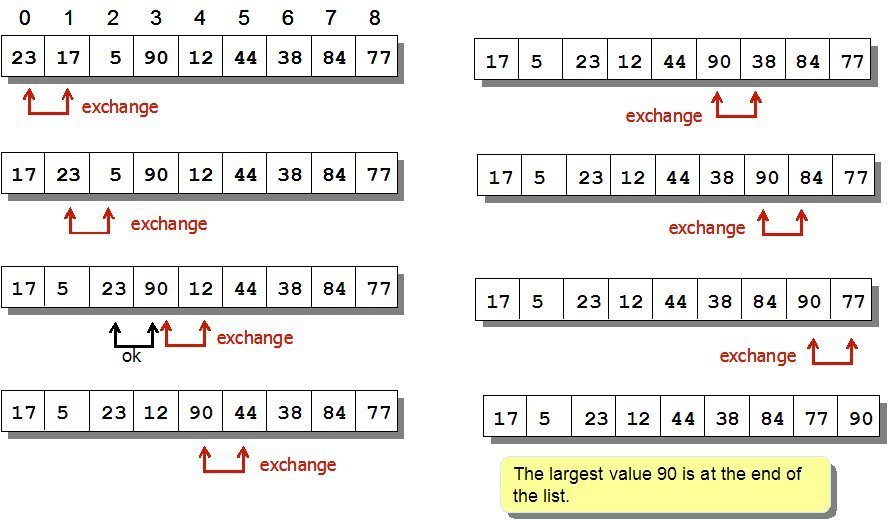
Time Complexity of Bubble Sort

Two nested for loops. First running for n times. Second for n, n-1,n-2, .... ,3,2,1 times.

f(n) = n+(n-1)+(n-2)+....+3+2+1

= n(n+1)/2

O(f(n)) = O(n^2)

Other sorting algorithms with quadratic running time

Selection Sort
Bubble Sort
Quick Sort (worst case)

Merge Sort

Sorts in O(nlogn) time.

Based on recursion and Divide and Conquer.

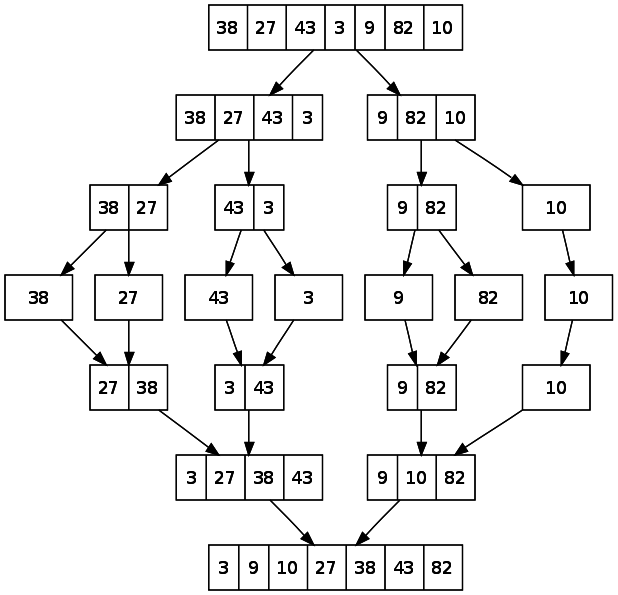
Other sorting algorithms

Counting Sort
Radix Sort

Searching algorithms

Naive method : O(n)
Binary Search : O(log n)

Note: Binary search works on sorted arrays.

Data Structures

Arrays

Array is just a list of some objects of certain datatype.

We have 1-D and 2-D arrays.

Each element is stored at a certain index and can be accessed using that index.

Vectors or ArrayList

Same as array but elements can be removed or inserted while executing.

Dictionaries or Hash Tables

Store a list of keys having a value associated with each of them.

Stacks (LIFO)

A list in which only the last element entered can be accessed or manipulated.

Queues (FIFO)

A list of objects in which only initially entered/first element can be accessed or manipulated.