Graphs
What are Graphs?
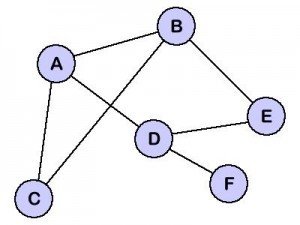


A Graph is a set of vertices and edges.
The edges can be directed on undirected.
Vertices represents any point, person, thing or anything.
Edges represent a certain relation between the vertices.
Representation
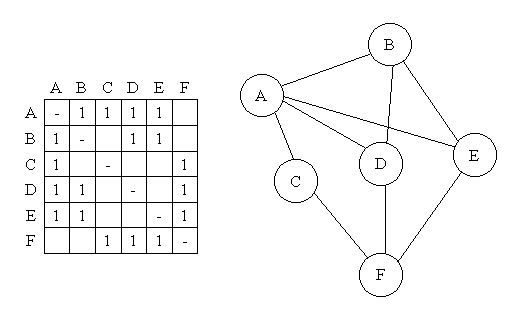
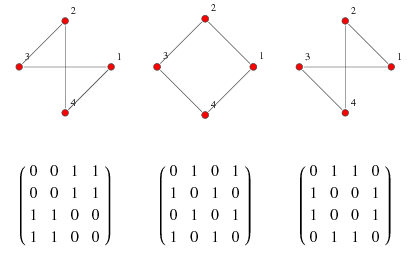
Adjacency Matrix
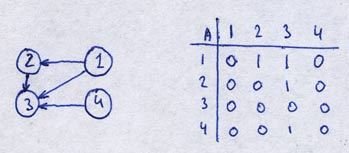
Topological Sort
Topological sort is used to convert a directed (acyclic) graph into a linear order such that if any event B requires that A be completed before B is initiated then A will occur before B in the ordering.
You decide to wake up at 7 am, catch a cab at 7:30 and reach office by 8. You would then want to have breakfast @ office by 8:30 which you definitely wouldn't be able to have unless you follow the above three. If you plan to attend the meeting at 8:40 after you have the breakfast by 8:30, then you want to finish your breakfast first.
You have to compute:
C =A+B
D= A+C
E = D+C
A = F+G
In which order they will be evaluated.
That's all Topological Sorting.
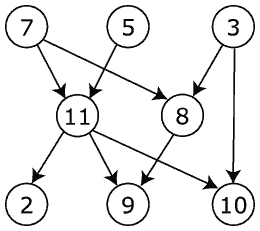
Lets order the previous examples and below one, notice the procedure and see what are the things required to produce the order.
Procedure
- Find a task which has indegree zero and add it to the order.
- Remove the task from the list.
- Repeat until all tasks are performed.
Algorithm
Preprocess the graph, make the adjacency matrix and store indegree of each vertice.
Add the vertice with indegree zero to the order, decrease the indegree of vertices which are connected to it.
Repeat adding vertices until all are add.
So try coding each step.
Pseudocode
//Input the graph
//Build the Adjacency Matrix - adj[][]
//Compute an array which contains indegree of each vertice - indegree[]
Stack cur //Initializing a stack
List order //Initializing a list in which final order will be saved
for each vertice
if(indegree[e]==0)
cur.push(e) //Adding all vertices with indegree zero
while(cur is not empty)
current_vertice=cur.pop()
order.add(current_vertice)
for each vertice v connected to current_vertice
--indegree[v] //Decreasing indegree if vertices
if(indegree[v]==0)
cur.push(v)
Problems on topological sort
- http://www.spoj.com/problems/PFDEP/
- http://www.spoj.com/problems/DEPEND/
- http://www.spoj.com/problems/TOPOSORT/
- UVA Problem No. : 124, 196, 200, 872, 10305
Breadth First Search
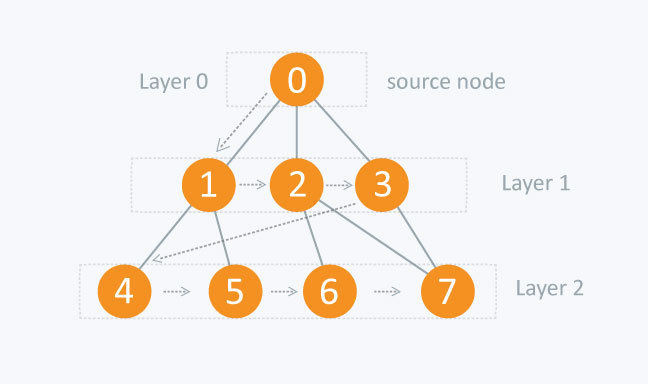
Breadth-first search (BFS) is an algorithm for traversing or searching graph data structures. It starts at some arbitrary node of a graph and explores the neighbor nodes first, before moving to the next level neighbors.
Traverse the vertices horizontally or layer-wise from a particular source vertex.
How it works
- From a source node, visit all the vertices which are connected to it.
- Then visit the vertices which are connected to those vertices which we have visited and are remained unvisited.
- Repeat this until every vertice is visited.


Things to store
- Whether a certain vertice is visited or not.
- A list which contains all the vertice to be visited in a specified order.
Things to do
- Visit a vertice and add all its children vertices in to_be_visited list.
- Before visiting a vertex check it is already visited or not.
- If not, visit it and add it to the visited.
Pseudocode
BFS (G, s) //where G is graph and s is source node.
Queue Q //Initializing a queue which will store the vertices to be visited
Q.enqueue( s )
visited[]
visited[s]=1
while ( Q is not empty)
// removing that vertex from queue,whose neighbour will be visited now.
v = Q.dequeue( )
//processing all the neighbours of v
for all neighbours w of v in Graph G
if visited[w]=0
Q.enqueue( w ) //stores w in Q to further visit its neighbour
visited[w]=1;deck
By Pulkit Goyal
deck
- 1,178



