The High-Dimensional Structure of
Visual Cortex Representations
A Dissertation Proposal
Outline
- Motivation
-
Projects
- Universal scale-free representations in human visual cortex
- Spatial-scale invariant properties of mammalian visual cortex
- Characterizing the representational content of different latent subspaces
- Timeline
Motivation
- Population codes in cortex are not fully understood
- Standard methods include
- decoding: "Can the neural responses do task ___ ?"
- encoding: "Can my model predict neural responses?"
What are the statistical properties of the cortical representations themselves?
Specifically, let's look at dimensionality.
A low-dimensional theory of visual cortex
Goal
Compress high-dimensional images onto a low-dimensional manifold that supports behavior while being robust to stimulus variation
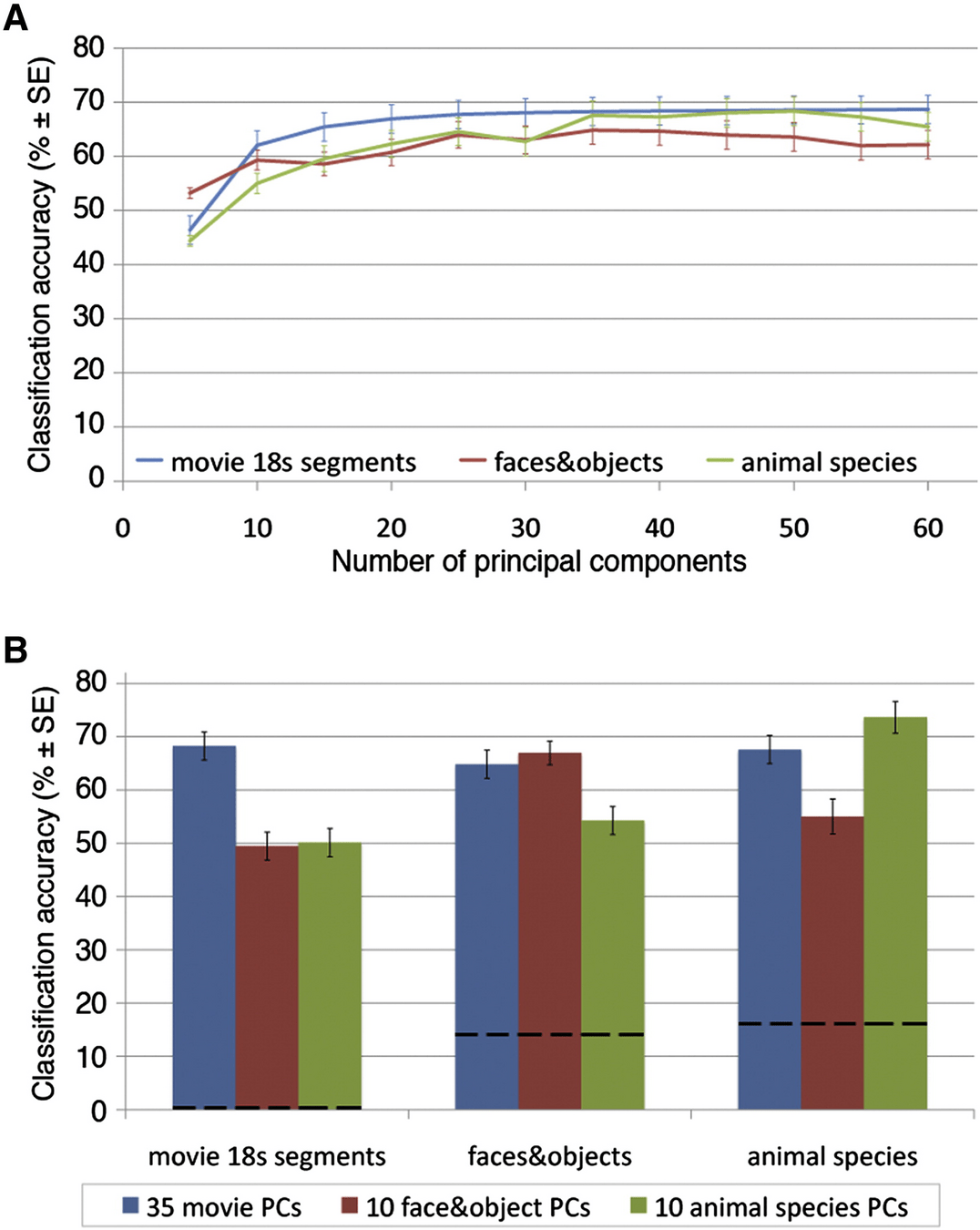
Haxby (2011), movie-viewing fMRI
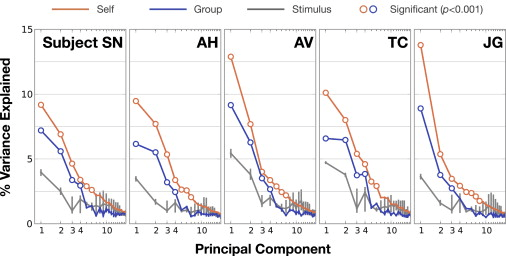
Huth (2012), movie-viewing fMRI, semantic space
Lehky (2014), objects, monkey electrophysiology

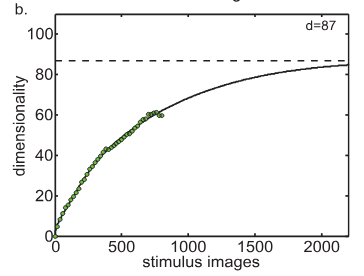
A high-dimensional theory of visual cortex
Benefits
Expressive enough to capture the complexity of the real world; supports performing a variety of tasks
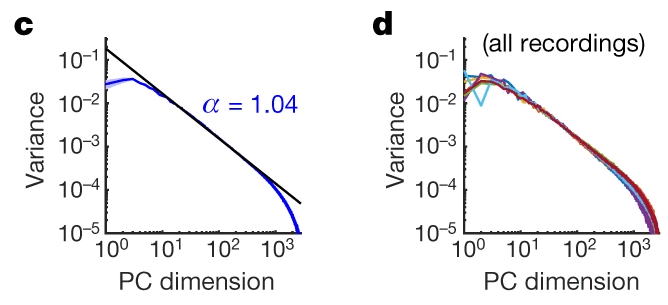
Stringer (2019), mouse visual cortex, ImageNet
mouse cortex also scales to ~10^6 dimensions, Manley et al. (2024)
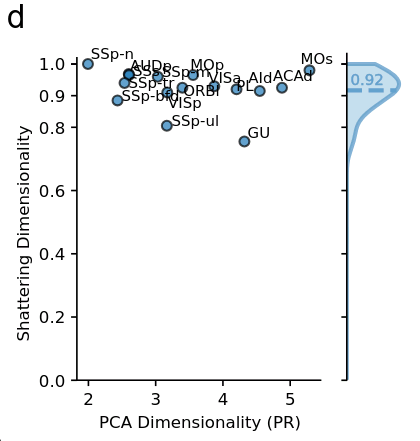
Posani (2024), mouse cortex during behavior
How can we resolve these contradictions?
Use new large-scale, high-quality fMRI datasets!
Project 1
Universal scale-free representations in human visual cortex
[manuscript under review]
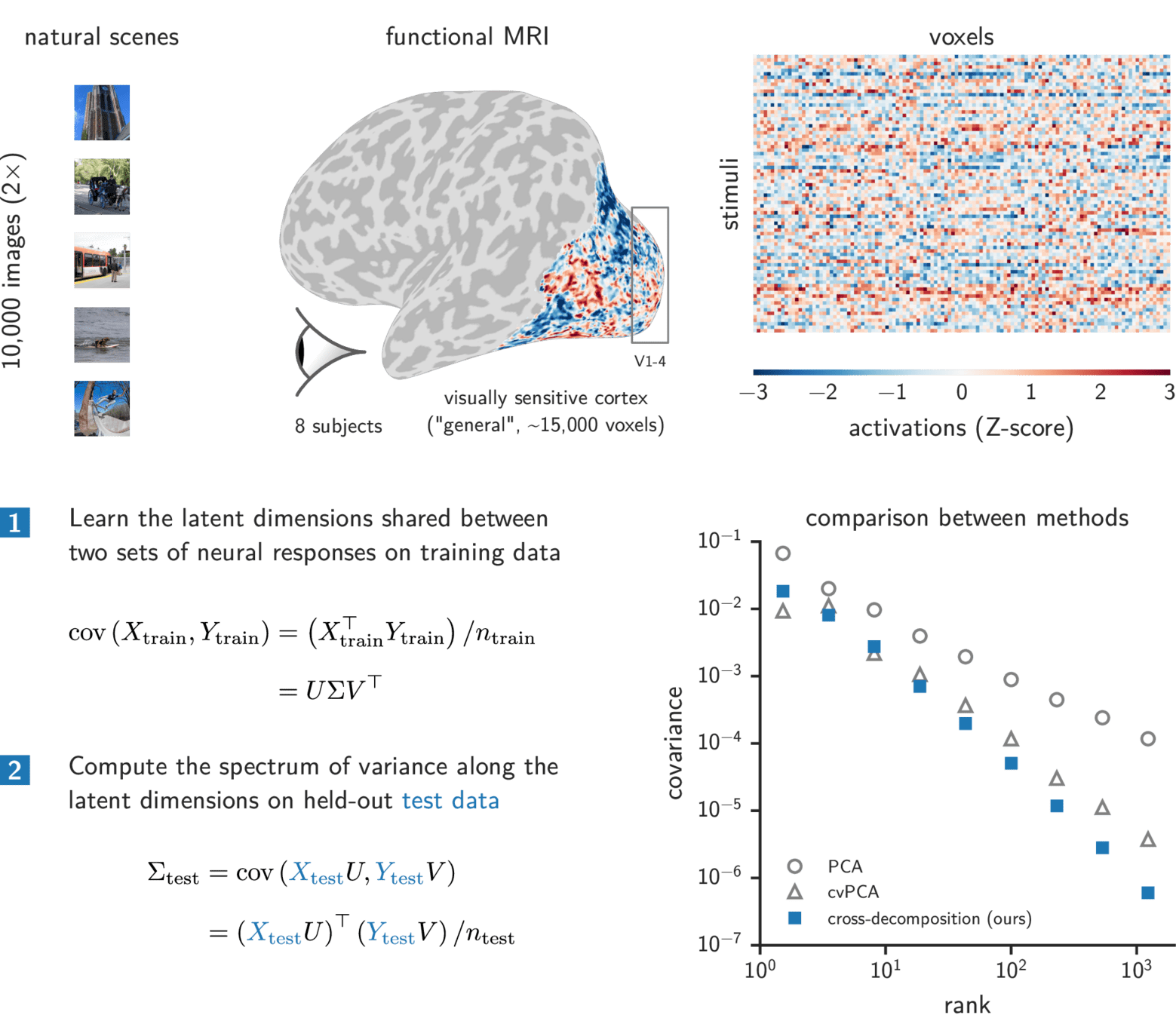
The Natural Scenes dataset

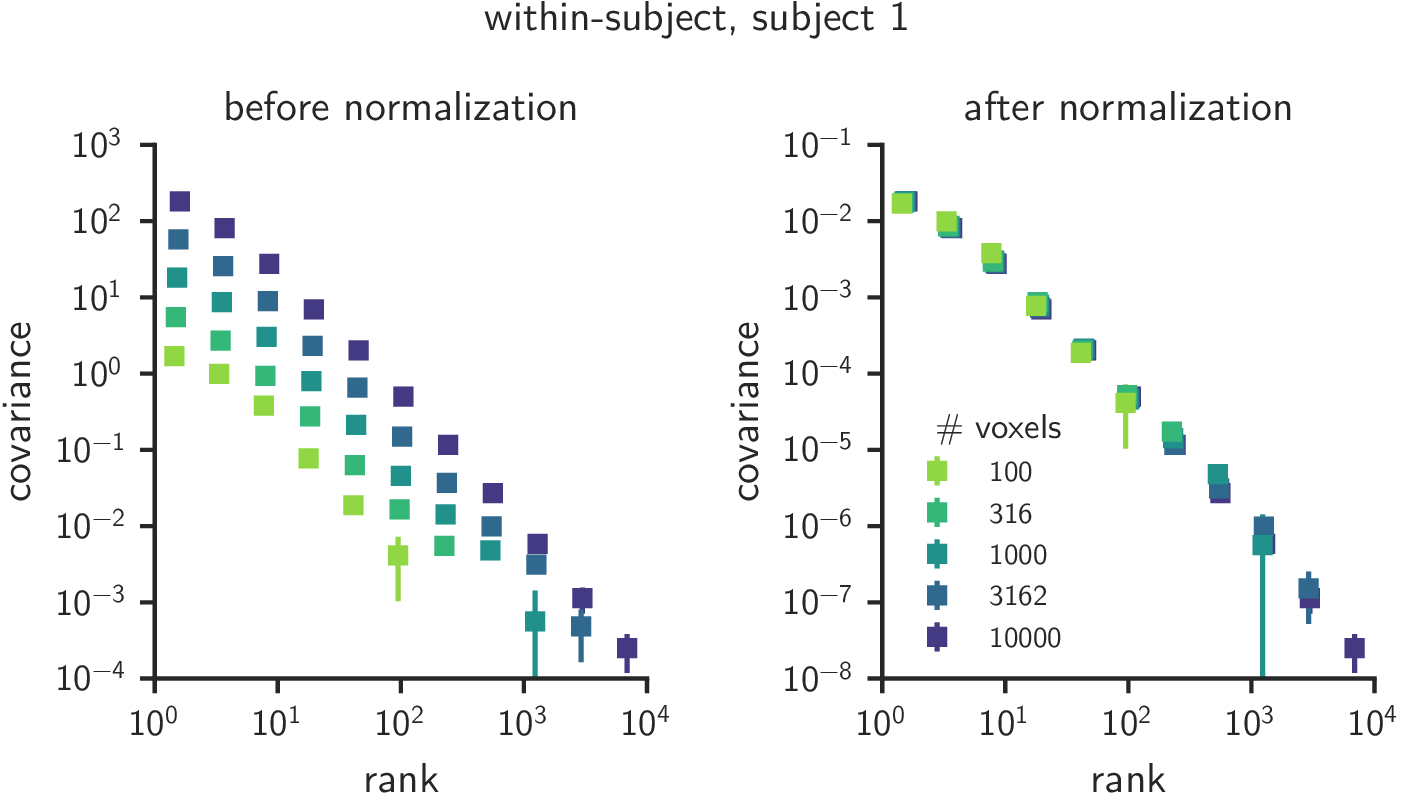
Cross-decomposition ~ cvPCA + hyperalignment

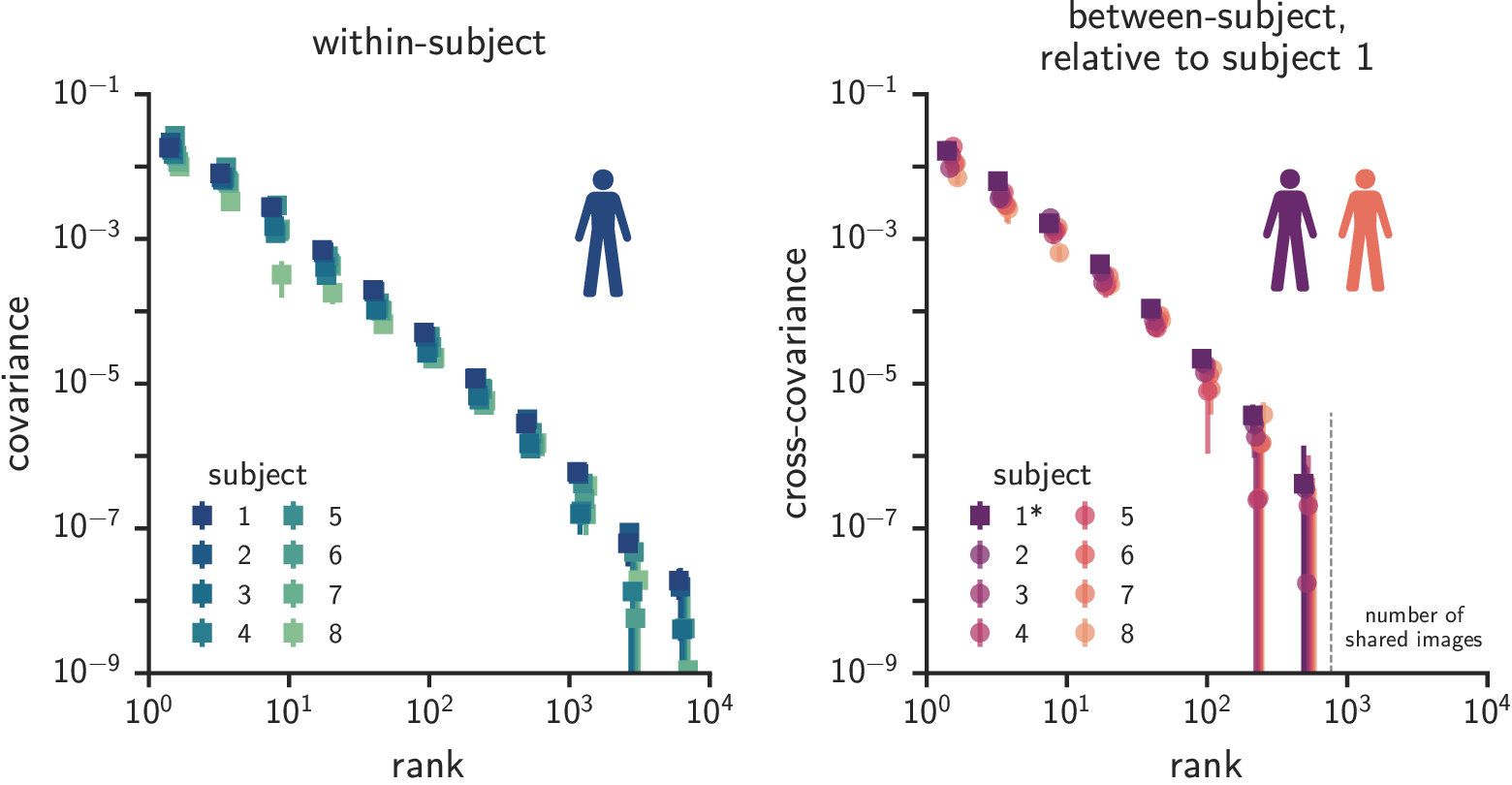
Universal scale-free covariance spectra
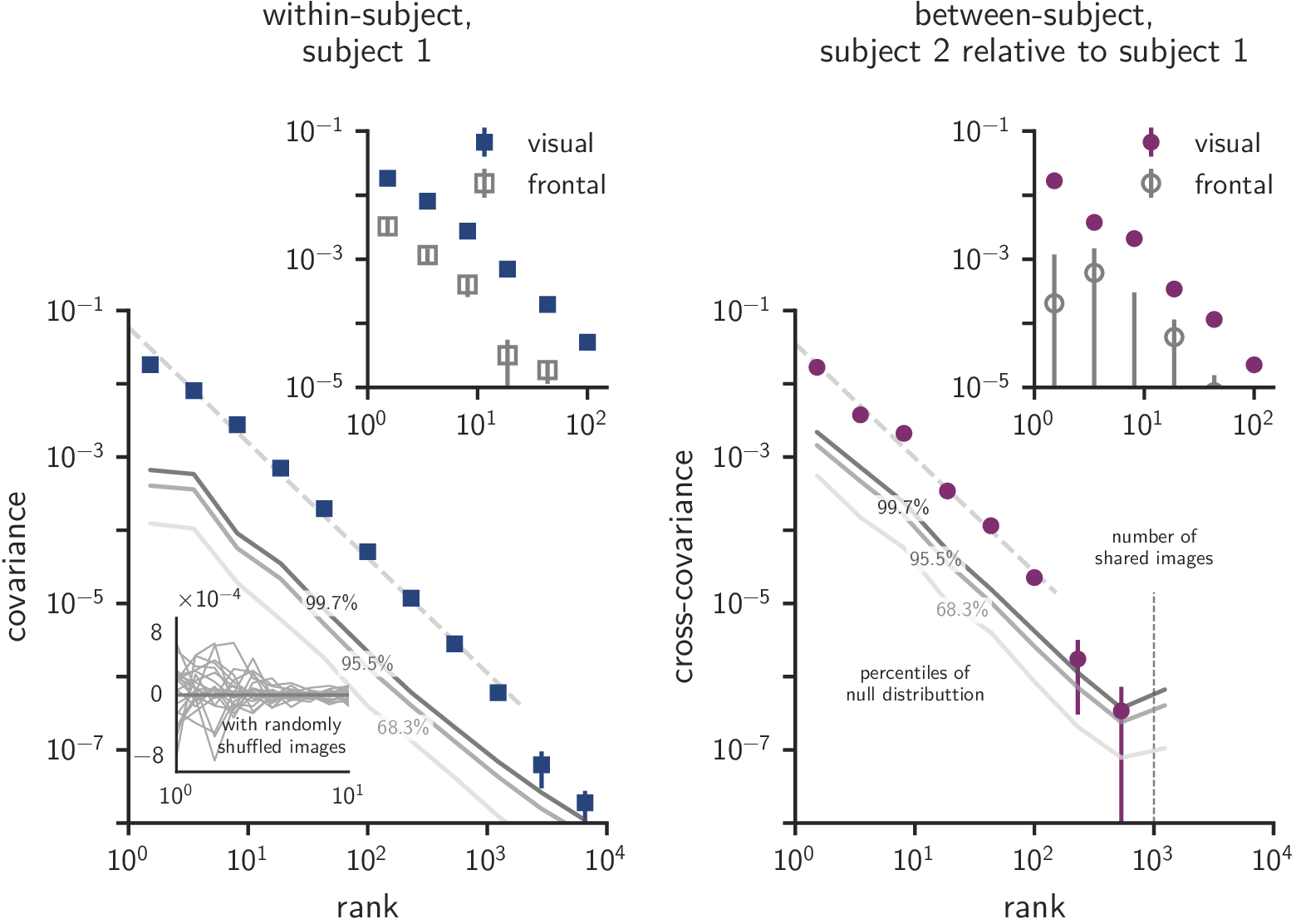
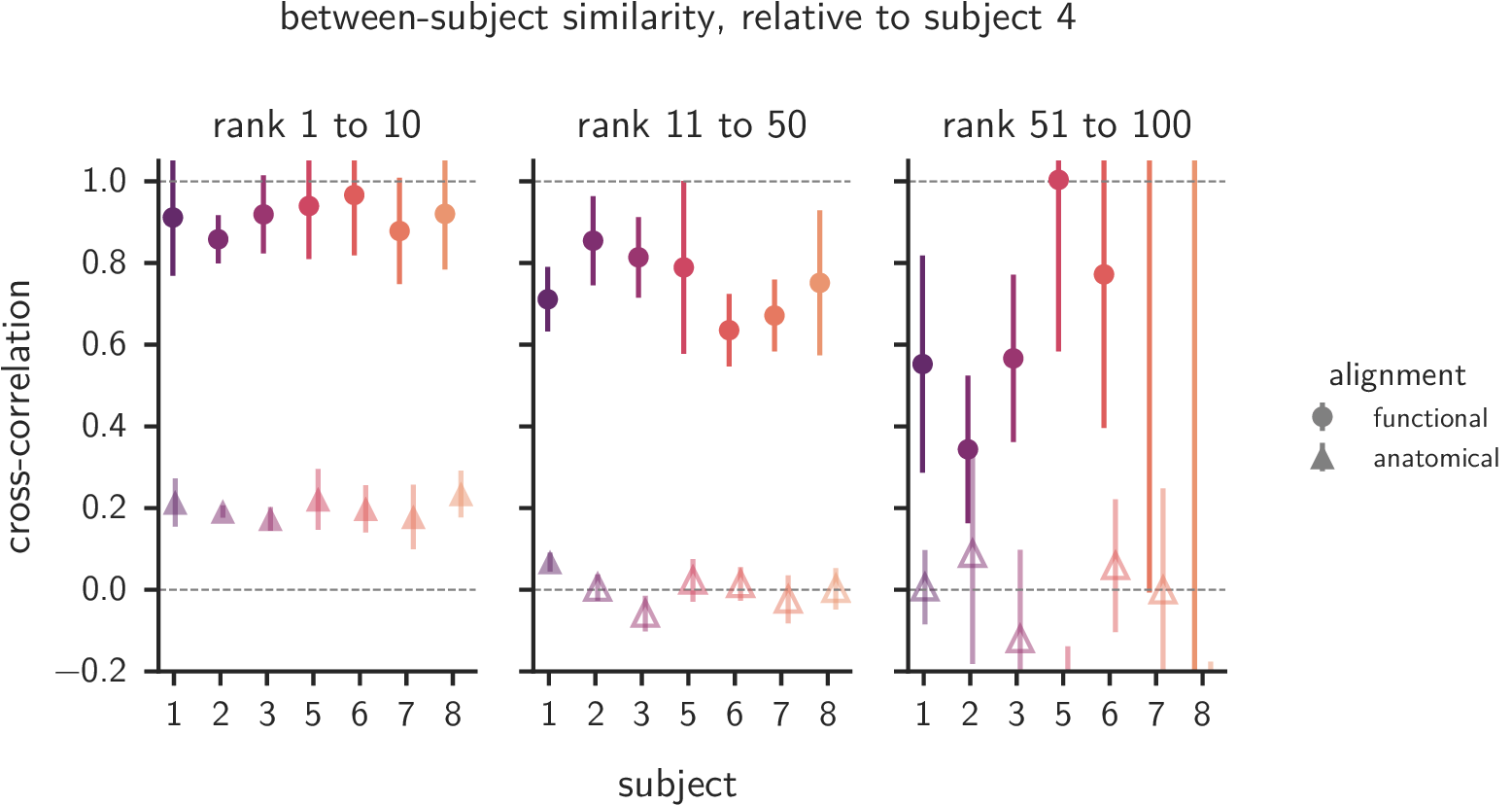
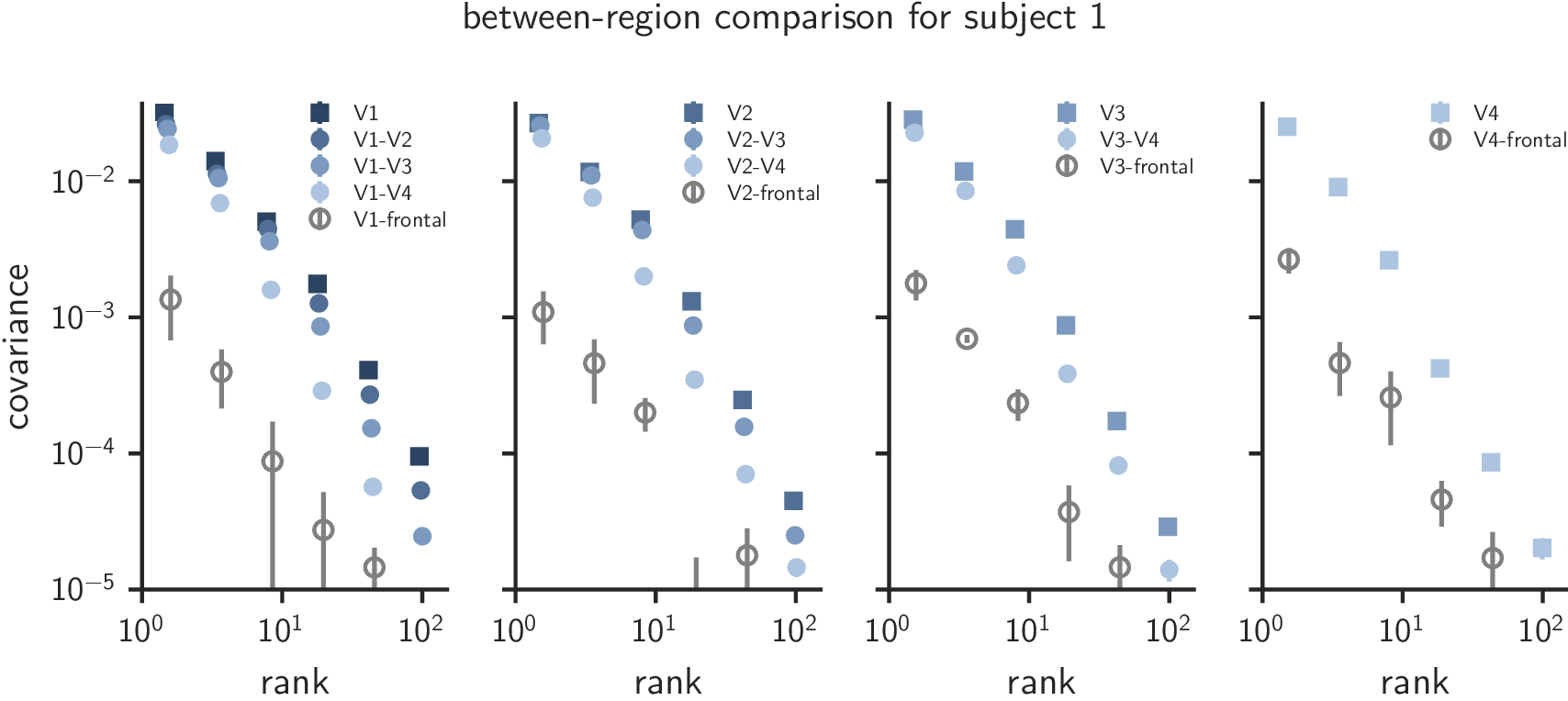
Anatomical alignment is insufficient

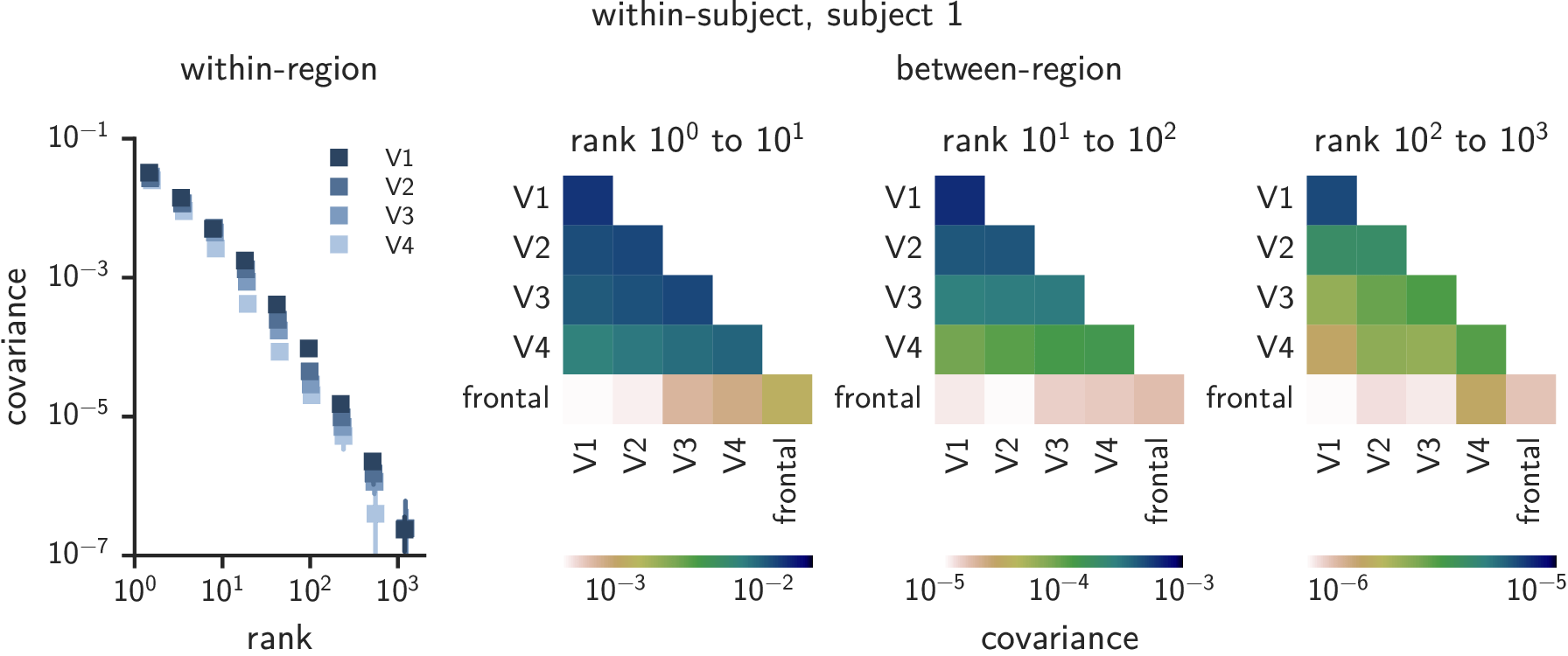
Systematic variation aross some ROIs
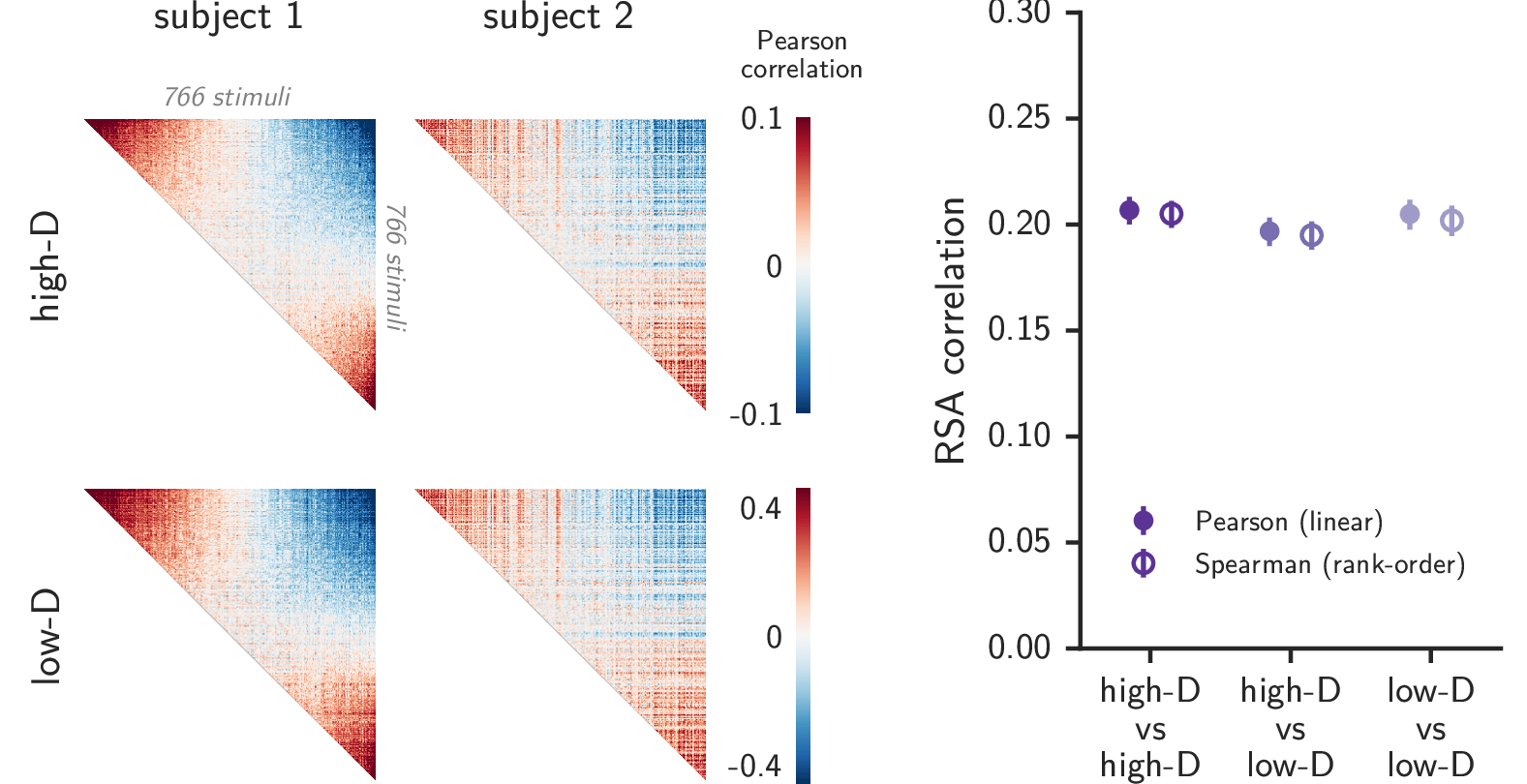
RSA is insensitive to high-rank dimensions
Summary
- Scale-free covariance spectra
- Detectable in fMRI data (!) with spectral binning
- Present everywhere in visual cortex
- High-dimensional structure shared between individuals
- Only detectable with spectral methods
Project 2
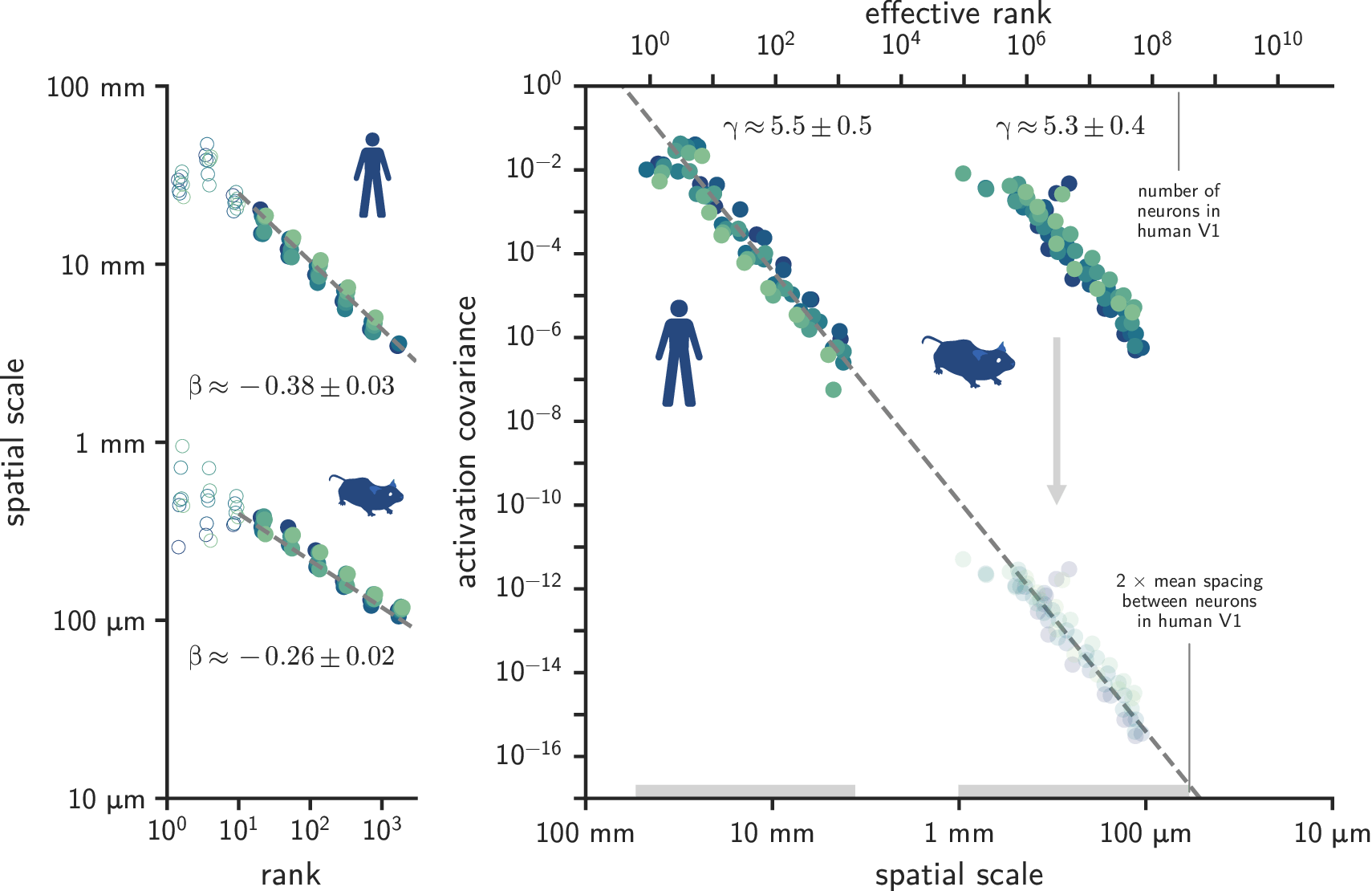
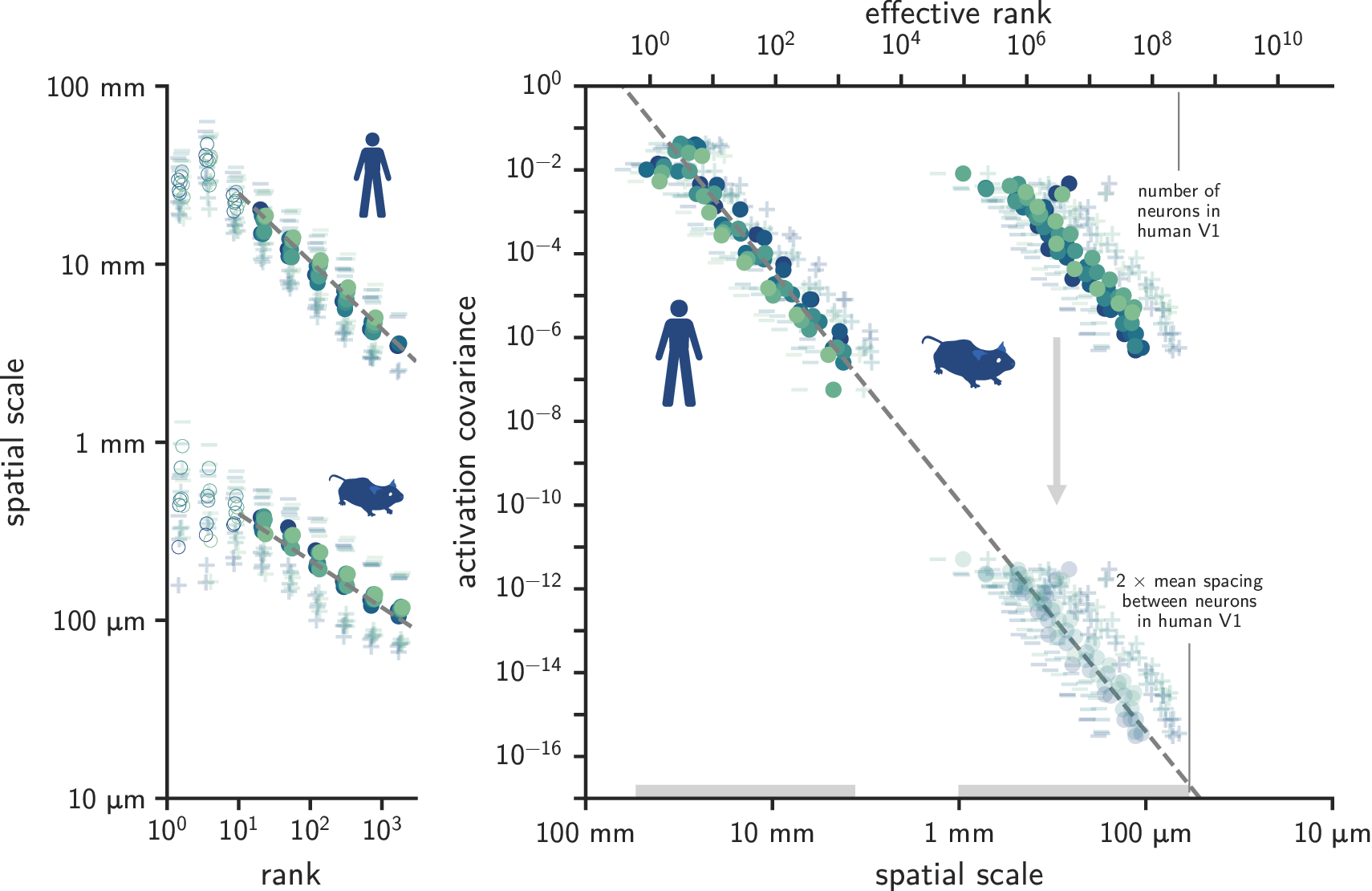
Spatial scale-invariant properties of mammalian visual cortex
[manuscript in preparation]
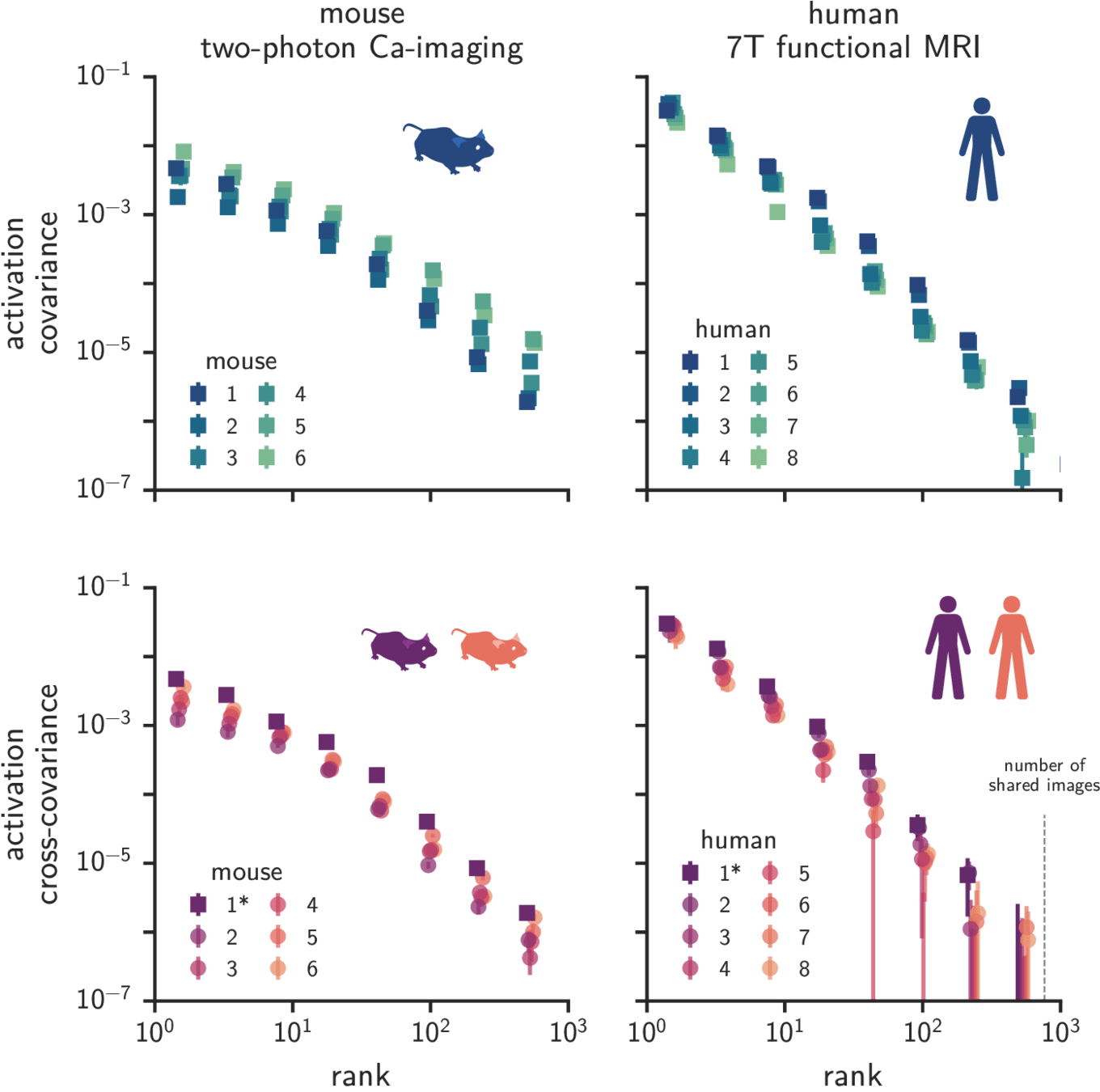
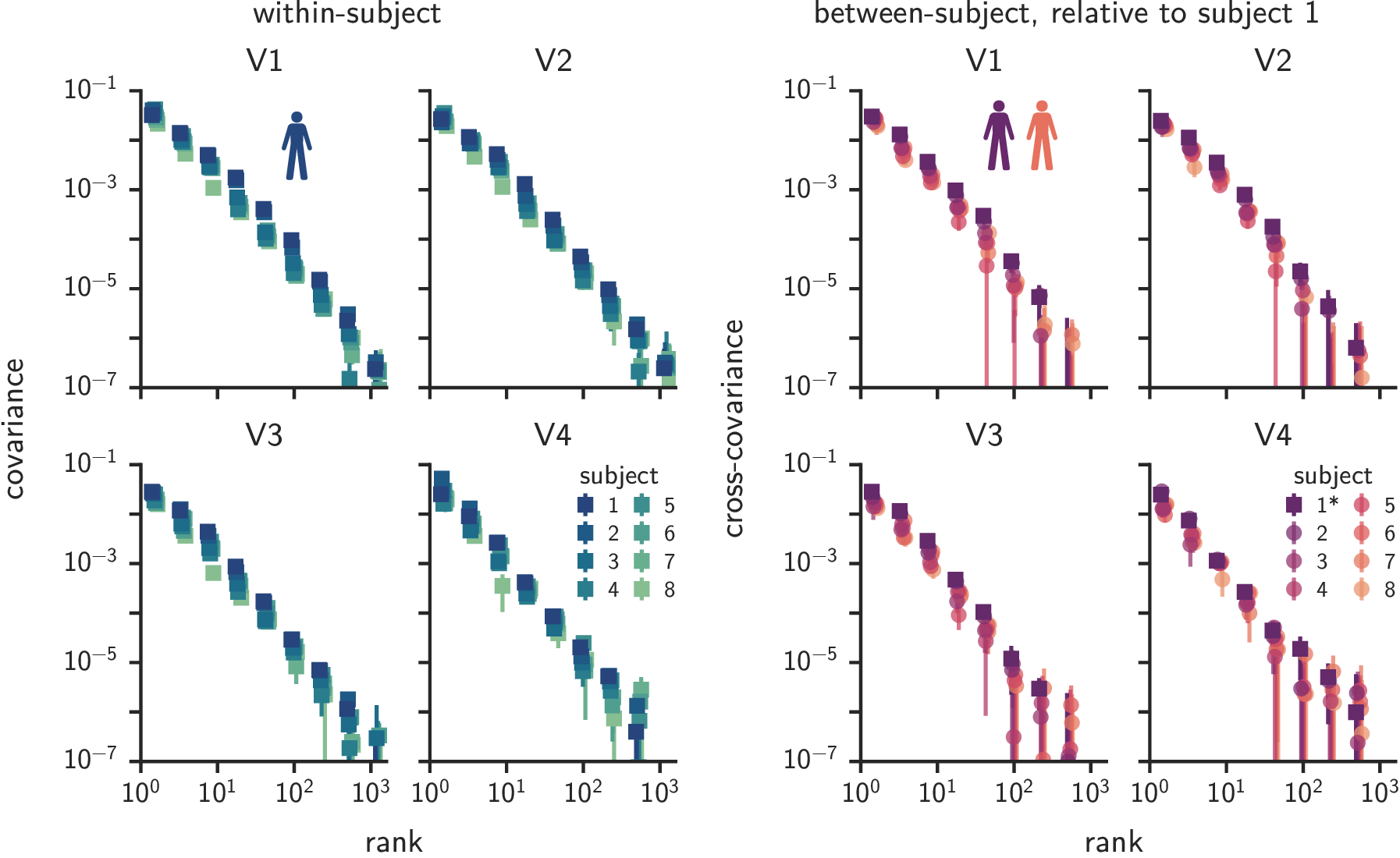
Similar covariance spectra in humans and mice*
Latent dimensions appear spatially structured
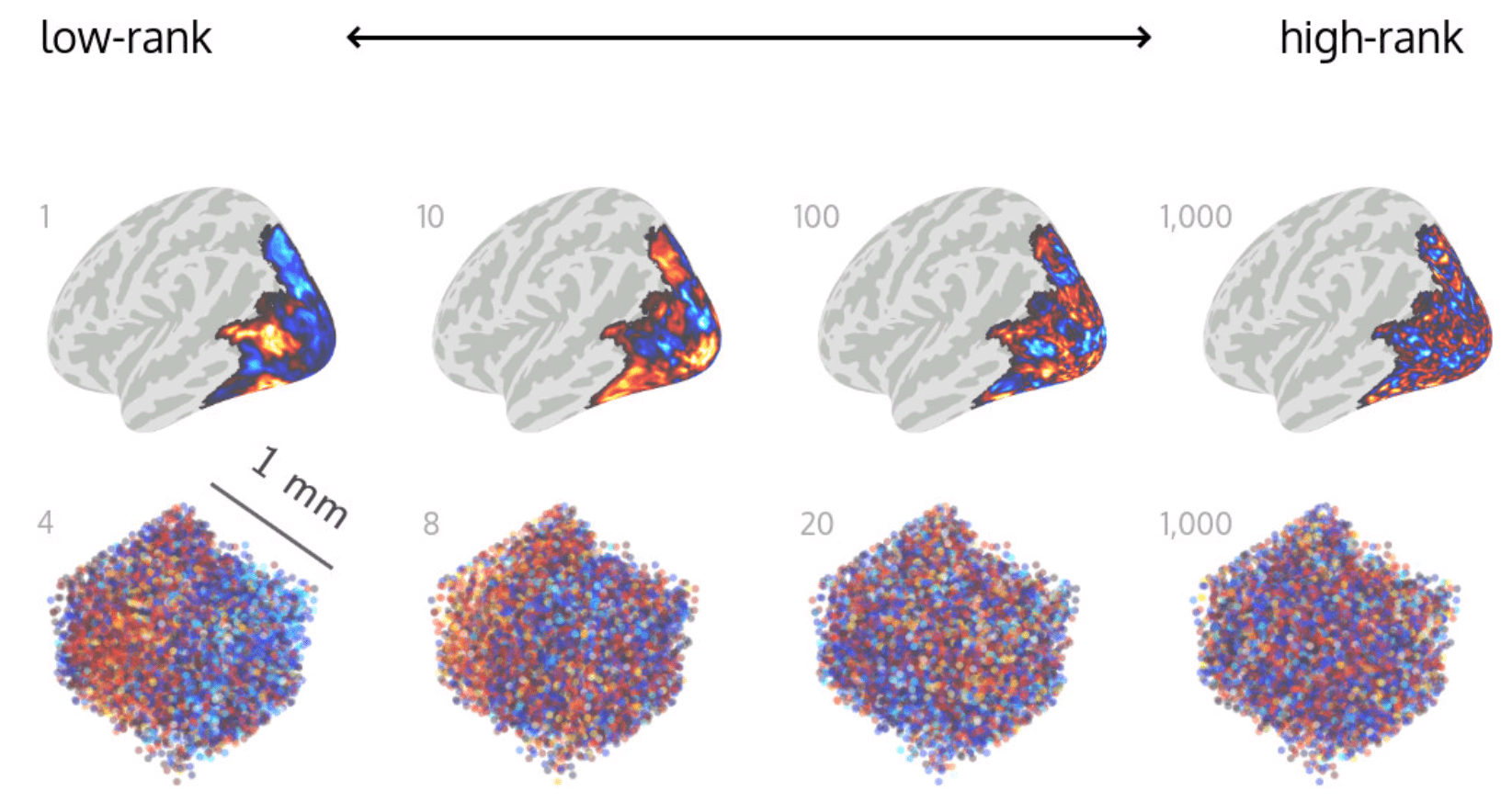
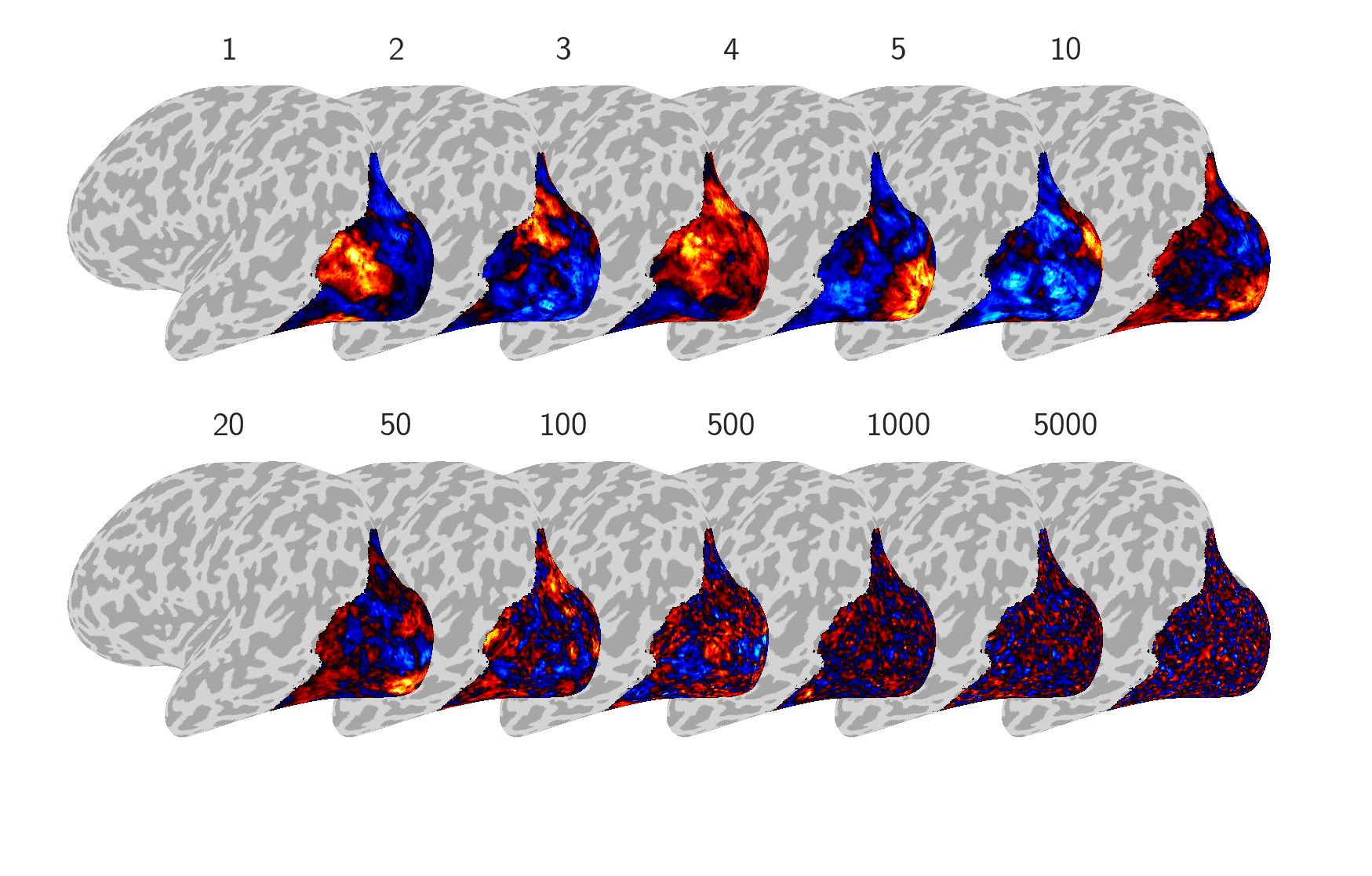
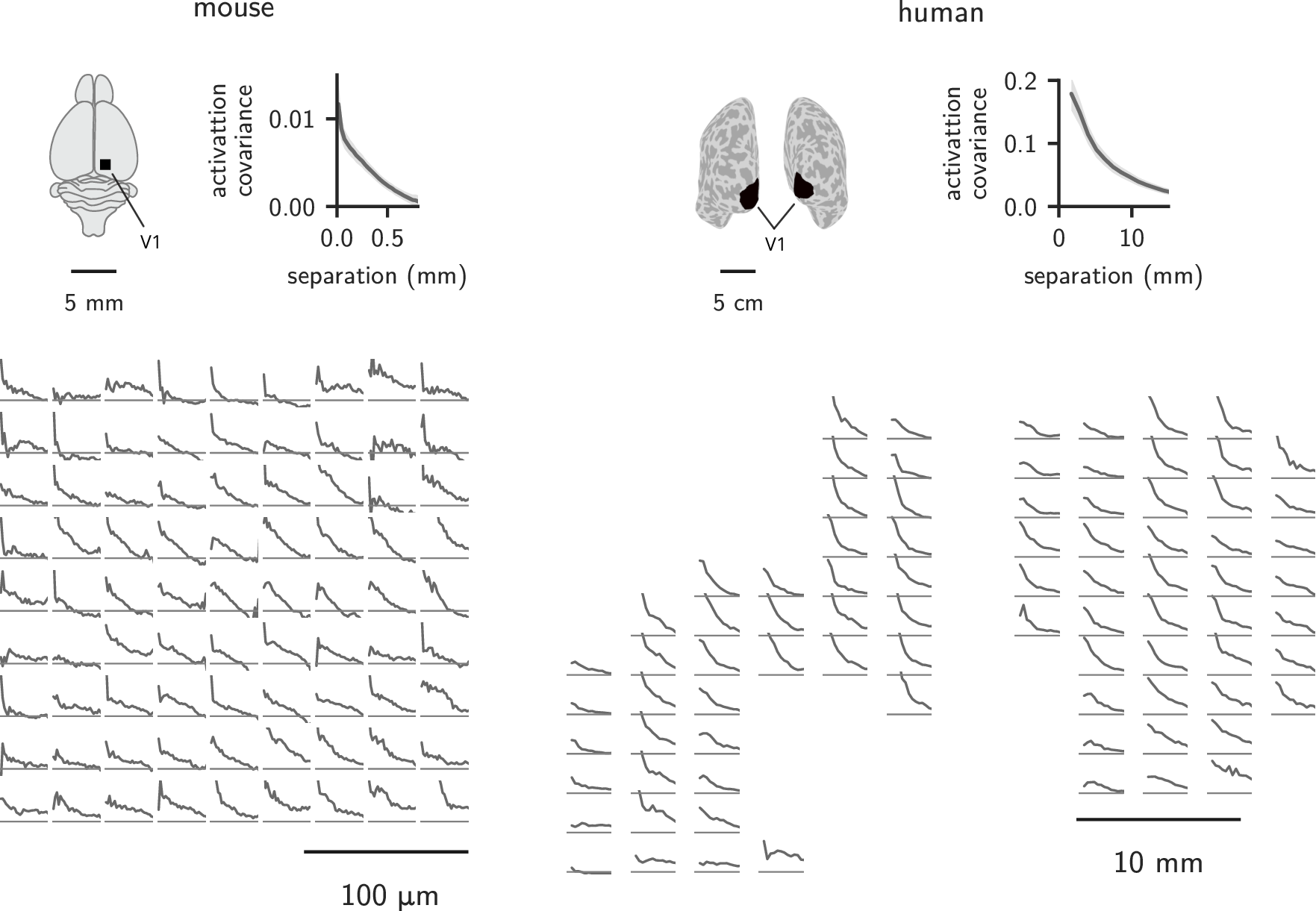
Covariance functions are spatially stationary
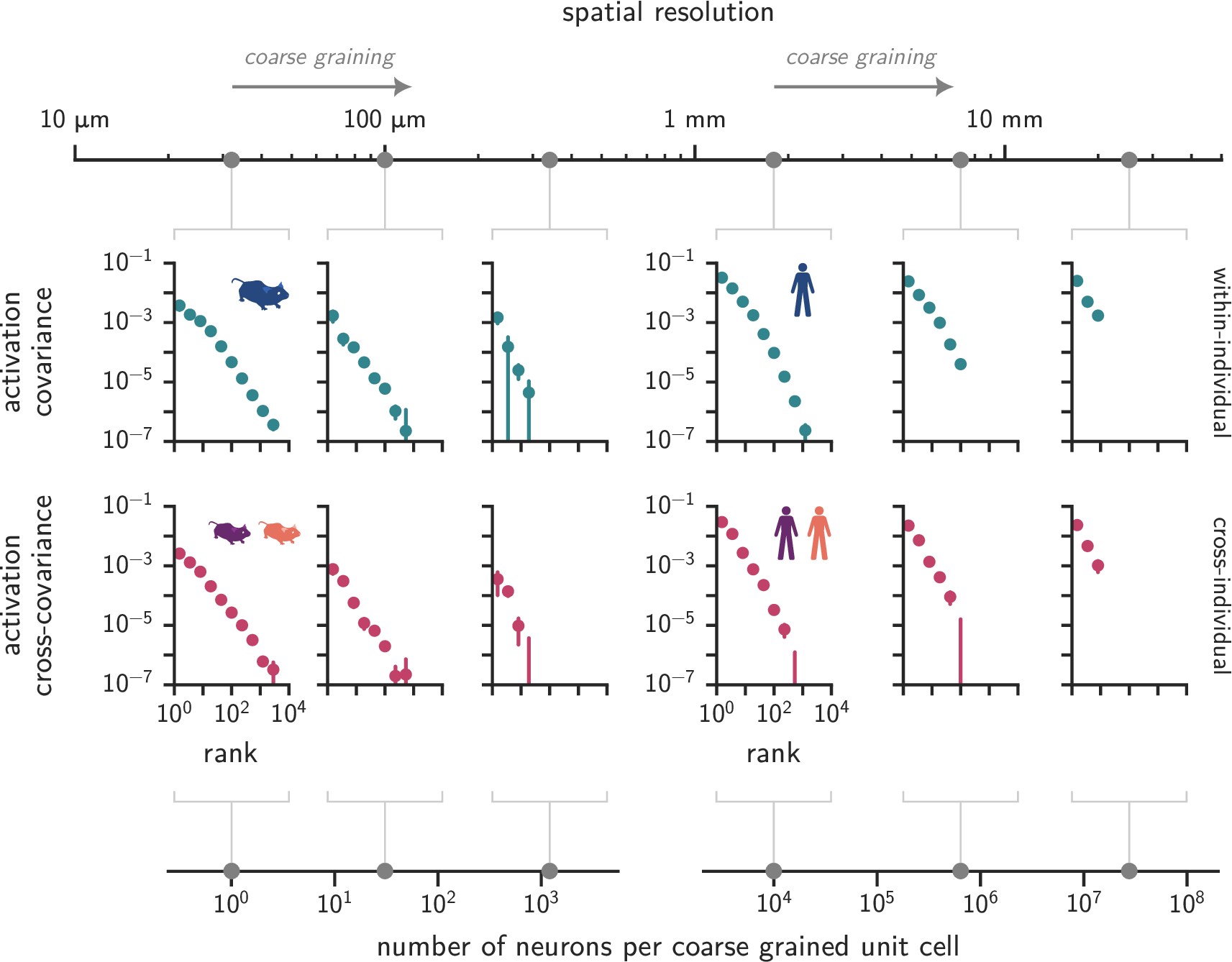
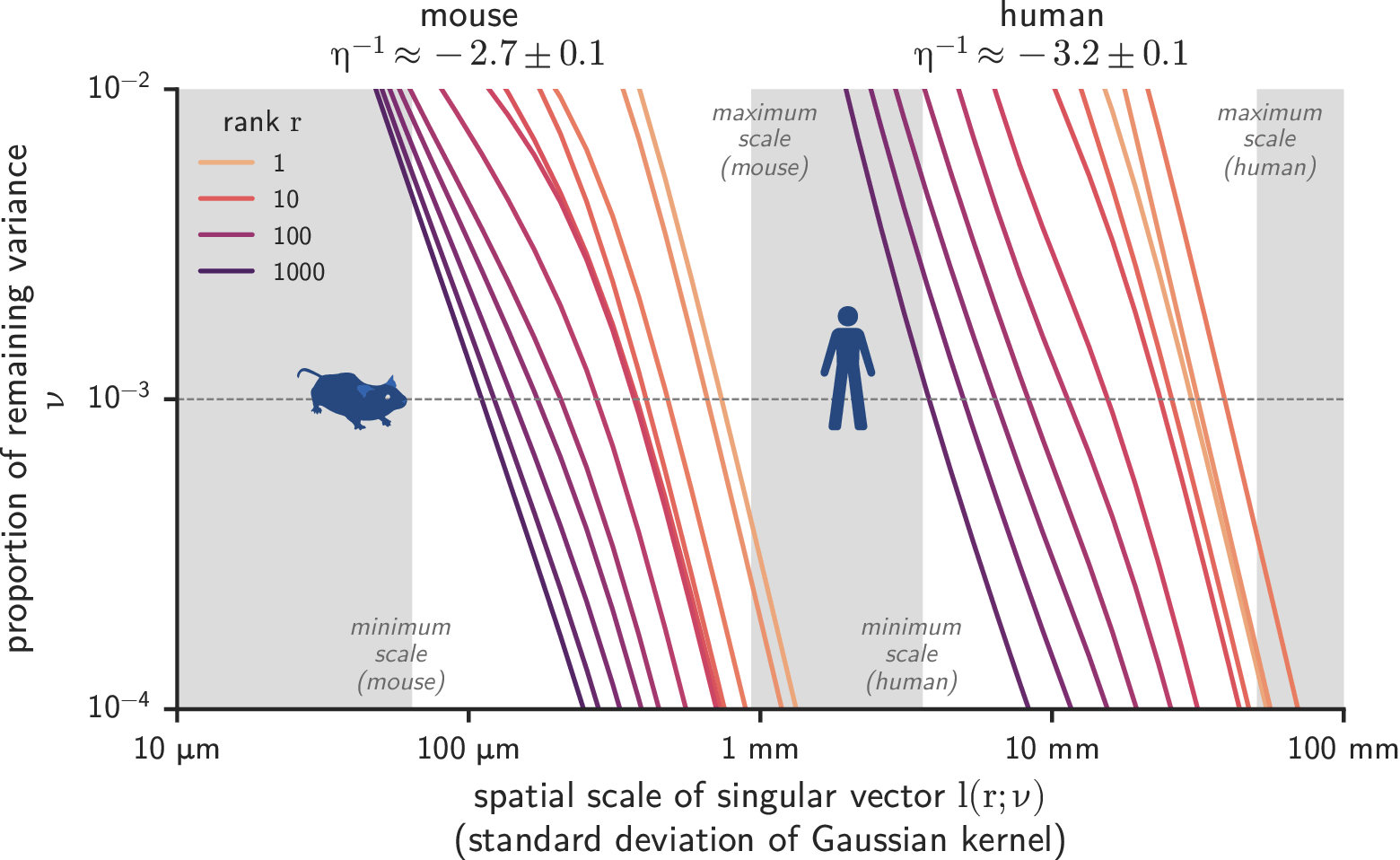
Covariance spectra are spatial scale-invariant
Some implications
- Universality across species: mouse visual cortex is perhaps not as much of an exception anymore
- Universality across scales: explains why similar phenomena are observed in measurements at different resolutions
How does this universal power spectrum arise?
Some possible explanations
- Theoretical constraints: the power-law exponent has an upper bound of -1 to maximize expressivity while being robust
- Physical scaffolding: scale-free structures in the connectivity patterns of neurons in cortex
- Generic learning mechanism: allows cortex to scale arbitrarily in size while maintaining the same representational format
Project 3
Characterizing the representational content of different latent subspaces
[planned; preliminary results]



What information is available at different ranks?

Fine-grained semantic annotations available
Hypothesis 1
coarse category information?

fine-grained distinctions?





Hypothesis 2
- CNNs
- AlexNet
- VGG-16
- ResNet-32
- Vision transformers
- Scattering network
- Untrained baselines
low-variance dimensions?
high-variance dimensions?
Testing these hypothesis: Proposed methods
-
Decoding category-level information at different levels of granularity from the neural representations
- linear classifiers (SVMs, logistic regression)
-
Encoding models to predict the activation in different latent subspaces of neural representations
- pretrained artificial neural networks
- linear regression + regularization
Is SNR too low in high-rank subspaces?
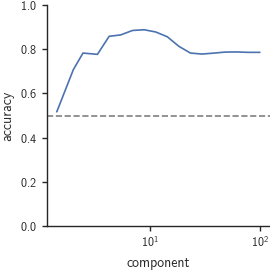
Apparently not.
As a simple proof-of-concept, a nearest centroid classifier can perform pairwise instance-level classification using information in all latent subspaces.
ranks 1-10
10-100
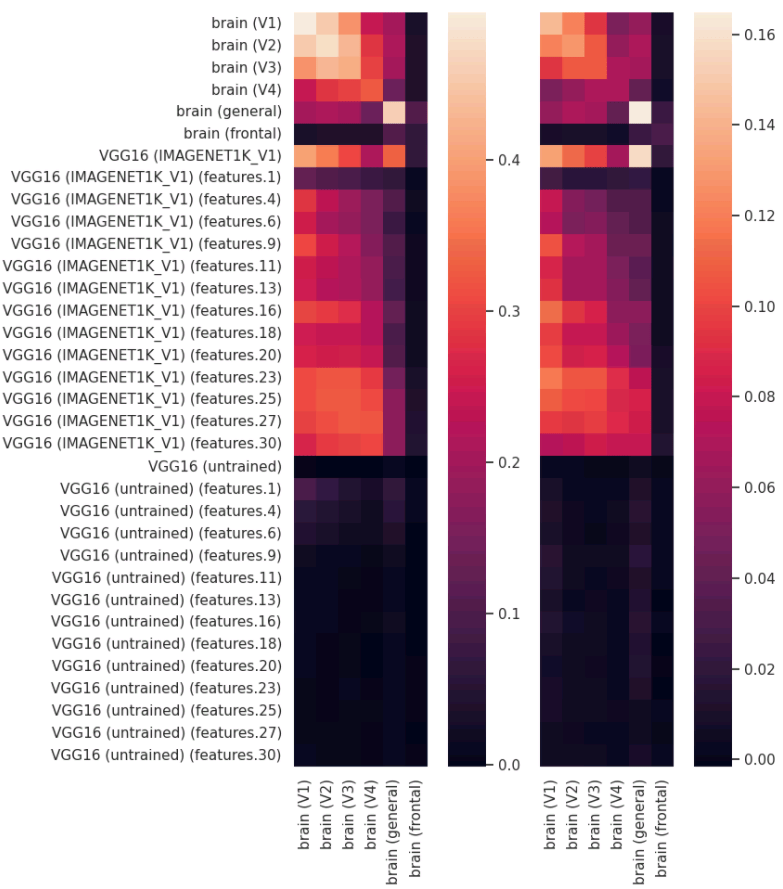

Preliminary results
Timeline
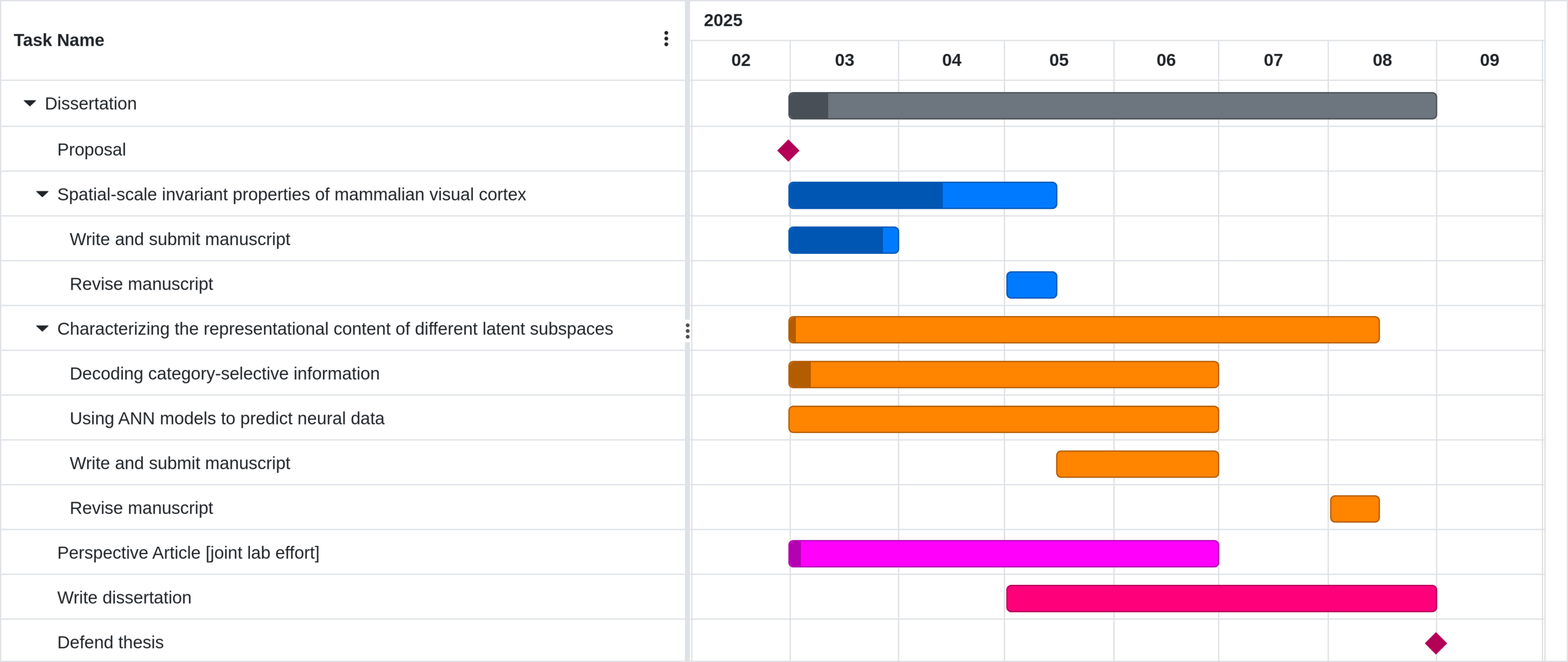
Dissertation Proposal
By raj-magesh
Dissertation Proposal
- 148



