Advancements in Fusion Energy: tritium fuel cycle and FESTIM's role in hydrogen transport simulation
Remi Delaporte-Mathurin and FESTIM contributors
Nuclear Fusion 101
+
+
Deuterium
Tritium
+
+
Helium
neutron
Fusion
What's the catch?
- The nuclei need to have enough energy to overcome the Coulomb barrier
- Fusion fuel needs to reach ~100 million K (plasma)
- How to contain a plasma at these temperatures?
Magnetic confinement
Jason Ginsberg
JET
- Joint European Torus
- UK Atomic Energy Authority (UKAEA)
- \( Q_\mathrm{plasma} = 0.7\) (1997)
- No longer operating
ITER
- International collaboration
- Located in Southern France
- \( Q_\mathrm{plasma} = 10\) (objective)
- First plasma in 2034
SPARC
- Private company Commonwealth Fusion Systems
- Spin off of MIT
- \( Q_\mathrm{plasma} = 5-10\) (objective)
- First plasma in 2026
ARC
- Private company Commonwealth Fusion Systems
- Power plant (electricity production) ~ 400 MW
- Will be sited in Virginia
Half-life: 12 years
\mathrm{T} \rightarrow \mathrm{He} + \mathrm{e}^-
☢
The tritium issue
Tritium is
- rare
- expensive
- hazardous
\mathrm{n} + ^6\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + 4.8 \ \mathrm{MeV}
\mathrm{n} + ^7\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + \mathrm{n} - 2.5 \ \mathrm{MeV}
\mathrm{TBR} = \mathrm{\frac{tritium \ produced}{tritium \ consumed}} > 1
❓How ❓
Lithium is used to breed tritium
\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}
\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}
Magnet
Breeding blanket
\mathrm{n} + \mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He}
The breeding blanket
Plasma
The breeding blanket is only one component of the fuel cycle
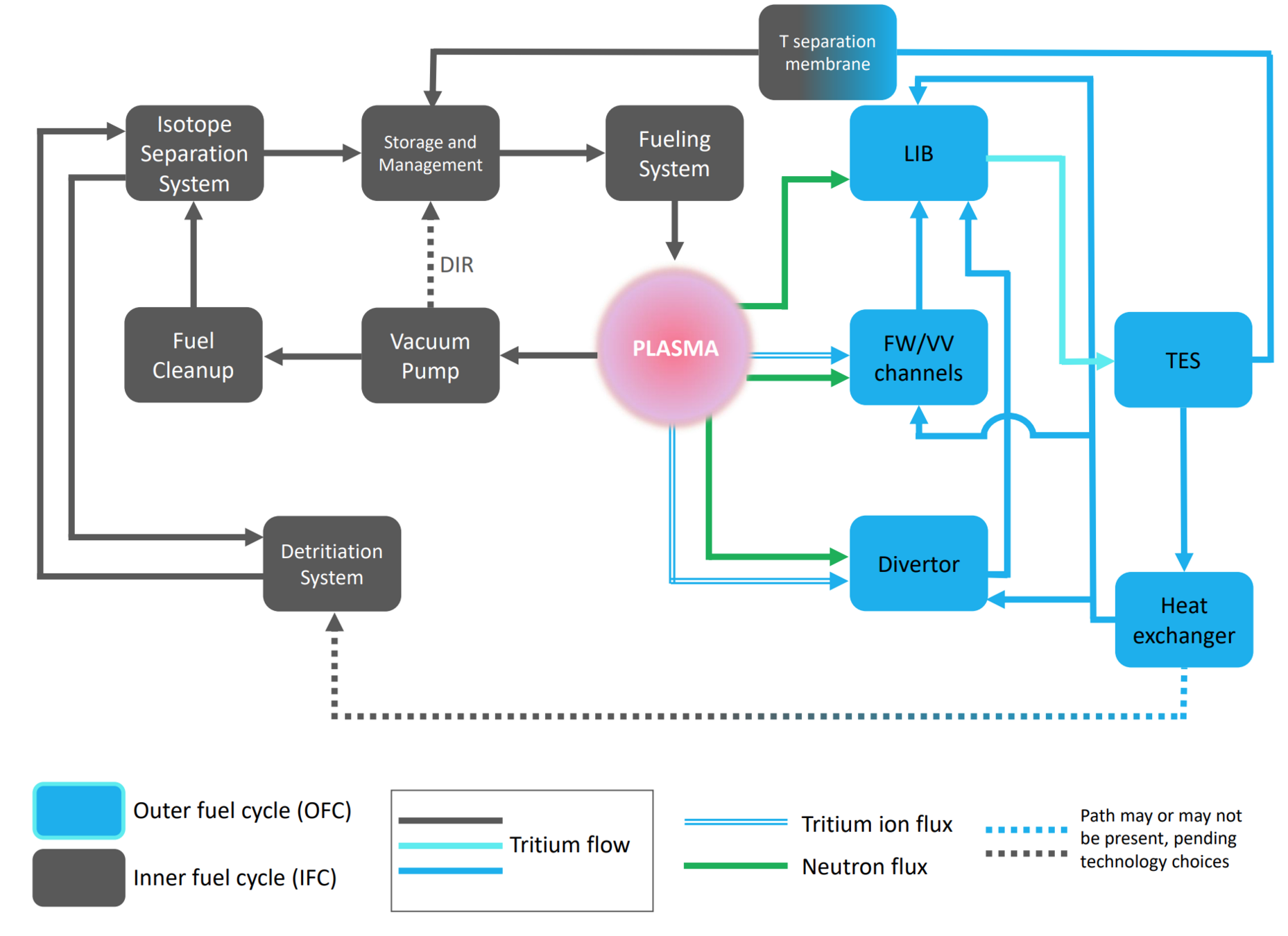
We need to study the behaviour of tritium in materials
Hydrogen transport in metals
Governing equations
\varphi_\mathrm{diffusion} = - D \ \left( \nabla c + \frac{Q\ c}{R \ T^2} \ \nabla{T} - \frac{c \ V_H}{R \ T} \nabla \sigma \right)
\( \varphi_\mathrm{diffusion} \): diffusion flux
\( D \): diffusion coefficient
\( c \): diffusive hydrogen concentration
\( S\): source term
Soret effect (or thermophoresis)
Stress assisted diffusion
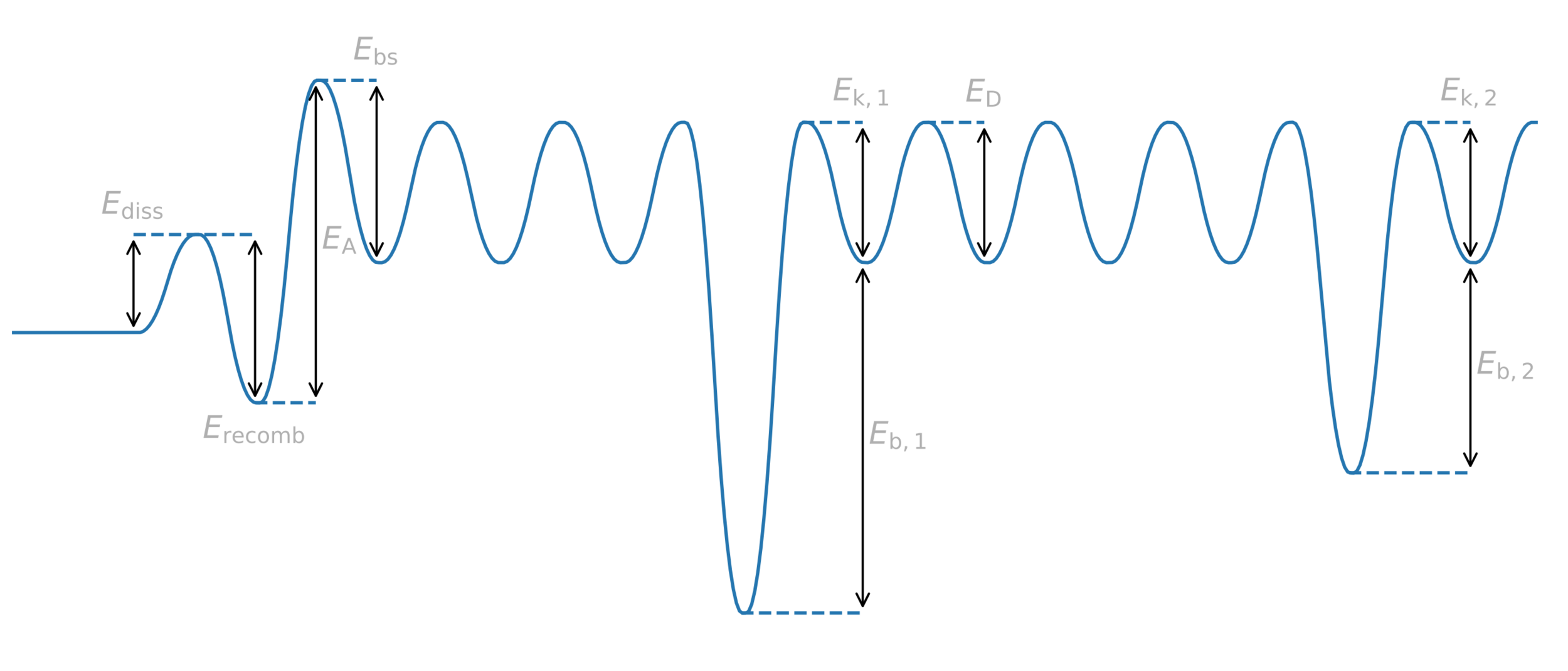
H
- vacancy
- grain boundary
- impurity
- chemical reaction
- ...
Governing equations
Trapping at defects
\mathrm{H} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{H}]_\mathrm{trap}
0D
\frac{\partial c_\mathrm{t}}{\partial t} = -\frac{\partial c_\mathrm{m}}{\partial t} = k \ c_\mathrm{m} \ n_\mathrm{free \ trap} - p c_\mathrm{t}
c_\mathrm{t}
Since \(n_\mathrm{trap} = n_\mathrm{free \ trap} + c_\mathrm{t} \)
c_\mathrm{m}
n_\mathrm{free \ trap}
Governing equations
\mathrm{H} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{H}]_\mathrm{trap}
c_\mathrm{t}
c_\mathrm{m}
n_\mathrm{free \ trap}
0D
\frac{\partial c_\mathrm{t}}{\partial t} = -\frac{\partial c_\mathrm{m}}{\partial t} = k \ c_\mathrm{m} \ (n_\mathrm{trap} - c_\mathrm{t}) - p c_\mathrm{t}
Total concentration of traps
Governing equations
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot \varphi_\mathrm{diffusion} + S - \sum \frac{\partial c_\mathrm{t,i}}{\partial t}
\frac{\partial c_\mathrm{t, i}}{\partial t} = k_i \ c_\mathrm{m} \ (n_\mathrm{trap,i} - c_\mathrm{t}) - p_i c_\mathrm{t}
McNabb & Foster model
Challenges
- Number of degrees of freedom
- Interface discontinuities
Governing equations
- D_1 \nabla c_1 = - D_2 \nabla c_2
\left( \frac{c_1}{K_{1}} \right)^2 =\left( \frac{c_2}{K_{2}} \right)^{\{1,2\} }
Recombination
Dissociation
Absorption
Trapping
Detrapping
Diffusion
Most processes are thermally activated
FESTIM: a FEniCS-based tool for hydrogen transport simulation
User inputs
- Material properties
- Trap properties
- Geometry
- Boundary conditions
- Initial conditions
- ...
T
FESTIM
Outputs
- H concentration fields \(c(x,t)\)
- Temperature field \(T(x,t)\)
- surface fluxes
- inventories
- average concentration
- ...
Heat transfer model
Hydrogen transport model(s)
📈5 years of development
📑14+ publications
🗣️130+ citations
🧑💻23+ contributors
🏛️27+ institutions using the code
🧑💻80+ Slack members
⭐~100 stars on GitHub
🧑💻4 user workshops
FESTIM in numbers
✅100% open-source
Source code: github.com/festim-dev/FESTIM
Tutorials: github.com/festim-dev/FESTIM-workshop
Documentation: festim.readthedocs.io
FESTIM is verified & validated
-
Validated against TDS, permeation experiments...
-
Verified against analytical solutions in many different problems
- New V&V online book
festim-vv-report.readthedocs.io
- 19 V&V cases in total (more to come)
Remi Delaporte-Mathurin and Jair Santana, FESTIM V&V Book, 2024, https://dspace.mit.edu/handle/1721.1/156690.
FESTIM from mesoscale to reactor scale
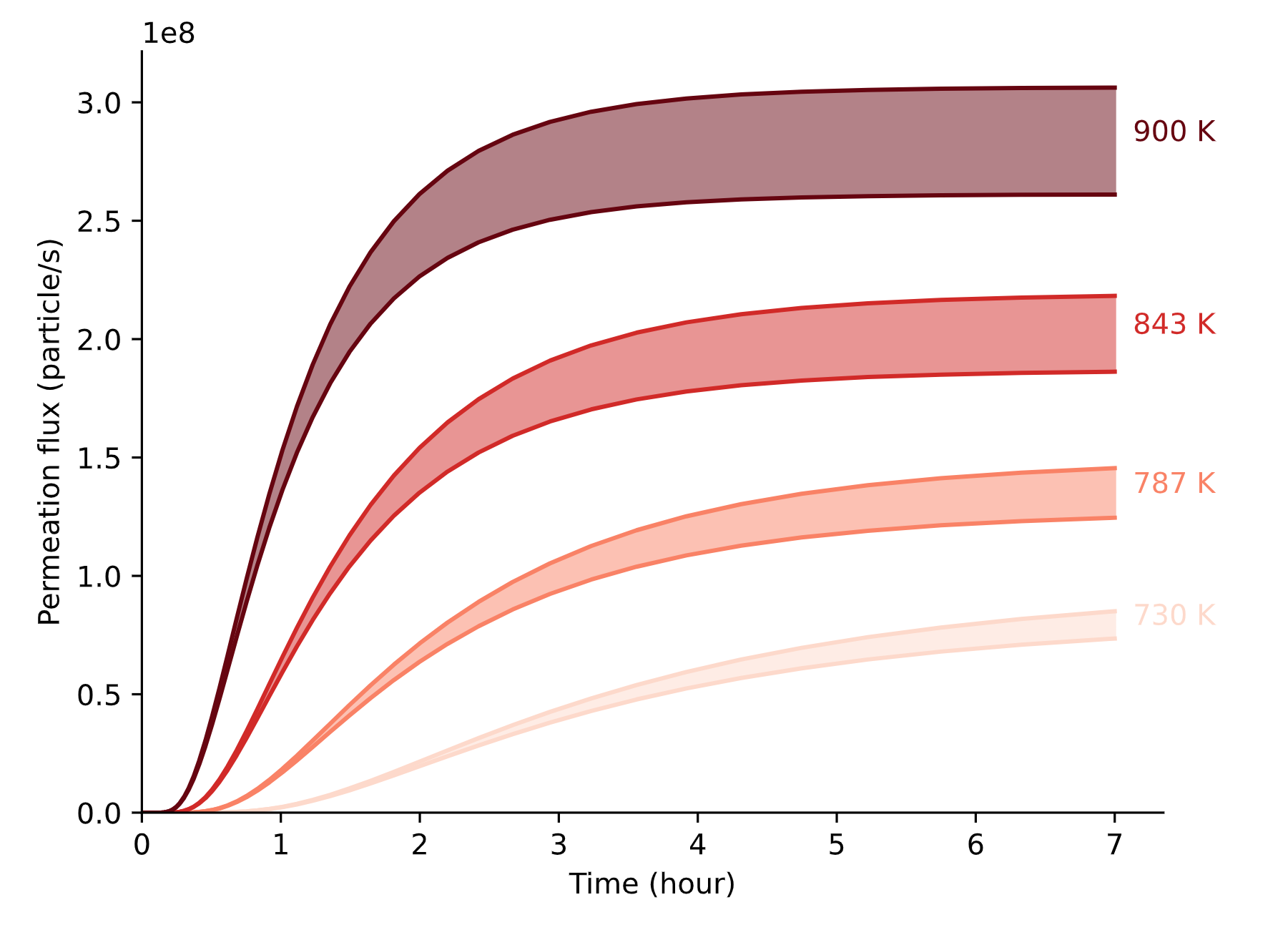
Gas driven permeation
J_\mathrm{left} = K_d \ P - K_r \ c^2
J_\mathrm{right} = - K_r \ c^2
Surface limited regime
Bulk limited regime
Transition to bulk limited as the permeation number \( W \) increases
High H pressure
Low H pressure
Permeation flux
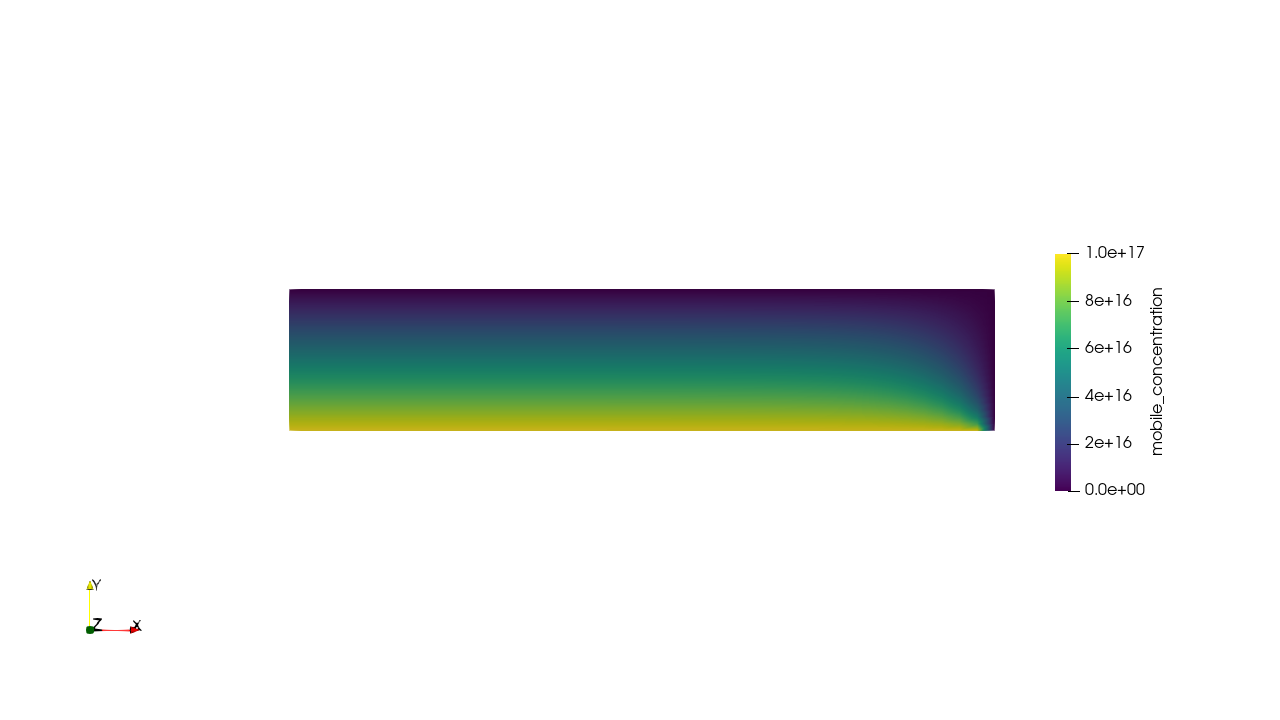
\( c = K_H \ P_\mathrm{up} \)
\( c = 0 \)
Permeation through the crucible wall
FLiBe
2D permeation through molten salts
\mathrm{flux} = 2 \pi \ \int_0^R r \ D \nabla c \ \cdot \mathbf{n} \ dr
HYPERION permeation rig
Permeation barriers
No barrier
with barrier
Permeation barrier
Substrate
High H pressure
Low H pressure
Permeation flux
Ongoing tritium permeation barriers development project at MIT
Conservation of chemical potential
\frac{c^-}{K_S^-} = \frac{c^+}{K_S^+}
TDS analysis: neutron damage
\frac{d n}{dt} = \Phi \ K \ (1 - \frac{n}{n_\mathrm{max}}) - A \ n
- New proposed model for neutron-induced trap creation
- Parameterised on TDS data (self-damaged W)
TDS analysis: neutron damage
- Model was used to simulate inventory evolution in PFCs
- Neglecting neutron traps could potentially underestimate inventories by several orders of magnitude after 1 FPY
- Need similar studies for structural materials!
TDS analysis: codeposits
- Simulation of W codeposited layers
- Influence of partial pressure
- 10 different traps!
Kinetic surface model
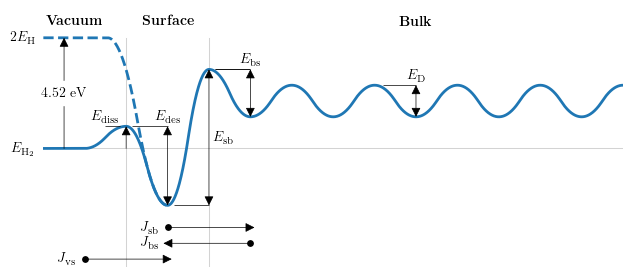
Kinetic surface model
V&V available at
github.com/KulaginVladimir/FESTIM-SurfaceKinetics-Validation
- D in damaged W (S. Markelj JNM 2016)
- Comparison with NRA (Nuclear Reaction Analysis) profiles
Kinetic surface model
V&V available at
github.com/KulaginVladimir/FESTIM-SurfaceKinetics-Validation
- H in oxidised W (A. Dunand et al 2022 Nucl. Fusion)
- Comparison with TDS spectra
Kinetic surface model
V&V available at
github.com/KulaginVladimir/FESTIM-SurfaceKinetics-Validation
- H in Ti (Hirooka et al 1981 JNM)
- Validation at 5 temperatures
H content (H/Ti)
Component scale modelling & multiphysics
Influence of ELMs on retention
- 1D model of a ITER monoblock
- Transient heat transfer simulation
- Varying surface heat flux
Metal Foil Pumps for DIR
- H is implanted in the first \( 10 \ \mathrm{nm} \)
- Super-permeation regime is attained at high recombination energy (upstream surface)
- Source code
Benedikt & Day, (2017) Fusion Engineering and Design
Trtitium retention studies
- Delaporte-Mathurin et al 2024 International Journal of Hydrogen Energy 63 786–802
- Delaporte-Mathurin et al 2024 Nucl. Fusion 64 026003
- ITER plasma facing components
- Transient estimation of tritium retention
- Tritium is trapped in colder regions
Retention (T/m3)
Detritiation studies
Tritium Breeding Blanket
- DEMO WCLL
- Complex 3D geometry
- Coupled to fluid dynamics
- Tritium generation in the LiPb volume (computed from neutronics)
Tritium extraction system
- Permeation Against Vacuum
- Complex 3D geometry
- Coupled with fluid dynamics
- Tritium extraction from permeable membranes
① neutrons are generated
② tritium is created from nuclear reactions
③ tritium is transported in the salt
④ tritium is released into the gas phase
⑤ tritium is collected and counted
MIT tritium breeding experiment
MIT tritium breeding experiment
Velocity
Temperature
Tritium concentration
For more details on experiment: Delaporte-Mathurin et al, Advancing Tritium Self-Sufficiency in Fusion Power Plants: Insights from the BABY Experiment (under review in Nucl. Fusion)
Towards FESTIM2
- Rewrite of FESTIM with FEniCSx
- Improved performances
- New physics and features
Spherical cavity trapping
see Zibrov and Schmid, NME, 2024
for complete description
- Implementation in FESTIM of the spherical cavity trapping model developed by Zibrov and Schmid
- Custom trapping equations
- Smooth implementation in FESTIM
Anisotropy
- Anisotropic materials can be simulated with very few modifications
- Composites
- Anisotropic microstructures
D = \begin{bmatrix}
D_{xx} & 0\\
0 & D_{yy}
\end{bmatrix}
\mathrm{H} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{H}]_\mathrm{trap}
\mathrm{D} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{D}]_\mathrm{trap}
\mathrm{D} + [\mathrm{H}]_\mathrm{trap} \ \substack{k_\mathrm{swap} \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1.2em] k_\mathrm{swap}} \ [\mathrm{D}]_\mathrm{trap} + \mathrm{H}
same underlying equations!
Can be represented by festim.Reaction
Isotope swapping
Trapping reactions
Swapping reaction
Isotope swapping
my_model.species = [
mobile_H,
mobile_D,
trapped_H,
trapped_D,
]
my_model.reactions = [
F.Reaction(
k_0=k_0,
E_k=0.39,
p_0=1e13,
E_p=1.2,
reactant1=mobile_H,
reactant2=empty_trap,
product=trapped_H,
volume=my_subdomain,
),
F.Reaction(
k_0=k_0,
E_k=0.39,
p_0=1e13,
E_p=1.2,
reactant1=mobile_D,
reactant2=empty_trap,
product=trapped_D,
volume=my_subdomain,
),
F.Reaction(
k_0=k_0,
E_k=0.1,
p_0=k_0,
E_p=0.1,
reactant1=mobile_H,
reactant2=trapped_D,
product=[mobile_D, trapped_H],
volume=my_subdomain,
),
]Usual trapping reactions
Swapping reaction
4 species are defined
Multi-isotope transport and multi-level trapping
- 2 isotopes, 1 trap (2 levels)
- 7 different species
- 6 reactions
\mathrm{H} + [\ \ \ ] \ \substack{p_1 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_1} \ [\mathrm{H}_1\mathrm{D}_0]
\mathrm{H} + [\mathrm{H}_1\mathrm{D}_0] \ \substack{p_2 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_2} \ [\mathrm{H}_2\mathrm{D}_0]
\mathrm{D} + [\ \ \ ] \ \substack{p_3 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_3} \ [\mathrm{H}_0\mathrm{D}_1]
\mathrm{D} + [\mathrm{H}_0\mathrm{D}_1] \ \substack{p_4 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_4} \ [\mathrm{H}_0\mathrm{D}_2]
\mathrm{H} + [\mathrm{H}_0\mathrm{D}_1] \ \substack{p_5 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_5} \ [\mathrm{H}_1\mathrm{D}_1]
\mathrm{D} + [\mathrm{H}_1\mathrm{D}_0] \ \substack{p_6 \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k_6} \ [\mathrm{H}_1\mathrm{D}_1]
✅Mixed domain can streamline multiphysics coupling
❌Some methods do not work for dissimilar materials (Henry vs Sieverts)
FESTIM 2 is much faster
3-30x
faster
HISP project: coupling FESTIM to plasma codes
RISP pulse
ITER FW divided in 60 bins
Data from DINA
Goal: find the best strategy for minimising ITER T inventory
HISP project: coupling FESTIM to plasma codes
- Multi isotopes
- Parametrisation for W, B, SS
- Testing different scenarios for detritiation in ITER
- Flexible enough to be reactor-and plasma code-agnostic
- Open-source development
github.com/kaelyndunnell/hisp
HISP project: coupling FESTIM to plasma codes
10 DT FP pulses
ICWC + RISP
GDC
Simulation time:
~ 60 s per bin (~ hour full reactor)
Next steps
- Release of FESTIM 2.0-alpha soon (FEniCSx support)
- Continue to improve our V&V process
festim-vv-report.readthedocs.io
- Improve coupling of FEniCS to external solvers (eg. OpenFOAM, OpenMC...) for multiphysics
- Don't hesitate to star the repository!
github.com/festim-dev/FESTIM
Advancements in Fusion Energy: tritium fuel cycle and FESTIM's role in hydrogen transport simulation (Dassault Systems Seminar)
By Remi Delaporte-Mathurin
