HYPERION
project
Motivation
FLiBe is considered for ARC's tritium breeding material
Understanding tritium transport in FLiBe is crucial
Motivation
- Hydrogen transport in materials is characterised by diffusivity and solubility
- These properties are temperature dependent
D = D_0 \ \exp{(-E_D/k_B \ T)}
S = S_0 \ \exp{(-E_S/k_B \ T)}
1/T (K-1)
Property
Pre-exp. factor
Activation energy
Motivation
Large deviation in literature
Solubility of hydrogen in FLiBe
Objective
To build an experiment to measure the hydrogen transport properties of FLiBe
Experiment principle
- Impose partial pressure of H on one side
- H permeates through the salt
- Measure the desorption flux on the other side
FLiBe
Experiment principle
- Impose partial pressure of H on one side
- H permeates through the salt
- Measure the desorption flux on the other side
- Fit with the master curve to identify \( \Phi \) and \(D\)
- Repeat for different temperature
FLiBe
\mathrm{downstream \; flux} = \frac{P_\mathrm{up} \Phi}{L} \left(1+2 \sum_{n=1}^{\infty} \left(-1\right)^{n} e^{- t\frac{\pi^{2}n^{2} D}{L^{2}}}\right)
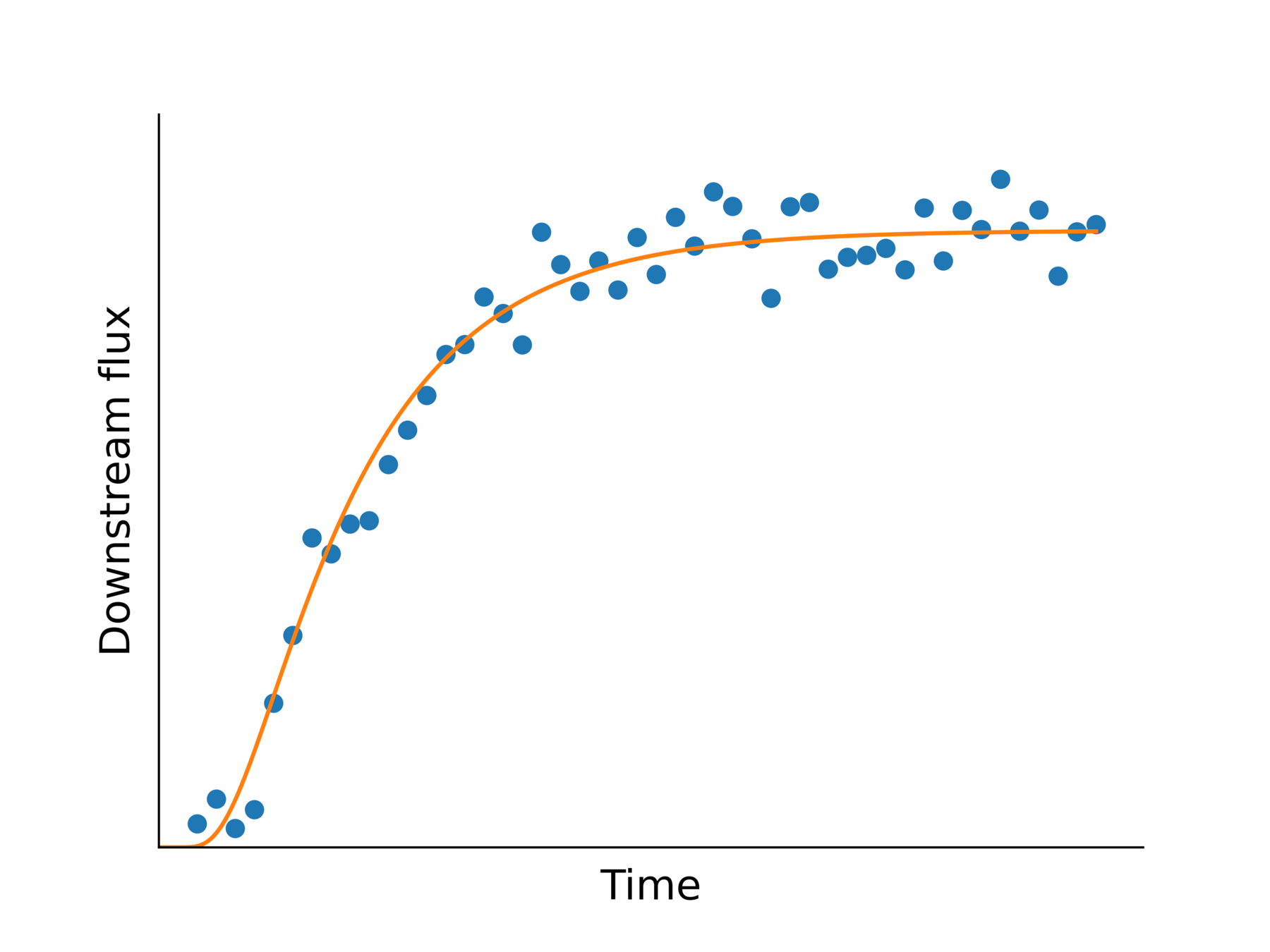
Experiment principle
FLiBe
Metal layer
Design specs and constraints
Subsystems
- Imposed partial pressure of hydrogen in the upstream volume
- Imposed flow rate in the downstream volume (around 20 ccm)
- Temperature measurements with TCs
Physics
- Minimise edge effects: small height to radius ratio
- Minimise resistance of metal membrane:
- small thickness
- permeable material
- Salt contamination: compatible metal (Ni)
- Minimise advection: homogeneous temperature in the salt
Space
- FLiBe = in a glovebox
- In furnace = diameter 3.5 inch ID
Study parameters
Temperature: 750 K - 970 K
Partial pressure: 1 Pa - 1000 Pa
Bonus: FLiBe thickness
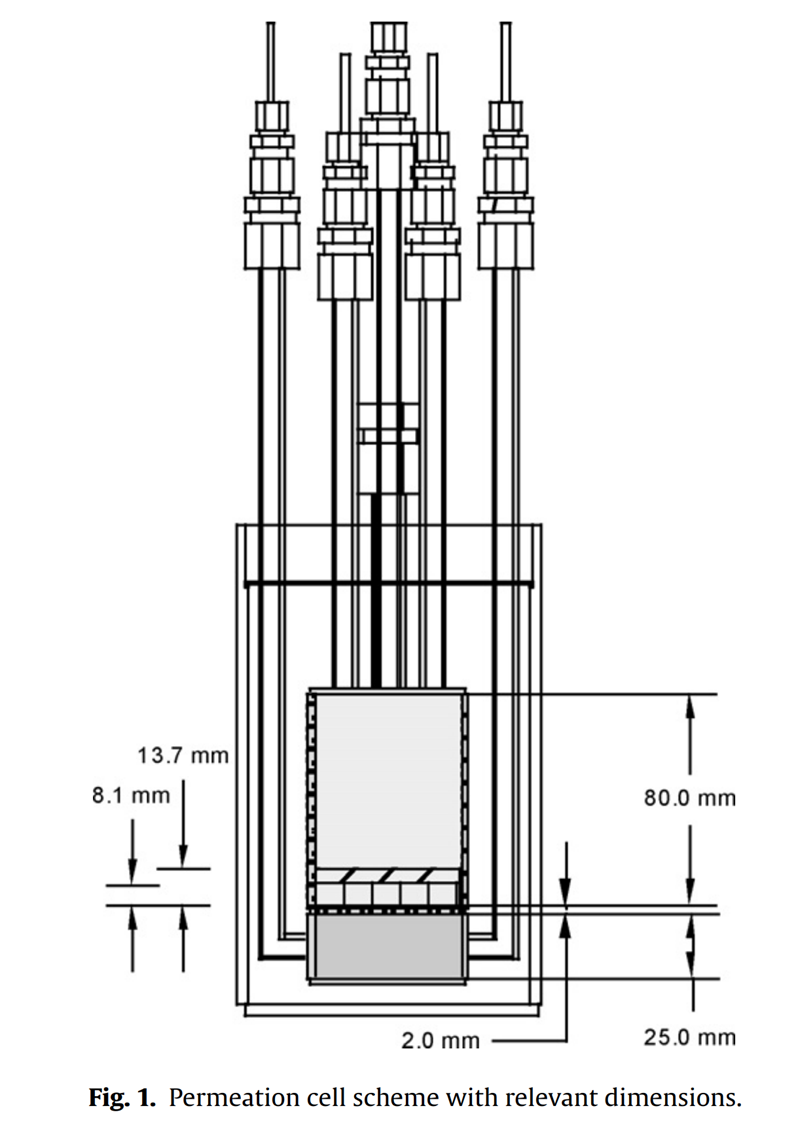
Calderoni's design
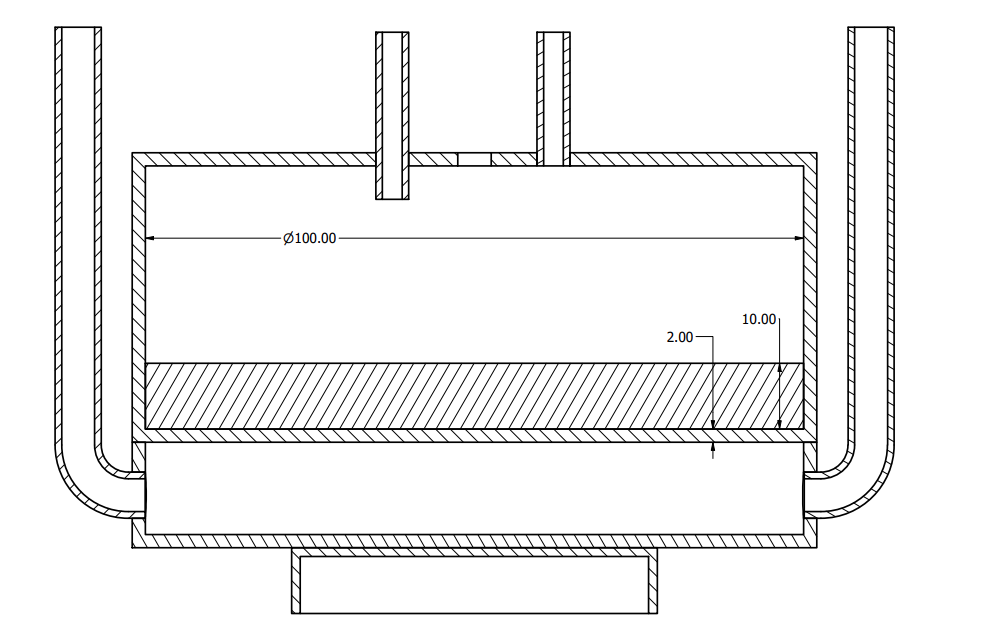
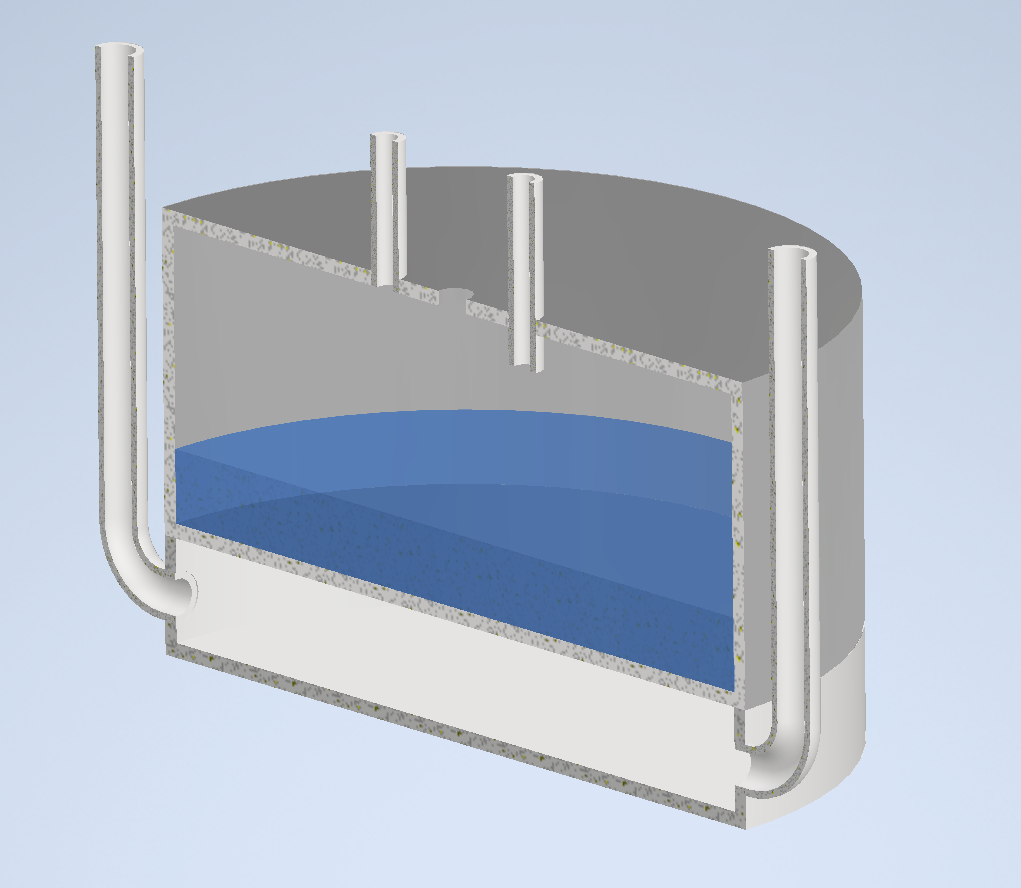
Our draft design
FLiBe
Metal membrane
Our draft design
H concentration
Permeation flux
H concentration
Our draft design
- 79 ml FLiBe
- Heating: furnace
- ΔT < 10℃
- Thermocouples for T measurements
- Lower/Upper volume in Ni200
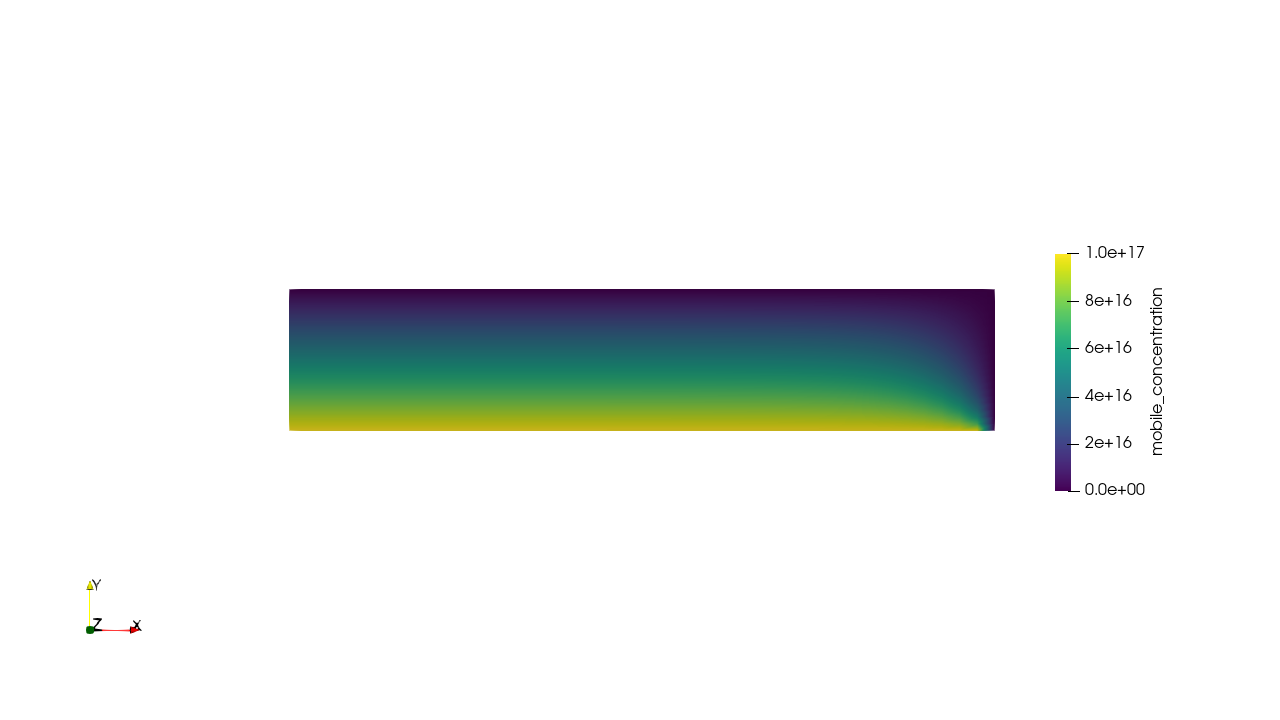
Transport through the salt was simulated with FESTIM
\( c = K_H \ P_\mathrm{up} \)
\( c = 0 \)
\( \mathrm{H \ m^{-3}} \)
Permeation through the crucible wall
FLiBe
The permeation fluxes are estimated w/wo edge effects
\mathrm{flux} = 2 \pi \ \int_0^R r \ D \nabla c \ \cdot \mathbf{n} \ dr
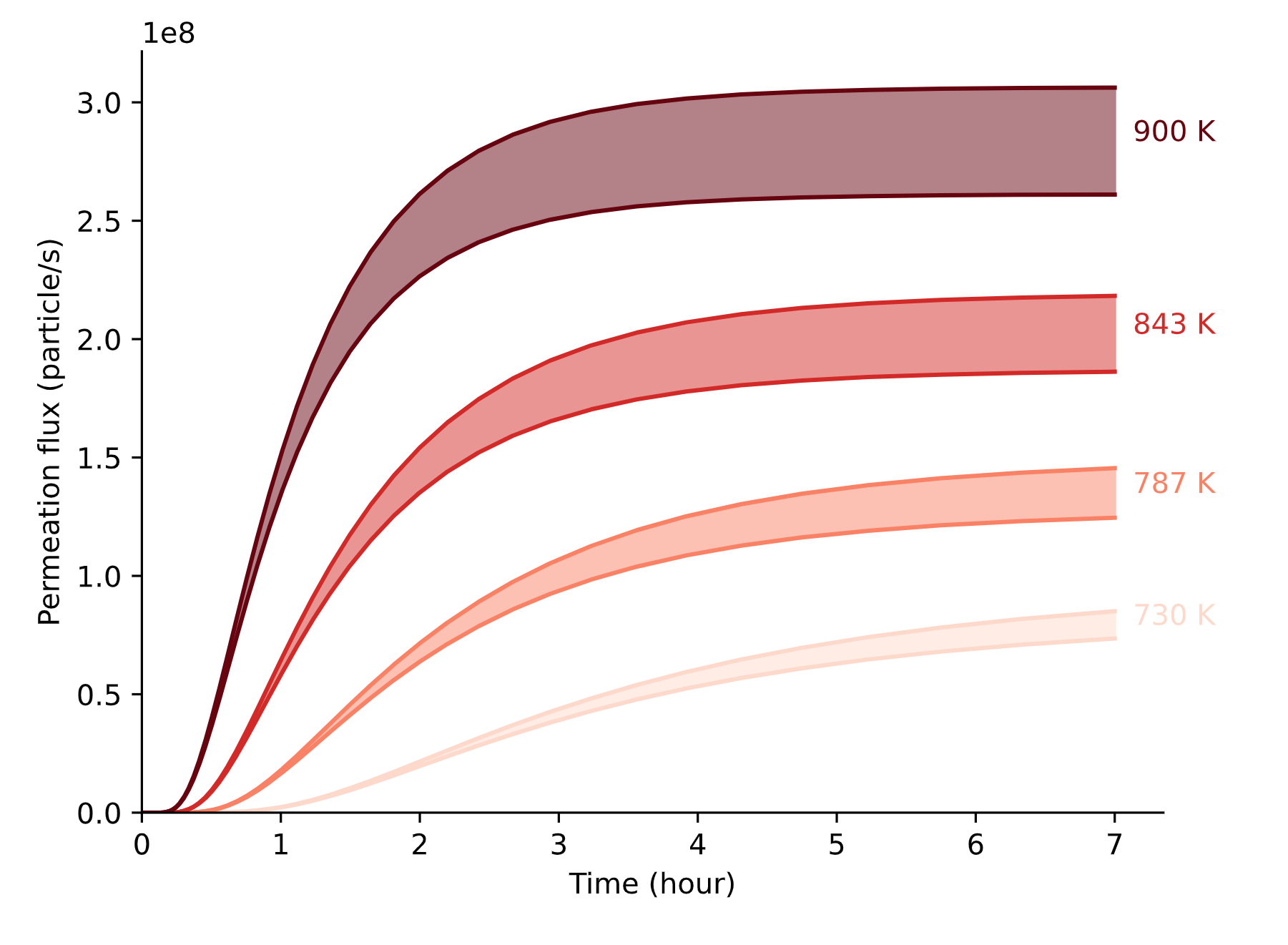
\( K_H = 10^{17} \ \mathrm{H \ m^{-3} \ Pa^{-1}}\)
\( D = 5.66\times10^{-7} \exp (-0.39 / k_B T) \ \mathrm{m^{2} \ s^{-1}}\)
\(P_\mathrm{up} = 1 \ \mathrm{Pa} \)
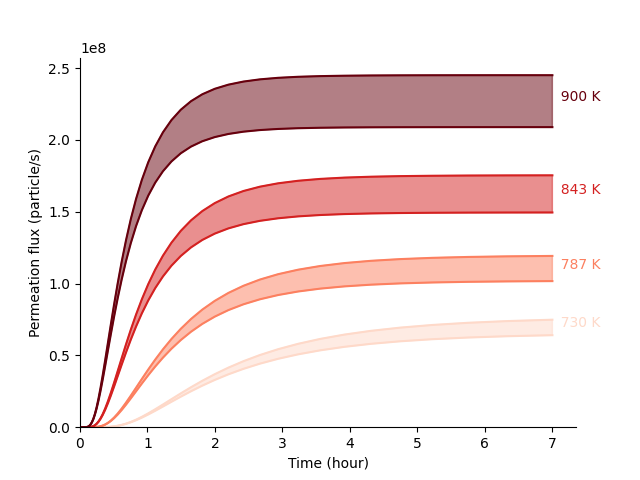
Permeation fluxes with h-to-d ratio of 1/10, 40 ml of salt
Timeline
Design
Crucible
Gas system
Manufacture
Crucible
Gas system
Test
Gas system
Temperature control
Hydrogen detection
Execute
Test with FLiNak
Experiment with FLiBe
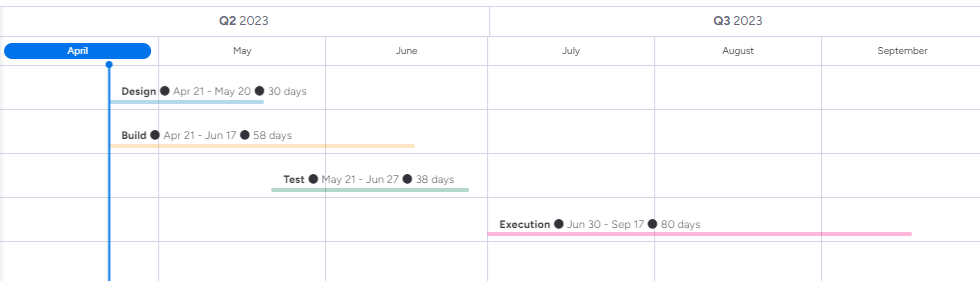
Timeline
Several solutions for accounting for edge effects
- Insulating the outside wall with permeation barriers (alumina?)
- Measure the H permeation through the walls
Permeation rig design presentation
By Remi Delaporte-Mathurin
