Tritium Transport in Breeding Blankets

Remi Delaporte-Mathurin

November 14th 2023

Tritium 101

\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}
800 \ \text{MWth} \approx 10^{20} \ \text{reactions/s} \approx 100 \ \text{kg/year}

Cost: $30,000 per gram

Half-life: 12 years

\mathrm{T} \rightarrow \mathrm{He} + \mathrm{e}^-

☢

\mathrm{n} + ^6\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + 4.8 \ \mathrm{MeV}
\mathrm{n} + ^7\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + \mathrm{n} - 2.5 \ \mathrm{MeV}
\mathrm{TBR} = \mathrm{\frac{tritium \ produced}{tritium \ consumed}}

❓How ❓

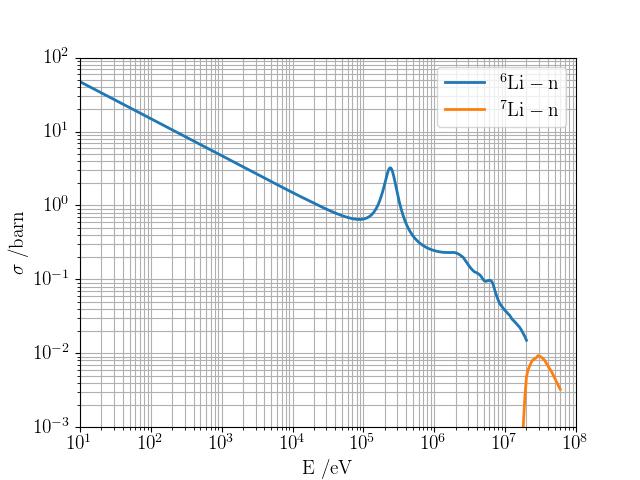
Lithium is used to breed tritium

\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}
\mathrm{n} + ^6\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + 4.8 \ \mathrm{MeV}
\mathrm{n} + ^7\mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He} + \mathrm{n} - 2.5 \ \mathrm{MeV}
\mathrm{D} + \mathrm{T} \rightarrow \mathrm{He} + \mathrm{n}

Magnet

Breeding blanket

\mathrm{n} + \mathrm{Li} \rightarrow \mathrm{T} + \mathrm{He}

The breeding blanket

There are several concepts of breeding blanket

FLiBe

Li

LiPb

Self

Water

He

He+Water

Liquid

Segmented

Choose your breeder

Choose your coolant

Choose your geometry

Li in ceramics

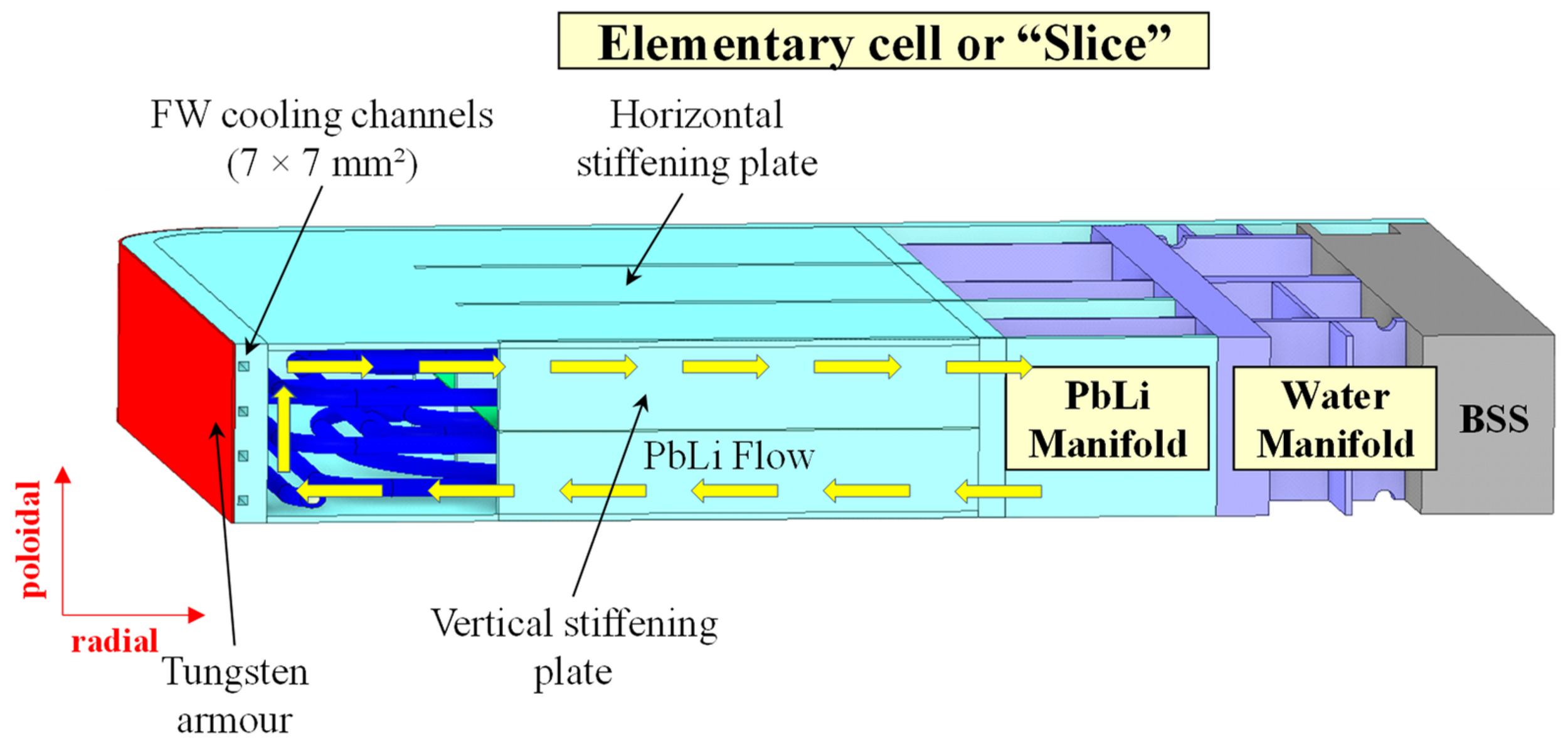
Water Cooled Lithium-Lead

First Light Fusion

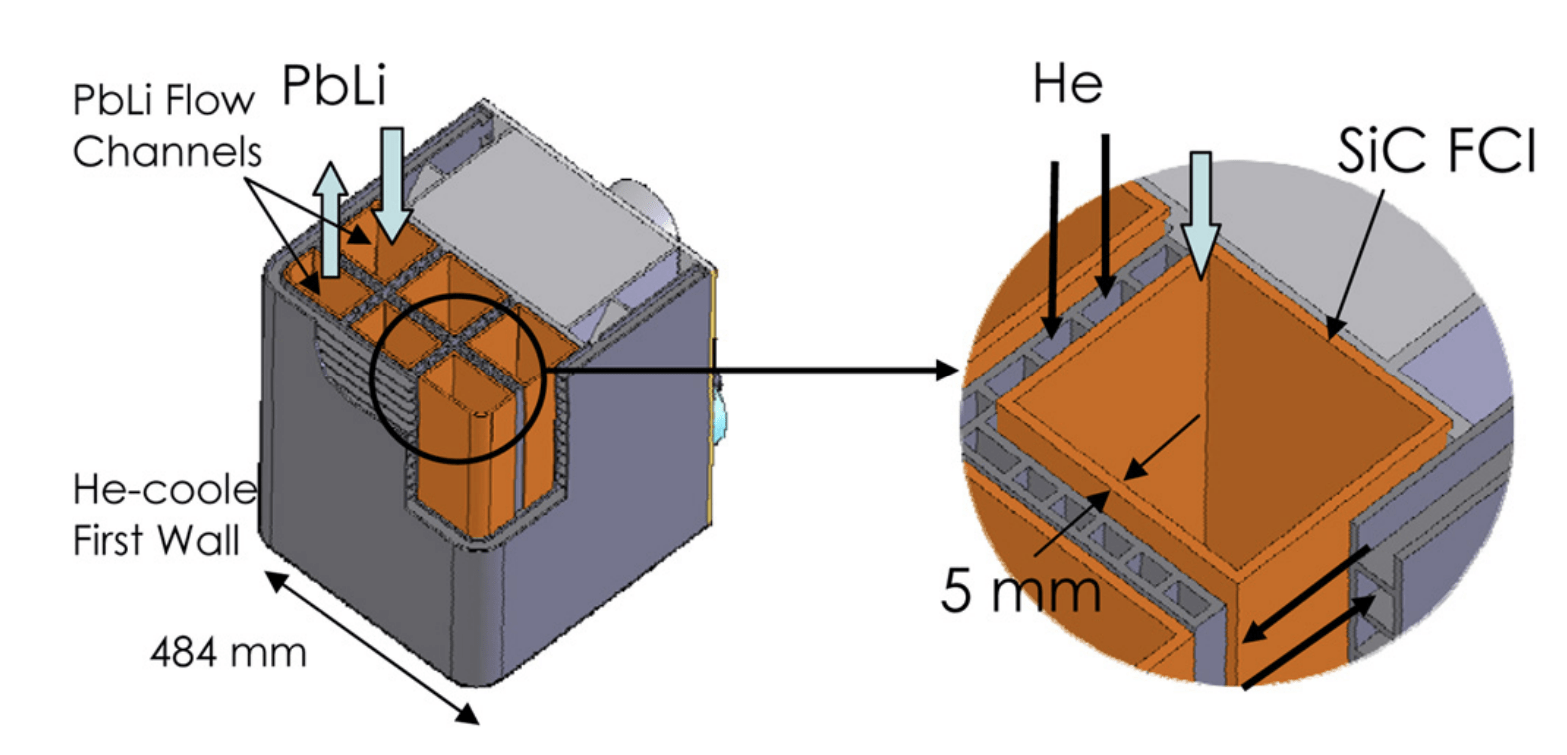
Dual Cooled Lithium-Lead

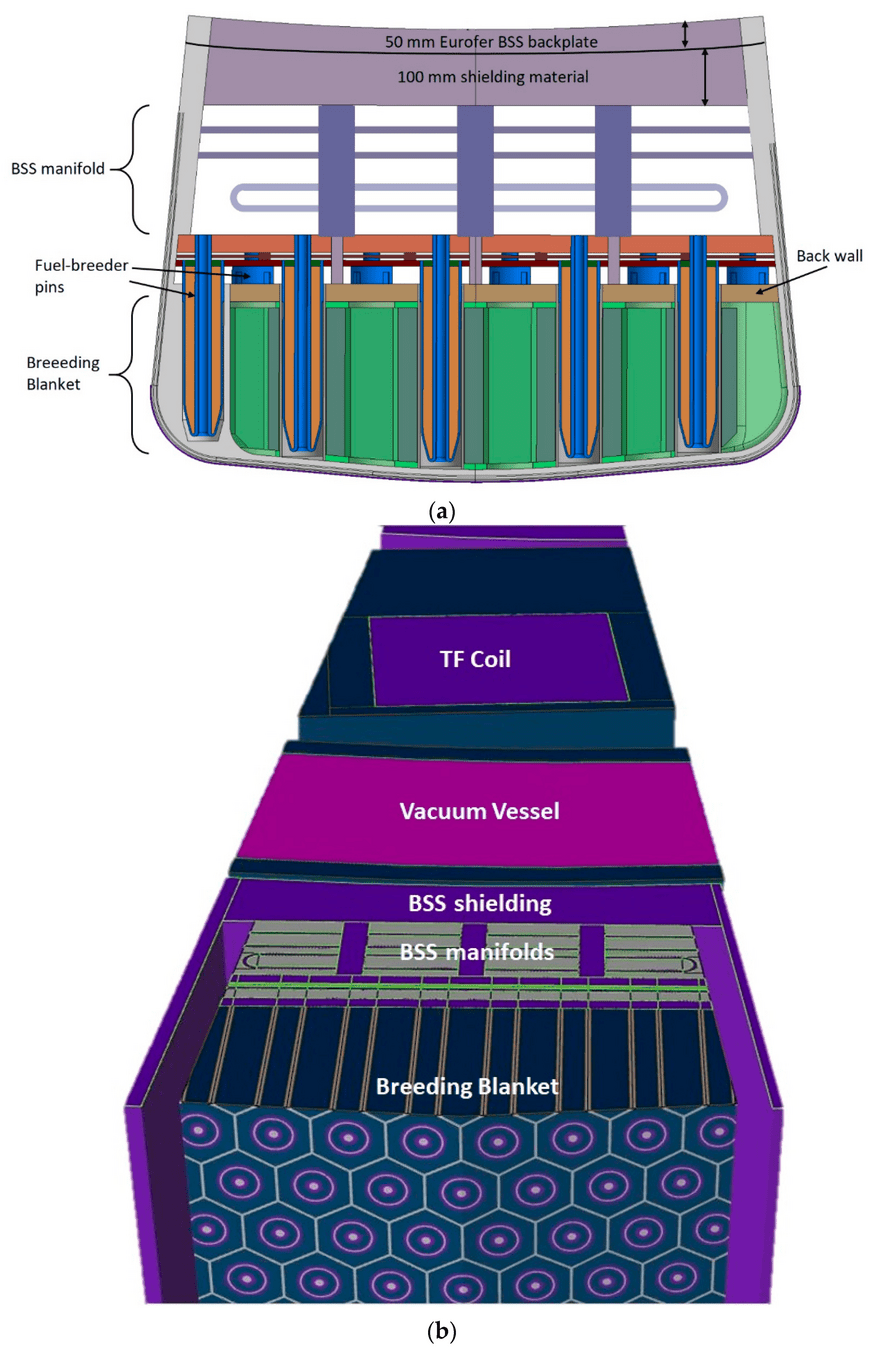
Helium Cooled Pebble Bed

⚛️Breeding tritium

🛡️Shield from neutrons

🔥Extract heat

Liquid Immersion Blanket

FLiBe

The LIB has many advantages

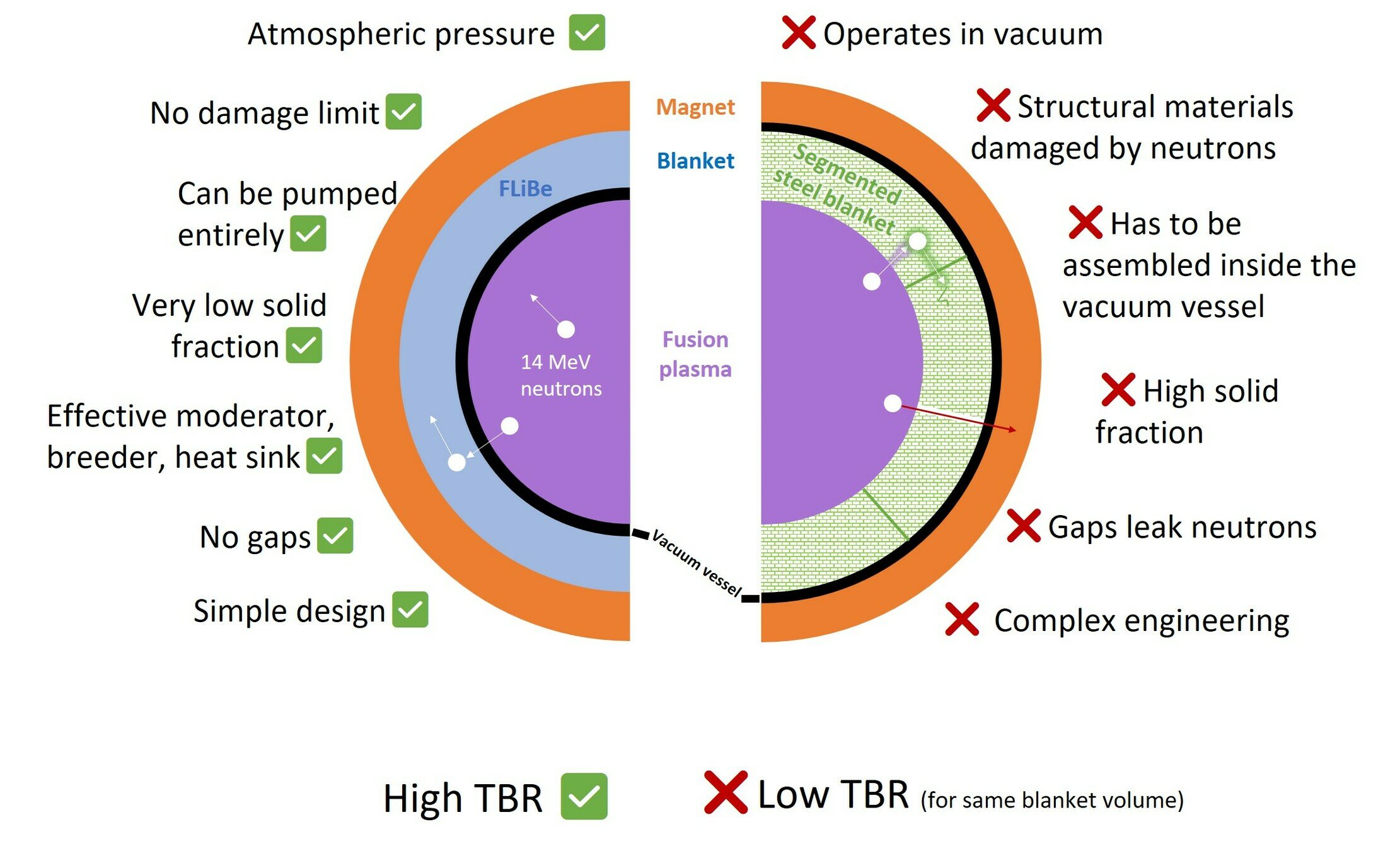
In order to design a breeding blanket we need to...

✅Understand T transport in the breeder

✅Understand the interaction of T with the solid materials

 

✅Develop and validate modelling tools for design optimisation

 

✅Demonstrate a proof a concept

Experimental techniques

FESTIM modelling

LIBRA experiment

Understanding Tritium Transport in Materials

Several mechanisms are at stake

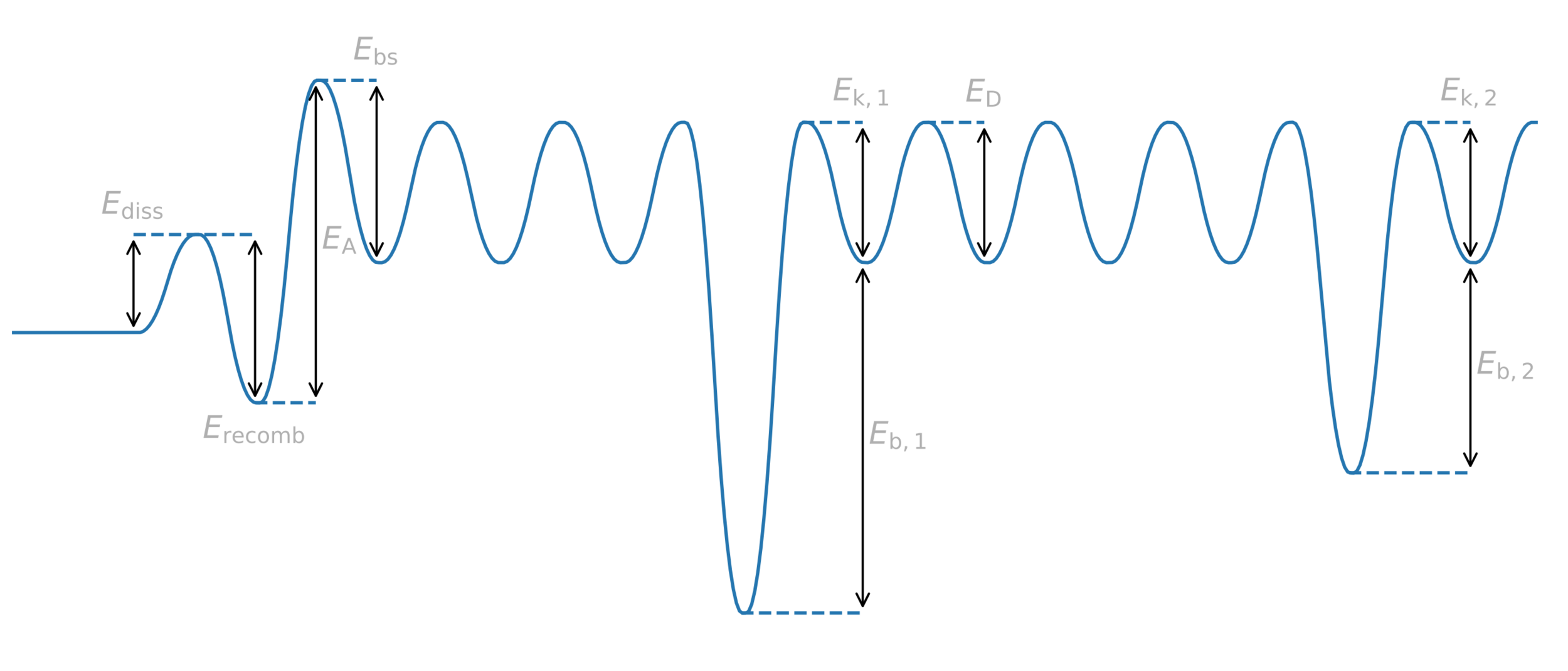
Processes are thermally activated

Dissociation/recombination

Diffusion

Trapping

Potential energy

These mechanisms are characterised by material properties

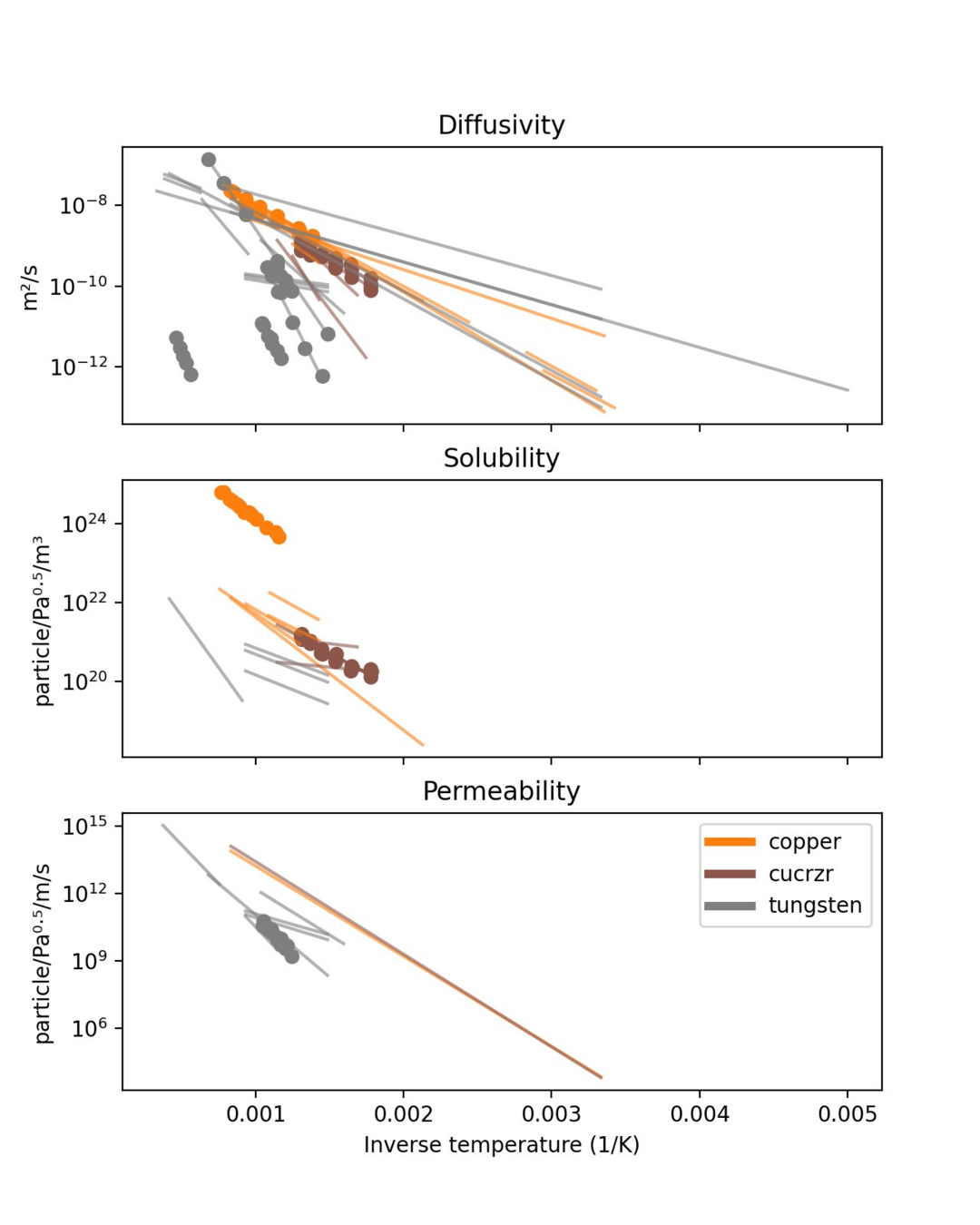
  • Diffusivity
  • Solubility
  • Permeability
  • Recombination coeff.
  • Dissociation coeff.
  • Trapping rate
  • Detrapping rate
X = X_0 \ \exp{\left( -E_X/k_B T \right)}

Arrhenius law

Properties can be calculated with Molecular Dynamics

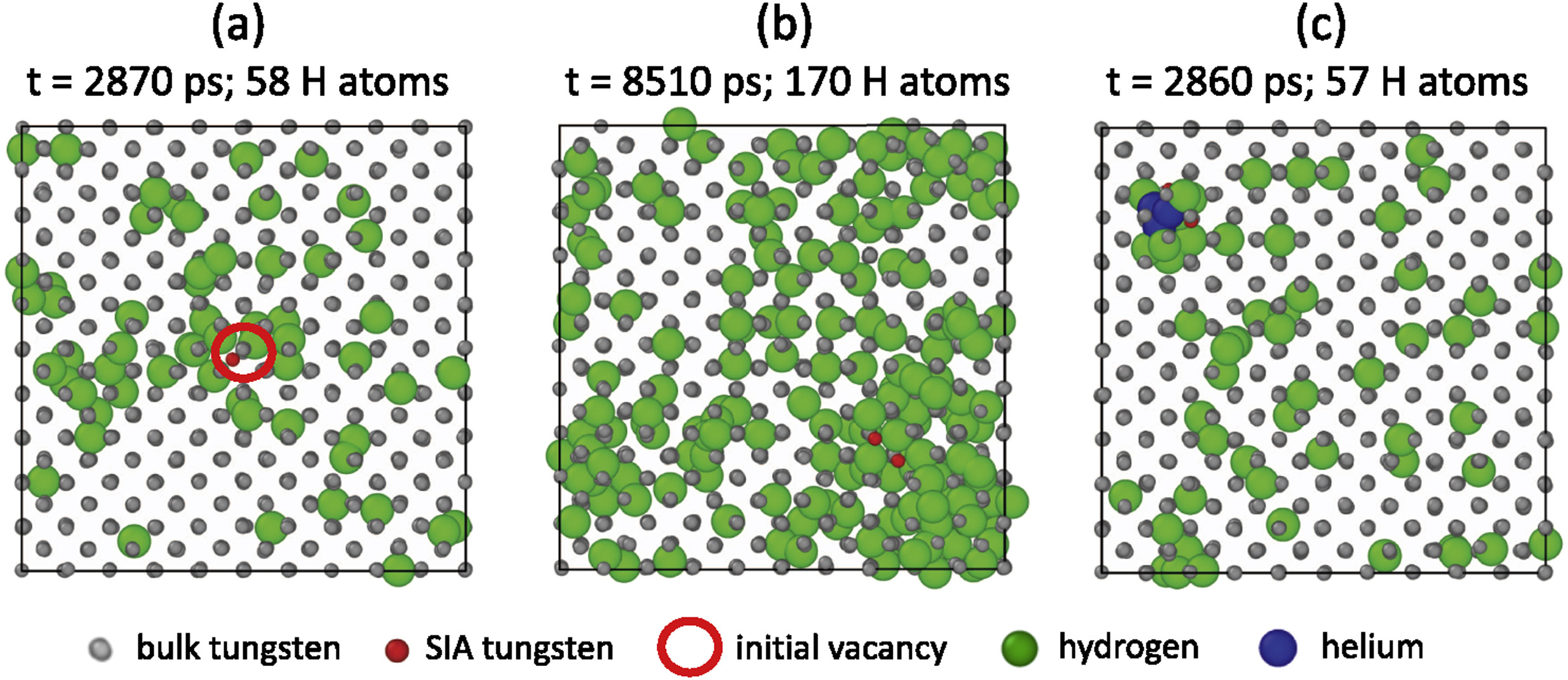
Grigorev et al Molecular dynamics simulation of hydrogen and helium trapping in tungsten, JNM, Volume 508, 2018

3 nm

Properties can also be measured experimentally

Thermo-desorption experiments provide information on retention

Stage 1: load with H

Stage 2: heat up to desorb H

Tungsten

Beryllium

Desorption flux (H m\(^{-2}\) s\(^{-1}\))

O.V Ogorodnikova et al Deuterium retention in tungsten in dependence of the surface conditions, JNM, 313–316, 2003

Baldwin et al Experimental study and modelling of deuterium thermal release from Be–D co-deposited layers, Nucl Fus, vol. 54, 2014

Permeation experiments measure the diffusivity and solubility

Sample

  1. Impose partial pressure of H on one side
  2. H permeates through the sample
  3. Measure the desorption flux on the other side

Sample

  1. Impose partial pressure of H on one side
  2. H permeates through the sample
  3. Measure the desorption flux on the other side
  4. Fit with the master curve to identify \( \Phi \) and \(D\)
  5. Repeat for different temperature
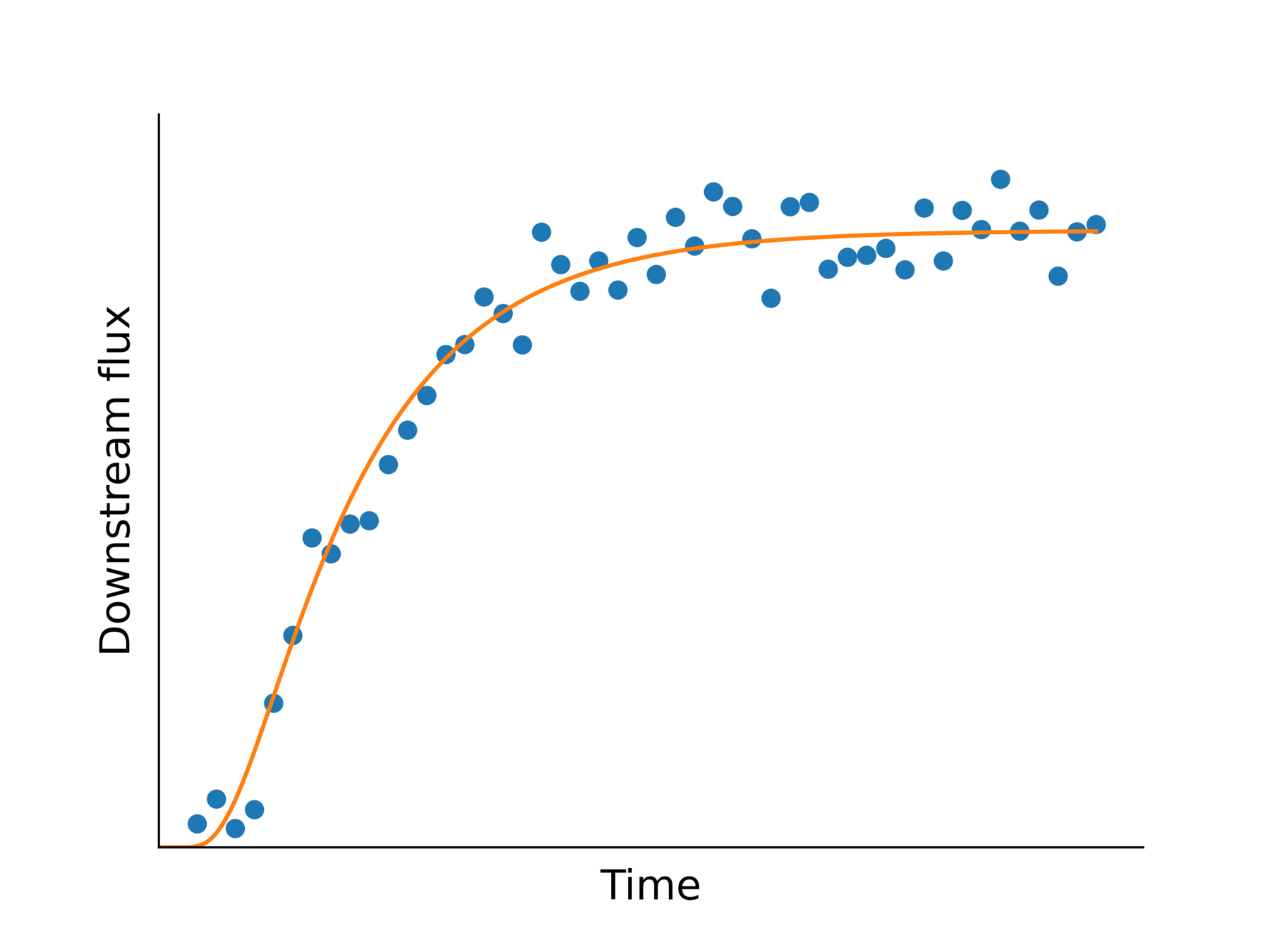
\mathrm{downstream \; flux} = \dfrac{\sqrt{P_\mathrm{up}} \Phi}{L} \left(1+2 \sum_{n=1}^{\infty} \left(-1\right)^{n} e^{- t\dfrac{\pi^{2}n^{2} D}{L^{2}}}\right)

Permeation experiments measure the diffusivity and solubility

What about molten salts?

FLiBe

metal membrane

FLiBe solubility

HYPERION project

Source: HTM database

HYPERION principle

H concentration

Permeation flux

H concentration

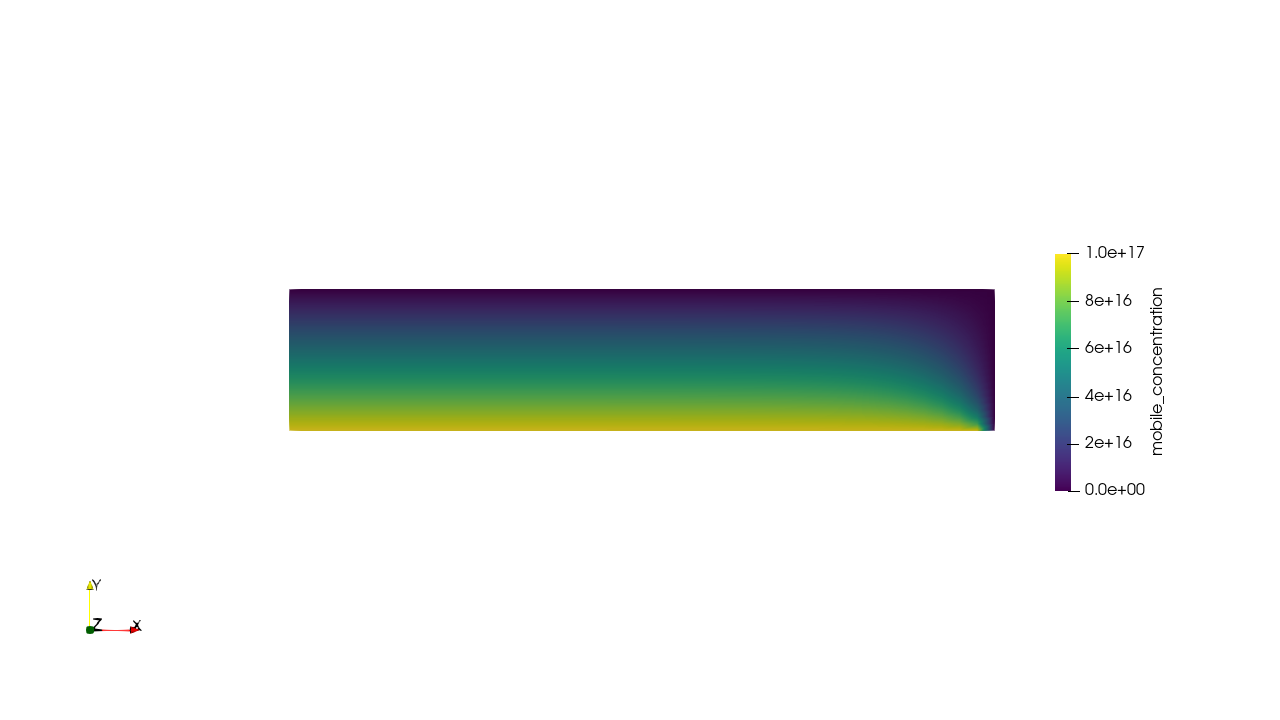
Transport through the salt was simulated with FESTIM

\( c = K_H \ P_\mathrm{up} \)

\( c = 0 \)

\( \mathrm{H \ m^{-3}} \)

Permeation through the crucible wall

FLiBe

The permeation fluxes are estimated w/wo edge effects

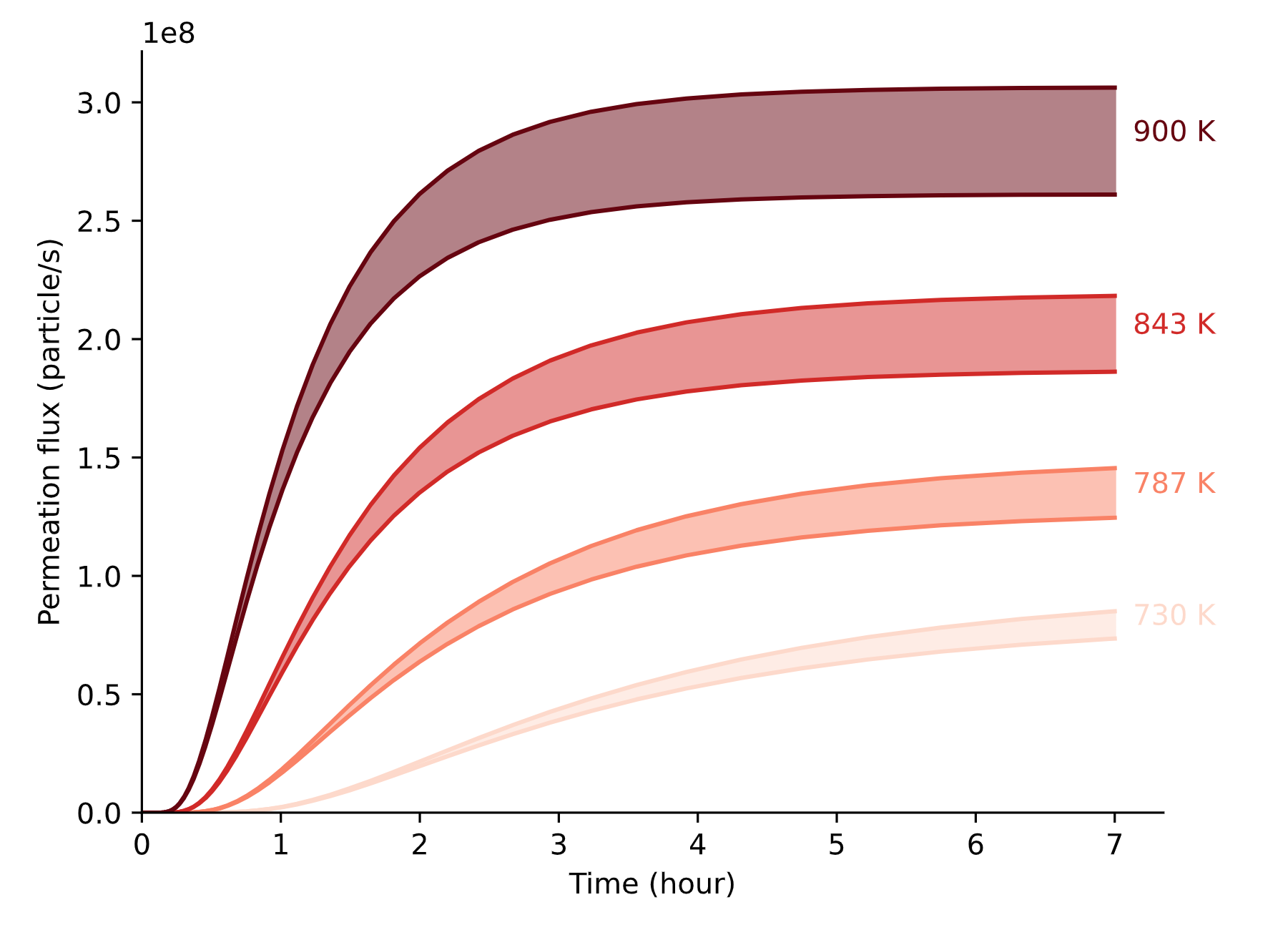
\mathrm{flux} = 2 \pi \ \int_0^R r \ D \nabla c \ \cdot \mathbf{n} \ dr

\( K_H = 10^{17} \ \mathrm{H \ m^{-3} \ Pa^{-1}}\) 

\( D = 5.66\times10^{-7} \exp (-0.39 / k_B T) \ \mathrm{m^{2} \ s^{-1}}\) 

\(P_\mathrm{up} = 1 \ \mathrm{Pa} \)

Component scale modelling with FESTIM

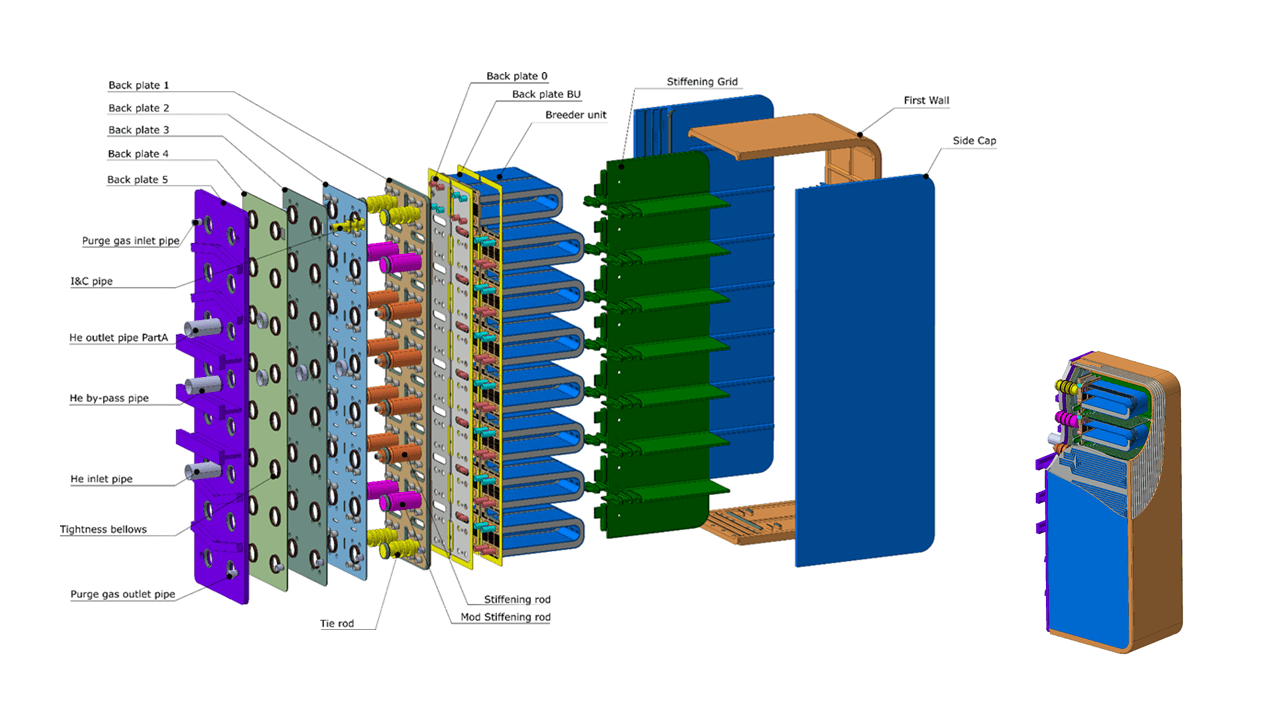
WCLL unit

At the macroscale, continuous fields can be used

Fick's second law of diffusion

= \nabla \cdot (D \nabla c_\mathrm{m})
J = -D \nabla c_\mathrm{m}

Fick's first law of diffusion

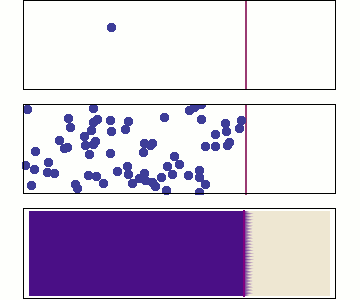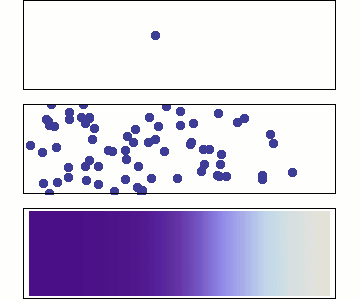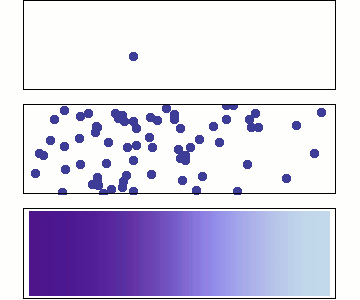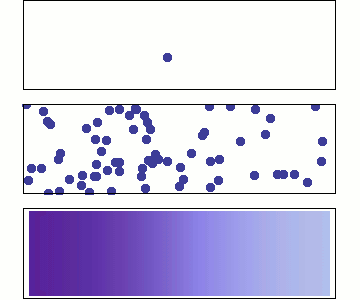
\frac{\partial c_\mathrm{m}}{\partial t} = -\nabla \cdot J

Trapping is modelled with reaction rate theory

\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D \nabla c_\mathrm{m}) - \sum \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p \ c_{\mathrm{t}, i}

McNabb & Foster model

\mathrm{H} + [\ \ \ ]_\mathrm{trap} \ \substack{p \\[-1em] \longleftarrow\\[-1em] \longrightarrow \\[-1em] k} \ [\mathrm{H}]_\mathrm{trap}
c_\mathrm{t}
c_\mathrm{m}
n_\mathrm{free}
n_\mathrm{free} = n - c_{\mathrm{t},i}
\rho C_p \frac{\partial T}{\partial t} = \nabla \cdot (\lambda \nabla T)
\frac{\partial c_\mathrm{m}}{\partial t} = \nabla \cdot (D(T) \nabla c_\mathrm{m}) - \frac{\partial c_{\mathrm{t}, i}}{\partial t}
\frac{\partial c_{\mathrm{t}, i}}{\partial t} = k(T) \ c_\mathrm{m} \ (n - c_{\mathrm{t}, i}) - p(T) \ c_{\mathrm{t}, i}

Hydrogen transport

Heat transfer

diffusion and trapping

FESTIM solves the H transport equations and heat transfer

\( T \)

Used at

Check it out on GitHub

FESTIM is a versatile tool

Thermo-desorption

Plasma facing components

Tungsten

Beryllium

Modelling permeation barriers

No barrier

Barrier

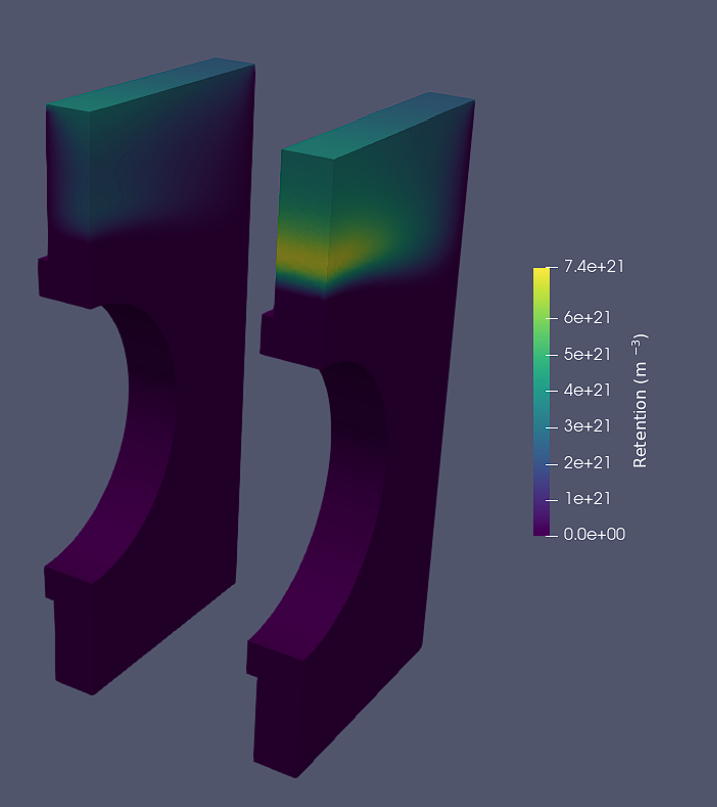
FESTIM has been used to simulate breeding blankets

Simulation of a WCLL breeding blanket from CAD files

1) Mesh generation

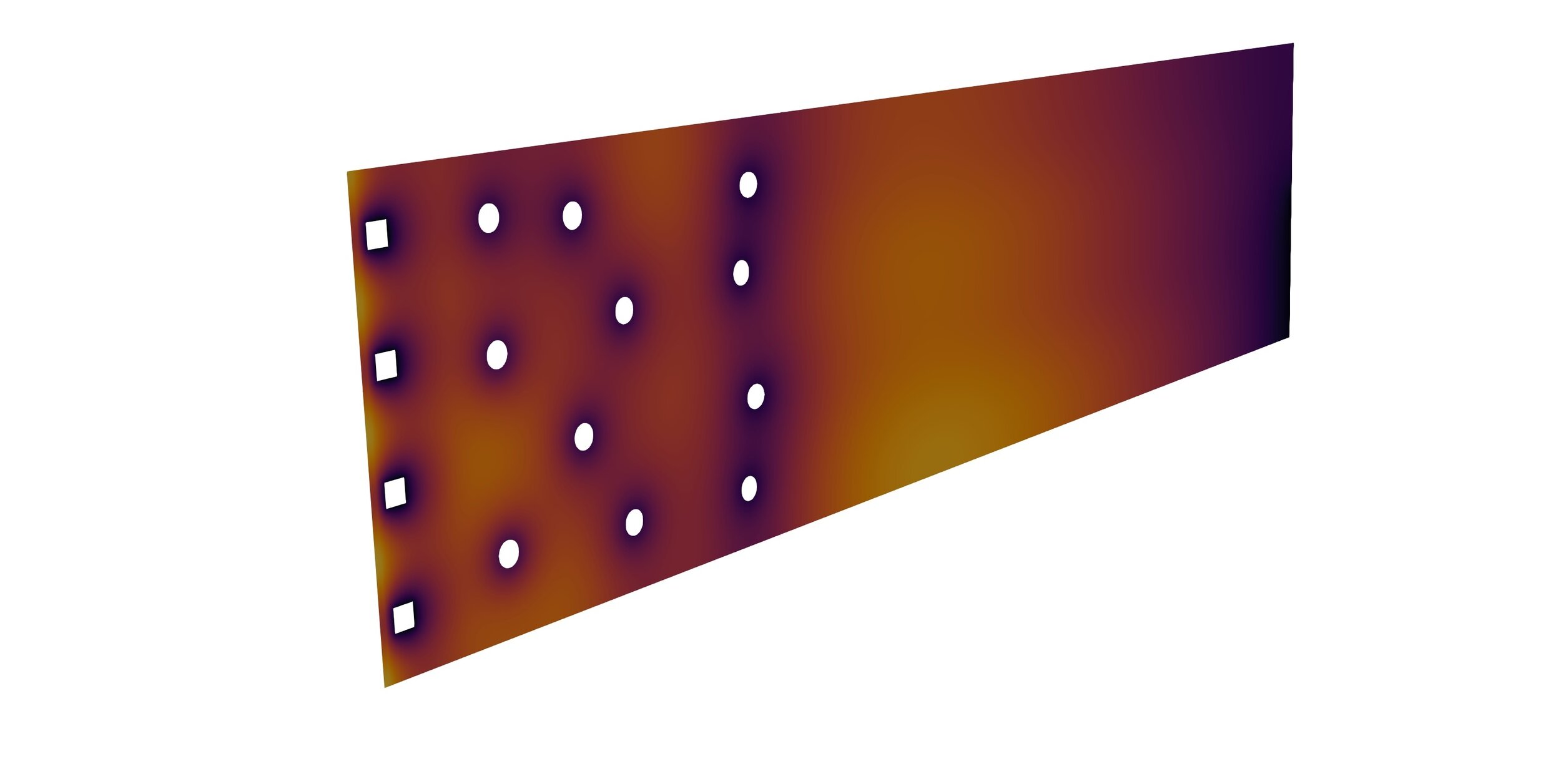
2) Heat transfer simulation

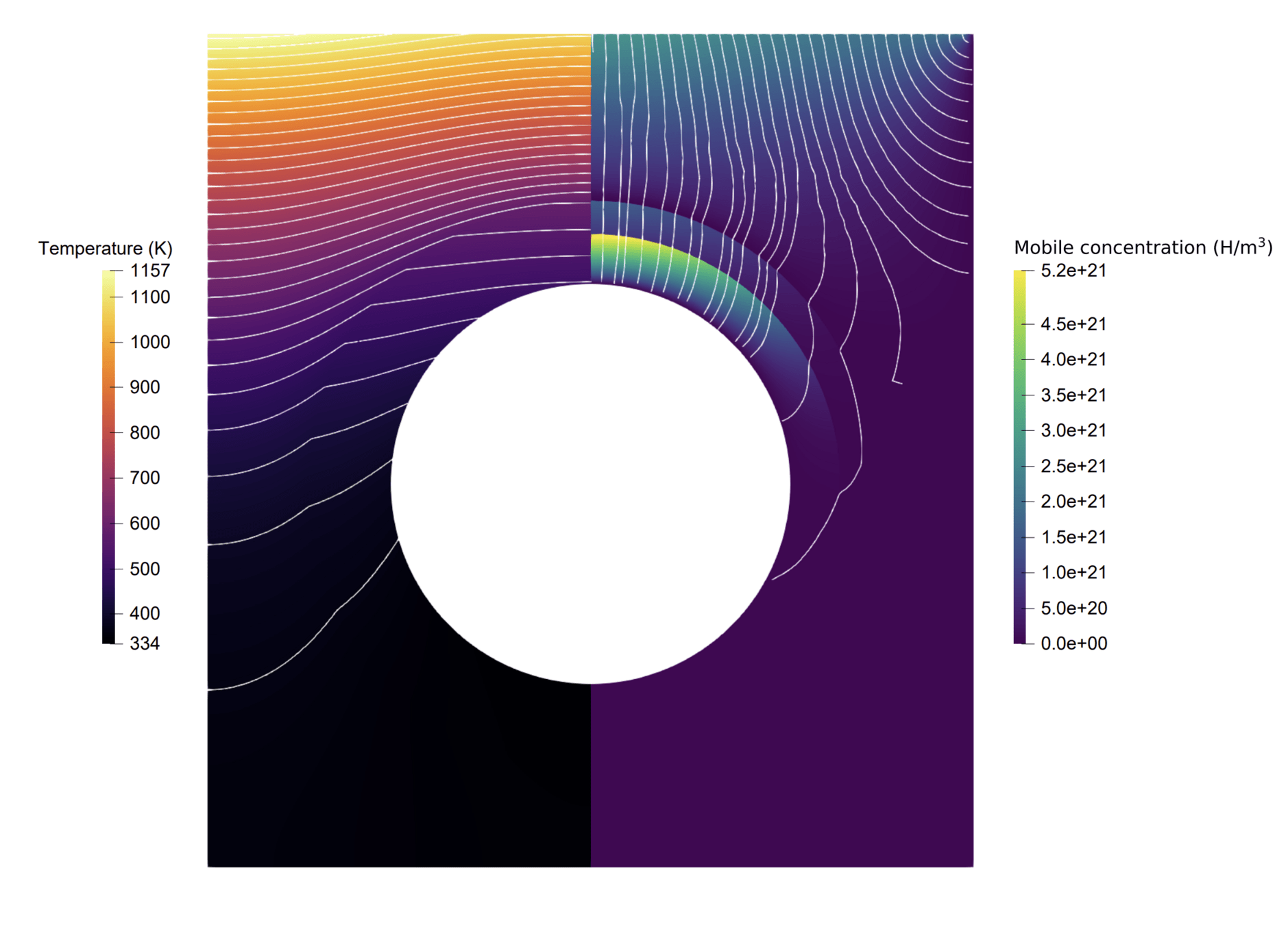
3) 2D slice

James Dark et al 2021 Nucl. Fusion 61 116076

Arena et al Energies 2023, 16, 2069

Simulation of a WCLL breeding blanket from CAD files

1) Mesh generation

2) Heat transfer simulation

3) 2D slice

4) Fluid dynamics

5) H transport

James Dark et al 2021 Nucl. Fusion 61 116076

In order to design a breeding blanket we need to...

✅Understand T transport in the breeder

✅Understand the interaction of T with the solid materials

 

✅Develop and validate modelling tools for design optimisation

Experimental techniques

FESTIM modelling

LIBRA experiment

✅Demonstrate a proof a concept

The EU-DEMO plan

Step 1. Build ITER...

Step 2. Plug some mockups in the Tritium Breeding System (TBS)

Step 3. Pick the best one and build a FULL SCALE prototype for DEMO

Step 4. Hope it works at scale 🤞

Plan B

There is no plan B.

ITER

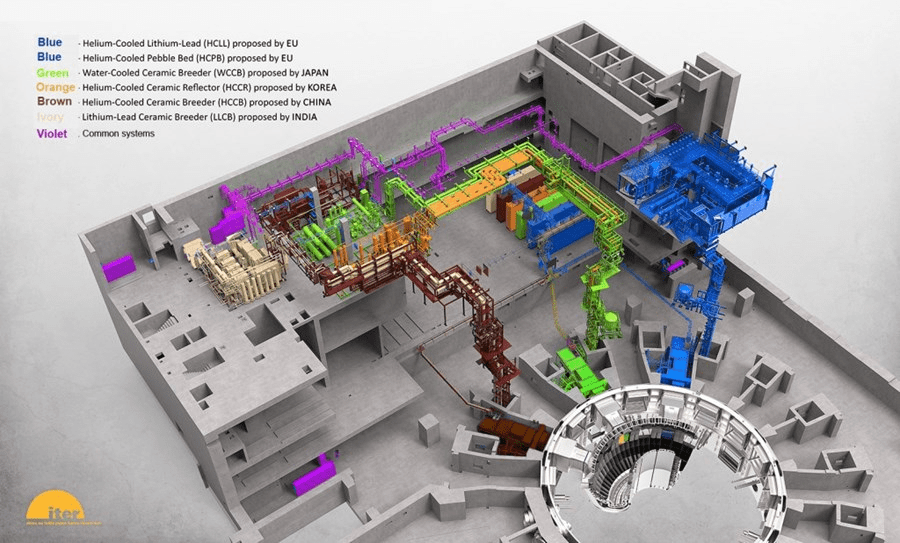
TBS

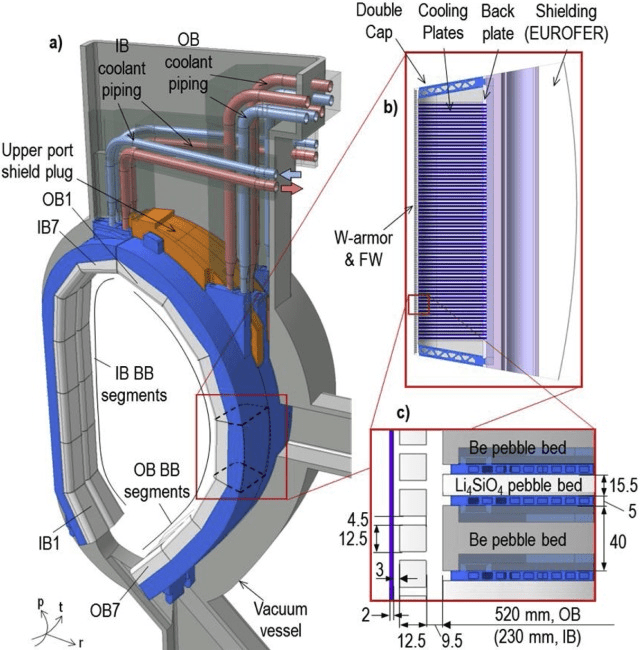
DEMO

Let's test it before ARC

What is the smallest blanket that can demonstrate a TBR of 1?

LIBRA

Liquid Immersion Blanket tritium Robust Accountancy

Objectives

🎯T self-sufficiency with DT neutrons

🎯Experience with molten salt handling

🎯Tritium extraction from molten salts

500L FLiBe

14 MeV neutron source

Inconel

double wall

Li + n → T + He

Neutron multiplier

The LIBRA experiment

Tritium transport

Transport mechanisms:

  • Diffusion
  • Advection

Release pathways:

  • Release gas/liquid interface
  • Permeation through walls

The LIBRA experiment

The LIBRA experiment

He

Tritium detection

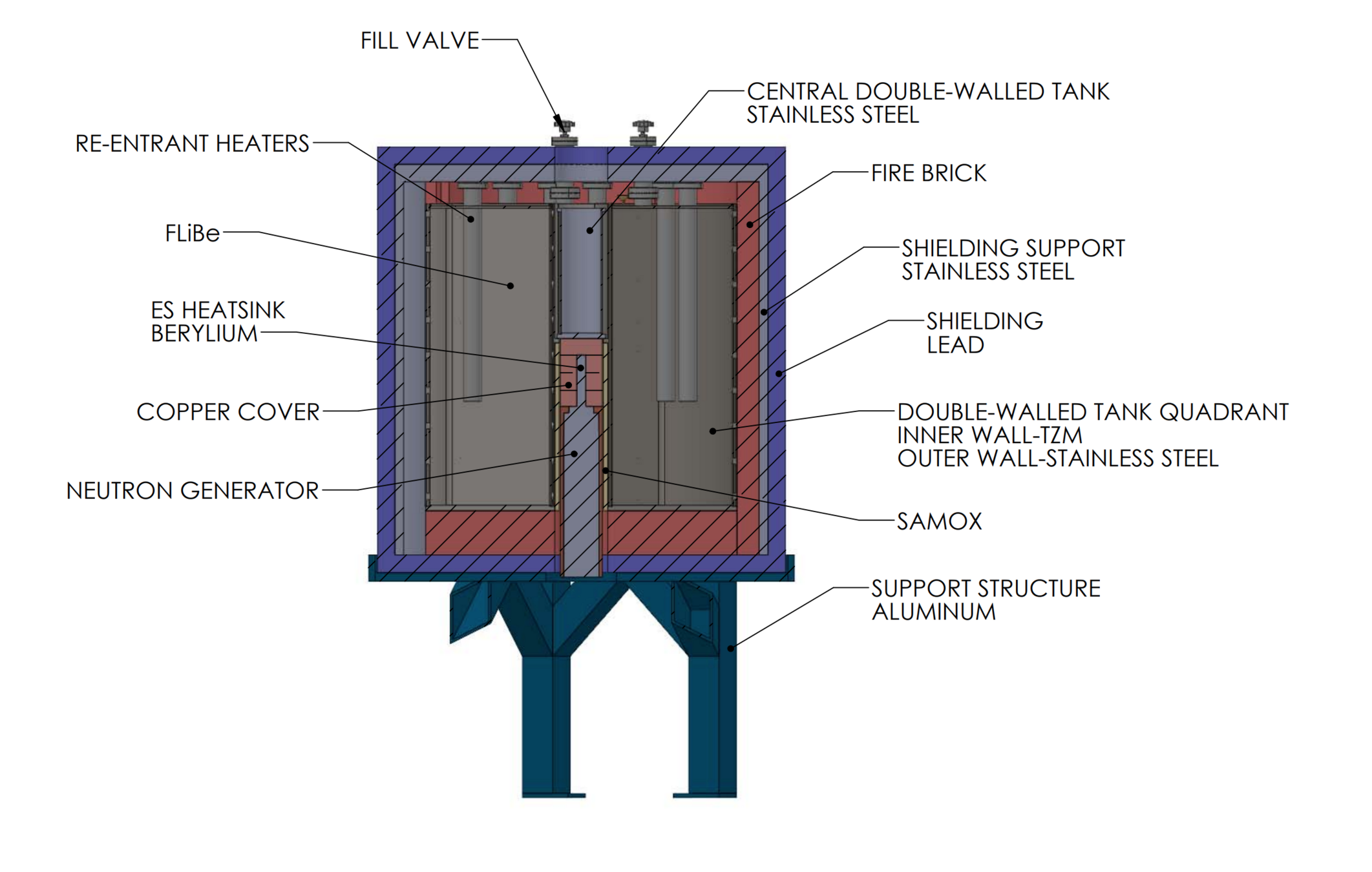
The actual design is a bit more complex

LIBRA was designed to achieve TBR ≈ 1

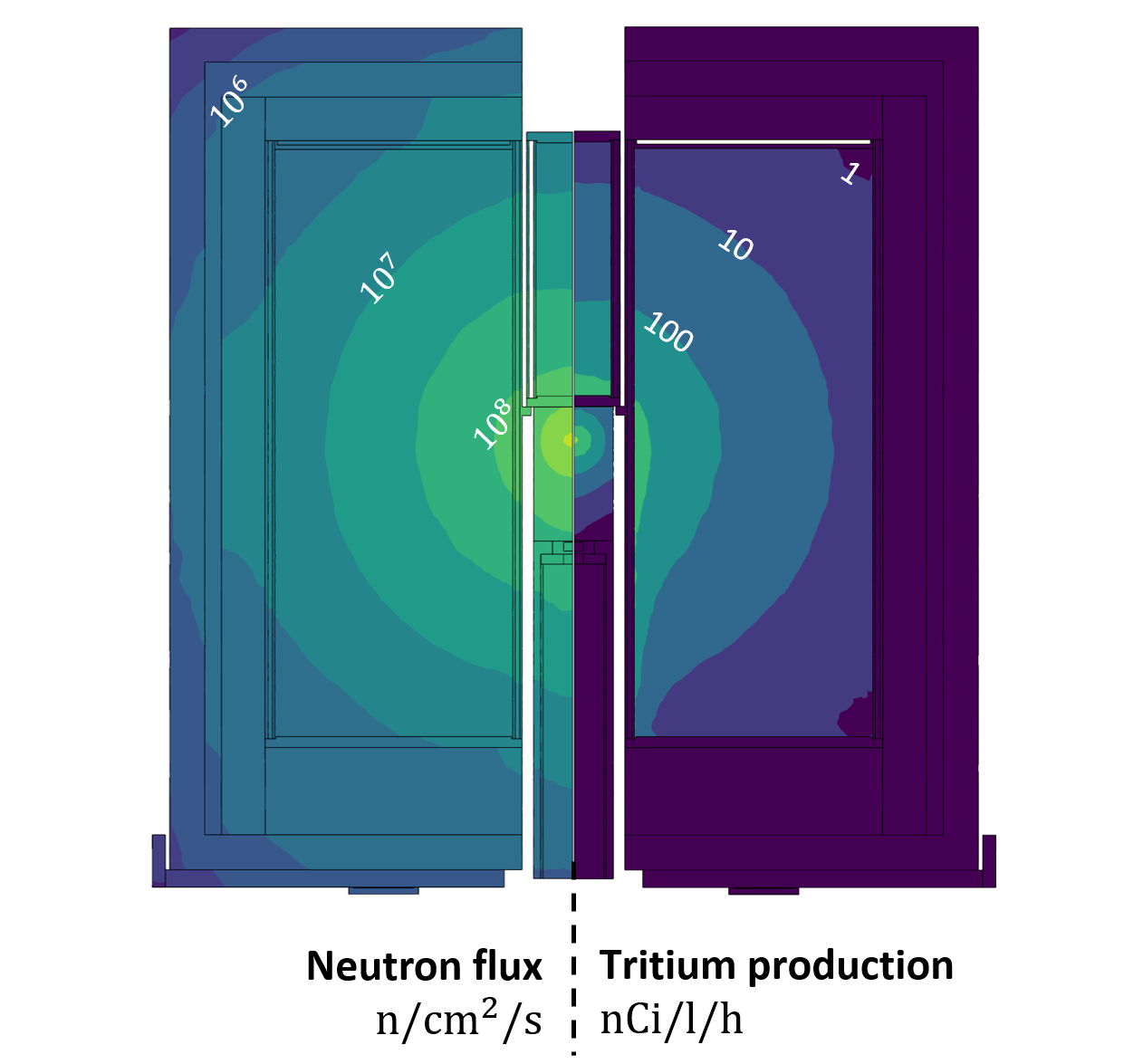
\mathrm{TBR} = \mathrm{\frac{T \ produced}{T \ consumed}}
= \mathrm{\frac{T \ produced}{neutron \ produced}}

Neutronics simulations

Let's start smaller

  • 14 MeV neutron generator \( 10^{10} \) n/s
  • 500 L of FLiBe

→ Never done at MIT ⚠️

The BABY programme

V \frac{d c_\mathrm{salt}}{dt} = S - \textcolor{#ff7f0e}{Q_\mathrm{wall}} - \textcolor{#2a7eb8}{Q_\mathrm{top}}
Q_i = A_i \ k_i \ (c_\mathrm{salt} - c_\mathrm{external}) \\ \approx A_i \ k_i \ c_\mathrm{salt}
S = \mathrm{TBR} \cdot \Gamma_n

100 mL

CLiF salt

Top release

Wall release

A simple 0D model is used to simulate BABY

= source - losses

inventory evolution

\(k\) mass transport coefficient

\(A\) surface area

neutron rate

  • 2 x 12 h irradiation
  • \( \mathrm{TBR} \approx 3 \times 10^{-4} \)
  • \( \Gamma_n \approx 4 \times 10^8 \) n/s (fitted)
  • Mass transport coeffs. \( k_i \) (fitted)

100 mL

CLiF salt

Top release

Wall release

THIS is what we can measure!

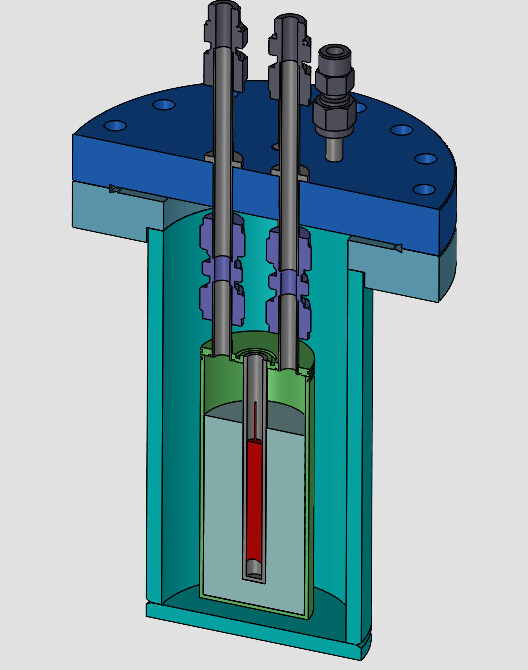
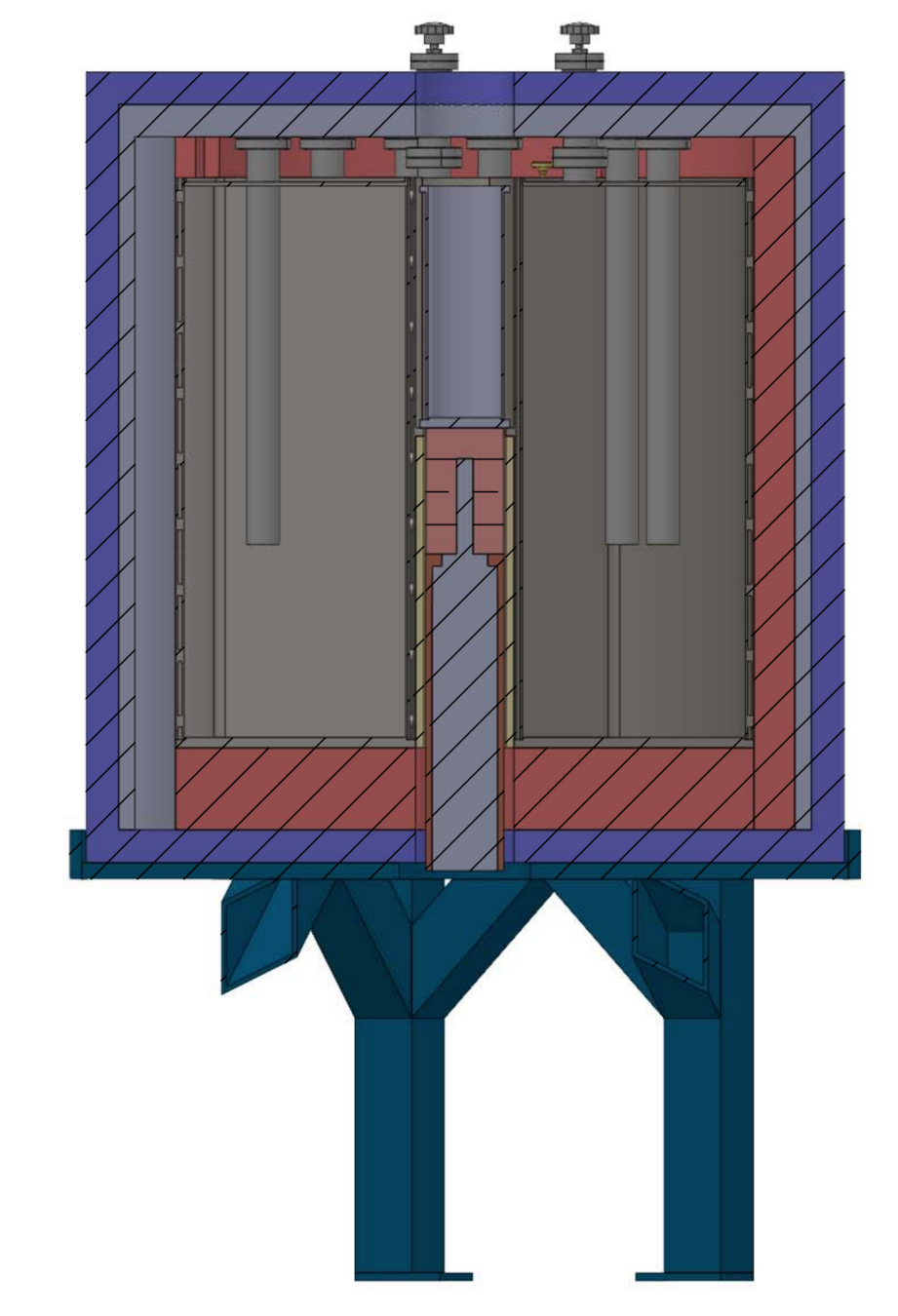
Kumagai's experiment

Salt crucible and two DT neutron sources

Tritium collection system

Temperature control

The BABY experiment breeds tritium at a smaller scale

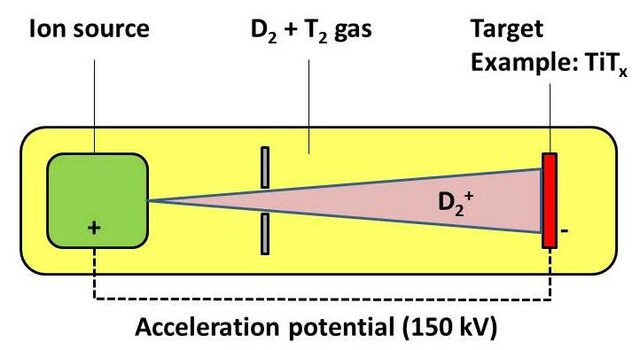
Bjørnstad, et al. (2014). The Current Status and Future Trends on Radioisotope Application in Industry.

HT, T2 → HTO

#1

#2

#3

#4

HTO, TF

HT, T2

Furnace

Tritium collection and accountancy

→ then analysed with Liquid Scintillation Counting

Liquid Scintillation Counting

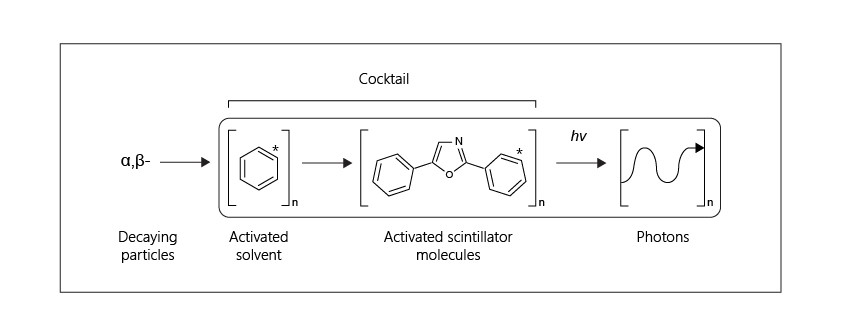
Counts between 0-18.6 keV for tritium detection

Theoretical activity (Bq)

Measured activity (Bq)

LSC tests

⏱️50 min

HTO, TF

HT, T2

15 Bq of tritium have been bred

Collected tritium

1 Bq = 10\(^{-15}\)  mole of T

Collection effiency 99.8%

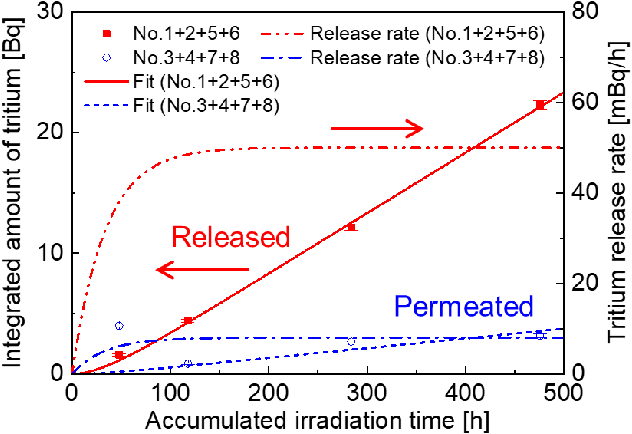
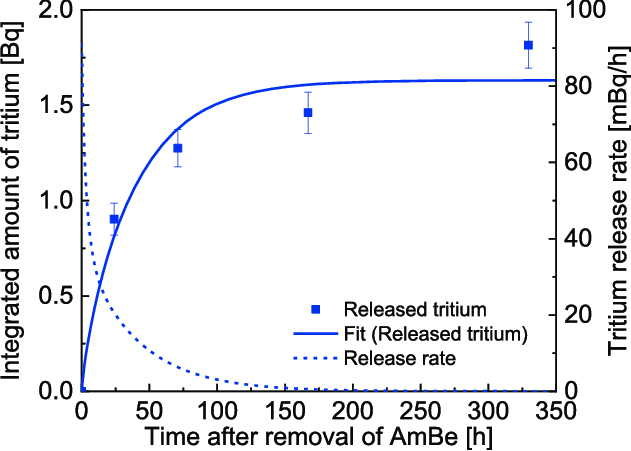
Cumulative tritium production agrees with simulation

Next experiments will give information on the wall desorption

Cumulative tritium release

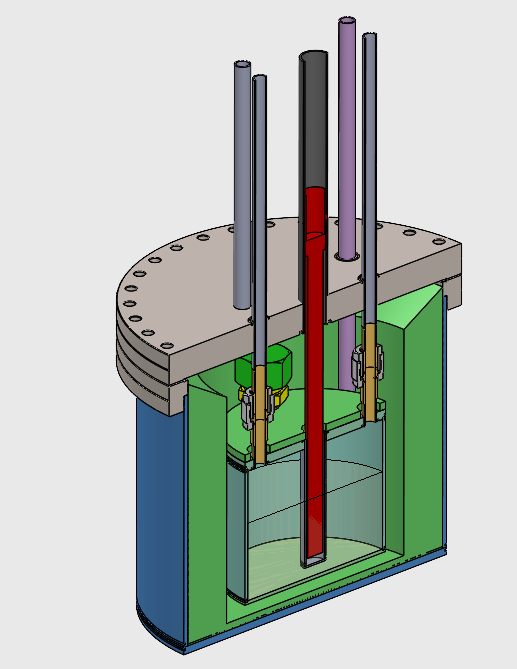
1L of salt

Top release gas sweep

Outer-vessel for capturing permeated tritium

Our next steps

  • Increase the volume of salt to 1L
  • Replace CLiF by FLiBe
  • Improve the neutron detection system
  • Build and validate FESTIM model of BABY
  • Demonstrate TBR = 1 with LIBRA

TBR

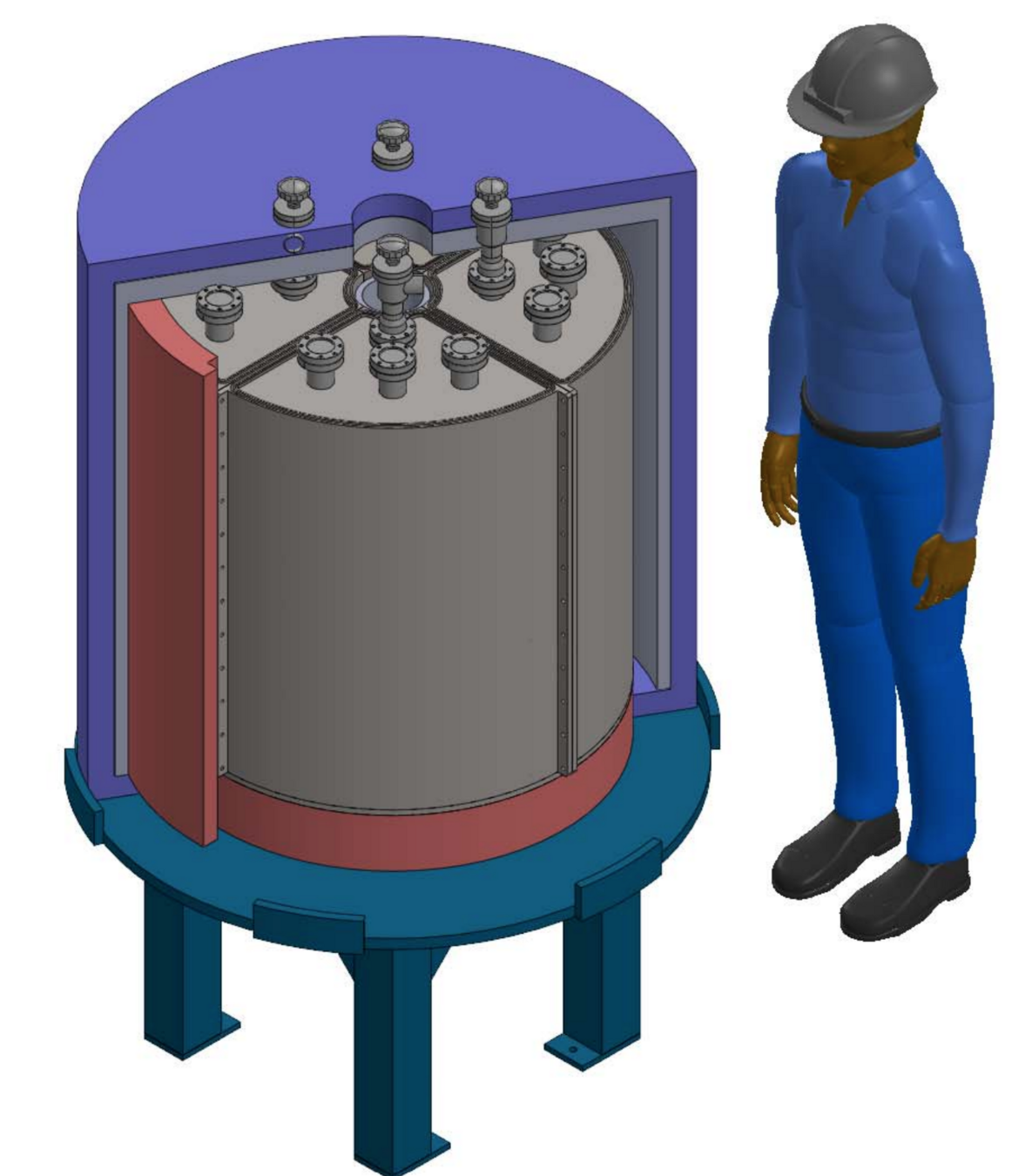
BABY

LIBRA

Takeaways

  • Tritium breeding is critical to the fusion economy
  • We have to de-risk the blanket technology before any pilot plant
  • LIBRA aims to be the world's first blanket demonstration
  • To design a full breeding blanket, we need:
    • Experiments to characterise materials
    • High-fidelity validated models

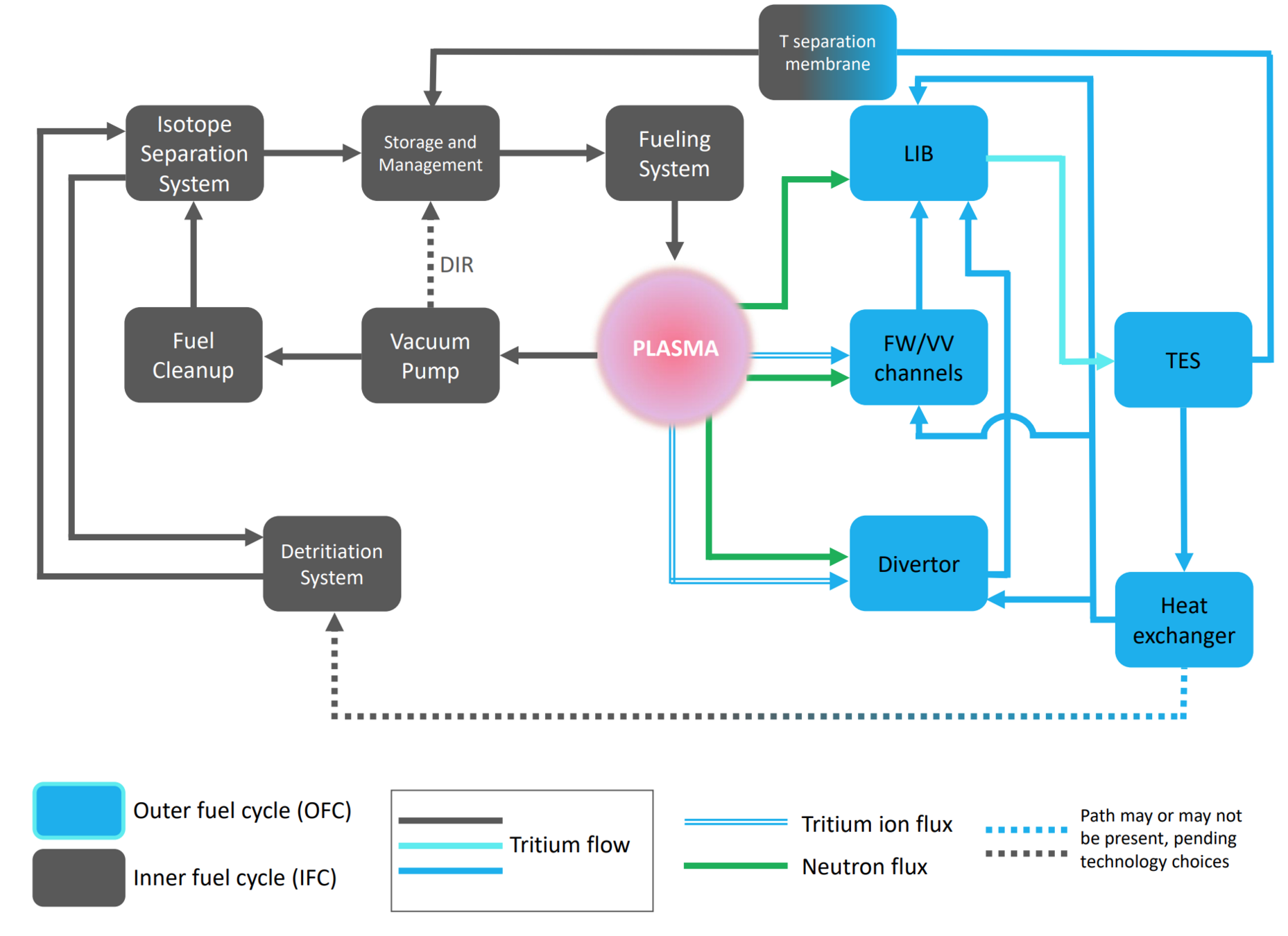
Meschini et al  Nucl Fus, 2023

Tritium breeding far from being the end of the journey

✅Can we breed enough tritium?

❓Can we extract it?

❓Can we separate it?

❓Can we store it?

❓Does it get trapped somewhere?

❓Can we recover it?

Thank you very much!

Any question?

Tritium Transport in Breeding Blankets (PSFC seminar)

By Remi Delaporte-Mathurin

Tritium Transport in Breeding Blankets (PSFC seminar)

  • 120

More from Remi Delaporte-Mathurin