Vpython 期末報告
磁瓶效應
磁瓶效應
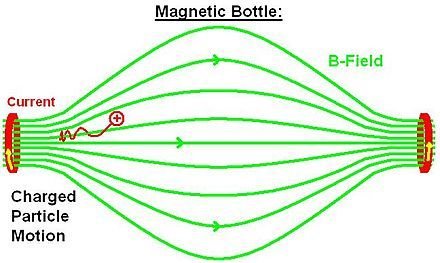
遇磁場密集處 => 反彈
會有部分角度及速度無法捕捉電子
研究動機
在這堂課中學了不少python運用方式,想要藉由python的程式運行產生的動畫來觀察螺線管產生磁場的情況,並利用必歐 - 沙伐定律以及勞倫茲力來輔助程式的編寫。螺線管產生之磁場
必歐 - 沙伐定律 (Biot–Savart law)
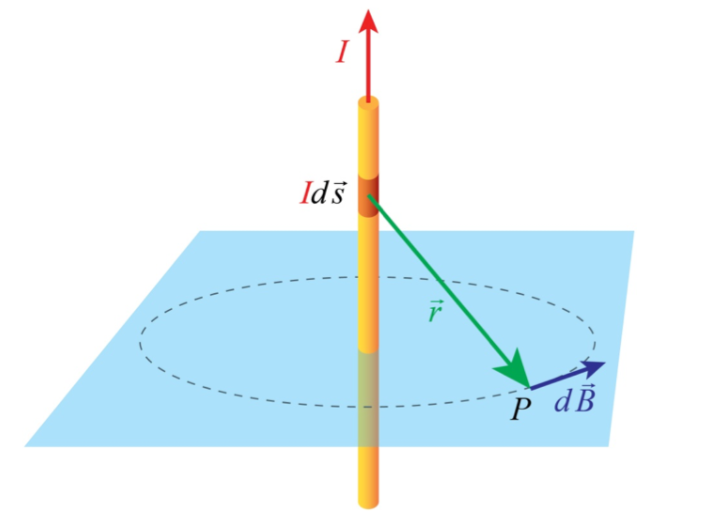
\vec{B}=\int \frac{\mu_{0}}{4 \pi} \frac{id\vec{s} \times \vec{r}}{r^{3}}
實作方法
將螺線管分割成很多小塊
求任意位置的磁場時 將所有小塊的磁場帶入定律做總和

# 自訂函式 magnetic, 計算某個位置的磁場
def magnetic(loc, segments):
field = vector(0, 0, 0)
for segment in segments:
axis = loc - segment.pos
field += mu*current/(4*pi)*mag(segment.axis)*cross(segment.axis, axis.norm())/mag(axis)**2
return field 程式實作
勞倫茲力
1892年,荷蘭物理學家亨德里克·勞侖茲提出了勞侖茲力
而勞倫茲力定律可以方程式表達為:
帶電粒子的電荷量
電場強度
帶電粒子速度
磁感應強度
勞
侖
茲
力
程式實作
\vec F = q (\vec E + \vec v \times \vec B)
# 計算羅倫茲力產生的加速度
def lorentz(v,B):
a=q*cross(v,B)/m
return a程式源碼
隨機位置速度測試
# 產生隨機位置速度小球
def randinit():
eposx = np.random.randint(low=60,high=140,size=10)
eposy = np.random.randint(low=-20,high=20,size=10)
evx = np.random.randint(low=-50,high=50,size=10)
evy = np.random.randint(low=-30,high=30,size=10)
electronic = [sphere(pos = vector(eposx[i],eposy[i],0),
v=vector(evx[i],evy[i],0),a=vector(0,0,0),
radius = 1.5,color = color.blue,
make_trail=True) for i in range(10)]
init=[[eposx[i],eposy[i],evx[i],evy[i]]for i in range(10)]
return electronic,initdef difdegree(v):
evx=[]
evy=[]
energy=[]
for i in range(360):
evx.append(v*cos(2*pi*i/360))
evy.append(v*sin(2*pi*i/360))
electronic = [sphere(pos = vector(100,0,0),v=vector(evx[i],evy[i],0),
a=vector(0,0,0),radius = 1.5,color = color.blue,
make_trail=True)for i in range(360)]
for i in range(360):
energy.append(0.5*m*((evx[i])**2+(evy[i])**2))
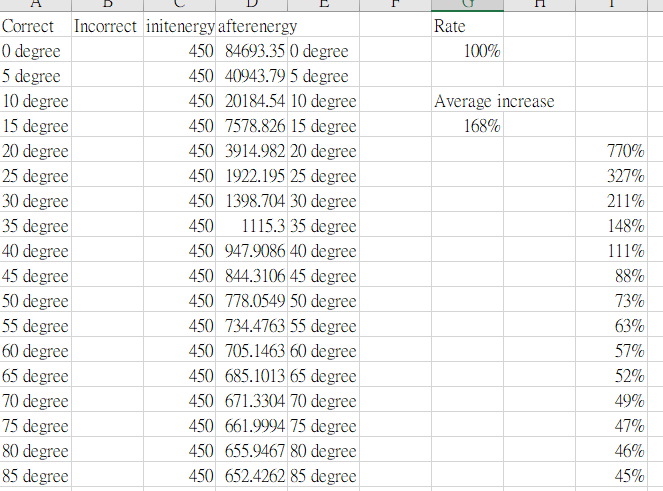
return electronic,energy相同速度位置、不同角度測試
while t<5:
electronic[i].a=lorentz(electronic[i].v,magnetic(electronic[i].pos,segs1+segs2))
electronic[i].v+=electronic[i].a*dt
electronic[i].pos+=electronic[i].v*dt
t+=dt球受磁場影響加速度
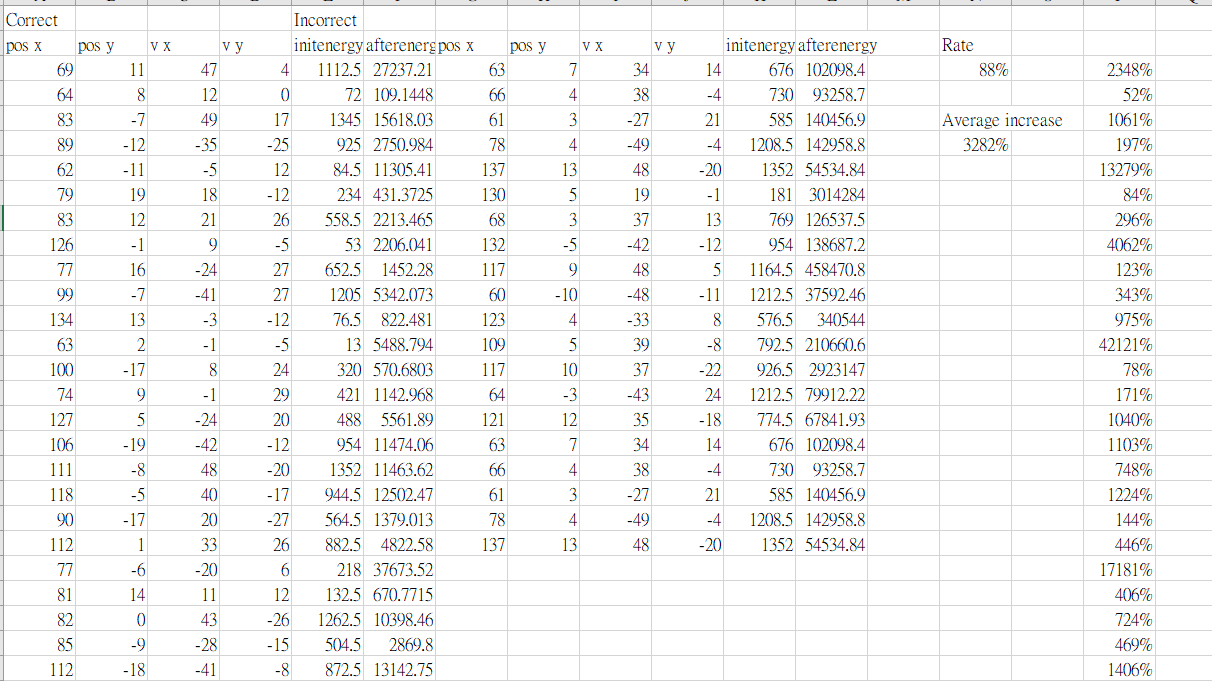
統計結果
首先我們用時間間隔為0.001測試
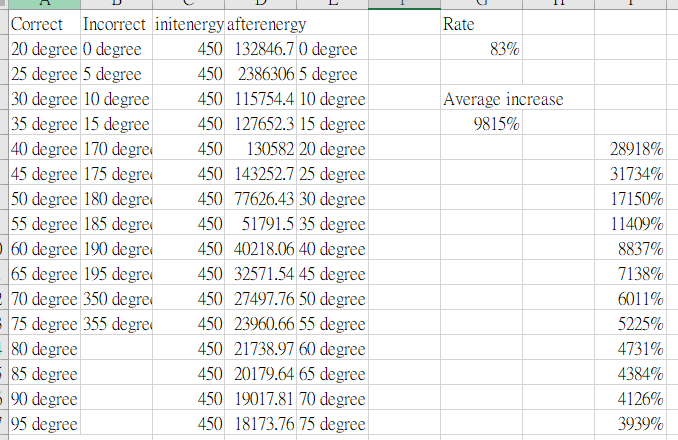
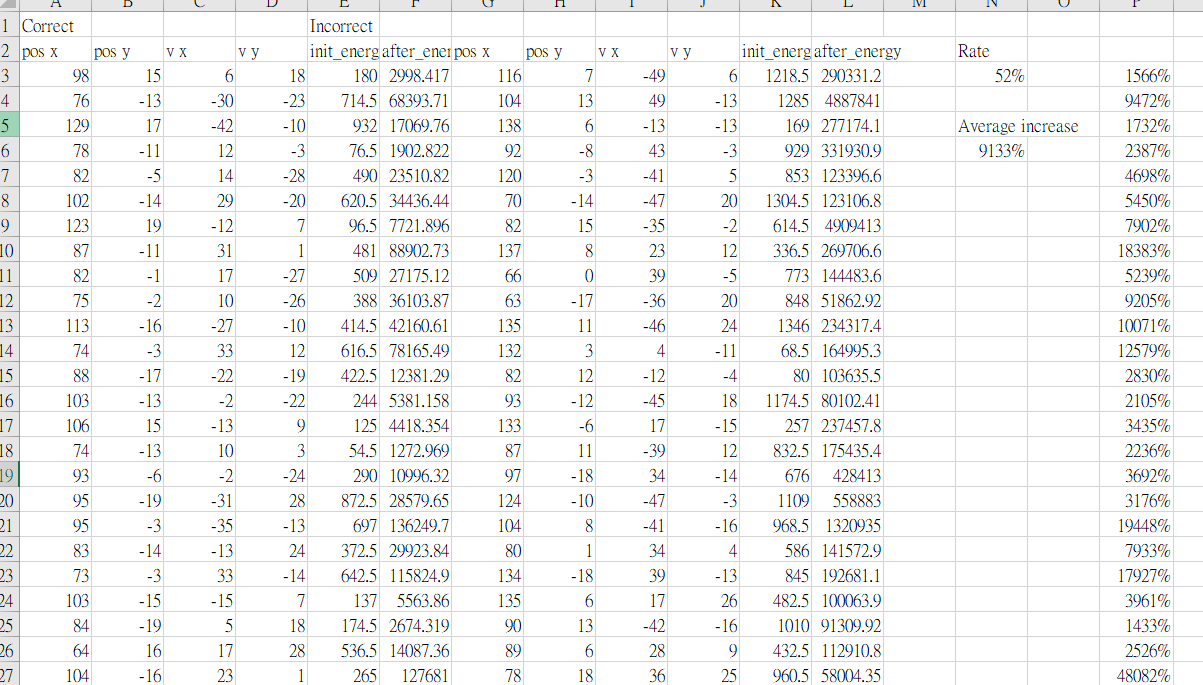
在來是間隔0.0001
GPU \|/
資料來源
研究心得
- 學習到的物理延伸
- 更多vpython工具的應用
- 遭遇眾多困難瓶頸
- 如何應付混分組員
如何成為混分組員

分工比例 :
梁棨理 27% 陳希愷 25% 張貽凱 24% 蘇煒元 24%
Vpython
By richardliang
Vpython
- 371



