Lecture 2
線性回歸(Linear Regression)
MACHINE LEARNING
training set
learning algorithm
f
y
x
線性回歸是甚麼?~?
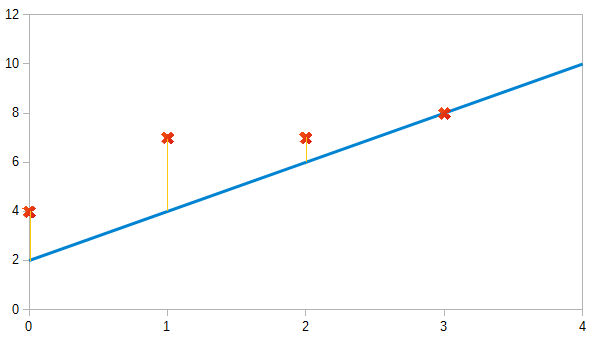
找到最符合散步圖的線性函數
Cost function
以下開始不負責任教學
J(\theta )=\frac{1}{m} \sum_{i=1}^{m}\frac{1}{2} (h_{\theta } (x^{(i)} )-y^{(i)} )^{2}
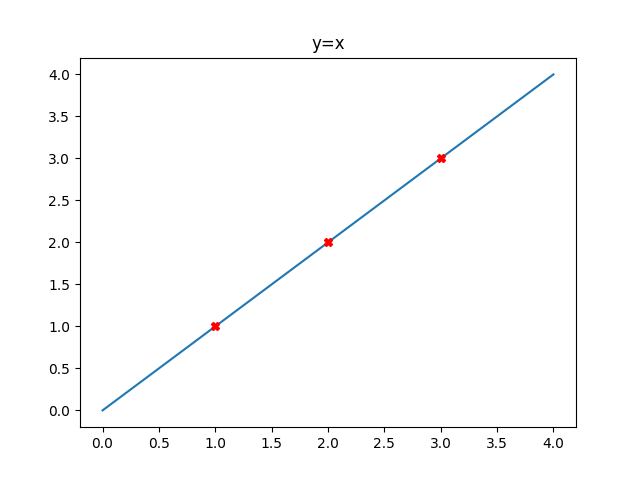
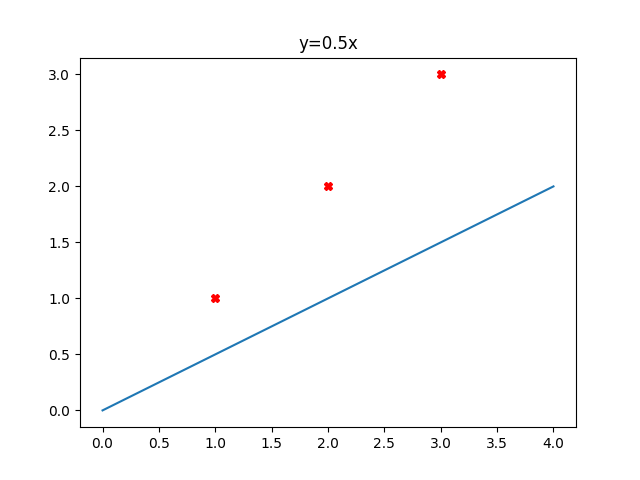
來看看函數的變化
\frac{1}{2\times 3} ((0-0)^{2} +(0-0)^{2}+(0-0)^{2}) = 0
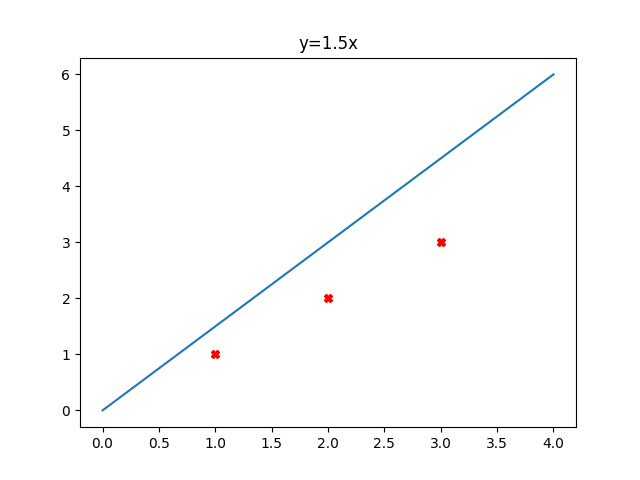
\frac{1}{2\times 3} ((1.5-1)^{2} +(3-2)^{2}+(4.5-3)^{2}) = 0.58
\frac{1}{2\times 3} ((0.5-1)^{2} +(1-2)^{2}+(1.5-3)^{2}) = 0.58
Cost function會怎麼變化?
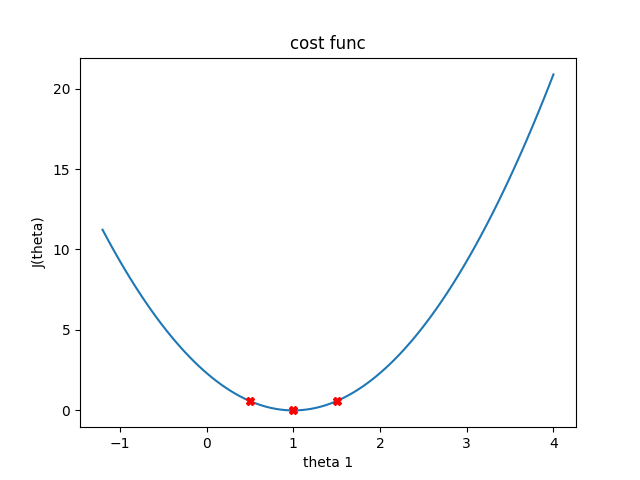
但是這只有一個變數 : 0
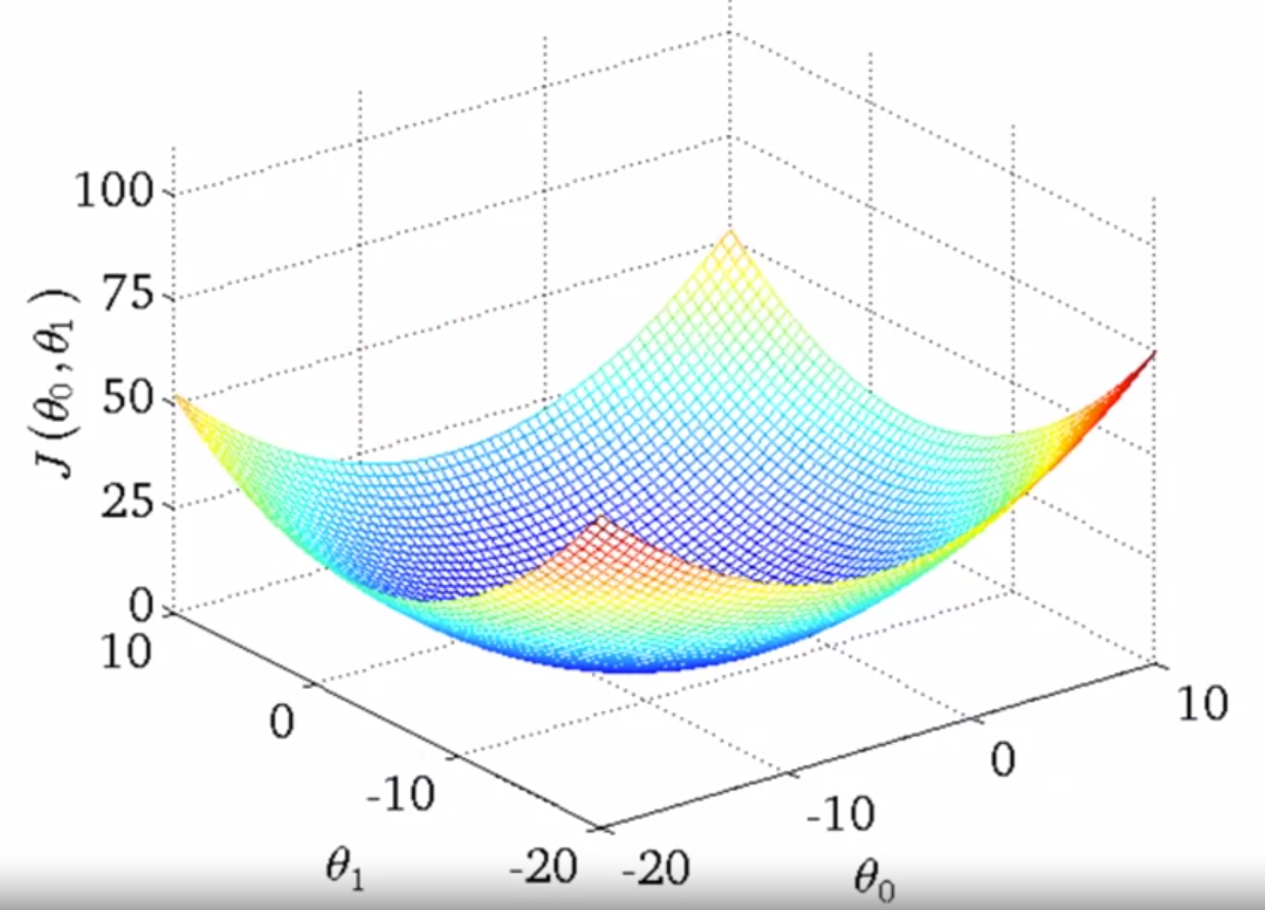
實際上可能長這樣(三圍)
the偷
怎麼讓機器能調整參數讓cost變小?
梯度下降法
Gradient descent
b= b-\alpha\frac{\partial }{\partial b} J(w,b)
w= w-\alpha\frac{\partial }{\partial w} J(w,b)
先來點數學
derivative
partial derivative
慢走不送
如果想求一個點的切線斜率怎麼辦?
用一個很小的變化量就可以知道了
y=x^{2}
求(3,9)、(3.001,9.006001)的斜率
\frac{9.006001-9}{3.001-3} =\frac{0.006001}{0.001}\approx 6
ㄜ不嚴謹的隨便講
\frac{\mathrm{d} }{\mathrm{d} x} (a_{1}x_{}^{n}+ a_{2}x_{}^{n-1}+ ...)= n\times a_{1}x_{}^{n-1}+(n-1)\times a_{2}x_{}^{n-2}+...
\frac{\partial }{\partial x} (x_{}^{m_{1}} y_{}^{n_{1}} +x_{}^{m_{2}} y_{}^{n_{2}}+...)=m_{1}x_{}^{m_{1}-1} y_{}^{n_{1}} +m_{2}x_{}^{m_{2}-1} y_{}^{n_{2}}+...
意義 : 函數圖型上點的切線斜率
意義 : 曲面上取xOz平面(垂直y軸)做的切線斜率
rOz...?
把另一個當常數看
# 在連續函數上,微分為0的為局部極值
#推到多變數就變偏微
Gradient
\nabla(x_{1},x_{2},...,x_{n})=(\frac{\partial f}{\partial x_{1}} ,\frac{\partial f}{\partial x_{2}},...\frac{\partial f}{\partial x_{n}} )
把所有方向的都考慮進去
目標?
梯度為0
最小值
如果要微分
小岔題
之後會用到
y=(2x^{2} -x)^{100}
要怎麼做?~?
chain rule
切入(?
\frac{\mathrm{d} y}{\mathrm{d} x} =\frac{\mathrm{d} y}{\mathrm{d} u} \frac{\mathrm{d} u}{\mathrm{d} x}
先降冪本身再微分
\frac{\mathrm{d} y}{\mathrm{d} x} =[100(2x^{2} -x)^{99}][4x-1]
粒子
來看微分在函數上的東東
y=x^{2}+2x
\Longrightarrow \frac{\mathrm{d} y}{\mathrm{d} x} =2x +2
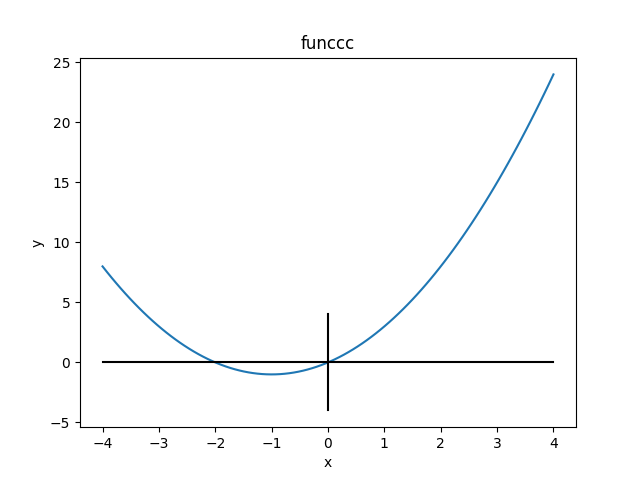
斜率為正 => 要變小,減掉(負)
斜率為負 => 要變大,減掉(負)
要把他趨向低點?
觀察微分
w= w-\alpha\frac{\partial }{\partial w} J(w,b)
下一個位置是先前的位置減掉位置梯度乘學習率(步長)
b= b-\alpha\frac{\partial }{\partial b} J(w,b)
那線性回歸的實作怎麼辦?
沒有微分的函式欸
分析一下(?
\frac{\partial }{\partial \theta_{0}} J(\theta_{0},\theta_{1})=\frac{\partial }{\partial \theta_{0}}\frac{1}{2m}\sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})^{2}
=\frac{\partial }{\partial \theta_{0}}\frac{1}{2m}\sum_{i=1}^{m} (w(x^{(i)})+b-y^{(i)})^{2}
=\frac{1}{m}\sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})^{}
\frac{\partial }{\partial \theta_{1}} J(\theta_{0},\theta_{1})=\frac{\partial }{\partial \theta_{1}}\frac{1}{2m}\sum_{i=1}^{m} (h_{\theta}(x^{(i}))-y^{(i)})^{2}
=\frac{\partial }{\partial \theta_{1}}\frac{1}{2m}\sum_{i=1}^{m} (w(x^{(i)})+b-y^{(i)})^{2}
=\frac{1}{m}\sum_{i=1}^{m} (h_{\theta}(x^{(i)})-y^{(i)})^{} x^{(i)}
好擠qwq
有關學習率
太小 ? 跑很慢
太大 ? 跑過頭沒辦法接近低點
石座
1. 很懶的framework
2. 直接np刻
沒很長我只有挖一點點空
加油OuO
如果真的不太懂...?
那就再看一次簡報(O)
不行的話
\這是一串結束/
ML L2
By richardliang
ML L2
- 499



