Epigenetic Modifications as dilute one dimensional Spin Glass systems
Ritam Das (MS19029)
IDC451
Epigenetic Modifications as dilute one dimensional Spin Glass systems
Epigenetic Modifications as dilute one dimensional Spin Glass systems
Epigenetic Modifications as dilute one dimensional Spin Glass systems
Epigenetic Modifications as dilute one dimensional Spin Glass systems
-
Magnetic systems characterised by disorder and frustration
-
Disorder in spins is analogous to positional disorder in chemical glass hence the name 'glass'
Disorder in Spin Glass Systems
Ferromagnetic
Interactions
Antiferromagnetic
Interactions
Disorder in Spin Glass Systems
Ferromagnetic
Interactions
Antiferromagnetic
Interactions
Disorder
F F F F F
AF AF AF AF AF
AF AF AF AF AF
AF AF AF AF AF
F F F F F
F F F F F
Frustration in Spin Glass Systems
Unfrustrated
Spins
Geometric
Frustration
Spin Glass
Frustration
AF
AF
AF
AF
AF
AF
AF
AF
AF
F
AF
Quantifying the Interactions
\mathcal{H} = -J_{ij} \sigma_i\sigma_j
J_{ij} > 0 \text{ : Ferromagnetic}
J_{ij} < 0 \text{ : Antiferromagnetic}
\text{Interaction Matrix}
}
}
\text{Spin States}
Quantifying the Interactions
\mathcal{H} = -J_{ij} \sigma_i\sigma_j
J_{ij} > 0 \text{ : Ferromagnetic}
J_{ij} < 0 \text{ : Antiferromagnetic}
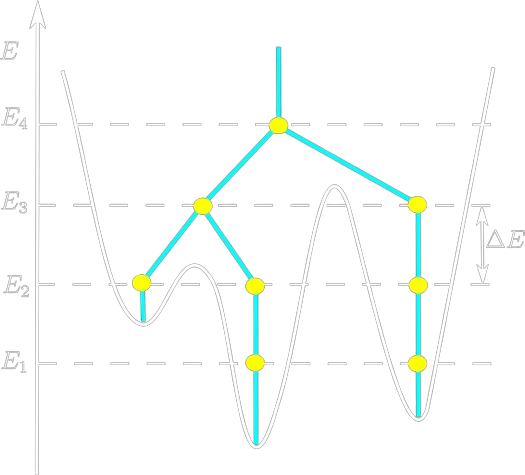
Multivalley Potential Landscape
Power of Spin Glasses
Depending on the choice of the J, spin glasses can be used to model a number of systems.
What are Epigenetic Modifications and why do we care?
Epigenetic Modifications
Today, this term is used to refer to heritable alterations that are not due to changes in DNA sequence
Epigenetic Modifications (historically) refer to the complex interactions between the genome and the environment
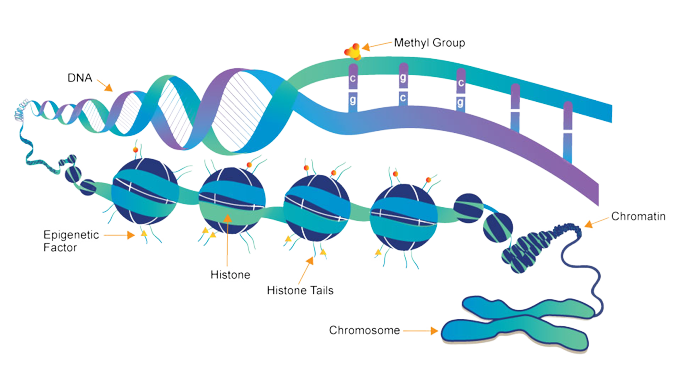
DNA
Methyl Group
Chromatin
Chromosome
Histone Tails
Histone
Epigenetic Factor
Folding your Genes
Epigenetic Modifications Activate or Silence Genes
Why do we care?
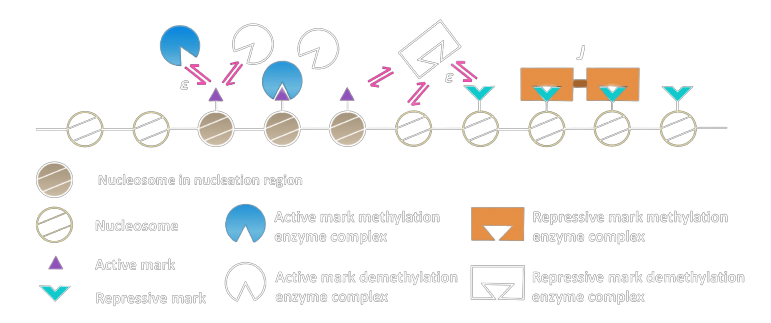
Loci are not independent of each other
Modifications at one site influence other loci in proximity
Proximity in Cartesian Space
Proximity in Genetic Space
\neq
The Problem
How do we quantify this influence of one site over the others?
Genes as Spins
*Inaccuracy for the sake of rhyme
*
Genes as Spins
*Inaccuracy for the sake of rhyme
*
States of epigenetic modifications are our spin states
Probability of contact between loci determines interaction matrix J
(\sigma)
The Spin States
\sigma
+1
-1
0
Type 1 Modification
Type 2 Modification
No Modification
One Dimensional Lattice
1
-1
0
1
1
-1
...
0
-1
1
L
The Interaction Matrix
Contact Probability Distribution
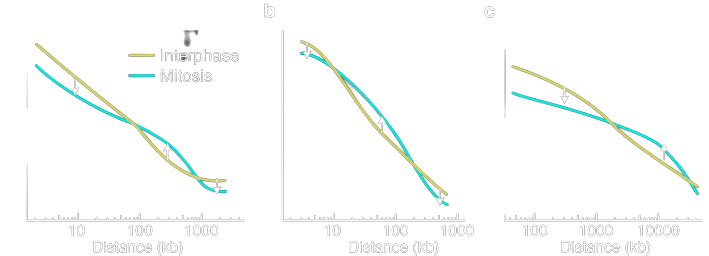
Fission Yeast
Budding Yeast
Human
(From HiC Data)
The Interaction Matrix
Probability of contact -
p(r)
- distance between two loci
r
J_{ij} =
\{
\pm 1, \text{with probability } p(r)
0\text{, otherwise}
The Hamiltonian
\sigma_i = \{+1, 0,-1\}
\mathcal{H} = -J_{ij} \sigma_i\sigma_j
-
Navigate through the rugged energy landscape
-
Find a (relatively) stable configuration
Our Goal
Simulations
- Monte Carlo Simulations
- Parallel Tempering Algorithm
- Two identical copies simulated parallely
Monte Carlo Algorithm
Start Random
Flip A Spin
ΔE < 0
Accept the change
Reject the change
Y
N
p > \min{(1, e^{-\beta\Delta H})}
N
Y
Monte Carlo Simulations using parallel tempering gives us an idea about the potential landscape for the system
Monte Carlo Simulations using parallel tempering gives us an idea about the potential landscape for the system
Monte Carlo Simulations using parallel tempering gives us an idea about the potential landscape for the system
Avenues to explore
- Appearance of glassy phase
- Ageing in spin glass vs Biological Ageing
- Addition of chemical potential to the Hamiltonian
\mathcal{H} = -J_{ij} \sigma_i\sigma_j + \Delta \sigma_i^2
References
- Koji Hukushima and Koji Nemoto. Exchange monte carlo method and application to spin glass simulations. Journal of the Physical Society of Japan, 65(6):1604–1608, 1996.
-
G Kotliar, PW Anderson, and Daniel L Stein. One-dimensional spin-glass model with long-range random interactions. Physical Review B, 27(1):602, 1983.
- L. Leuzzi, G. Parisi, F. Ricci-Tersenghi, and J. J. Ruiz-Lorenzo. Dilute one-dimensional spin glasses with power law decaying interactions. Phys. Rev. Lett., 101:107203, Sep 2008.
-
Fabrizio Olmeda, Tim Lohoff, Stephen Clark, Laura Benson, Felix Krueger, Wolf Reik, and Steffen Rulands. Inference of emergent spatio-temporal processes in single-cell genomics. In APS March Meeting Abstracts, volume 2021, pages S13–009, 2021.
-
Guang Shi and D. Thirumalai. From hi-c contact map to three-dimensional organization of interphase human chromosomes. Phys. Rev. X, 11:011051, Mar 2021.
Thank You
Questions?
14-MS19029-Epigenetics_Spin_Glass
By ritamdas
14-MS19029-Epigenetics_Spin_Glass
Slides for IDC451
