Ne prennez pas la modèlisation à la légère
Par Thomas Bracher
Comment font ils pour avoir un modèle qui marche ?
L'ambiguïté dans le modèle
EmailChoosen
EmailConfirmed
UserValidated
Modèle = Abstraction
Exemple de modèle
- Modèle mental
- Diagrammes
- Spécifications
- Le code
Comment valider leur cohérence ?
Comment valider leur cohérence ?
LES MÉTHODES FORMELLES
Pourquoi utiliser des outils ?
Process 1
db.modify(x -> x + 1)
Process 2
db.modify(x -> x * 2)
x = 1
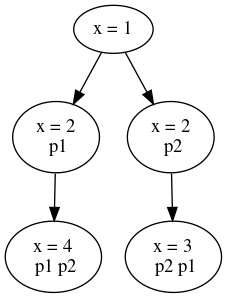
Process 1
tmp = db.get(x) db.set(x, tmp + 1)
Process 2
tmp = db.get(x) db.set(x, tmp * 2)
x = 1
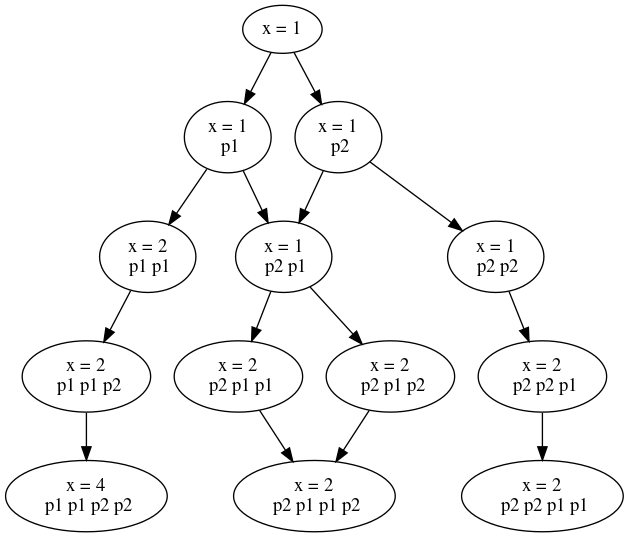
State explosion problem
Vérifier la pensée magique
- les user story
- les tests unitaires
- le langage naturel
Les familles de méthodes formelles
Coq
Require Import Arith.
Require Import List.
Require Import Omega.
(* Require Import listkit. *)
(** [cutn] breaks a list into prefix, suffix at [n]. *)
Definition cutn A n (xs : list A) := (firstn n xs, skipn n xs).
(** [cutn n] is inverse of [(++)] when [n] equals the length of the first arg to [(++)]. *)
Lemma cutn_app:
forall A n (xs ys : list A),
n = length xs -> cutn A n (xs ++ ys) = (xs, ys).
Proof.
induction n; destruct xs; simpl; easy||auto.
intros.
unfold cutn in *.
simpl.
lapply (IHn xs ys).
- congruence.
- omega.
Qed.Tables de vérité
| has_id | is_green | healthy | ok ? |
|---|---|---|---|
| T | F | F | F |
| T | F | T | T |
| T | T | F | F |
| T | T | T | T |
| F | T | F | F |
| F | T | T | T |
| F | F | T | F |
| F | F | F | F |
DRAKON
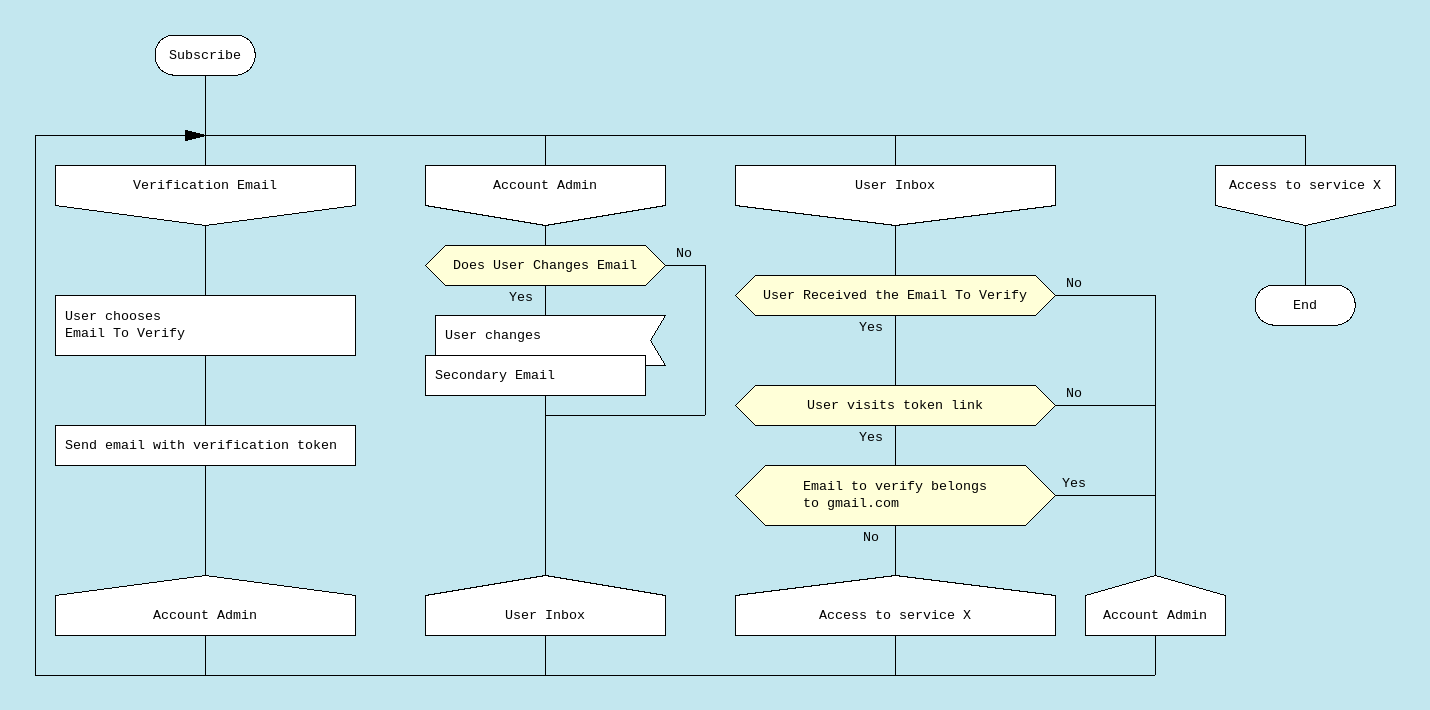
XP : System metaphor
- Design itératif
- Ubiquitous language ?
- Partage du modèle mental
Alloy Analyzer :
lightweight formal verification
Des concepts familiers
- Proche de l'orienté objet
- Théorie des sets
- Algèbre relationnel
Les sets, tuples et atomes
Book = {(B0)}
Name = {(N0), (N1), (N2)}
names = {(B0, N0), (B0, N2)}
name1 = {(N1)}
-- Opération de lien (->)
{(B0)} -> {(N1), (N2)} = {(B0, N1), (B0, N2)}ajouter et jointurer
Book = {(B0)}
Name = {(N0), (N1), (N2)}
names = {(B0, N0), (B0, N2)}
name1 = {(N1)}
-- Addition (+)
names + Book -> name1 = {(B0, N0), (B0, N1), (B0, N2)}
Book + Name = {(B0), (N0), (N1), (N2)}
-- Jointure (.)
Book.names = {(B0)} . {(B0, N0), (B0, N2)}
Book.names = {(N0), (N2)}
names.Name = {(B0, N0), (B0, N2)} . {(B0, N0), (B0, N2)}
names.Name = {(B0)}Le carnet d'adresses
Découverte de la syntaxe
sig Name, Addr {}
sig Book {
// addresses = {(B0, N0, A0), (B0, N1, A2), (B1, N2, A0)}
addresses: Name -> lone Addr
}
run {} for 3sig Name, Addr {}
sig Book {
addresses: Name -> lone Addr
}
pred show (b: Book) {
// {(B0)} . {(B0, N0, A0), (B0, N1, A2), (B1, N2, A0)}
// {(N0, A0), (N1, A2)}
#b.addresses > 1
}
run show for 3 but 1 Booksig Name, Addr {}
sig Book {
addresses: Name -> lone Addr
}
pred add (b, b': Book, n: Name, a: Addr) {
b'.addresses = b.addresses + n -> a
}
pred showAdd (b, b': Book, n: Name, a: Addr) {
add [b, b', n, a]
#Name.(b'.addresses) > 1
}
run showAdd for 3 but 2 Booksig Name, Addr {}
sig Book {
addresses: Name -> lone Addr
}
pred add (b, b': Book, n: Name, a: Addr) {
b'.addresses = b.addresses + n -> a
}
pred del (b, b': Book, n: Name) {
b'.addresses = b.addresses - n -> Addr
}
fun lookup (b: Book, n: Name): set Addr {
n.(b.addresses)
}
pred showAdd (b, b': Book, n: Name, a: Addr) {
add [b, b', n, a]
#Name.(b'.addresses) > 1
}
run showAdd for 3 but 2 Bookassert delUndoesAdd {
all b, b', b'': Book , n: Name, a: Addr |
add[b, b', n, a] and del[b', b'', n] implies b.addresses = b''.addresses
}
check delUndoesAdd for 3assert delUndoesAdd {
all b, b', b'': Book , n: Name, a: Addr |
no n.(b.addresses) and add[b, b', n, a] and del[b', b'', n]
implies b.addresses = b''.addresses
}Jusqu'ici, on a :
- Posé les bases de notre modèle
- Généré des exemples avec facilité
- Mis à l'epreuve notre modèle mental
2ème itération
Introduction des alias et des groupes
abstract sig Target {}
sig Addr extends Target {}
abstract sig Name extends Target {}
sig Alias, Group extends Name {}
sig Book { addresses: Name -> Target }
pred show (b: Book) { some b.addresses }
run show for 3 but 1 Book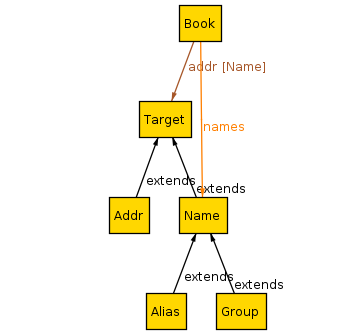
abstract sig Target {}
sig Addr extends Target {}
abstract sig Name extends Target {}
sig Alias, Group extends Name {}
sig Book { addresses: Name -> Target } {
no n: Name | n in n.^addresses
}
fact { all b: Book | no n: Name | n in n.^(b.addresses) }
pred show (b: Book) { some b.addresses }
run show for 3 but 1 Bookabstract sig Target {}
sig Addr extends Target {}
abstract sig Name extends Target {}
sig Alias, Group extends Name {}
sig Book { addresses: Name -> Target } {
no n: Name | n in n.^addresses
all a: Alias | lone a.addresses
}
pred show (b: Book) { some Alias.(b.addresses) }
run show for 3 but 1 Bookabstract sig Target {}
sig Addr extends Target {}
abstract sig Name extends Target {}
sig Alias, Group extends Name {}
sig Book {
names: set Name,
addresses: names -> some Target
} {
no n: Name | n in n.^addresses
all a: Alias | lone a.addresses
}
pred show (b: Book) { some Alias.(b.addresses) }
run show for 3 but 1 Bookpred add (b, b': Book, n: Name, t: Target) { b'.addresses = b.addresses + n -> t }
pred del (b, b': Book, n: Name, t: Target) { b'.addresses = b.addresses - n -> t }
fun lookup (b: Book, n: Name): set Addr { n.^(b.addresses) & Addr }abstract sig Target { }
sig Addr extends Target { }
abstract sig Name extends Target { }
sig Alias, Group extends Name { }
sig Book {
names: set Name,
addresses: names->some Target
} {
no n: Name | n in n.^addresses
all a: Alias | lone a.addresses
}
pred add [b, b': Book, n: Name, t: Target] { b'.addresses = b.addresses + n->t }
pred del [b, b': Book, n: Name, t: Target] { b'.addresses = b.addresses - n->t }
fun lookup [b: Book, n: Name] : set Addr { n.^(b.addresses) & Addr }
assert delUndoesAdd {
all b, b', b'': Book, n: Name, t: Target |
no n.(b.addresses) and add [b, b', n, t] and del [b', b'', n, t]
implies b.addresses = b''.addresses
}
check delUndoesAdd for 3
assert addIdempotent {
all b, b', b'': Book, n: Name, t: Target |
add [b, b', n, t] and add [b', b'', n, t]
implies b'.addresses = b''.addresses
}
check addIdempotent for 3
assert addLocal {
all b, b': Book, n, n': Name, t: Target |
add [b, b', n, t] and n != n'
implies lookup [b, n'] = lookup [b', n']
}
check addLocal for 3 but 2 Book
assert lookupYields {
all b: Book, n: b.names | some lookup [b,n]
}
check lookupYields for 4 but 1 BookTracer la cynématique du modèle
module tour/addressBook
open util/ordering [Book] as BookOrder
abstract sig Target { }
sig Addr extends Target { }
abstract sig Name extends Target { }
sig Alias, Group extends Name { }
sig Book {
names: set Name,
addresses: names->some Target
} {
no n: Name | n in n.^addresses
all a: Alias | lone a.addresses
}
pred add [b, b': Book, n: Name, t: Target] { b'.addresses = b.addresses + n->t }
pred del [b, b': Book, n: Name, t: Target] { b'.addresses = b.addresses - n->t }
fun lookup [b: Book, n: Name] : set Addr { n.^(b.addresses) & Addr }
pred init [b: Book] { no b.addresses }
fact traces {
init [first]
all b: Book-last | let b' = b.next | some n: Name, t: Target |
add [b, b', n, t] or del [b, b', n, t]
}
pred show { }
run show for 4assert lookupYields { all b: Book, n: b.names | some lookup [b, n] }
check lookupYields for 3 but 4 Book
t in Addr or some lookup [b, t]
no b.addresses.n or some n.(b.addresses) - tÉtait-ce bien utile ?
- Les bugs sont "triviaux"
- Les tests unitaires suffisent
- Beaucoup de code pour rien
Hmm, pas exactement
- Apple Mail a ce bug
- Les bugs sont toujours triviaux
- Alloy s'apprend
Les forces d'Alloy
- Incrémental
- Pas dépendant du runtime
- Peu de maths
- Pas de fausse alarme
- Les graphiques générés
Minute honnêteté
Ça n'est pas mon usage d'Alloy
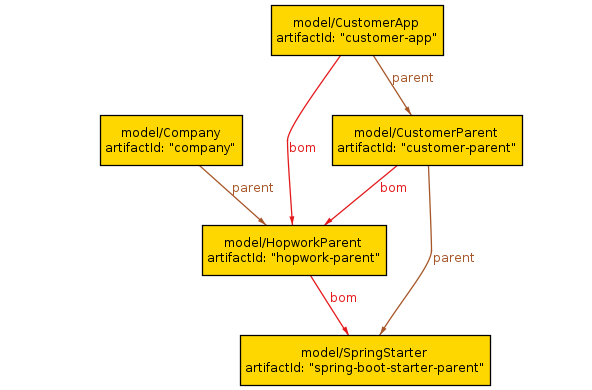
Pas de miracle
- Formuler des spécifications cohérentes
- Communiquer les besoins
- Comprendre les contraintes du système
Les alternatives
- Les systèmes de type fort
- La programmation par contrat
- Property-based testing
MÉTHODES FORMELLES
pensez-y quand même
Bibliographie
- Le Blog d'Hillel Wayne
- Alloy Tutorial
- Software Abstractions: Logic, Language, and Analysis by Daniel Jackson
Merci pour votre attention
modelling
By Thomas Bracher
modelling
- 362


