Dynamic Mode Decomposition
Journal Club - 03/22/2019
Outline
- Context
- Theoretical aspects
- Examples
- Conclusion
- Dynamic Mode Decomposition (DMD) was first introduced by the Fluid Dynamics community
Schmid, Dynamic Mode Decomposition of Numerical and Experimental Data, JFM, 2010
Context
- The DMD extracts coupled spatial temporal modes from a dynamical system
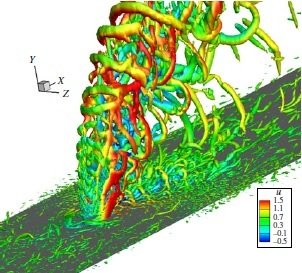
Chai et al., Numerical study of high speed jets in crossflow, JFM, 2015
Vorticity contour
DMD mode, St = 0,43
DMD mode, St = 1
- Robotics (Berger et al. (2015))
- Neuroscience (Brunton et al. (2014))
- Disease modeling (Proctor et al. (2015))
- Finances (Mann et al. (2015))
- Control systems (Proctor etal. (2015))
- ...
Context
- DMD is a "data-driven" technique applied in many other fields:
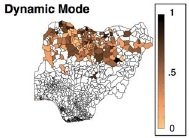
Theoretical aspects
Let's consider a dynamical system evolving as follows:
\frac{d\vec{x}}{dt} = f(\vec{x}, t)
- Fluid Dynamics: Navier-Stokes equations
- Electro-Magnetism: Maxwell equations
- Quantum Mechanics: Schrödinger equation
Linear dynamical system
\frac{d\vec{x}}{dt} = A \vec{x}
Nonlinear dynamical system
approximation
\vec{x} \in \mathbb{R}^n
where
and .
n >> 1
f(\vec{x}, t)
Note: is unknown and is measurable.
\vec{x}
1. Collect data
Decompose the dynamical system into successive snapshots separated by :
x_i=x(t_i) \in \mathbb{R}^n
Theoretical aspects
m \approx 1e^3
For a fluid dynamic problem: and .
n \approx 1e^9
where and
- m is the total snapshot number,
- n is the dimension of observables.
x_1
x_2
x_3
x_m
\Delta t
2. Organize into matrices
X = \begin{bmatrix}
| & | & & |\\
x_1 & x_2 & ... & x_{m-1}\\
| & | & & |
\end{bmatrix}
X' = \begin{bmatrix}
| & | & & |\\
x_2 & x_3 & ... & x_{m}\\
| & | & & |
\end{bmatrix}
The columns are evolving in time along with the system dynamics
is the equal to shifted by in the future.
Theoretical aspects
\Delta t
X, X' \in \mathbb{R}^{n\times(m-1)}
So, we have
\frac{d\vec{x}}{dt} = A \vec{x}
and
X
X'
x_{k+1}=A x_k
3. DMD
Find the best fit linear operator A that advances into .
X'= A X
A = X' X^\dagger
Now, let's compute the eigenvalues and eigenvectors of ,
which are the DMD eigenvalues and DMD modes of the dynamical system.
We have to find another way...
X
X'
Moore-Penrose
pseudo-inverse
A \in \mathbb{R}^{n\times n}
A
PROBLEM:
Computationally prohibitive!
Theoretical aspects
(Exact DMD)
X = \begin{bmatrix}
| & | & & |\\
x_1 & x_2 & ... & x_{m-1}\\
| & | & & |
\end{bmatrix}
X' = \begin{bmatrix}
| & | & & |\\
x_2 & x_3 & ... & x_{m}\\
| & | & & |
\end{bmatrix}
4. DMD Algorithm
X = U_r \Sigma_r V_r^*
Theoretical aspects
Objective: work on a lower rank version of .
A
a.
(Fluid Dynamics: r is about a few hundred modes)
rank-r truncation
b.
A = X' X^\dagger = X' V_r \Sigma_r^{-1} U_r^*
\tilde{A} = U_r^* A U_r = U_r^* X' V_r \Sigma_r^{-1}
Similarity transform of to the low rank subspace:
A
\tilde{A} \in \mathbb{R}^{r\times r}
SVD of :
X
4. DMD Algorithm
Theoretical aspects
c.
Eigendecomposition of :
\tilde{A}
\tilde{A} W = \Lambda W
d.
Coming back into high dimensional space:
\Phi = X' V_r \Sigma_r^{-1} W
- DMD modes:
- DMD eigenvalues:
\Lambda
(remains unchange since it is a similarity transformation)
(not orthogonal)
W = \begin{bmatrix}
| & | & & |\\
w_1 & w_2 & ... & w_{r}\\
| & | & & |
\end{bmatrix}
\Lambda = \begin{bmatrix}
\lambda_1 & ... & 0\\
\vdots & \ddots & \\
0 & ... & \lambda_r
\end{bmatrix}
4. DMD Prediction
Theoretical aspects
x(t) = \sum_{k=1}^{r} \phi_k e^{\omega_k t} b_k = \Phi e^{\Omega t} b
b = \Phi^\dagger x(0)
at t = 0,
vector of mode amplitudes
transformed eigenvalues
DMD modes
We are able to simulate the system in the future by chosing t.
where
\Omega = \frac{log(\Lambda)}{\Delta t}
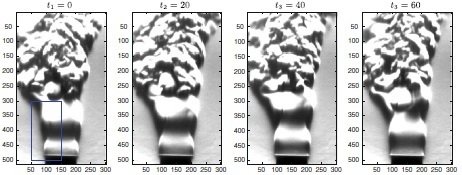
1. Helium jet experiment (Schmid et al. (2010))
Examples
\rho_{jet}/\rho_{amb} = 0.14
Re = \frac{u_{jet}D}{\nu} = 940
kinematic molecular viscosity
D = 19\text{mm}
Schlieren Visualization showing density variations
Jet characteristics:
At such conditions, "the jet is characterized by a pocket of absolute instability near the nozzle exit which manifests itself in a self-sustained, axisymmetric, oscillatory behavior of the jet".
1. Helium jet experiment (Schmid et al. (2010))
Examples
Schlieren Visualization showing density variations
Schlieren Visualization showing density variations
Interrogation window
- greyscale colormap from the snapshots
- 100 snapshots
- Sampling: 1.6KHz
512 \times 512 \text{ pixels}
\lambda_i
\lambda_r
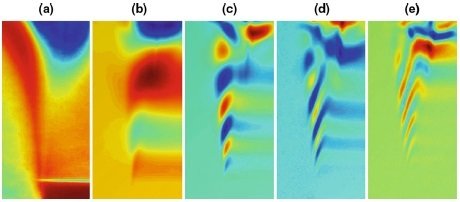
DMD Spectrum
DMD modes
a
b
c
d
ee
2. a) Sensorimotor mapping (Brunton et al. (2016))
Examples
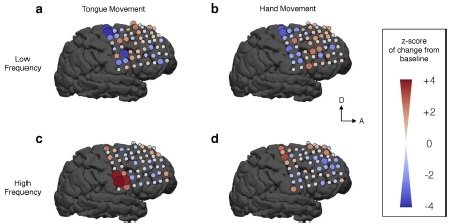
Objective: study the cortical activity during the movement of the tongue and the hands in a frequency-dependent way.
Motor mapping:
- sampling: 1Khz
- 2s recording window
- low-freq: 8 - 32Hz
- high-freq: 75-100Hz
Sensorimotor map with DMD modes
At high frequencies, results are "consistent with known organization of the human sensimotor cortex".
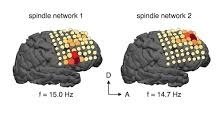
2. b) Sleep spindle network detection (Brunton et al. (2016))
Examples
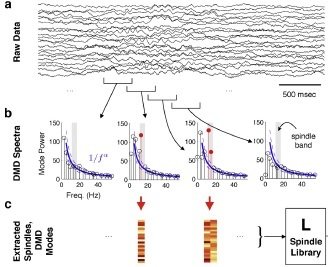
- DMD spectra of windowed ECoG data (300ms)
"Sleep spindle are distinctive, transient oscillations around 14Hz that are characteristic of non-rapid eye movement (NREM) sleep"
- Human ECoG recordings
- spindle modes around 14Hz
- spindle modes are gathered in L
"our algorithm reliably identifies most spindle-type events detected by the author's vusal inspection of the data".
- 200 samples/s
- 20-30 min recording window
Conclusion
Principal components analysis (PCA)
Fourier Transform
DMD
Possible DataLab applications:
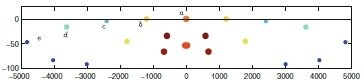
- Application to geo-spatial human locations using data from CMU (http://mocap.cs.cmu.edu/)
Takeishi et al., Bayesian Dynamic Mode Decomposition (2017)
- Video analysis separating video frames into background (low-rank) and foreground (sparse) components in real-time
Grosek et al., Dynamic Mode Decomposition for Real-Time Background/Foreground Separation in Video (2014)
Merci de votre attention!
Dynamic Mode Decomposition
By Sami Yamouni
