More symplectic structures
on the space of space curves
Joint with Martin Bauer & Peter Michor
September 2024 @ TU Wien
Sadashige Ishida (ISTA)

Overview
On the space of space curves, only one symplectic structure was known.
We found more.
Symplectic structure is a sandbox
for Hamiltonian dynamics
Space with
a symplectic structure Ω
A function H
Dynamics VH
Symplectic structure is a sandbox
for Hamiltonian dynamics
A symplectic structure Ω is a 2-form on a manifold X s.t.
Symplectic structure is a sandbox
for Hamiltonian dynamics
A symplectic structure Ω is a 2-form on a manifold X s.t.
- closed i.e. dΩ=0
Symplectic structure is a sandbox
for Hamiltonian dynamics
A symplectic structure Ω is a 2-form on a manifold X s.t.
- non-degenerate i.e. the map ♭:TX→T∗X v→Ω(v,⋅) is injective
- closed i.e. dΩ=0
Symplectic structure is a sandbox
for Hamiltonian dynamics
Symplectic structure is a sandbox
for Hamiltonian dynamics
For H:X→R,
Hamiltonian vector field VH∈Γ(TM) is the one
dH=Ω(VH,⋅).
Symplectic structure is a sandbox
for Hamiltonian dynamics
For H:X→R,
Hamiltonian vector field VH∈Γ(TM) is the one
dH=Ω(VH,⋅).
The Hamiltonian dynamics
x˙=VH(x).
Why Hamiltonian dynamics?
Has nice properties.
E.g.
- H is preserved in dynamics.
- If H is invariant under some group action, there is a conserved quantity.
Spaces with symplectic structures
and Hamiltonian dynamics
T∗Mn
T∗SDiff(M)
Celestial mechanics
C∞(M,C)
Schrödinger equation
Incompressible fluids
Spaces with symplectic structures
and Hamiltonian dynamics
T∗Mn
T∗SDiff(M)
C∞(M,C)
Schrödinger equation
Incompressible fluids
Space curves
Celestial mechanics
The space of space curves
Imm(S1,R3)={c:S1→R3,∂θc=0 ∀θ∈S1}
Parametrized curves
The space of space curves
Imm(S1,R3)={c:S1→R3,∂θc=0 ∀θ∈S1}
Parametrized curves
TcImm(S1,R3)=C∞(S1,R3)
Tangent space

The space of space curves
UImm(S1,R3)=Imm(S1,R3)/Diff+(S1)
Unparametrized curves a.k.a. shape space
The space of space curves
UImm(S1,R3)=Imm(S1,R3)/Diff+(S1)
Unparametrized curves a.k.a. shape space
UImm(S1,R3)
Imm(S1,R3)
↓⏐π
↷
Diff+(S1)
The space of space curves
UImm(S1,R3)=Imm(S1,R3)/Diff+(S1)
Unparametrized curves a.k.a. shape space
Tangent space
T[c]UImm(S1,R3)=TcImm(S1,R3)/kerdπc
UImm(S1,R3)
Imm(S1,R3)
↓⏐π
↷
Diff+(S1)
The space of space curves
UImm(S1,R3)=Imm(S1,R3)/Diff+(S1)
Unparametrized curves a.k.a. shape space
Tangent space
T[c]UImm(S1,R3)=TcImm(S1,R3)/kerdπc
UImm(S1,R3)
Imm(S1,R3)
↓⏐π
↷
Diff+(S1)
{a.∂θc∣a∈C∞(S1)}
curve tangent
The space of space curves
UImm(S1,R3)=Imm(S1,R3)/Diff+(S1)
Unparametrized curves a.k.a. shape space
Tangent space
T[c]UImm(S1,R3)=TcImm(S1,R3)/kerdπc
≂{h∈TcImm(S1,R3)∣h⊥∂θc}
UImm(S1,R3)
Imm(S1,R3)
↓⏐π
↷
Diff+(S1)
{a.∂θc∣a∈C∞(S1)}
curve tangent
Canonical symplectic structure on UImm(S1,R3)
The Marsden-Weinstein structure
Ω[c]:T[c]UImm×T[c]UImm→R,
Canonical symplectic structure on UImm(S1,R3)
Ω[c]:T[c]UImm×T[c]UImm→R,
The Marsden-Weinstein structure
Ω[c]([h],[k])=∫S1⟨Dsc×h,k⟩ds
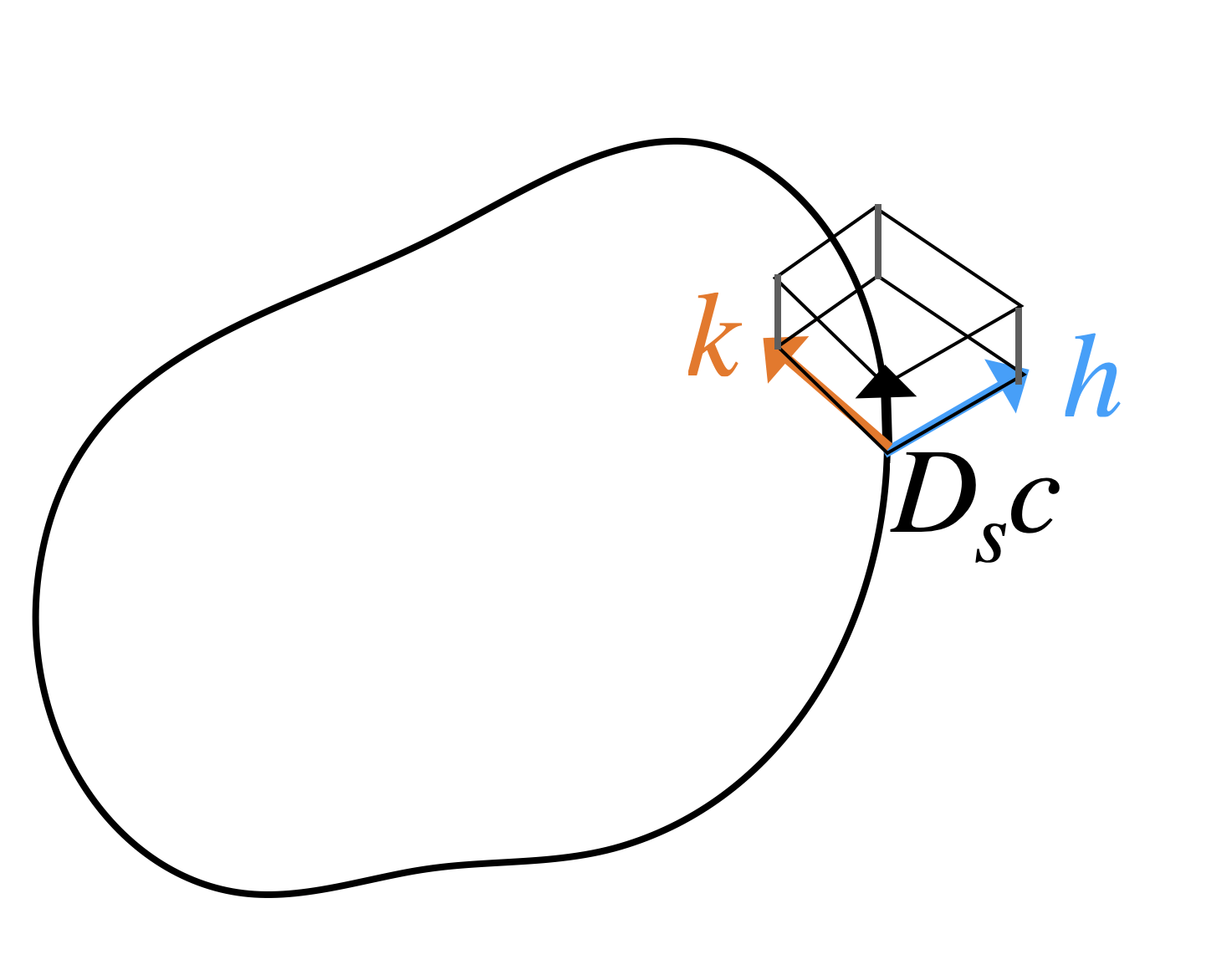
where
Ds=∣∂θc∣∂θ,ds=∣∂θc∣dθ
unit tangent
Canonical symplectic structure on UImm(S1,R3)
Ω[c]:T[c]UImm×T[c]UImm→R,
Symplectic!
The Marsden-Weinstein structure
Ω[c]([h],[k])=∫S1⟨Dsc×h,k⟩ds
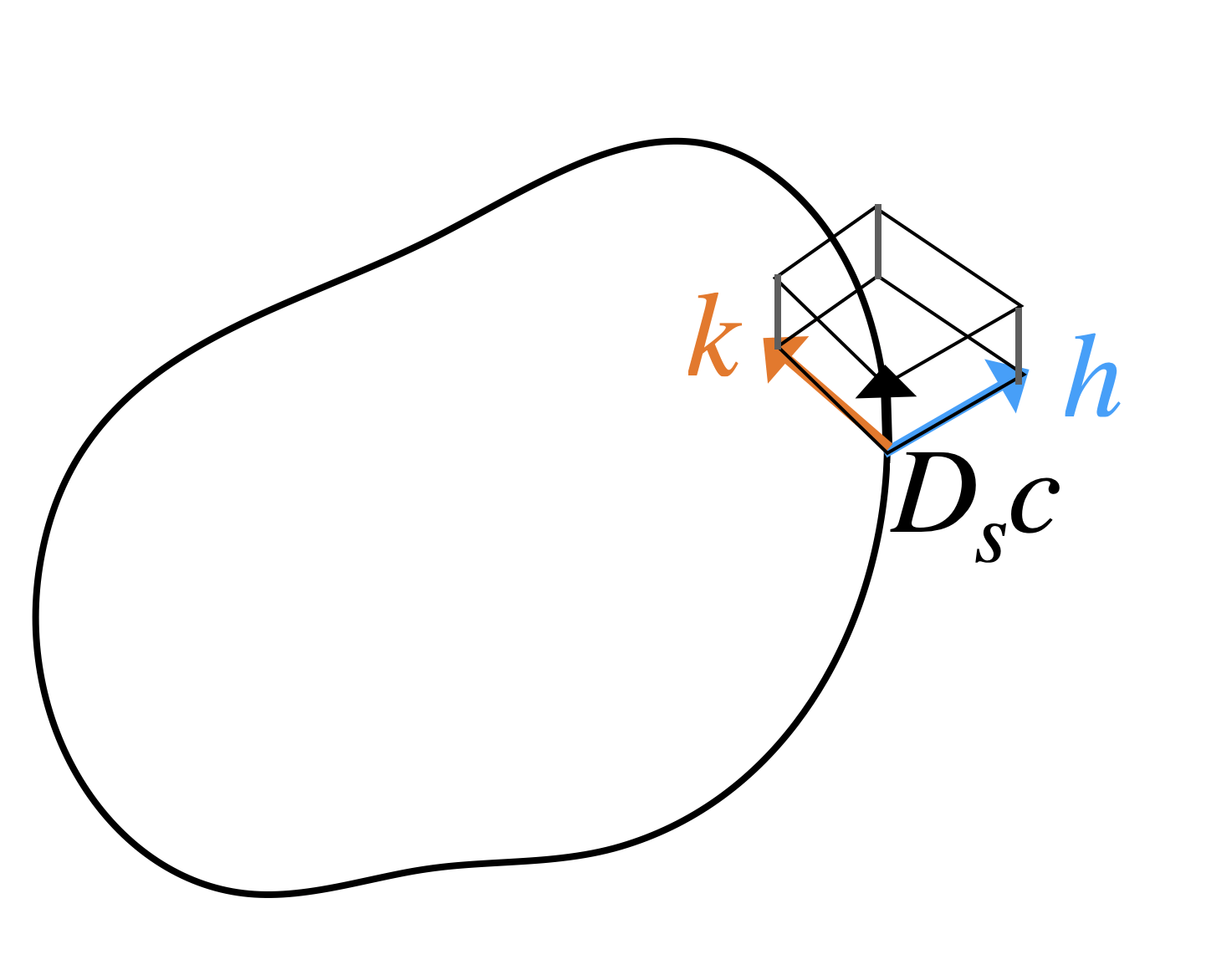
where
Ds=∣∂θc∣∂θ,ds=∣∂θc∣dθ
unit tangent
Canonical symplectic structure on UImm(S1,R3)
Ω[c]:T[c]UImm×T[c]UImm→R,
Closed dΩ=0,
Symplectic!
The Marsden-Weinstein structure
Ω[c]([h],[k])=∫S1⟨Dsc×h,k⟩ds
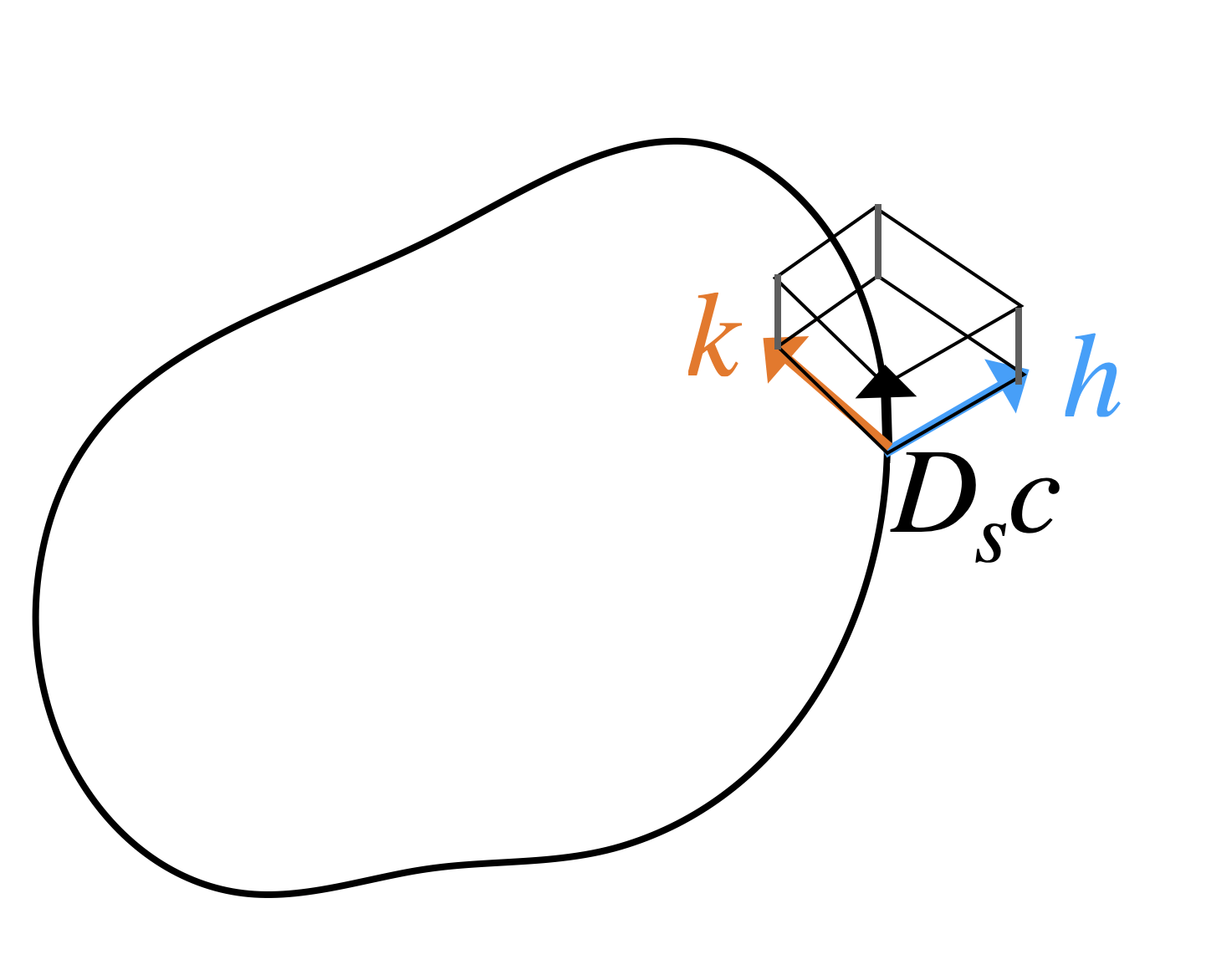
where
Ds=∣∂θc∣∂θ,ds=∣∂θc∣dθ
unit tangent
Canonical symplectic structure on UImm(S1,R3)
Ω[c]:T[c]UImm×T[c]UImm→R,
Closed dΩ=0,
Symplectic!
The Marsden-Weinstein structure
Ω[c]([h],[k])=∫S1⟨Dsc×h,k⟩ds
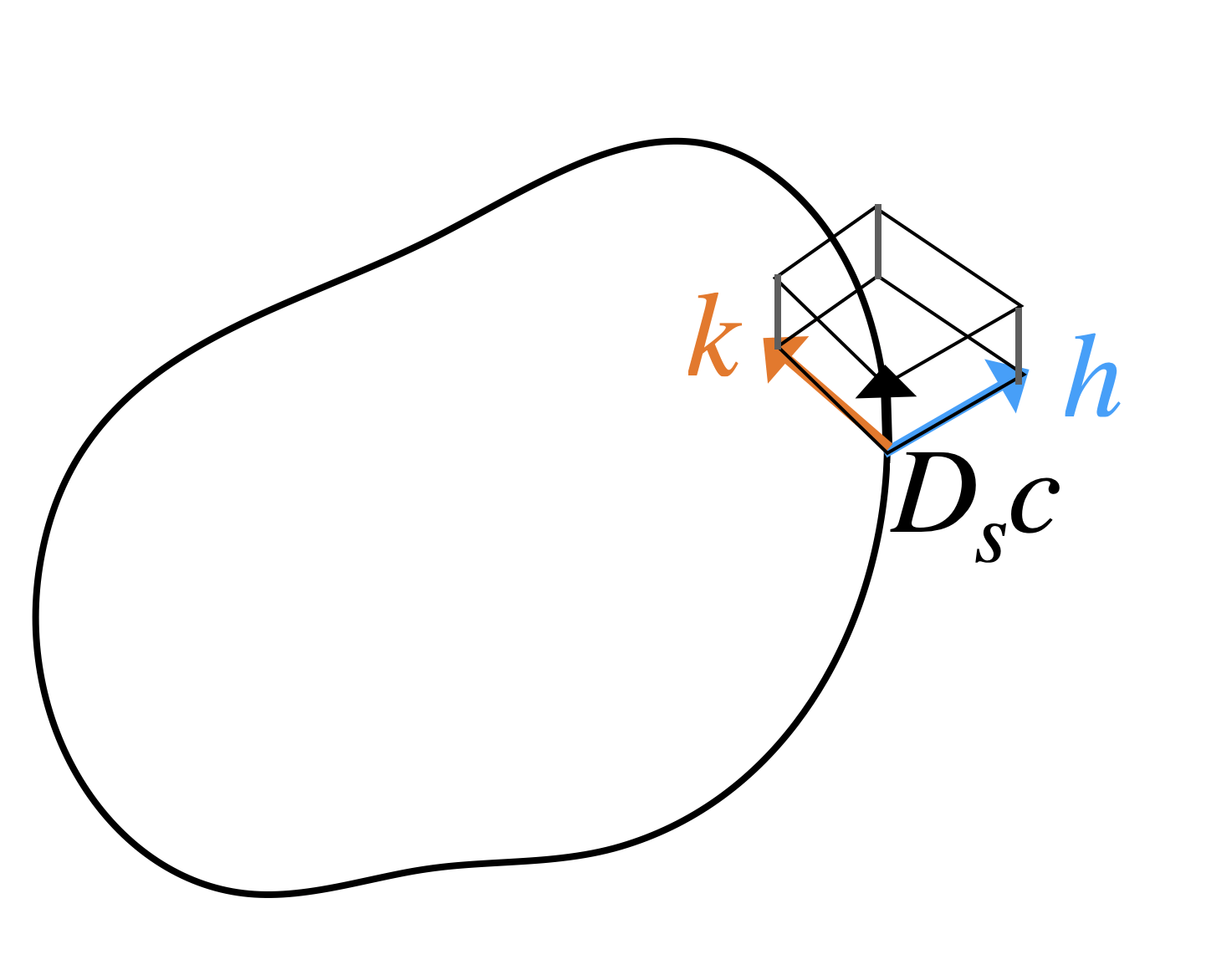
where
Ds=∣∂θc∣∂θ,ds=∣∂θc∣dθ
Non-degenerate kerΩ[c]=[0]={a.Dsc∣a∈C∞(S1)}
unit tangent
Hamiltonian flow
E.g.
Hamiltonian H=Length([c])
Binormal flow
Dynamics VH=[Dsc×Ds2c]
Hamiltonian flow
E.g.
Hamiltonian H=Length([c])
Binormal flow
Dynamics VH=[Dsc×Ds2c]
A completely integrable system
More symplectic structures?
More symplectic structures?
Remember
A symplectic structure Ω defines a Hamiltonian dynamics VH via dH=Ω(VH,⋅).
More symplectic structures?
A different Ω defines different VH.
Remember
A symplectic structure Ω defines a Hamiltonian dynamics VH via dH=Ω(VH,⋅).
More symplectic structures?
A different Ω defines different VH.
But only one Ω is known on UImm.
Remember
A symplectic structure Ω defines a Hamiltonian dynamics VH via dH=Ω(VH,⋅).
More symplectic structures?
A different Ω defines different VH.
We found more.
But only one Ω is known on UImm.
Remember
A symplectic structure Ω defines a Hamiltonian dynamics VH via dH=Ω(VH,⋅).
Hint 1. Trend in shape analysis
Hint 1. Trend in shape analysis
a Riemannian metric on Imm
g(h,k)=∫S1⟨h,k⟩ds
Hint 1. Trend in shape analysis
a Riemannian metric on Imm
g(h,k)=∫S1⟨h,k⟩ds
a suitable operator
L:TImm→TImm.
Hint 1. Trend in shape analysis
a Riemannian metric on Imm
g(h,k)=∫S1⟨h,k⟩ds
New metric gL(h,k):=g(h,Lk)
a suitable operator
L:TImm→TImm.
e.g. Lc=idc,
gcid(h,k)=∫S1⟨h,k⟩ds
Hint 1. Trend in shape analysis
e.g. Lc=idc,
gcid(h,k)=∫S1⟨h,k⟩ds
e.g. Lc=λ(c) with a conformal factor λ:Imm→R>0
gcλ(h,k)=λ(c)∫S1⟨h,k⟩ds
Hint 1. Trend in shape analysis
e.g. Lc=idc,
gcid(h,k)=∫S1⟨h,k⟩ds
e.g. Sobolev-type differential operator Lc=id−Ds2
gcid−Ds2(h,k)=∫S1⟨h,k⟩−⟨h,Ds2k⟩ds=∫S1⟨h,k⟩+⟨Dsh,Dsk⟩ds
Hint 1. Trend in shape analysis
e.g. Lc=λ(c) with a conformal factor λ:Imm→R>0
gcλ(h,k)=λ(c)∫S1⟨h,k⟩ds
Hint 2. Liouville form
Ω is exact
i.e. there is a 1-form Θ s.t. Ω=dΘ.
Hint 2. Liouville form
Ω is exact
Θ is given by
Θ[c]([h])=31∫S1⟨Dsc×c,h⟩ ds=gid(31Dsc×c,h).
i.e. there is a 1-form Θ s.t. Ω=dΘ.
Hint 1 + Hint 2
Let's define a 1-form
Θ[c]L([h]):=gL(31Dsc×c,h)=31∫S1⟨Dsc×c,Lh⟩ds
Hint 1 + Hint 2
and a 2-form ΩL:=dΘL
Let's define a 1-form
Θ[c]L([h]):=gL(31Dsc×c,h)=31∫S1⟨Dsc×c,Lh⟩ds
ΩL:=dΘL
Does ΩL define a symplectic structure on UImm?.
Hint 1 + Hint 2
with Θ[c]L([h]):=31∫S1⟨Dsc×c,Lh⟩ds
Closeness. OK because it is exact dΩL=ddΘL=0
ΩL:=dΘL
Does ΩL define a symplectic structure on UImm?.
Hint 1 + Hint 2
with Θ[c]L([h]):=31∫S1⟨Dsc×c,Lh⟩ds
Closeness. OK because it is exact dΩL=ddΘL=0
ΩL:=dΘL
Does ΩL define a symplectic structure on UImm?.
Hint 1 + Hint 2
with Θ[c]L([h]):=31∫S1⟨Dsc×c,Lh⟩ds
Non-degeneracy on UImm ?
i.e. kerΩcL=[0]={a.Dsc∣a∈C∞(S1)}
Closeness. OK because it is exact dΩL=ddΘL=0
ΩL:=dΘL
Does ΩL define a symplectic structure on UImm?.
Non-degeneracy on UImm ?
i.e. kerΩcL=[0]={a.Dsc∣a∈C∞(S1)}
Need to check case by case.
Hint 1 + Hint 2
with Θ[c]L([h]):=31∫S1⟨Dsc×c,Lh⟩ds
Symplectic structure
induced by a conformal factor
Ωλ:=dΘλ
Theorem
With a conformal factor λ:UImm→R>0,
is a symplectic structure on UImm
Symplectic structure
induced by a conformal factor
Ωλ:=dΘλ
Theorem
With a conformal factor λ:UImm→R>0,
is a symplectic structure on UImm
if Θλ is NOT invariant under scaling (c→c+tc with t∈R×).
Symplectic structure
induced by a conformal factor
Ωλ:=dΘλ
Theorem
With a conformal factor λ:UImm→R>0,
is a symplectic structure on UImm
If Θλ is invariant under scaling, Ωλ is NOT symplectic on UImm,
but becomes symplectic in another space! (Check out our paper)
if Θλ is NOT invariant under scaling (c→c+tc with t∈R×).
Open problem
Is there a non-conformal L making ΩL:=dΘL symplectic?
Open problem
Is there a non-conformal L making ΩL:=dΘL symplectic?
Conjecture
Squared curvature L∣θ=1+κc2(θ) defines a symplectic structure.
Open problem
Is there a non-conformal L making ΩL:=dΘL symplectic?
Conjecture
Squared curvature L∣θ=1+κc2(θ) defines a symplectic structure.
Result in preparation
Squared scale L∣θ=∣c(θ)∣2 defines a symplectic structure.
Simulation of Hamiltonian dynamics
Remember, different symplectic structures induce different dynamics from the same Hamiltonian.
(Marsden-Weinstein)
Ωcid
ΩcLength(c)−1/10
ΩcLength(c)2
Simulation of Hamiltonian dynamics
Hamiltonian dynamics VH of total squared-scale H(c)=∫S1∣c∣2ds
H is preserved in all of them.
Future work
Future work
Our paper has a disclaimer
We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation
Future work
Symplectic structure on the space of discrete space curves?
Toward a symplectic integrator for space curves
Our paper has a disclaimer
We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation
Future work
Symplectic structure on the space of discrete space curves?
Toward a symplectic integrator for space curves
Looking for a collaborator!
Our paper has a disclaimer
We do not guarantee any correctness of (even short-time behavior) dynamics in our simulation
Thanks!
Preprint: arXiv 2407.19908
Sadashige.Ishida@ist.ac.at

old_symplectic_curves
By sdsgisd
old_symplectic_curves
- 170
