INTRODUCTION TO QUANTUM COMPUTATION

 

Sean Bae

Quantum
Mechanics &
Computation

Part 1

  • Motivation
  • Fun video
  • History
  • Literature
  • Applications

Part 2

  • Formalism
  • Insights
  • Algorithms
  • State-of-the-art

1 + 1 = ?

i\hbar\frac{\partial|\psi (t)\rangle}{\partial t} = [-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + V]|\psi (t) \rangle
iℏ∂∣ψ(t)⟩∂t=[−ℏ22m∂2∂x2+V]∣ψ(t)⟩i\hbar\frac{\partial|\psi (t)\rangle}{\partial t} = [-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} + V]|\psi (t) \rangle
|\psi (t)\rangle = ?
∣ψ(t)⟩=?|\psi (t)\rangle = ?
P = NP?
P=NP?P = NP?

Polynomial Time

"Easy problems"

T(n) \in \mathcal{O}(poly(n))
T(n)∈O(poly(n))T(n) \in \mathcal{O}(poly(n))
10^{10} + 10^{10} = 2 \times 10^{10}
1010+1010=2×101010^{10} + 10^{10} = 2 \times 10^{10}
10^{10} \times 10^{10} = 10^{20}
1010×1010=102010^{10} \times 10^{10} = 10^{20}
15 = 3 \times 5
15=3×515 = 3 \times 5
1539218309217839021739021 = ?
1539218309217839021739021=?1539218309217839021739021 = ?
3\times 17\times 30180751161134098465471
3×17×301807511611340984654713\times 17\times 30180751161134098465471

Non-deterministic Polynomial Time

"hard problems"

T(n) \in \mathcal{O}(2^{n})
T(n)∈O(2n)T(n) \in \mathcal{O}(2^{n})
P \subseteq NP
P⊆NPP \subseteq NP

Does being able to quickly RECOGNIZE (NP) correct answers mean there's also a quick way to FIND (P) them?

Moore's Law

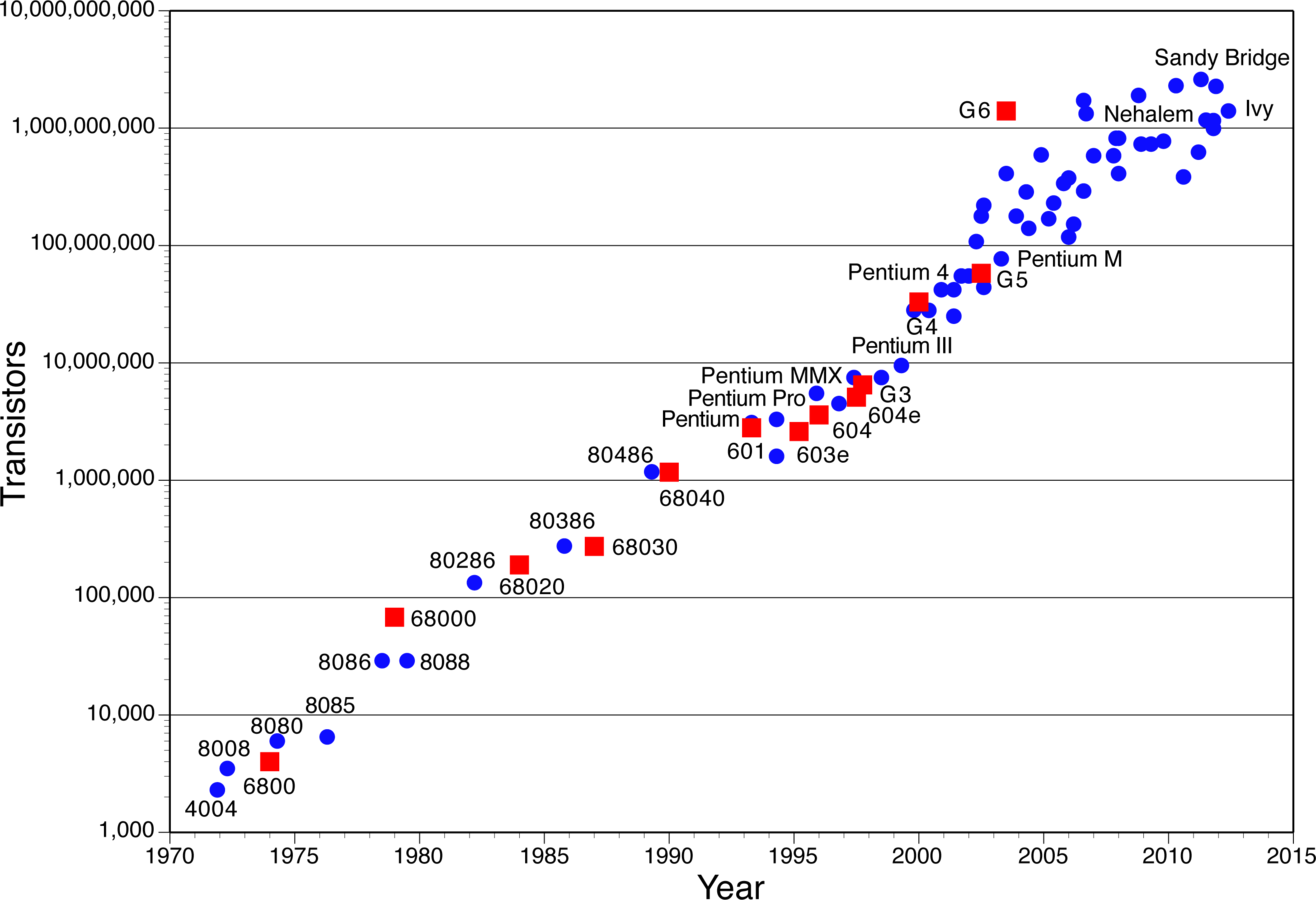
Extended Church-Turing Thesis

Any "reasonable" model of computation can be simulated on a (probabilistic) Turing Machine with at most polynomial simulation overhead

Axioms of Quantum Mechanics

  • Superposition
  • Measurement
  • Unitary Evolution
|cat\rangle = \frac{1}{\sqrt{2}}(|dead\rangle + |alive\rangle)
∣cat⟩=12(∣dead⟩+∣alive⟩)|cat\rangle = \frac{1}{\sqrt{2}}(|dead\rangle + |alive\rangle)
  1. Trap a cat in a box
  2. A radioactive material in the box will decay with 50% probability and kill the cat in 1 hour
  3. Wait for 1 hour
  4. Is the cat is both dead and alive??

Schrödinger's Cat

Bits

0
00
1
11

Qubits = Quantum Bits

|0\rangle
∣0⟩|0\rangle
|1\rangle
∣1⟩|1\rangle

Spin Qubit

Quantum Parallelism

Quantum Entanglement

100,000 light years

Milky Way

COLLEGE PARK, MD

Milky Way

ME

YOU

ME

YOU

ME

YOU

ME

YOU

|\downarrow\rangle
∣↓⟩|\downarrow\rangle
|\uparrow\rangle
∣↑⟩|\uparrow\rangle

ME

YOU

|\downarrow\rangle
∣↓⟩|\downarrow\rangle
|\uparrow\rangle
∣↑⟩|\uparrow\rangle

ME

YOU

Information travelled faster than the speed of light?

"Spukhafte Fernwirkung!"

("Spooky action at a distance")

Albert Einstein

"God does not play dice with the universe"

Albert Einstein

John Bell

1964

"Don't tell God what to do with his dice"

Niels Bohr

Practical use of entanglement?

ME

YOU

|\psi\rangle
∣ψ⟩|\psi\rangle
\frac{1}{\sqrt{2}}|\downarrow\uparrow\rangle +\frac{1}{\sqrt{2}}|\uparrow\downarrow\rangle
12∣↓↑⟩+12∣↑↓⟩\frac{1}{\sqrt{2}}|\downarrow\uparrow\rangle +\frac{1}{\sqrt{2}}|\uparrow\downarrow\rangle

ME

YOU

|\psi\rangle
∣ψ⟩|\psi\rangle

Average Human 

\sim 10^{27}
∼1027\sim 10^{27}

Qubits

PARTICLE CHAMBER

Champaign

Paris

SCANNER

PARTICLE CHAMBER

SCANNER

PARTICLE CHAMBER

PARTICLE CHAMBER

SCANNER

SCANNER

Champaign

Paris

SCANNER

PARTICLE CHAMBER

PARTICLE CHAMBER

SCANNER

Champaign

Paris

SCANNER

PARTICLE CHAMBER

PARTICLE CHAMBER

SCANNER

Champaign

Paris

SCANNER

PARTICLE CHAMBER

PARTICLE CHAMBER

SCANNER

Champaign

Paris

SCANNER

PARTICLE CHAMBER

PARTICLE CHAMBER

SCANNER

Champaign

Paris

We are ready to solve some interesting problems.

Computational Complexity Zoo

EXP

PSPACE

NP

NP-Complete

P

Computational Complexity Zoo

EXP

PSPACE

NP

NP-Complete

P

BQP

Bounded Error

Quantum

 Polynomial Time

"solves with probability > 2/3"

Peter Shor

1994

Bell Labs

Non-trivial Square Root of 1 modulo N

x^2 \equiv 1\text{ }(\text{mod}\ N) \text{ and }\ x \neq \pm 1
x2≡1 (mod N) and  x≠±1x^2 \equiv 1\text{ }(\text{mod}\ N) \text{ and }\ x \neq \pm 1

Non-trivial Square Root of 1 modulo N

x^2-1 \equiv 0\text{ }(\text{mod}\ N)
x2−1≡0 (mod N)x^2-1 \equiv 0\text{ }(\text{mod}\ N)
N|(x + 1)(x - 1)
N∣(x+1)(x−1)N|(x + 1)(x - 1)
\text{gcd}(N, x + 1) \text{ and gcd}(N, x -1) \text{ are factors of }N
gcd(N,x+1) and gcd(N,x−1) are factors of N\text{gcd}(N, x + 1) \text{ and gcd}(N, x -1) \text{ are factors of }N

Factoring 15

4^2=16\equiv 1 \text{ }(\text{mod } 15) \text{ and } 4 \neq \pm 1\text{ }(\text{mod } 15)
42=16≡1 (mod 15) and 4≠±1 (mod 15)4^2=16\equiv 1 \text{ }(\text{mod } 15) \text{ and } 4 \neq \pm 1\text{ }(\text{mod } 15)
\text{gcd}(15, 5) = 5 \text{ and gcd}(15, 3) = 3
gcd(15,5)=5 and gcd(15,3)=3\text{gcd}(15, 5) = 5 \text{ and gcd}(15, 3) = 3
15 = 3 \times 5
15=3×515 = 3 \times 5

RSA Cryptography

Fun Facts

  • Largest number factored is 56,153 [2014]
  • Factoring 2048 bit integer (RSA)
    • Classical
      • 10 years
      • $10^6 trillion
      • 10^6 terawatts
    • Quantum
      • 16 hours
      • $100 billion
      • 10 megawatts

Computational Complexity Zoo

EXP

PSPACE

NP

NP-Complete

P

BQP

NP-Complete Problems

  • Protein Folding
  • Traveling Salesman Problem (TSP)
  • Boolean Satisfiability Problem

NP-Complete Problems

  • Protein Folding
  • Traveling Salesman Problem (TSP)
  • Boolean Satisfiability Problem
  • Battleship
  • Tetris
  • Super Mario Bros
  • Candy Crush
  • Sudoku

5 Minute Break

Formalism

|0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}
∣0⟩=(10)|0\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}
|1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
∣1⟩=(01)|1\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle = \alpha\begin{pmatrix}1 \\ 0\end{pmatrix} + \beta\begin{pmatrix}0 \\ 1\end{pmatrix} = \begin{pmatrix}\alpha \\ \beta\end{pmatrix}
∣ψ⟩=α∣0⟩+β∣1⟩=α(10)+β(01)=(αβ)|\psi\rangle = \alpha|0\rangle + \beta|1\rangle = \alpha\begin{pmatrix}1 \\ 0\end{pmatrix} + \beta\begin{pmatrix}0 \\ 1\end{pmatrix} = \begin{pmatrix}\alpha \\ \beta\end{pmatrix}
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
\langle\psi| = |\psi\rangle^\dagger = \alpha^*\langle0|+ \beta^*\langle1|
⟨ψ∣=∣ψ⟩†=α∗⟨0∣+β∗⟨1∣\langle\psi| = |\psi\rangle^\dagger = \alpha^*\langle0|+ \beta^*\langle1|
\langle0| = (1, 0)
⟨0∣=(1,0)\langle0| = (1, 0)
\langle1| = (0, 1)
⟨1∣=(0,1)\langle1| = (0, 1)
\langle0|1\rangle = (1, 0)\begin{pmatrix}0 \\ 1\end{pmatrix} = 0
⟨0∣1⟩=(1,0)(01)=0\langle0|1\rangle = (1, 0)\begin{pmatrix}0 \\ 1\end{pmatrix} = 0
|\psi_2\rangle = \alpha_{00}|00\rangle + \alpha_{01}|01\rangle + \alpha_{10}|10\rangle + \alpha_{11}|11\rangle
∣ψ2⟩=α00∣00⟩+α01∣01⟩+α10∣10⟩+α11∣11⟩|\psi_2\rangle = \alpha_{00}|00\rangle + \alpha_{01}|01\rangle + \alpha_{10}|10\rangle + \alpha_{11}|11\rangle
|\psi_1\rangle = \alpha_{0}|0\rangle + \alpha_{1}|1\rangle
∣ψ1⟩=α0∣0⟩+α1∣1⟩|\psi_1\rangle = \alpha_{0}|0\rangle + \alpha_{1}|1\rangle
\text{N-qubit system is a }2^N\text{ dimensional complex vector space}
N-qubit system is a 2N dimensional complex vector space\text{N-qubit system is a }2^N\text{ dimensional complex vector space}
...
......
\text{What exactly are these }\alpha\text{'s and }\beta\text{'s?}
What exactly are these α's and β's?\text{What exactly are these }\alpha\text{'s and }\beta\text{'s?}
|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle = \alpha|0\rangle + \beta|1\rangle
i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂Ψ∂t=−ℏ22m∂2Ψ∂x2+VΨi\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi

Schrödinger Equation in 1D

i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂Ψ∂t=−ℏ22m∂2Ψ∂x2+VΨi\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi

Assumption: 

\Psi \text{ is real}
Ψ is real\Psi \text{ is real}

Complex

i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂Ψ∂t=−ℏ22m∂2Ψ∂x2+VΨi\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi

Assumption: 

\Psi \text{ is real}
Ψ is real\Psi \text{ is real}

Complex

Real

i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂Ψ∂t=−ℏ22m∂2Ψ∂x2+VΨi\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi

Assumption: 

\Psi \text{ is real}
Ψ is real\Psi \text{ is real}

Complex

Real

Contradiction!

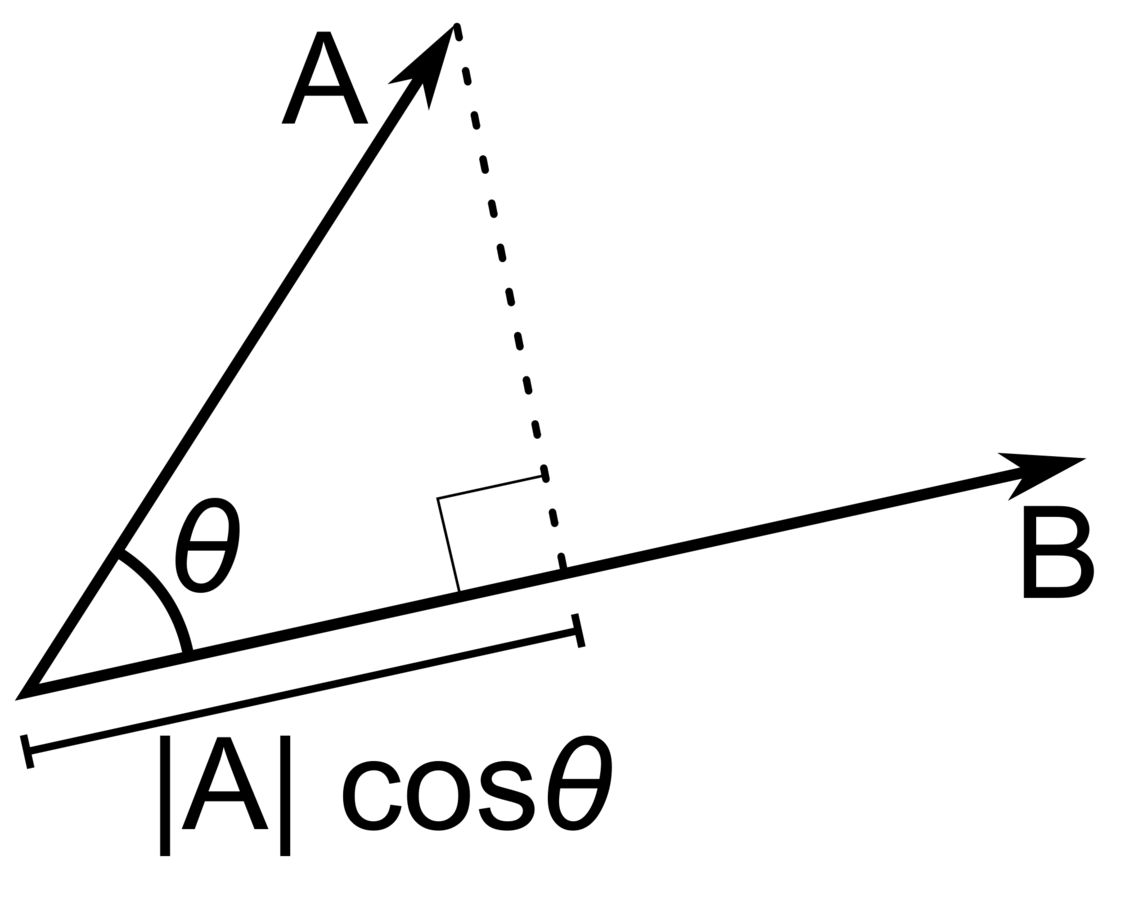
Inner Product (Dot Product)

\text{For basis vectors }|i\rangle \text{ and } |j\rangle \text{, } \langle i|j\rangle = \delta_{ij}
For basis vectors ∣i⟩ and ∣j⟩, ⟨i∣j⟩=δij\text{For basis vectors }|i\rangle \text{ and } |j\rangle \text{, } \langle i|j\rangle = \delta_{ij}
\text{In functional space, }\langle\phi |\psi\rangle = \int_{-\infty}^{+\infty} \phi^* \psi dx
In functional space, ⟨ϕ∣ψ⟩=∫−∞+∞ϕ∗ψdx\text{In functional space, }\langle\phi |\psi\rangle = \int_{-\infty}^{+\infty} \phi^* \psi dx
\delta_{ij} = \left\{ \begin{array}{ll} 0 & i\neq j \\ 1 & i = j \end{array} \right.
δij={0i≠j1i=j\delta_{ij} = \left\{ \begin{array}{ll} 0 & i\neq j \\ 1 & i = j \end{array} \right.

Geometric Interpretation of Inner Product

Born Interpretation of QM

\text{Probability of measuring } |\phi_n\rangle \text{ from } |\psi\rangle \text{ is }|\langle \phi_n|\psi\rangle|^2
Probability of measuring ∣ϕn⟩ from ∣ψ⟩ is ∣⟨ϕn∣ψ⟩∣2\text{Probability of measuring } |\phi_n\rangle \text{ from } |\psi\rangle \text{ is }|\langle \phi_n|\psi\rangle|^2
\text{and if you observe } |\phi_n\rangle \text{ then the new state is } |\phi_n\rangle
and if you observe ∣ϕn⟩ then the new state is ∣ϕn⟩\text{and if you observe } |\phi_n\rangle \text{ then the new state is } |\phi_n\rangle

Observables

U = \sum_n \lambda_n|\phi_n\rangle \langle \phi_n|
U=∑nλn∣ϕn⟩⟨ϕn∣U = \sum_n \lambda_n|\phi_n\rangle \langle \phi_n|
U|\phi_m \rangle = \lambda_m |\phi_m \rangle
U∣ϕm⟩=λm∣ϕm⟩U|\phi_m \rangle = \lambda_m |\phi_m \rangle
\hat{H}|\psi_n \rangle = E_n |\psi_n \rangle
H^∣ψn⟩=En∣ψn⟩\hat{H}|\psi_n \rangle = E_n |\psi_n \rangle

Measurement Example

\text{Let }|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
Let ∣ψ⟩=12(∣0⟩+∣1⟩)\text{Let }|\psi\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
\text{Probability of measuring } |0\rangle \text{ from } |\psi\rangle \text{ is }|\langle 0|\psi\rangle|^2
Probability of measuring ∣0⟩ from ∣ψ⟩ is ∣⟨0∣ψ⟩∣2\text{Probability of measuring } |0\rangle \text{ from } |\psi\rangle \text{ is }|\langle 0|\psi\rangle|^2
\langle 0|\psi\rangle = \langle 0 | (\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )) = \frac{1}{\sqrt{2}} \langle 0|0\rangle + \frac{1}{\sqrt{2}} \langle 0|1\rangle
⟨0∣ψ⟩=⟨0∣(12(∣0⟩+∣1⟩))=12⟨0∣0⟩+12⟨0∣1⟩\langle 0|\psi\rangle = \langle 0 | (\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle )) = \frac{1}{\sqrt{2}} \langle 0|0\rangle + \frac{1}{\sqrt{2}} \langle 0|1\rangle
= \frac{1}{\sqrt{2}} \delta_{00} + \frac{1}{\sqrt{2}} \delta_{01} = \frac{1}{\sqrt{2}}
=12δ00+12δ01=12= \frac{1}{\sqrt{2}} \delta_{00} + \frac{1}{\sqrt{2}} \delta_{01} = \frac{1}{\sqrt{2}}

Normalization Rule

\langle\psi |\psi\rangle = 1
⟨ψ∣ψ⟩=1\langle\psi |\psi\rangle = 1
\forall |\psi\rangle = \alpha |0\rangle + \beta |1\rangle
∀∣ψ⟩=α∣0⟩+β∣1⟩\forall |\psi\rangle = \alpha |0\rangle + \beta |1\rangle
|\alpha|^2 + |\beta|^2 = 1
∣α∣2+∣β∣2=1|\alpha|^2 + |\beta|^2 = 1

Normalization Rule

\langle\psi |\psi\rangle = 1
⟨ψ∣ψ⟩=1\langle\psi |\psi\rangle = 1
\forall |\psi\rangle = \alpha |0\rangle + \beta |1\rangle
∀∣ψ⟩=α∣0⟩+β∣1⟩\forall |\psi\rangle = \alpha |0\rangle + \beta |1\rangle
|\alpha|^2 + |\beta|^2 = 1
∣α∣2+∣β∣2=1|\alpha|^2 + |\beta|^2 = 1

Qubit is a unit vector!

Dimension of Wave Function

\text{Recall in functional space, }\langle\psi |\psi\rangle = \int_{-\infty}^{+\infty} \psi^* \psi dx = 1
Recall in functional space, ⟨ψ∣ψ⟩=∫−∞+∞ψ∗ψdx=1\text{Recall in functional space, }\langle\psi |\psi\rangle = \int_{-\infty}^{+\infty} \psi^* \psi dx = 1
\text{Dimension of }[\psi] = \frac{1}{\sqrt{m}}
Dimension of [ψ]=1m\text{Dimension of }[\psi] = \frac{1}{\sqrt{m}}

How can we mathematically manipulate qubits to do interesting computation?

Unitary Evolution

\text{A matrix }U\text{ is unitary if } UU^\dagger = U^\dagger U = I
A matrix U is unitary if UU†=U†U=I\text{A matrix }U\text{ is unitary if } UU^\dagger = U^\dagger U = I
\text{Quantum states go through unitary evolution.}
Quantum states go through unitary evolution.\text{Quantum states go through unitary evolution.}

Logic Gates

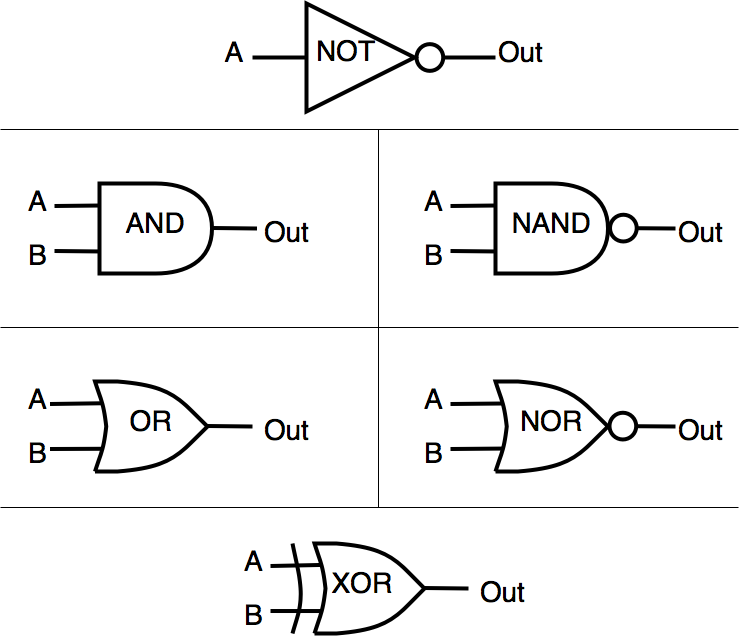
Quantum Gates

X = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}
X=(0110)X = \begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix}
H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix}
H=12(111−1)H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix}
Z = \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}
Z=(100−1)Z = \begin{pmatrix} 1 & 0\\ 0 & -1 \end{pmatrix}
CNOT = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}
CNOT=(1000010000010010)CNOT = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 \end{pmatrix}

Quantum Teleportation Protocol

How do you find a needle

in a haystack?

How do you find a needle

in a haystack?

Grover's Algorithm

Unstructured Search

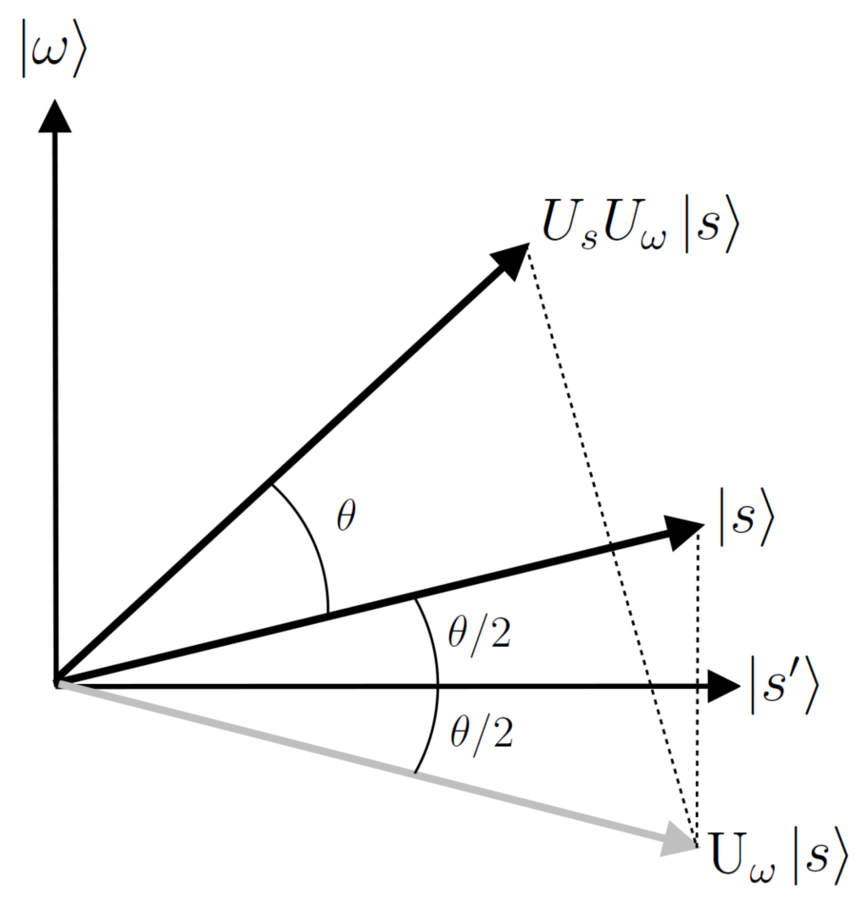
T(N) = O(\sqrt{N})
T(N)=O(N)T(N) = O(\sqrt{N})

Our discussion of qubit has been abstract

Our discussion of qubit has been abstract

 

How can we realize a physical qubit?

p

e-

|0\rangle
∣0⟩|0\rangle

Hydrogen

p

e-

|1\rangle
∣1⟩|1\rangle

Hydrogen

p

e-

e-

|\psi\rangle
∣ψ⟩|\psi\rangle

Hydrogen

Particle in a Box

m
mm
0
00
l
ll
|\psi (t)\rangle = \text{ }?
∣ψ(t)⟩= ?|\psi (t)\rangle = \text{ }?

Schrödinger Equation

i\hbar\frac{d|\psi\rangle}{dt} = \hat{H} |\psi\rangle
iℏd∣ψ⟩dt=H^∣ψ⟩i\hbar\frac{d|\psi\rangle}{dt} = \hat{H} |\psi\rangle
|\psi (t)\rangle = e^{-i\frac{\hat{H}}{\hbar}t} |\psi (t=0)\rangle
∣ψ(t)⟩=e−iH^ℏt∣ψ(t=0)⟩|\psi (t)\rangle = e^{-i\frac{\hat{H}}{\hbar}t} |\psi (t=0)\rangle

General Solution

|\psi (t)\rangle = e^{i\frac{\hat{H}}{\hbar}t} |\psi (t=0)\rangle
∣ψ(t)⟩=eiH^ℏt∣ψ(t=0)⟩|\psi (t)\rangle = e^{i\frac{\hat{H}}{\hbar}t} |\psi (t=0)\rangle
|\psi (t=0)\rangle = \sum_n c_n|\psi_n \rangle
∣ψ(t=0)⟩=∑ncn∣ψn⟩|\psi (t=0)\rangle = \sum_n c_n|\psi_n \rangle
|\psi (t)\rangle = \sum_n c_n e^{-iE_n t/\hbar}|\psi_n \rangle
∣ψ(t)⟩=∑ncne−iEnt/ℏ∣ψn⟩|\psi (t)\rangle = \sum_n c_n e^{-iE_n t/\hbar}|\psi_n \rangle

Particle in a Box

|\psi_n\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{n\pi}{l}x)}
∣ψn⟩=2lsin(nπlx)|\psi_n\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{n\pi}{l}x)}
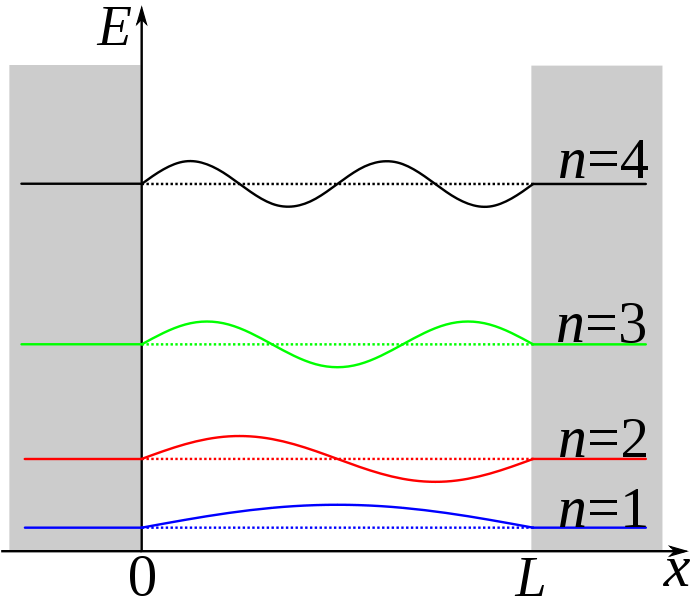
E_n = \frac{n^2\pi^2 \hbar^2}{2ml^2}
En=n2π2ℏ22ml2E_n = \frac{n^2\pi^2 \hbar^2}{2ml^2}

Particle in a Box

|0\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{\pi}{l}x)}
∣0⟩=2lsin(πlx)|0\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{\pi}{l}x)}
E_1 = \frac{\pi^2 \hbar^2}{2ml^2}
E1=π2ℏ22ml2E_1 = \frac{\pi^2 \hbar^2}{2ml^2}
|1\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{2\pi}{l}x)}
∣1⟩=2lsin(2πlx)|1\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{2\pi}{l}x)}
E_2 = \frac{2\pi^2 \hbar^2}{ml^2}
E2=2π2ℏ2ml2E_2 = \frac{2\pi^2 \hbar^2}{ml^2}

Particle in a Box

|\psi\rangle = \alpha |0\rangle + \beta |1\rangle
∣ψ⟩=α∣0⟩+β∣1⟩|\psi\rangle = \alpha |0\rangle + \beta |1\rangle
|\psi (t)\rangle = \alpha |0\rangle e^{-\frac{iE_1 t}{\hbar}} + \beta |1\rangle e^{-\frac{iE_2 t}{\hbar}}
∣ψ(t)⟩=α∣0⟩e−iE1tℏ+β∣1⟩e−iE2tℏ|\psi (t)\rangle = \alpha |0\rangle e^{-\frac{iE_1 t}{\hbar}} + \beta |1\rangle e^{-\frac{iE_2 t}{\hbar}}
|\psi (t)\rangle = e^{-\frac{iE_1 t}{\hbar}} (\alpha |0\rangle + \beta |1\rangle e^{-\frac{i(\Delta E)t}{\hbar}})
∣ψ(t)⟩=e−iE1tℏ(α∣0⟩+β∣1⟩e−i(ΔE)tℏ)|\psi (t)\rangle = e^{-\frac{iE_1 t}{\hbar}} (\alpha |0\rangle + \beta |1\rangle e^{-\frac{i(\Delta E)t}{\hbar}})
\Delta E \approx 10 \text{ eV}
ΔE≈10 eV\Delta E \approx 10 \text{ eV}
\nu = \frac{\Delta E}{h} = 2.5 \times 10^{15} \text{ Hz}
ν=ΔEh=2.5×1015 Hz\nu = \frac{\Delta E}{h} = 2.5 \times 10^{15} \text{ Hz}
\therefore \text{Atomic qubits are controlled optically via interactions with light pulses}
∴Atomic qubits are controlled optically via interactions with light pulses\therefore \text{Atomic qubits are controlled optically via interactions with light pulses}

Solving NP-Complete Problems

Quantum Adiabatic Optimization

\hat{H}(s) = (1-s)\hat{H}_B + s\hat{H}_P
H^(s)=(1−s)H^B+sH^P\hat{H}(s) = (1-s)\hat{H}_B + s\hat{H}_P
\Delta (\hat{H}) = |E_2 - E_1|
Δ(H^)=∣E2−E1∣\Delta (\hat{H}) = |E_2 - E_1|
T \propto O(\frac{1}{{\Delta (\hat{H}(s))}^3})
T∝O(1Δ(H^(s))3)T \propto O(\frac{1}{{\Delta (\hat{H}(s))}^3})

State-of-the-art

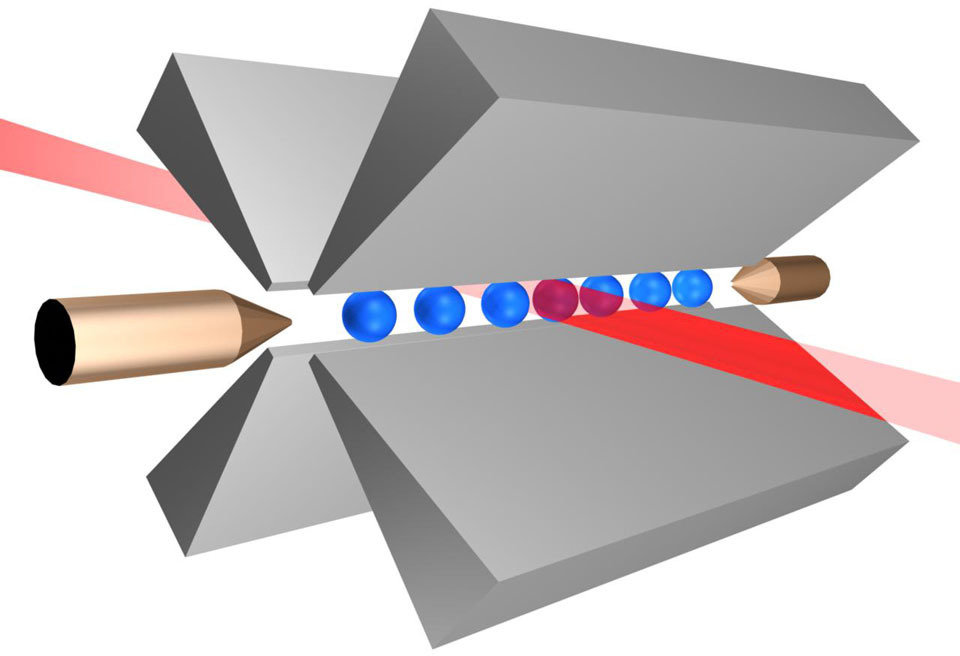
Trapped Atomic Ion

  • very long (>>1s) memory
  • <20 coherent qubits
  • engineering needed
  • connection reconfigurable

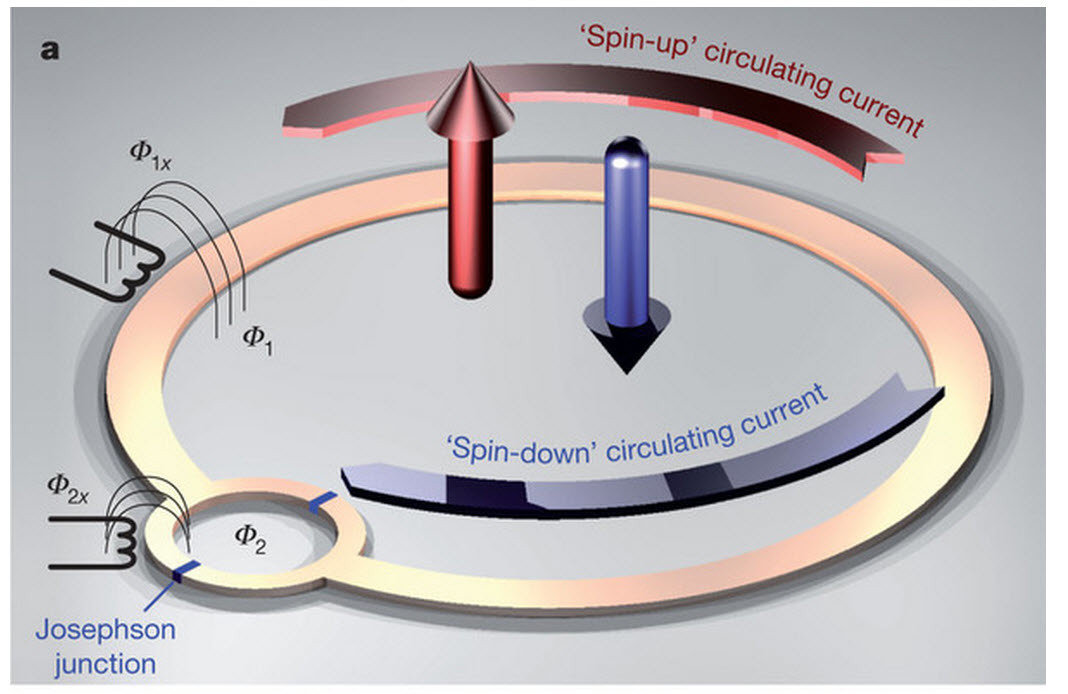
Superconducting Loop

  • short (10^-6s) memory
  • <10 coherent qubits
  • printable circuits and VLSI
  • not reconfigurable
\vec{\nabla} \cdot \vec{E} = 0
∇⃗⋅E⃗=0\vec{\nabla} \cdot \vec{E} = 0

Maxwell's Equations

\text{Cannot create a stable equilibrium with a static potential.}
Cannot create a stable equilibrium with a static potential.\text{Cannot create a stable equilibrium with a static potential.}

Q & A

Copy of Quantum Computation

By seanbae

Made with Slides.com

Copy of Quantum Computation

  • 624

More from seanbae