QUANTUM PHYSICS:
Whimsical Laws of Nature at the Most Fundamental Level
Sean Bae


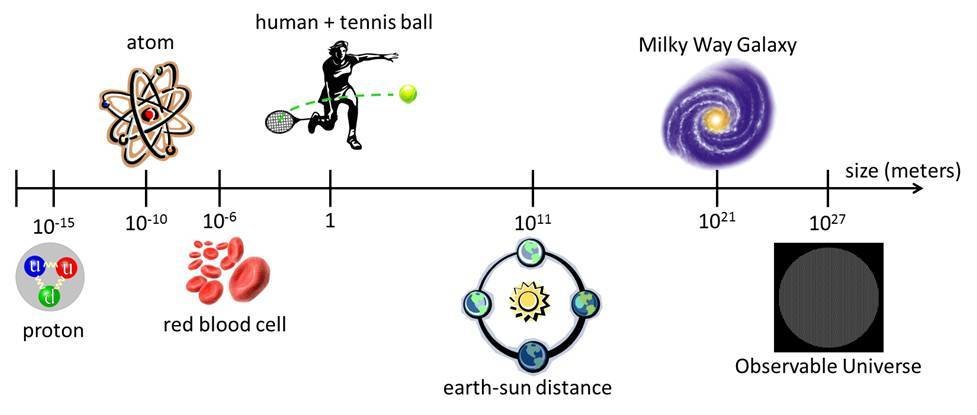
Quantum Mechanics in 3 Minutes
- Wave-particle Duality
- State and Measurement
- Applications
F = ma
F=ma
Newtonian Mechanics
F = ma
F=ma
Newtonian Mechanics

F = ma
F=ma
Newtonian Mechanics


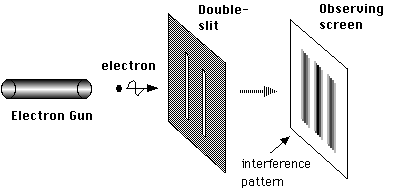
Wave-Particle Duality
Superposition
- An electron can exist in two places at the same time
- Quantum state can exist in multiple states simultaneously as long as they are not observed
Measurement
- Superposition collapses
- Forces the electron to take a stand and exist in only one position
- Complete knowledge of a system is forbidden
- Heisenberg's Uncertainty Principle
|\text{cat}\rangle = \frac{1}{\sqrt{2}}(|\text{dead}\rangle + |\text{alive}\rangle)
∣cat⟩=√21(∣dead⟩+∣alive⟩)
- Trap a cat in a box
- A radioactive material in the box will decay with 50% probability and kill the cat in 1 hour
- Wait for 1 hour
- Is the cat is both dead and alive??
Schrödinger's Cat
Quantum Entanglement


100,000 light years
Milky Way

COLLEGE PARK, MD
Milky Way

ME
YOU



ME
YOU

ME
YOU



ME
YOU
|\downarrow\rangle
∣↓⟩
|\uparrow\rangle
∣↑⟩

ME
YOU
|\downarrow\rangle
∣↓⟩
|\uparrow\rangle
∣↑⟩

ME
YOU
Information travelled faster than the speed of light?

"Spukhafte Fernwirkung!"
("Spooky action at a distance")
Albert Einstein

"God does not play dice with the universe"
Albert Einstein
John Bell
1964
Practical use of entanglement?
Measurement
\text{Systems do not have definite properties until measured}
Systems do not have definite properties until measured
von Neumann
Many worlds
Copenhagen
(\sum_i c_i|a_i\rangle)\otimes|\text{measurement device ready}\rangle\otimes |\text{observer ready}\rangle
(∑ici∣ai⟩)⊗∣measurement device ready⟩⊗∣observer ready⟩
\text{No collapse of wave function}
No collapse of wave function
(\sum_i c_i|a_i\rangle)\otimes|\text{measurement device shows i}\rangle\otimes |\text{observer sees i}\rangle
(∑ici∣ai⟩)⊗∣measurement device shows i⟩⊗∣observer sees i⟩
\text{but does not define what constitutes a measurement}
but does not define what constitutes a measurement

Many Worlds Interpretation
i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂t∂Ψ=−2mℏ2∂x2∂2Ψ+VΨ
Schrödinger Equation in 1D
i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂t∂Ψ=−2mℏ2∂x2∂2Ψ+VΨ
Assumption:
\Psi \text{ is real}
Ψ is real
Complex
i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂t∂Ψ=−2mℏ2∂x2∂2Ψ+VΨ
Assumption:
\Psi \text{ is real}
Ψ is real
Complex
Real
i\hbar\frac{\partial\Psi}{\partial t} = -\frac{\hbar^2}{2m}\frac{\partial^2 \Psi}{\partial x^2} + V\Psi
iℏ∂t∂Ψ=−2mℏ2∂x2∂2Ψ+VΨ
Assumption:
\Psi \text{ is real}
Ψ is real
Complex
Real
Contradiction!
Dimension of Wave Function
\text{Recall in functional space, }\langle\psi |\psi\rangle = \int_{-\infty}^{+\infty} \psi^* \psi dx = 1
Recall in functional space, ⟨ψ∣ψ⟩=∫−∞+∞ψ∗ψdx=1
\text{Dimension of }[\psi] = [\frac{1}{\sqrt{L}}]
Dimension of [ψ]=[√L1]
How can we mathematically manipulate qubits to do interesting computation?
Logic Gates
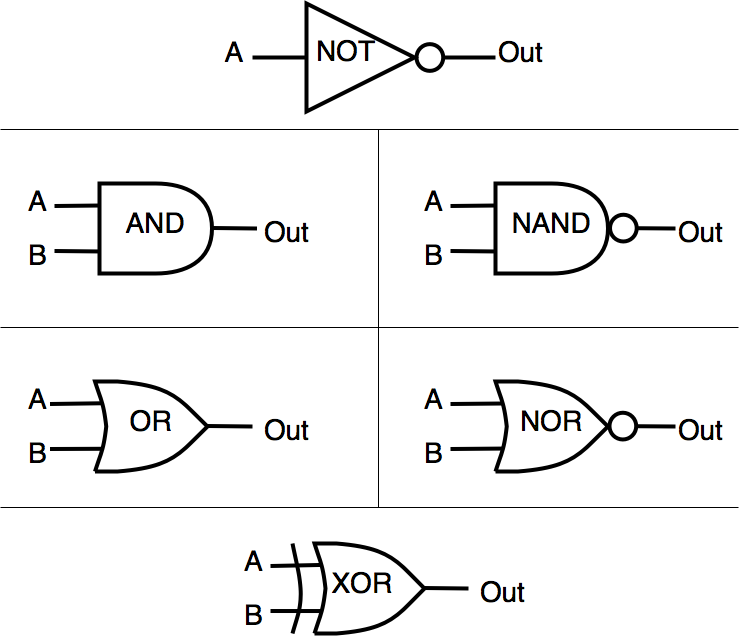
Logic Circuit
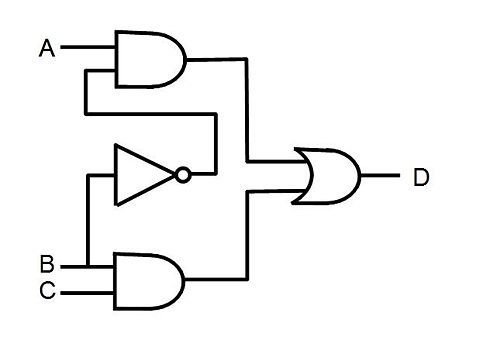
\text{Any Turing computable function can be converted into the form:}
Any Turing computable function can be converted into the form:
f : \{0,1\}^n \rightarrow \{0,1\}^m
f:{0,1}n→{0,1}m
Logic Circuit

\text{Any Turing computable function can be converted into the form:}
Any Turing computable function can be converted into the form:
\text{NAND and FANOUT are universal}
NAND and FANOUT are universal
Quantum Gates
|0100\rangle
∣0100⟩
|\text{result}\rangle
∣result⟩
Gate
|0\rangle\otimes |1\rangle\otimes |0\rangle = |0\rangle|1\rangle|0\rangle = |010\rangle
∣0⟩⊗∣1⟩⊗∣0⟩=∣0⟩∣1⟩∣0⟩=∣010⟩
Simplified Notation
Quantum Gates
|0100\rangle
∣0100⟩
|\text{result}\rangle
∣result⟩
Gate
|0\rangle\otimes |1\rangle\otimes |0\rangle = |0\rangle|1\rangle|0\rangle = |010\rangle
∣0⟩⊗∣1⟩⊗∣0⟩=∣0⟩∣1⟩∣0⟩=∣010⟩
Simplified Notation
Evolution operator U act for finite time according to the Schrödinger Equation
Quantum Gates
|000\rangle + |001\rangle +
∣000⟩+∣001⟩+
|\text{result}\rangle
∣result⟩
Gate
|0\rangle\otimes |1\rangle\otimes |0\rangle = |0\rangle|1\rangle|0\rangle = |010\rangle
∣0⟩⊗∣1⟩⊗∣0⟩=∣0⟩∣1⟩∣0⟩=∣010⟩
Simplified Notation
One gate operation acts on all components
|010\rangle + |100\rangle + |110\rangle
∣010⟩+∣100⟩+∣110⟩
Quantum Gates
|\psi\rangle
∣ψ⟩
|\text{result}\rangle
∣result⟩
Gate
|0\rangle\otimes |1\rangle\otimes |0\rangle = |0\rangle|1\rangle|0\rangle = |010\rangle
∣0⟩⊗∣1⟩⊗∣0⟩=∣0⟩∣1⟩∣0⟩=∣010⟩
Simplified Notation
\text{Can act on }2^{N} \text{ basis states in 1 clock cycle}
Can act on 2N basis states in 1 clock cycle
Qubit
\mathcal{H} \cong \mathbb{C}^2
H≅C2
|\psi\rangle = \alpha |0\rangle + \beta |1\rangle
∣ψ⟩=α∣0⟩+β∣1⟩
|\alpha |^2 + |\beta |^2 = 1
∣α∣2+∣β∣2=1
State Space
Generalized Qubit
Normalization
Quantum Gates
X = \text{X gate (NOT)}
X=X gate (NOT)
H = \text{Hadamard gate}
H=Hadamard gate
Z = \text{Z-gate}
Z=Z-gate
X|0\rangle = |1\rangle
X∣0⟩=∣1⟩
X|1\rangle = |0\rangle
X∣1⟩=∣0⟩
Z|0\rangle = |0\rangle
Z∣0⟩=∣0⟩
Z|1\rangle = -|1\rangle
Z∣1⟩=−∣1⟩
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
Quantum Teleportation Protocol
|\Psi\rangle = |\psi\rangle_t\otimes|\psi^{-}\rangle_{a,b}
∣Ψ⟩=∣ψ⟩t⊗∣ψ−⟩a,b
|\psi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|01\rangle \pm |10\rangle)
∣ψ±⟩=√21(∣01⟩±∣10⟩)
|\phi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|00\rangle \pm |11\rangle)
∣ϕ±⟩=√21(∣00⟩±∣11⟩)
Quantum Teleportation Protocol
|\Psi\rangle = |\psi\rangle_t\otimes|\psi^{-}\rangle_{a,b}
∣Ψ⟩=∣ψ⟩t⊗∣ψ−⟩a,b
=\frac{1}{\sqrt{2}}(\alpha |0\rangle_{t0} + \beta |1\rangle_{t1})\otimes(|01\rangle_{a,b} - |10\rangle_{a,b})
=√21(α∣0⟩t0+β∣1⟩t1)⊗(∣01⟩a,b−∣10⟩a,b)
|\psi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|01\rangle \pm |10\rangle)
∣ψ±⟩=√21(∣01⟩±∣10⟩)
|\phi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|00\rangle \pm |11\rangle)
∣ϕ±⟩=√21(∣00⟩±∣11⟩)
\text{Expand the terms}
Expand the terms
Quantum Teleportation Protocol
|\Psi\rangle = |\psi\rangle_t\otimes|\psi^{-}\rangle_{a,b}
∣Ψ⟩=∣ψ⟩t⊗∣ψ−⟩a,b
=\frac{1}{\sqrt{2}}(\alpha |0\rangle_{t0} + \beta |1\rangle_{t1})\otimes(|01\rangle_{a,b} - |10\rangle_{a,b})
=√21(α∣0⟩t0+β∣1⟩t1)⊗(∣01⟩a,b−∣10⟩a,b)
=\frac{1}{2}[(\alpha |1\rangle_{b1} - \beta |0\rangle_{b0} ) |\phi^+\rangle_{t,a} + (\alpha |1\rangle_{b1} + \beta |0\rangle_{b0} )|\phi^-\rangle_{t,a}
=21[(α∣1⟩b1−β∣0⟩b0)∣ϕ+⟩t,a+(α∣1⟩b1+β∣0⟩b0)∣ϕ−⟩t,a
+ (\beta |1\rangle_{b1} - \alpha |0\rangle_{b0} )|\psi^+\rangle_{t,a} - (\alpha |0\rangle_{b0} + \beta |1\rangle_{b1} )|\psi^-\rangle_{t,a}]
+(β∣1⟩b1−α∣0⟩b0)∣ψ+⟩t,a−(α∣0⟩b0+β∣1⟩b1)∣ψ−⟩t,a]
|\psi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|01\rangle \pm |10\rangle)
∣ψ±⟩=√21(∣01⟩±∣10⟩)
|\phi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|00\rangle \pm |11\rangle)
∣ϕ±⟩=√21(∣00⟩±∣11⟩)
\text{Alice makes a measurement in Bell basis}
Alice makes a measurement in Bell basis
Quantum Teleportation Protocol
|\Psi\rangle = |\psi\rangle_t\otimes|\psi^{-}\rangle_{a,b}
∣Ψ⟩=∣ψ⟩t⊗∣ψ−⟩a,b
=\frac{1}{\sqrt{2}}(\alpha |0\rangle_{t0} + \beta |1\rangle_{t1})\otimes(|01\rangle_{a,b} - |10\rangle_{a,b})
=√21(α∣0⟩t0+β∣1⟩t1)⊗(∣01⟩a,b−∣10⟩a,b)
=\frac{1}{2}[(\alpha |1\rangle_{b1} - \beta |0\rangle_{b0} ) |\phi^+\rangle_{t,a} + (\alpha |1\rangle_{b1} + \beta |0\rangle_{b0} )|\phi^-\rangle_{t,a}
=21[(α∣1⟩b1−β∣0⟩b0)∣ϕ+⟩t,a+(α∣1⟩b1+β∣0⟩b0)∣ϕ−⟩t,a
+ (\beta |1\rangle_{b1} - \alpha |0\rangle_{b0} )|\psi^+\rangle_{t,a} - (\alpha |0\rangle_{b0} + \beta |1\rangle_{b1} )|\psi^-\rangle_{t,a}]
+(β∣1⟩b1−α∣0⟩b0)∣ψ+⟩t,a−(α∣0⟩b0+β∣1⟩b1)∣ψ−⟩t,a]
|\psi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|01\rangle \pm |10\rangle)
∣ψ±⟩=√21(∣01⟩±∣10⟩)
|\phi^{\pm}\rangle = \frac{1}{\sqrt{2}}(|00\rangle \pm |11\rangle)
∣ϕ±⟩=√21(∣00⟩±∣11⟩)
\text{Bob applies the correct gates to retrieve Alice's qubit}
Bob applies the correct gates to retrieve Alice's qubit
Deutsch-Josza Algorithm
\text{Oracle } f : \{0,1\}^{n} \rightarrow \{0,1\}
Oracle f:{0,1}n→{0,1}
| x | f0 | f1 | f2 | f3 |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
\text{Is } f \text{ constant or balanced?}
Is f constant or balanced?
n = 1
n=1
Deutsch-Josza Algorithm
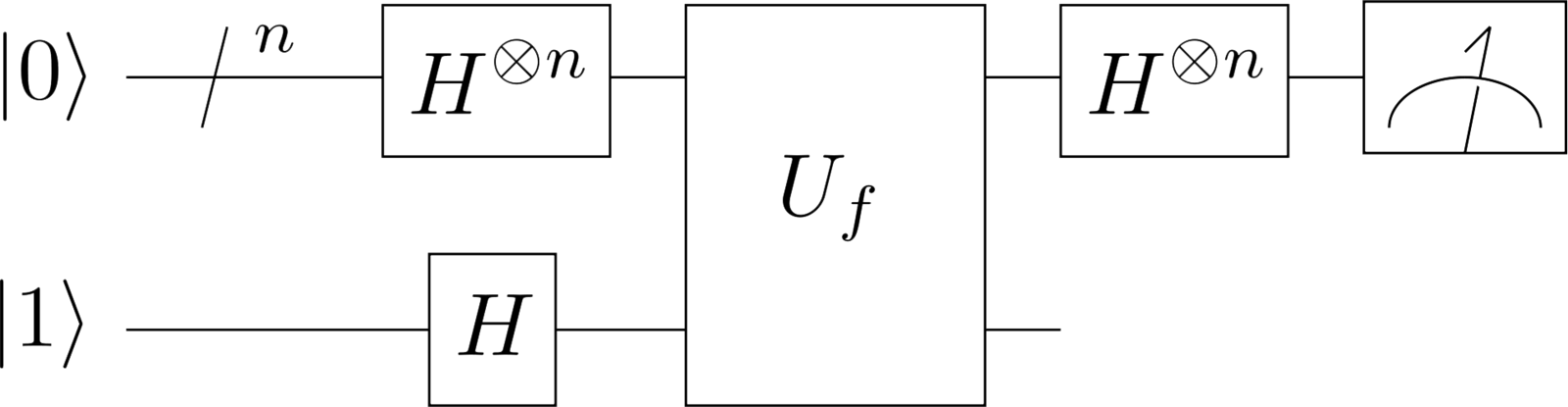
Classical: 2 queries
Quantum: 1 query
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
Deutsch-Josza Algorithm
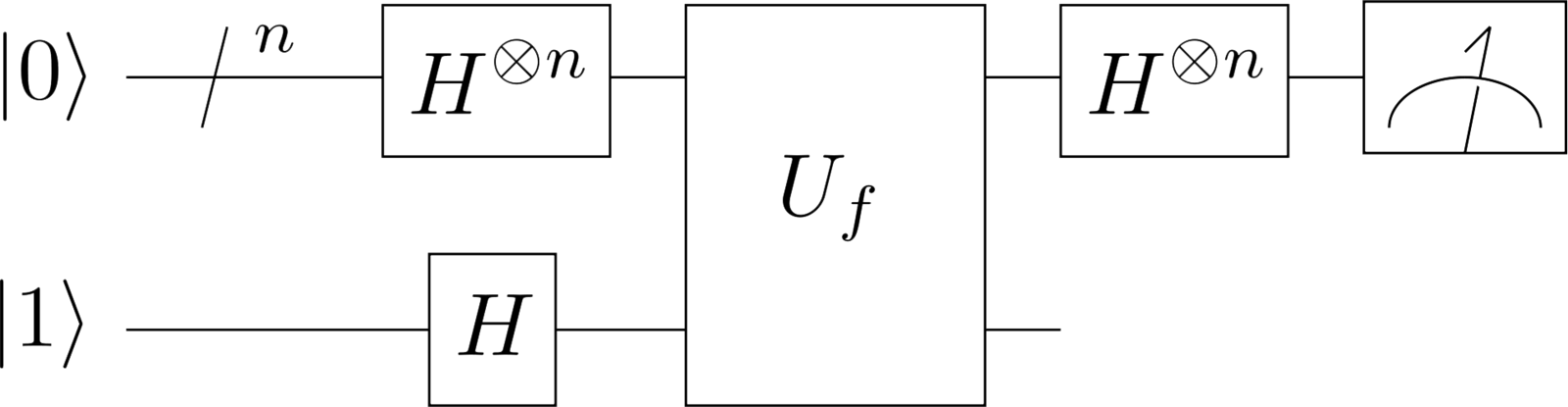
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\text{Apply the Hadamard gates}
Apply the Hadamard gates
Deutsch-Josza Algorithm
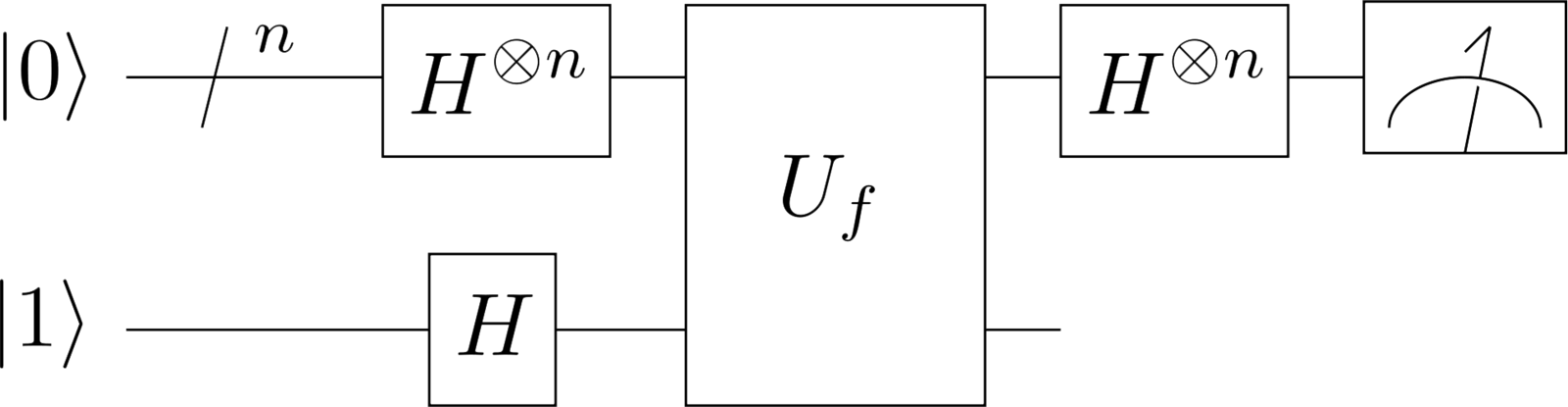
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle |0\oplus f(0)\rangle + |1\rangle |0\oplus f(1)\rangle + |0\rangle |1\oplus f(0)\rangle + |1\rangle |1\oplus f(1)\rangle)
→21(∣0⟩∣0⊕f(0)⟩+∣1⟩∣0⊕f(1)⟩+∣0⟩∣1⊕f(0)⟩+∣1⟩∣1⊕f(1)⟩)
\text{Apply the Oracle gate}
Apply the Oracle gate
Deutsch-Josza Algorithm
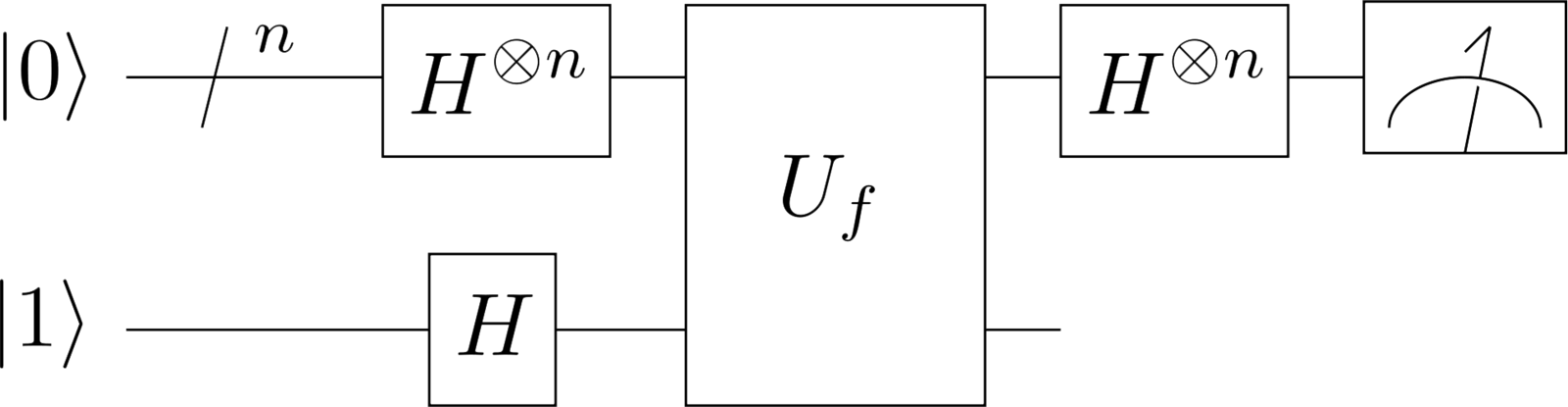
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle |0\oplus f(0)\rangle + |1\rangle |0\oplus f(1)\rangle + |0\rangle |1\oplus f(0)\rangle + |1\rangle |1\oplus f(1)\rangle)
→21(∣0⟩∣0⊕f(0)⟩+∣1⟩∣0⊕f(1)⟩+∣0⟩∣1⊕f(0)⟩+∣1⟩∣1⊕f(1)⟩)
\text{Reorganize the terms}
Reorganize the terms
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)(-1)^{f(0)}\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)(−1)f(0)√21(∣0⟩−∣1⟩)
Deutsch-Josza Algorithm
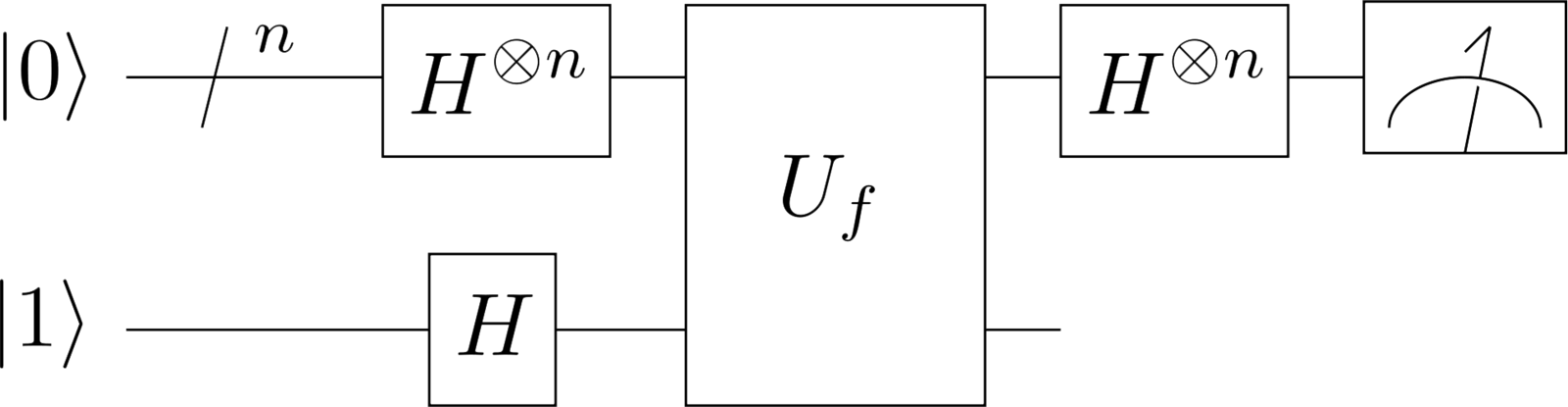
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle |0\oplus f(0)\rangle + |1\rangle |0\oplus f(1)\rangle + |0\rangle |1\oplus f(0)\rangle + |1\rangle |1\oplus f(1)\rangle)
→21(∣0⟩∣0⊕f(0)⟩+∣1⟩∣0⊕f(1)⟩+∣0⟩∣1⊕f(0)⟩+∣1⟩∣1⊕f(1)⟩)
\text{Discard the second qubit}
Discard the second qubit
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)(-1)^{f(0)}\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)(−1)f(0)√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)
Deutsch-Josza Algorithm
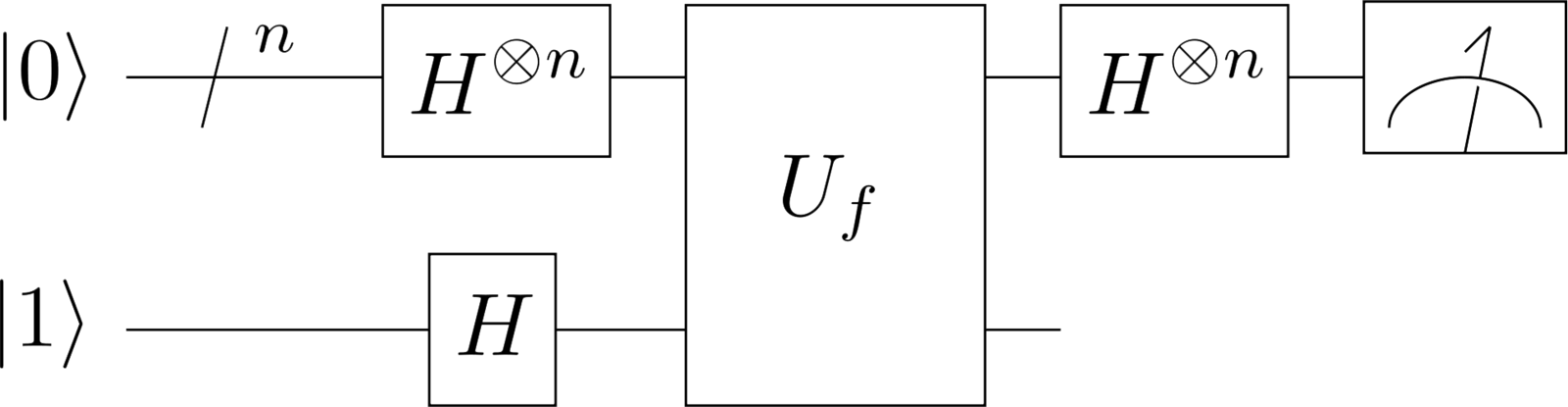
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle |0\oplus f(0)\rangle + |1\rangle |0\oplus f(1)\rangle + |0\rangle |1\oplus f(0)\rangle + |1\rangle |1\oplus f(1)\rangle)
→21(∣0⟩∣0⊕f(0)⟩+∣1⟩∣0⊕f(1)⟩+∣0⟩∣1⊕f(0)⟩+∣1⟩∣1⊕f(1)⟩)
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)(-1)^{f(0)}\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)(−1)f(0)√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle + |1\rangle + (-1)^{f(0)\oplus f(1)}|0\rangle - (-1)^{f(0)\oplus f(1)}|1\rangle)
→21(∣0⟩+∣1⟩+(−1)f(0)⊕f(1)∣0⟩−(−1)f(0)⊕f(1)∣1⟩)
\text{Apply the Hadamard gates}
Apply the Hadamard gates
Deutsch-Josza Algorithm
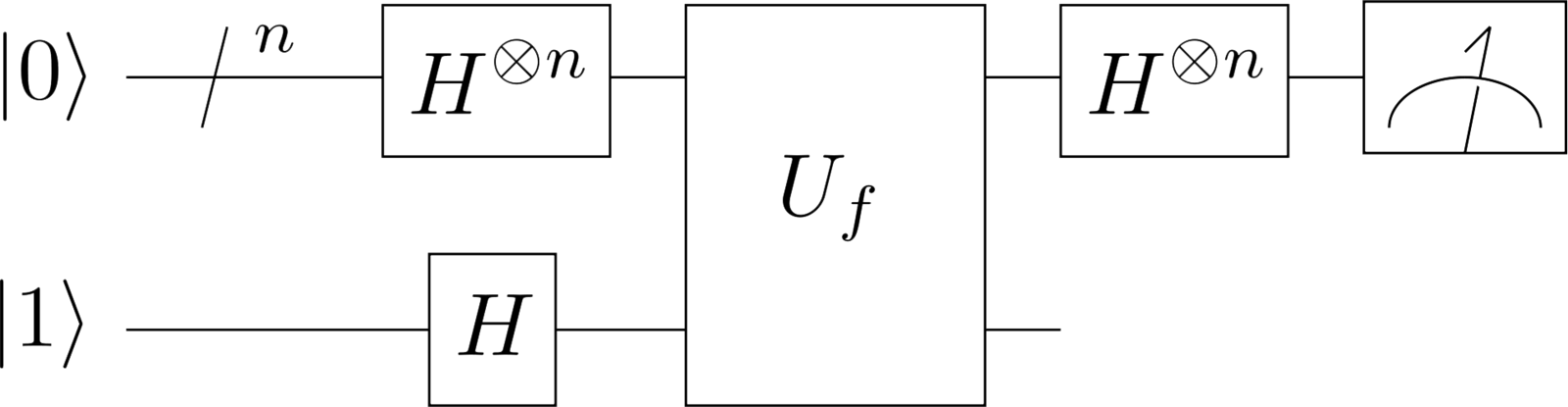
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle |0\oplus f(0)\rangle + |1\rangle |0\oplus f(1)\rangle + |0\rangle |1\oplus f(0)\rangle + |1\rangle |1\oplus f(1)\rangle)
→21(∣0⟩∣0⊕f(0)⟩+∣1⟩∣0⊕f(1)⟩+∣0⟩∣1⊕f(0)⟩+∣1⟩∣1⊕f(1)⟩)
\rightarrow \frac{1}{2}(|0\rangle + |1\rangle + (-1)^{f(0)\oplus f(1)}|0\rangle - (-1)^{f(0)\oplus f(1)}|1\rangle)
→21(∣0⟩+∣1⟩+(−1)f(0)⊕f(1)∣0⟩−(−1)f(0)⊕f(1)∣1⟩)
\rightarrow \frac{1}{2}[(1 + (-1)^{f(0)\oplus f(1)})|0\rangle + (1 - (-1)^{f(0)\oplus f(1)})|1\rangle]
→21[(1+(−1)f(0)⊕f(1))∣0⟩+(1−(−1)f(0)⊕f(1))∣1⟩]
\text{Reorganize the terms}
Reorganize the terms
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)(-1)^{f(0)}\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)(−1)f(0)√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)
Deutsch-Josza Algorithm
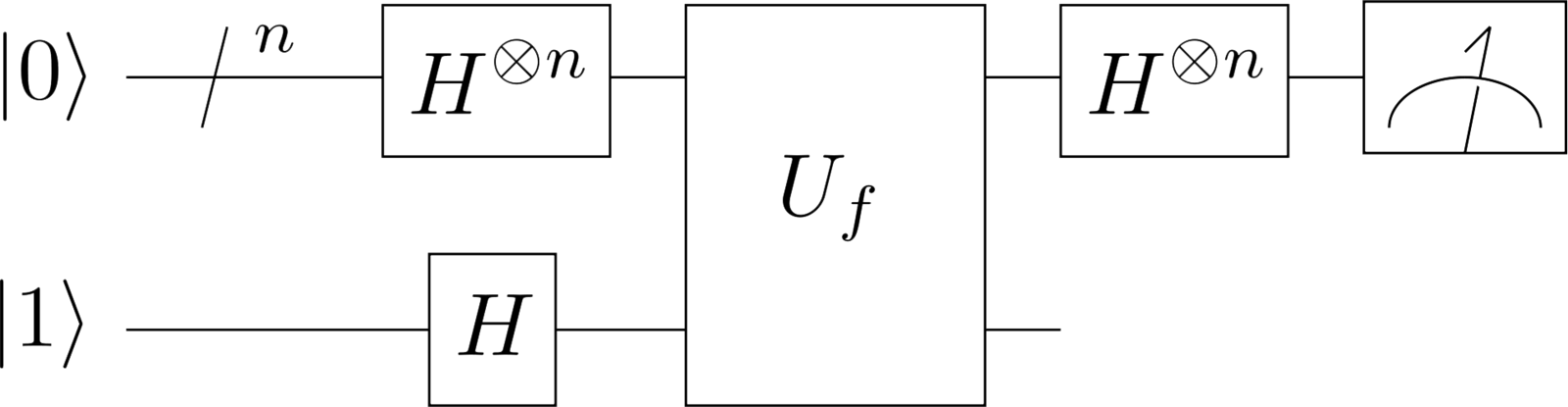
U_f |x\rangle |y\rangle = |x\rangle |y\oplus f(x)\rangle
Uf∣x⟩∣y⟩=∣x⟩∣y⊕f(x)⟩
|01\rangle \rightarrow \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
∣01⟩→√21(∣0⟩+∣1⟩)√21(∣0⟩−∣1⟩)
H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)
H∣0⟩=√21(∣0⟩+∣1⟩)
H|1\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
H∣1⟩=√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{2}(|0\rangle |0\oplus f(0)\rangle + |1\rangle |0\oplus f(1)\rangle + |0\rangle |1\oplus f(0)\rangle + |1\rangle |1\oplus f(1)\rangle)
→21(∣0⟩∣0⊕f(0)⟩+∣1⟩∣0⊕f(1)⟩+∣0⟩∣1⊕f(0)⟩+∣1⟩∣1⊕f(1)⟩)
\rightarrow \frac{1}{2}(|0\rangle + |1\rangle + (-1)^{f(0)\oplus f(1)}|0\rangle - (-1)^{f(0)\oplus f(1)}|1\rangle)
→21(∣0⟩+∣1⟩+(−1)f(0)⊕f(1)∣0⟩−(−1)f(0)⊕f(1)∣1⟩)
\rightarrow \frac{1}{2}[(1 + (-1)^{f(0)\oplus f(1)})|0\rangle + (1 - (-1)^{f(0)\oplus f(1)})|1\rangle]
→21[(1+(−1)f(0)⊕f(1))∣0⟩+(1−(−1)f(0)⊕f(1))∣1⟩]
\text{if measured } |0\rangle \text{, then } f \text{ is constant, and balanced otherwise}
if measured ∣0⟩, then f is constant, and balanced otherwise
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)(-1)^{f(0)}\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)(−1)f(0)√21(∣0⟩−∣1⟩)
\rightarrow \frac{1}{\sqrt{2}}(|0\rangle + (-1)^{f(0)\oplus f(1)}|1\rangle)
→√21(∣0⟩+(−1)f(0)⊕f(1)∣1⟩)
How do you find a needle
in a haystack?
How do you find a needle
in a haystack?

Unstructured Search
Classical
T(N) = \mathcal{O}(N)
T(N)=O(N)
Quantum
T(N) = \mathcal{O}(\sqrt{N})
T(N)=O(√N)
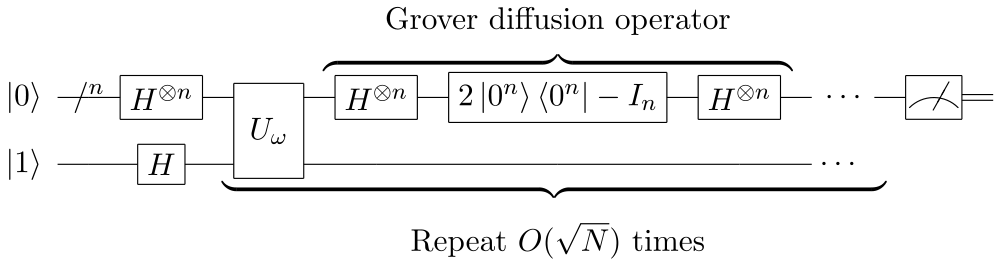
Unstructured Search
Classical
T(N) = \mathcal{O}(N)
T(N)=O(N)
Quantum
T(N) = \mathcal{O}(\sqrt{N})
T(N)=O(√N)
Our discussion of qubit has been abstract
Our discussion of qubit has been abstract
How can we realize a physical qubit?
p
e-
|0\rangle
∣0⟩
Hydrogen
p
e-
|1\rangle
∣1⟩
Hydrogen
p
e-
e-
|\psi\rangle
∣ψ⟩
Hydrogen
Particle in a Box
m
m
0
0
l
l
|\psi (t)\rangle = \text{ }?
∣ψ(t)⟩= ?
Schrödinger Equation
i\hbar\frac{d}{dt}|\psi\rangle = \hat{H} |\psi\rangle
iℏdtd∣ψ⟩=H^∣ψ⟩
Schrödinger Equation
i\hbar\frac{d}{dt}|\psi\rangle = \hat{H} |\psi\rangle
iℏdtd∣ψ⟩=H^∣ψ⟩
|\psi (t)\rangle = e^{-i\frac{\hat{H}}{\hbar}t} |\psi (0)\rangle
∣ψ(t)⟩=e−iℏH^t∣ψ(0)⟩
\text{General solution for differential equation}
General solution for differential equation
General Solution
|\psi (t)\rangle = e^{-i\frac{\hat{H}}{\hbar}t} |\psi (0)\rangle
∣ψ(t)⟩=e−iℏH^t∣ψ(0)⟩
General Solution
|\psi (t)\rangle = e^{-i\frac{\hat{H}}{\hbar}t} |\psi (0)\rangle
∣ψ(t)⟩=e−iℏH^t∣ψ(0)⟩
|\psi (0)\rangle = \sum_n c_n|\psi_n \rangle
∣ψ(0)⟩=∑ncn∣ψn⟩
\text{WLOG, initial state is a superposition of arbitrary basis states}
WLOG, initial state is a superposition of arbitrary basis states
General Solution
|\psi (t)\rangle = e^{-i\frac{\hat{H}}{\hbar}t} |\psi (0)\rangle
∣ψ(t)⟩=e−iℏH^t∣ψ(0)⟩
|\psi (0)\rangle = \sum_n c_n|\psi_n \rangle
∣ψ(0)⟩=∑ncn∣ψn⟩
|\psi (t)\rangle = \sum_n c_n e^{-iE_n t/\hbar}|\psi_n \rangle
∣ψ(t)⟩=∑ncne−iEnt/ℏ∣ψn⟩
\text{Plug the second equation into the first equation}
Plug the second equation into the first equation
Particle in a Box
|\psi_n\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{n\pi}{l}x)}
∣ψn⟩=√l2sin(lnπx)
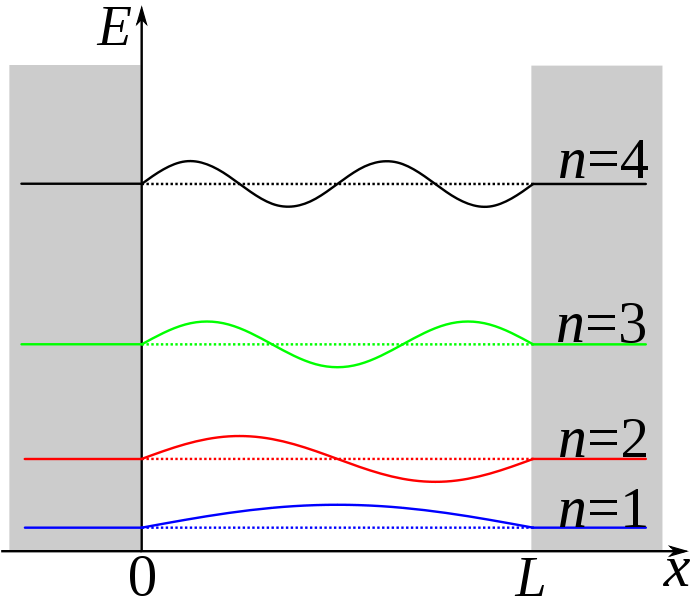
E_n = \frac{n^2\pi^2 \hbar^2}{2ml^2}
En=2ml2n2π2ℏ2
Particle in a Box
|0\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{\pi}{l}x)}
∣0⟩=√l2sin(lπx)
E_1 = \frac{\pi^2 \hbar^2}{2ml^2}
E1=2ml2π2ℏ2
|1\rangle = \sqrt{\frac{2}{l}}\sin{(\frac{2\pi}{l}x)}
∣1⟩=√l2sin(l2πx)
E_2 = \frac{2\pi^2 \hbar^2}{ml^2}
E2=ml22π2ℏ2
Particle in a Box
|\psi(0)\rangle = \alpha |0\rangle + \beta |1\rangle
∣ψ(0)⟩=α∣0⟩+β∣1⟩
|\psi (t)\rangle = \alpha |0\rangle e^{-\frac{iE_1 t}{\hbar}} + \beta |1\rangle e^{-\frac{iE_2 t}{\hbar}}
∣ψ(t)⟩=α∣0⟩e−ℏiE1t+β∣1⟩e−ℏiE2t
|\psi (t)\rangle = e^{-\frac{iE_1 t}{\hbar}} (\alpha |0\rangle + \beta |1\rangle e^{-\frac{i(\Delta E)t}{\hbar}})
∣ψ(t)⟩=e−ℏiE1t(α∣0⟩+β∣1⟩e−ℏi(ΔE)t)
\Delta E \approx 10 \text{ eV}
ΔE≈10 eV
\nu = \frac{\Delta E}{h} = 2.5 \times 10^{15} \text{ Hz}
ν=hΔE=2.5×1015 Hz
\therefore \text{Atomic qubits are controlled optically via interactions with light pulses}
∴Atomic qubits are controlled optically via interactions with light pulses
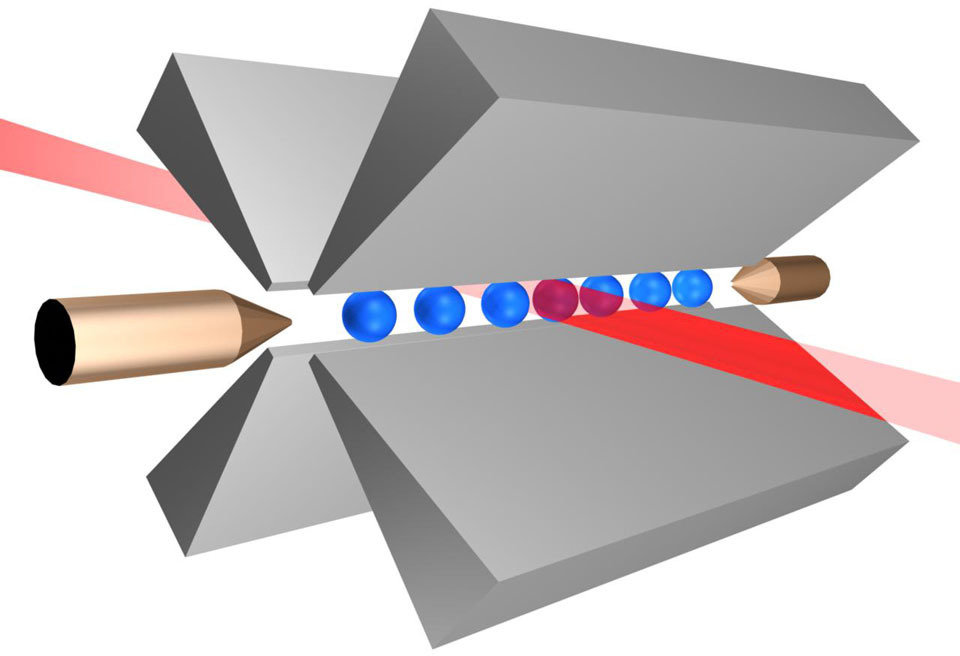
State-of-the-art
Trapped Atomic Ion
- very long (>>1s) memory
- <20 coherent qubits
- engineering needed
- connection reconfigurable
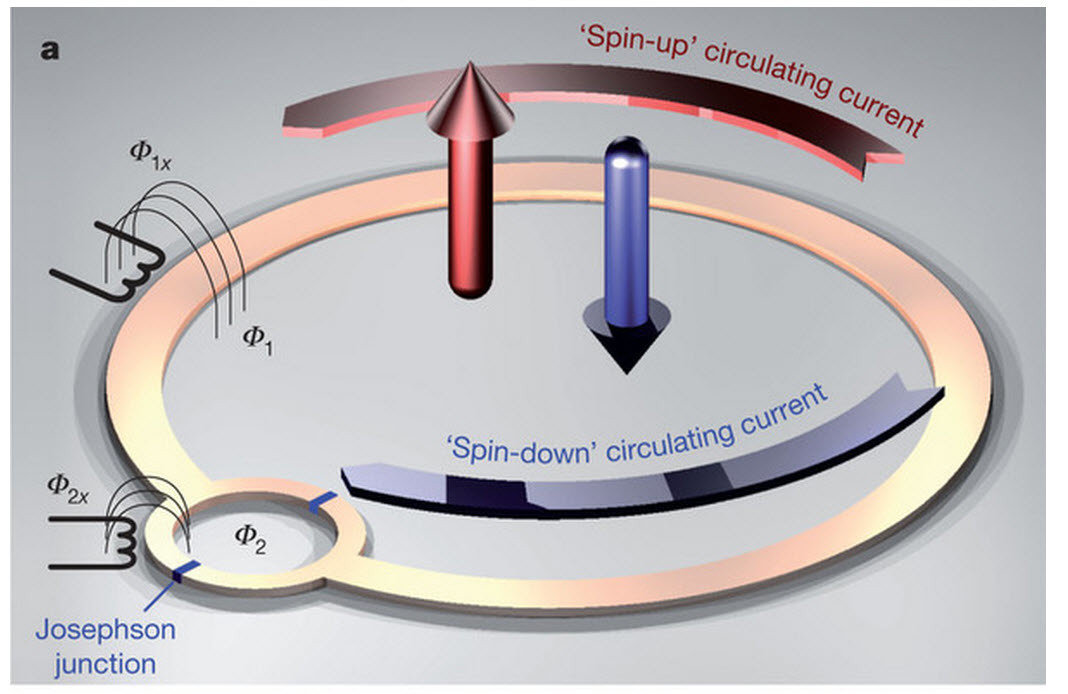
Superconducting Loop
- short (10^-6s) memory
- <10 coherent qubits
- printable circuits and VLSI
- not reconfigurable
Q & A
Quantum Physics: INAG 110
By seanbae
Quantum Physics: INAG 110
- 883



