Algorithm Sort
Sean Chou
Sort type
- Bubble Sort
- Insertion Sort
- Selection Sort
- Quick Sort
- Heap Sort
- Merge Sort
Complexity Table
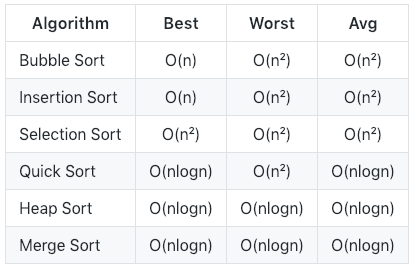
Bubble Sort
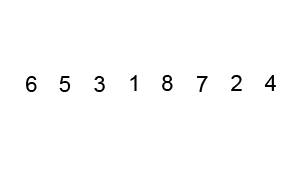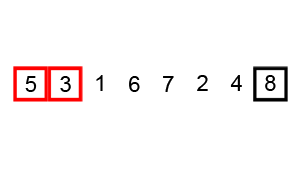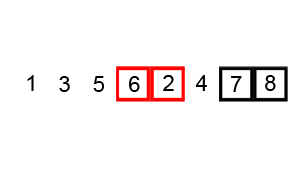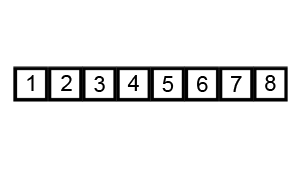
兩兩互相比較,每回合將最大值升到最高格子,像氣泡往上升一樣
function bubblesort(array) {
var n = array.length;
for (var i = 0; i < n-1; i++) {
for (var j = 0; j<n-i-1; j++) {
if(array[j] > array[j+1]) {
var temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
return array;
}Insertion Sort
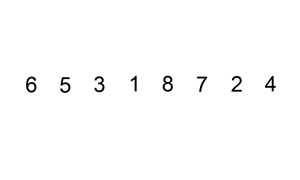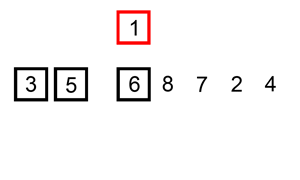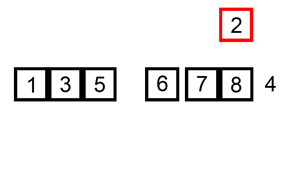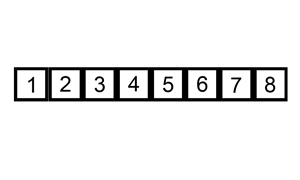
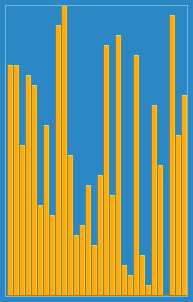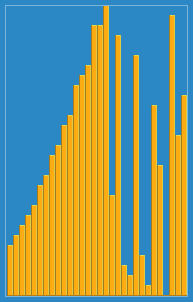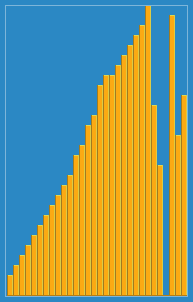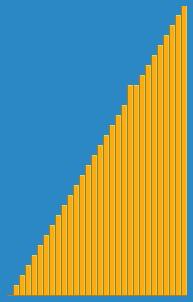
把第i筆資料插入前面(i-1)筆已經排序好的陣列中
function insertionsort(array) {
for (var i = 1; i < array.length; i++) {
// 從目前的第 i 個(target) 往前找到第一個
// 把這個 target 推到合適的位置
for (var j = i; j > 0; j--) {
if(array[j] < array[j-1]) {
var temp = array[j];
array[j] = array[j-1];
array[j-1] = temp;
}
}
}
return array;
}Selection Sort
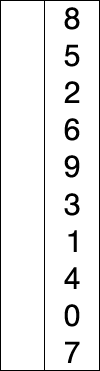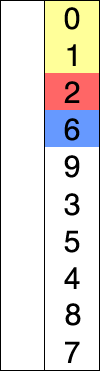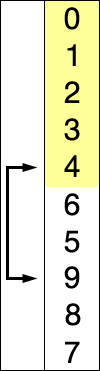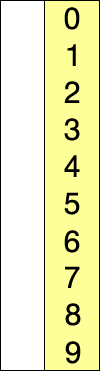

每次從第 i 到 n 筆中挑出最小值,和前面第 i 筆交換
function selectionsort(array) {
var min = 0;
var idx = 0;
for (var i = 0; i < array.length; i++) {
// 要交換的目標 = idx
idx = i;
min = array[i];
// 從當前的 i 往後找比 i 小數值定為 idx
for (var j = i+1; j < array.length; j++) {
if(array[j] < min ){
min = array[j];
idx = j;
}
}
// 將這回合找到最小的 idx 換到 i 的位置
_swap(i, idx, array);
}
return array;
}Quick Sort
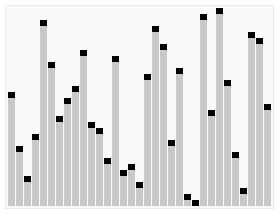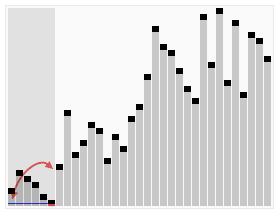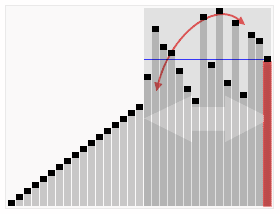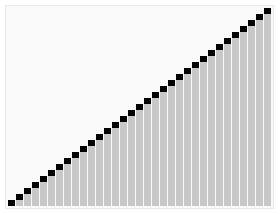
- 隨意找出一個 pivot (p)
- 每回合比較把小的放 p 左邊,大的放 p 右邊
- 做完之後分兩邊繼續做 (divide and conquer)
Partition
區分 pivot 兩邊數值的方法叫做 partition
Partition 作法一
1. 每回合都從兩邊去各自找第一個大於pivot值 & 小於pivot值的位置
2. 將這兩個位置互換
3. 繼續往第二個值去做,做到兩邊重疊後就停止
4. 把 pivot 換到中間
const i = left;
const j = right;
// 先將第一個當成pivot
const pivot = array[i];
const length = array.length;
while(true) {
// 從頭(left)開始找第一個大於pivot值的位置i
while(i < length-1 && array[i] <= pivot) {
i++;
}
// 從尾(right)開始找第一個小於pivot值的位置j
while(j >= left && array[j] > pivot) {
j--;
}
// 假如i超過j了就要結束這回合
if(i>=j) {
break;
}
// 移動i,j的元素
_swap(i, j, array);
}
// 最後將pivot換到中間
_swap(left, j, array);Partition 作法二
1. i 初始為 -1 的位置,每回合都從前面開始找第一個大於pivot值的位置 j
2. 將 i 的位置往前一格並且與目前這個 j 位置互換
3. j 繼續往第二個值去做,一找到大於pivot值的位置就重複第二步驟
4. 整個數列做完後,把 pivot 換到中間
const pivot = arr[end];
let i = start - 1;
for (let j = start; j < end; j++) {
if (arr[j] < pivot) {
i++;
_swap(i, j, arr);
}
}
i++;
_swap(i, end, arr);
return i;Heap Sort
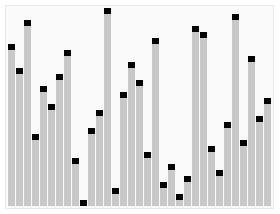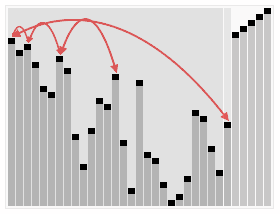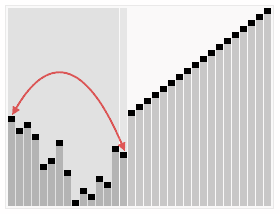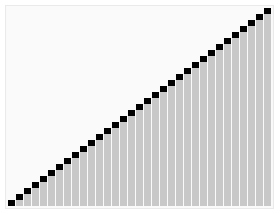
- 轉為 Heap Tree (Complete Binary Tree)
- 再轉換為 Max Heap
- 把 root 刪除,並把最後一個放到 root
- 接著剩下的繼續做
- Max heap
- 刪除 root
- 最後一個搬到 root
Heap Tree (Complete Binary Tree)
每個節點最多有兩個子節點 (Binary Tree)
子節點有左右之分 (Binary Tree)
除了最後一階層之外的階層,都必預完全有左與右節點 (Complete Binary Tree)
Code
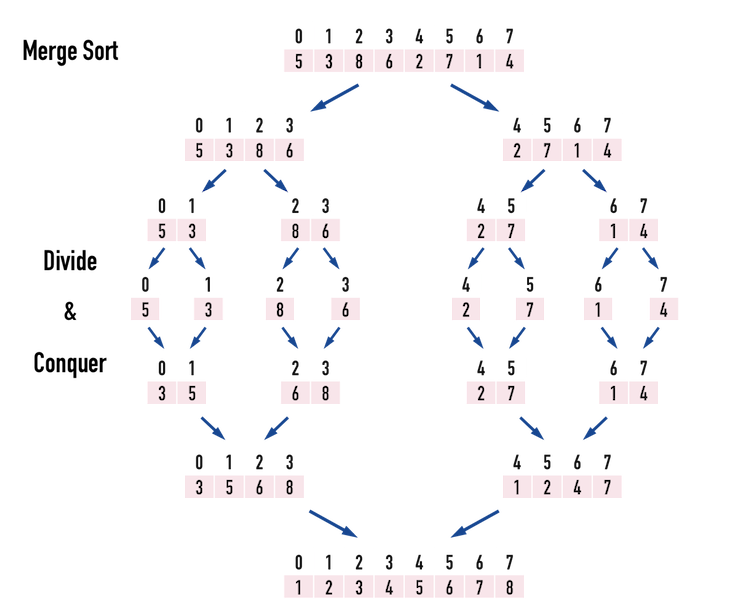
Merge Sort
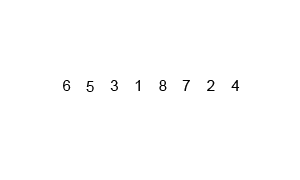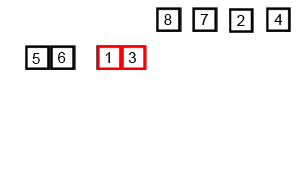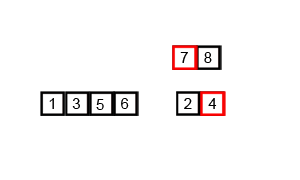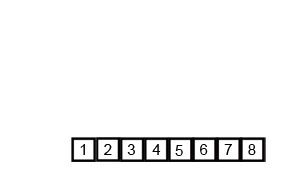
Divide and conquer
把目標切成子問題,處理過後再將結果合併。
1. 將數列不斷的對半切
2. 從最小問題比較大小並排序
3. 合併排序好的子數列
const mergesort = {
sort: (array) => {
if (array.length <= 1) {
return array;
}
const mid = Math.floor(array.length / 2);
const leftArray = array.slice(0, mid);
const rightArray = array.slice(mid, array.length);
const leftSortedArray = mergesort.sort(leftArray);
const rightSortedArray = mergesort.sort(rightArray);
return mergesort.merge(leftSortedArray, rightSortedArray);
},
merge: (leftArray, rightArray) => {
let sortedArray = [];
// 兩兩從陣列拿第一個比較出小的放入新的陣列
while (leftArray.length && rightArray.length) {
const elm = leftArray[0] < rightArray[0] ?
leftArray.shift() : rightArray.shift();
sortedArray.push(elm);
}
// 如果左右兩邊數量不一樣,做完之後再把多出來的(比較大)加到最後
if (leftArray.length) {
sortedArray = sortedArray.concat(leftArray);
}
if (rightArray.length) {
sortedArray = sortedArray.concat(rightArray);
}
return sortedArray;
}
};Reference
-
https://medium.com/@realdennis/javascript-%E5%BE%9Earray%E7%9A%84sort%E6%96%B9%E6%B3%95-%E8%81%8A%E5%88%B0%E5%90%84%E5%AE%B6%E7%80%8F%E8%A6%BD%E5%99%A8%E7%9A%84%E5%AF%A6%E4%BD%9C%E7%AE%97%E6%B3%95-c23a335b1b80
Algorithm Sort
By Sean Chou
Algorithm Sort
- 237

