DAT259: Deep Learning
An Exploratory Data Analysis of Uncertainty Estimation in Neural Networks
Sean Meling Murray, 2018
Roadmap
- What is the theory?
- Which tools have we used?
- What have we found out?
- What is the problem?
Are You Sure You Are Making the Right Decision?
Deep learning models have been wildly successful at a range of predictive tasks, but they have lacked a principled way of expressing uncertainty about their predictions.
Uncertainty approximations are critical in many practical applications, such as self-driving cars or AI-assisted diagnostic medicine.
These papers introduce a mathematically principled approach to uncertainty estimation in different kinds of neural networks
Applies MC dropout to a binary diagnostic setting in health care
Gal et. al. (2016)
Leibig et. al. (2017)
Monte Carlo Dropout
Is the approximated uncertainty obtained from MC dropout in convolutional neural networks a useful quantity for a multi-class setting?
Problem statement
Additionally, we examine if there is any information to be gained from establishing a connection between the uncertainty and the runner-up prediction.
Neural Networks
z(l) = W(l)a(l-1) + b(l)
a(1) = x
\text{for } l=2, ..., L \text{ do}:
a(l) = \sigma[z(l)]
\text{end}
\hat{y} = a(L)
Neural networks are essentially a cascade of
matrix multiplications followed by non-linear transformations.
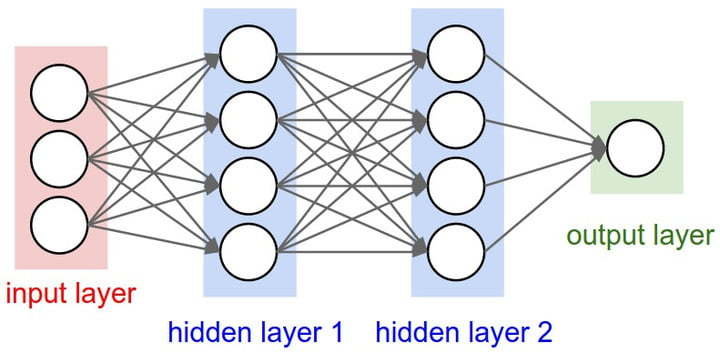
Image source: https://www.digitaltrends.com/cool-tech/what-is-an-artificial-neural-network/
Convolutional Neural Networks
S(k, i, j) = \sum_{l,m,n} I(l, i + m, j + n) K(l,k,m,n)
CNNs are a specialized kind of network that take advantage of the grid-like topology of image and time-series data.
Feature map
Image,input
Kernel, filter, feature, receptive field
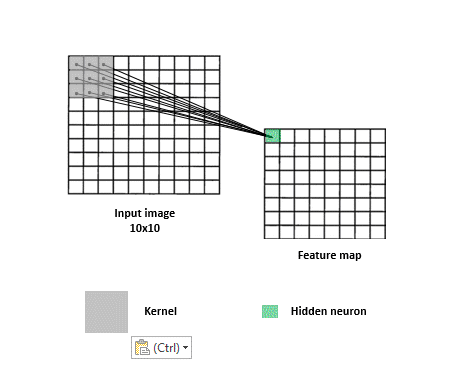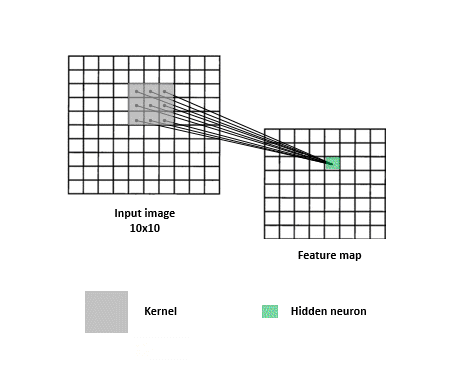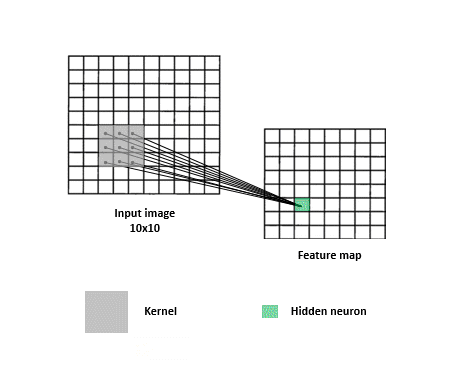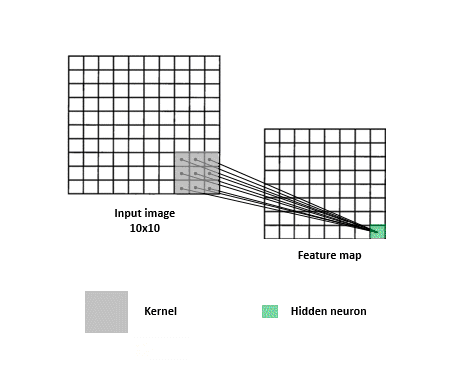
2D map that indicates the presence of a feature in the input
Dropout
Dropout is a regularisation technique used to prevent overfitting in neural networks.
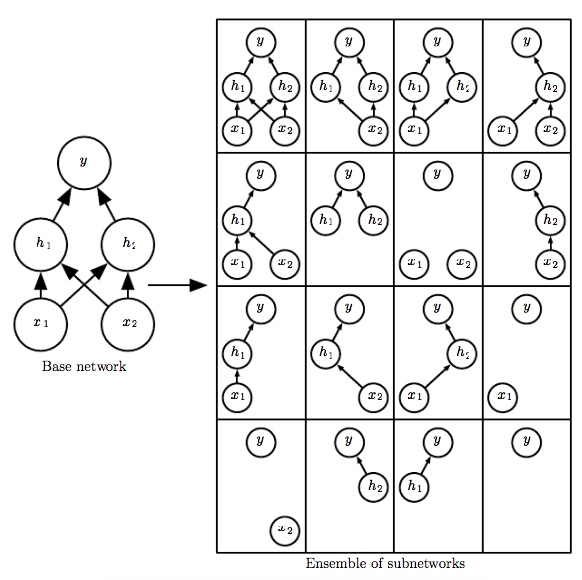
Image source: deeplearningbook.org
Temporarily removes all connections from a node to the rest of the network at training time.
At test time dropout is turned off and weights are scaled to match expected output, can be viewed as model averaging.
Monte Carlo Dropout
- An image is fed forward through the network T times (we use T=100). Each time the image is fed through is called a stochastic forward pass (SFP).
- Each SFP pass returns a slightly different vectors of class predictions.
- Finally we calculate the standard deviation in class predictions over all forward passes. This is our estimated uncertainty.
- To make a prediction we average the 100 vectors. The class corresponding to the largest element in the resulting vector is our final prediction.
- Leaving dropout on at test time turns a NN into a Bayesian NN. This allows us to obtain principled uncertainty estimates.
Simple LeNet
architecture
- Easy to see what's going on.
- Trains quickly, easy to experiment.
- Same baseline model as used by Gal et. al. (2016).
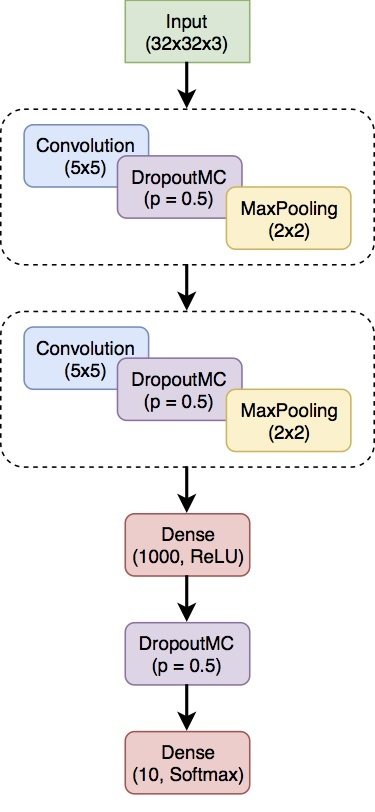
Experimental setup
- Image classification: Predict which of the 10 classes an image in the CIFAR-10 dataset belongs to.
- 50.000 training images, 10.000 test images.
- At test time, average T = 100 SFP and calculate predictive mean and standard deviation, check if we predicted correctly.
Results
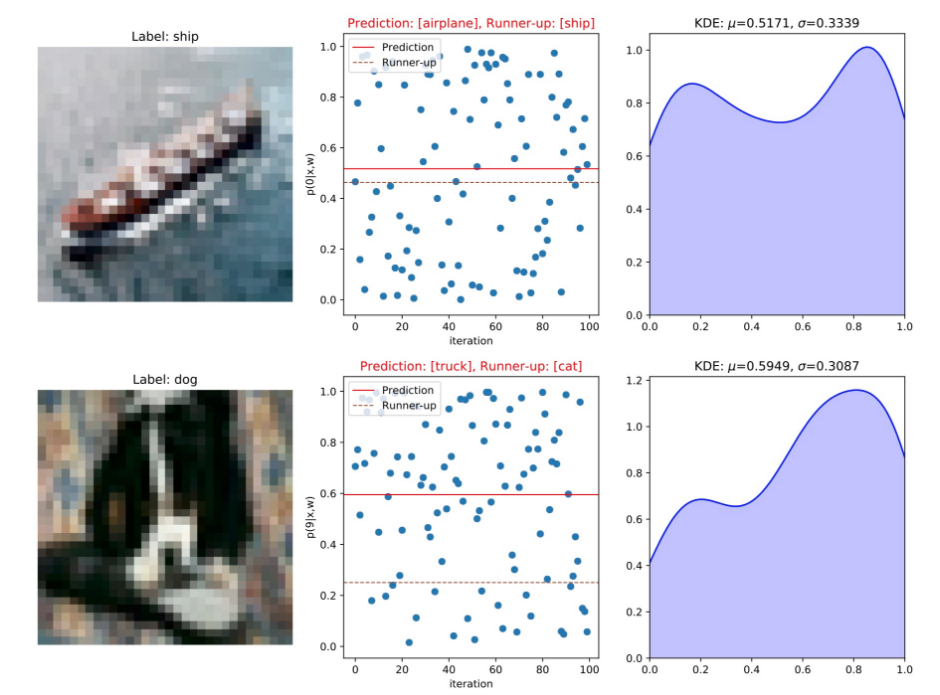
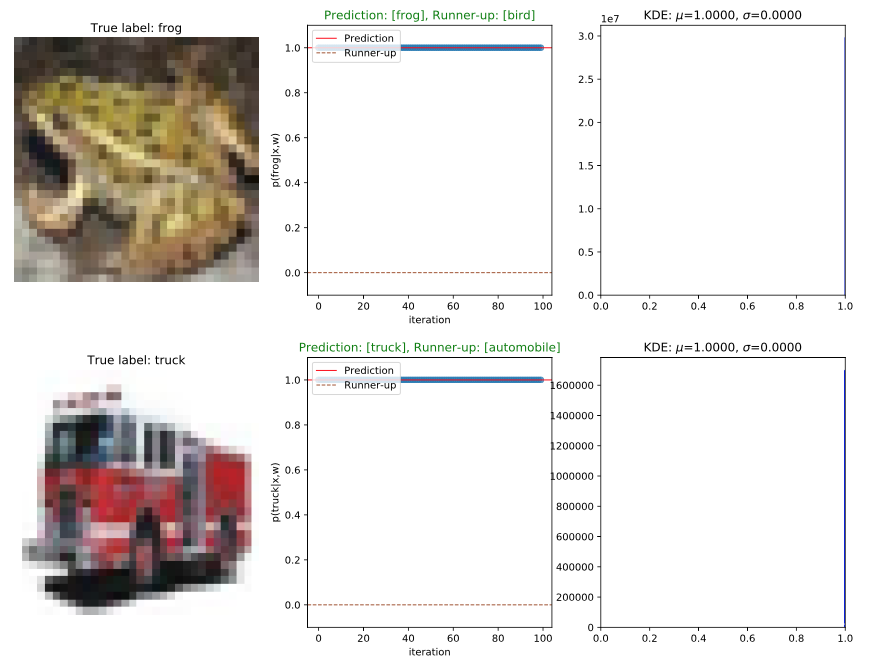
Results
| Correct | n | uncertainty |
|---|---|---|
| 0 | 2084 | 0.1802 |
| 1 | 7916 | 0.1021 |
(Note: Validation accuracy was 76.14%.)
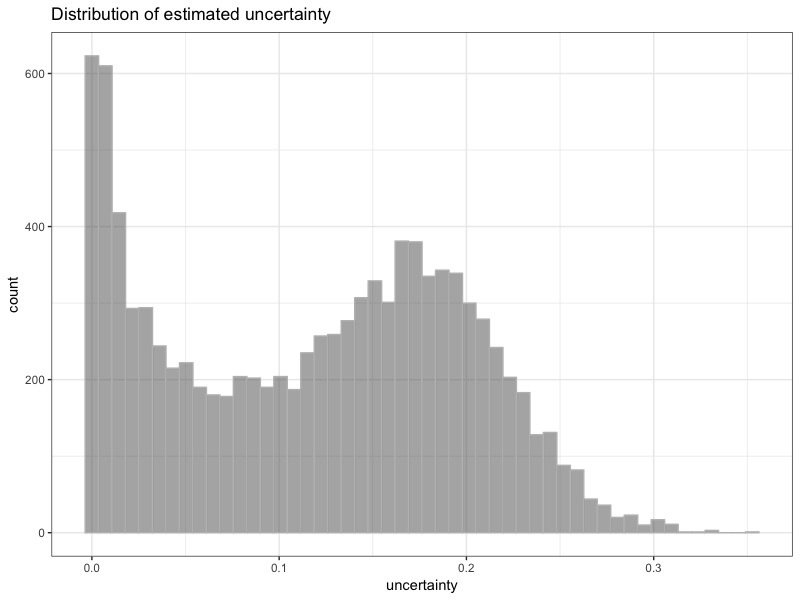
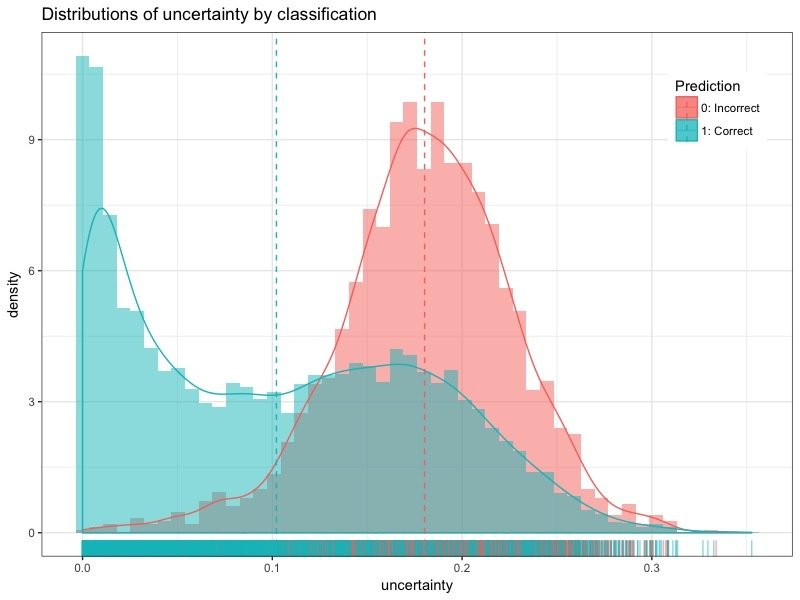
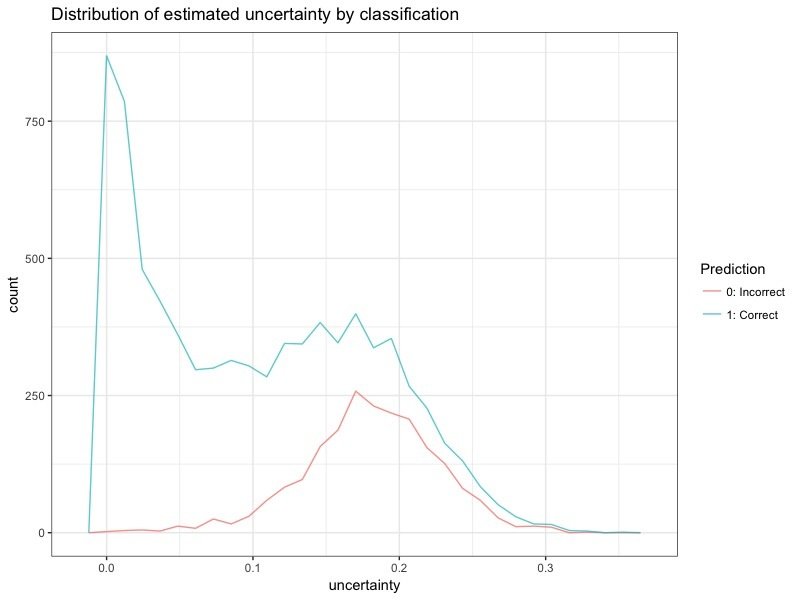
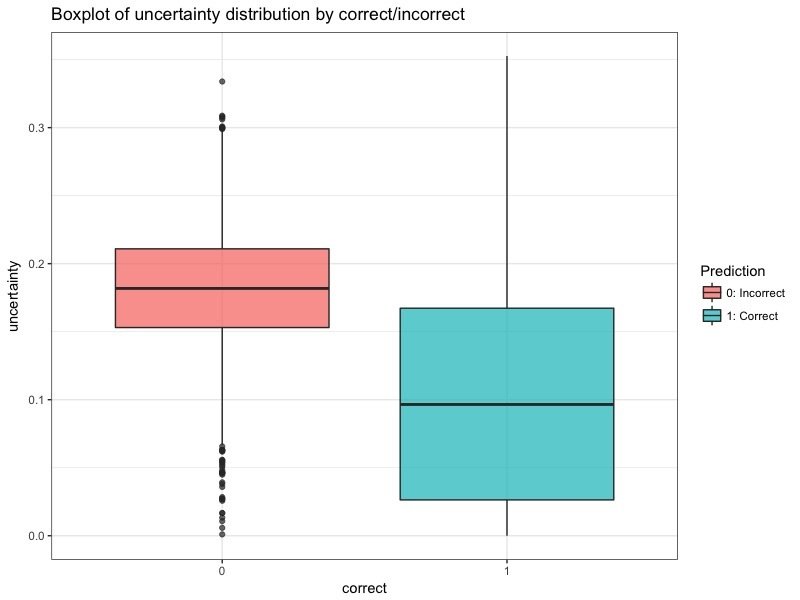
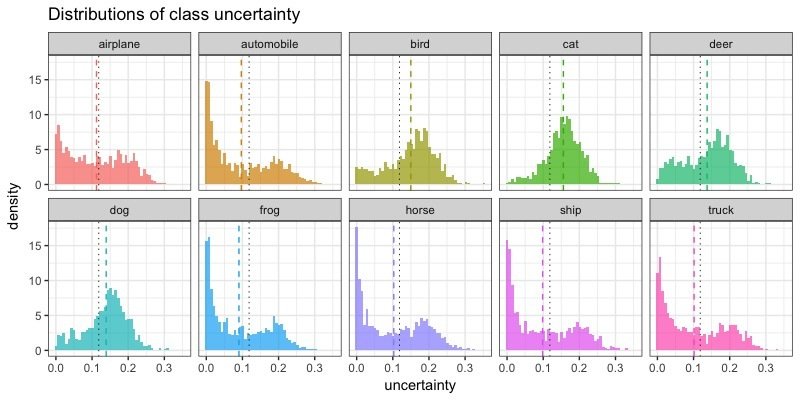
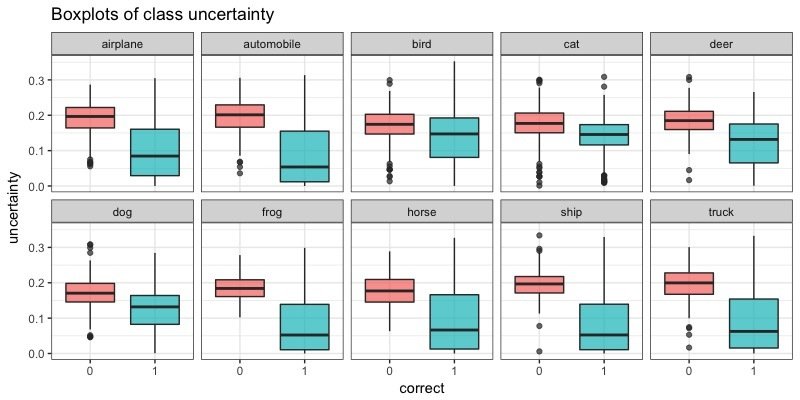
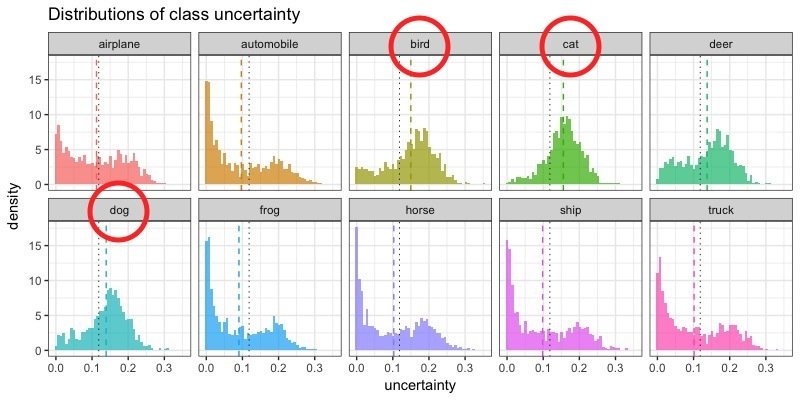
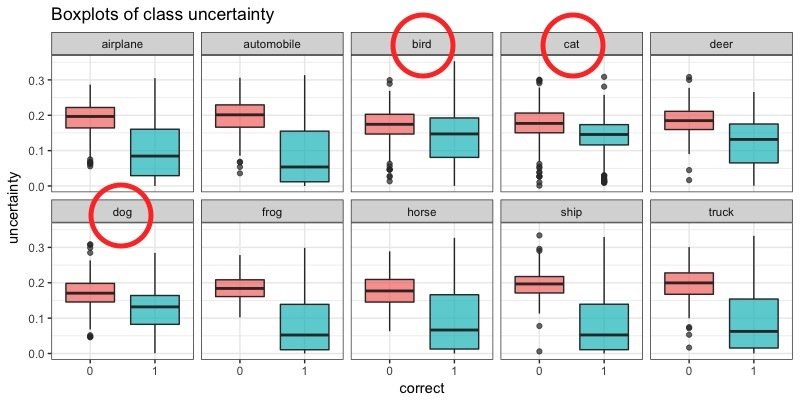
Uncertainty distributions
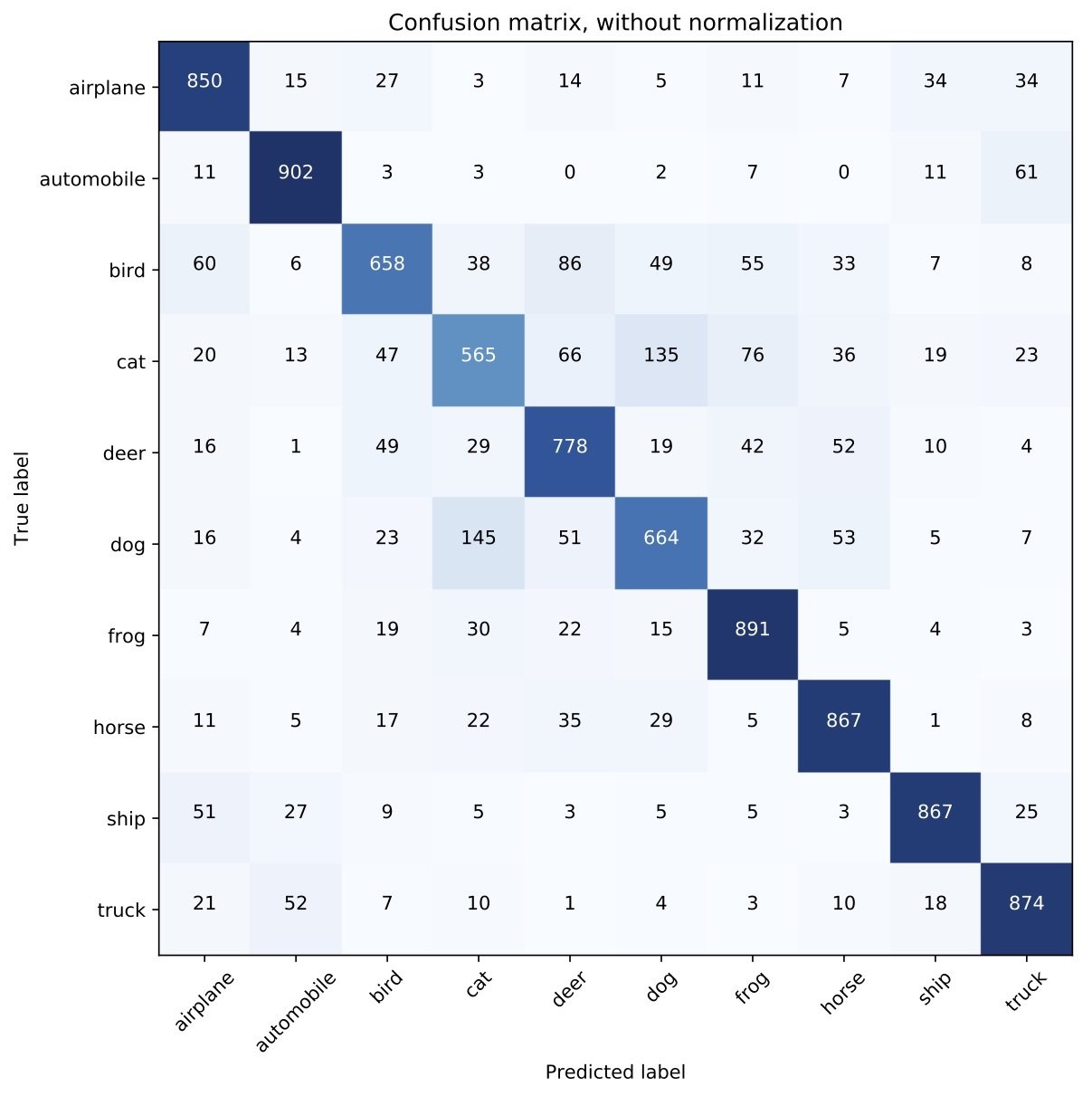
Confusion matrix
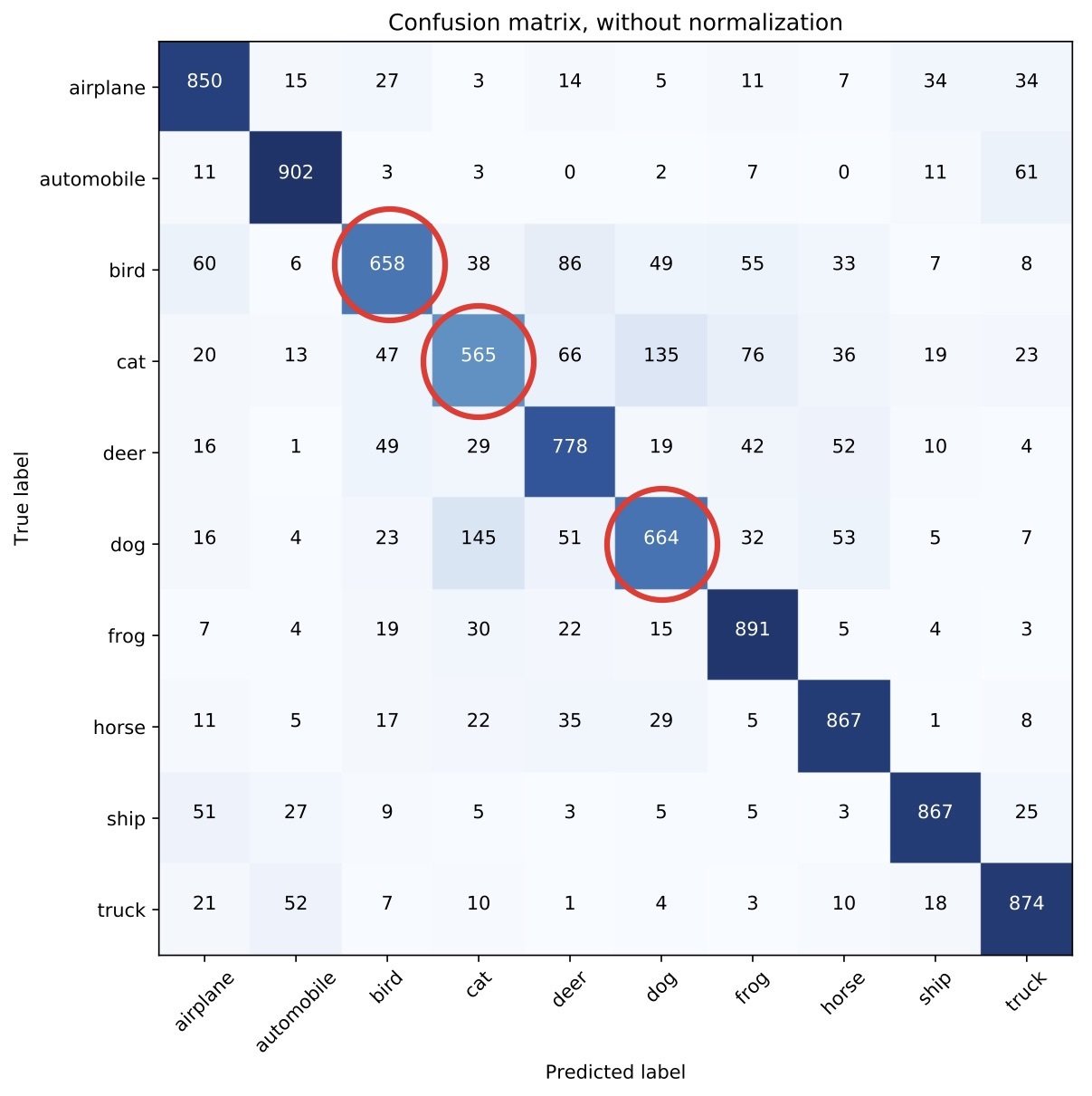
Class-specific uncertainty
Uncertainty and predictions
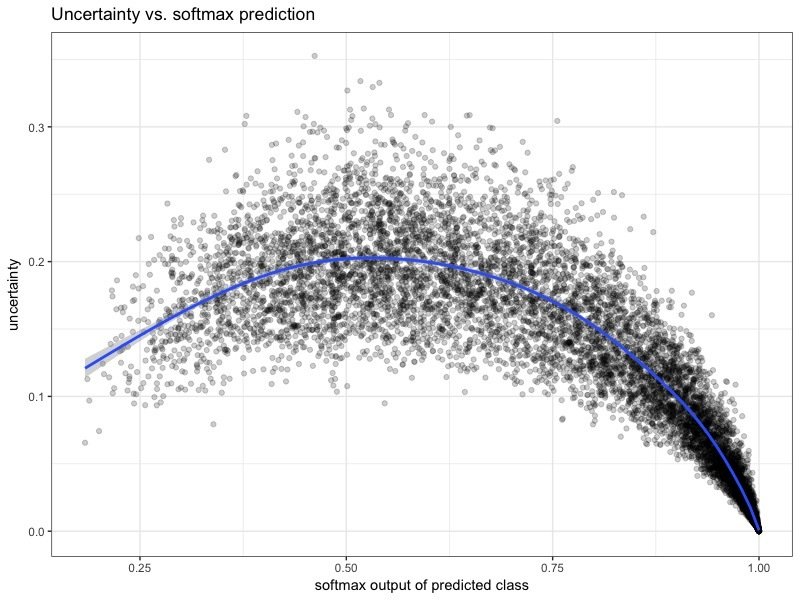
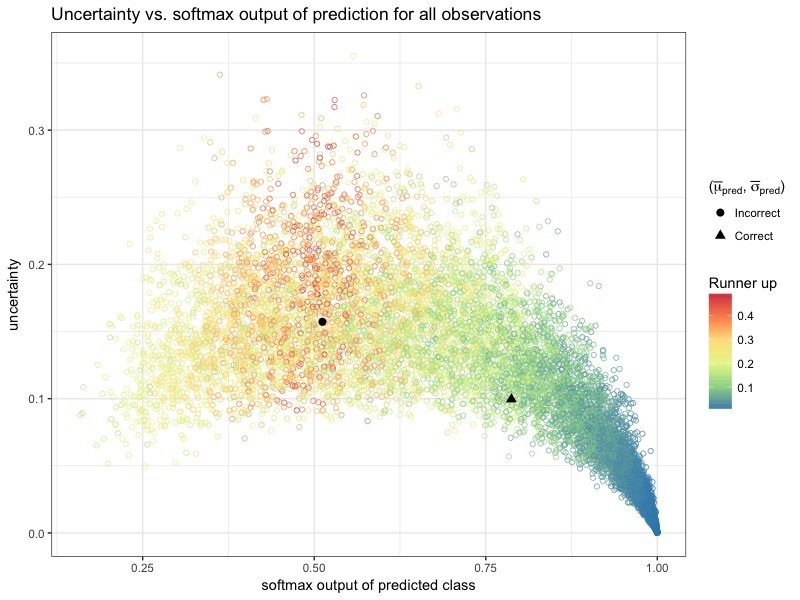
Can we learn anything from the runner up predictions?
| Correct | n |
|---|---|
| 0 | 921 |
| 1 | 9071 |
If we had used runner up predictions in the cases where the model misclassifies:
Accuracy goes from
79.16 \% \rightarrow 90.71 \%
Suggests that the runner up prediction contains useful information.
Can we learn anything from the runner up predictions?
| Runner up correct |
n |
prob1 |
prob2 |
uncertainty |
|---|---|---|---|---|
| 0 | 921 | 0.5085 | 0.2156 | 0.1780 |
| 1 | 1163 | 0.5740 | 0.2644 | 0.1819 |
| Correct | n |
|---|---|
| 0 | 2084 |
| 1 | 7916 |
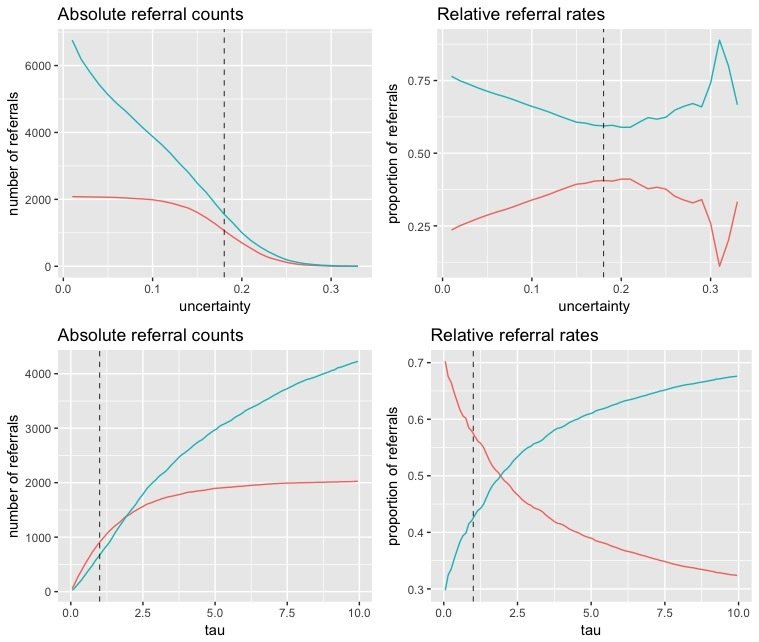
How can we make use of approximated uncertainty?
Leibig et. al. (2017) explore MC dropout in a binary setting:
Define a referral threshold based on uncertainty, and measure accuracy of predictions after referral to a human expert.
In a multi-class setting, we propose incorporating the runner up prediction for use in referrals.
Can we leverage the runner up predictions?
\tau = \dfrac{\hat{\mu}_k - \hat{\mu}_j}{\hat{\sigma}_k}
ratio of two different measures of uncertainty
softmax prediction
softmax runner up
uncertainty associated with prediction
0
1
Infinity
Idea:
\tau \leq 1
Can we leverage the runner up predictions?
| referral criteria | correct | incorrect |
|---|---|---|
| uncertainty >= .18 | 1556 | 1064 |
| tau <= 1 | 673 | 907 |
false negatives
Summary
- Approximated uncertainty values mirror the confusion matrix.
- Approximated uncertainty is higher for incorrectly classified images.
- Empirically show that could be a useful quantity for reducing false negatives in referrals in a multi-class setting.
- MC dropout seems to capture a useful measure for quantifying uncertainty. Perhaps best suited for a binary classification setting?
\tau
Trained using fastai framework
- Pros: Implementation of best practices and novel/overlooked methods (learning rate finder, annealing schedules, differential learning rates, adaptive max/avg. pooling, test-time augmentation, etc.).
- Pros: Simple to use, easy to train high-performing, state-of-the-art models quickly.
- Dedicated to making deep learning more accessible through MOOC and fastai module built on PyTorch.
Trained using fastai framework
- Cons: Difficult to do non-standard experiments.
Thank you!
DAT259: Deep Learning
By Sean Meling Murray
DAT259: Deep Learning
Project presentation for DAT259: Deep Learning course at Western University of Applied Science.
