Machine Learning
Sebastian David Ariza Coll
Ing. Universidad del Norte
Hands-on Machine Learning with Scikit-Learn & TensorFlow, by Aurelien Geron.
Esta presentación contiene material de los siguientes recursos:
¿Qué es Machine Learning?
Industria
¿Por qué usar ML?
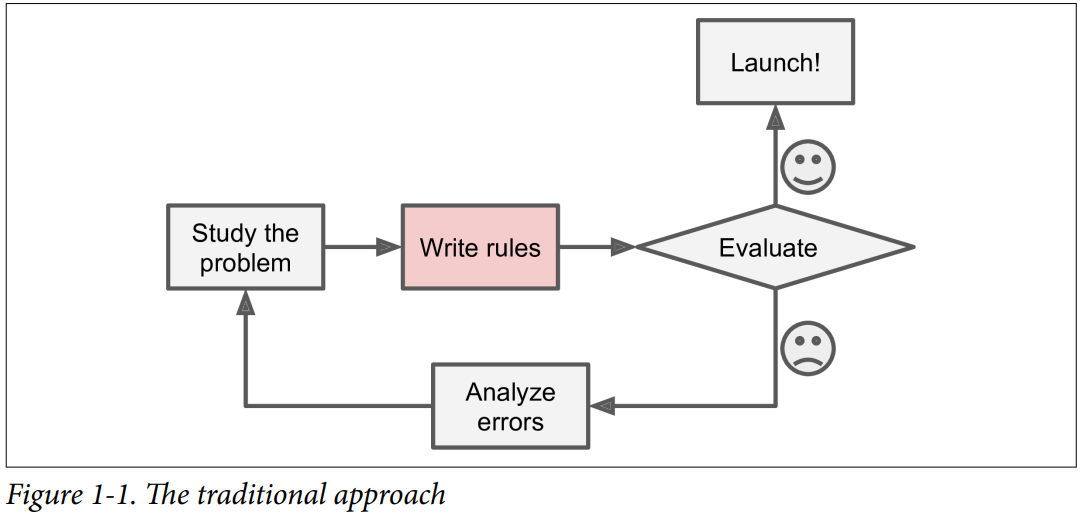
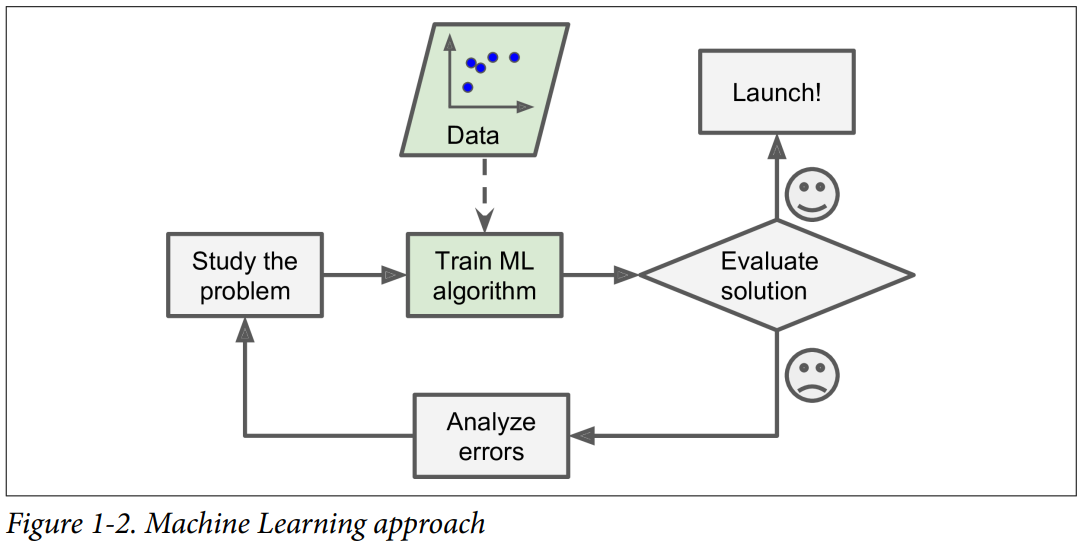
Actualmente, muchas de las aplicaciones que usan ML fueron creadas usando reglas "hand-code" (Aprendizaje humano)
El ML puede ayudar a los humanos a aprender
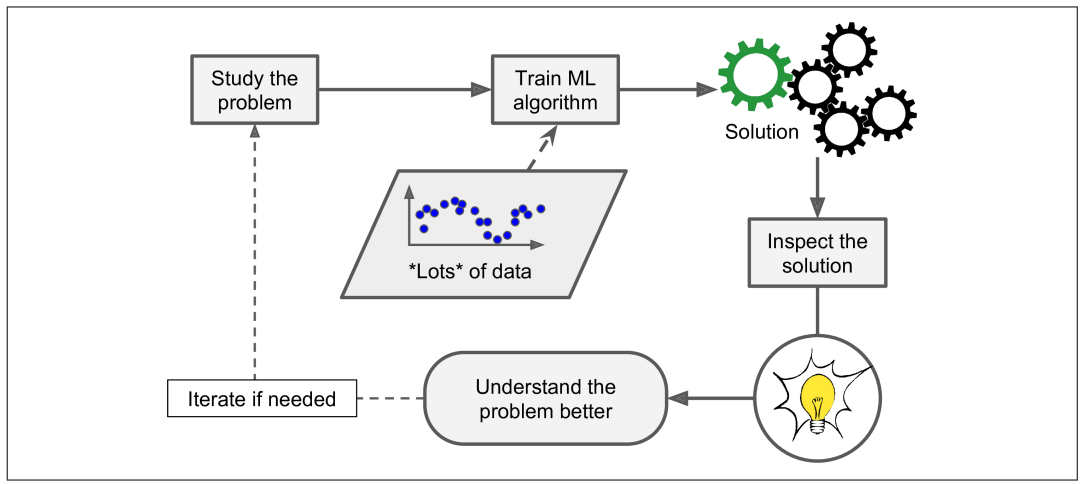
En resumen...
- Problemas para los cuales las soluciones existentes requieren mucho ajuste manual o largas listas de reglas: un algoritmo de aprendizaje automático a menudo puede simplificar el código y funcionar mejor.
- Problemas complejos para los que no existe una buena solución utilizando un método tradicional: las mejores técnicas de Machine Learning pueden encontrar una solución.
- Entornos fluctuantes: un sistema de Machine Learning puede adaptarse a nuevos datos.
- Obtener información sobre problemas complejos y grandes cantidades de datos.
Background
EDA
Exploratory Data Analysis
Análisis exploratorio de los datos
Tipos de ML
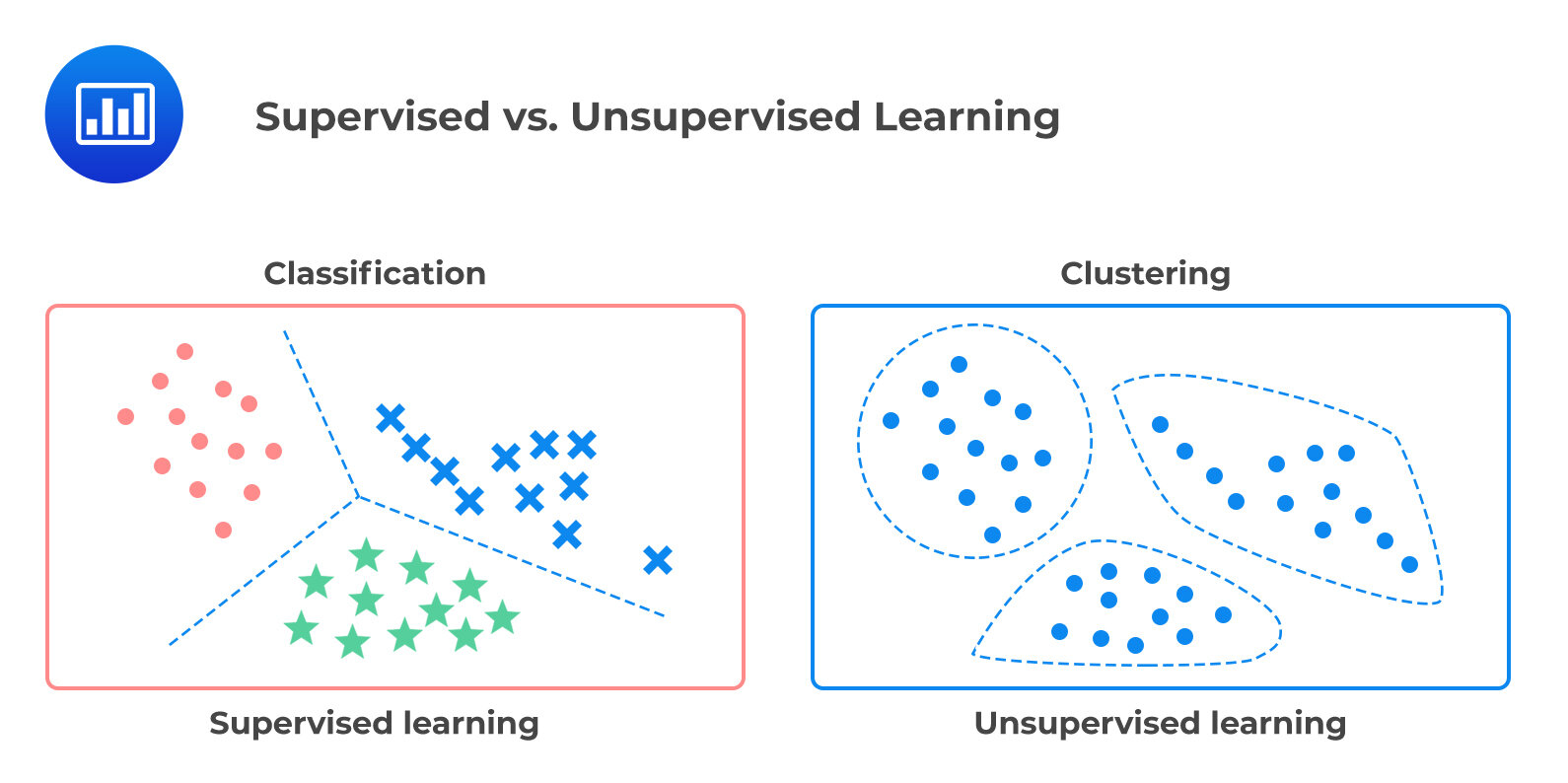
Aprendizaje supervisado
Modelos de Machine Learning
En el contexto de ML, los modelos paramétricos pueden ser vistos como una estructura para soluciones de problemas inversos:
y = f(\beta,{\bf z}) + \epsilon
Donde es una observación, es un vector de parámetros, es el número de parámetros, las variables están almacenadas en el vector , es el número de variables, , y puede ser descrito por alguna función de densidad de probabilidad.
y
\beta \in \Re^{p \times 1}
p
{\bf z} \in \Re^{v \times 1}
v
f : \Re^{p \times 1} \times \Re^{v \times 1} \rightarrow 1
\epsilon
Un modelo simple
Modelo lineal
y = \sum_{i=1}^{v}{\beta_{i} \cdot z_{i}+\epsilon}, \epsilon \sim \mathcal{N}(0, \sigma^2)
Solución general - Forma cerrada
\beta = (Z^\mathsf{T} Z)^{-1} Z^\mathsf{T}y
Un modelo simple
Modelo lineal
y = \sum_{i=1}^{v}{\beta_{i} \cdot z_{i}+\epsilon}, \epsilon \sim \mathcal{N}(0, \sigma^2)
Solución general - Forma cerrada
\beta = (Z^\mathsf{T} Z)^{-1} Z^\mathsf{T}y
Introduction to Machine Learning
By Sebastian David Ariza Coll
