Https and cryptography
HTTP
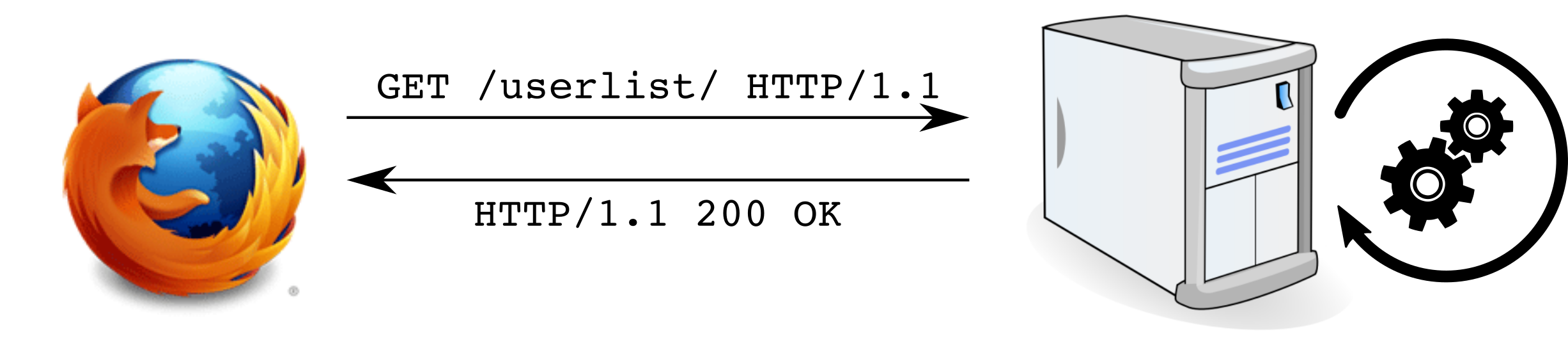
HTTPS

Symmetric encrpytion
Symmetric encryption
XOR - One time pad


Secret key:
011010100010
Secret key:
011010100010
Symmetric encryption
XOR - One time pad


Secret key:
011010100010
Message 1:
101
Secret key:
011010100010
101 XOR 011 =110
Bob decipher:
110 XOR 011 = 101
Symmetric encryption
XOR - One time pad


Secret key:
011010100010
Message 2:
111
Secret key:
011010100010
111 XOR 010 =101
Bob decipher:
101 XOR 010 = 111
Symmetric encryption
XOR - One time pad
Pros
- Very fast
- Perfect encrypting if the secret key is random
Cons
- Need a key as long as the message
- Very dangerous to use the same key twice
One time pad
Use the same key twice

Secret key:

Message:
Result:

XOR
=



XOR
=
One time pad
Use the same key twice

Secret key:

Message:
Result:

XOR
=



XOR
=

XOR
=
One time pad
Use the same key twice

Secret key:

Message:
Result:

XOR
=



XOR
=

M1 S M1 XOR S
M2 S M2 XOR S
M1 XOR S XOR M2 XOR S = M1 XOR M2
Other issues
Small change in plain
Small change in ciphered
Historical algorithms (substitution, XOr, Vigenere, Enigma...)
Small change in plain
Small change in ciphered
Historical algorithms (substitution, XOr, Vigenere, Enigma...)
Small change in plain
Almost all ciphered changed
Modern algorithms (DES, AES, ...)
Data Encryption Standard
Input (64 bits)
000100111011
Left half (32 bits)
000100
Right half (32 bits)
111011
Input (64 bits)
000100111011
Left half (32 bits)
000100
Right half (32 bits)
111011
Out left (32 bits)
111011
Input (64 bits)
000100111011
Left half (32 bits)
000100
Right half (32 bits)
111011
Cipher
Function
Secret Key
Out left (32 bits)
111011
Input (64 bits)
000100111011
Left half (32 bits)
000100
Right half (32 bits)
111011
Cipher
Function
Secret Key
XOR
Out right (32 bits)
011100
Out left (32 bits)
111011
Input (64 bits)
000100111011
Left half (32 bits)
000100
Right half (32 bits)
111011
Cipher
Function
Secret Key
XOR
Out right (32 bits)
011100
Out left (32 bits)
111011
A single round of DES
Input (64 bits)
Initial Permutation
{
16 rounds
Final Permutation
Output (64 bits)
Complete DES
Input (64 bits)
Initial Permutation
{
16 rounds
Final Permutation
Output (64 bits)
Complete DES
Key (56 bits)
Sub-key 1
Sub-key 16
Input (64 bits)
Initial Permutation
{
16 rounds
Final Permutation
Output (64 bits)
Complete DES
Key (56 bits)
Sub-key 1
Sub-key 16
Key schedule
Data
Encryption
Standard
is now broken
A
E
S
is the new standard
Advanced
Encryption
Standard
is the new standard
Symmetric encryption
AES


Secret key:
011010100010
Secret key:
011010100010
c = AES(message, secret_key)
Bob decipher:
message = AES_decipher(c, secret_key)
Symmetric encryption
AES


Secret key:
011010100010
Secret key:
011010100010
c = AES(message, secret_key)
Bob decipher:
message = AES_decipher(c, secret_key)
?
Key exchange
Asymmetric cryptography
(e.g. RSA)

Public RSA key \(K_p\)
Secret RSA key \(K_s\)
Asymmetric cryptography
(e.g. RSA)

Public RSA key \(K_p\)
Secret RSA key \(K_s\)
Asymmetric cryptography
(e.g. RSA)

Public RSA key \(K_p\)
Secret RSA key \(K_s\)

\(ciph\) = RSA_cipher("Hello!", \(K_p\))
RSA_decipher(\(ciph, K_s\))
➡️ "Hello!"
Asymmetric cryptography is heavy
Key exchange v.1

\(ciph\) = RSA_cipher("E563 65AC", \(K_p\))

Public RSA key \(K_p\)
Secret RSA key \(K_s\)

\(ciph\) = RSA_cipher("E563 65AC", \(K_p\))

Public RSA key \(K_p\)
Secret RSA key \(K_s\)
AES-key
Key exchange v.1

\(ciph\) = RSA_cipher("E563 65AC", \(K_p\))

Public RSA key \(K_p\)
Secret RSA key \(K_s\)
AES-key
AES(message, "E536 65AC")
Key exchange v.1



Key exchange v.2
Metaphor: agree on a color


Define yellow as common color




Define yellow as common color
Alice's secret color
Bob's secret color




Define yellow as common color
Alice's secret color
Bob's secret color
My color mixed with the common one




Define yellow as common color
Alice's secret color
Bob's secret color
My color mixed with the common one
My color mixed with the common one




Define yellow as common color
Alice's secret color
Bob's secret color
My color mixed with the common one
My color mixed with the common one



+

Define yellow as common color
Alice's secret color
Bob's secret color
My color mixed with the common one
My color mixed with the common one



\(\ \)
+ =

Define yellow as common color
Alice's secret color
Bob's secret color
My color mixed with the common one
My color mixed with the common one



+ =
= +
secret shared color




Define a base \(g\) and a prime \(p\)

Alice's secret number: \(a\)
Bob's secret number: \(b\)
My color mixed with the common one



Define a base \(g\) and a prime \(p\)
The result of \(g^a~\text{mod} ~p\)
The result of \(g^b~\text{mod} ~p\)

Alice's secret number: \(a\)
Bob's secret number: \(b\)
My color mixed with the common one


\({(g^b)}^a \text{mod} p\) =
= \({(g^a)}^b \text{mod} p\)
secret shared key
Define a base \(g\) and a prime \(p\)
The result of \(g^a~\text{mod} ~p\)
The result of \(g^b~\text{mod} ~p\)

Diffie-Hellman
key exchange





Hi Alice, I'm Bob, let us define shared secret keys!
Hi Bob, I'm Alice, let us define shared secret keys!





Hi Alice, I'm Bob, let us define shared secret keys!
Hi Bob, I'm Alice, let us define shared secret keys!
Man in the middle
attack
Need to authenticate the server first
Need to authenticate the server first

Asymmetric cryptography
(e.g. RSA)

Public key \(K_p\)
Secret key \(K_s\)

\(ciph\) = RSA_cipher("Hello!", \(K_p\))
RSA_decipher(\(ciph, K_s\))
➡️ "Hello!"
Asymmetric cryptography
(e.g. RSA)

Public key \(K_p\)
Secret key \(K_s\)

\(ciph\) = RSA_cipher("Hello!", \(K_p\))
RSA_decipher(\(ciph, K_s\))
➡️ "Hello!"
RSA is used to ensure
confidentiality
Asymmetric cryptography
(e.g. RSA)

Public key \(K_p\)
Secret key \(K_s\)

RSA_cipher(\(sign, K_p\))
➡️ "Hi Bob!"
RSA_decipher("Hi Bob!", \(K_s\)) = \(sign\)
Asymmetric cryptography
(e.g. RSA)

Public key \(K_p\)
Secret key \(K_s\)

RSA_decipher("Hi Bob!", \(K_s\)) = \(sign\)
RSA_cipher(\(sign, K_p\))
➡️ "Hi Bob!"
RSA is used to ensure
authenticity

Public key \(K_p\)
Secret key \(K_s\)

RSA_cipher(\(sign, K_p\))
➡️ "Hi Bob!"
RSA is used to ensure
authenticity

RSA_decipher("Hi Bob!", \(K_s\)) = \(sign\)
\(sign\)
The signature has to change!

Public key \(K_p\)
Secret key \(K_s\)

RSA_cipher(\(sign, K_p\))
➡️ "0111001..."
RSA is used to ensure
authenticity
RSA_decipher("0111001...", \(K_s\)) = \(sign\)
"Sign this long random string: 0111001..."
Bob challenges Alice

Certificate authorities
A few well known compagnies
| CA | Public key |
|---|---|
| DigiCert | 1652 az512 |
| GeoTrust | a142 684a |
| GlobalSign | a654 Fa32 |

Certificate authorities
A few well known compagnies
0. The server's owner asks for a couple of a RSA public/secret key to a CA.
The PK is signed by the CA.




Certificate authorities
A few well known compagnies



1. "Hey, here is a very long random string \(c\) (for challenge), sign it plz!"


Certificate authorities
A few well known compagnies

2. The server compute the signature with its private key


1. "Hey, here is a very long random string \(c\) (for challenge), sign it plz!"


Certificate authorities
A few well known compagnies

2. The server compute the signature with its private key


1. "Hey, here is a very long random string \(c\) (for challenge), sign it plz!"

3. "Sure, here is the signature of your string and the certified public key."


Certificate authorities
A few well known compagnies


3. "Sure, here is the signature of your string and the certified public key."
| CA | Public key |
|---|---|
| DigiCert | 1652 az512 |
| GeoTrust | a142 684a |
| GlobalSign | a654a32 |
4. The browser checks the signature of the challenge
AND the signature of the public key.

Chain of CAs







Chain of CAs






Need to trust all the intermediate CAs!
SSL sum up
- The client check the identity of the server
- Client and server exchange a symmetric secret key
- Client and server communicate by encrypting data with the symmetric key.
SSL sum up
- The client check the identity of the server
Certificate Authorities, signature (e.g. with RSA) - Client and server exchange a symmetric secret key
Asymmetric encryption (e.g. with RSA or Diffie-Hellman)
- Client and server communicate by encrypting data with the symmetric key.
e.g. AES
SSL sum up
- The client check the identity of the server
Certificate Authorities, signature (e.g. with RSA) - Client and server exchange a symmetric secret key
Asymmetric encryption (e.g. with RSA or Diffie-Hellman)
- Client and server communicate by encrypting data with the symmetric key.
e.g. AES
SSL handshake
SSL record
HTTPS & Cryptography - TWTS 07
By sebbes
HTTPS & Cryptography - TWTS 07
- 934



