Rolling
S
Copes
c
h
o
o
L
План на сегодня
- Основные понятия алгоритмизации
- Big O
- Сортировки
- Структуры данных
- Что-то интересное
Алгоритм
(Wiki) набор инструкций, описывающих порядок действий исполнителя для достижения некоторого результата. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.
пошаговый набор инструкций для выполнения задачи
Основные
Свойства алгоритмов
Дискретность
Алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после выполнения предыдущего шага.
Пример
Свойства алгоритмов
class Person {
getUp() {...}
takeShower() {...}
haveBreakfast() {...}
getDressed() {...}
goToWork() {
getUp();
takeShower();
haveBreakfast();
getDressed();
}
}Определенность
Каждый шаг алгоритма должен быть четко и недвусмысленно определен и не должен допускать произвольной трактовки исполнителем.
Пример
Свойства алгоритмов
let numbers = [1, 2, 3, 4];
let doubles = getDoubles(numbers);
function getDoubles(array) {
return numbers.map(function(x) {
return x * 2;
});
}
// doubles - [2, 4, 6, 8]
// numbers - [1, 2, 3, 4]Результативность (конечность)
Алгоритм должен приводить к решению поставленной задачи за конечное число шагов.
Пример
Свойства алгоритмов
while(true) {
doSmth();
} let counter = 10;
while(counter > 0) {
console.log(counter--);
}
/*************************************/
let isModalActive = true;
while(isModalActive) {
showSmth();
//do some staff
}
/*if user press Close button*/
closeHandler() {
isModalActive = false;
}Массовость
Алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся только исходными данными.
Пример
Свойства алгоритмов
let smallArray = [1,2,3,4];
let bigArray = [1,2,3,4,6,.....,43,34];
let namesArray = ['Emma', 'Olivia',..., 'Meilani'];
getLastItem(array) {
return array[array.length - 1];
}РЕкурсия
... – это вызов функции самой себя, как правило, с другими аргументами.
Math.pow(2,3); //8
// pow(x, n) = x * pow(x, n - 1);
// pow(2, 3) = 2 * pow(2, 2)
function pow(x, n) {
return n !== 1 ? x * pow(x, n - 1) : x;
}Любая рекурсия может быть переделана в цикл. Как правило, вариант с циклом будет эффективнее.
function pow(x, n) {
let result = x;
for (let i = 1; i < n; i++) {
result *= x;
}
return result;
}Любой рекурсивный алгоритм может быть реализован с помощью итераций
При любом вложенном вызове JavaScript запоминает текущий контекст выполнения в специальной внутренней структуре данных – «стеке контекстов».
У каждого вызова функции есть свой «контекст выполнения» (execution context).
Контекст включает в себя не только переменные, но и место в коде, так что когда вложенный вызов завершится - можно будет легко вернуться назад.
К примеру: { x: 2, n: 3, строка 3 }
А зачем эта замена рекурсии?!
Размер стека вызовов в различных браузерах
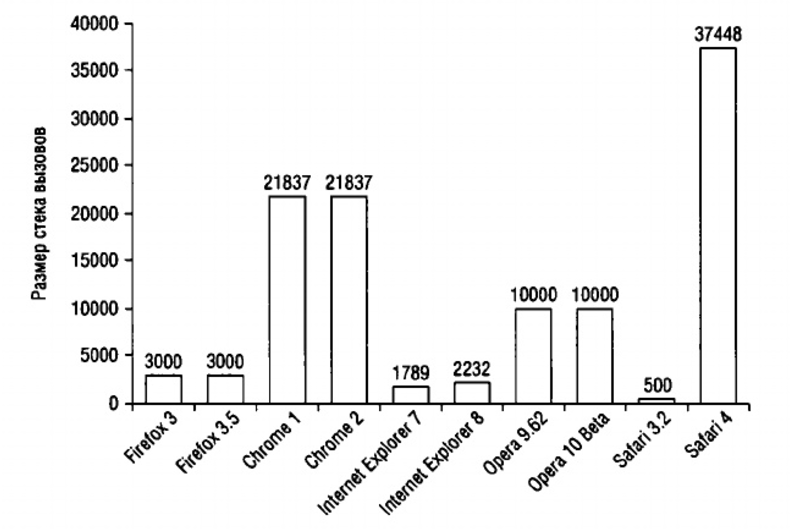
Фибоначчи
Теперь очевидным решением будет:
var recursive = function(n) {
if(n <= 2) {
return 1;
} else {
return this.recursive(n - 1) + this.recursive(n - 2);
}
};Фибоначчи
Решение без рекурсии...
let loopingFib = function(n) {
let a = 0, b = 1, f = 1;
for(let i = 2; i <= n; i++) {
f = a + b;
a = b;
b = f;
}
return f;
};формула...
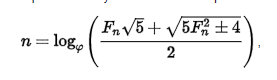
где:
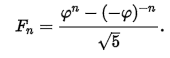
где:
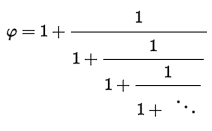
Фибоначчи
Решение c мемоизаций(?!)
let memo = [];
let fib = function(n) {
if (memo[n] !== undefined) return memo[n];
let current = 0;
let next = 1;
for (let i = 0; i < n; i++) {
memo[i] = current;
[current, next] = [next, current + next]; //swap
}
return current;
};Мемоизация — сохранение результатов выполнения функций для предотвращения повторных вычислений. Это один из способов оптимизации
Фибоначчи
Сравнение скорости работы алгоритма с мемоизацией и без
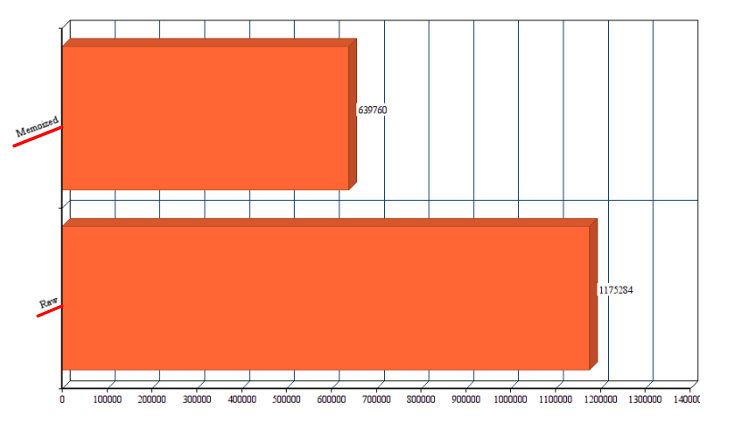
Для больших чисел n количество вызовов функции растёт очень быстро. Уже для n=50 это порядка 40 миллиардов вызовов.
Используя идею мемоизации, то есть кеширования промежуточного результата, можно добиться уменьшения количества вызовов для n=50 до всего лишь 99.
Мемоизация полезна, когда вы передаёте в функцию заранее известный набор аргументов и когда результат функции будет всегда одинаковым при одинаковых аргументах. Если же функция не даёт одинакового результата при тех же аргументах, то мемоизация будет бесполезна.
Cинтаксис
result = ++variable
result = --variable
result = variable++
result = variable--
/*************************/
variable = 1;
result1 = variable++;
result2 = ++variable;
variable //3
result1 //1
result2 //3
result1 = expression1 && expression2
result2 = expression1 || expression2 let a = {b: 3};
a.b > 2 && doSmth();
function foo(a) {
let variable = a || [1,2,3];
//do something
} function foo(a = [1,2,3]) {
console.log(a);
//do something
}typeof (2 === 11 % 3) === 'boolean' // 'string'...Cинтаксис
// 14 is 00000000000000000000000000001110
let temp = 14;
temp <<= 2;
console.log(temp);
// 56 is 00000000000000000000000000111000
Output: 56 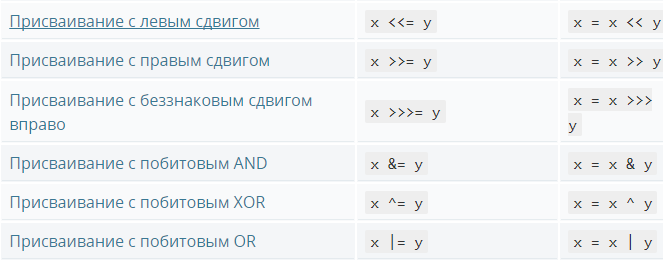
/** Convert a decimal number to binary **/
var toBinary = function(decNum){
return parseInt(decNum,10).toString(2);
}
/** Convert a binary number to decimal **/
var toDecimal = function(binary) {
return parseInt(binary,2).toString(10);
} function binToDec(number){
return number.split('').reverse().reduce(function(x, y, i){
return (y === '1') ? x + Math.pow(2, i) : x;
}, 0);
}А если без parseInt...

Системы счисления
Попробуем сделать перевод из десятичной в двоичную

Реализация
function decToBinary(decNumber) {
}
let stack = [];let binString = "";while(decNumber > 0) {
let rem = decNumber % 2;
stack.push(rem);
decNumber = Math.floor(decNumber / 2); // ~~(decNumber / 2)
}while(stack.length) {
binString = binString + stack.pop(); // binString.concat(stack.pop());
}return binString;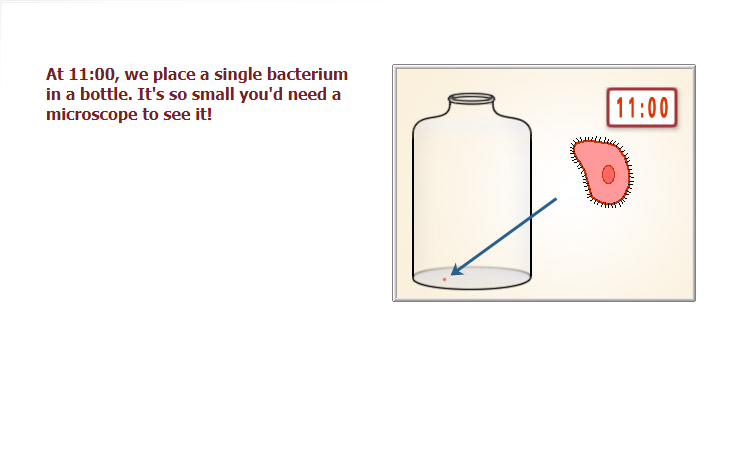




BiG O
Для оценки производительности алгоритмов можно использовать разные подходы. Самый бесхитростный - просто запустить каждый алгоритм на нескольких задачах и сравнить время исполнения.
Другой способ - математически оценить время исполнения подсчетом операций.
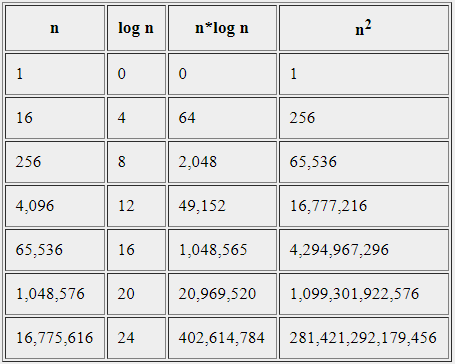
Если считать, что числа в таблице соответствуют микросекундам, то для задачи с n=1048576 элементами алгоритму с временем работы O(log n) потребуется 20 микросекунд, алгоритму со временем O(n) - 17 минут, а алгоритму с временем работы O( n*n ) - более 12 дней...
разберемся
Как оценивать сложность алгоритма
Наилучшей является оценка O(1)... В этом случае время вообще не зависит от n, т.е постоянно при любом количестве элементов.
let array = [1,2,3,4];
array[0]; //1
array.unshift(5);
array[0]; //5
задача
Поиск максимального элемента в массиве.
let array = [1,2,3,4,5,6,7,8,9,10,12,0,100];
let max = array[0];
for (let i = 0; i < array.length; i++) {
if ( array[i] >= max ) {
max = array[i];
}
}Предположим, что наш процессор способен выполнять как единые инструкции следующие операции:
- Присваивать значение переменной
- Находить значение конкретного элемента в массиве
- Сравнивать два значения
- Инкрементировать значение
- Основные арифметические операции (например, сложение и умножение)
2 операции
2 операции на инициализацию for
+ по 2 на итерацию цикла
задача
Поиск максимального элемента в массиве.
if ( array[i] >= max ) { ...Но тело if может запускаться, а может и нет, в зависимости от актуального значения из массива. Если произойдёт так, что array[ i ] > max, то у нас запустятся две дополнительные команды: поиск в массиве и присваивание
array2 = [ 4, 3, 2, 1 ];array1 = [ 1, 2, 3, 4 ];Когда мы анализируем алгоритмы, мы чаще всего рассматриваем наихудший сценарий.
Таким образом, в наихудшем случае в теле цикла из нашего кода запускается четыре инструкции, и мы имеем f( n ) = 4 + 2n + 4n = 6n + 4.
Поэтому первое, что мы сделаем,
это отбросим 4 и оставим только
f( n ) = 6n.Мы отбрасываем те элементы функции, которые при росте n возрастают медленно, и оставляем только те, что растут сильно.
Второй вещью, на которую можно не обращать внимания, является множитель перед n. Так что наша функция превращается в f( n ) = n.
Что дальше
ПРАКТИЧЕСКАЯ РЕКОМЕНДАЦИЯ
Практическая рекомендация: простые программы можно анализировать с помощью подсчёта в них количества вложенных циклов. Одиночный цикл в n итераций даёт f( n ) = n. Цикл внутри цикла f( n ) = n*N. Цикл внутри цикла внутри цикла — f( n ) = n*N*N.
И так далее.
ПРАКТИЧЕСКАЯ РЕКОМЕНДАЦИЯ
Практическая рекомендация: если у нас имеется серия из последовательных for-циклов, то асимптотическое поведение (сложность, оценку сложности) программы определяет наиболее медленный из них. Два вложенных цикла, идущие за одиночным, тоже самое, что и вложенные циклы сами по себе.
Говорят, что вложенные циклы доминируют над одиночными.
Итак
O() - асимптотическая оценка алгоритма на худших входных данных
При оценке O() константы не учитываются.
При оценке за функцию берется количество операций, возрастающее быстрее всего.
График роста O(n)

Пример с улучшением кода
let array = [1,2,3,4,5,6,7,8,9,10,12,0,100];
let max = array[0];
for (let i = 0; i < array.length; i++) {
if ( array[i] >= max ) {
max = array[i];
}
}let array = [1,2,3,4,5,6,7,8,9,10,12,0,100];
let max = array[0];
let length = array.length;
for (let i = 1; i < length; i++) {
if ( array[i] > max ) {
max = array[i];
}
}Алгоритмы сортировки
Глупая
Пузырьковая
Шейкарная
Слиянием
Быстрая
Пирамидальная сортировка
Выбором
Шелла
Сортировка прямыми включениями
Поразрядная
Блочная
.....
Виды сортировок:
Оценка сортировок
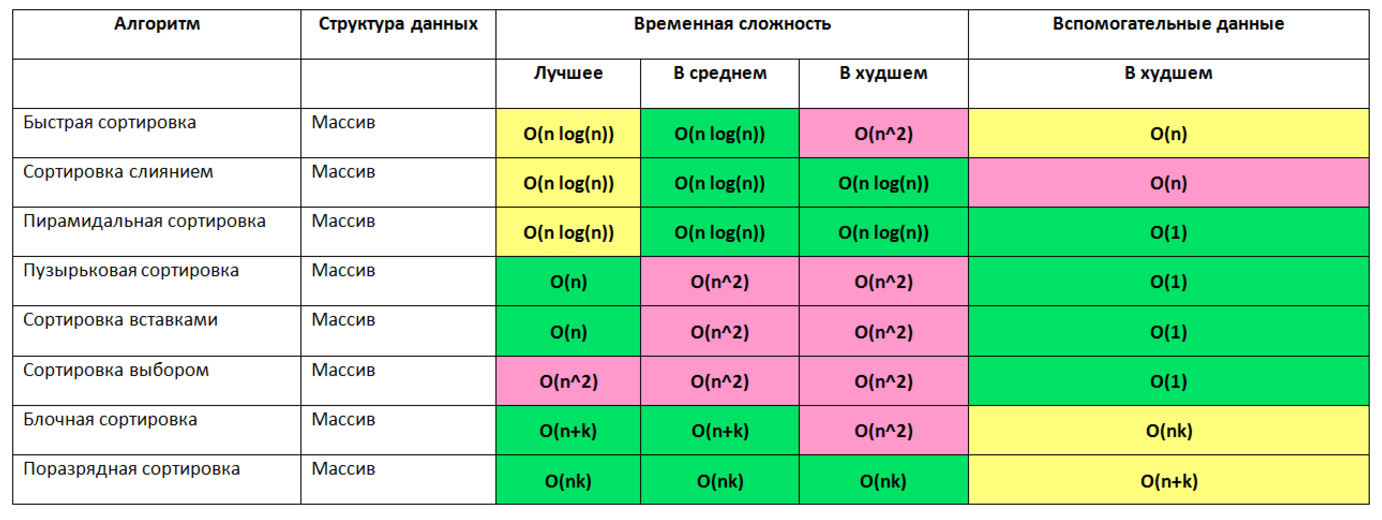
Глупая сортировка
«Так любой дурак сортировать умеет» — скажете Вы и будете абсолютно правы. Именно поэтому сортировку и прозвали «глупой».

Просматриваем массив слева-направо и по пути сравниваем соседей. Если мы встретим пару взаимно неотсортированных элементов, то меняем их местами и возвращаемся в самое начало.
Пузырьковая сортировка

Принцип действий прост: обходим массив от начала до конца, попутно меняя местами неотсортированные соседние элементы. В результате первого прохода на последнее место «всплывёт» максимальный элемент. Теперь снова обходим неотсортированную часть массива (от первого элемента до предпоследнего) и меняем по пути неотсортированных соседей.
Продолжая в том же духе
(сортировка простыми обменами)
O(n^2)
Пузырьковая сортировка
function bubbleSort(array) {
return array;
}
for (var i=0; i < length - 1; i++) {
for(var j = 1; j < length - i; j++) {
if(array[j-1] > array[j]) {
var temp = array[j-1];
array[j-1] = array[j];
array[j] = temp;
}
}
}
bubbleSort([5,90,2,3,5,7,1,4]); //[1, 2, 3, 4, 5, 5, 7, 90] var length = array.length;Шейкерная сортировка

Пузырьковая сортировка + задвигать максимумы не только в конец, а ещё и в начало перебрасывать минимумы то у нас получается…
Начинается процесс как в «пузырьке»: "перекатываем" максимум в конец. После этого разворачиваемся на 180 градусов и идём в обратную сторону, при этом уже "перекатывая" в начало не максимум, а минимум. Отсортировав в массиве первый и последний элементы, снова повторяем...
Имеем:
Когда же конец:
заканчиваем процесс, оказавшись в середине списка.
O(n^2)
Merge sort

O(N*LOG N)
принцип работы
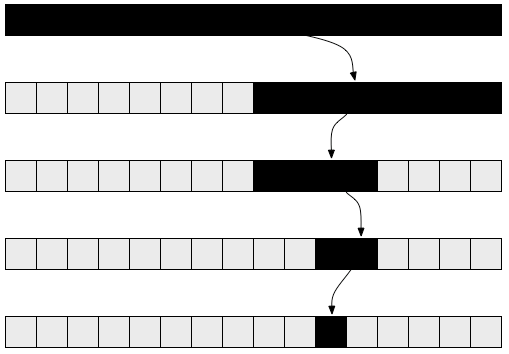
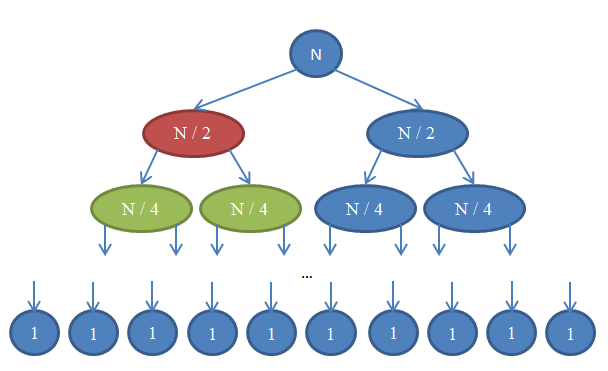
Merge sort
function merge(left, right) { //Вспомогательная функция.
let result = [];
while (left.length > 0 && right.length > 0) {
if (left[0] < right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
return result.concat(left).concat(right);
}
function mergeSort(array) { //Функция сортировки слиянияем.
if (array.length < 2) {
return array;
}
let middle = Math.floor(array.length / 2);
let left = array.slice(0, middle);
let right = array.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}Merge sort (2)
function mergeSort(array) { //используем функцию merge() из предыдущего примера
if (array.length < 2) {
return array;
}
var work= [];
var length = array.length;
for (var i=0; i < length - 1; i++) {
work.push(array[i]);
}
work.push([]); // в случае нечетного числа элементов
for(var lim = length; lim > 1; lim = Math.floor((lim + 1)/2)) {
for(var j=0, k=0; k < lim; j++, k++) {
work[j] = merge(work[k], work[k + 1]);
}
work[j] = [];
}
return work[0];
}Без рекурсии, без перформанса.. :)
В целом, пример плохого mergeSort (опасно для здоровья)
Quick sort
http://me.dt.in.th/page/Quicksort/

Принцип работы
1. Выбираем опорный элемент
2. Добиваемся того, чтобы элементы меньше опорного оказываются слева от опорного, а элементы больше опорного — справа.
3. К подмассивам слева и справа от опорного применяются первые два шага, если в этих подмассивах больше одного элемента.

QUICK sort
function quickSort(array) {
if (array.length < 2) {
return array;
}
let a = [], b = [], p = array[0];
for (let i = 1; i < array.length; i++) {
if (array[i] < p) {
a[a.length] = array[i];
} else {
b[b.length] = array[i];
}
}
return quickSort(a).concat(p, quickSort(b));
}O(N^2) в худшем случае
Array.prototype.sort()
var fruit = ['cherries', 'apples', 'bananas'];
fruit.sort(); // ['apples', 'bananas', 'cherries'];
var scores = [1, 10, 21, 2];
scores.sort(); // [1, 10, 2, 21];
var things = ['word', 'Word', '1 Word', '2 Words'];
things.sort(); // ['1 Word', '2 Words', 'Word', 'word'];Array.prototype.sort()
function compareNumbers(a, b) {
return a - b;
}var numbers = [4, 2, 5, 1, 3];
numbers.sort(function(a, b) {
return a - b;
});
// [1, 2, 3, 4, 5]Array.prototype.sort()
var items = [
{ name: 'Edward', value: 21 },
{ name: 'Sharpe', value: 37 },
{ name: 'And', value: 45 },
{ name: 'The', value: -12 },
{ name: 'Magnetic', value: 13 },
{ name: 'Zeros', value: 37 }
];
function compare(a, b) {
if (a < b) {
return -1;
}
if (a > b) {
return 1;
}
// a === b
return 0;
}
// sort by value
items.sort(function (a, b) {
return a.value - b.value;
});
// sort by name
items.sort(function(a, b) {
var nameA = a.name.toUpperCase(); // ignore upper and lowercase
var nameB = b.name.toUpperCase(); // ignore upper and lowercase
if (nameA < nameB) {
return -1;
}
if (nameA > nameB) {
return 1;
}
// names must be equal
return 0;
});Cтруктуры данных
Массив
Доступ
O(1)
Удаление
O(1)
Вставка
O(1)
Поиск
O(n)
slice splice push shift unshift join reverse.....
Список
Доступ
O(n)
Удаление
O(1)
Вставка
O(1)
Поиск
O(n)
length add remove insertAfter traverse head tail numberOfValues

Реализуем
function Node(data) {
this.data = data;
this.next = null;
}function SinglyLinkedList() {
this.head = null;
this.tail = null;
this.numberOfValues = 0;
}SinglyLinkedList.prototype.length = function() {
return this.numberOfValues;
};SinglyLinkedList.prototype.add = function(data) {
var node = new Node(data);
if(!this.head) {
this.head = node;
this.tail = node;
} else {
this.tail.next = node;
this.tail = node;
}
this.numberOfValues++;
};SinglyLinkedList.prototype.remove = function(data){
var previous = this.head;
var current = this.head;
while(current) {
if(current.data === data) {
if(current === this.head) {
this.head = this.head.next;
}
if(current === this.tail) {
this.tail = previous;
}
previous.next = current.next;
this.numberOfValues--;
} else {
previous = current;
}
current = current.next;
}
};....insertAfter = function(data, afterElement) {
}var list = new SinglyLinkedList();
list.add(1);
list.add(2);
list.add(3);
list.length(); //3
list.remove(2);
list.insertAfter(1, 2); //1,2,3var node = new Node(data);Стек
Доступ
O(n)
Удаление
O(1)
Вставка
O(1)
Поиск
O(n)
push(value) pop() peek()
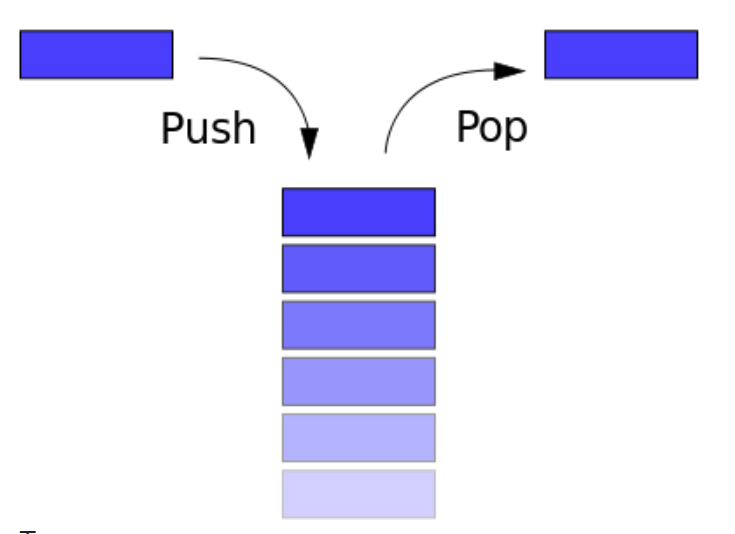
Реализуем
function Stack() {
this.stack = [];
}Stack.prototype.push = function(value) {
this.stack.push(value);
};Stack.prototype.pop = function() {
return this.stack.pop();
};Stack.prototype.peek = function() {
return this.stack[this.stack.length - 1];
};var stack = new Stack();
stack.push(1);
stack.push(2); //1,2
stack.peek(); //2
stack.pop(); //1очередь
Доступ
O(n)
Удаление
O(n)
Вставка
O(1)
Поиск
O(n)
enqueue, dequeue, peek..
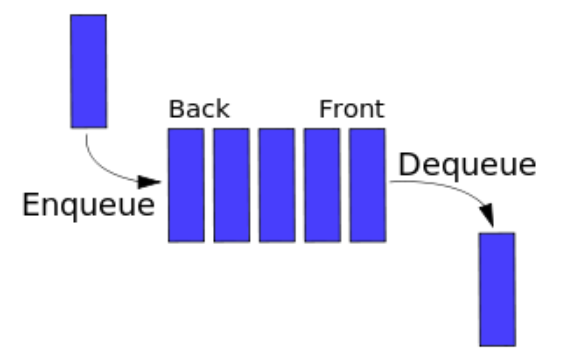
Реализуем
function Queue() {
this.queue = [];
}Queue.prototype.enqueue = function(value) {
this.queue.push(value);
};Queue.prototype.dequeue = function() {
return this.queue.shift();
};Queue.prototype.peek = function() {
return this.queue[0];
};
var queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.peek();
queue.dequeue();
ХЭШ таблица
Удаление
O(1)
Вставка
O(1)
Поиск
O(1)
calculateHash, add, search, remove..
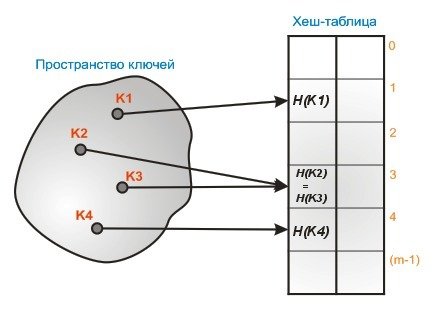
ХЭШ таблица
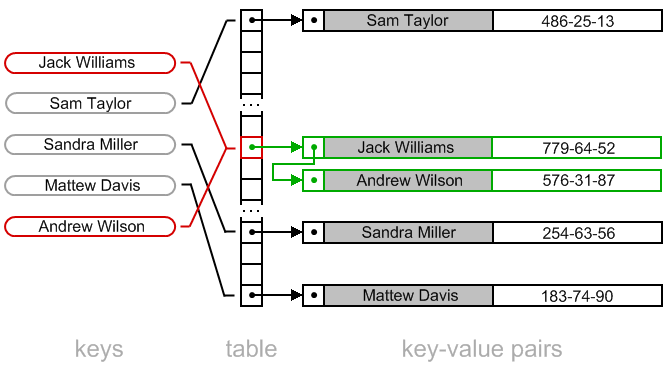
Коллизии
Парадокс дней рождения

ДЕРЕВО

ДЕРЕВО
Виды деревьев
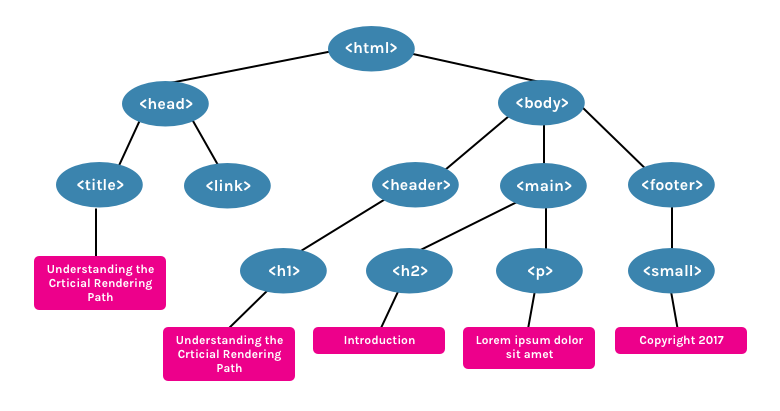
ДЕРЕВО
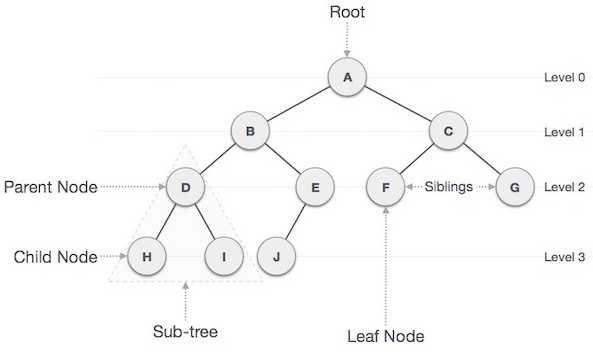
Доступ
O(n)
Удаление
Вставка
Поиск
O(n)
O(n)
O(n)
Двоичное ДЕРЕВО поиска

Доступ
O(LOGN)
Удаление
O(LOGN)
Вставка
O(LOGN)
Поиск
O(LOGN)
Реализуем
function Node(data) {
this.data = data;
this.left = null;
this.right = null;
}
function BinarySearchTree() {
this.root = null;
}BinarySearchTree.prototype.add = function(data) {
var node = new Node(data);
if(!this.root) {
this.root = node;
} else {
var current = this.root;
while(current) {
if(node.data < current.data) {
if(!current.left) {
current.left = node;
break;
}
current = current.left;
} else if (node.data > current.data) {
if(!current.right) {
current.right = node;
break;
}
current = current.right;
} else {
break;
}
}
}
};var bsTree = new BinarySearchTree();
bsTree.add(5);
bsTree.add(3);
bsTree.add(7);
bsTree.add(2);
bsTree.add(4);
bsTree.add(4);
bsTree.add(6);
bsTree.add(8); 5 | 3 7 | 2 4 6 8Реализуем
BinarySearchTree.prototype.getMax = function(node) {
if(!node) {
node = this.root;
}
while(node.right) {
node = node.right;
}
return node.data;
};BinarySearchTree.prototype.contains = function(data) {
var current = this.root;
while(current) {
if(data === current.data) {
return true;
}
if(data < current.data) {
current = current.left;
} else {
current = current.right;
}
}
return false;
};Реализуем удаление
BinarySearchTree.prototype.remove = function(data) {
var that = this;
var removeNode = function(node, data) {
if(!node) {
return null;
}
if(data === node.data) {
if(!node.left && !node.right) {
return null;
}
if(!node.left) {
return node.right;
}
if(!node.right) {
return node.left;
}
} else if(data < node.data) {
node.left = removeNode(node.left, data);
return node;
} else {
node.right = removeNode(node.right, data);
return node;
}
};
this.root = removeNode(this.root, data);
};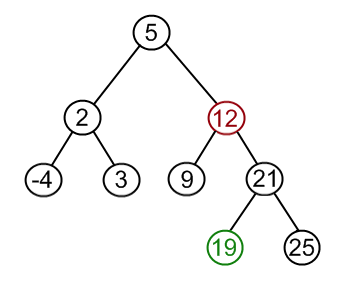
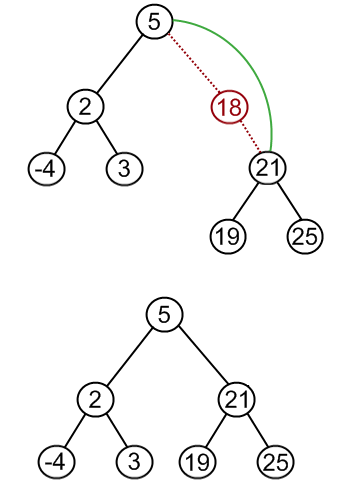
// 2 children
var temp = that.getMin(node.right);
node.data = temp;
node.right = removeNode(node.right, temp);
return node;Обход дерева
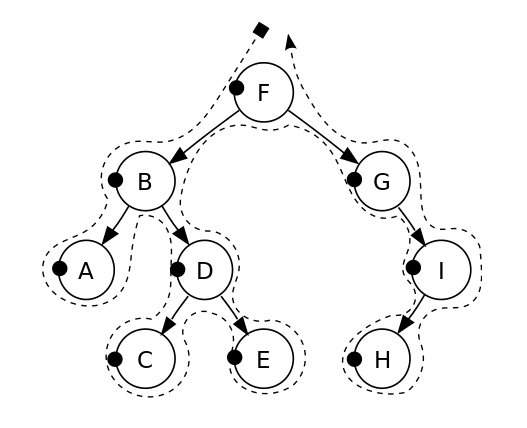
Реализуем
BinarySearchTree.prototype.traverse = function(fn) {
var current = this.root;
this.inOrder(current, fn);
};BinarySearchTree.prototype.inOrder = function(node, fn) {
if(node) {
this.inOrder(node.left, fn);
if(fn) {
fn(node);
}
this.inOrder(node.right, fn);
}
};binarySearchTree.traverse(function(node) { console.log(node.data); }); //2 3 4 5 6 7 8Что-то интересное...

Граф

Граф

Нейронные сети
Виды графов
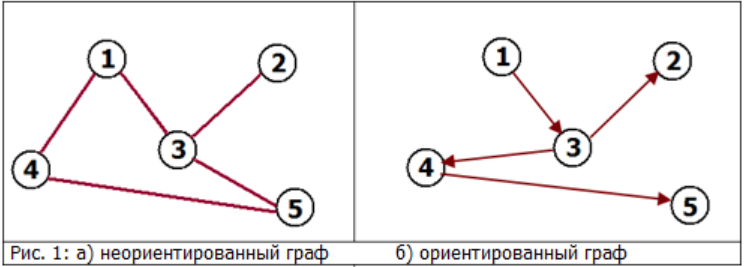
Представление графов


lodash
https://lodash.com/docs
Зачем очередной раз изобретать велосипед, когда до нас уже столько сделано....

JSPerf
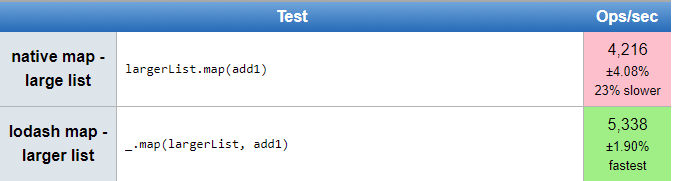
https://jsperf.com/
Интересные задачи
https://www.interviewcake.com/all-questions/javascript
Для каждой из задач можно увидеть оптимальный путь решения (алгоритм)
Полезные ссылки
http://www.thatjsdude.com/interview/js1.html
https://khan4019.github.io/front-end-Interview-Questions/sort.html
https://github.com/mr-mig/every-programmer-should-know
CODEWARS ЗАДАЧИ:

Algorithms
By sergey_kovalchuk
Algorithms
Fundamental algorithms and data structures.
- 5,693



