Darboux & ε-Reformulation of the Definite Integral
in 30 minutes!
Topics to Cover
11/7/2020
Darboux Definition of the Definite Integral
ε-Reformulation Definition of the Definite Integral
HOW and WHEN to use these definitions to:
1. Prove when a function is integrable over a specified interval [a, b]
2. Prove the definite integral properties (Theorem 4 through Theorem 7 in Spivak)
But first...
Darboux definition of the Definite Integral
Let \space a, b \in \R, a < b.
Suppose \space f \space is\space bounded.
Let \space P = \{ti\}, where \space 0\leq i \leq n.
Then \space we \space say \space f \space is \space integrable \space on \space [a,b] \space IFF
sup\{L(f, P)\} = inf\{U(f, P)\} = Area \space
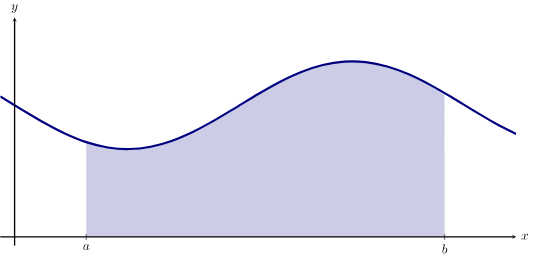
What does this mean geometrically speaking?
Darboux definition of the Definite Integral
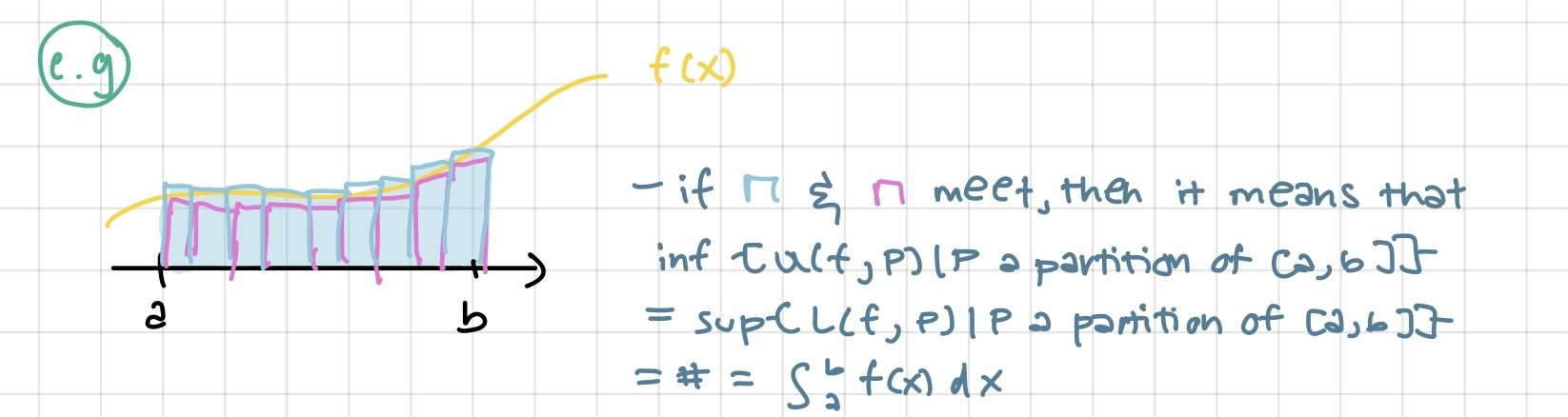
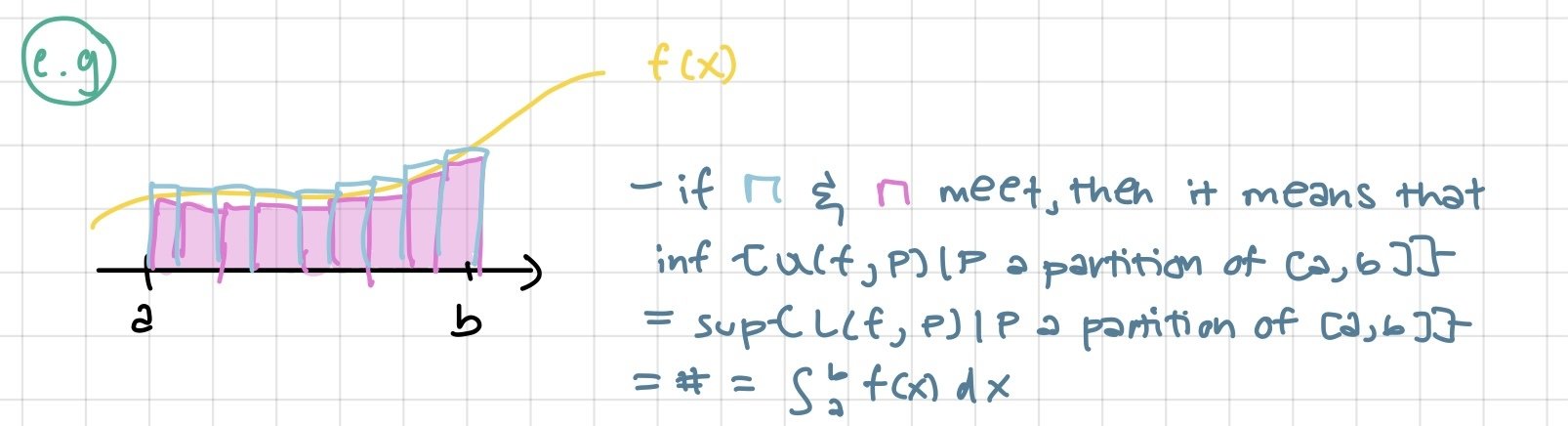
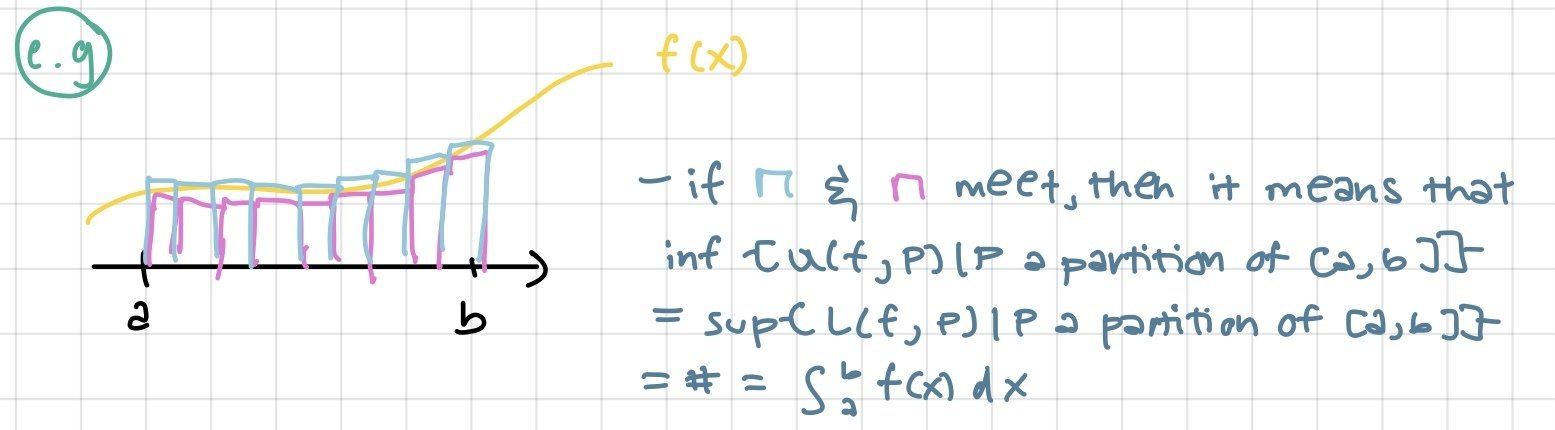
Lower sum of f on P
Higher sum of f on P
ε-Reformulation definition of the Definite Integral (restatement)
If \space f \space is \space bounded \space on \space [a, b] \space then \space f \space is \space integrable
on \space [a, b] \space IFF \space \forall \epsilon > 0, \space there \space is \space a \space partition \space P
of \space [a, b] \space s.t, \space U(f, P) - L(f, P) < \epsilon
What does this mean geometrically speaking? How is this a restatement?
ε-Reformulation definition of the Definite Integral (restatement)
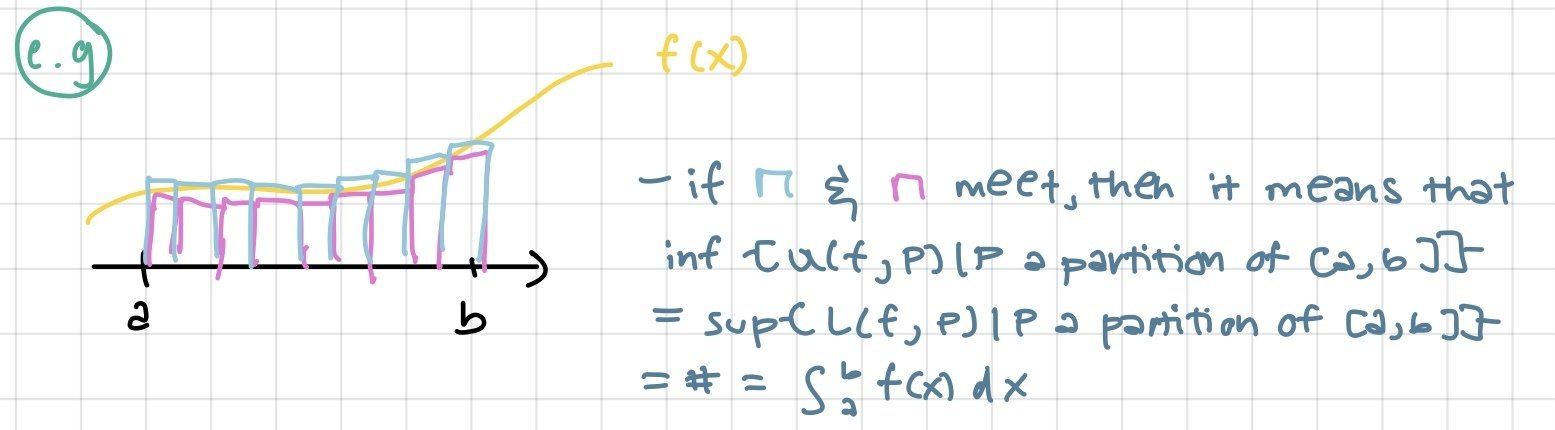
If we choose a partition and compute its upper and lower sums and the difference between these sums is < ε, then the upper and lower sum estimates can be made infinitely close to one another. I.e, they result in practically the same number and represent the area!
Recall ε is an infinitely small number
restatement bc this is the same idea as Darboux: upper and lower sums equal to each other and the area of the curve
When/how do we use these definitions when we have the Riemann sum definition?
WHEN: to prove that a function, f, is not integrable over an interval [a, b].
HOW:
Darboux defn:
We simply show that the supremum of the lower sums of f on P does not equal to the infimum of the upper sums f on p.
Epsilon defn:
We assume that the definition is false, and choose a value of epsilon (after computing U(f, P) - L(f, P) that contradicts the definition.
When/how do we use these definitions when we have the Riemann sum definition?
WHEN: to prove that a function, f, is integrable over an interval [a, b].
HOW:
Darboux defn:
We prove the definition. I.e, compute the lower and upper sums of f on P and show the infimum of the upper sum and supremum of the lower sum are equivalent.
Epsilon defn:
We choose a value of epsilon that is greater than the difference of the upper and lower sum of f on P
Prove a fcn is integrable over [a, b]
deck
By sheeza aziz
