Intro to Machine Learning
Lecture 2: Linear regression and regularization
Shen Shen
Feb 9, 2024
(many slides adapted from Tamara Broderick)
Logistical issues? Personal concerns?
We’d love to help out at
6.390-personal@mit.edu
Logistics
- 11am Section 3 and 4 are completely full and we have many requests to switch. Physical space packed.
- If at all possible, please help us by signup/switch to other slots.
- OHs start this Sunday, please also join our Piazza
- Thanks for all the assignments feedback. We are adapting on-the-go but these certainly benefit future semesters.
- Start to get assignments due now. (first up, exercises 2, keep an eye on the "due")
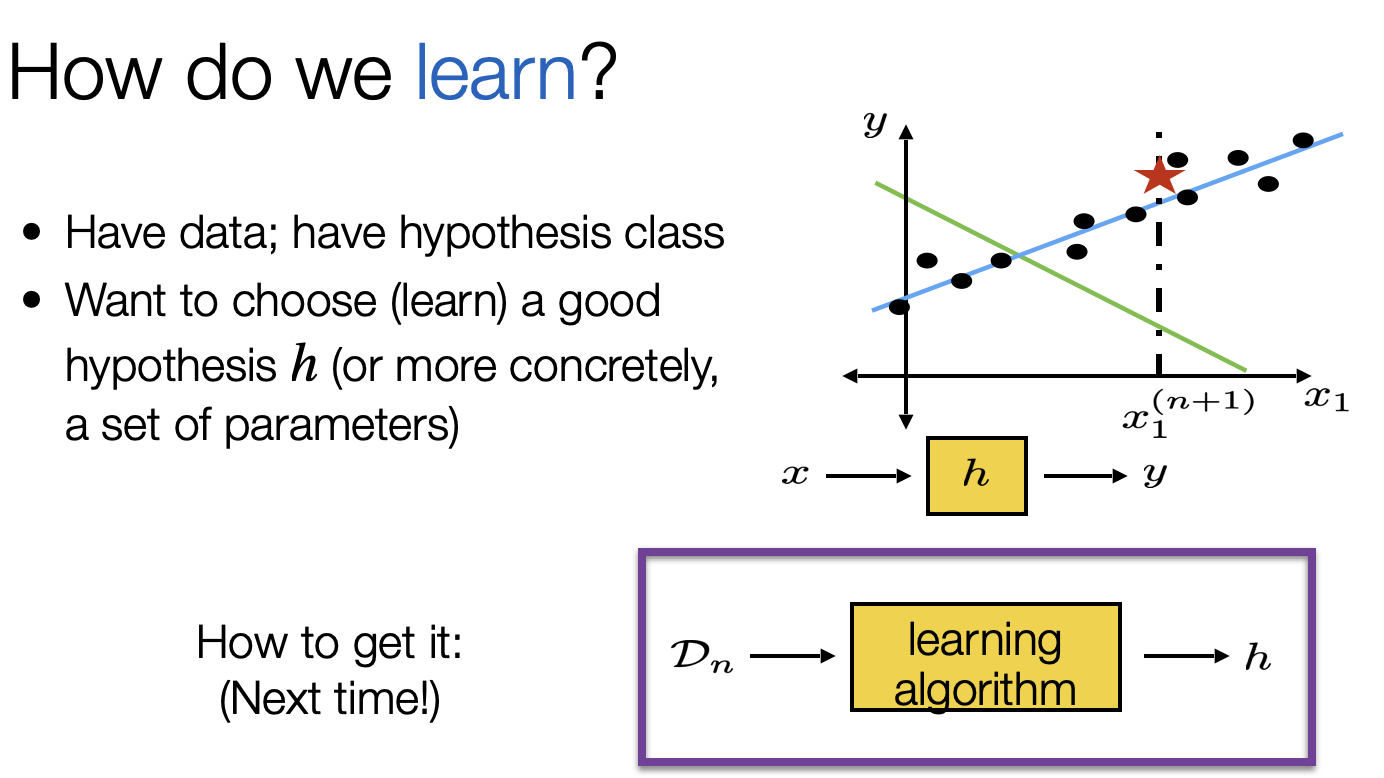
How do Lectures fit in the course components/line up?
Optimization + first-principle physics
5min primer to an optimization problem
using OLS
Outline
- Recap of last (content) week.
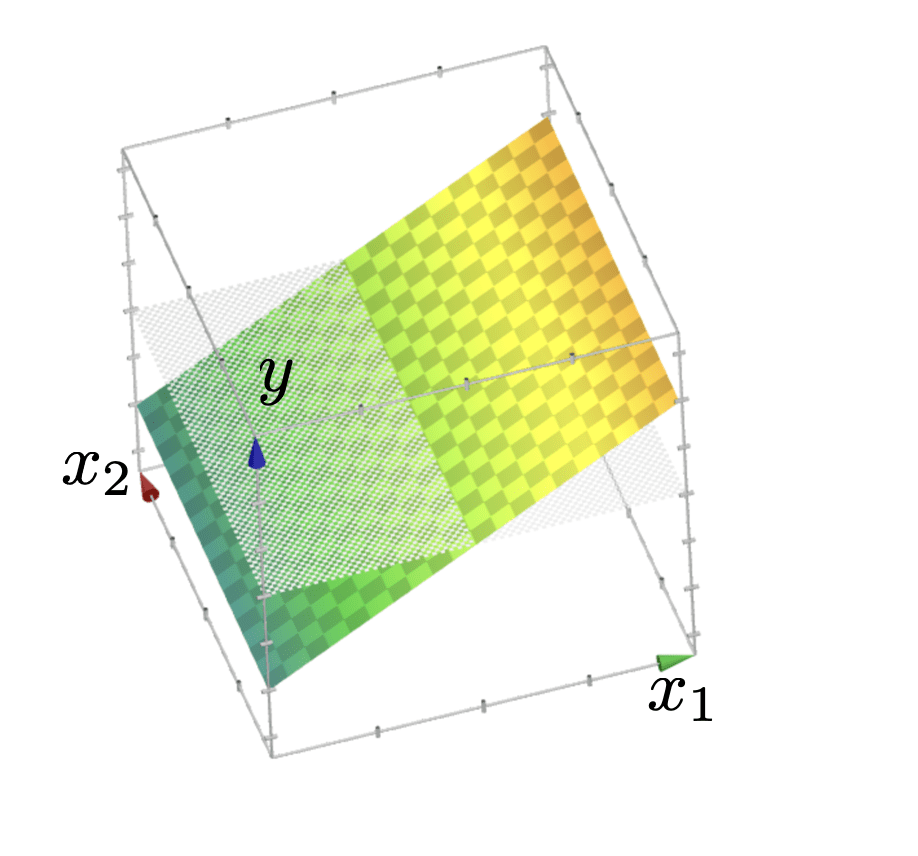
- Ordinary least-square regression
- Analytical solution (when exists)
- Cases when analytical solutions don't exist
- Practically, visually, mathamtically
- Regularization
- Hyperparameter, cross-validation
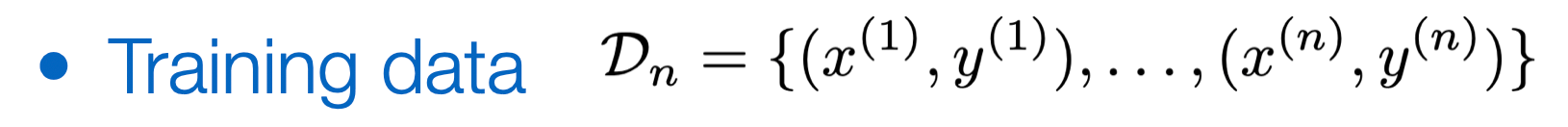
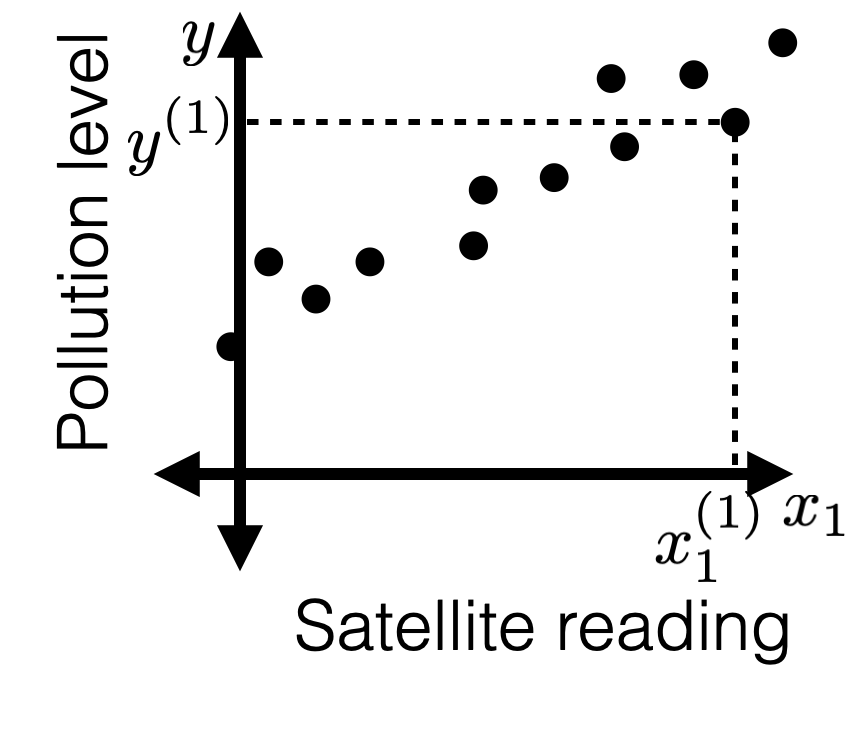
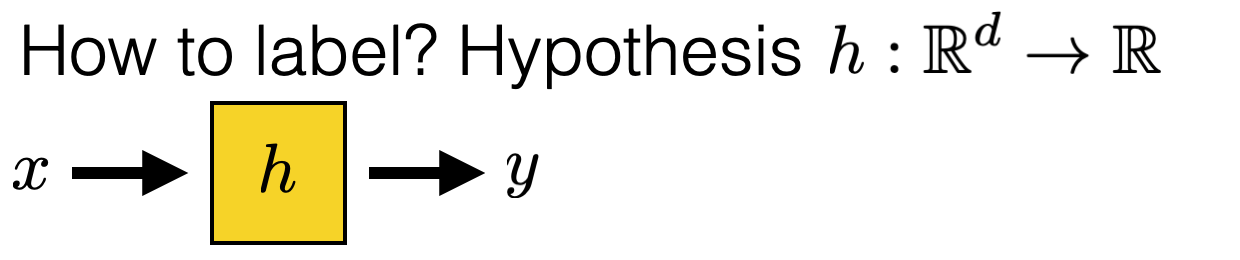
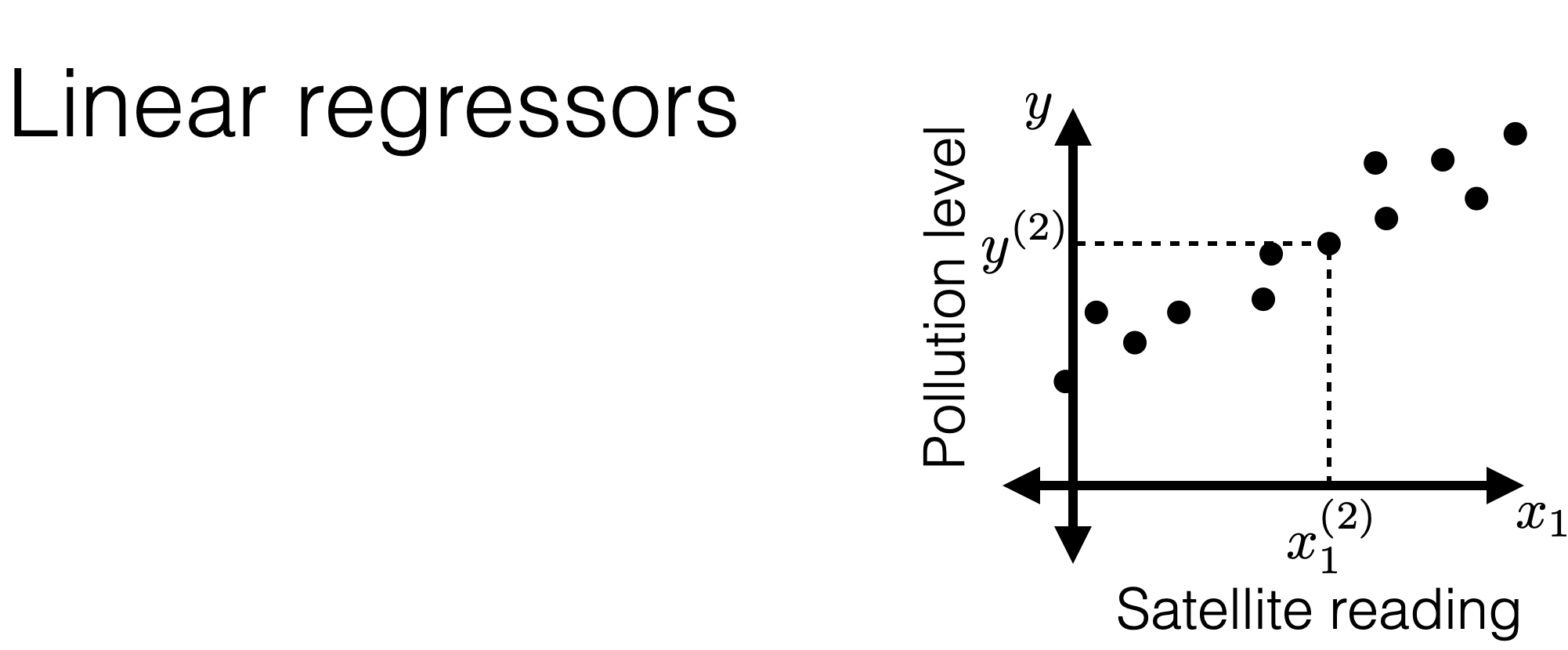
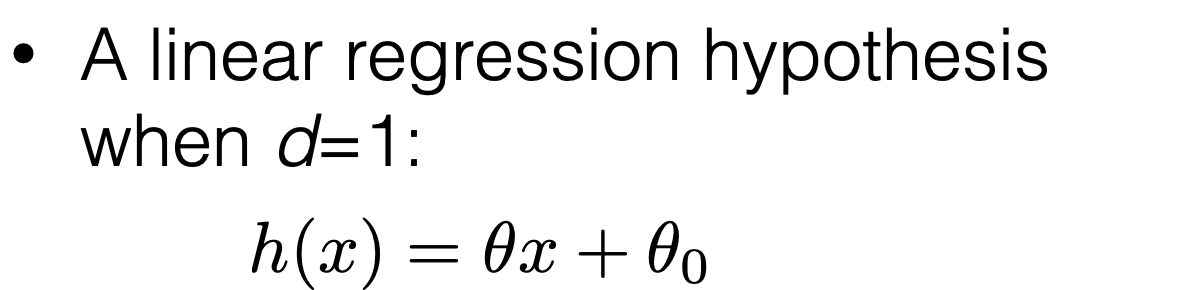
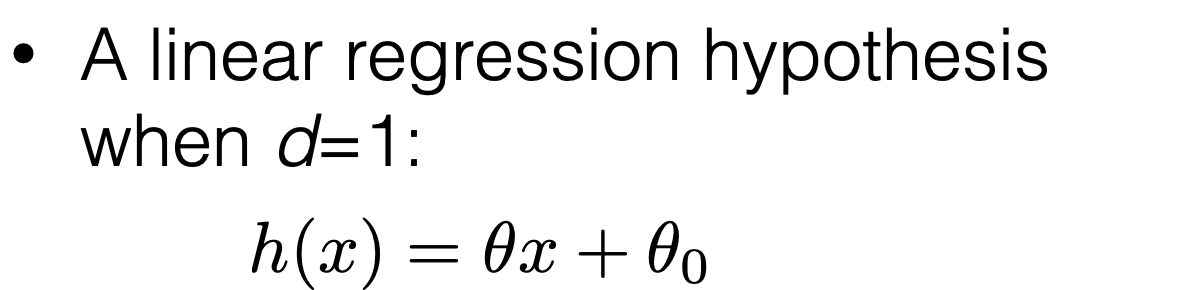
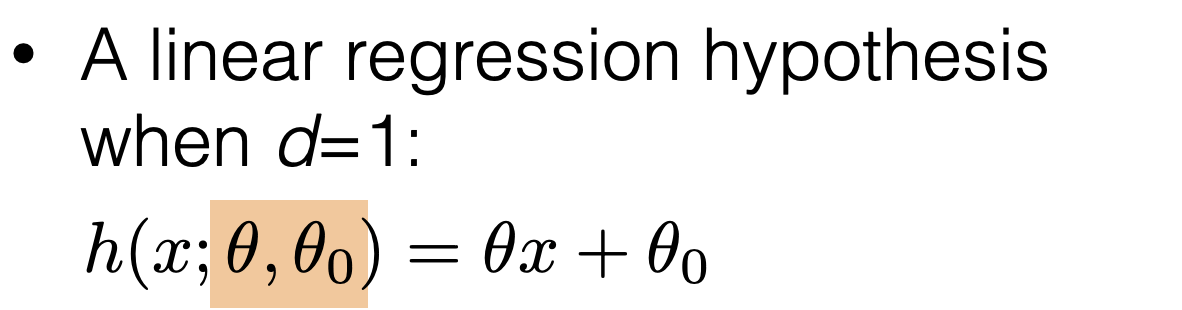
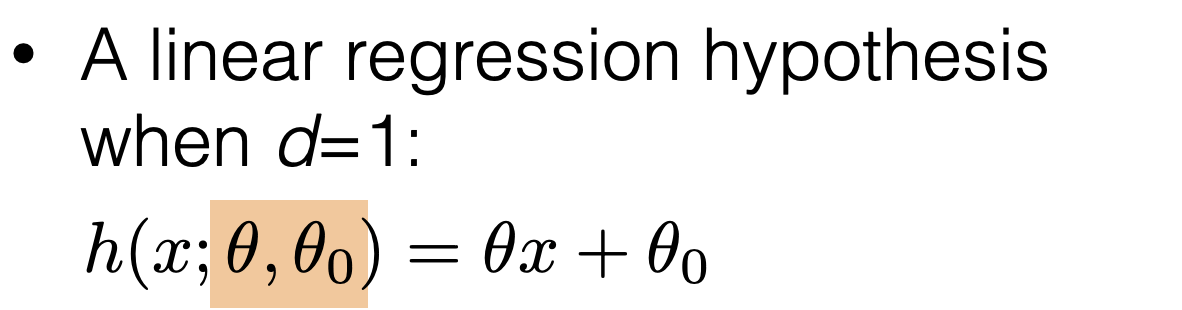
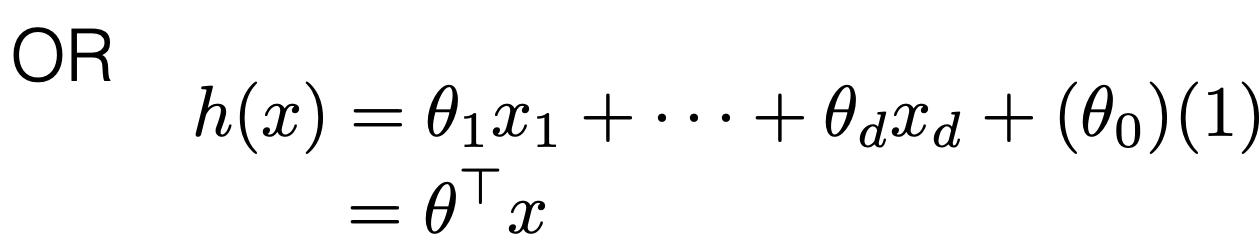
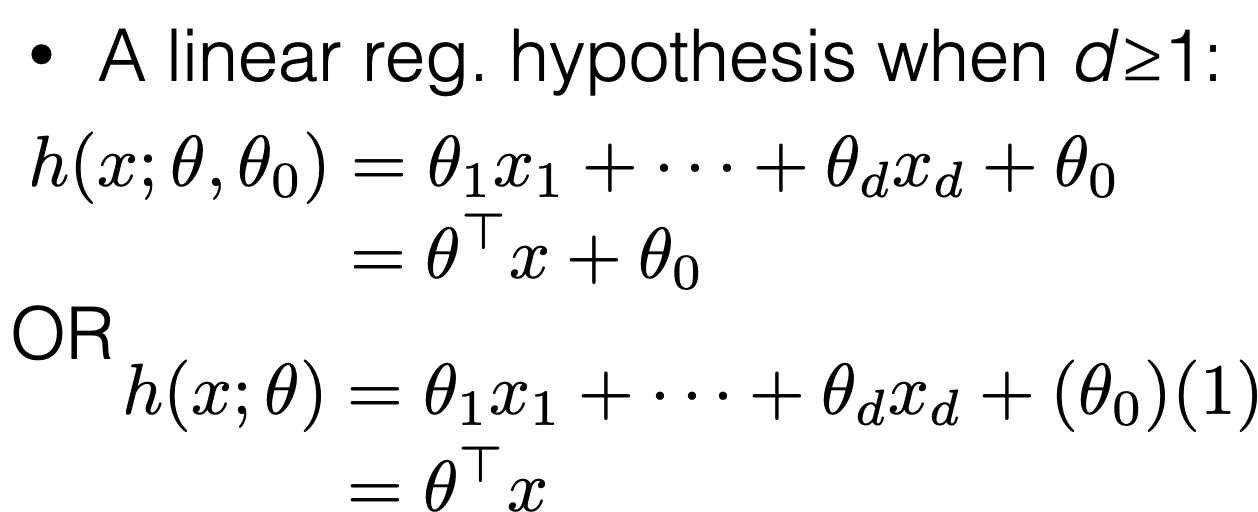
Outline
- Recap of last (content) week.
- Ordinary least-square regression
- Analytical solution (when exists)
- Cases when analytical solutions don't exist
- Practically, visually, mathemtically
- Regularization
- Hyper-parameter, cross-validation
\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}
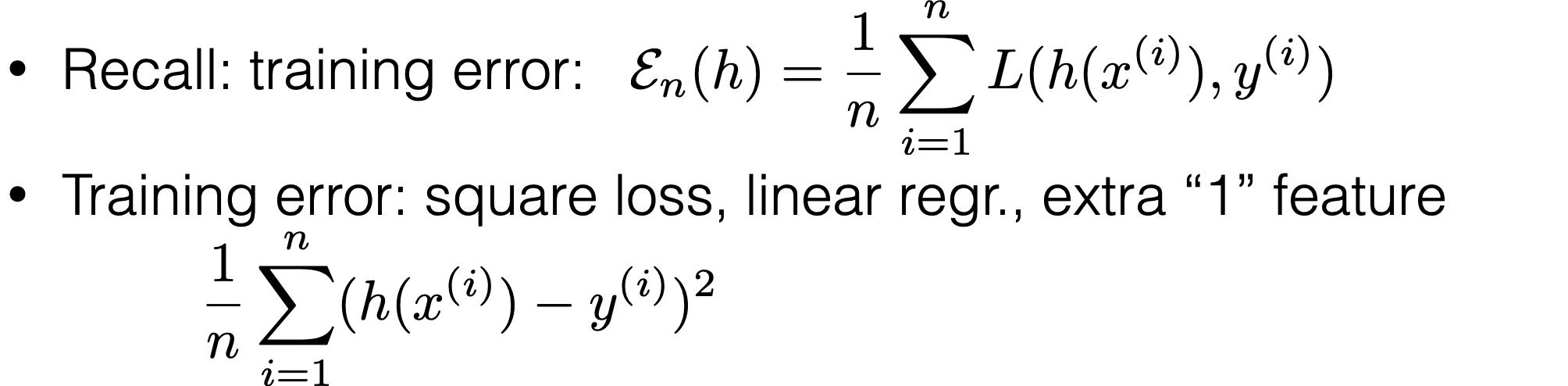
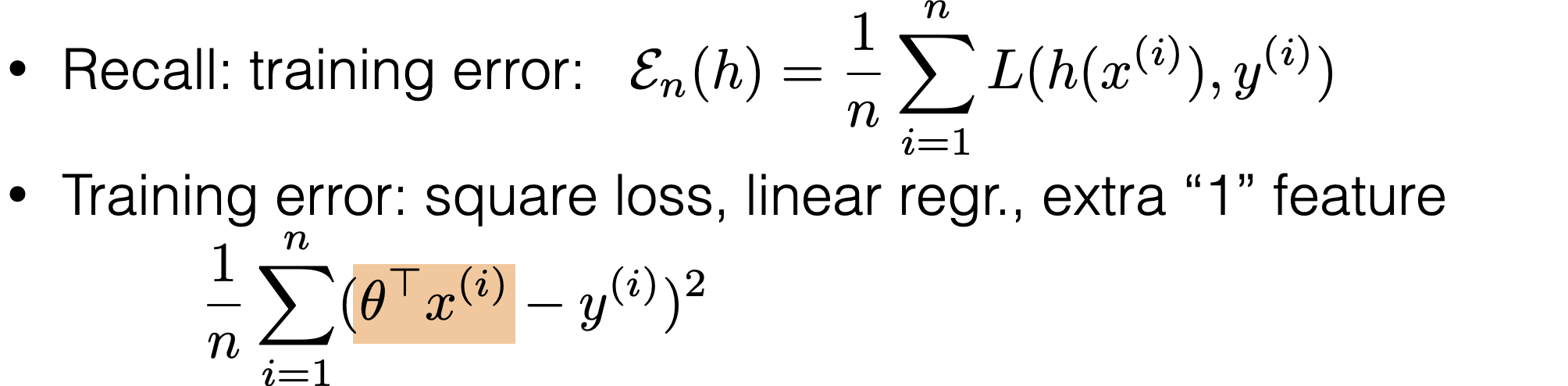
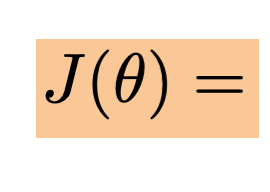
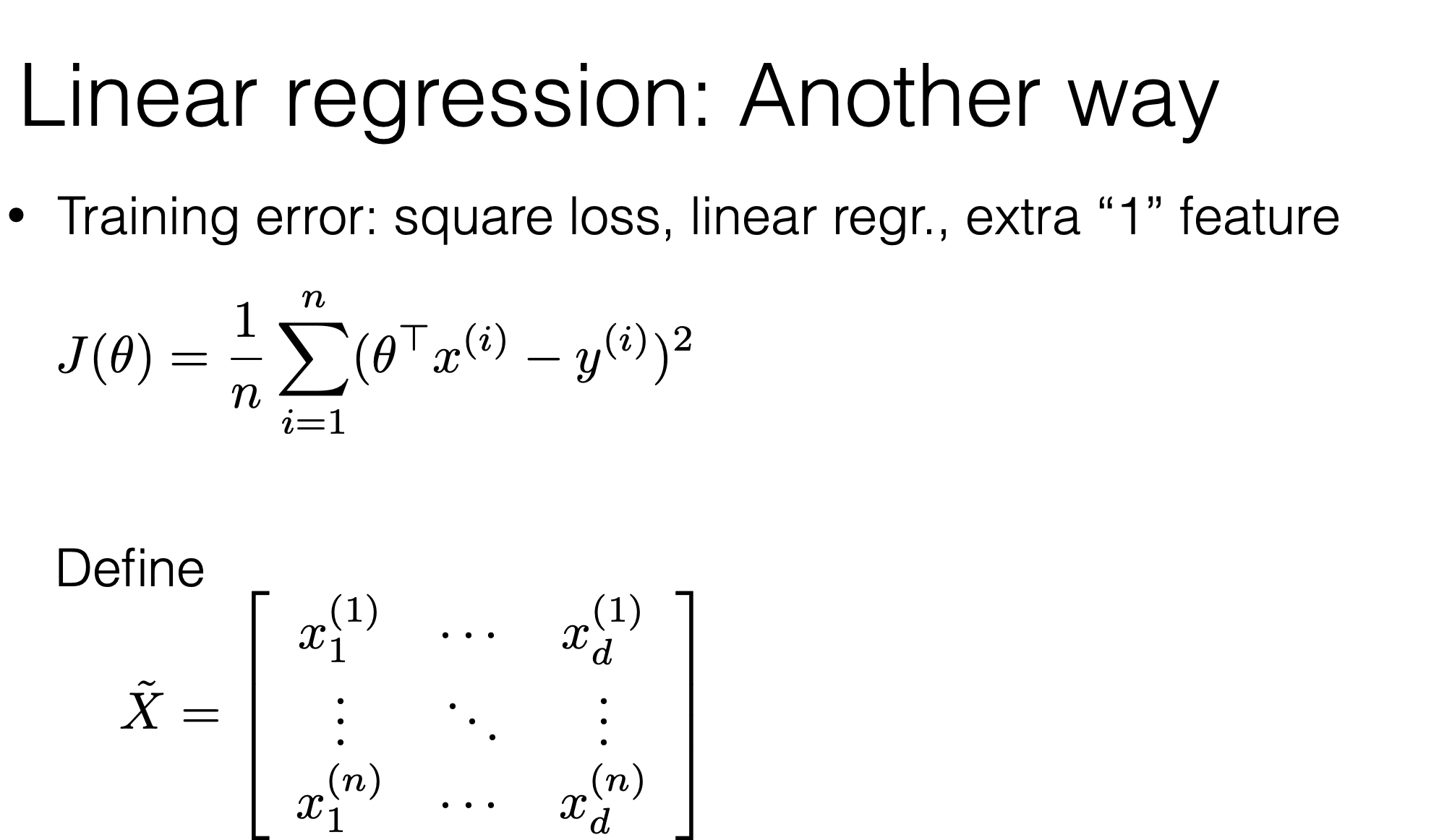
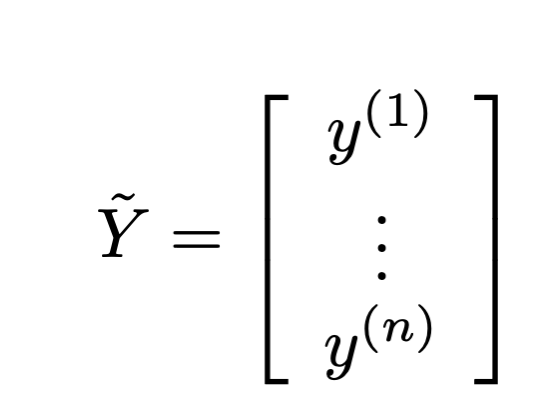
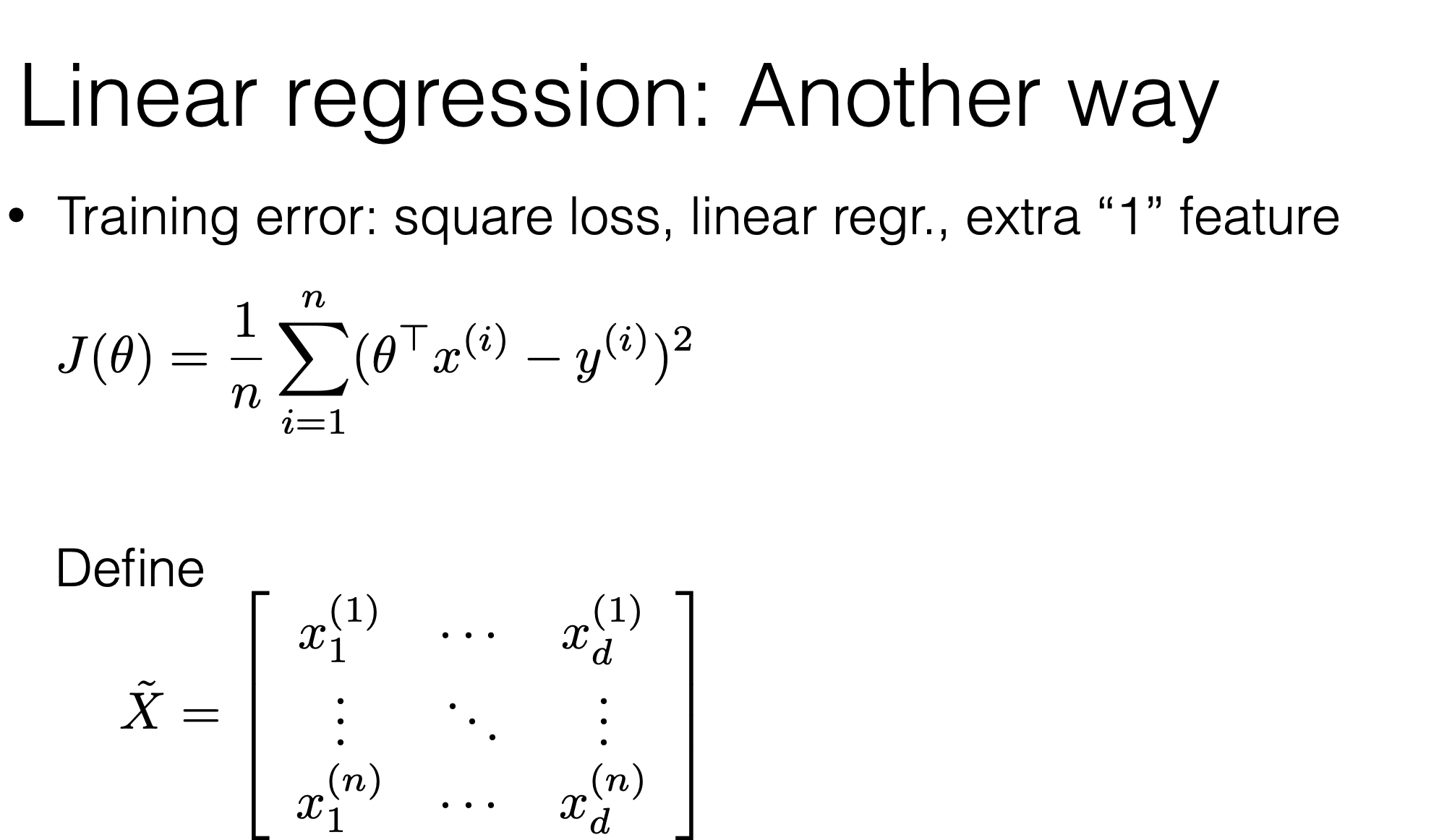
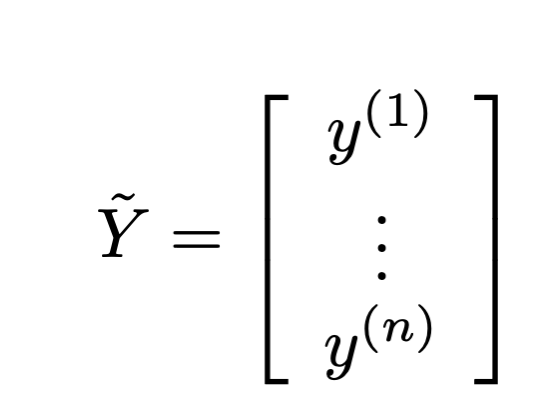
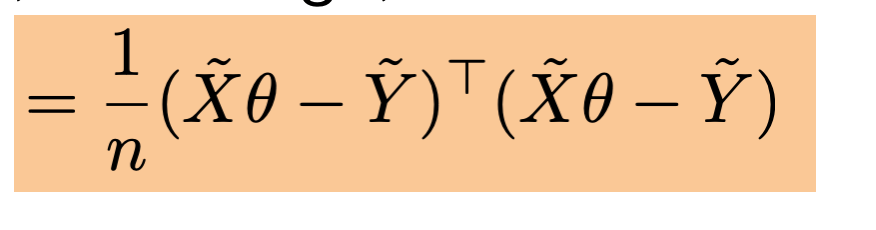
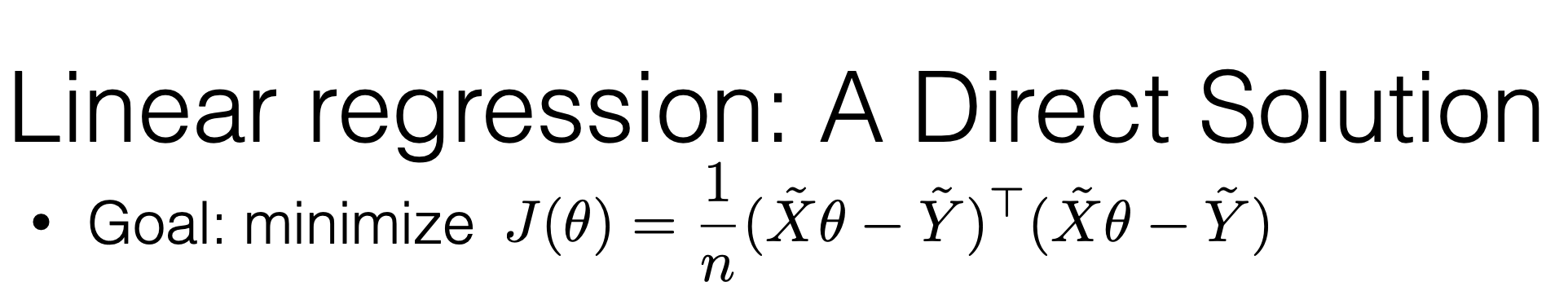
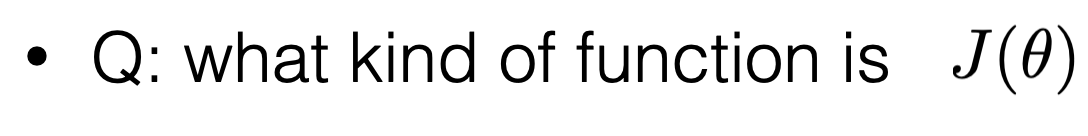
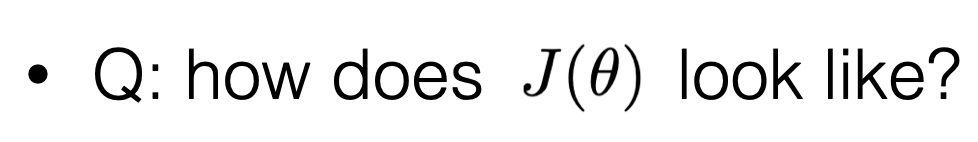
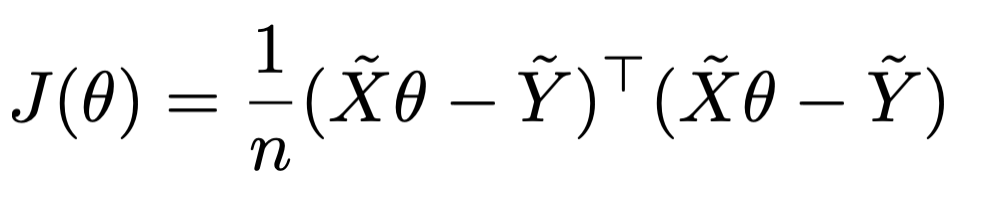
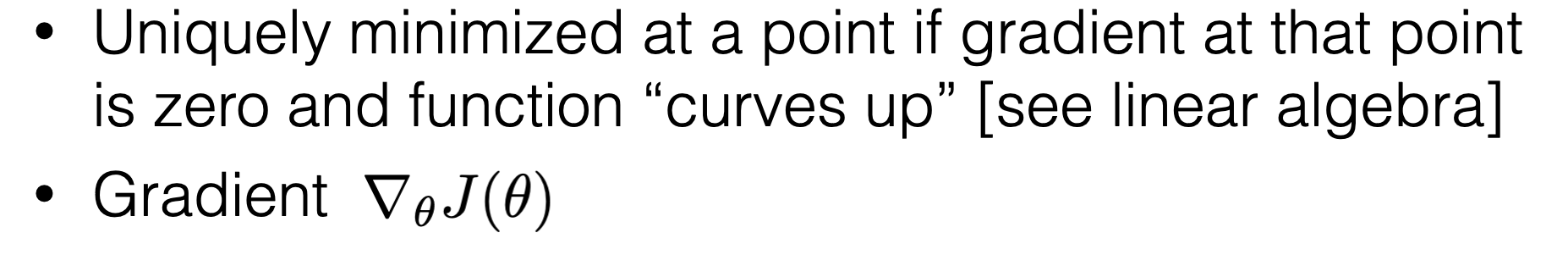
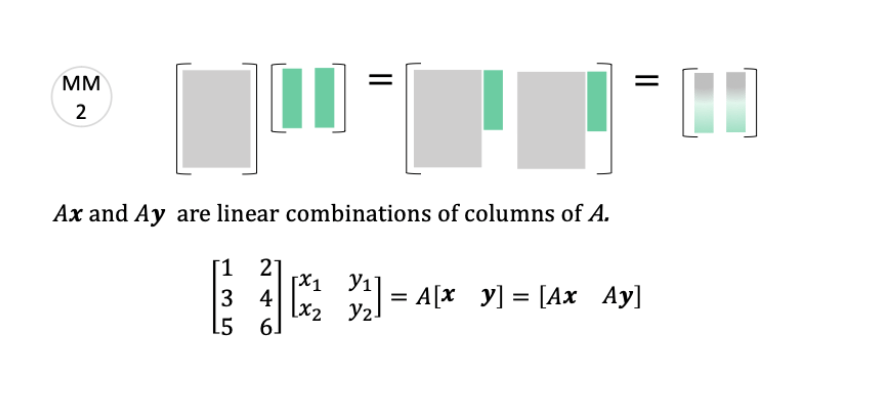
- When \(\theta^*\) exists, guaranteed to be unique minimizer of
\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}
\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}
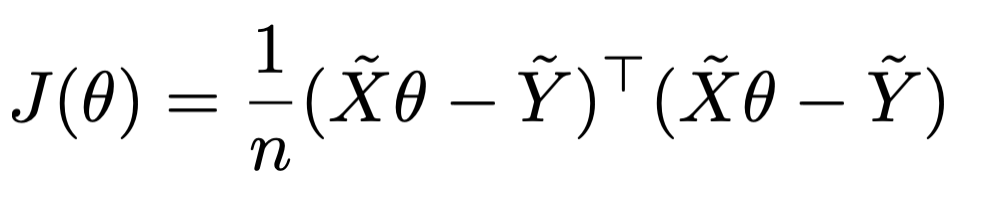
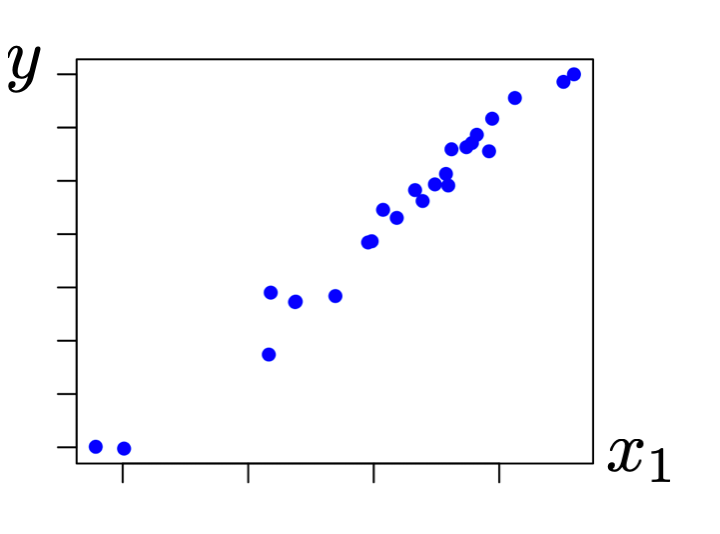
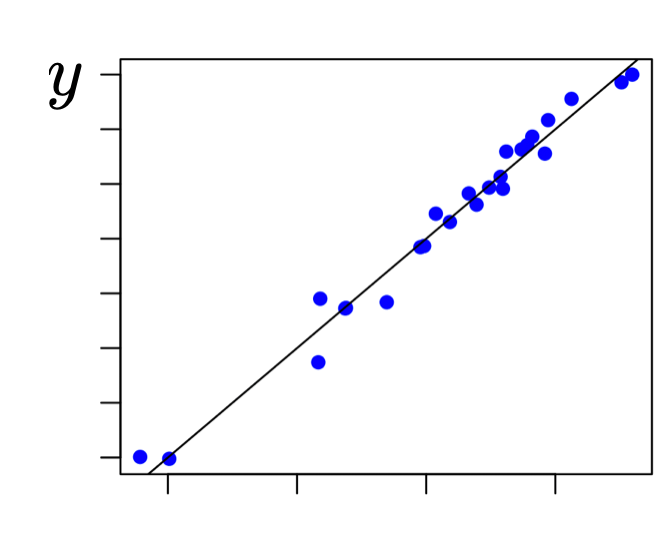
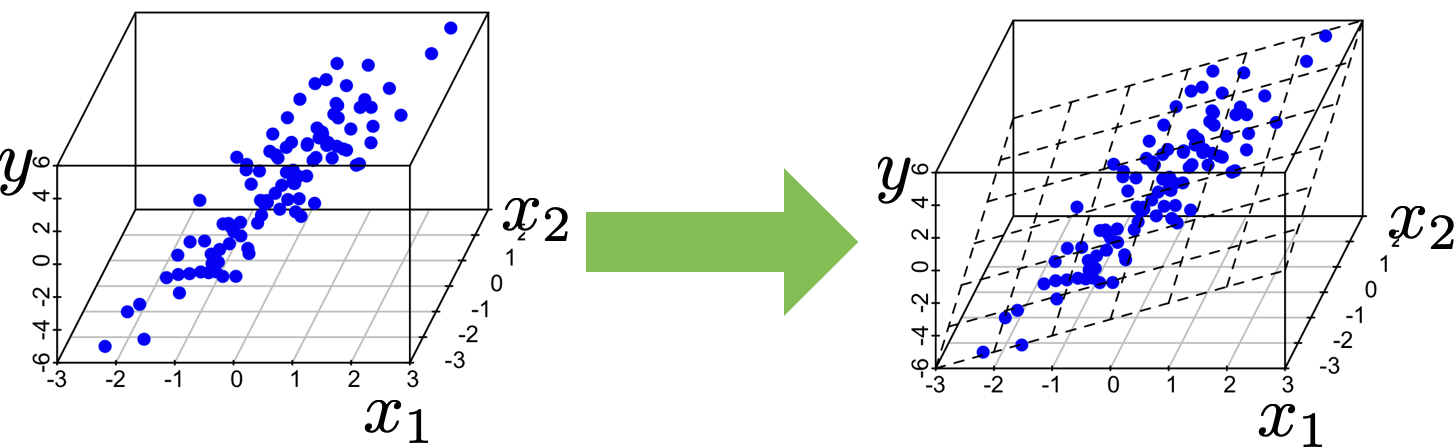
Now, the catch:
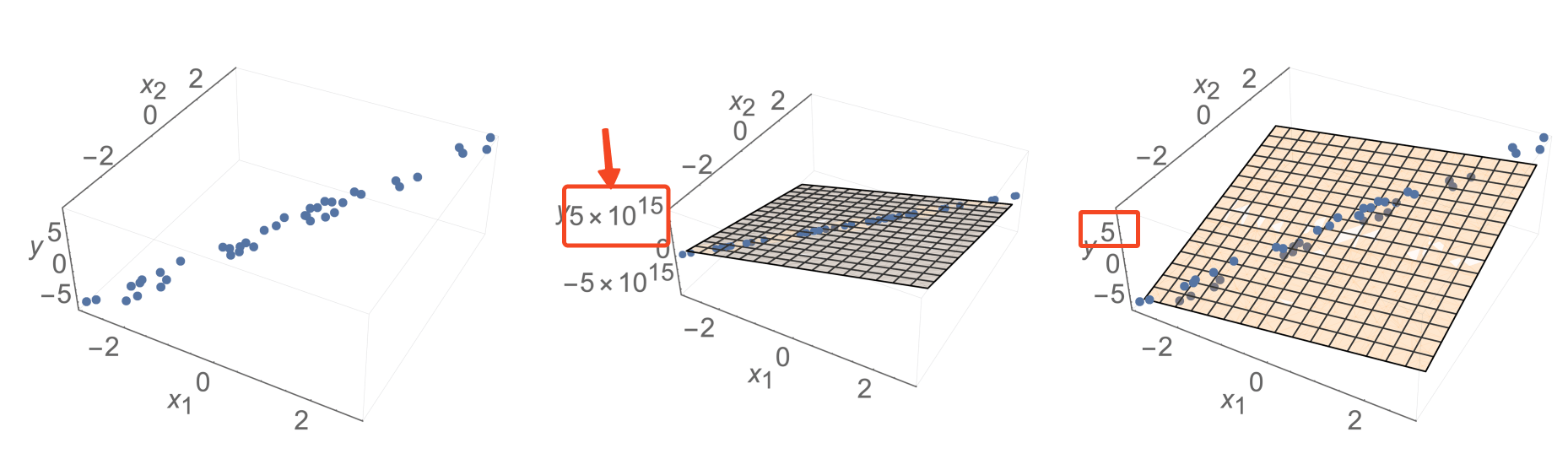
may not be well-defined
- \(\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}\) is not well-defined if \(\left(\tilde{X}^{\top} \tilde{X}\right)\) is not invertible
- Indeed, it's possible that\(\left(\tilde{X}^{\top} \tilde{X}\right)\) is not invertible.
- In particular,\(\left(\tilde{X}^{\top} \tilde{X}\right)\) is not invertible if and only if \(\tilde{X}\) is not full column rank
\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}
Now, the catch:
is not well-defined
if \(\tilde{X}\) is not full column rank
- if \(n\)<\(d\)
- if columns (features) in \( \tilde{X} \) have linear dependency
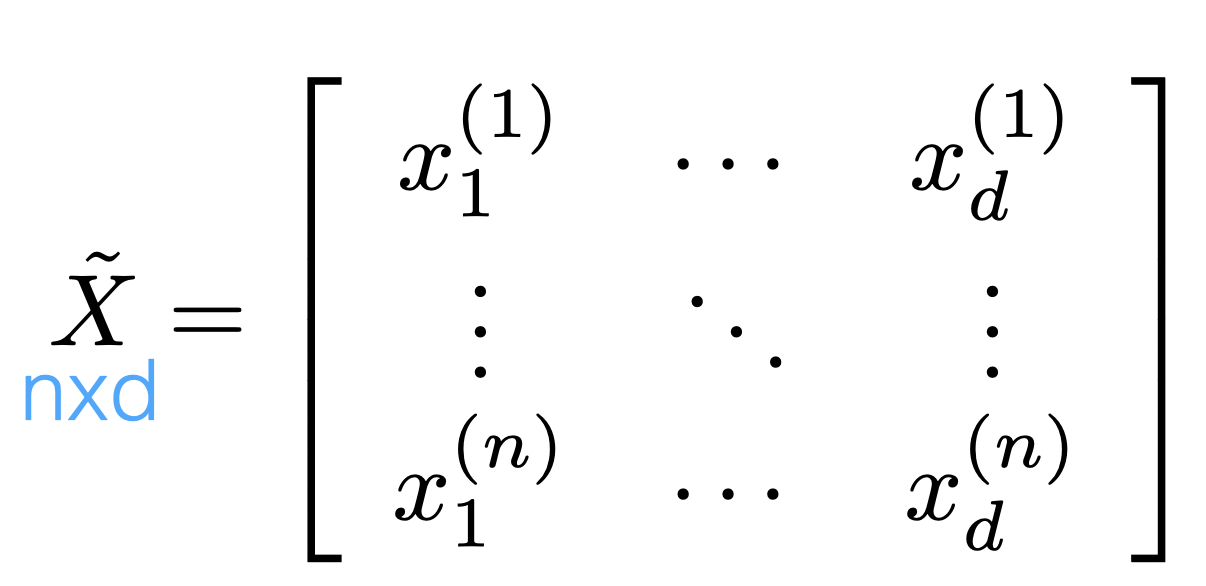
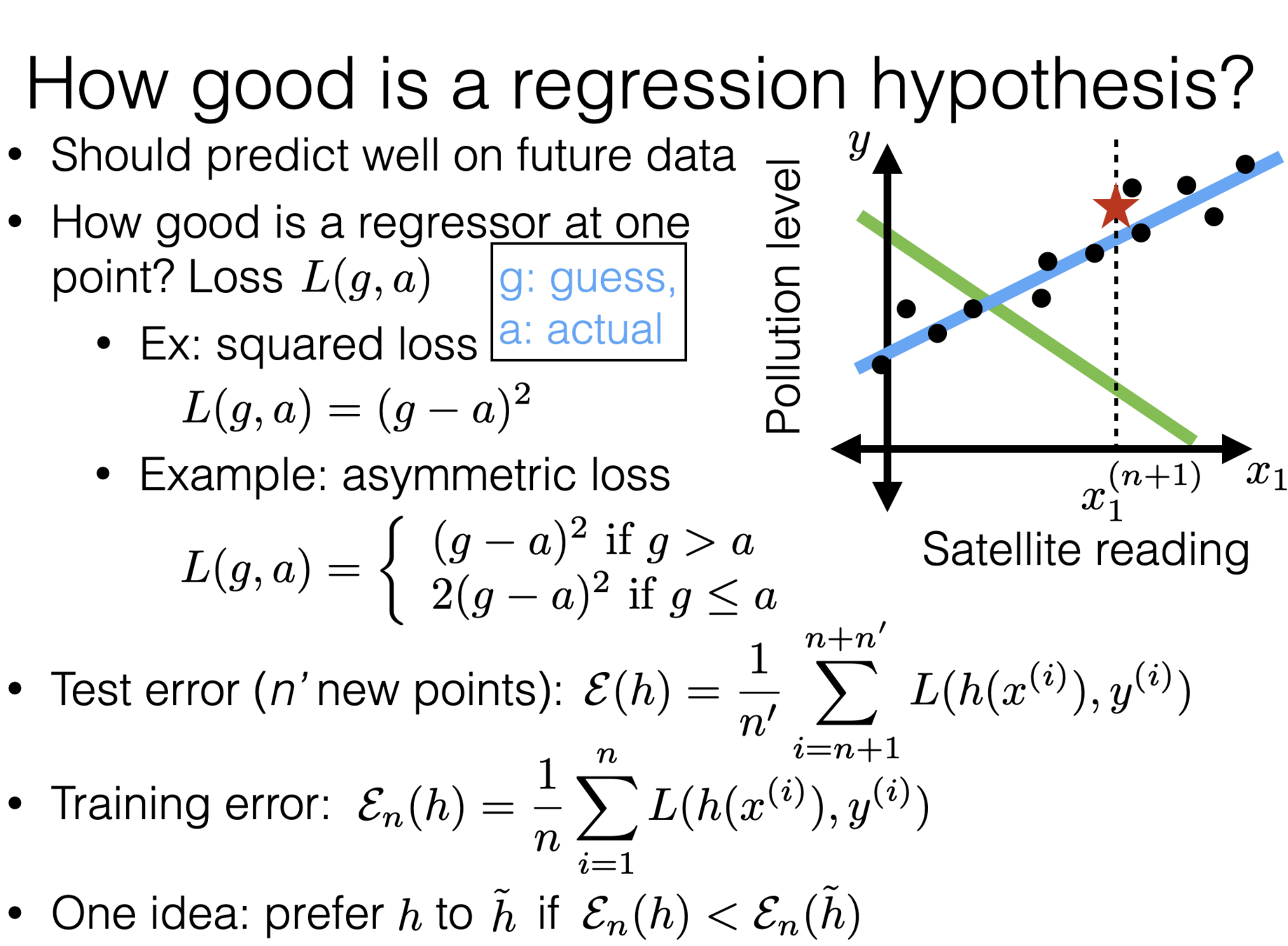
Recall
indeed \(\tilde{X}\) is not full column rank
\theta^*=\left(\tilde{X}^{\top} \tilde{X}\right)^{-1} \tilde{X}^{\top} \tilde{Y}
Recap:
- if \(n\)<\(d\) (i.e. not enough data)
- if columns (features) in \( \tilde{X} \) have linear dependency (i.e., so-called co-linearity)
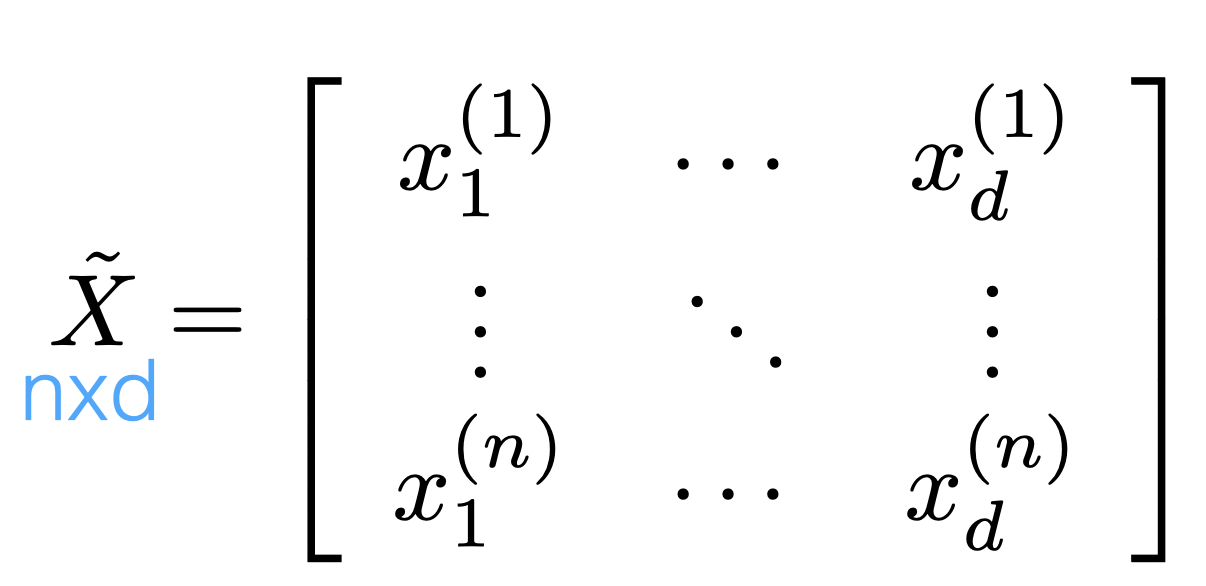
- Both cases do happen in practice
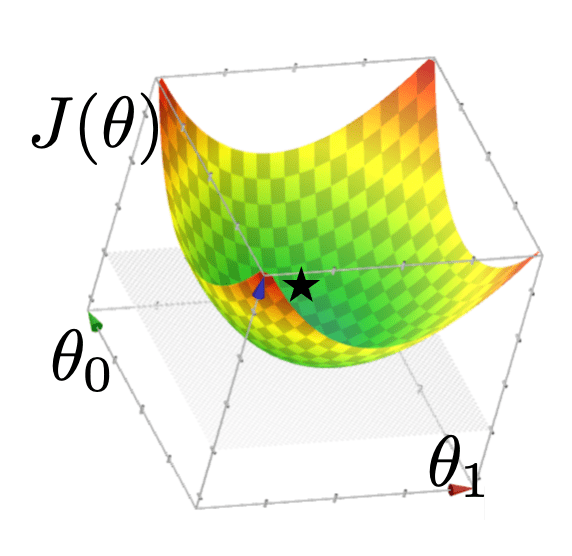
- In both cases, loss function is a "half-pipe"
- In both cases, infinitily-many optimal hypotheses
- Side-note: sometimes noise can resolve invertabiliy issue, but undesirable
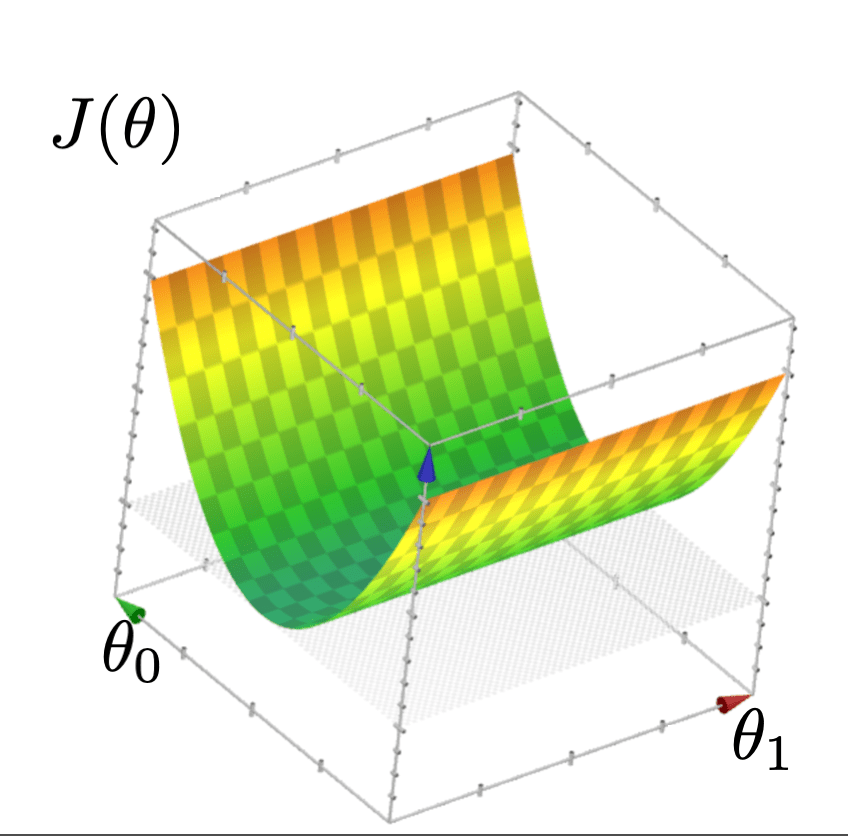
is not defined
Outline
- Recap of last (content) week.
- Ordinary least-square regression
- Analytical solution (when exists)
- Cases when analytical solutions don't exist
- Practically, visually, mathemtically
- Regularization
- Hyper-parameter, cross-validation
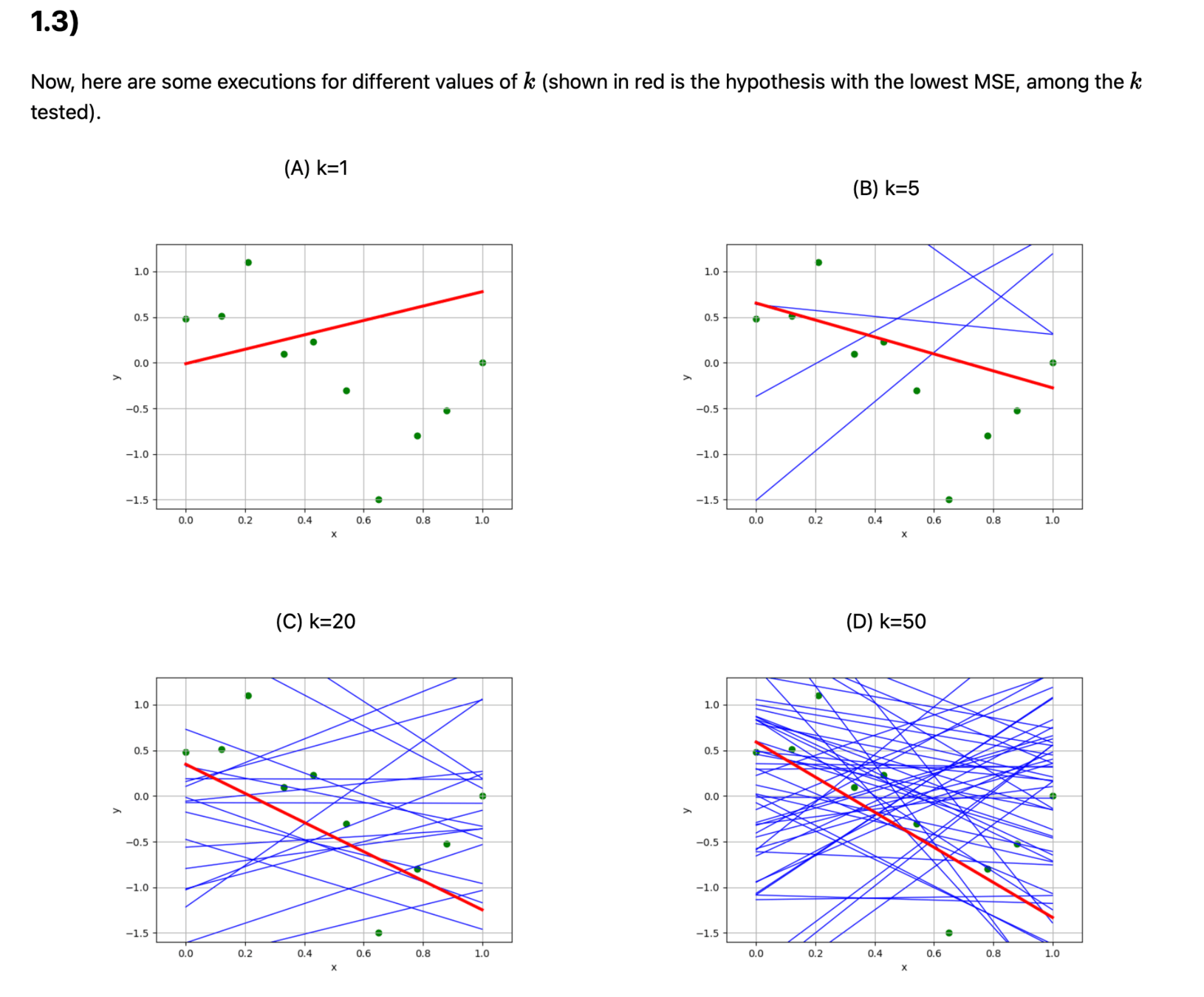
Regularization
🥰
🥺
Ridge Regression Regularization
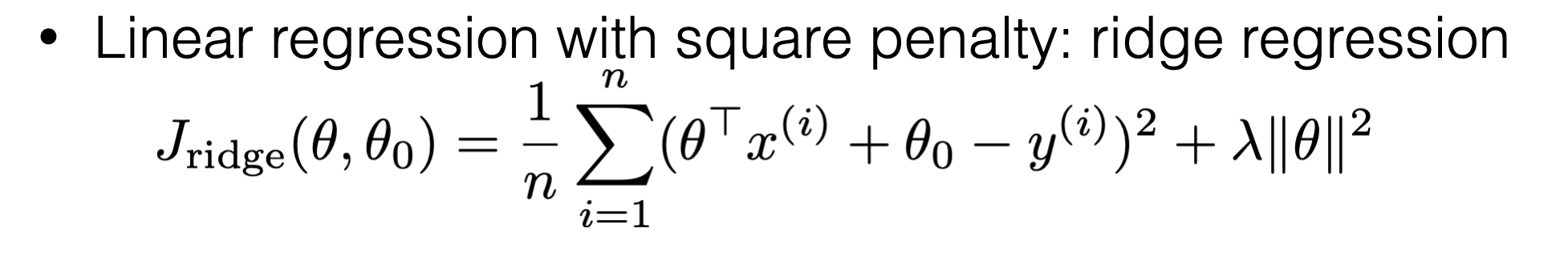
Ridge Regression Regularization
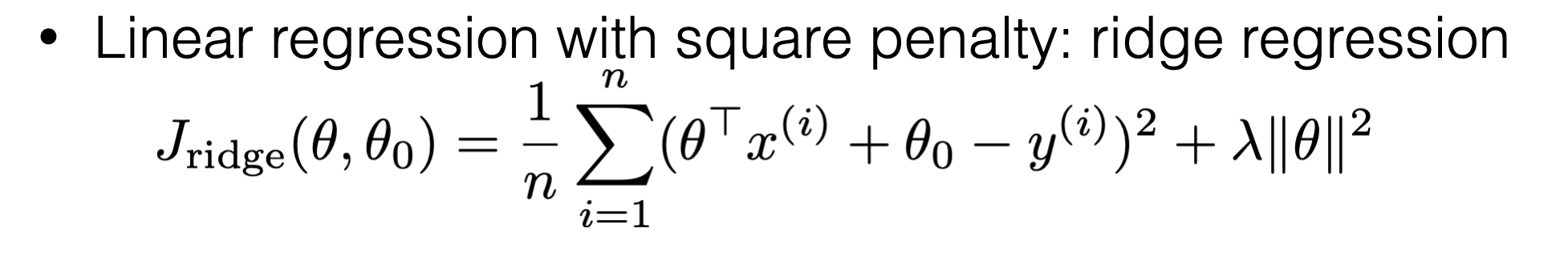
Ridge Regression Regularization
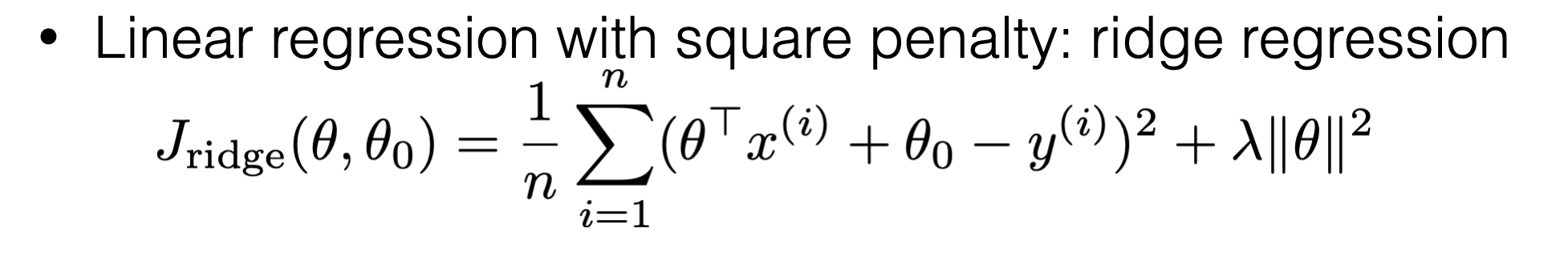
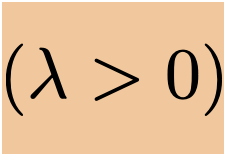
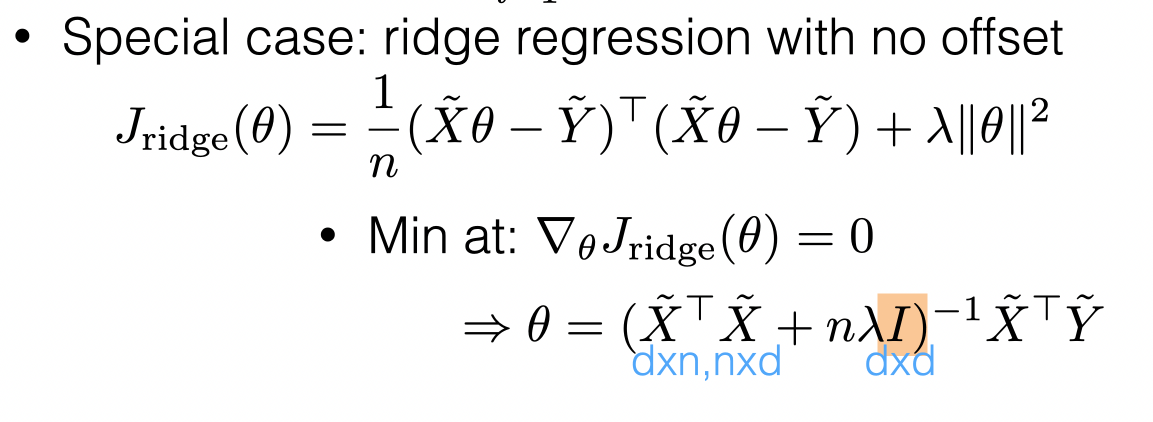
\(\lambda\) is a hyper-parameter
Outline
- Recap of last (content) week.
- Ordinary least-square regression
- Analytical solution (when exists)
- Cases when analytical solutions don't exist
- Practically, visually, mathemtically
- Regularization
- Hyper-parameter, cross-validation
Cross-validation
Cross-validation
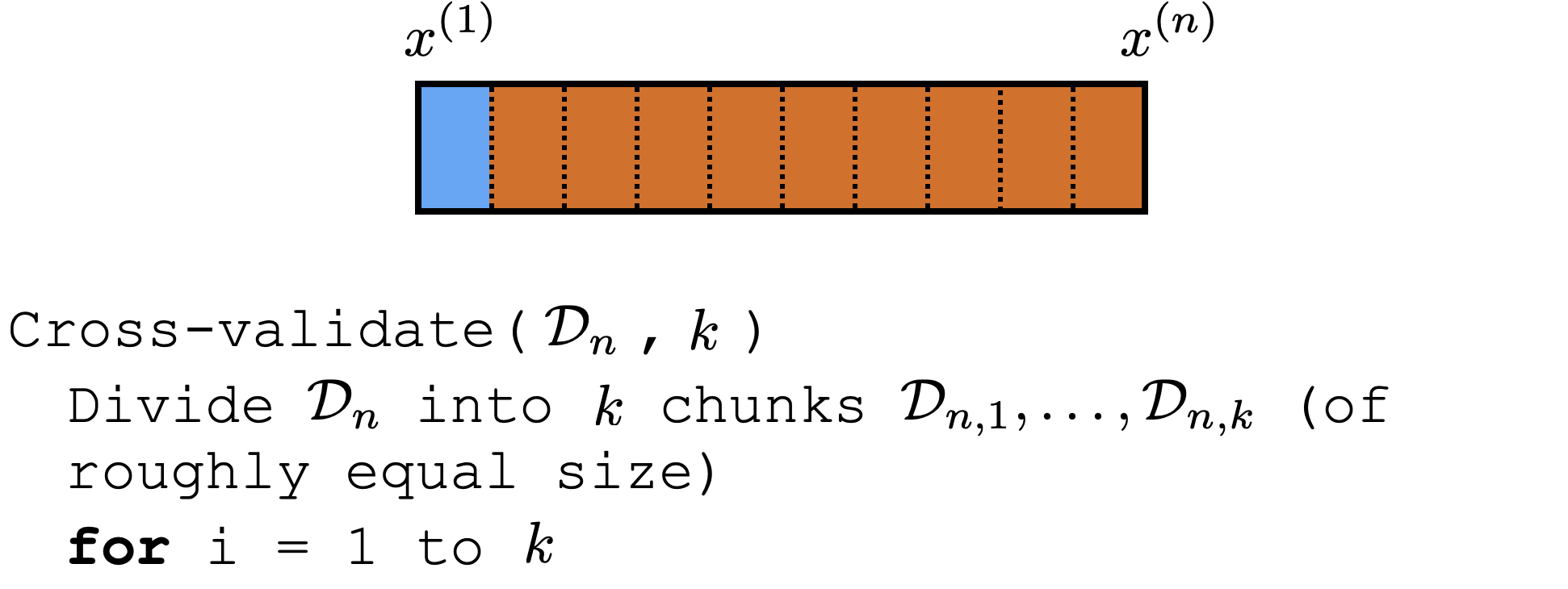
Cross-validation
\dots
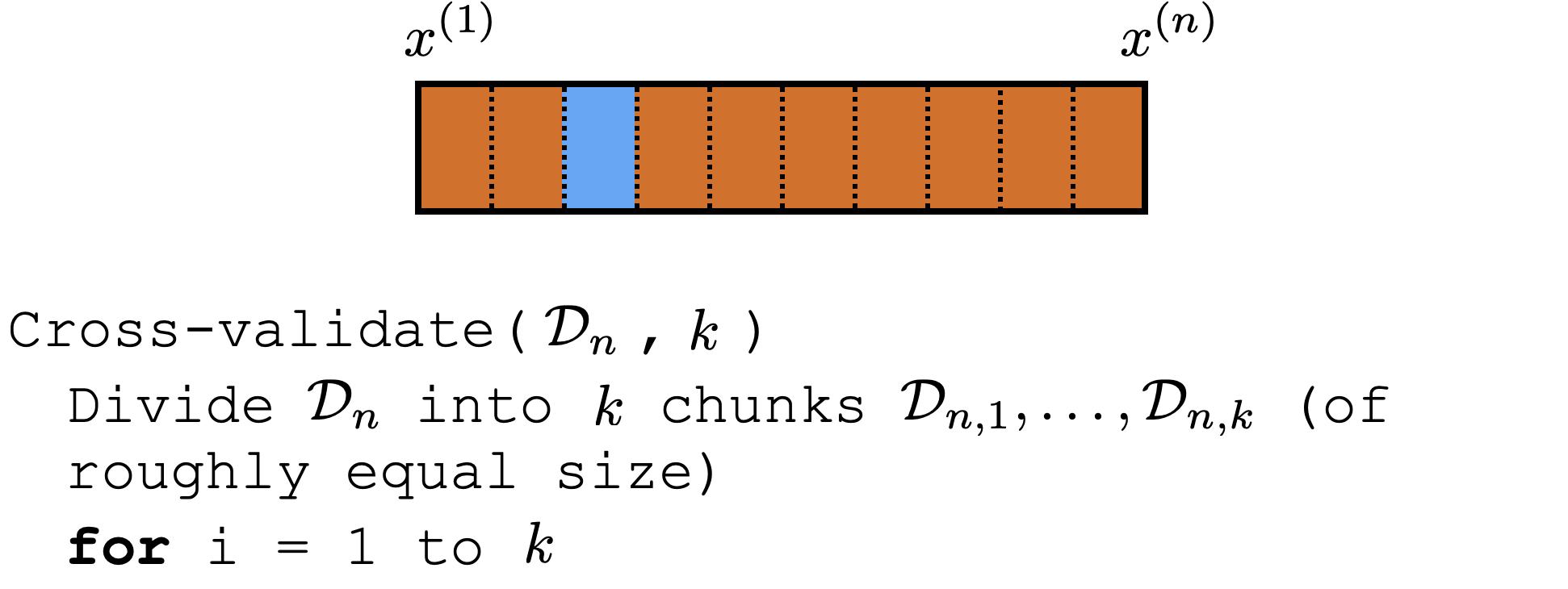
Cross-validation
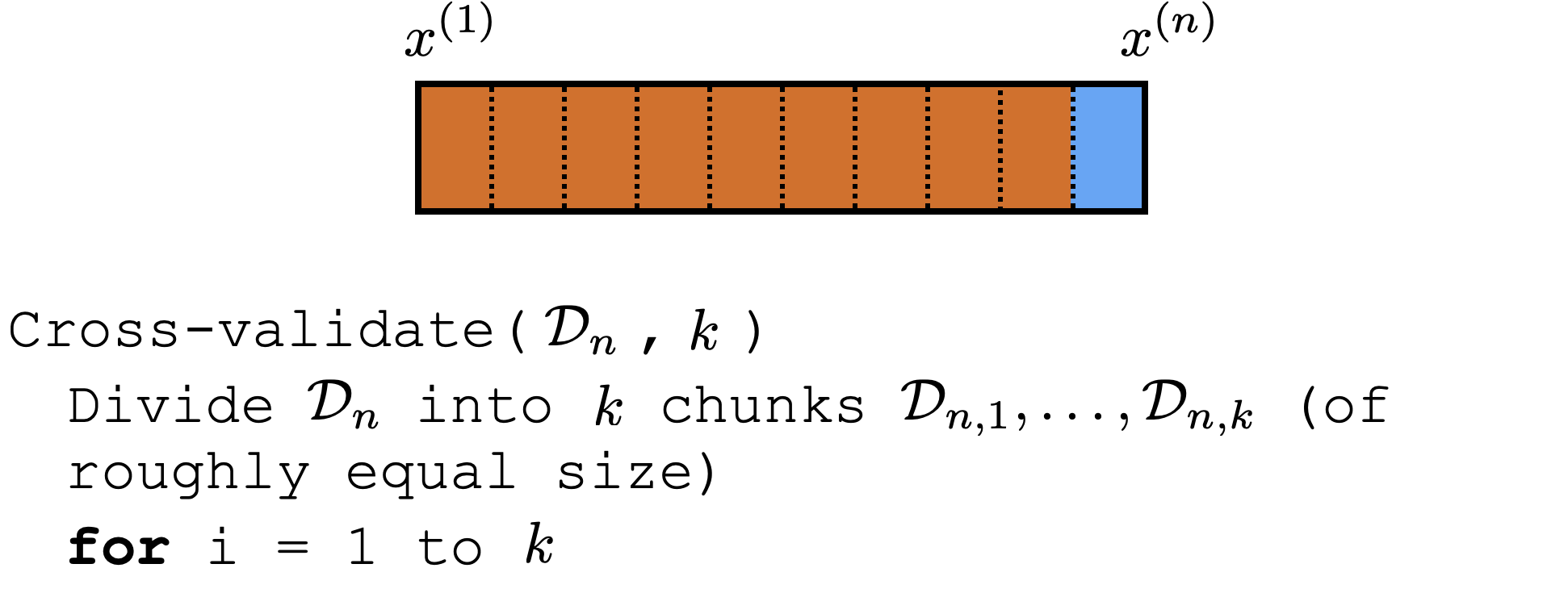
Cross-validation
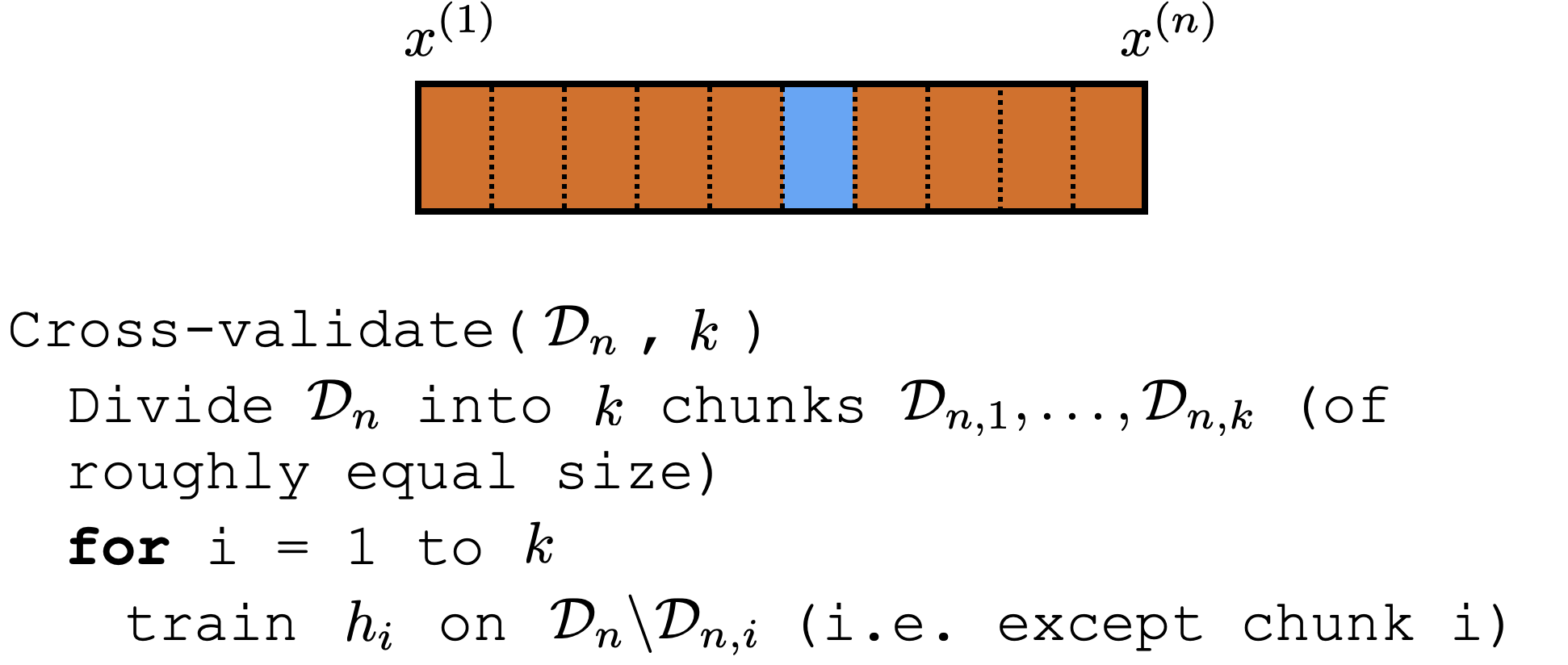
Cross-validation
Cross-validation
Cross-validation
Comments about cross-validation
-
good idea to shuffle data first
-
a way to "reuse" data
-
not evaluating a hypothesis, but rather
-
evaluating learning algorithm. (e.g. hypothesis class, hyper-parameter)
-
Could e.g. have an outer loop for picking good hyper-parameter/class
Summary
- One strategy for finding ML algorithms is to reduce the ML problem to an optimization problem.
- For the ordinary least squares (OLS), we can find the optimizer analytically, using basic calculus! Take the gradient and set it to zero. (Generally need more than gradient info; suffices in OLS)
- Two ways to approach the calculus problem: write out in terms of explicit sums or keep in vector-matrix form. Vector-matrix form is easier to manage as things get complicated (and they will!) There are some good discussions in the lecture notes.
Summary
- What does it mean to well posed.
- When there are many possible solutions, we need to indicate our preference somehow.
- Regularization is a way to construct a new optimization problem
- Least-squares regularization leads to the ridge-regression formulation. Good news: we can still solve it analytically!
- Hyper-parameters and how to pick them. Cross-validation
Thanks!
We'd love it for you to share some lecture feedback.
introml-sp24-lec2
By Shen Shen
