Fusion Energy
Nuclear Physics 303 course

 

 

 

 

 

 

 

 

Presented at Sheffield University on 19/2/2018

by  Jonathan Shimwell

Image by Volker Steger

by Jonathan Shimwell

Fusion Energy, Physics 303 course

Objectives

  • Why and when
  • Reasons for selecting the DT reaction
  • Methods of achieving nuclear fusion
  • Lawson criteria
  • Fusion technology

by Jonathan Shimwell

Fusion Energy, Physics 303 course

Fusion energy has excellent credentials

  • Safe (no run away chain reactions)
  • High energy density (337GJ/g)
  • Clean (reaction waste product is helium)
  • Low Carbon (no CO2 emitted during operation)
  • Produces no long lived radioactivity (Only activated materials)
  • An abundant and distributed fuel source (Lithium and Deuterium)

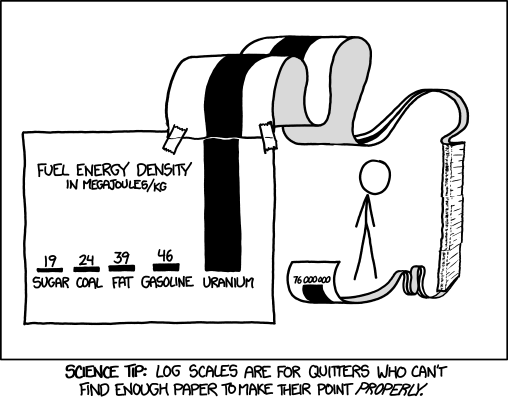
by Jonathan Shimwell

Fusion Energy, Physics 303 course

When will fusion be achieved?

  • Funding
  • The demand for a new energy source
  • Political will
  • Scientific and engineering capacity
  • Unknown unknowns

"Fusion will be ready when society needs it"

Lev Artsimovich, Father of the Tokamak

by Jonathan Shimwell

Fusion Energy, Physics 303 course

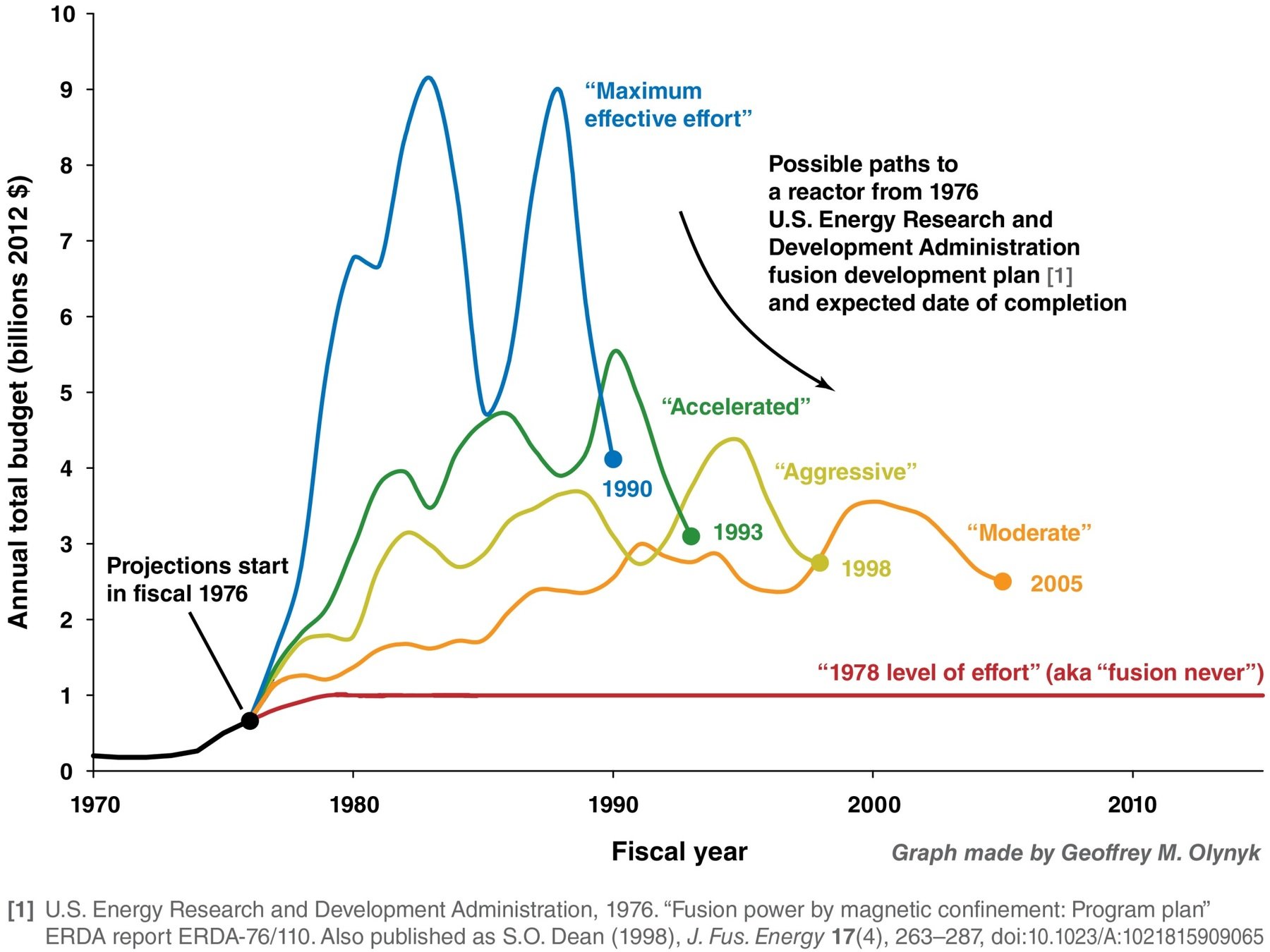
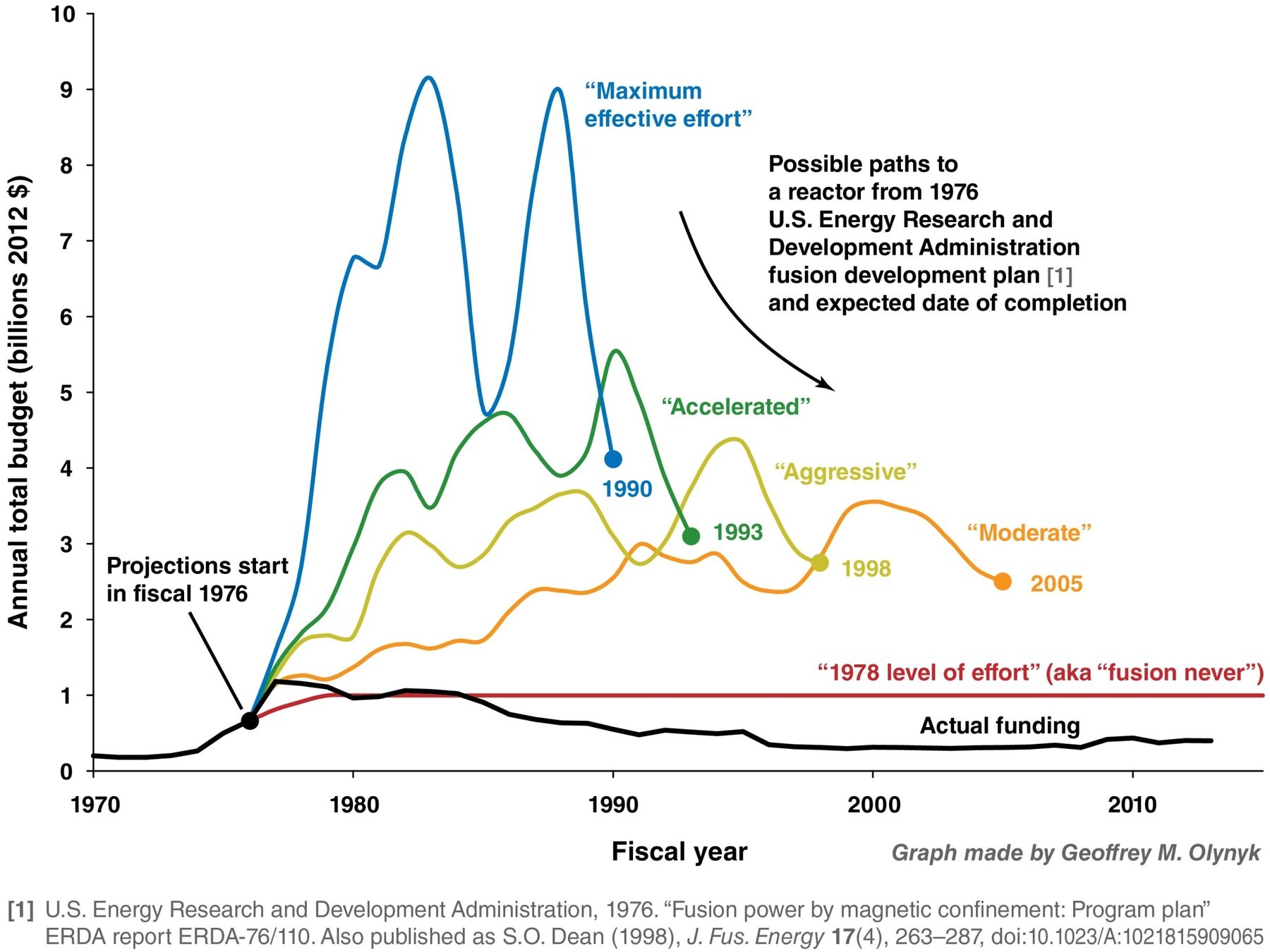
The need for a new energy source

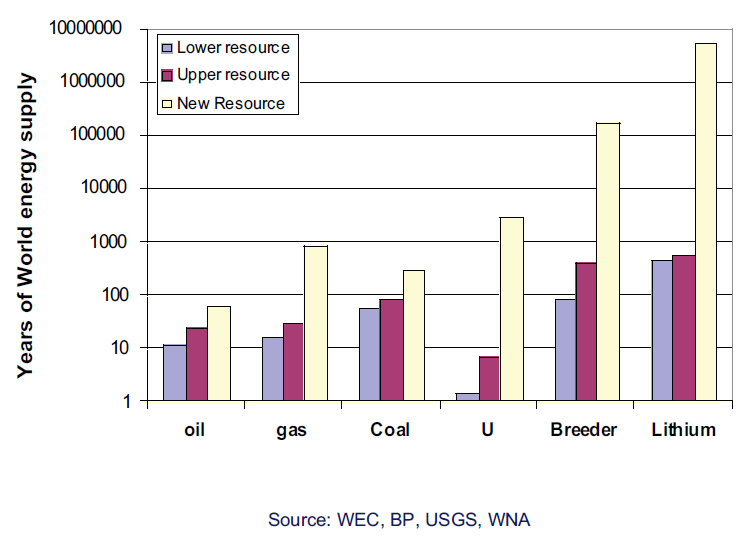
Data source WEC, BP, USGS and WNA data from presentation by  Steven Cowley

Unknown unknowns

link

What is fusion

  • A fusion reaction is the joining of two smaller atoms to form heavier ones.
  • A large amount of energy is released during this process .

 

Deuterium (D)

Tritium (T)

Helium 4

3.5MeV

1/5 of the energy

Neutron

14.1MeV

4/5 of the energy

Helium 5

17.6MeV

Energy emitted from nuclear reactions

  • Calculation of fusion energy  from binding energy

          H3 + H2 = He4 + n

          Binding energy before = 3 x 2.83 + 2 x 1.11

          Binding energy after = 4 x 7.07
          Difference in binding energy is 17.57 MeV

  • Calculation of fission energy from mass difference

      U235 + n= Ba145 + Kr87 + 4n

      Mass before = 235.04393u + 1.00866u

      Mass after = 144.92752u + 86.91335u + 4 x 1.00866u

      Mass difference = 0.17708u = 164.95MeV

proton mass = 1.672623E-27 kg

neutron mass = 1.674929E-27 kg

1 atomic mass unit = 1.660540E-27 kg

Maximum energy emitted from fission and fusion per gram

17.6 MeV emitted per DT fusion

Assuming every D reacts with a T.
1 gram of material.

~200MeV emitted per U235 fission

Assuming 100% U235 enrichment .
Assuming ever U235 fissions.
Ignoring decay heat.
1 gram of material.

 

number\ of\ moles =\frac{mass}{molar \ mass}
number of moles=massmolar massnumber\ of\ moles =\frac{mass}{molar \ mass}
0.2 =\frac{1}{5}
0.2=150.2 =\frac{1}{5}
number \ of \ atoms = number\ of\ moles \times Avogadro's \ constant
number of atoms=number of moles×Avogadro′s constantnumber \ of \ atoms = number\ of\ moles \times Avogadro's \ constant
0.0042 =\frac{1}{235}
0.0042=12350.0042 =\frac{1}{235}
0.0042 \times 6.02 \times 10^{23} = 2.56\times 10^{21}
0.0042×6.02×1023=2.56×10210.0042 \times 6.02 \times 10^{23} = 2.56\times 10^{21}
0.2 \times 6.02 \times 10^{23} = 1.204\times 10^{23}
0.2×6.02×1023=1.204×10230.2 \times 6.02 \times 10^{23} = 1.204\times 10^{23}
1g\ gram\ of\ DT\ fuel\ 1.1\times 10^{24}\ J
1g gram of DT fuel 1.1×1024 J1g\ gram\ of\ DT\ fuel\ 1.1\times 10^{24}\ J
1g\ gram\ of\ U^{235}fuel\ 0.5\times 10^{24}\ J
1g gram of U235fuel 0.5×1024 J1g\ gram\ of\ U^{235}fuel\ 0.5\times 10^{24}\ J

Typical fusion reactions

H2 + H2 = H3 + H1                  Q=4MeV

H2 + H2 = He3 + n                   Q=3.3MeV

H2 + He3 = He4 + H1              Q=18.3MeV

N14 + H1 = O15                       Q=7.35MeV

H2 + H1 = He3                         Q=5.49MeV

C12 + H1 = N13                        Q=12.86MeV

He3 + He3 = He4 + 2 H1         Q=1.95MeV

C13 + H1 = N14                        Q=7.55MeV

H1 + H1 = H2                            Q=0.42MeV

N15 + H1 = C12 + He4             Q=4.96MeV

H2 + H3 = He4 +n                   Q=17.6MeV

Fusion cross section

  • The DT reaction has a higher probability of occurring
  • The DT reaction has a lower threshold temperature
  • The DT reaction releases large amounts of energy 17.6MeV

Main methods of achieving fusion

Magnetic

confinement

Gravitational

confinement

Inertial

confinement

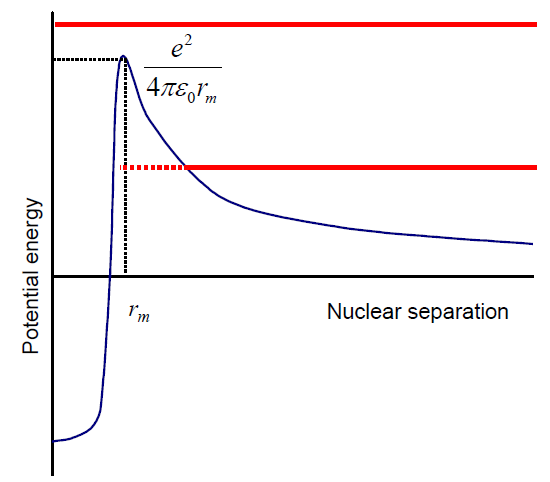
Gravitation confinement

  • The repulsive coulomb force is overcome by gravitational forces and tunneling

 

  • Extremely large masses are required as gravity is a relatively weak force.

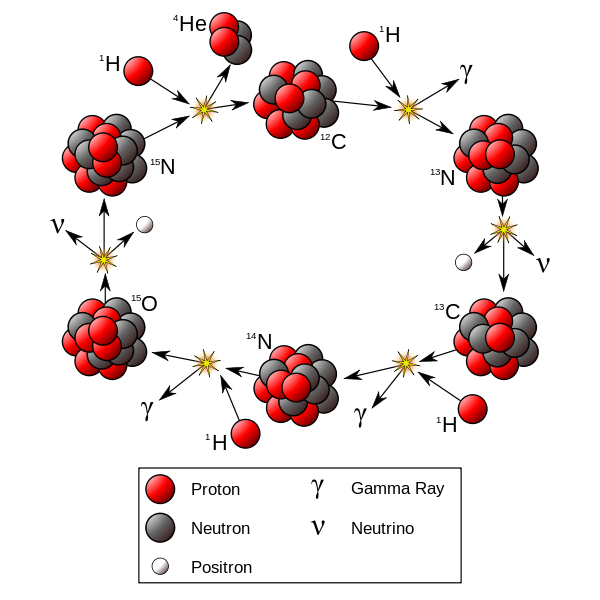
The CNO cycle

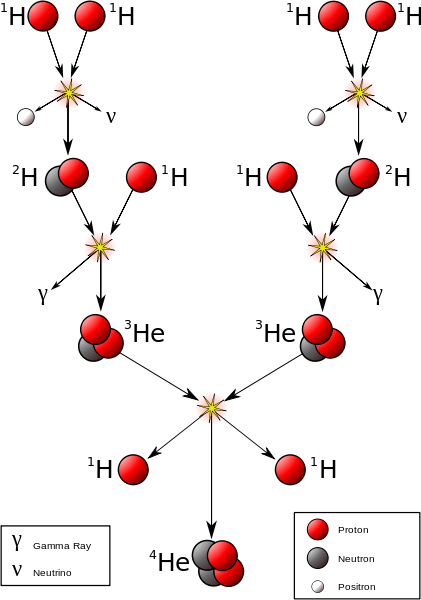
The Proton-Proton reaction

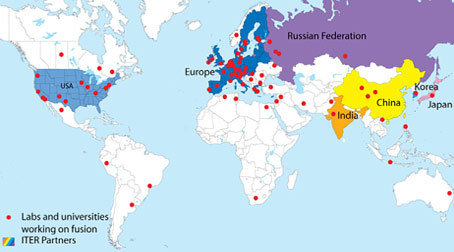
Fusion research around the world

Fusion research around the world

Inertial Confinement

Inertial Confinement

Indirect drive

Direct drive

Inertial Confinement

link

Magnetic Confinement

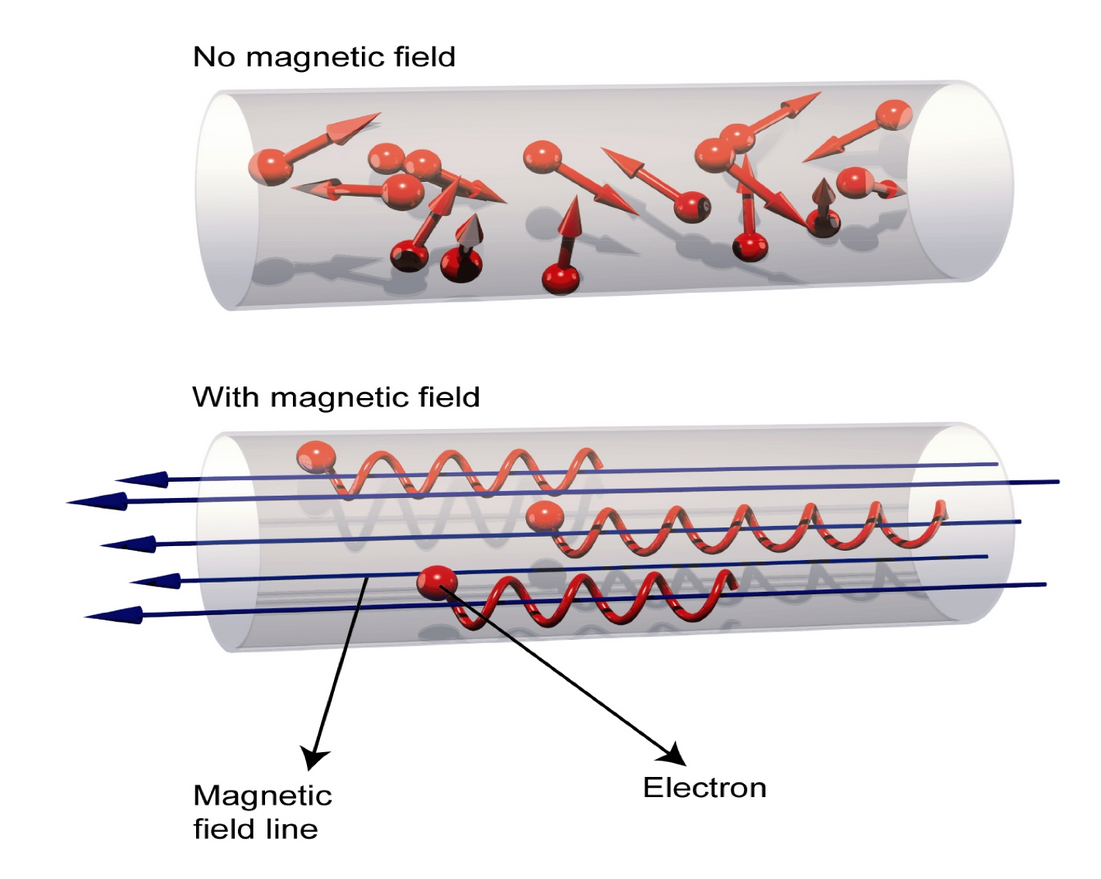
Magnetic Confinement

Poloidal and toroidal magnets

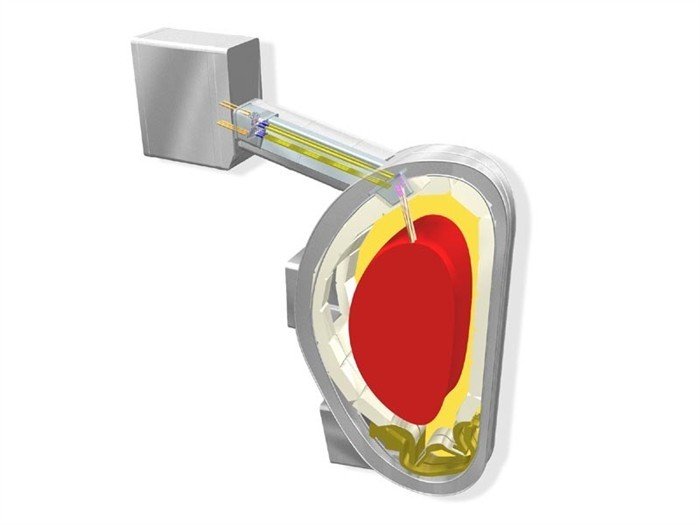
Magnetic Confinement

Magnetic Confinement

link

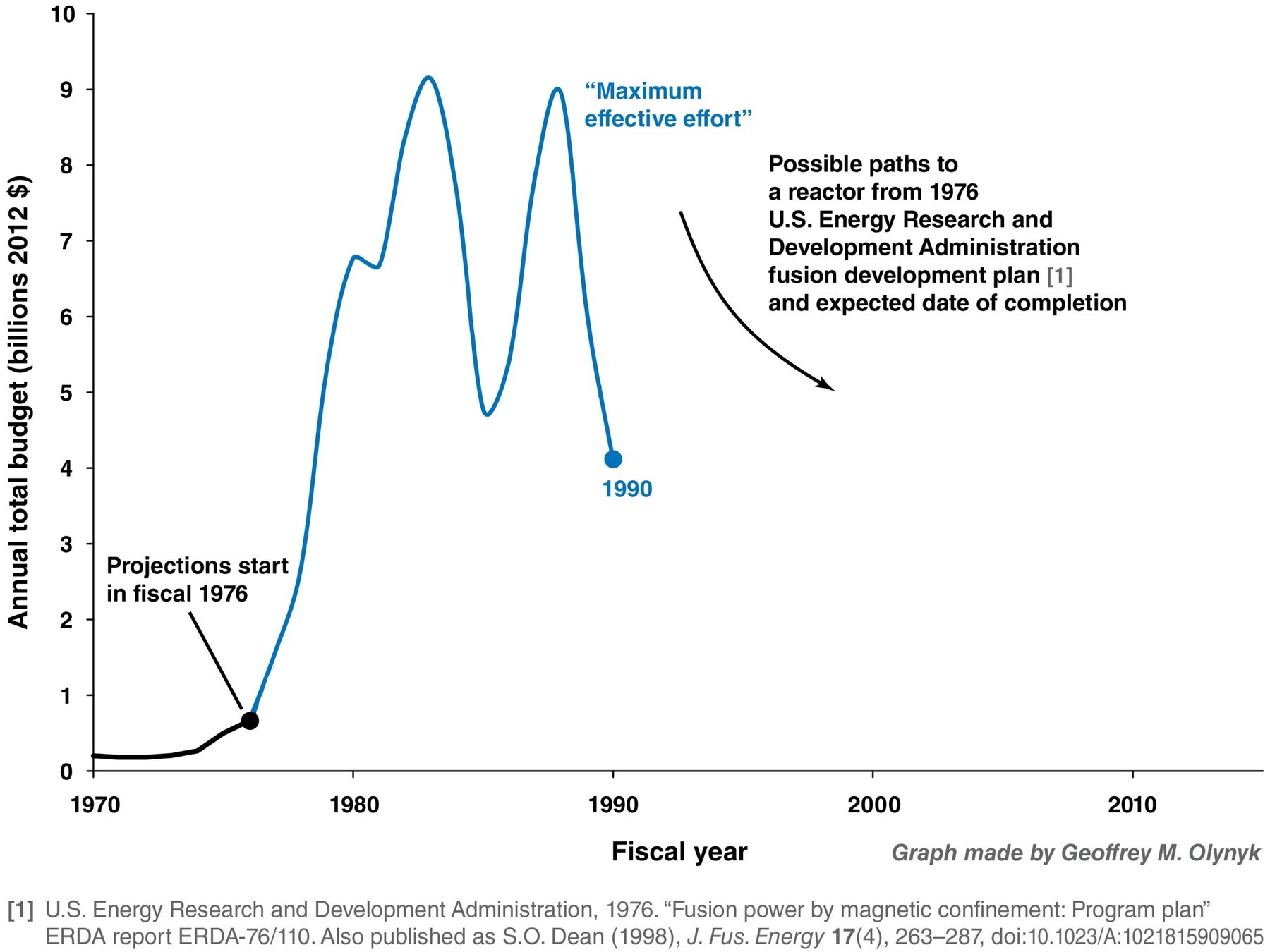
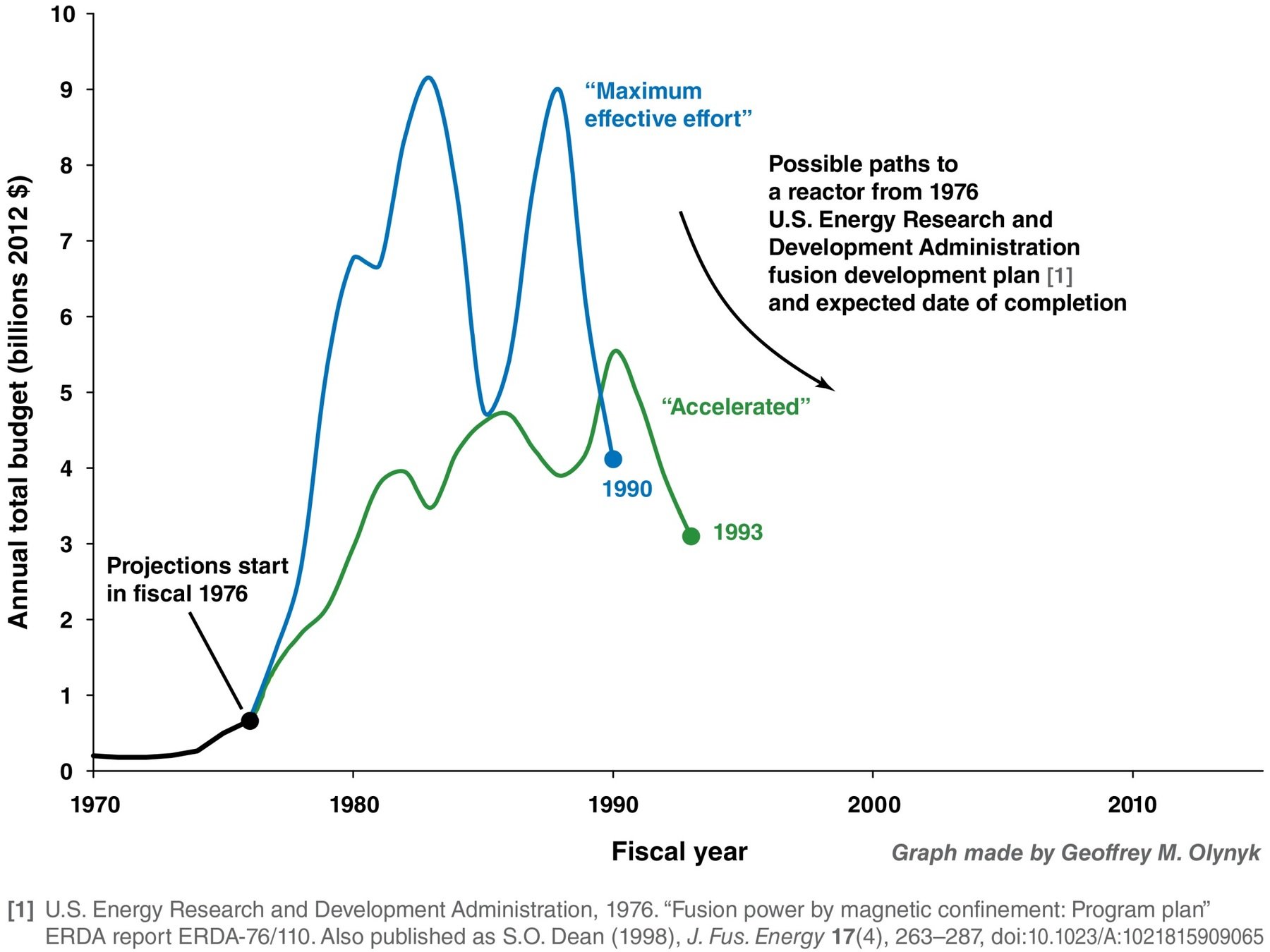
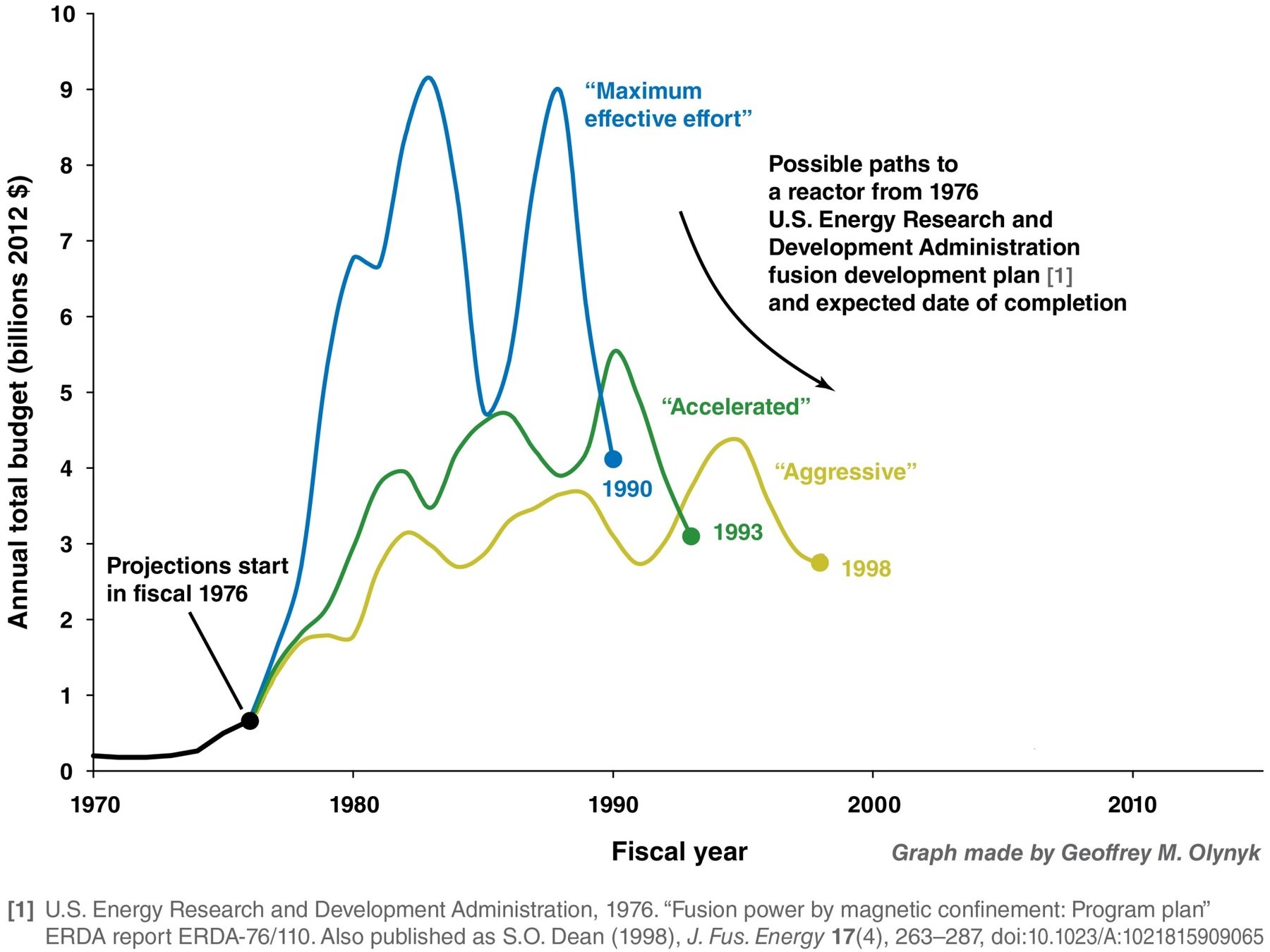
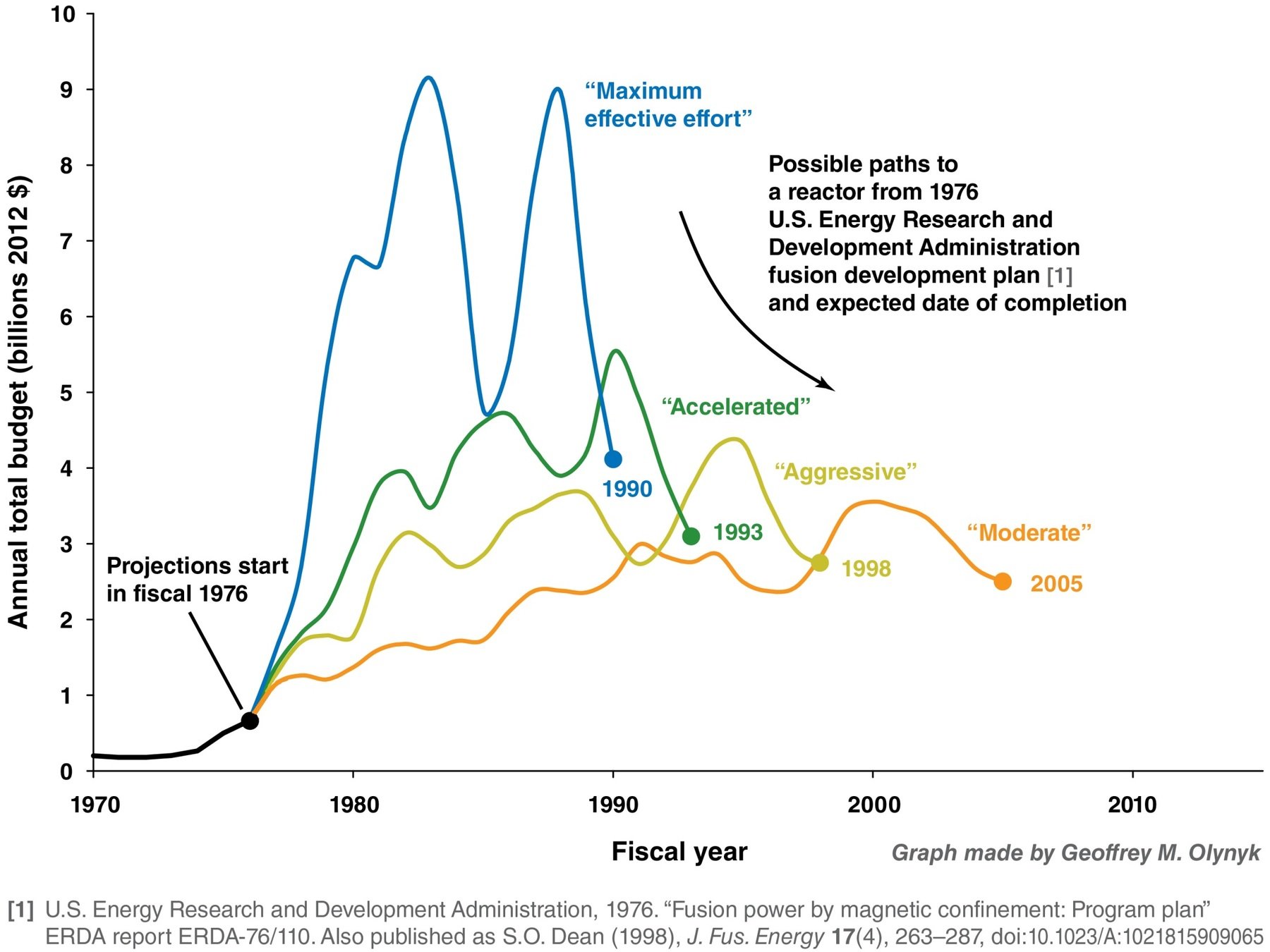
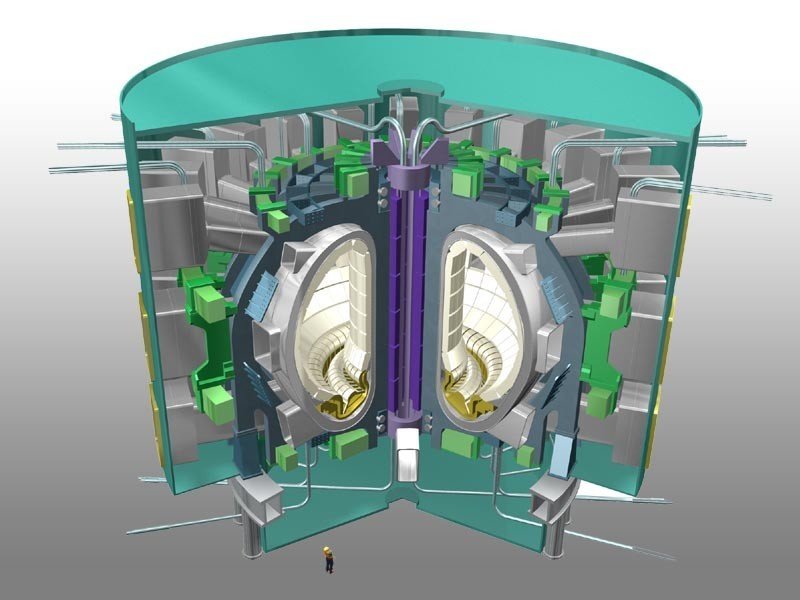
Magnetic Confinement Roadmap

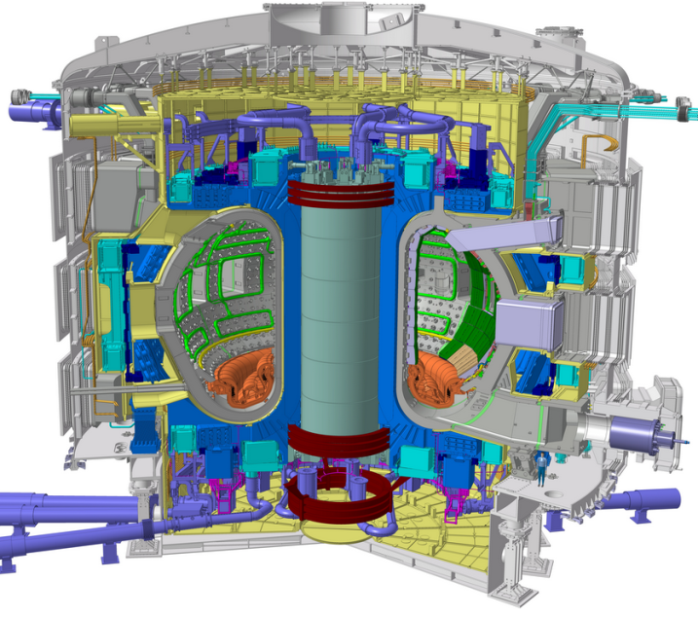
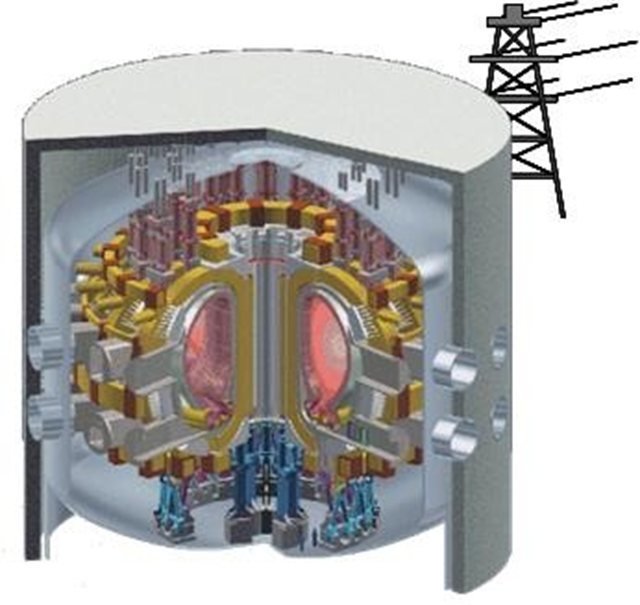
ITER reactor

800m3 plasma volume

500MW thermal

DEMO reactor

1000-3500m3 plasma volume

4000MW thermal

JET reactor

80m3 plasma volume

16MW thermal

Tore Supra

25m3 plasma volume

0MW thermal

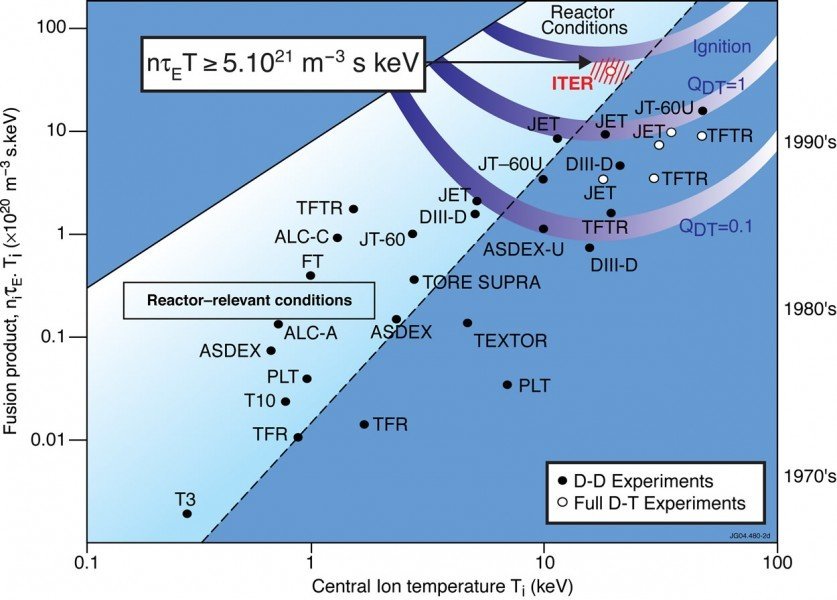
Ignition


The point where a fusion reaction becomes self-sustaining instead of requiring a constant input of energy. In the case of DT fusion the plasma is heated by the energetic alpha particle that is emitted during fusion reactions. This is also known as self heated plasma

 

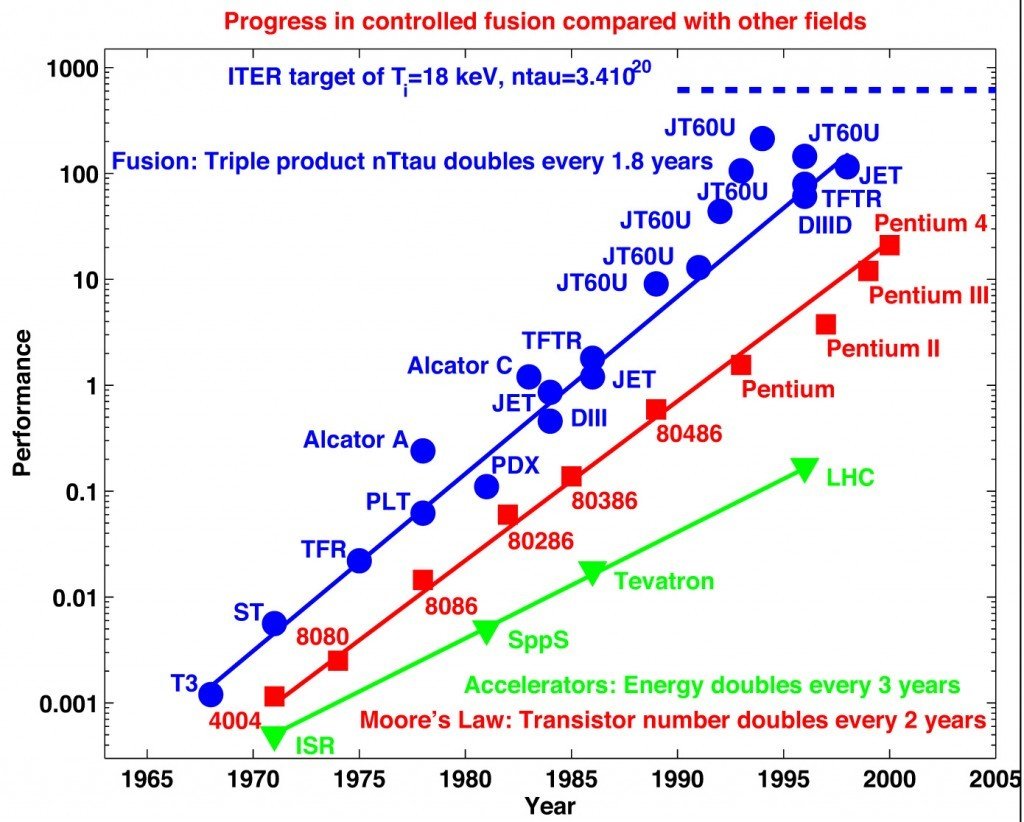
Lawson criteria

The lawson criteria defines the general requirements (temperature, density and confinement time) of a reactor to reach a self sustaining reaction (ignition).

n_e\tau \geq
neτ≥n_e\tau \geq
12K_BT_e
12KBTe12K_BT_e
Q<\sigma v>
Q<σv>Q<\sigma v>

Confinement time

Boltzmann constant

Temperature of electrons

Number density of electrons

Energy released per fission

Cross section of reaction

Average velocity of ions

Derivation of Lawson Criterion for DT fusion

\tau = \frac{w}{P_{loss}}
τ=wPloss\tau = \frac{w}{P_{loss}}
w = \int_{}^{}( \frac{3}{2}k_Bn_eT_e+\frac{3}{2}k_Bn_DT_D +\frac{3}{2}k_Bn_tT_t)dV
w=∫(32kBneTe+32kBnDTD+32kBntTt)dVw = \int_{}^{}( \frac{3}{2}k_Bn_eT_e+\frac{3}{2}k_Bn_DT_D +\frac{3}{2}k_Bn_tT_t)dV
n_e = n_{ions} = n_D + n_t
ne=nions=nD+ntn_e = n_{ions} = n_D + n_t
w =\frac{3}{2}k_BT_e(n_e+0.5n_e+0.5n_e)V
w=32kBTe(ne+0.5ne+0.5ne)Vw =\frac{3}{2}k_BT_e(n_e+0.5n_e+0.5n_e)V
P_{loss} = \frac{3k_BT_en_eV}{\tau}
Ploss=3kBTeneVτP_{loss} = \frac{3k_BT_en_eV}{\tau}
R = n_Dn_t<\sigma_fv>V
R=nDnt<σfv>VR = n_Dn_t<\sigma_fv>V
RQ = n_Dn_t<\sigma_fv>VQ
RQ=nDnt<σfv>VQRQ = n_Dn_t<\sigma_fv>VQ
RQ \geq P_{loss}
RQ≥PlossRQ \geq P_{loss}
\frac{1}{4}n_e^2<\sigma_fv>QV \geq \frac{3k_BT_en_eV}{\tau}
14ne2<σfv>QV≥3kBTeneVτ\frac{1}{4}n_e^2<\sigma_fv>QV \geq \frac{3k_BT_en_eV}{\tau}
n_e\tau \geq \frac{12k_BT_e}{Q<\sigma_fv>}
neτ≥12kBTeQ<σfv>n_e\tau \geq \frac{12k_BT_e}{Q<\sigma_fv>}
V = volume
V=volumeV = volume
v = velocity
v=velocityv = velocity
R = reaction \ rate
R=reaction rateR = reaction \ rate
w = stored \ energy \ in \ plasma
w=stored energy in plasmaw = stored \ energy \ in \ plasma
P_{loss} = rate \ of \ energy \ loss
Ploss=rate of energy lossP_{loss} = rate \ of \ energy \ loss
k_B = Boltzmann \ constant
kB=Boltzmann constantk_B = Boltzmann \ constant
\sigma_f = fusion \ cross \ section
σf=fusion cross section\sigma_f = fusion \ cross \ section
\tau = confinement \ time
τ=confinement time\tau = confinement \ time
T = temperature \ of \ tritium (T_t), \ deuterium (T_D), \ electrons \ (T_e), \ ions \ (T_i)
T=temperature of tritium(Tt), deuterium(TD), electrons (Te), ions (Ti)T = temperature \ of \ tritium (T_t), \ deuterium (T_D), \ electrons \ (T_e), \ ions \ (T_i)
n = number \ density \ of \ tritium (n_t), \ deuterium \ (n_D), \ electrons \ (n_e)
n=number density of tritium(nt), deuterium (nD), electrons (ne)n = number \ density \ of \ tritium (n_t), \ deuterium \ (n_D), \ electrons \ (n_e)
Q = energy \ released \ by \ reaction
Q=energy released by reactionQ = energy \ released \ by \ reaction
RQ = \frac{1}{4}n_e^2<\sigma_fv>QV
RQ=14ne2<σfv>QVRQ = \frac{1}{4}n_e^2<\sigma_fv>QV

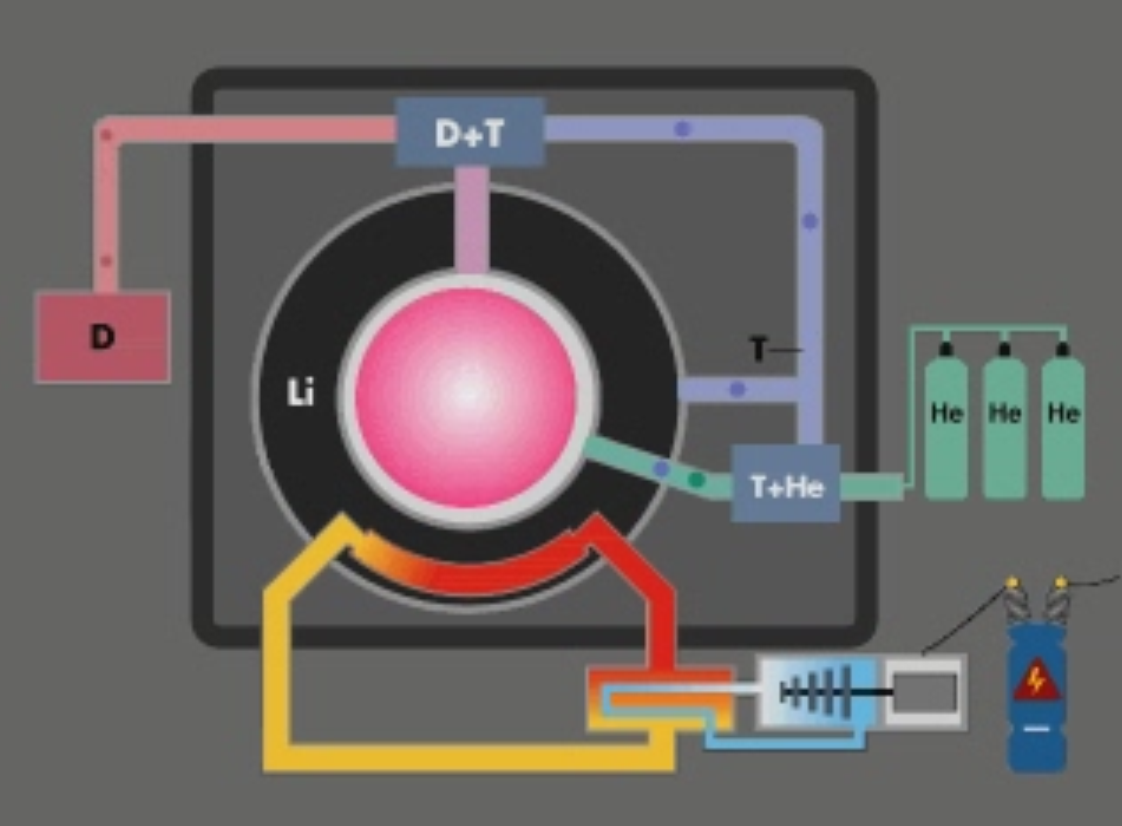
Fusion Technology

electricity from fusion

Breeder blankets

  • To generate sufficient tritium fuel to sustain the reactor.
  • To convert kinetic energy of the neutrons to thermal energy.
  • To shield the exterior components from neutrons.

Fuel Cycle

Fuel Cycle

Fuel Cycle

Fuel Cycle

Key reactions in breeder blankets

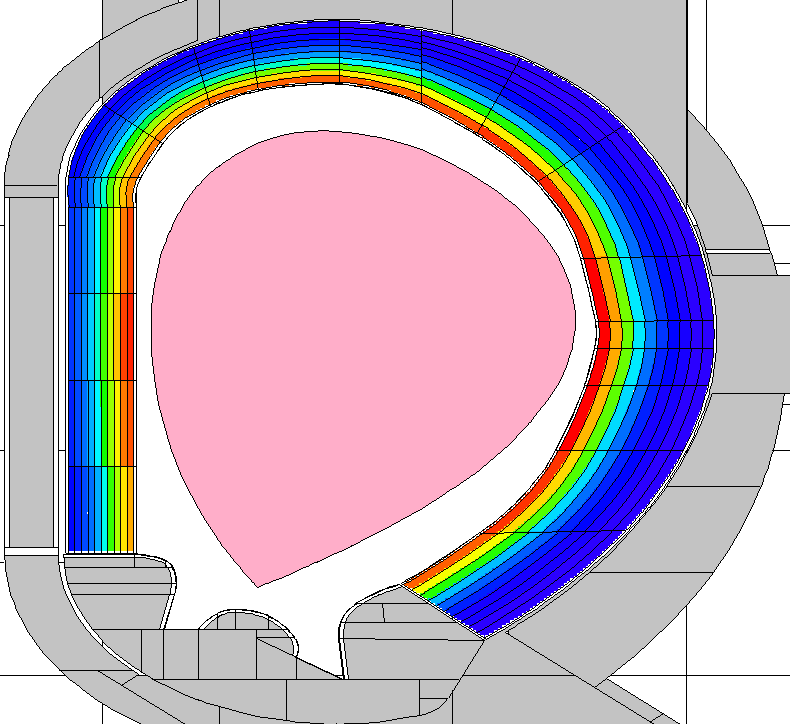
Questions

Which isotope is depleted?
Why at the front?
What is the best isotope for the front?

Li^6 + n = He^4 + H^3
Li6+n=He4+H3Li^6 + n = He^4 + H^3
Li^7 + n = He^4 + H^3 + n
Li7+n=He4+H3+nLi^7 + n = He^4 + H^3 + n
Be^9 + n = 2He^4 + 2n
Be9+n=2He4+2nBe^9 + n = 2He^4 + 2n
1\times 10^{21}
1×10211\times 10^{21}
neutrons
neutronsneutrons
per second
persecondper second

Fuel Cycle

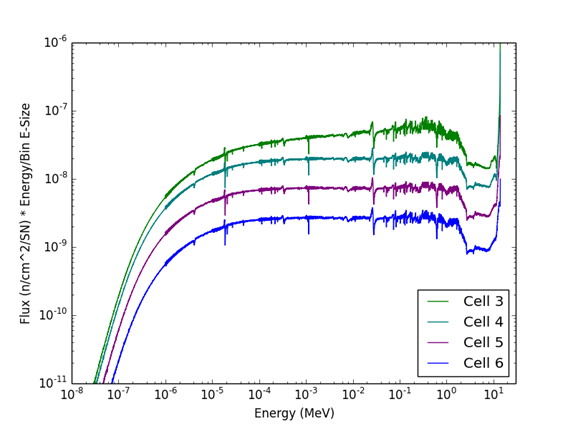
Neutron spectra at different depths in the blanket.

Neutrons are moderated by the material and lose energy.

Neutrons are also captured by some reactions.

Selecting suitable materials

Fuel Cycle - tritium breeding

Fuel Cycle - neutron multiplication

Radioactivity

Target

Nuclide

n,2n

n,g

n,p

n,pn

n,d

n,t

n,nd

n,a

n,He3

n,pd

n = neutron

g = gamma

t = tritium

p = proton

d = deuterium

He = helium

Common neutron induced reactions

Neutron number

Proton number

Radioactivity - activation

Radioactivity - fission products

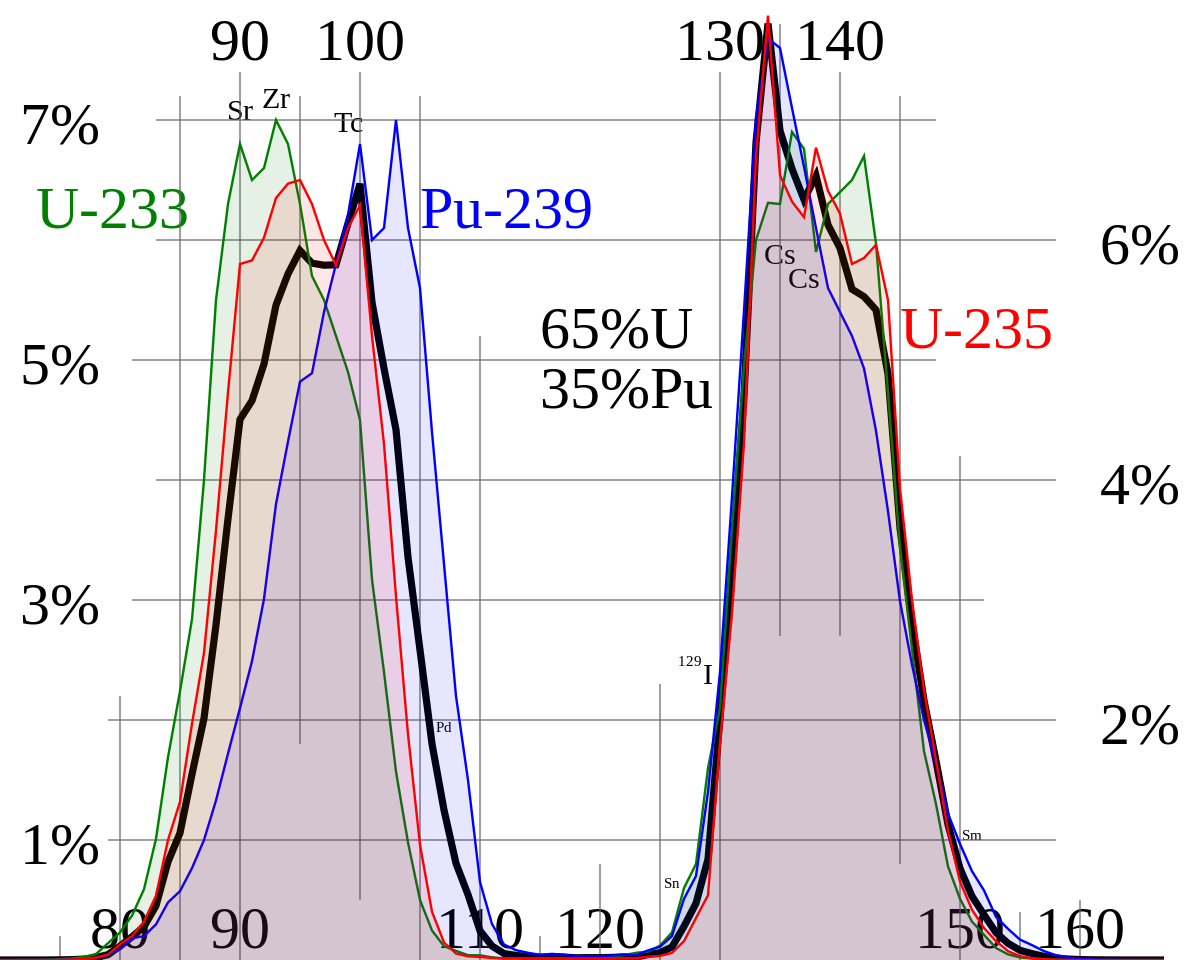
Atomic number

Percentage of fission products

Radioactivity - fission products

EU Roadmap for fusion energy

  • 3 main reactors (JET, ITER, DEMO) demonstrating large steps in understanding and performance.

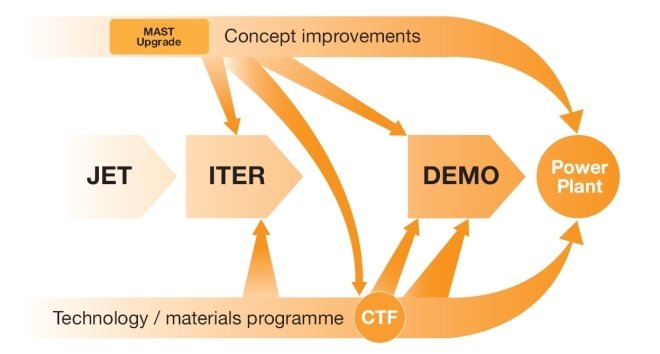
Image source www.ccfe.ac.uk/mast_upgrade.aspx

  • Many smaller reactors testing, validating and experimenting on different plasma physics regimes, component designs, materials and feeding into the design of larger ground breaking reactors

Lots of interesting physics to learn

Banana orbits

run away electrons

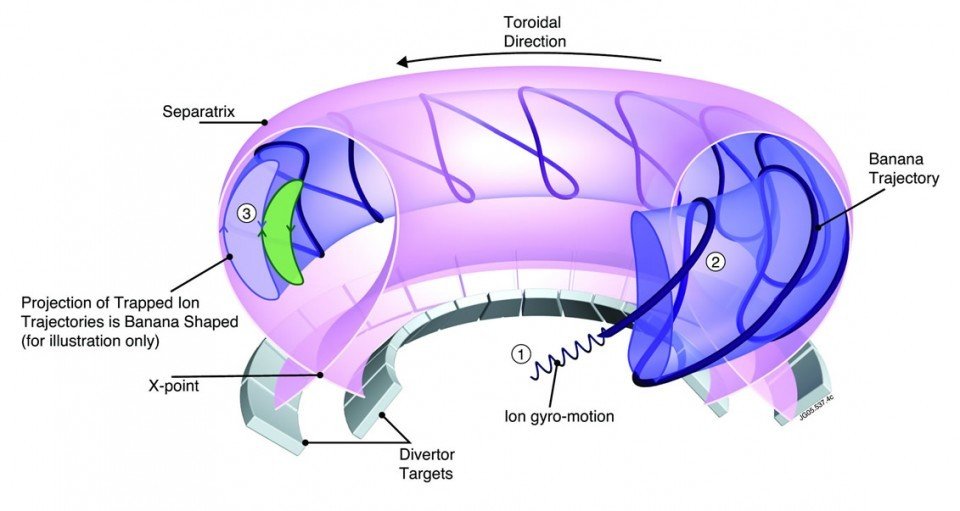
Stellarators

3D printing components

Neutral particle accelerators

Robotic maintainance

Plasma instabilities such as sausage, kink, balloon and elms

Further opportunists

Masters Degrees

PhD

Jobs

Fusion Energy Msc
The University of York

European Masters of Science in Nuclear Fusion and Engineering Physics
Organised by the European Commission

The physics and technology of nuclear reactors, MSc
University of Birmingham

Nuclear Energy, MPhil
University of Cambridge

Fusion Doctorial Training Network, PhD Organised by several universities and research organisations.

 

Doctoral Programme in nuclear fusion science and engineering
Organised by 18 European Universities

Nuclear First Doctorial Training Centre University of Manchester and University of Sheffield.

Summer placements, graduate recruitment and work experience at CCFE near Oxford

PhD open days hosted by UKAEA and CCFE with repreentatives from  UK universities
 

Summer placements, graduate recruitment at Fusion 4 Energy in Barcelona

Summer placements, graduate recruitment at ITER in France

Fusenet the European fusion education network with funding oppertunities

Fusion Energy

By Jonathan Shimwell

Made with Slides.com

Fusion Energy

Sheffield University Nuclear Physics 303 course 2018

  • 618

More from Jonathan Shimwell