Crypto
Whoami
-
sicc
-
輔仁大學資工系四年級
-
112 NISRA 會長
- ...
為什麼我們需要密碼
-
在資訊安全的三個要素
-
機密性 (Confidentiality)
-
完整性 (Integrity)
-
可用性 (Availability)
-
為什麼我們需要密碼
-
在資訊安全的三個要素
-
機密性 (Confidentiality)
-
完整性 (Integrity)
-
可用性 (Availability)
-

為什麼我們需要密碼
-
在資訊安全的三個要素
-
機密性 (Confidentiality)
-
完整性 (Integrity)
-
可用性 (Availability)
-

我們需要的是什麼樣的密碼
- 一個足夠強度的密碼

我們需要的是什麼樣的密碼

密碼學必備 - 現代
- 機密性(Confidentiality):確保訊息只有被授權者才能取得
- 完整性(Integrity):偵測訊息是否遭受竄改
- 身分認證(Authentication):傳送方與接受方需驗證識別
- 不可否認性(Non-Reputation):提供訊息傳送方與接受方的交易證明
密碼學簡介
密碼學簡介
- 可分為古典密碼學與現代密碼學
- 源於希臘語 kryptós「隱藏的」,和 gráphein「書寫」
- 古典密碼學
- 創造力與技巧的展現
- 現代密碼學
- 電腦科學與數學
密碼學簡介
- 密碼學 == 數學 + 邏輯
- 數學 == 要記得與計算很多東西
- 邏輯 == 要思考很多東西
- 記得與計算 == 頭很痛
- 思考 == 頭很痛
- 密碼學 == 頭很痛 + 頭很痛
- 密碼學 == 頭超級痛
密碼學簡介
- 加密 Encrypt
- 指將明文經過某種程序轉換成密文,該程序稱為加密。
- 指將明文經過某種程序轉換成密文,該程序稱為加密。
- 解密 Decrypt
- 指將密文經過某種程序轉換成明文,該程序稱為解密。
- 指將密文經過某種程序轉換成明文,該程序稱為解密。
- 明文 Plaintext
- 加密前的訊息。
- 加密前的訊息。
- 密文 (ciphertext / cyphertext)
- 加密後的訊息。
密碼學簡介
- 演算法 Algorithm
- 解決問題的程序或方法。
- 解決問題的程序或方法。
- 密碼學演算法
- 密碼學相關問題(如加密、解密、簽章...)的演算法。
- 密碼學相關問題(如加密、解密、簽章...)的演算法。
- 金鑰 / 密鑰 Key
- 加解密時所使用的「鑰匙」。
密碼學簡介
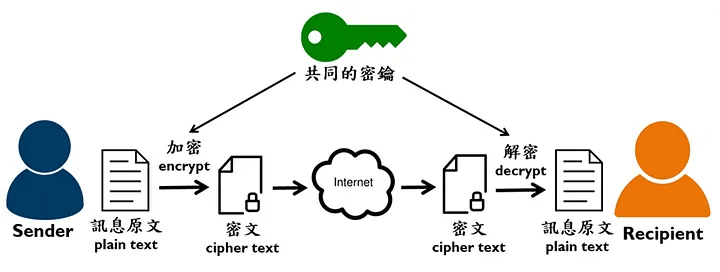
- Key 的作用
密碼學
- 本課程不會教如何設立密碼
-
但可以學到如何建立一個安全的密碼
-
但可以學到如何建立一個安全的密碼
- 不會教如何破解別人的密碼
-
最快的方式是社交工程
-
最快的方式是社交工程
- 不會因為密碼學而直接變成超強駭客
- 但可以搭配組合計(請自行研究)
密碼學與資安
- 不要使用未公開的密碼演算法
- 低強度的密碼 < 直接沒有密碼
-
聊勝於無 (x)
-
聊勝於無 (x)
- 任何密碼總有一天會被破解
- 密碼只是資訊安全的一部分
編碼 vs 加密
介紹編碼和加密的差別
編碼
- 編碼 (Encoding)
- 是資訊從一種形式或格式轉換為另一種形式的過程。
- 是資訊從一種形式或格式轉換為另一種形式的過程。
- 解碼 (Decoding)
- 編碼的逆過程,即將資料從另一種形式轉換回來。
編碼
- 編碼是資訊從一種形式或格式轉換為另一種形式的過程;解碼則是編碼的逆過程。
- 編碼不具任何安全性,只要知道編碼方式都可以解碼得到明文

如果去問 Gemini 就 ...
Binary encode
- 二進位
- 電腦由一堆 0 和 1 組成(bits)
- 常常以八個為一組看(8 bits = 1 byte)
- 相當於短除法連除 16 的結果
| Decimal | Binary |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| ... | ... |
Hex encode
- 十六進制
- 0 ~ 9, A, B, C, D, E, F 共 16個符號
- 相當於短除法連除 16 的結果
| Decimal | Hex |
|---|---|
| ... | ... |
| 8 | 8 |
| 9 | 9 |
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
| 16 | 10(x10) |
| 17 | 11(x11) |
| ... | ... |
ASCII
- 將常會用到的字進行編碼,讓電腦之間好溝通
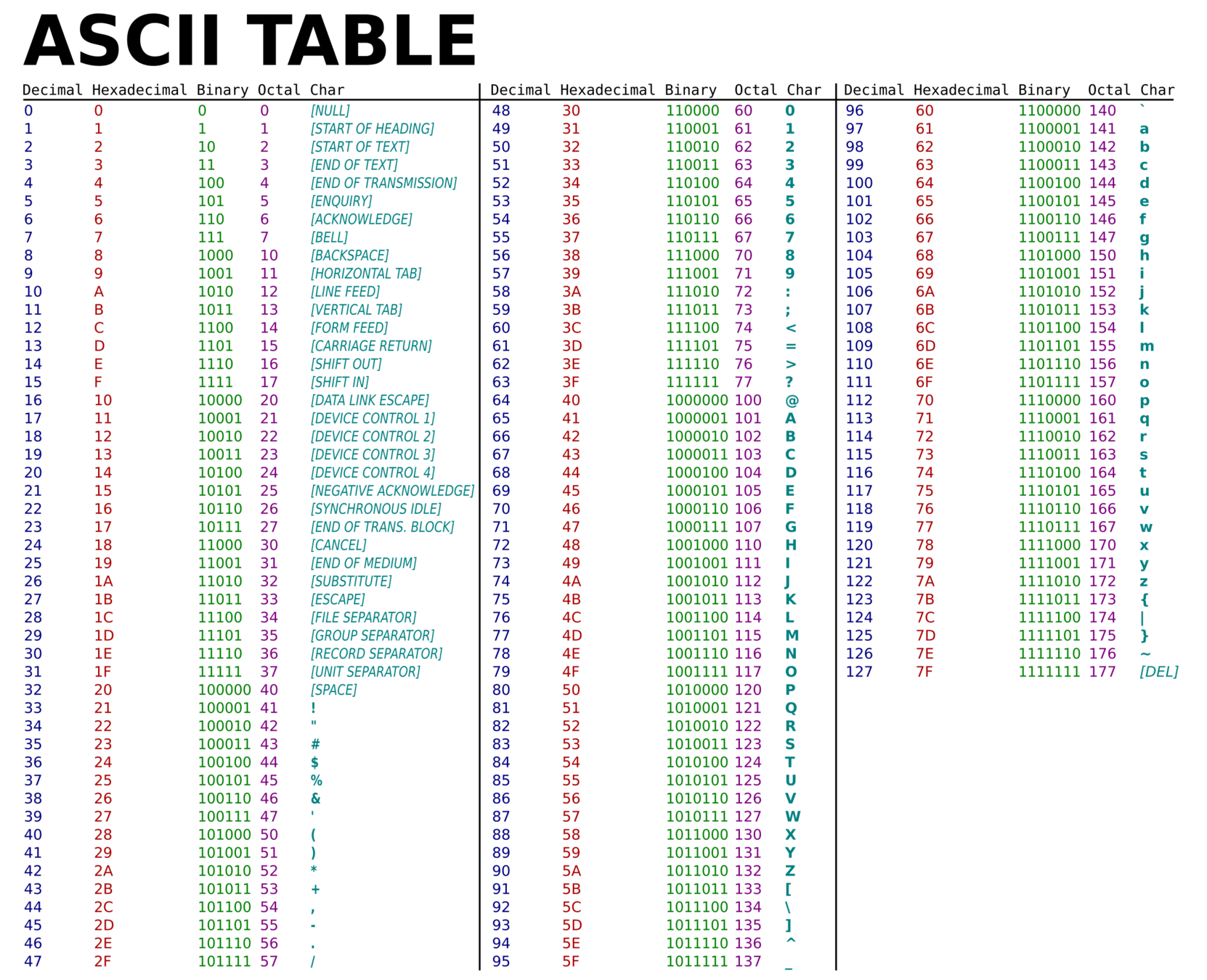
Base encode
- Base 32
- A ~ Z , 2~7
- Base 45
- A ~ Z , 0 ~ 9, $, %, *, +, -, ., /, :, (空白)
- Base 58
- 1 ~ 9 (0 除外), A ~ Z (O 除外), a ~ z (o 除外)
- Base 62
- 0 ~ 9, A ~ Z, a ~ z
- Base 64
- 0 ~ 9, A ~ Z, a ~ z, +, /
Base64
- 用於傳輸資料(如圖片)
- ASCII 一個字元 8 bits
- Base64 一字元只有6 bits
- 如果原文不整除3,結尾會出現對應數量的= 用以補足
Base64
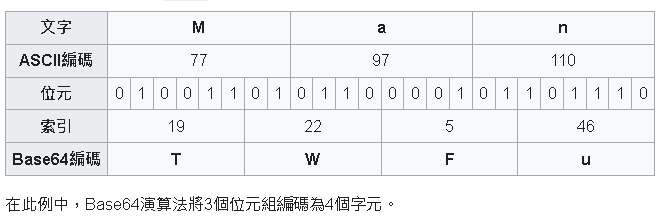
Base64
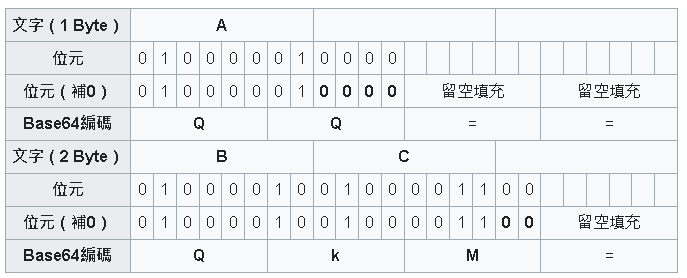
URL encode
- 為了避開有特殊意義的符號(如 '&', ' ', '=', '#', '?')
- 編碼為 ‘%’ 加上該字元之 ASCII (Hex表示)
- Eg. 昨天 Web II 的內容
Lab 1
Lab 1:Base64
Lab 2: URL
cyberchef 解題
- 來自 Base64 的神祕句子
Lab 2
- 來自 Base64 的神祕句子
- 但轉回去好像又不太一樣
摩斯密碼
-
編碼的一種
感覺漢堡比較有趣

加密
- 加密(英語:Encryption)是將原始資訊(稱為明文)轉換為另一種形式(稱為密文),使之不可讀的過程。
- 經過一些酷酷的演算法 (通常都是數學家發明的)
- 舉例: AES、DES ...
古典密碼學
古典密碼學
-
移項式加密
-
改變順序
-
改變順序
-
替換式加密
- 改變內容
- 單表加密
- 多表加密
替換式加密
-
替換密碼是字母作有系統的代換,直到訊息被替換成其它難以解讀的字。
- 單表加密
- 凱撒密碼、阿特巴希密碼
- 凱撒密碼、阿特巴希密碼
- 多表加密
- 維吉尼亞密碼、自動密鑰密碼
凱薩加密
- Caesar cipher
- 凱撒加密、凱撒變換、變換加密
- 凱撒加密、凱撒變換、變換加密
- 明文中的所有字母都在字母表上向後(或向前)按照一個固定數目進行偏移後被替換成密文。
- 容易被頻率分析或暴力破解攻擊
凱薩加密
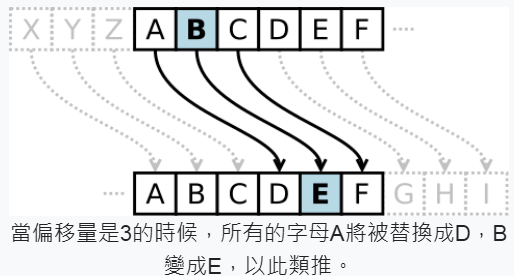
凱薩加密
- 假設 ROT 3
明文: ABCDEFGHIJKLMNOPQRSTUVWXYZ
DEFGHIJKLMNOPQRSTUVWXYZABC
ROT 3
Lab3
- 猜猜我是 ROT ?
阿特巴希密碼
- 阿特巴希密碼將字母表整個扭轉:
- 第一個字母 "A" 與最後一個 "Z" 相替換,
- 第二個 "B" 與倒數第二個 "Y" 相替換,如此類推。
簡單替換式密碼
- 簡易替換密碼(可以理解為一種建立替換表的方式)
- 傳統上會先把一個關鍵詞寫在字母表最前面,再刪去重
複字母, - 這樣就能得到一個替換表。
- Keyword:"HELLO"
- HELLOABCDEFGHIJKLMNOPQRSTUVWXYZ
- HEL
LOABCDEFGHIJKLMNOPQRSTUVWXYZ - HELOABCDFGIJKMNPQRSTUVWXYZ
簡單替換式密碼
- 簡易替換密碼(可以理解為一種建立替換表的方式)
- 傳統上會先把一個關鍵詞寫在字母表最前面,再刪去重
複字母, - 這樣就能得到一個替換表。
- Keyword:"HELLO"
- HELLOABCDEFGHIJKLMNOPQRSTUVWXYZ
- HEL
LOABCDEFGHIJKLMNOPQRSTUVWXYZ - HELOABCDFGIJKMNPQRSTUVWXYZ
- 可以對替換表再進行偏移(凱撒密碼)或翻轉(阿特巴希密碼)
波雷費密碼 - 補充
- Playfair cipher
- 一種對稱式密碼
- 首種雙字母取代的加密法。
字頻分析
- 大部分語言中,字母或字符使用的頻率並不是平均的
- 以英文為例,很明顯母音的使用頻率更高
- ETAOINSHRDLU
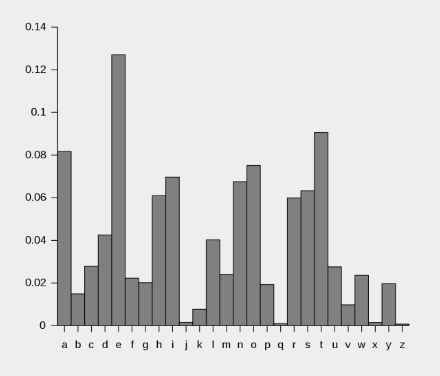
單表加密攻擊
-
爆破
-
已知為凱撒密碼,只有26種可能
-
已知為凱撒密碼,只有26種可能
-
字頻分析
- 最常出現的字母:e, t, a, o, i
- 最常出現的單字:the, to, of, and
- 自動化分析:https://quipqiup.com/
字頻分析
-
攻擊者能夠更加容易地進行攻擊
-
因為單表加密只是將字元做替換,所以頻率並不會變。
-
如果我們知道一段英文是由單表加密所得。我們對這段英文做字頻分析,發現 ”X” 的出現的頻率最高。
- 那我們合理猜測 ”X” 很有可能替換了 ”E”
維吉尼亞加密
- 利用表格內容進行加密
- 包括了26行字母表,每一行都由前一行向左偏移一位得到。
維吉尼亞加密
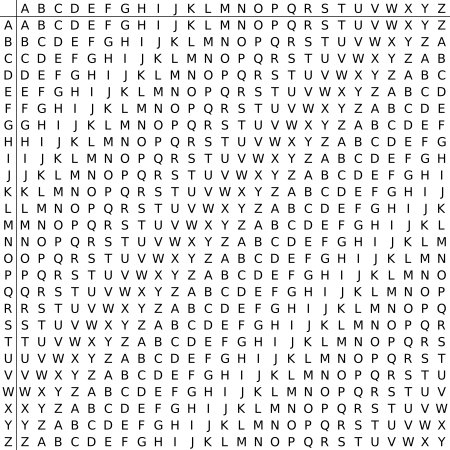
明文
密鑰
維吉尼亞加密
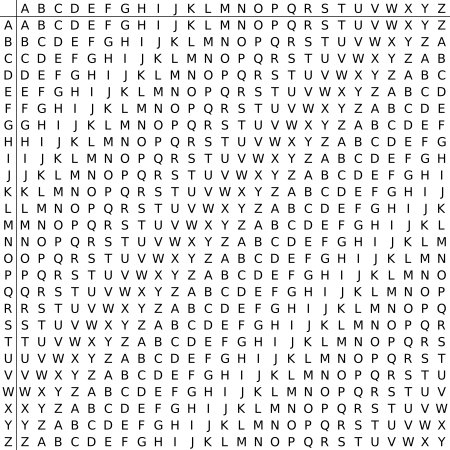
- 明文: H
- 密鑰: O
- 密文: V
維吉尼亞加密
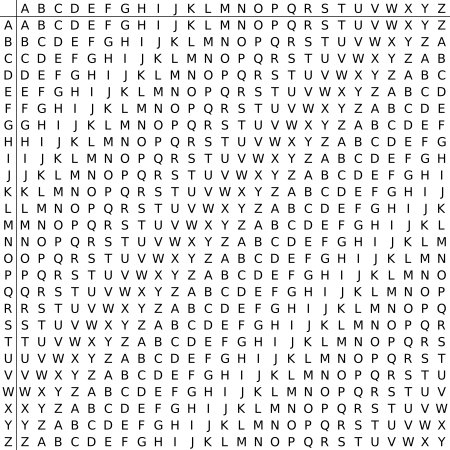
- 密文: V
- 密鑰: O
- 明文: ?
維吉尼亞加密
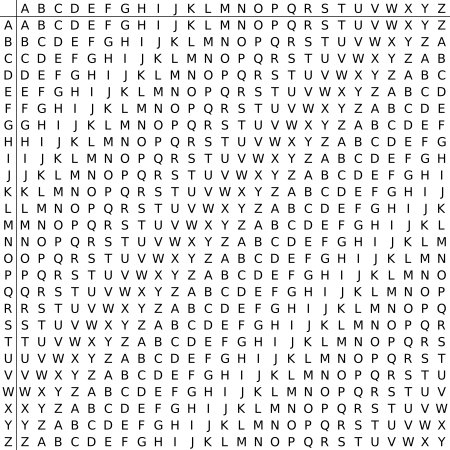
- 密文: V
- 密鑰: O
- 明文: H
Lab4
- 維吉尼亞~
多表加密攻擊
- 卡西斯基試驗
- Index of coincidence
- ...etc
卡西斯基試驗
- Kasiski examination
- 針對有邏輯文章的維吉尼亞加密
- 需要明文與密文就能夠得到密鑰組成
卡西斯基試驗
- 密鑰:ABCDEF AB CDEFA BCD EFABCDEFABCD
- 明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
- 密文:CSASXT IT UKSWT GQU GWYQVRKWAQJB
卡西斯基試驗
- 密鑰:ABCDEF AB CDEFA BCD EFABCDEFABCD
- 明文:CRYPTO IS SHORT FOR CRYPTOGRAPHY
- 密文:CSASXT IT UKSWT GQU GWYQVRKWAQJB
卡西斯基試驗
- 密文:DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
-
DYDUXRMH
- 相距為 18 個字元
- 可以推測密鑰長度為 2,3,6,9,18
-
NQD
- 相距為 20 個字元
- 可推測密鑰長度為 2,4,5,10,20
卡西斯基試驗
- 密文:DYDUXRMHTVDVNQDQNWDYDUXRMHARTJGWNQD
-
DYDUXRMH
- 相距為 18 個字元
- 可以推測密鑰長度為 2,3,6,9,18
-
NQD
- 相距為 20 個字元
- 可推測密鑰長度為 2,4,5,10,20
- 取兩者的交集可以知道密鑰長度為 2
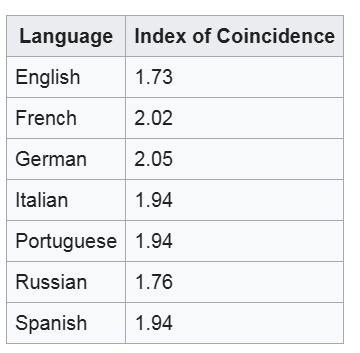
IOC
-
Index of coincidence
- 兩個文本並排放置,並計算相同字母在兩個文本中出現
在相同位置的次數。此計數稱為巧合指數,或簡稱IoC
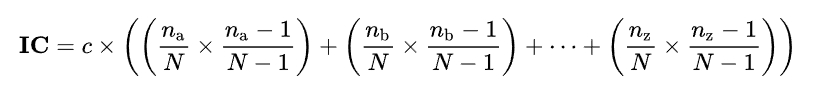
IOC
- 可以理解為 “文本” 的 “BMI”
- 是一段文本 “有序程度” 的指標
- 無序 -> IOC 低
- 有序 -> IOC 高
IOC
- 假設文本共100字
- 統計每個字母出現的次數
- 如果a出現了8次
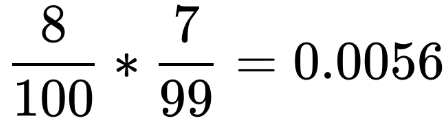
a 連續出現的機率 =
IOC
- 假設加總完得到0.065
- 我們再將 0.065 乘以 26(字母總數)得到 1.69
- 那我們說這段文本的 IoC 為 1.69
IOC
- IoC反應一段文本 “有多不隨機”
- 假設一段完全隨機的英文(260個字,每個字母各10個)
- 一段完全隨機的文本的IoC會逼近 1 (當文本長度趨近無限)
而文本 “越有序” 、 “越不隨機” ,其IoC就會越高
IOC
- 字母機率加總的部分可以理解為一段文字的有序程度。
(越高越有序)
- 之所以要乘以字母個數,是因為要讓不同語言之間可以互
相比較。(同語言比較可以不用乘字母個數)
IOC
- 字母機率加總的部分可以理解為一段文字的有序程度。
(越高越有序)
- 之所以要乘以字母個數,是因為要讓不同語言之間可以互
相比較。(同語言比較可以不用乘字母個數)
IOC
-
字母多的語言,IoC上限更高
- 因為可以理解為字母越多的語言,天生有序化程度就更低。
(因為他字母多)
- 假設他還能全部文本都是一個字母,則他的IoC會更高
- 30個字母的語言組成的文本只有一個字母和3個字母的語言組成的文本只有一個字母,是不一樣的
IOC
- 一個猴群分香蕉。(社會化程度)
- 分的越均勻,IoC越低。
- 分的越不均勻,IoC越高。(香蕉集中在某幾個猴子手裡)
- 這樣我們就得出 IoC的下限 是 1(完全隨機的文本,逼近 1)
- IoC的上限 是1乘以(該語言字母總數)(英文為 26)
IOC
- 一段有意義的文本:
一次性密碼本
-
規則:
-
1 “關鍵字”必須是完全隨機的(有意義就容易被破解)
-
2 關鍵字的長度需要與明文等長
-
3 只能加密一次,用完即銷毀
-
一次性密碼本
-
規則:
-
1 “關鍵字”必須是完全隨機的(有意義就容易被破解)
-
2 關鍵字的長度需要與明文等長
-
3 只能加密一次,用完即銷毀
-
缺點: 難用
移向式加密
- 字元本身不改變,但字元位置依照一定規則進行移動、變換
移向式加密
| 1 | 2 | 3 |
|---|---|---|
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 1 | 4 | 7 |
|---|---|---|
| 2 | 5 | 8 |
| 3 | 6 | 9 |
密碼棒
- 1.由一條加工過、且有夾帶訊息的皮革繞在一個木棒所組成
- 2.在古希臘,文書記載著斯巴達人用此於軍事上的訊息傳遞
- 3.密碼接受者需使用一個相同尺寸的棒子讓他將密碼條繞在上面解讀

密碼棒
-
密碼棒加密
- 1. 將要加密的明文分為N個一組
- 2. 再從每組的選出一個字母連起來
- 3. 最後,形成一段無規律的密文
- 1. 將要加密的明文分為N個一組
密碼棒 - 1
- 原 THEREISALWAYSONLYONETRUTH(明文長度為25)
將要加密的明文由左到右變成為5*5的陣列
T H E R E
I S A L W
A Y S O N
L Y O N E
T R U T H
密碼棒 - 2
-
再從上到下抄一遍的到密文
T H E R E
I S A L W
A Y S O N
L Y O N E
T R U T H
TIALTHSYYREASOURLONTEWNEH
密碼棒
-
密碼棒解密
-
由上至下抄一遍密文
-
由左至右再抄成一段完整的句子
-
得到原先的明文
-
密碼棒 - 2
T H E R E
I S A L W
A Y S O N
L Y O N E
T R U T H
TIALTHSYYREASOURLONTEWNEH
-
由上至下抄一遍密文
密碼棒 - 2
T H E R E
I S A L W
A Y S O N
L Y O N E
T R U T H
THEREISALWAYSONLYONETRUTH
-
由左至右再抄成一段完整的句子
密碼棒 - practice
-
密文:SLAOCEYRY1HYT310ASFU
-
這是一個長寬4*5的密碼棒做成的密文,請解出明文
密碼棒 - practice
- 密文:SLAOCEYRY1HYT310ASFU
S C Y T A
L E 1 3 S
A Y H 1 F
O R Y 0 U
明文:SCYTALE13SAYH1FORY0U
Lab5
- 密碼棒~
中國式密碼
- 一種移項式密碼
- 將訊息的字母由右而左、上下交替排列,最後將排列出的結果從左到右,一列一列寫出,成為密文。
中國式密碼

- 明文: The rabbit is cute.
古典密碼學的總結
- 總之,就是被時代淘汰的東西
- 算力增長的時代,暴力破解不需要花上多久時間(只要有錢)
現代密碼學
現代密碼學
-
加密不再限於書寫文字
-
基於各種複雜的數學
-
加密簡單破解難
- 對稱式加密及非對稱式加密
柯克霍夫原則
- 密碼系統即便做不到數學上不可破解,也應在實際程度上無法破解
- 即使加密方式公開,只要密鑰沒有洩露,密文仍無法破譯。
現代密碼學
- 對稱式加密:
- 加密解密用同把金鑰
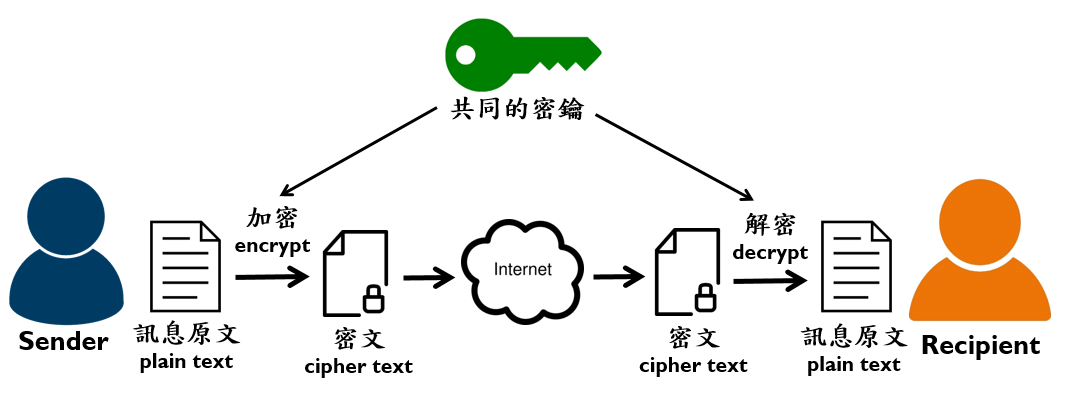
區塊加密法/串流加密法
- 區塊加密
- 常用於已知訊息長度的情況
- 將明文分成一塊一塊等長的模組分別加密
- AES DES
- 串流加密
- 常用於需要即時回應,或是訊息長度未定的情況
- 對明文逐bit 加密
串流加密法
- XOR
- A ⊕ A = 0
- (A ⊕ B) ⊕ B = A
| A | B | A ⊕ B | (A ⊕ B )⊕ B |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
串流加密法
- 攻擊:
- 已知明文與密文時可以直接回推Key (明文⊕密文= 金鑰)
- 遇到一長串Null (0x00) 時會直接寫出Key,而這在二進制檔案中是很常見的事情
- 如果Key 長度等於Plaintext,又Key 完全隨機且不重用,是被證實無法破解的。
- 已知明文與密文時可以直接回推Key (明文⊕密文= 金鑰)
非對稱式加密
- 利用公鑰加密,用私鑰解密
- RSA
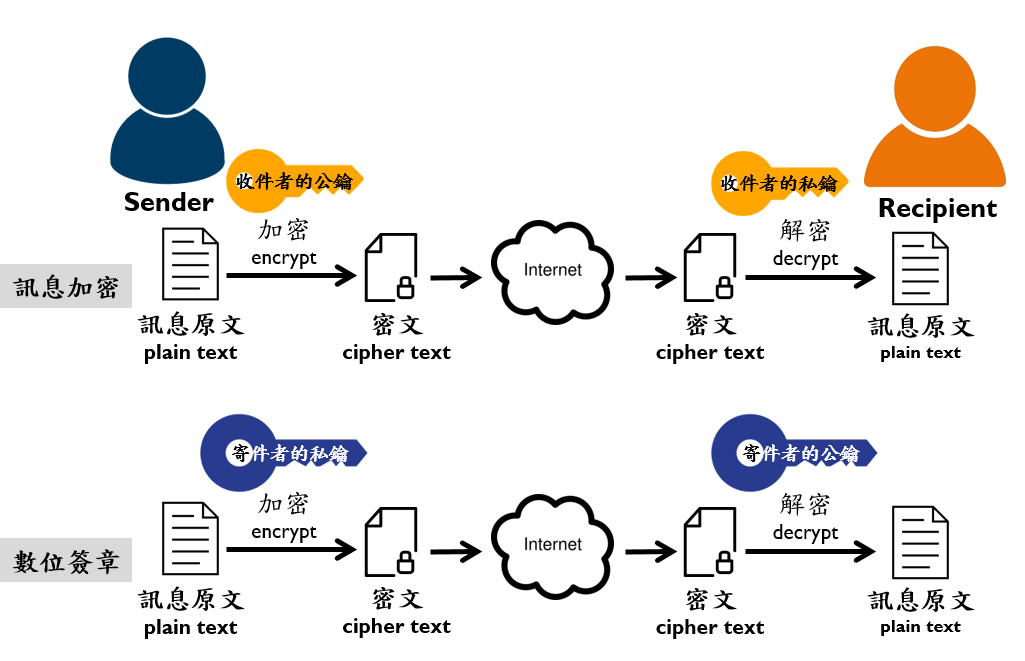
非對稱式加密
- 利用公鑰加密,用私鑰解密
- RSA

Hash(雜湊、哈希)
- 將任意長度的字串轉成固定長度
- 雪崩效應:字串即使只有動一個字,Hash 結果差異很大
- md5(1234) = 81dc9bdb52d04dc20036dbd8313ed055
- md5(1235) = 9996535e07258a7bbfd8b132435c5962
- 無法回推:可以從X 算出Hash(X),但無法從Hash(X) 算出X
- 抗碰撞:很難找到兩個不同字串X 與X’ 符合Hash(X) = Hash(X’)
- md5, sha256,bcrypt
數位簽章(Digital Signature)
- 類似於在紙上簽名,證明這份資料是我認可的
- 只有擁有私鑰的人可以簽章,所有人都可以驗證簽章
- 因為訊息很長,所以通常會先將訊息Hash 過再簽章
- 基於非對稱式加密系統的應用
- 具有不可否認性(Non-repudiation)
資料來源
- Google 爸爸
- Chatgpt
- NISRA 的各位學長姐
- Gemini ...(?
- 還有網路上的各路大神

Crypto
By sicc
Crypto
- 109



